Prediction and Analysis of the Relationship between Energy Mix Structure and Electric Vehicles Holdings Based on Carbon Emission Reduction Constraint: A Case in the Beijing-Tianjin-Hebei Region, China
Abstract
:1. Introduction
- (1)
- This paper constitutes a perfect indicator system for the factors influencing Power generation in the Beijing-Tianjin-Hebei region using the grey correlation method including: employment population, GDP per capita, consumer price index, electricity consumption for domestic consumption, coal price;
- (2)
- The Extreme learning machine optimized by Improved particle swarm optimization (IPSO-ELM) model is first applied in the field of energy mix prediction which has higher precision than the Extreme Learning Machine (ELM) predictive method; this method not only greatly improves the forecasting accuracy but also decreases the possibility of trapping a local minimum;
- (3)
- This paper pioneered a model of a correlational relationship between electric energy structure and number of electric vehicles under carbon constraint and calculated the maximum number of electric vehicles under the carbon emission reduction target.
2. Methodology
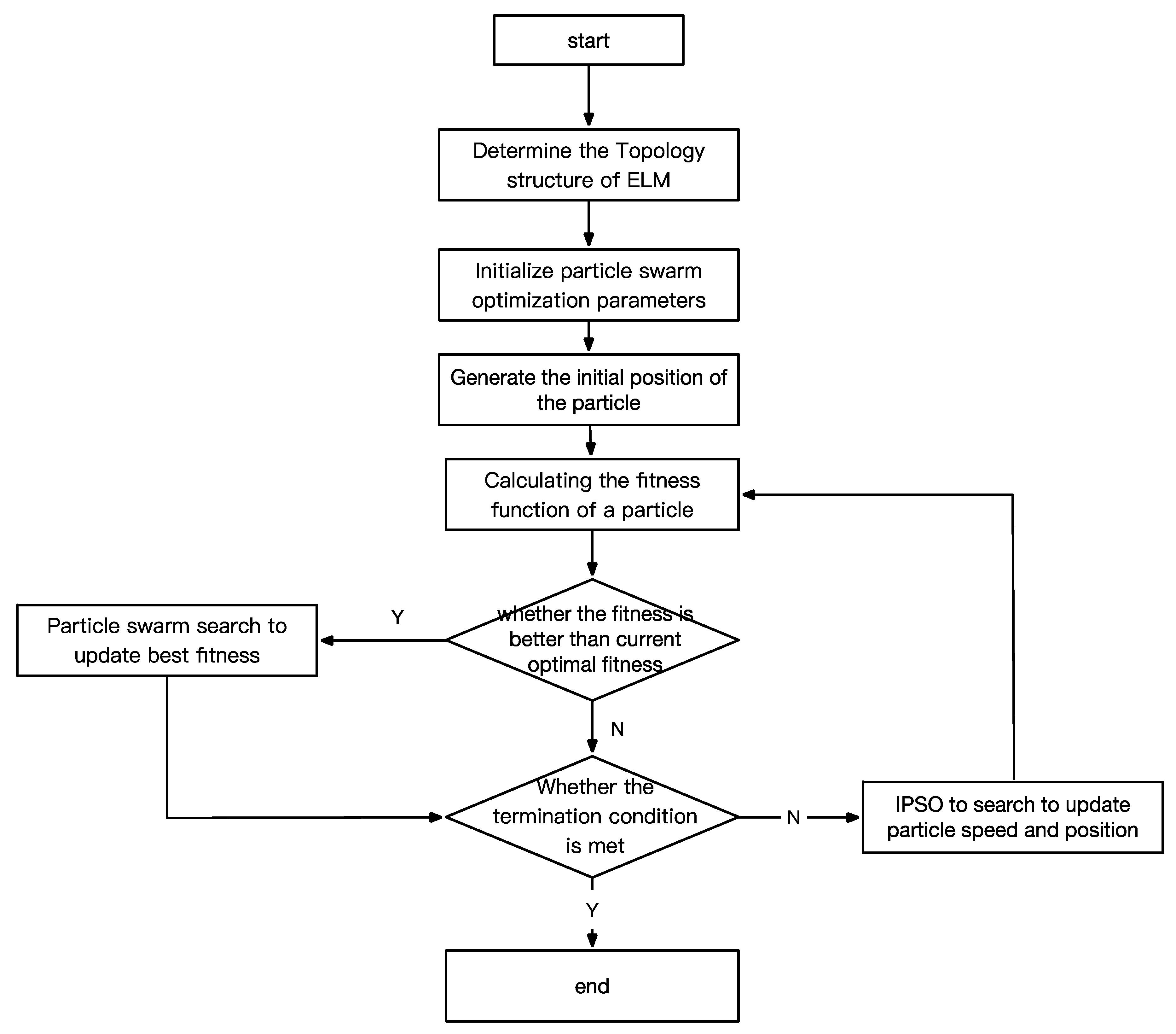
2.1. Improved Particle Swarm Optimization (IPSO)
- Step 1
- Initialize the decision vector P, P is a zero vector and the dimension is equal to the particle population of the particle group;
- Step 2
- Judge whether is established, if it is established, then ; otherwise, . Here, is the judgment accuracy, this paper set the for 10−5;
- Step 3
- If , it is determined that the i-th particle loses the optimization function and the particle position is reset to a random sequence.
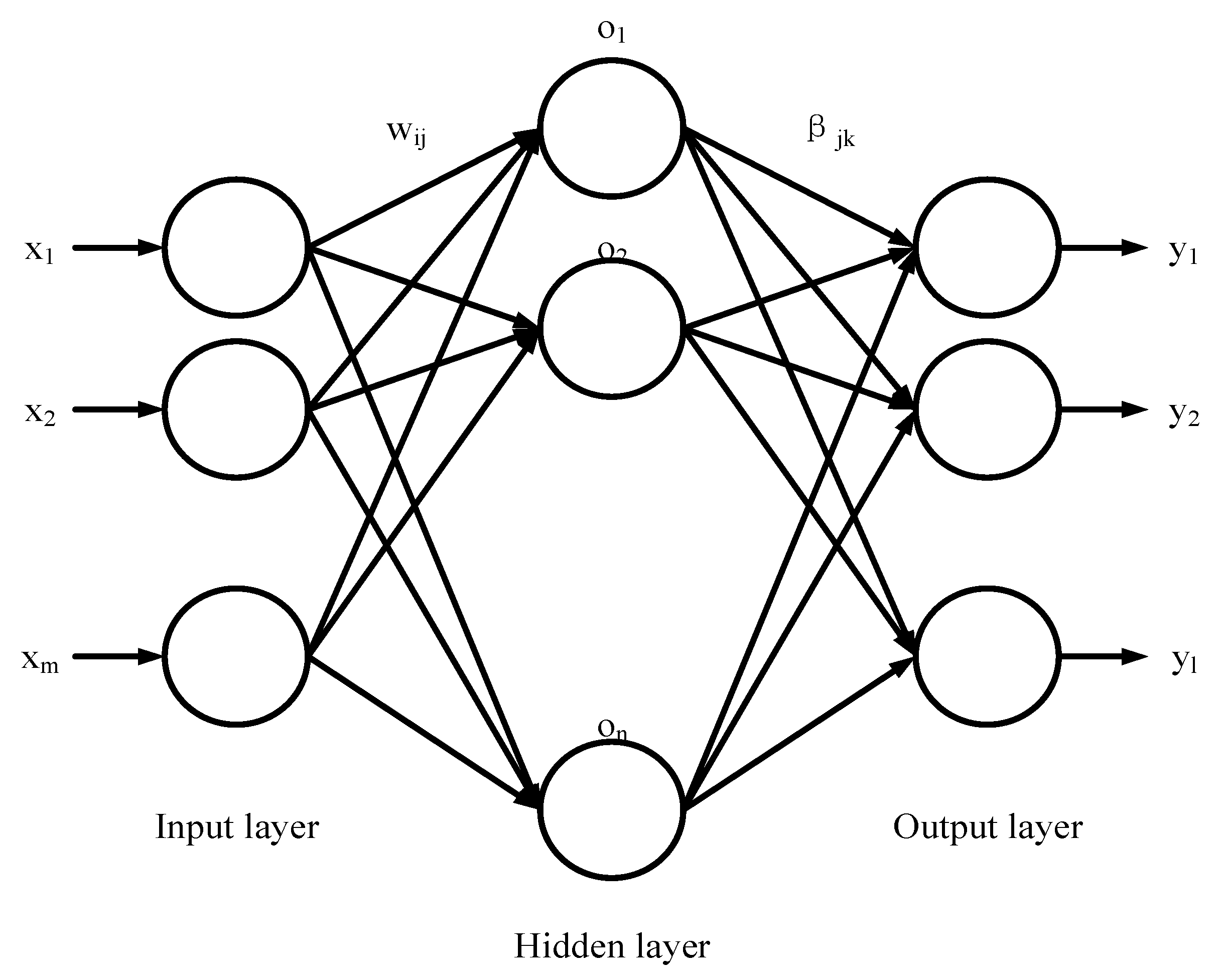
2.2. Extreme Learning Machine
2.3. Extreme Learning Machine Optimized by Improved Particle Swarm Optimization
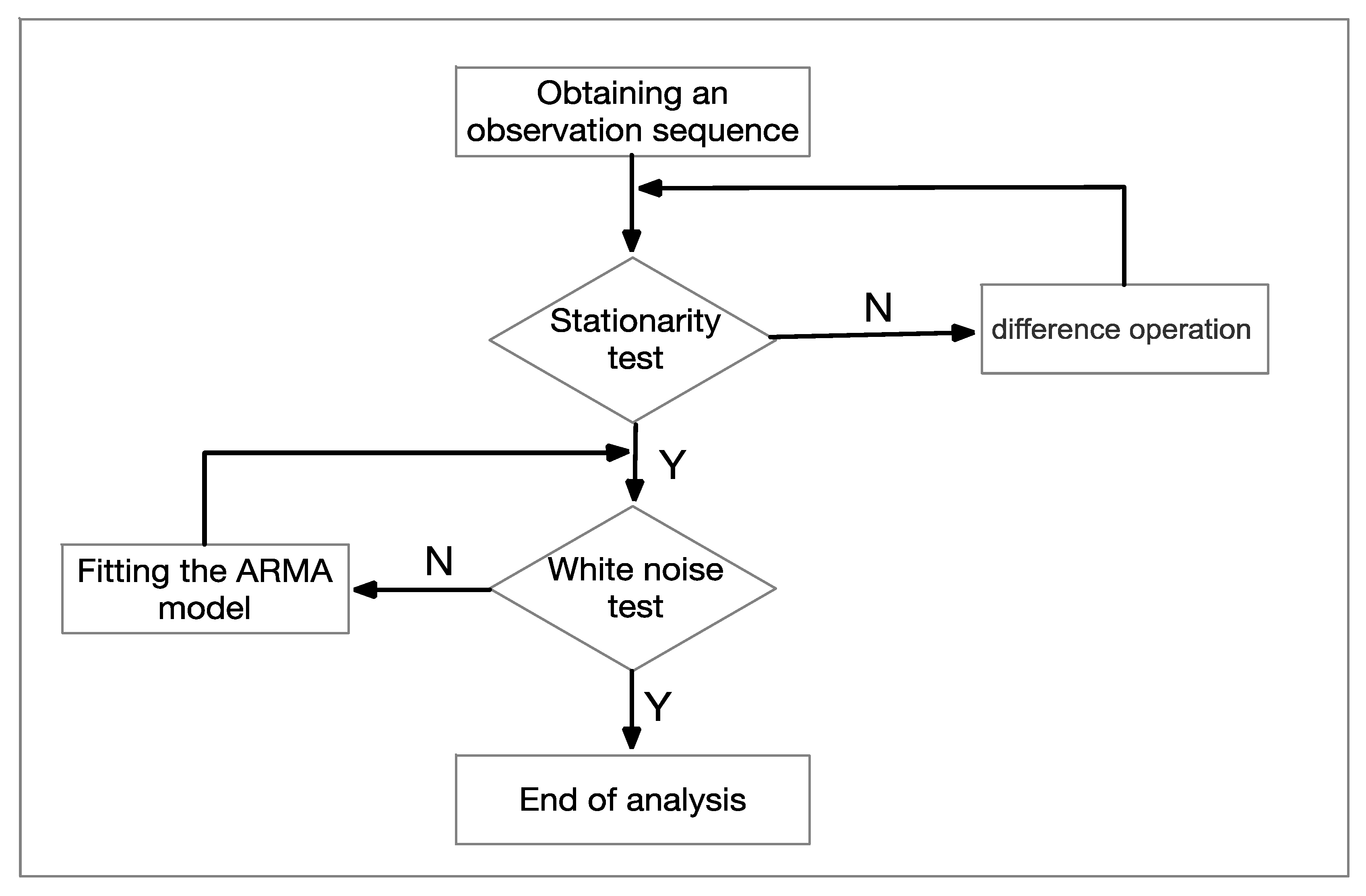
2.4. Autoregressive Integrated Moving Average Model (ARIMA)
3. Electric Vehicles Ownership Calculation
3.1. Model of Correlational Relationship between Electric Energy Structure and Electric Vehicles Number under Carbon Constraint
- (1)
- Power consumption of electric vehicles ()is 100 km of electricity consumption per electric vehicle; k is electric vehicles holdings; is the charging efficiency of electric vehicles; is line loss rate during power transfer; S is the average annual travel distance of each electric car.
- (2)
- Carbon emissions from electric vehicles ()are the average carbon emissions factors of clean energy power generation; are carbon emissions factors of thermal power generation; is clean power generation in the Beijing-Tianjin-Hebei region (kW h); is the total power generation in the Beijing-Tianjin-Hebei region (kW h).In the whole life cycle, clean energy produces fewer carbon emissions, so, in this paper, clean energy will not be classified using the average clean energy carbon emissions; in order to facilitate statistics and calculations, the energy prediction structures are only divided into clean energy generation and thermal power generation.
- (3)
- Carbon emissions from traditional fuel vehicles ()are carbon emissions factors from three types of traditional fuel vehicles; is the amount of energy consumed per fuel vehicle per year; is the fuel consumption or natural gas volume of a traditional car of 100 km is traditional fuel cars holdings; is the proportion of three types of traditional fuel vehicles.
- (4)
- A relationship between energy mix structure and electric vehicles holdingsIn order to study the maximum value of electric vehicles under the existing energy structure in the Beijing-Tianjin-Hebei region and ensures that the carbon emissions of electric vehicles are not higher than the traditional cars, a relationship between energy mix structure and electric vehicles holdings is established. In other words, when , the value of k is the maximum value of the electric car in this case. The formula is calculated as follows:
3.2. Energy Consumption Per 100 km (q)
3.3. Charging Efficiency of Electric Vehicles ()
3.4. Carbon Emission Coefficient for Different Energy Forms
3.5. Clean Power Generation and Total Power Generation Forecasting
3.5.1. Input Selection
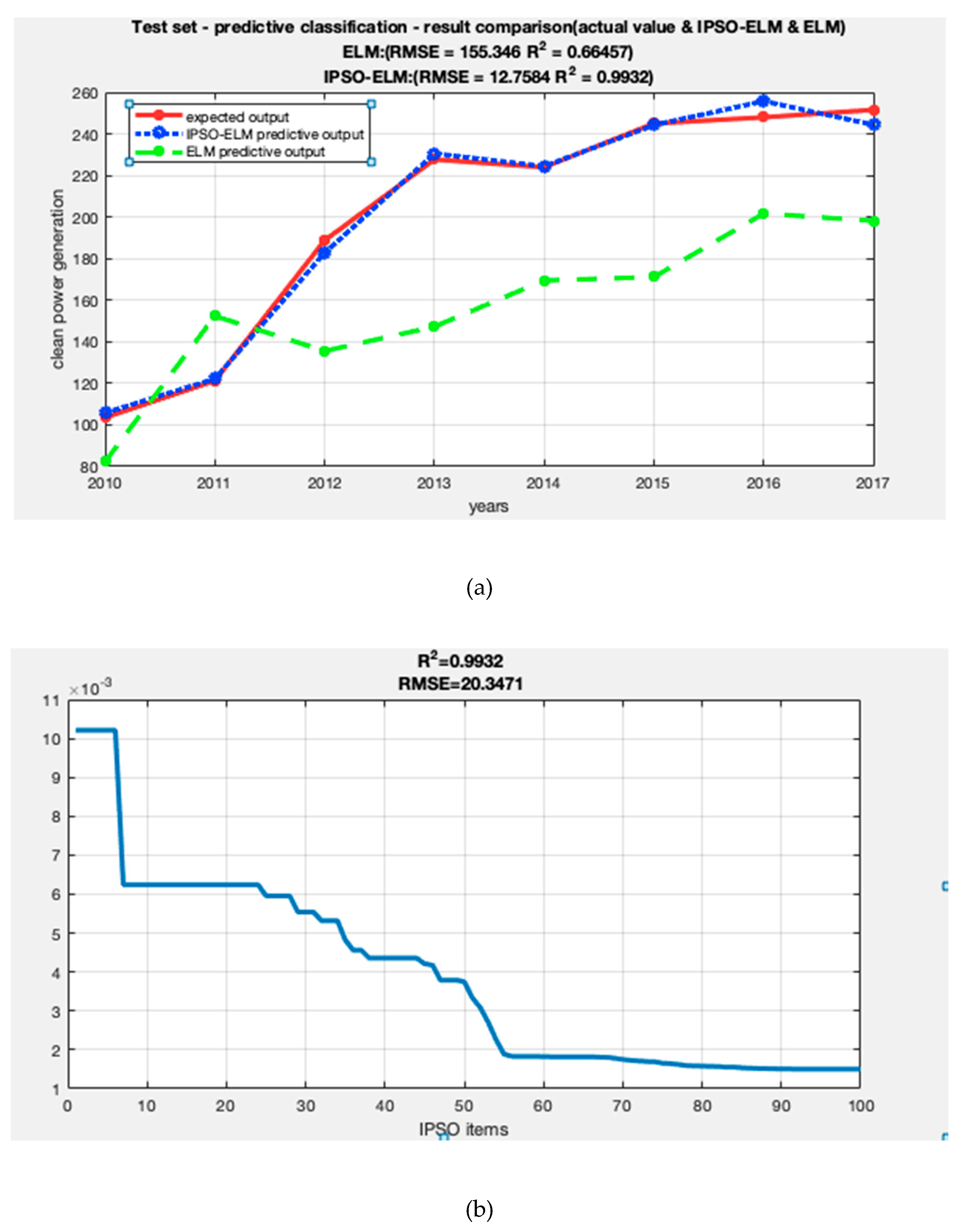
3.5.2. Model Error Analysis
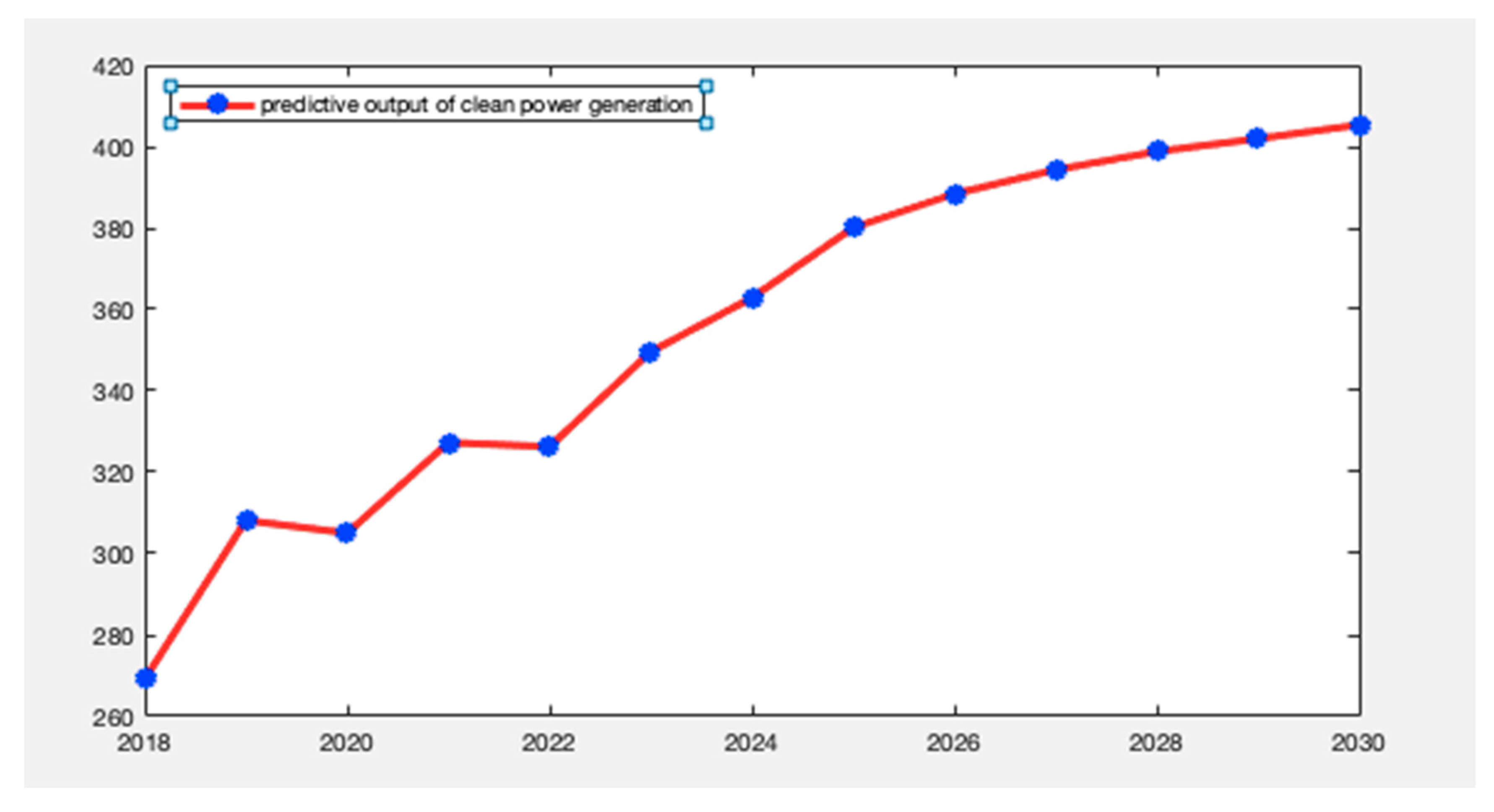
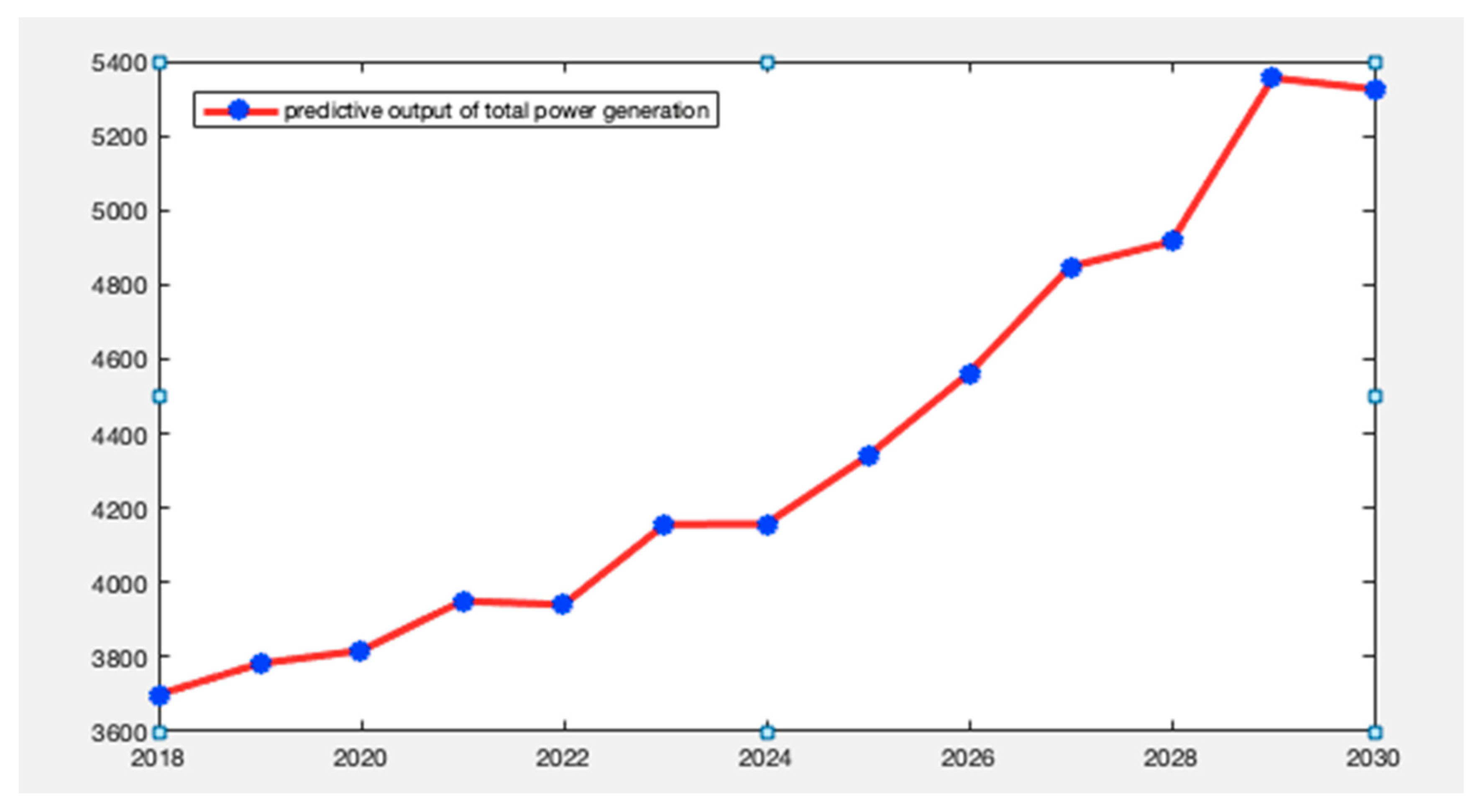
3.5.3. Forecast of Power Generation in the Beijing-Tianjin-Hebei Region from 2018 to 2030
4. Results
- (a)
- The comprehensive line loss rate () used to calculate the carbon emissions is 6.17% [37];
- (b)
- The energy consumption per 100 km of traditional fuel vehicles is calculated based on the average fuel consumption on the market. This paper assumes that fuel vehicles consume 8 L per 100 km (, ) and natural gas-fueled vehicles consume 5.3 kg of natural gas per 100 km () by data statistics;
- (c)
- In traditional fuel cars, the ratio of gasoline vehicles (), diesel vehicles and natural gas vehicles are 12:5:3 [38].
- (a)
- The maximum quantity of electric vehicles under the carbon emission reduction target by eliminating clean energy is 0.4385 million and 0.6167 million with the ratio of the number of electric vehicles to the number of traditional cars is 0.75 and 0.78, which shows that under the existing energy mix structure, electric vehicles cannot completely replace traditional vehicles to ensure carbon emission reduction.
- (b)
- In order to achieve a complete replacement of traditional fuel vehicles for electric vehicles, the minimum proportion of clean energy generation is 0.314 and 0.323 in 2020 and 2030, respectively, which shows it is necessary to introduce a large amount of clean energy, such as inter-regional power trading. Only in this way, with the carbon emission reduction target, can electric cars completely replace traditional fuel cars.
5. Conclusions
- (a)
- The main factors affecting regional clean power generation and total generation include: employment population, installed capacity, regional per capita GDP, total domestic consumption of electricity and coal price;
- (b)
- In consideration of the life cycle of environmental emissions of different energy sources, whether the large-scale development of electric vehicles can achieve environmental protection and carbon emission reduction depends on the regional electricity structure and clean energy utilization;
- (c)
- With the growth speed of clean power generation in the Beijing-Tianjin-Hebei region predicted by the IPSO-ELM method, when the number of officially planned electric vehicles is reached in 2020 and 2030, the carbon emissions of the large-scale adoption of electric vehicles are not lower than those of traditional fuel vehicles. That is to say, according to the prediction result of the generation of clean energy, the goal of carbon emission reduction by the large-scale development of electric vehicles cannot be achieved. It is necessary for local power grids to increase the proportion of clean energy consumption and the amount of clean power trading across provinces.
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Year | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | Y1 | Y2 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1982 | 12.8 | 2825.1 | 544.4 | 2.6 | 68.996 | 3326.4 | 101.8 | 12.345 | 25.730 | 0.583 | 29.165 |
| 1983 | 13 | 2844.3 | 489.9 | 2.4 | 70.521 | 3672.9 | 100.5 | 12.645 | 26.380 | 0.625 | 31.275 |
| 1984 | 11.9 | 2767.6 | 488.8 | 2.4 | 71.724 | 4378.5 | 102.2 | 13.354 | 27.210 | 0.671 | 33.553 |
| 1985 | 11.5 | 2511.9 | 721 | 2.2 | 72.821 | 5405.4 | 117.6 | 14.139 | 31.960 | 0.731 | 36.552 |
| 1986 | 12.1 | 2804.1 | 665.3 | 2.3 | 73.817 | 6066.9 | 106.8 | 14.603 | 34.760 | 0.800 | 40.006 |
| 1987 | 12.3 | 2631.9 | 683.9 | 2.4 | 75.048 | 7005.6 | 108.6 | 15.333 | 47.290 | 0.885 | 44.260 |
| 1988 | 12.7 | 2558.1 | 673.3 | 2.4 | 76.233 | 8605.8 | 120.4 | 16.137 | 51.230 | 0.970 | 48.523 |
| 1989 | 13.2 | 2626.2 | 442.2 | 1.9 | 76.933 | 9569.7 | 117.2 | 16.497 | 56.340 | 1.041 | 52.047 |
| 1990 | 12.7 | 2325 | 697.3 | 1.9 | 78.121 | 10,357.2 | 105.4 | 17.005 | 61.670 | 1.106 | 55.287 |
| 1991 | 12.5 | 2536.6 | 747.9 | 2.1 | 79.294 | 11,925.9 | 111.9 | 18.203 | 70.930 | 1.206 | 60.298 |
| 1992 | 12.8 | 2712.5 | 541.5 | 2.2 | 80.217 | 14,559.3 | 109.9 | 20.376 | 85.130 | 1.342 | 67.097 |
| 1993 | 13 | 2669.8 | 506.7 | 2.6 | 80.901 | 18,887.4 | 119.0 | 22.369 | 113.650 | 1.492 | 74.609 |
| 1994 | 13.7 | 2470.5 | 813.2 | 2.5 | 81.650 | 25,477.2 | 124.9 | 24.619 | 126.830 | 1.648 | 82.414 |
| 1995 | 13.3 | 2519.1 | 572.5 | 2.6 | 82.435 | 31,789.8 | 117.3 | 26.336 | 140.440 | 1.784 | 89.205 |
| 1996 | 12.7 | 2418.7 | 700.9 | 2.6 | 83.216 | 36,829.8 | 111.6 | 28.567 | 159.410 | 1.916 | 95.800 |
| 1997 | 13.1 | 2596.5 | 430.9 | 2.5 | 83.975 | 40,446.0 | 105.3 | 29.087 | 166.600 | 2.076 | 101.874 |
| 1998 | 13.1 | 2420.7 | 731.7 | 2.3 | 84.746 | 42,814.8 | 102.4 | 29.678 | 160.200 | 1.705 | 99.701 |
| 1999 | 13.1 | 2594 | 266.9 | 2.4 | 85.442 | 45,101.7 | 100.6 | 31.484 | 143.980 | 1.156 | 109.411 |
| 2000 | 12.8 | 2667.2 | 371.1 | 2.5 | 87.712 | 49,067.0 | 103.5 | 33.999 | 140.190 | 1.361 | 120.111 |
| 2001 | 12.9 | 2611.7 | 338.9 | 2.4 | 87.754 | 54,390.0 | 103.1 | 37.056 | 150.590 | 0.668 | 125.234 |
| 2002 | 13.2 | 2588.4 | 370.4 | 2.3 | 88.147 | 61,187.0 | 98.2 | 40.242 | 167.810 | 0.974 | 142.507 |
| 2003 | 12.9 | 2260.2 | 444.9 | 2.5 | 88.565 | 70,687.0 | 100.2 | 51.638 | 173.540 | 0.969 | 160.057 |
| 2004 | 13.5 | 2515.4 | 483.5 | 2.4 | 130.242 | 84,161.0 | 101.0 | 61.202 | 210.000 | 1.027 | 179.921 |
| 2005 | 13.2 | 2576.1 | 410.7 | 2.4 | 140.281 | 96,009.0 | 101.5 | 70.518 | 240.000 | 1.338 | 192.104 |
| 2006 | 13.4 | 2192.7 | 318 | 2.2 | 154.877 | 107,360.0 | 100.9 | 76.232 | 270.000 | 2.992 | 203.509 |
| 2007 | 14 | 2351.1 | 483.9 | 2.2 | 170.558 | 127,728.0 | 102.4 | 86.248 | 304.810 | 1.827 | 226.759 |
| 2008 | 13.4 | 2391.4 | 626.3 | 2.2 | 191.767 | 146,133.0 | 105.1 | 96.029 | 418.550 | 12.484 | 215.336 |
| 2009 | 13.3 | 2511.8 | 480.6 | 2.2 | 226.492 | 154,095.0 | 98.5 | 108.293 | 394.350 | 6.299 | 240.088 |
| 2010 | 12.6 | 2382.9 | 522.5 | 2.3 | 257.692 | 175,518.0 | 102.4 | 117.936 | 453.310 | 10.352 | 285.120 |
| 2011 | 13.4 | 2485.7 | 720.6 | 2.2 | 272.462 | 200,840.0 | 105.6 | 126.941 | 498.430 | 12.130 | 321.102 |
| 2012 | 12.9 | 2450.2 | 733.2 | 2.2 | 306.040 | 217,232.0 | 103.3 | 135.965 | 500.230 | 18.879 | 330.043 |
| 2013 | 12.8 | 2371.1 | 578.9 | 2.1 | 342.108 | 233,662.0 | 103.3 | 141.563 | 520.260 | 22.770 | 340.354 |
| 2014 | 14.1 | 2344.1 | 461.5 | 2.1 | 377.331 | 245,210.0 | 101.6 | 152.770 | 529.250 | 22.398 | 348.939 |
| 2015 | 13.7 | 2420.2 | 458.6 | 2.1 | 405.265 | 254,712.0 | 101.8 | 153.270 | 548.930 | 24.499 | 354.200 |
| 2016 | 15.2 | 2530.3 | 432.3 | 2 | 428.031 | 276,313.0 | 101.4 | 159.678 | 610.250 | 24.798 | 367.200 |
| 2017 | 16.1 | 2638.4 | 467.2 | 2.1 | 426.198 | 288,065.1 | 101.3 | 158.843 | 600.084 | 25.156 | 371.741 |
| Year | X5 | X6 | X7 | X8 | X9 |
|---|---|---|---|---|---|
| 2018 | 449.670 | 294,109.7 | 101.0 | 169.847 | 634.037 |
| 2019 | 469.534 | 313,876.4 | 99.0 | 168.116 | 663.942 |
| 2020 | 485.237 | 317,094.0 | 101.1 | 177.035 | 676.726 |
| 2021 | 496.431 | 335,087.3 | 100.4 | 178.350 | 675.639 |
| 2022 | 502.985 | 339,166.9 | 98.3 | 183.811 | 677.093 |
| 2023 | 504.992 | 358,870.7 | 100.5 | 188.778 | 695.090 |
| 2024 | 502.769 | 366,171.5 | 99.3 | 190.563 | 727.932 |
| 2025 | 496.835 | 388,416.9 | 97.7 | 199.067 | 759.835 |
| 2026 | 487.890 | 398,163.0 | 99.8 | 197.606 | 775.905 |
| 2027 | 476.781 | 421,017.7 | 98.1 | 208.925 | 776.274 |
| 2028 | 464.459 | 430,701.0 | 97.2 | 205.204 | 775.972 |
| 2029 | 451.933 | 451,843.4 | 99.0 | 218.130 | 790.668 |
| 2030 | 440.225 | 459,846.2 | 97.1 | 213.525 | 821.796 |
| Year | Y1 | Y2 | Year | Y1 | Y2 |
|---|---|---|---|---|---|
| 2018 | 26.913 | 369.919 | 2024 | 36.285 | 415.745 |
| 2019 | 30.815 | 378.226 | 2025 | 38.011 | 433.933 |
| 2020 | 30.504 | 381.739 | 2026 | 38.840 | 456.195 |
| 2021 | 32.727 | 395.024 | 2027 | 39.430 | 484.839 |
| 2022 | 32.625 | 394.073 | 2028 | 39.880 | 491.566 |
| 2023 | 34.962 | 415.616 | 2029 | 40.195 | 535.526 |
| 2030 | 40.536 | 532.525 |
| Year | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 |
|---|---|---|---|---|---|---|---|---|---|
| the number of traditional fuel cars (million) | 2.561 | 2.791 | 3.180 | 3.725 | 4.217 | 4.756 | 5.477 | 6.399 | 7.389 |
| year | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
| the number of traditional fuel cars (million) | 8.939 | 11.008 | 12.685 | 14.432 | 15.950 | 17.351 | 18.825 | 20.670 | 22.380 |
References
- Hua, H.; Yong, C.; Qi, L. Bi-level multi-objective optimization dispatch of electric vehicles and new energy sources with the priority of satisfaction and cleanliness. Electr. Meas. Instrum. 2018, 55, 59–66, 79. [Google Scholar]
- Chen, Z.; Liu, Q.; Xiao, X.; Liu, N.; Yan, X. Integrated Mode and Key Issues of Renewable Energy Sources and Electric Vehicles’ Charging and Discharging Facilities in Microgrid. Trans. China Electrotech. Soc. 2013, 28, 1–14. [Google Scholar] [CrossRef]
- Baptista, P.; Ribau, J.; Bravo, J.; Silva, C.; Adcock, P.; Kells, A. Fuel cell hybrid taxi life cycle analysis. Energy Policy 2011, 39, 4683–4691. [Google Scholar]
- Deluchi, M.A. Addendum to emissions of greenhouse gases from the use of transportation fuels and electricity. Effect of 1992 revision of global warming potential (GWP) by the Intergovernmental Panel on Climate Change (IPCC). In Office of Scientific & Technical Information Technical Reports; Argonne National Lab.: Argonne, IL, USA, 1992. [Google Scholar]
- Hacknhy, J.; Neufville, R.D. Life cycle model of alternative fuel vehicles: Emissions, energy and cost tradeoffs. Transp. Res. Part A: Policy Pr. 2001, 35, 243–266. [Google Scholar]
- Ou, X.M.; Zhang, X.L.; Qin, Y.N.; Qi, T.Y. Life cycle analysis of electric vehicle charged by advanced technologies coal-power in future China. J. China Coal Soc. 2010, 35, 169–172. [Google Scholar]
- Shi, X.Q.; Li, X.N.; Yang, J.X. Research on Carbon Reduction Potential of Electric Vehicles for Low-Carbon Transportation and Its Influencing Factors. Chin. J. Environ. Sci. 2013, 34, 385–394. [Google Scholar]
- Tang, B.J.; Ma, Y.; Wei, Y.M. Analysis of Energy Conservation and Emission Reduction of New Energy Vehicles in Beijing during the “13th Five-Year Plan”. J. Beijing Inst. Technol. (Soc. Sci. Ed.) 2016, 18, 13–17. [Google Scholar] [CrossRef]
- Mishina, Y.; Muromachi, Y. Are potential reductions in CO2 emissions via hybrid electric vehicles actualized in real traffic? Case Jpn. Transp. Res. Part D 2017, 50, 372–384. [Google Scholar] [CrossRef]
- Mills, G.; Macgill, I. Assessing greenhouse gas emissions from electric vehicle operation in Australia using temporal vehicle charging and electricity emission characteristics. Int. J. Sustain. Transp. 2017, 11, 20–30. [Google Scholar] [CrossRef]
- Wang, G. Study on the Current Situation and Development Trend of Electric Vehicle Technology. Adv. Power Syst. Hydroelectr. Eng. 2017, 33, 97–100. [Google Scholar]
- Doucette, R.T.; McCulloch, M.D. Modeling the prospects of plug-in hybrid electric vehicles to reduce CO2 emissions. Appl. Energy 2011, 88, 2315–2323. [Google Scholar] [CrossRef]
- Patrick, J.; Sonja, B.; Wolf, F. Assessing CO2 emissions of electric vehicles in Germany in 2030. Transp. Res. Part A 2015, 78, 68–83. [Google Scholar]
- Thiel, C.; Perujo, A.; Mercier, A. Cost and CO2 aspects of future vehicle options in Europe under new energy policy scenarios. Energy Policy 2010, 38, 7142–7151. [Google Scholar] [CrossRef]
- Nanaki, E.A.; Koroneos, C.J. Comparative economic and environmental analysis of conventional, hybrid and electric vehicles—the case study of Greece. J. Clean. Prod. 2013, 53, 261–266. [Google Scholar] [CrossRef]
- Huang, Y.; Ji, J.; Ma, X. Greenhouse gas emissions reduction from battery electric automobile: A study based on EIO-LCA model. China Environ. Sci. 2012, 32, 947–953. [Google Scholar]
- Van den Broek, M.; Faaij, A.; Turkenburg, W. Planning for an electricity sector with carbon capture and Storage: Case of the Netherlands. Int. J. Greenh. Gas Control 2008, 2, 105–129. [Google Scholar] [CrossRef]
- Brady, J.; O’Mahony, M. The potential impacts of electric vehicles on climate change and urban air quality. Transp. Res. Part D 2011, 16, 188–193. [Google Scholar] [CrossRef]
- Yu, C.; Tan, Z.F.; Jiang, H.Y. Grey Incidence Analysis and Forecast on Energy Consumption and Economy Growth of China. J. Electr. Power 2007, 22, 424–427, 431. [Google Scholar] [CrossRef]
- Liu, R.Y.; Zhang, J.; Huang, Q.; Lei, B.D. Energy Forecast Model Based on Combination of GM(1,1) and Neural Network. In Proceedings of the 2009 International Conference on Computational Intelligence and Software Engineering, Wuhan, China, 11–13 December 2009. [Google Scholar]
- Yan, X.; Mu, L. Research on GM(1,1) Energy Prediction Model Based on Genetic Algorithm Optimization. China Manag. Inf. 2009, 12, 95–97. [Google Scholar]
- Gorucu, F.B.; Geris, P.U.; Gumrah, F. Artificial neural network modeling for forecasting gas consumption. Energy Sources 2004, 26, 299–307. [Google Scholar] [CrossRef]
- Szoplik, J. Forecasting of natural gas consumption with artificial neural networks. Energy 2015, 85, 208–220. [Google Scholar] [CrossRef]
- Junchen, L.; Xiucheng, D.; Jian, G. Dynamical modeling of natural gas consumption in China. Nat. Gas Ind. 2010, 30, 127–129. [Google Scholar] [CrossRef]
- Anand, A.; Suganthi, L. Hybrid GA-PSO Optimization of Artificial Neural Network for Forecasting Electricity Demand. Energies 2018, 11, 728. [Google Scholar] [CrossRef]
- Qin, H.S.; Wei, D.Y.; Li, J.H.; Zhang, L.; Feng, Y.Q. A Particle Swarm Optimization with Variety Factor. Appl. Mech. Mater. 2013, 239, 1291–1297. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: A new learning scheme of feedforward neural networks. In Proceedings of the IEEE International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 25–29 July 2004. [Google Scholar]
- Luo, J.-X.; Luo, D.; Hu, Y.-M. A new online extreme learning machine with varying weights and decision level fusion for fault detection. Control Decis. 2018, 33, 1033–1040. [Google Scholar]
- Wang, Y.W.; Shen, Z.Z.; Yan, B.H.; Yang, Y. Application of ARIMA and hybrid ARIMA-GRNN models in forecasting AIDS incidence in China. Chin. J. Dis. Control Prev. 2018, 22, 1287–1290. [Google Scholar] [CrossRef]
- Ensslen, A.; Schücking, M.; Jochem, P.; Steffens, H.; Fichtner, W.; Wollersheim, O.; Stella, K. Empirical carbon dioxide emissions of electric vehicles in a French-German commuter fleet test. J. Clean. Prod. 2016, 142, 263–278. [Google Scholar] [CrossRef]
- Vaka, R.; Keshri, R.K. Review on Contactless Power Transfer for Electric Vehicle Charging. Energies 2017, 10, 636. [Google Scholar] [CrossRef]
- Yu, S.; Wei, Y.M.; Guo, H.; Ding, L. Carbon emission coefficient measurement of the coal-to-power energy chain in China. Appl. Energy 2014, 114, 290–300. [Google Scholar] [CrossRef]
- Pan, Z.; Ma, Z.; Li, X.; Wu, T.; Xiu, B. Comparative study of impacts of coal chain and nuclear power chain in china on health, environment and climate. Radiat. Prot. 2001, 21, 129–145. [Google Scholar]
- BJX.com.cn. Available online: http://news.bjx.com.cn/html/20171225/869765.shtml (accessed on 25 December 2017).
- Yang, N.; Li, H.; Yuan, J.; Li, S.; Wang, X. Medium-and Long-term Load Forecasting Method Considering Grey Correlation Degree Analysis. Proc. CSU-EPSA 2018, 30, 108–114. [Google Scholar]
- Guo, W.Q.; Shi, S.; Zhang, X.; Li, K.K.; She, J.L.; Gao, W.Q. Short-term power generation prediction based on BPneural network optimized by genetic algorithm. J. Shaanxi Univ. Sci. Technol. (Nat. Sci. Ed.) 2017, 35, 159–163, 178. [Google Scholar]
- Min, T.; Xinghua, W.; Qing, L. Application of Support Vector Machine Based on Particle Swarm Optimization in Low Voltage Line Loss Prediction. In Proceedings of the Joint International Mechanical, Electronic and Information Technology Conference (JIMET), Chongqing, China, 18–20 December 2015. [Google Scholar]
- Chinabaogao. Available online: http://zhengce.chinabaogao.com/nengyuan/2017/11203021512017.html (accessed on 15 February 2017).

| Car Manufacturer | BYD | SAIC Roewe | Chery | JAC | Geely | Changan |
|---|---|---|---|---|---|---|
| Model | E6 | E50 | eQ | iEV | Conti | EODO |
| Electricity consumption per 100 km | 20 | 15 | 15 | 14 | 14 | 16 |
| Average energy consumption per 100 km | 15.7 | |||||
| Manufacturer | BYD | SAIC Roewe | Chery | JAC | Geely | Changan |
|---|---|---|---|---|---|---|
| E6 | E50 | eQ | iEV | Conti | EODO | |
| SOH 100% | 87.6% | 87.5% | 86.3% | 86.9% | 87.2% | 87.6% |
| SOH 90% | 86.5% | 86.9% | 85.5% | 86.1% | 87.1% | 86.9% |
| Battery temperature 25 °C | 88.1% | 88% | 87.1% | 87.5% | 88.4% | 88.9% |
| Battery temperature 45 °C | 83.1% | 84.1% | 83.4% | 84.1% | 84.1% | 85.1% |
| Comprehensive efficiency | 86.33% | 86.63% | 85.58% | 86.15% | 86.70% | 87.13% |
| Average comprehensive efficiency | 86.42 | |||||
| Fuel | Carbon Emissions (kg) |
|---|---|
| Gasoline (L) () | 2.36 |
| Diesel (L) () | 2.63 |
| Liquefied natural gas (kg) () | 1.964 |
| Thermal power generation (kW h) | 1.303 |
| Hydroelectric power (kW h) | 0.026 |
| Nuclear power generation (kW h) | 0.029 |
| Wind power generation (kW h) | 0.026 |
| Solar energy generation (kW h) | 0.085 |
| Clean power generation average (kW h) | 0.0415 |
| Influencing Factors | Score | Influencing Factors | Score |
|---|---|---|---|
| average temperature | −0.363 | GDP per capita | 0.910 |
| sunshine hours | 0.431 | consumer price index | 0.834 |
| precipitation | 0.088 | electricity consumption for domestic consumption | 0.888 |
| average wind speed | 0.436 | coal price | 0.879 |
| employment population | 0.959 |
| Influencing Factors | Score | Influencing Factors | Score |
|---|---|---|---|
| average temperature | −0.359 | GDP per capita | 0.991 |
| sunshine hours | 0.413 | consumer price index | 0.813 |
| precipitation | 0.102 | electricity consumption for domestic consumption | 0.986 |
| average wind speed | 0.374 | coal price | 0.991 |
| employment population | 0.944 |
| Parameter | Set Quantity |
|---|---|
| the max-generation | 40 |
| the size of population | 40 |
| The maximum number of iterations | 300 |
| Parameter | Index | ELM | IPSO-ELM |
|---|---|---|---|
| Forecast of clean power generation | R² | 66.46% | 99.32% |
| RMSE | 155.346 | 12.76 | |
| Forecast of total power generation | R² | 91.73% | 99.29% |
| RMSE | 241.20 | 62.48 |
| Year | Clean Power Generation | Total Power Generation |
|---|---|---|
| 2020 | 30.504 | 381.738 |
| 2030 | 40.535 | 532.525 |
| Year | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 | 2024 |
| traditional fuel cars(million) | 23.99 | 24.31 | 25.56 | 26.02 | 26.9 | 27.35 | 28.09 |
| Year | 2025 | 2026 | 2027 | 2028 | 2029 | 2030 | |
| traditional fuel cars(million) | 28.8 | 29.08 | 29.87 | 30.32 | 33.98 | 36.09 |
| Year | 2020 | 2030 |
|---|---|---|
| Clean power generation (billion kW h) | 30.041 | 40.535 |
| Total power generation (billion kW h) | 381.739 | 532.525 |
| The maximum quantity of electric vehicles under the carbon emission reduction target by eliminating clean energy (million units) | 18.37 | 26.86 |
| the number of traditional fuel cars (million units) | 23.06 | 32.57 |
| the ratio of the number of electric vehicles to the number of traditional cars | 0.75 | 0.78 |
| the proportion of clean energy generation to achieve a complete replacement of traditional fuel vehicles for electric vehicles | 0.314 | 0.323 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Zhao, D.; Mi, Z.; Fan, L. Prediction and Analysis of the Relationship between Energy Mix Structure and Electric Vehicles Holdings Based on Carbon Emission Reduction Constraint: A Case in the Beijing-Tianjin-Hebei Region, China. Sustainability 2019, 11, 2928. https://doi.org/10.3390/su11102928
Wang W, Zhao D, Mi Z, Fan L. Prediction and Analysis of the Relationship between Energy Mix Structure and Electric Vehicles Holdings Based on Carbon Emission Reduction Constraint: A Case in the Beijing-Tianjin-Hebei Region, China. Sustainability. 2019; 11(10):2928. https://doi.org/10.3390/su11102928
Chicago/Turabian StyleWang, Weijun, Dan Zhao, Zengqiang Mi, and Liguo Fan. 2019. "Prediction and Analysis of the Relationship between Energy Mix Structure and Electric Vehicles Holdings Based on Carbon Emission Reduction Constraint: A Case in the Beijing-Tianjin-Hebei Region, China" Sustainability 11, no. 10: 2928. https://doi.org/10.3390/su11102928
APA StyleWang, W., Zhao, D., Mi, Z., & Fan, L. (2019). Prediction and Analysis of the Relationship between Energy Mix Structure and Electric Vehicles Holdings Based on Carbon Emission Reduction Constraint: A Case in the Beijing-Tianjin-Hebei Region, China. Sustainability, 11(10), 2928. https://doi.org/10.3390/su11102928




