Social Security and Sustainable Economic Growth: Based on the Perspective of Human Capital
Abstract
:1. Introduction
2. Literature Review and Research Hypothesis
3. Variables and Data
3.1. Measurement of Total Factor Productivity: A measure of Economic Sustainability
3.2. Measurement of Variables
4. Does the Threshold Effect Exist?
5. The Impact of Social Security on Productivity
5.1. Measurement Model Setting
5.2. Estimation Results and Analysis
5.3. Robustness Test
6. Conclusions and Policy Recommendations
Author Contributions
Funding
Conflicts of Interest
References
- Butter, F.A.G.D.; Kock, U. Social Security, Economic Growth and Poverty: Theoretical Considerations and Guidelines for Institutional Arrangements. Res. Memo. 2001, 5, 1–21. [Google Scholar]
- Sala-I-Martin, X. A Positive Theory of Social Security. Scand. J. Econ. 1996, 1, 277–304. [Google Scholar] [CrossRef]
- Lucas, R.E. On the Mechanics of Economic Development. J. Monet. Econ. 1988, 22, 3–42. [Google Scholar] [CrossRef]
- Fan, G.; Zhang, X.J. Welfare catching up and growth trap: Lessons from Latin America. Manag. World 2008, 9, 12–24. (In Chinese) [Google Scholar]
- Zheng, B.W. 40 years of social security in China: Experience summary and reform orientation. Chin. Popul. Sci. 2018, 4, 2–17. (In Chinese) [Google Scholar]
- Zhang, Y.H. The structural contradiction between Latin America’s welfare catching up and social expenditure. Comp. Econ. Soc. Syst. 2018, 4, 139–147. (In Chinese) [Google Scholar]
- Barro, R.J. Government Spending in A Simple Model of Endogenous Growth. J. Political Econ. 1990, 98, 103–126. [Google Scholar] [CrossRef]
- Feldstein, M. Social Security, Induced Retirement, and Aggregate Capital Accumulation. J. Political Econ. 1974, 82, 905–926. [Google Scholar] [CrossRef]
- Kotlikoff, L.J. Privatization of Social Security: How it Works and Why it Matters. Tax Policy Econ. 1996, 10, 1–32. [Google Scholar] [CrossRef]
- Sun, Y.X.; Xiao, Z.G. The reform of social security system and the rebalancing of China’s internal and external economy. Financ. Res. 2013, 6, 74–88. (In Chinese) [Google Scholar]
- Jia, J.X.; Guo, Q.W.; Ning, J. Traditional cultural beliefs, social security and economic growth. World Econ. 2011, 8, 3–18. (In Chinese) [Google Scholar]
- Guo, K.M.; Gong, L.T. Social Security, Family Pension and Economic Growth. Financ. Res. 2012, 1, 78–90. (In Chinese) [Google Scholar]
- Lu, C.C.; Liu, H.J. Does Social Security Promote Regional Economic Growth? A Dynamic Spatial Panel Model Analysis Based on Time and Space Effect and Decomposition. J. Huazhong Univ. Sci. Technol. (Soc. Sci. Ed.) 2017, 2, 55–66. (In Chinese) [Google Scholar]
- Glomm, G.; Kaganovich, M. Distributional Effects of Public Education in an Economy with Public Pensions. Int. Econ. Rev. 2003, 44, 917–937. [Google Scholar] [CrossRef]
- Nelson, R.; Phelps, E. Investment in Humans, Technological Diffusion and Economic Growth. Am. Econ. Rev. 1966, 56, 69–75. [Google Scholar]
- Scicchitano, S. On the complementarity between on-the-job training and R&D: A brief overview. Econ. Bull. 2007, 15, 1–11. [Google Scholar]
- Benhabib, J.; Spiegel, M. The Role of Human Capital in Economic Development Evidence from Aggregate Cross Country Data. J. Monet. Econ. 1994, 34, 143–173. [Google Scholar] [CrossRef]
- Redding, S. Low-skill, Low-quality Trap: Strategic Complementarities between Human Capital and R&D. Econ. J. 1996, 106, 458–470. [Google Scholar] [CrossRef]
- Scicchitano, S. Complementarity between Heterogeneous Human Capital and R&D: Can Job-training Avoid Low Development Traps? Empirica 2010, 37, 361–380. [Google Scholar] [CrossRef]
- Anand, S.; Ravallion, M. Human Development in Poor Countries: On the Role of Private Incomes and Public Services. J. Econ. Perspect. 1993, 7, 133–150. [Google Scholar] [CrossRef] [Green Version]
- Nordhaus, W.D. The Health of Nations: Irving Fisher and the Contribution of Improved Longevity to Living Standards. Cowles Found. Discuss. Pap. 1998, 64, 399–405. [Google Scholar] [CrossRef]
- Barro, R.J. Determinants of Economic Growth: A Cross Country Empirical Study. Am. J. Agric. Econ. 2003, 85, 1087–1088. [Google Scholar] [CrossRef]
- Fogel, R.W. Economic Growth, Population Theory, and Physiology: The Bearing of Long Term Processes on the Making of Economic Policy. Am. Econ. Rev. 1994, 84, 369–395. [Google Scholar] [CrossRef]
- Mimoun, M.B.; Raies, A. Education and Economic Growth: The Role of Public Expenditures Allocation. Econ. Bull. 2009, 29, 2404–2416. [Google Scholar]
- Pietro, G.D. Equality of Opportunity in Italian University Education: Is There Any Role for Social Welfare Spending. Int. J. Educ. Dev. 2003, 23, 5–15. [Google Scholar] [CrossRef]
- Fan, J.B.; Yang, T.Y. Social Welfare Expenditure, Human Capital and China’s Economic Growth—Based on the Research of Provincial Panel Data. Contemp. Econ. Manag. 2012, 7, 13–18. (In Chinese) [Google Scholar]
- Guo, Q.W.; Jia, J.X.; Zhao, Z.Y. Chinese Traditional Cultural Beliefs, Human Capital Accumulation and Family Endowment Security Mechanism. Econ. Res. 2007, 8, 58–72. [Google Scholar]
- Peng, H.R.; Shen, S.G. Pay-as-you-go pension insurance and economic growth: Theoretical model and Chinese experience. World Econ. 2007, 10, 67–75. (In Chinese) [Google Scholar]
- Lin, Z.J.; Gong, L.T. Retirement age, years of education and social security. China Econ. Q. 2008, 1, 211–230. (In Chinese) [Google Scholar]
- Ehrlich, I.; Kim, J. Social Security, Demographic Trends, and Economic Growth: Theory and Evidence from the International Experience. Rev. Econ. Dyn. 2007, 10, 55–77. [Google Scholar] [CrossRef]
- Shen, Y. The Impact of Social Security on Human Capital and Its Economic Growth—Based on China’s Data from 1989 to 2008. Soc. Secur. Res. 2012, 4, 69–76. (In Chinese) [Google Scholar]
- Caliendo, F.; Findley, T.S. Myopia, Education, and Optimal Social Security. SSRN Electron. J. 2018, 1, 1–37. [Google Scholar] [CrossRef]
- Bucciol, A.; Cavalli, L.; Fedotenkov, I. A large scale OLG model for the analysis of the redistributive effects of policy reforms. Eur. J. Political Econ. 2017, 48, 104–127. [Google Scholar] [CrossRef]
- Zhou, H.; Tang, L.R. Can market competition force companies to be kind to employees?—Micro evidence from manufacturing companies. Manag. World 2015, 11, 135–144. (In Chinese) [Google Scholar]
- Easterly, W.; Levine, R. It’s Not Factor Accumulation: Stylized Facts and Growth Models. World Bank Econ. Rev. 2001, 15, 177–219. [Google Scholar] [CrossRef]
- Fare, R.S.; Grosskopf, S.; Norriss, M.; Zhang, Z. Productivity Growth, Technical Progress, and Efficiency Change in Industrialized Countries. Am. Econ. Rev. 1994, 84, 66–83. [Google Scholar] [CrossRef]
- Lai, P.Y. Productivity Dilemma of China’s Economic Growth: Expanding Growth under Investment. World Econ. 2016, 39, 75–94. (In Chinese) [Google Scholar]
- Zhong, S.C.; Mao, Y.H. Re-measurement and Decomposition of China’s Total Factor Productivity—Based on the Perspective of Multi-factor Technology Progressive Deviation. Econ. Rev. 2017, 1, 3–14. (In Chinese) [Google Scholar]
- Romer, M.P. Endogenous Technological Change. J. Political Econ. 1990, 98, 71–102. [Google Scholar] [CrossRef]
- Hansen, B.E. Threshold Effects in Non-Dynamic Panels: Estimation, Testing, and Inference. J. Econom. 1999, 93, 345–368. [Google Scholar] [CrossRef]
- Windmeijer, F. A Finite Sample Correction for The Variance of Linear Efficient Two-Step GMM Estimators. J. Econom. 2005, 126, 25–51. [Google Scholar] [CrossRef]
- Bond, S.R. Dynamic Panel Data Models: A Guide to Micro Data Methods and Practice. Port. Econ. J. 2002, 1, 141–162. [Google Scholar] [CrossRef]
- Levin, A.; Lin, C.F.; Chu, C. Unit Root Tests in Panel Data: Asymptotic and Finite-sample Properties. J. Econom. 2002, 108, 1–24. [Google Scholar] [CrossRef]
- Im, K.S.; Pesaran, M.; Shin, Y. Testing for Unit Roots in Heterogeneous Panels. J. Econom. 2003, 115, 53–74. [Google Scholar] [CrossRef]
- Han, C.; Phillips, C.B. GMM Estimation for Dynamic Panels with Fixed Effects and Strong Instruments at Unity. Econom. Theory 2010, 26, 119–151. [Google Scholar] [CrossRef]
- Elhorst, J.P. Unconditional Maximum Likelihood Estimation of Linear and Log-linear Dynamic Models for Spatial Panels. Geogr. Anal. 2005, 37, 85–106. [Google Scholar] [CrossRef]

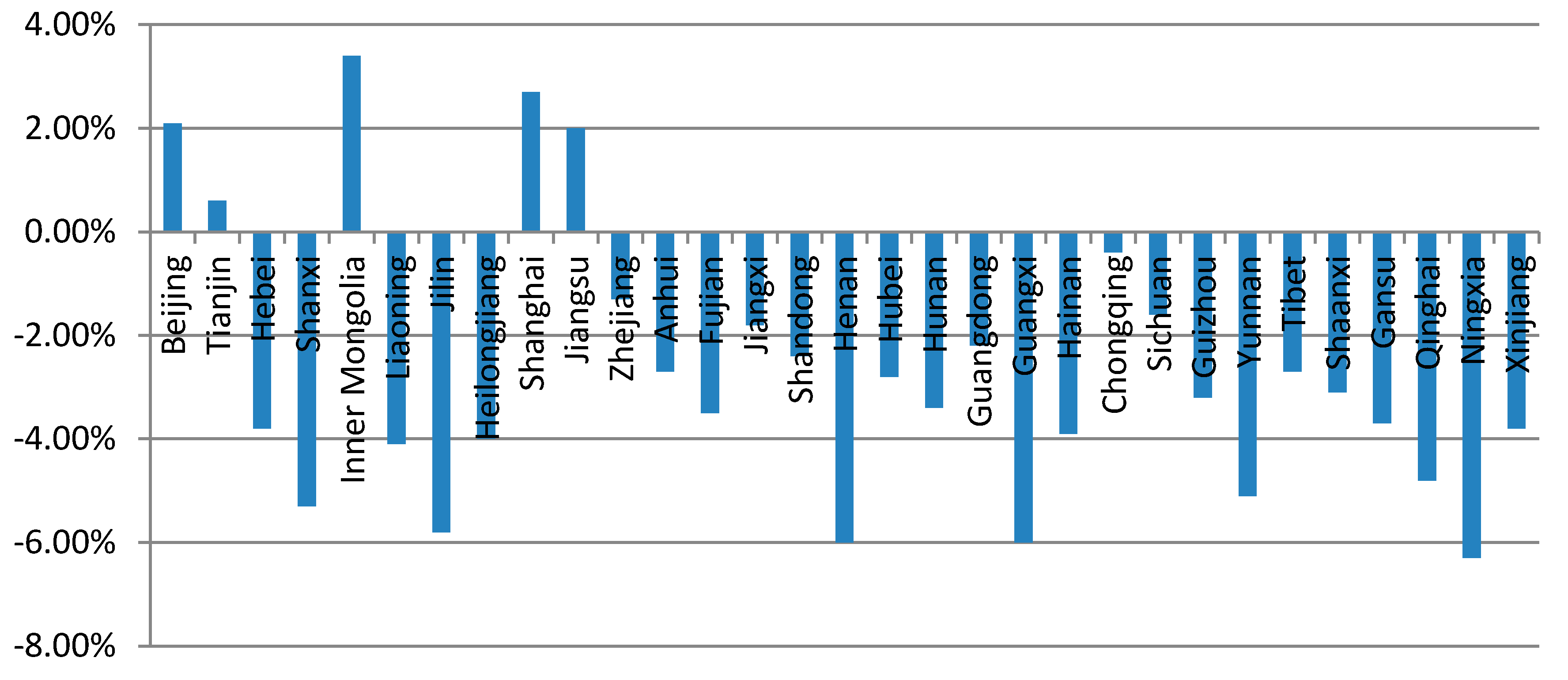
| Mean | Changes from 2007 to 2016 | Mean | Changes from 2007 to 2016 | Mean | Changes from 2007 to 2016 | |
|---|---|---|---|---|---|---|
| Beijing | 0.0227 | 0.0097 | 11.5894 | 1.2187 | 2.4693 | 3.7363 |
| Tianjin | 0.0164 | 0.0060 | 10.2753 | 0.9657 | 1.3344 | 2.0430 |
| Hebei | 0.0194 | 0.0100 | 8.6279 | 0.8078 | 0.2109 | 0.3489 |
| Shanxi | 0.0332 | 0.0112 | 9.1641 | 0.9193 | 0.1703 | 0.2146 |
| Inner Mongolia | 0.0281 | 0.0118 | 8.9235 | 1.3263 | 0.1235 | 0.1779 |
| Liaoning | 0.0343 | 0.0154 | 9.5547 | 0.9848 | 0.4150 | 0.3497 |
| Jilin | 0.0300 | 0.0045 | 9.1443 | 0.7367 | 0.2044 | 0.2611 |
| Heilongjiang | 0.0365 | 0.0170 | 9.0803 | 0.6760 | 0.3280 | 0.3625 |
| Shanghai | 0.0232 | 0.0131 | 10.6278 | 0.5895 | 1.9471 | 1.4680 |
| Jiangsu | 0.0098 | 0.0034 | 9.0217 | 1.0771 | 2.1356 | 2.4769 |
| Zhejiang | 0.0093 | 0.0076 | 8.7448 | 1.0102 | 2.6584 | 3.1456 |
| Anhui | 0.0281 | 0.0032 | 8.1148 | 1.3206 | 0.5357 | 0.9284 |
| Fujian | 0.0109 | 0.0023 | 8.4528 | 0.9789 | 0.7958 | 1.5183 |
| Jiangxi | 0.0264 | 0.0097 | 8.6141 | 0.5043 | 0.2303 | 0.6380 |
| Shandong | 0.0117 | 0.0048 | 8.6407 | 0.8030 | 0.6336 | 0.7425 |
| Henan | 0.0217 | 0.0076 | 8.5574 | 0.6315 | 0.2644 | 0.4408 |
| Hubei | 0.0252 | 0.0073 | 8.9187 | 0.8739 | 0.3874 | 0.5946 |
| Hunan | 0.0256 | 0.0043 | 8.7694 | 0.9405 | 0.2881 | 0.4096 |
| Guangdong | 0.0113 | 0.0053 | 9.1226 | 0.9326 | 1.3709 | 1.7707 |
| Guangxi | 0.0235 | 0.0104 | 8.3603 | 0.7295 | 0.1402 | 0.2671 |
| Hainan | 0.0389 | 0.0168 | 8.7864 | 0.7969 | 0.1204 | 0.1764 |
| Chongqing | 0.0336 | 0.0064 | 8.4470 | 1.3492 | 0.6592 | 1.2248 |
| Sichuan | 0.0324 | 0.0143 | 8.0518 | 0.8696 | 0.4505 | 0.6336 |
| Guizhou | 0.0321 | 0.0066 | 7.4636 | 0.9238 | 0.1722 | 0.2457 |
| Yunnan | 0.0435 | 0.0111 | 7.4800 | 1.2066 | 0.1271 | 0.2048 |
| Tibet | 0.0913 | 0.1304 | 4.8223 | 0.4675 | 0.0505 | 0.0505 |
| Shaanxi | 0.0316 | 0.0062 | 8.9425 | 0.8726 | 0.4660 | 1.1777 |
| Gansu | 0.0543 | 0.0250 | 7.8999 | 1.3820 | 0.1391 | 0.2653 |
| Qinghai | 0.0844 | 0.0121 | 7.5619 | 0.6157 | 0.1010 | 0.1886 |
| Ningxia | 0.0371 | 0.0241 | 8.3998 | 1.3329 | 0.1765 | 0.3481 |
| Xinjiang | 0.0341 | 0.0265 | 8.8457 | 0.5870 | 0.1737 | 0.2235 |
| Threshold Model | F Value | P | 10% Threshold Value | 5% Threshold Value | 1% Threshold Value |
|---|---|---|---|---|---|
| Single threshold | 10.313 | 0.0020 | 2.9113 | 4.1216 | 6.5654 |
| Double threshold | 8.7487 | 0.0020 | 2.6150 | 3.8296 | 6.3304 |
| Triple threshold | 0.6102 | 0.4375 | 2.9795 | 4.0144 | 7.0600 |
| Threshold | Estimated Value | 95% Confidence Interval |
|---|---|---|
| First threshold value | 7.5138 | [7.5138, 8.0390] |
| Second threshold values | 9.3523 | [7.7525, 9.8776] |
| LLC Test | IPS Test | |
|---|---|---|
| −4.5832(0.0000) | −4.0892(0.0000) | |
| −10.0108(0.0000) | −7.2362(0.0000) | |
| −6.8059(0.0000) | −4.9425(0.0000) | |
| −1.7075(0.0439) | −5.9247(0.0000) |
| I | II | III | |
|---|---|---|---|
| 0.4787 (12.79) *** | 0.5087 (8.83) *** | 0.4401 (5.51) *** | |
| −0.2070 (−1.17) | −0.0098 (−0.05) | 1.3694 (2.15) ** | |
| 0.0039 (2.00) * | |||
| 0.0061 (2.32) ** | 0.0084 (2.81) *** | ||
| −0.4438 (−2.50) ** | |||
| 0.0334 (2.51) ** | |||
| 0.0001 (0.02) | −0.0047 (−0.64) | −0.0104 (−1.60) | |
| −0.0056 (−1.39) | −0.0034 (−0.64) | −0.0088 (−1.51) | |
| Constant term | 0.3299 (7.49) *** | 0.3052 (4.20) *** | 0.3956 (4.67) *** |
| AR(2) | 0.458 | 0.408 | 0.474 |
| Hansen | 1.000 | 1.000 | 1.000 |
| Difference-in-Hansen | 1.000 | 1.000 | 1.000 |
| Ⅳ Han–Philips Moment Estimator | Ⅴ Space System Moment Estimator | Ⅵ Space Han–Philips Moment Estimator | |
|---|---|---|---|
| 0.3618 (0.96) | 0.3799 (1.01) | 0.3459 (0.91) | |
| 3.4918 (1.50) | 4.6900 (2.08) ** | 3.4639 (1.50) | |
| 0.0165 (1.96) * | 0.0156 (1.98) ** | 0.0123 (1.33) | |
| −1.1354 (−1.64) * | −1.4666 (−2.20) ** | −1.1054 (−1.65) * | |
| 0.0767 (1.68) * | 0.1040 (2.21) ** | 0.0733 (1.63) * | |
| −0.0217 (−1.42) | −0.0075 (−0.48) | −0.0243 (−1.58) | |
| −0.0196 (−1.52) | −0.0165 (−1.36) | −0.0243 (−1.81) * | |
| Constant term | 0.6285 (51.72) *** | 0.5819 (33.44) *** | 0.6406 (50.60) *** |
| Space item | 0.0067 (2.17) ** | 0.0002 (1.13) | |
| Wald-test | 19.49 | 26.95 | 21.01 |
| F-test | 2.49 | 3.37 | 2.63 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Zou, X.; Sha, L. Social Security and Sustainable Economic Growth: Based on the Perspective of Human Capital. Sustainability 2019, 11, 662. https://doi.org/10.3390/su11030662
Zhang M, Zou X, Sha L. Social Security and Sustainable Economic Growth: Based on the Perspective of Human Capital. Sustainability. 2019; 11(3):662. https://doi.org/10.3390/su11030662
Chicago/Turabian StyleZhang, Ming, Xiaorong Zou, and Long Sha. 2019. "Social Security and Sustainable Economic Growth: Based on the Perspective of Human Capital" Sustainability 11, no. 3: 662. https://doi.org/10.3390/su11030662
APA StyleZhang, M., Zou, X., & Sha, L. (2019). Social Security and Sustainable Economic Growth: Based on the Perspective of Human Capital. Sustainability, 11(3), 662. https://doi.org/10.3390/su11030662




