GIS Multi-Criteria Analysis by Ordered Weighted Averaging (OWA): Toward an Integrated Citrus Management Strategy
Abstract
:1. Introduction
- An approach that combined AHP with OWA in a GIS environment is proffered. The present study focuses on an integrated citrus management strategy. Specifically, a GIS-based overlay analysis was performed to identify the optimum site for the citrus production that fulfilled all of the desired attributes.
- Accordingly, this research tries to develop a new method, which is proposed by applying a novel GIS-based MCDM methodology for the assessment of citrus production.
- A spatial framework adopting the AHP and OWA into the ArcGIS is used to evaluate the potential for the future expansion of citrus in Ramsar, Iran.
- GIS is used for an important improvement to the conventional map overlay approaches.
- How can the citrus susceptibility problems be solved using a GIS-based OWA operator with a multi-criteria approach?
- How can the critical factors by their relative weights, which are imported in GIS-based OWA capabilities, help decision makers with the citrus planning procedure now and in the future?
2. Materials and Methods
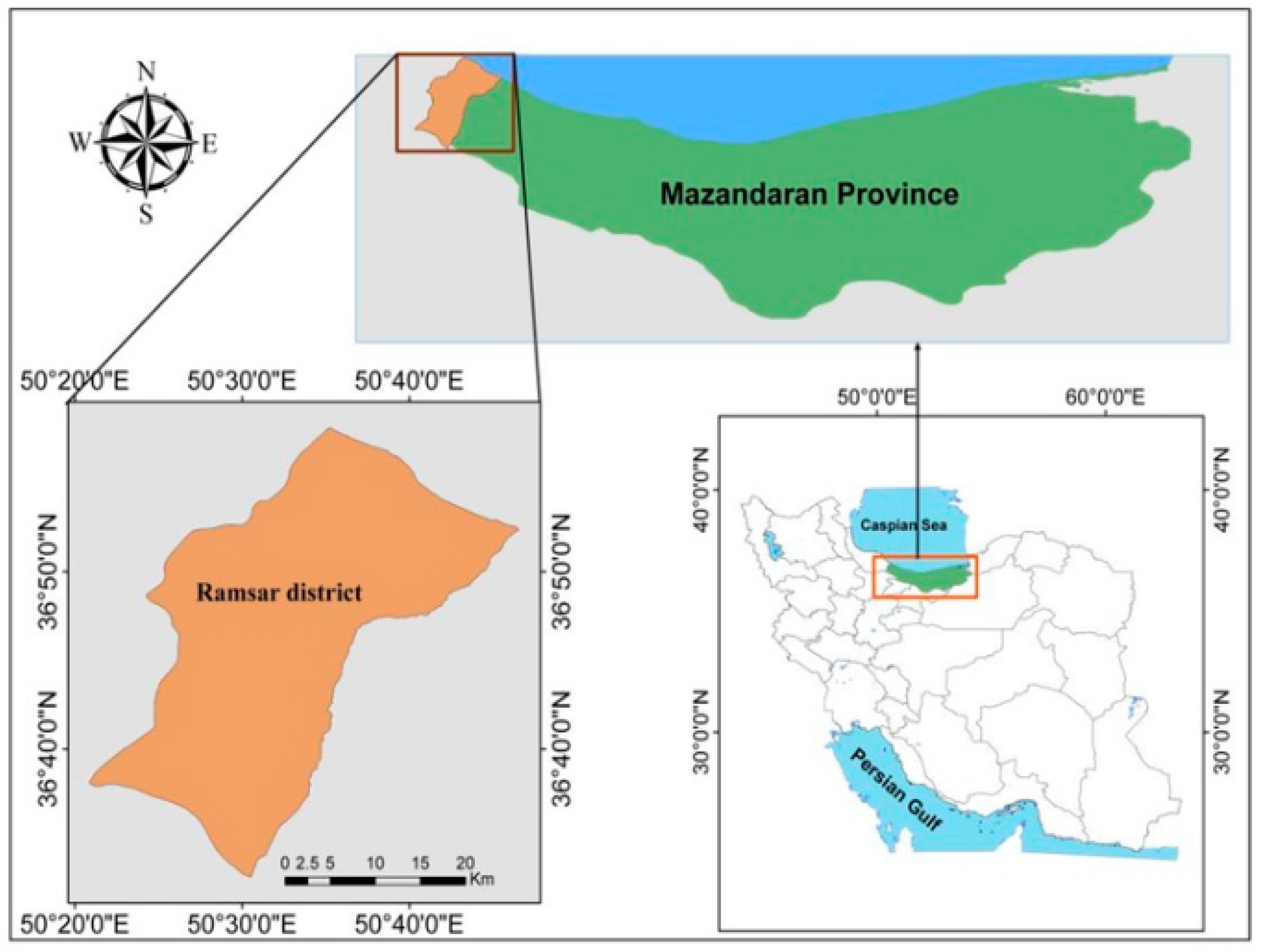
2.1. Study Site
2.2. Methodology
2.2.1. Data Collection and Preparation
2.2.2. Ordered Weighted Averaging (OWA) Method
3. Results
4. Discussion
5. Conclusions and Perspectives
Author Contributions
Funding
Conflicts of Interest
References
- Memarbashi, E.; Hossein Azadi, H.; Barati, A.K.; Fatemeh Mohajeri, F.; Van Passel, S.; Witlox, F. Land-Use Suitability in Northeast Iran: Application of AHP-GIS Hybrid Model. Isprs Int. J. Geo-Inf. 2017, 6, 396. [Google Scholar] [CrossRef]
- Zabihi, H.; Alizadeh, M.; Vogeler, I.; Ahmad, A.; Nor Said, M.; Ramezani Gourabi, B. Land allocation based on spatial analysis using artificial neural networks and GIS in Ramsar, Iran. Model. Earth Syst. Environ. 2017, 3, 1515–1527. [Google Scholar] [CrossRef]
- Pandey, B.; Seto, K.C. Urbanization and agricultural land loss in India: Comparing satellite estimates with census data. J. Environ. Manag. 2015, 148, 53–66. [Google Scholar] [CrossRef] [PubMed]
- Antonelli, M.; Siciliano, G.; Turvani, M.E.; Rulli, M.C. Global investments in agricultural land and the role of the EU: Drivers, scope and potential impacts. Land Use Policy. 2015, 47, 98–111. [Google Scholar] [CrossRef]
- Lee, T.M.; Yeh, H.C. Applying remote sensing techniques to monitor shifting wetland vegetation: A case study of Danshui River estuary mangrove communities, Taiwan. Ecol. Eng. 2009, 35, 487–496. [Google Scholar] [CrossRef]
- Cordioli, M.; Pironi, C.; De Munari, E.; Marmiroli, N.; Lauriola, P.; Ranzi, A. Combining land use regression models and fixed site monitoring to reconstruct spatiotemporal variability of NO2 concentrations over a wide geographical area. Sci. Total Environ. 2017, 74, 1075–1084. [Google Scholar] [CrossRef] [PubMed]
- Van den Bossche, J.; De Baets, B.; Verwaeren, J.; Botteldooren, D.; Theunis, J. Development and evaluation of land use regression models for black carbon based on bicycle and pedestrian measurements in the urban environment. Environ. Model. Softw. 2018, 99, 58–69. [Google Scholar] [CrossRef] [Green Version]
- Pan, G.; Pan, J. Research in crop land suitability analysis based on GIS. Comput. Comput. Technol. Agric. 2012, 365, 314–325. [Google Scholar]
- Aramburu Merlos, F.A.; Monzon, J.P.; Mercau, J.L.; Taboada, M.; Andrade, F.H.; Hall, A.J.; Jobbagy, E.; Cassman, K.G.; Grassini, P. Potential for Crop Production Increase in Argentina Through Closure of Existing Yield Gaps. Field Crop. Res. 2015, 184, 145–154. [Google Scholar] [CrossRef]
- Lamb, A.; Green, R.; Bateman, I.; Broadmeadow, M.; Bruce, T.; Burney, J.; Carey, P.; Chadwick, D.; Crane, E.; Field, R.; et al. The potential for land sparing to offset greenhouse gas emissions from agriculture. Nat. Clim. Chang. 2016, 6, 488–492. [Google Scholar] [CrossRef] [Green Version]
- Shen, J.; Huete, A.; Nguyen Tran, N.; Devadas, R.; Xuanlong Ma, X.; Eamus, D.; Yu, Q. Diverse sensitivity of winter crops over the growing season to climate and land surface temperature across the rainfed cropland-belt of eastern Australia. Agric. Ecosyst. Environ. 2017, 254, 99–110. [Google Scholar] [CrossRef]
- Malczewski, J. Ordered weighted averaging with fuzzy quantifiers: GIS-based multi-criteria evaluation for land-use suitability analysis. Int. J. Appl. Earth Obs. Geoinf. 2006, 8, 270–277. [Google Scholar] [CrossRef]
- Montgomery, B.; Dragićević, S.; Dujmović, J.; Schmidt, M. A GIS-based Logic Scoring of Preference method for evaluation of land capability and suitability for agriculture. Comput. Electron. Agric. 2016, 124, 340–353. [Google Scholar] [CrossRef]
- Grima, N.; Singh, S.J.; Smetschka, B. Improving payments for ecosystem services (PES) outcomes through the use of Multi-Criteria Evaluation (MCE) and the software OPTamos. Ecosyst. Serv. 2018, 29, 47–55. [Google Scholar] [CrossRef]
- Cover, S.J. Integrating multi-criteria evaluation with of the geographical information systems. Int. J. Geogr. Inf. Syst. 1991, 5, 321–339. [Google Scholar]
- Voogd, H. Multicriteria Evaluation for Urban and Regional Planning; Pion Limited: London, UK, 1983. [Google Scholar]
- Gorsevski, P.V.; Cathcart, S.C.; Mirzaei, G.; Jamali, M.M.; Ye, X.; Gomezdelcampo, E. A group-based spatial decision support system for wind farm site selection in Northwest Ohio. Energy Policy 2013, 55, 374–385. [Google Scholar] [CrossRef]
- Krois, J.; Schulte, A. GIS-based multi-criteria evaluation to identify potential sites for soil and water conservation techniques in the Ronquillo watershed, northern Peru. Appl. Geogr. 2014, 51, 131–142. [Google Scholar] [CrossRef]
- Dragićević, S.; Lai, T.; Balram, S. GIS-based multi-criteria evaluation with multiscale analysis to characterize urban landslide susceptibility in data-scarce environments. Habitat Int. 2015, 45, 114–125. [Google Scholar] [CrossRef]
- Flocard, F.; Ierodiaconou, D.; Coghlan, I.R. Multi-criteria evaluation of wave energy projects on the south-east Australian coast. Renew. Energy 2016, 99, 80–94. [Google Scholar] [CrossRef]
- Pujadas, P.; Pardo-Bosch, F.; Aguado-Renter, A.; Aguado, A. MIVES multi-criteria approach for the evaluation, prioritization, and selection of public investment projects. A case study city Barcelona. Land Use Policy 2017, 64, 29–37. [Google Scholar] [CrossRef]
- Mardani, A.; Zavadskas, E.K.; Khalifah, Z.; Jusoh, A.; Nor, K.M. Multiple criteria decision-making techniques in transportation systems: A systematic review of the state-of-the-art literature. Transport 2016, 31, 359–385. [Google Scholar] [CrossRef]
- Podvezko, V. Application of AHP technique. J. Bus. Econ. Manag. 2009, 10, 181–189. [Google Scholar] [CrossRef] [Green Version]
- Ramanathan, R. Data envelopment analysis for weight derivation and aggregation in the analytic hierarchy process. Comput. Oper. Res. 2006, 33, 1289–1307. [Google Scholar] [CrossRef]
- Velasquez, M.; Hester, P.T. An analysis of multi-criteria decision making methods. Int. J. Oper. Res. 2013, 10, 56–66. [Google Scholar]
- Ishizaka, A.; Nemery, P. Multi-Criteria Decision Analysis: Methods and Software; Wiley: Chichester, UK, 2013. [Google Scholar]
- Saaty, T.L.; Vargas, L.G. Prediction, Projection and Forecasting; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1991; p. 251. [Google Scholar]
- Marinoni, O. Implementation of the analytical hierarchy process with VBA in ArcGIS. Comput. Geosci. 2004, 30, 637–646. [Google Scholar] [CrossRef]
- Zhang, J.; Su, Y.; Wu, J.; Liang, H. GIS based land suitability assessment for tobacco production using AHP and fuzzy set in Shandong province of China. Comput. Electron. Agric. 2015, 114, 202–211. [Google Scholar] [CrossRef]
- Bozda˘g, A.; Yavuz, F.; Günay, A.S. AHP and GIS based land suitability analysis for Cihanbeyli (Turkey) County. Environ. Earth Sci. 2016, 75, 1–15. [Google Scholar]
- Yager, R.R. On ordered weighted averaging aggregation operators in multi-criteria decision making. IEEE Trans. Syst. Man Cybern. 1988, 18, 183–190. [Google Scholar] [CrossRef]
- Wanderer, T.; Herle, S. Creating a spatial multi-criteria decision support system for energy related integrated environmental impact assessment. Environ. Impact Assess. Rev. 2015, 52, 2–8. [Google Scholar] [CrossRef]
- Shen, J.; Lu, H.; Zhang, Y.; Song, X.; He, L. Vulnerability assessment of urban ecosystems driven by water resources, human health and atmospheric environment. J. Hydrol. 2016, 536, 457–470. [Google Scholar] [CrossRef]
- Malczewski, J.; Chapman, T.; Flegel, C.; Walters, D.; Shrubsole, D.; Healy, M.A. GIS-multi-criteria evaluation with ordered weighted averaging (OWA): A case study of developing watershed management strategies. Environ. Plan. 2003, A 35, 1769–1784. [Google Scholar] [CrossRef]
- Makropoulos, C.; Butler, D. Spatial ordered weighted averaging: Incorporating spatially variable attitude towards risk in spatial multi- criteria decision-making. Environ. Model. Softw. 2005, 21, 69–84. [Google Scholar] [CrossRef]
- Aydin, N.Y.; Kentel, E.; Duzgun, S. GIS-based environmental assessment of wind energy systems for spatial planning: A case study from Western Turkey. Renew. Sustain. Energy Rev. 2010, 14, 364–373. [Google Scholar] [CrossRef]
- Nadi, S.; Delavar, M.R. Multi-criteria, personalized route planning using quantifier-guided ordered weighted averaging operators. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 322–335. [Google Scholar] [CrossRef]
- Ferretti, V.; Pomarico, S. Ecological land suitability analysis through spatial indicators: An application of the Analytic Network Process technique and Ordered Weighted Average approach. Ecol. Indic. 2013, 34, 507–519. [Google Scholar] [CrossRef]
- Rahman, M.A.; Rusteberg, B.; Uddin, M.S.; Lutz, A.; Saada, M.A.; Sauter, M. An integrated study of spatial multi-criteria analysis and mathematical modelling for managed aquifer recharge site suitability mapping and site ranking at Northern Gaza coastal aquifer. J. Environ. Manag. 2013, 124, 25–39. [Google Scholar] [CrossRef] [PubMed]
- Mokarram, M.; Hojati, M. Using ordered weight averaging (OWA) aggregation for multi-criteria soil fertility evaluation by GIS (case study: Southeast Iran). Comput. Electron. Agric. 2017, 132, 1–13. [Google Scholar] [CrossRef]
- Yager, R.R. Quantifier guided aggregation using OWA operators. Int. J. Intell. Syst. 1996, 11, 49–73. [Google Scholar] [CrossRef]
- Eastman, J.R. IDRISI for Windows, Version 2.0: Tutorial Exercises Graduate School of Geography; Clark University: Worcester, MA, USA, 2001. [Google Scholar]
- Malczewski, J.; Rinner, C. Exploring multi-criteria decision strategies in GIS with linguistic quantifiers: A case study of residential quality evaluation. J. Geogr. Syst. 2005, 7, 249–256. [Google Scholar] [CrossRef]
- Abudeif, A.M.; Abdel Moneim, A.A.; Farrag, A.F. Multicriteria decision analysis based on analytic hierarchy process in GIS environment for siting nuclear power plant in Egypt. Ann. Nucl. Energy 2015, 75, 682–692. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytical Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Boroushaki, S.; Malczewski, J. Implementing an extension of the analytical hierarchy process using ordered weighted averaging operators with fuzzy quantifiers in ArcGIS. Comput. Geosci. 2008, 34, 399–410. [Google Scholar] [CrossRef]
- Tiwari, D.N.; Loof, R.; Paudyal, G.N. Environmental-economic decision-making in lowland irrigated agriculture using multi-criteria analysis techniques. Agric. Syst. 1999, 60, 99–112. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Jankowski, P.; Blaschke, T. A GIS based spatially-explicit sensitivity and uncertainty analysis approach for multi-criteria decision analysis. Comput. Geosci. 2014, 64, 81–95. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xue, R.; Wang, C.; Liu, M.L.; Zhang, D.; Li, K.; Li, N. A new method for soil health assessment based on Analytic Hierarchy Process and meta-analysis. Sci. Total Environ. 2019, 650, 2771–2777. [Google Scholar] [CrossRef] [PubMed]
- Mandal, B.; Mandal, S. Analytical hierarchy process (AHP) based landslide susceptibility mapping of Lish river basin of eastern Darjeeling Himalaya, India. Adv. Space Res. 2018, 62, 3114–3132. [Google Scholar] [CrossRef]
- Kundu, S.; Khare, D.; Mondal, A. Landuse change impact on sub-watersheds prioritization by analytical hierarchy process (AHP). Ecol. Inform. 2017, 42, 100–113. [Google Scholar] [CrossRef]
- Liang, R.; Song, S.; Shi, Y.; Shi, Y.; Lu, Y.; Zheng, X.; Xu, X.; Wang, Y.; Han, X. Comprehensive assessment of regional selenium resources in soils based on the analytic hierarchy process: Assessment system construction and case demonstration. Sci. Total Environ. 2017, 605–606, 618–625. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Li, J.; Sui, H.; He, L.; Cao, X.; Li, Y. Evaluation and determination of soil remediation schemes using a modified AHP model and its application in a contaminated coking plant. J. Hazard. Mater. 2018, 353, 300–311. [Google Scholar] [CrossRef] [PubMed]
- Saaty, T.L. How to make a decision: The analytic hierarchy process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Sumathi, V.R.; Natesan, U.; Sarkar, C. GIS-based approach for optimized siting of municipal solid waste landfill. Waste Manag. 2008, 28, 2146–2160. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Yu, Y.; Khan, S. Spatial sensitivity analysis of multi-criteria weights in GIS-based land suitability evaluation. Environ. Model. Softw. 2010, 25, 1582–1591. [Google Scholar] [CrossRef]
- Statistical Center of Iran, Archives Bureau. 2018. Available online: https://www.amar.org.ir/ (accessed on 9 February 2019).
- Ramsar Agriculture Organization, Census Bureau. 2016. Available online: http://jkmaz.ir/ramsar (accessed on 9 February 2019).
- Ramsar Meteorological Administration, Archives Bureau. 2018. Available online: https://www.irimo.ir/far/wd/701 (accessed on 9 February 2019).
- Coltro, L.; Mourad, A.L. Assessing the environmental profile of orange production in Brazil. Int. J. Life Cycle Assess. 2009, 14, 656–664. [Google Scholar] [CrossRef]
- García-Tejero, I.; Romero-Vicente, R.; Jiménez-Bocanegra, J.A.; Martínez-García, G.; Durán-Zuazo, V.H.; Muriel-Fernández, J.L. Response of citrus trees to deficit irrigation during different phenological periods in relation to yield, fruit quality, and water productivity. Agric. Water Manag. 2010, 97, 689–699. [Google Scholar] [CrossRef]
- Wu, W.; Liu, H.; Dai, H.; Li, W.; Sun, P. The management and planning of citrus orchards at a regional scale with GIS. Precis. Agric. 2011, 12, 44–54. [Google Scholar] [CrossRef]
- Hatfield, J.L.; Boote, K.J.; Kimball, B.A.; Ziska, L.H.; Izaurralde, R.C.; Ort, D.; Thomson, A.M.; Wolfe, D. Climate Impacts on Agriculture: Implications for Crop Production. Agron. J. 2011, 103, 351–370. [Google Scholar] [CrossRef]
- Milkha, M.S.; Garg, A.K.; Manchanda, J.S.; Dercon, G.; Nguyen, M.N. Biological nitrogen fixation by soybean and fate of applied 15N-fertilizer in succeeding wheat under conventional tillage and conservation agriculture practices. Nutr. Cycl. Agroecosyst. 2017, 107, 79–89. [Google Scholar]
- Mathbout, S.; Lopez-Bustins, J.A.; Martin-Vide, J.; Bech, J.; Rodrigo, F.S. Spatial and temporal analysis of drought variability at several time scales in Syria during 1961–2012. Atmos. Res. 2018, 200, 153–168. [Google Scholar] [CrossRef]
- ESRI. ArcGIS 9.3; ESRI: Redlands, CA, USA; Available online: http://www.esri.com/software/arcgis (accessed on 9 September 2011).
- Saaty, T.L. The analytic hierarchy and analytic network processes for the measurement of intangible criteria and for decision-making. In Multiple Criteria Decision Analysis State of the Art Surveys; Greco, S., Ehrgott, M., Figueira, J.R., Eds.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Wang, Y.M.; Parkan, C. A minimax disparity approach for obtaining OWA operator weights. Inf. Sci. 2005, 175, 20–29. [Google Scholar] [CrossRef]
- Heumann, B.W.; Walsh, S.J.; McDaniel, P.M. Assessing the application of a geographic presence-only model for land suitability mapping. Ecol. Inform. 2011, 6, 257–269. [Google Scholar] [CrossRef] [Green Version]
- Burnside, N.; Smith, R.; Waite, S. Habitat suitability modeling for calcareous grassland restoration on the South Downs, United Kingdom. J. Environ. Manag. 2002, 65, 209–221. [Google Scholar] [CrossRef]
- Malczewski, J. GIS-Based Land-Use Suitability Analysis: A Critical Overview. Prog. Plan. 2004, 62, 3–65. [Google Scholar] [CrossRef]
- Drobne, S.; Lisec, A. Multi-attribute Decision Analysis in GIS: Weighted Linear Combination and Ordered Weighted Averaging. Informatica 2009, 33, 459–474. [Google Scholar]
- Romano, G.; Dal Sasso, P.; Trisorio Liuzzi, G.; Gentile, F. Multi-criteria decision analysis for land suitability mapping in a rural area of Southern Italy. Land Use Policy 2015, 45, 131–143. [Google Scholar] [CrossRef]
- Jiang, H.; Eastman, J.R. Application of fuzzy measures in multi-criteria evaluation in GIS. Int. J. Geogr. Inf. Sci. 2000, 14, 173–184. [Google Scholar] [CrossRef] [Green Version]
- Sadiq, R.; Tesfamariam, S. Environmental decision-making under uncertainty using intuitionistic fuzzy analytic hierarchy process (IF-AHP). Stoch. Environ. Res. Risk Assess. 2009, 23, 75–91. [Google Scholar] [CrossRef]
- Okur, A.; Nasibov, E.; Kiliç, M.; Yavuz, M. Using OWA aggregation technique in QFD: A case study in education in a textile engineering department. Qual. Quant. 2009, 43, 999–1009. [Google Scholar] [CrossRef]





| Quantifier | Order Weights | GIS Combination Procedure | ORness | Trade-Off | |
|---|---|---|---|---|---|
| 0 | At least one | Vi1 = 1; Vik = 0, (1 < k ≤ n) | OWA (OR) | 1.0 | 0 |
| At least a few | a | OWA | a | a | |
| A few | a | OWA | a | a | |
| Half | Vik = 1; Vi1 = 0, (1 ≤ k ≤ n) | OWA (WLC) | 0.5 | 1 | |
| Most | a | OWA | a | a | |
| Almost all | a | OWA | a | a | |
| All | Vin = 1; Vik = 0, (1 ≤ k < n) | OWA (AND) | 0 | 0 |
| Criteria | Model Application | Description |
|---|---|---|
| Elevation | Constraint mapping and suitability mapping | Elevation until 700 m could not be a limiting factor in citrus tree production [62]. Lower values denote higher importance. The elevation is the most vital environmental factor in nearly all of the models [69]. |
| Maximum temperature | Constraint mapping and suitability mapping | The temperature should not be high (over 38 °C); otherwise, evapotranspiration would be high, which will require artificial irrigation. Due to water scarcity, the lower the value, the greater the suitability of the site and the higher the preference. |
| Minimum temperature | Constraint mapping and suitability mapping | The parameter is considered the function of the degreening process, except for the extreme minimum temperature (less than 0 °C because of chilling and freeze injury), which is not suitable. Higher values denote high site suitability. |
| Slope angle | Constraint mapping and suitability mapping | Steeper slopes have negative effects on picking up fruits (more than 26°). Furthermore, runoff, nutrient losses, and soil fertility are proportional to the slope angle. Flat areas enhance high performance, which is suitable for citrus orchards. Lower values mean higher priority. |
| Rainfall | Constraint mapping and suitability mapping | Rainfall less than 400 mm in the hottest month (from June to August) is not guaranteed. The places that received more than 800 mm per year are considered as potential sites. The higher the value, the higher the priority (except in flowering stages and runoff disaster). |
| Comparative Importance | Suitability Rating | Numerical Expression |
|---|---|---|
| Equal importance | Not suitable | 1 |
| Moderate importance of one over another | Marginally suitable | 3 |
| Essential or strong importance | Moderately suitable | 5 |
| Very strong importance | Highly suitable | 7 |
| Extreme importance | Optimally suitable | 9 |
| Intermediate values | 2,4,6,8 | |
| Suitability Criterion | Elevation | Maximum Temperature | Minimum Temperature | Slope Angle | Rainfall |
|---|---|---|---|---|---|
| Elevation | 1 | 5 | 3 | 7 | 5 |
| Maximum temperature | 1/5 | 1 | 1/3 | 3 | 1/2 |
| Minimum temperature | 1/3 | 3 | 1 | 5 | 3 |
| Slope angle | 1/7 | 1/3 | 1/5 | 1 | 1/5 |
| Rainfall | 1/5 | 2 | 1/3 | 5 | 1 |
| Σ | 1.87 | 11.3 | 4.86 | 21 | 9.7 |
| Suitability Criterion | Elevation | Maximum Temperature | Minimum Temperature | Slope Angle | Rainfall | Weights |
|---|---|---|---|---|---|---|
| Elevation | 0.53 | 0.44 | 0.61 | 0.30 | 0.43 | 0.462 |
| Maximum temperature | 0.10 | 0.08 | 0.06 | 0.14 | 0.15 | 0.106 |
| Minimum temperature | 0.17 | 0.26 | 0.20 | 0.25 | 0.30 | 0.236 |
| Slope angle | 0.07 | 0.02 | 0.04 | 0.05 | 0.02 | 0.042 |
| Rainfall | 0.13 | 0.17 | 0.06 | 0.26 | 0.10 | 0.144 |
| Σ | 1 | 1 | 1 | 1 | 1 |
| (n) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| (RI) | 0 | 0 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 | 1.49 | 1.51 | 1.48 | 1.56 | 1.57 | 1.59 |
| Different Suitability Classes | Area (Hectare) | Percent |
|---|---|---|
| Unsuitable | 4956.98 | 3.2 |
| Moderate | 66,359.46 | 90.1 |
| Suitable | 2348.01 | 6.7 |
| Total | 71,316.44 | 100 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zabihi, H.; Alizadeh, M.; Kibet Langat, P.; Karami, M.; Shahabi, H.; Ahmad, A.; Nor Said, M.; Lee, S. GIS Multi-Criteria Analysis by Ordered Weighted Averaging (OWA): Toward an Integrated Citrus Management Strategy. Sustainability 2019, 11, 1009. https://doi.org/10.3390/su11041009
Zabihi H, Alizadeh M, Kibet Langat P, Karami M, Shahabi H, Ahmad A, Nor Said M, Lee S. GIS Multi-Criteria Analysis by Ordered Weighted Averaging (OWA): Toward an Integrated Citrus Management Strategy. Sustainability. 2019; 11(4):1009. https://doi.org/10.3390/su11041009
Chicago/Turabian StyleZabihi, Hasan, Mohsen Alizadeh, Philip Kibet Langat, Mohammadreza Karami, Himan Shahabi, Anuar Ahmad, Mohamad Nor Said, and Saro Lee. 2019. "GIS Multi-Criteria Analysis by Ordered Weighted Averaging (OWA): Toward an Integrated Citrus Management Strategy" Sustainability 11, no. 4: 1009. https://doi.org/10.3390/su11041009
APA StyleZabihi, H., Alizadeh, M., Kibet Langat, P., Karami, M., Shahabi, H., Ahmad, A., Nor Said, M., & Lee, S. (2019). GIS Multi-Criteria Analysis by Ordered Weighted Averaging (OWA): Toward an Integrated Citrus Management Strategy. Sustainability, 11(4), 1009. https://doi.org/10.3390/su11041009








