An Improved Power Management Strategy for MAS-Based Distributed Control of DC Microgrid under Communication Network Problems
Abstract
:1. Introduction
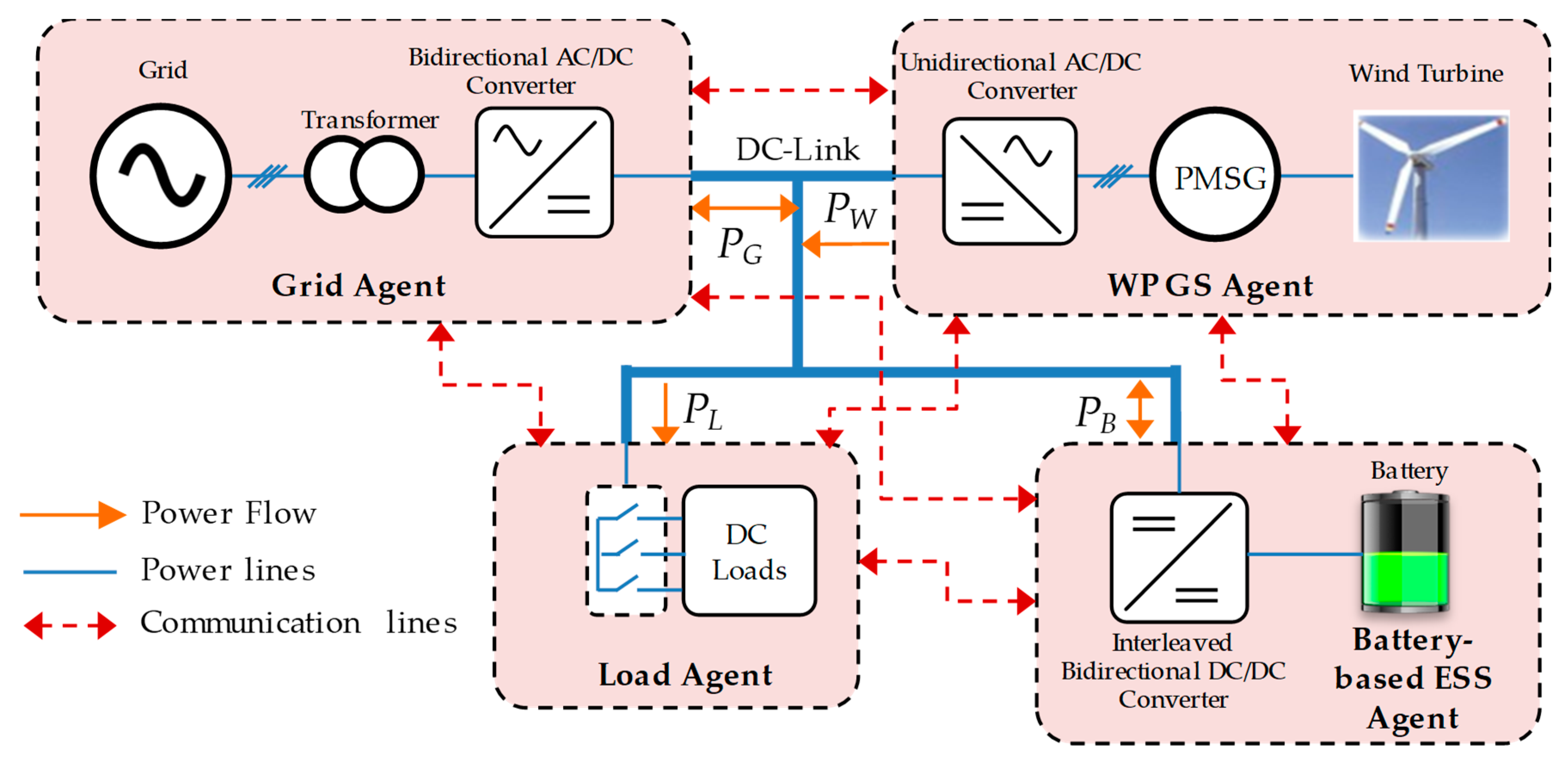
2. System Configuration of DCMG with MAS-based Distributed Control
2.1. MAS-based Distributed Control of DCMG
2.2. System Communication Topology
3. Power Management and Control Strategy of Local Agents
3.1. Control Strategy of Grid Agent
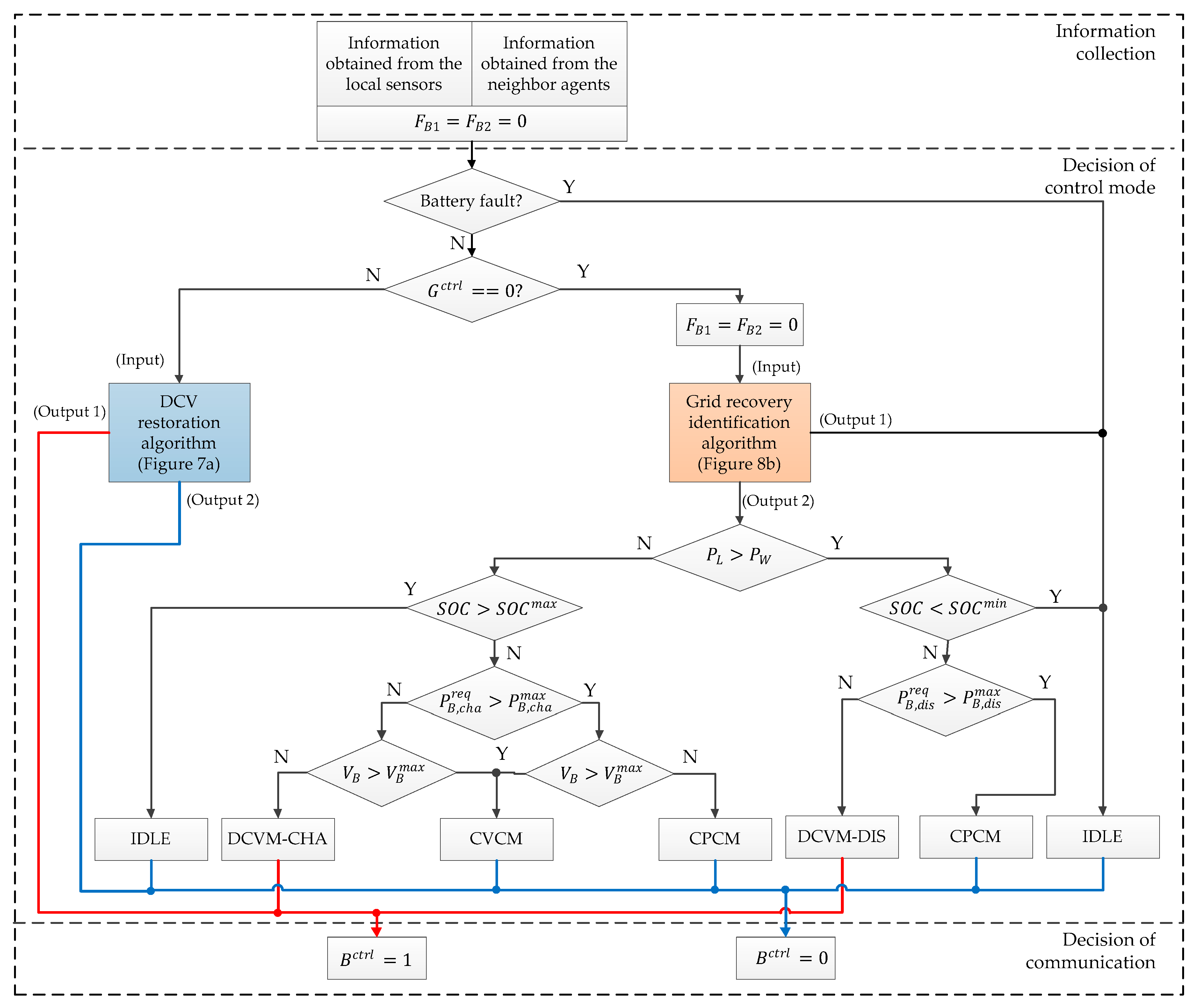
3.2. Control Strategy of Battery Agent
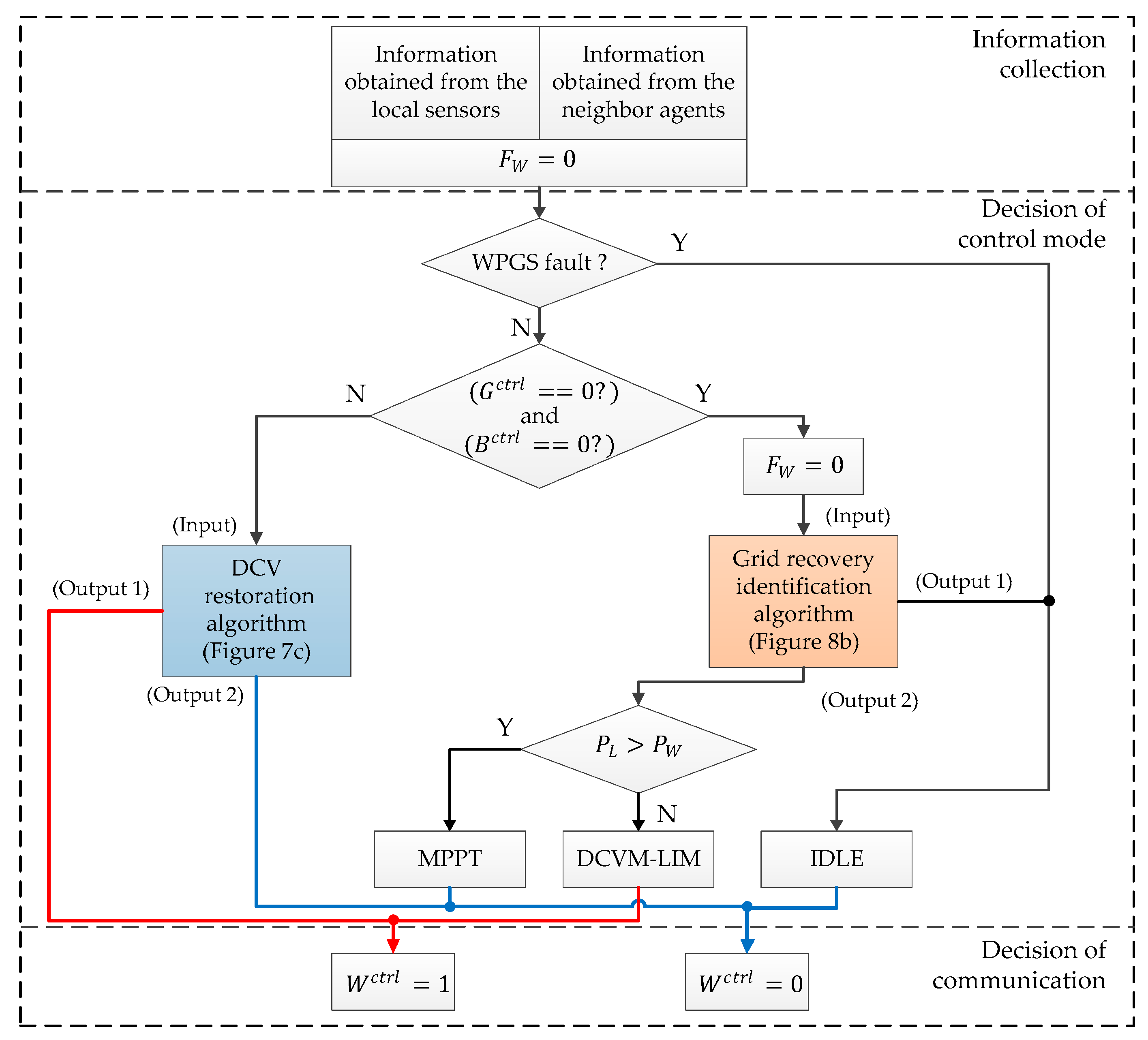
3.3. Control Strategy of WPGS Agent
3.4. Control Strategy of Load Agent
4. Proposed Control Strategies under Communication Network Problems
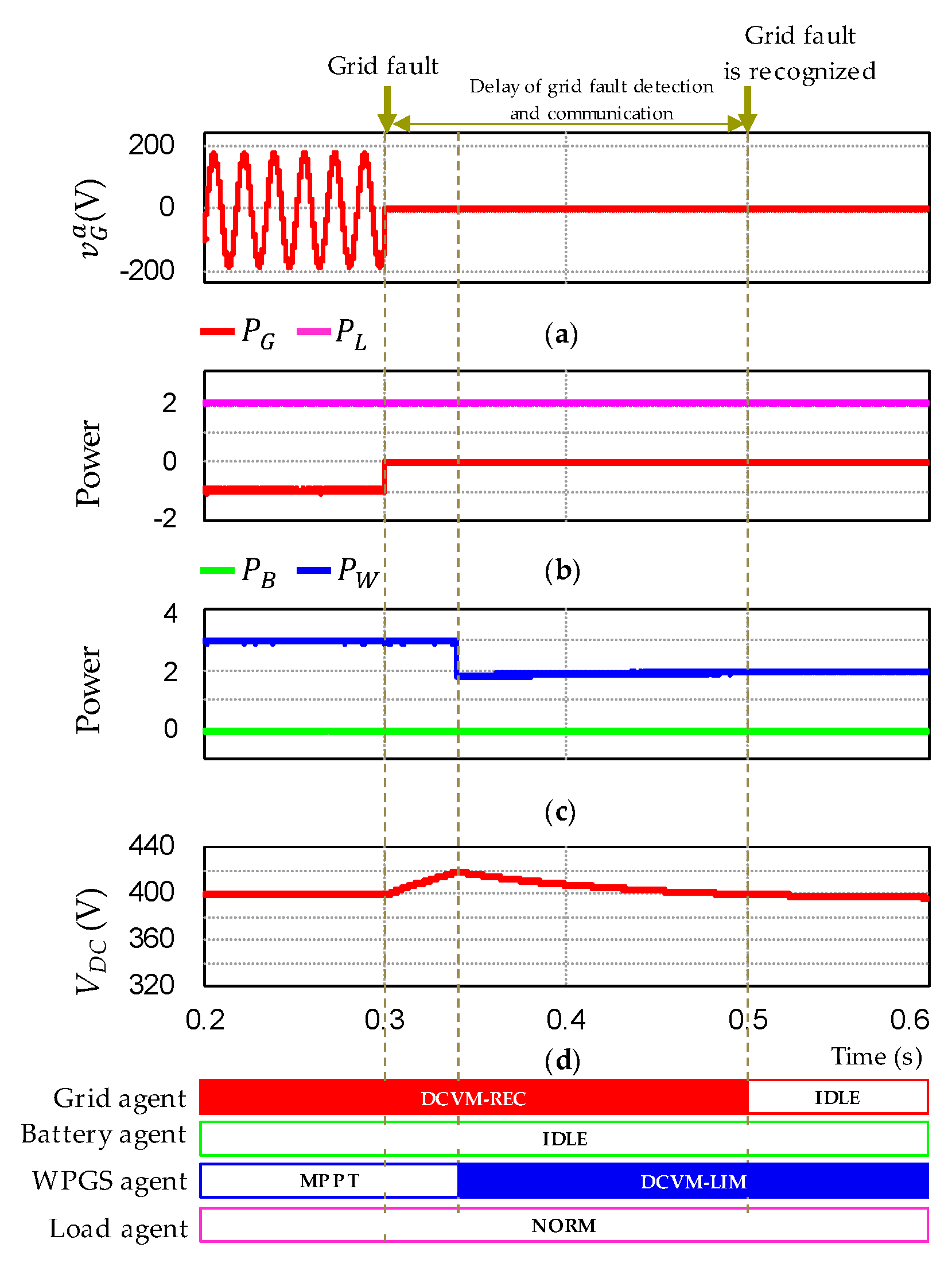
4.1. Control Strategy for Grid Fault Case
4.2. Control Strategy for Grid Recovery Case
5. Simulation Results
5.1. Grid-connected Case
5.2. Islanded Case
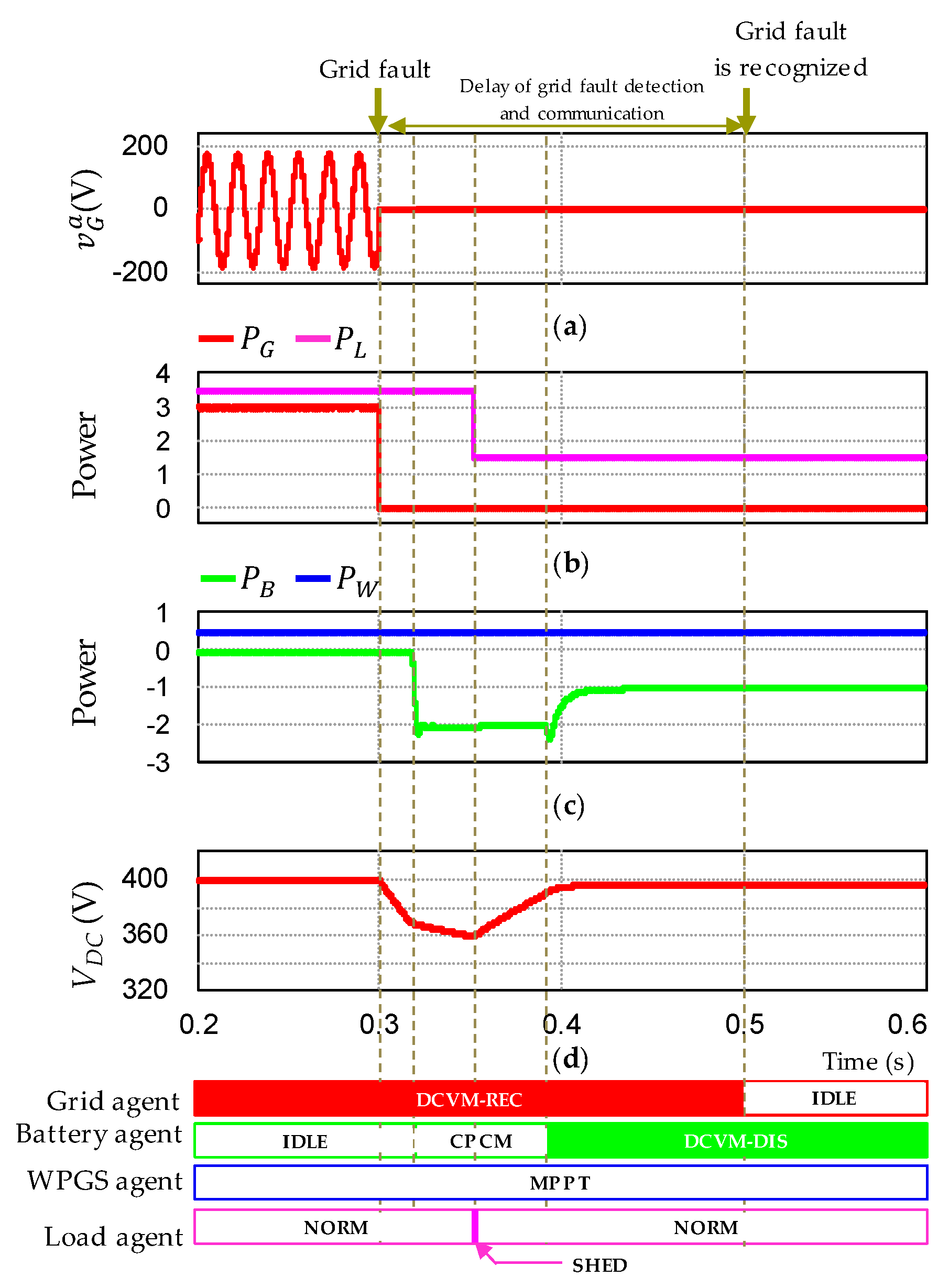
5.3. Case of Communication Problems
6. Experimental Results
6.1. Grid-connected Case
6.2. Islanded Case
6.3. Case of Communication Problems
7. Conclusions
- i)
- A MAS-based distributed control technique has been developed for PMS of DCMG including four agents of the grid, WPGS, battery, and load. In the PMS, by investigating the information obtained from both the local measurements and the neighboring agents via communication lines, all the agents determine not only optimal operating modes for local controllers but also the proper information to be transmitted in order to guarantee the system power balance under various conditions. By using this control scheme, the drawbacks of the existing centralized and decentralized controls are eliminated. In particular, the control mode of the agents can be determined locally without CC, which contributes to avoid the common single point of failure as in the centralized control. Since each agent is controlled by its own local controller, the computational burden is shared by local controllers. In addition, the problem related to communication failure can be avoided by using the proposed reliability improvement algorithm. As compared to the decentralized control, the problems related to the lack of exchanged information can be solved by means of communication network.
- ii)
- In order to deal with the system power imbalance caused by the delay in grid fault detection and communication, the DCV restoration algorithm is proposed in this paper. By using this scheme, as soon as abnormal level of the DCV is detected, the DCV can be restored stably to the nominal value irrespective of unbound time delay even under the communication network problems, which contributes to prevent the system malfunction and collapse of DCMG.
- iii)
- To recognize the grid recovery reliably even under communication failure, the grid recovery identification algorithm is introduced in this study. By detecting the frequency of the current pattern on the DC-link, the battery and WPGS agents can effectively identify the grid recovery even in the presence of communication failure. Therefore, the conflict in the DCV control by different voltage control sources can be avoided.
Author Contributions
Funding
Conflicts of Interest
Abbreviation
| AC | Alternating current |
| ACMG | AC microgrid |
| CC | Central controller |
| CPCM | Constant power control mode |
| CVCM | Constant voltage control mode |
| DC | Direct current |
| DCMG | DC microgrid |
| DCV | DC-link voltage |
| DCVM | DC-link voltage control mode |
| DCVM-CHA | DC-link voltage control mode by battery charging |
| DCVM-DIS | DC-link voltage control mode by battery discharging |
| DCVM-INV | DC-link voltage control mode by inverter mode of grid agent |
| DCVM-LIM | DC-link voltage control mode by limiting output power of WPGS |
| DCVM-REC | DC-link voltage control mode by converter mode of grid agent |
| DG | Distributed generation |
| ESS | Energy storage system |
| GO | Grid operator |
| MAS | Multiagent system |
| MPPT | Maximum power point tracking |
| PMS | Power management strategy |
| PMSG | Permanent magnet synchronous generator |
| RECO | Load reconnection |
| RES | Renewable energy source |
| SCCM | Special current control mode |
| SHED | Load shedding |
| SOC | State of charge |
| WPGS | Wind power generation system |
| NORM | Normal load state |
| C | Battery rated capacity |
| cos | Power factor of induction machine |
| DC-link capacitance | |
| , | Flags in control strategy of battery agent |
| Frequency of special current pattern for grid identification algorithm | |
| Detected frequency for grid identification algorithm | |
| , , | Flags in control strategy of grid agent |
| Flag in control strategy of WPGS agent | |
| a-phase grid current | |
| Battery current | |
| Battery current with special current pattern | |
| Output of high pass filter | |
| , , | Indications of DCV control ability by grid, battery, and WPGS agents |
| State of grid | |
| Voltage constant of PMSG | |
| Rated speed of wind turbine generator | |
| Rated speed of induction machine | |
| Output power of battery agent | |
| , | Maximum and required battery charging power |
| , | Maximum and required battery discharging power |
| Output power of grid agent | |
| , | Maximum and required power injected to the grid from DCMG |
| , | Maximum and required power supplied from the grid to DCMG |
| Rated power of PMSG | |
| Rated power of induction machine | |
| Total load power, and power of load 1, load 2, load 3 | |
| Output power of WPGS agent | |
| Supply-demand power relationship | |
| , | Maximum and minimum battery state of charge |
| Time delay for load shedding | |
| a-phase grid voltage | |
| , | Battery voltage and maximum battery voltage |
| , | DCV, nominal DCV |
| DCV thresholds for grid fault case | |
| DCV thresholds for grid recovery case | |
| Rated voltage of induction machine |
References
- Hatziargyriou, N.; Asano, H.; Iravani, R.; Marnay, C. Microgrids. IEEE Power Energy Mag. 2007, 5, 78–94. [Google Scholar] [CrossRef]
- Farrokhabadi, M.; Koenig, S.; Canizares, C.A.; Bhattacharya, K.; Leibfried, T. Battery Energy Storage System Models for Microgrid Stability Analysis and Dynamic Simulation. IEEE Trans. Power Syst. 2018, 33, 2301–2312. [Google Scholar] [CrossRef]
- Mohammadi, F.; Nazri, G.-A.; Saif, M. A Bidirectional Power Charging Control Strategy for Plug-in Hybrid Electric Vehicles. Sustainability 2019, 11, 4317. [Google Scholar] [CrossRef] [Green Version]
- Sanjeev, P.; Padhy, N.P.; Agarwal, P. Peak Energy Management Using Renewable Integrated DC Microgrid. IEEE Trans. Smart Grid 2018, 9, 4906–4917. [Google Scholar] [CrossRef]
- Mohammadi, F.; Nazri, G.-A.; Saif, M. A New Topology of a Fast Proactive Hybrid DC Circuit Breaker for MT-HVDC Grids. Sustainability 2019, 11, 4493. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, T.V.; Kim, K.-H. Power Flow Control Strategy and Reliable DC-Link Voltage Restoration for DC Microgrid under Grid Fault Conditions. Sustainability 2019, 11, 3781. [Google Scholar] [CrossRef] [Green Version]
- El-Hendawi, M.; Gabbar, H.A.; El-Saady, G.; Ibrahim, E.-N.A. Control and EMS of a Grid-Connected Microgrid with Economical Analysis. Energies 2018, 11, 129. [Google Scholar] [CrossRef] [Green Version]
- Xu, L.; Chen, D. Control and Operation of a DC Microgrid with Variable Generation and Energy Storage. IEEE Trans. Power Deliv. 2011, 26, 2513–2522. [Google Scholar] [CrossRef]
- Dragičević, T.; Lu, X.; Vasquez, J.C.; Guerrero, J.M. DC Microgrids-Part I: A Review of Control Strategies and Stabilization Techniques. IEEE Trans. Power Electron. 2016, 31, 4876–4891. [Google Scholar]
- Dehkordi, N.M.; Sadati, N.; Hamzeh, M. Fully Distributed Cooperative Secondary Frequency and Voltage Control of Islanded Microgrids. IEEE Trans. Energy Convers. 2017, 32, 675–685. [Google Scholar] [CrossRef]
- Gao, L.; Liu, Y.; Ren, H.; Guerrero, J.M. A DC Microgrid Coordinated Control Strategy Based on Integrator Current-Sharing. Energies 2017, 10, 1116. [Google Scholar] [CrossRef] [Green Version]
- Kumara, J.; Agarwalb, A.; Agarwala, V. A Review on Overall Control of DC Microgrids. J. Energy Storage 2019, 21, 113–138. [Google Scholar] [CrossRef]
- Yazdanian, M.; Mehrizi-Sani, A. Distributed Control Techniques in Microgrids. IEEE Trans. Smart Grid 2014, 5, 2901–2909. [Google Scholar] [CrossRef]
- Logenthiran, T.; Naayagi, R.T.; Woo, W.L.; Phan, V.-T.; Abidi, K. Intelligent Control System for Microgrids Using Multiagent System. IEEE J. Emerg. Sel. Topics Power Electron. 2015, 3, 1036–1045. [Google Scholar] [CrossRef]
- Qi, X.; Luo, Y.H.; Zhang, Y.; Zhou, G.; Wei, Z. Novel Distributed Optimal Control of Battery Energy Storage System in an Islanded Microgrid with Fast Frequency Recovery. Energies 2018, 11, 1955. [Google Scholar] [CrossRef] [Green Version]
- Dehkordi, N.M.; Sadati, N.; Hamzeh, M. Distributed Robust Finite-Time Secondary Voltage and Frequency Control of Islanded Microgrids. IEEE Trans. Power Syst. 2017, 32, 3648–3659. [Google Scholar] [CrossRef]
- Dou, C.; Zhang, Z.; Yue, D.; Zheng, Y. MAS-Based Hierarchical Distributed Coordinate Control Strategy of Virtual Power Source Voltage in Low-Voltage Microgrid. IEEE Access 2017, 5, 11381–11390. [Google Scholar] [CrossRef]
- Lai, J.; Lu, X.; Li, X.; Tang, R.-L. Distributed Multiagent-Oriented Average Control for Voltage Restoration and Reactive Power Sharing of Autonomous Microgrids. IEEE Access 2018, 6, 25551–25561. [Google Scholar] [CrossRef]
- Morstyn, T.; Hredzak, B.; Agelidis, V.G. Communication Delay Robustness for Multi-Agent State of Charge Balancing Between Distributed AC Microgrid Storage Systems. In Proceedings of the 2015 IEEE Conference on Control Applications (CCA), Sydney, Australia, 21–23 September 2015; pp. 181–186. [Google Scholar]
- Chen, F.; Chen, M.; Li, Q.; Meng, K.; Guerrero, J.M.; Abbott, D. Multiagent-Based Reactive Power Sharing and Control Model for Islanded Microgrids. IEEE Trans. Sustain. Energy 2016, 7, 1232–1244. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Chen, F.; Chen, M.; Guerrero, J.M.; Abbott, D. Agent-Based Decentralized Control Method for Islanded Microgrids. IEEE Trans. Smart Grid 2016, 7, 637–649. [Google Scholar] [CrossRef] [Green Version]
- Dou, C.; Yue, D.; Zhang, Z.; Ma, K. MAS-Based Distributed Cooperative Control for DC Microgrid Through Switching Topology Communication Network with Time-Varying Delays. IEEE Syst. J. 2019, 13, 615–624. [Google Scholar] [CrossRef]
- Lai, J.; Zhou, H.; Hu, W.; Lu, X.; Zhong, L. Synchronization of Hybrid Microgrids with Communication Latency. Math. Probl. Eng. 2015, 2015, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Dou, C.; Yue, D.; Zhang, Z.; Guerrero, J.M. Hierarchical Delay-Dependent Distributed Coordinated Control for DC Ring-Bus Microgrids. IEEE Access 2017, 5, 10130–10140. [Google Scholar] [CrossRef]
- Dou, C.; Yue, D.; Guerrero, J.M.; Xie, X.; Hu, S. Multiagent System-Based Distributed Coordinated Control for Radial DC Microgrid Considering Transmission Time Delays. IEEE Trans. Smart Grid 2016, 8, 2370–2381. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Hredzak, B. Distributed Finite-Time Multiagent Control for DC Microgrids with Time Delays. IEEE Trans. Smart Grid 2018, 10, 2692–2701. [Google Scholar] [CrossRef]
- Zhang, Z.; Dou, C.; Yue, D.; Zhang, B.; Li, F. Neighbor-Prediction-Based Networked Hierarchical Control in Islanded Microgrids. Int. J. Electr. Power Energy Syst. 2019, 104, 734–743. [Google Scholar] [CrossRef]
- Gaeini, N.; Amani, A.M.; Jalili, M.; Yu, X. Cooperative Secondary Frequency Control of Distributed Generation: The Role of Data Communication Network Topology. Int. J. Electr. Power Energy Syst. 2017, 92, 221–229. [Google Scholar] [CrossRef]
- IEEE. IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces, IEEE Std.1547; IEEE: New York, NY, USA, 2018. [Google Scholar]
- Tran, T.V.; Yoon, S.-J.; Kim, K.-H. An LQR-Based Controller Design for an LCL-Filtered Grid-Connected Inverter in Discrete-Time State-Space under Distorted Grid Environment. Energies 2018, 11, 2062. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Panda, S.K.; Xu, J. Development of a New Mathematical Model of Three Phase PWM Boost Rectifier Under Unbalanced Supply Voltage Operating Conditions. In Proceedings of the 2006 37th IEEE Power Electronics Specialists Conference, Jeju, Korea, 18–22 June 2006; pp. 1–7. [Google Scholar]
- Hegazy, O.; Mierlo, J.V.; Lataire, P. Control and Analysis of an Integrated Bidirectional DC/AC and DC/DC Converters for Plug-in Hybrid Electric Vehicle Applications. J. Power Electron. 2011, 11, 408–417. [Google Scholar] [CrossRef] [Green Version]

















| Communication Line | Exchange Data | Data Type | Data Information |
|---|---|---|---|
| 1 | Double | Maximum power supplied from grid to DCMG | |
| Double | Maximum power injected to grid from DCMG | ||
| Binary | 00: Grid has fault. | ||
| 11: Grid is recovered. | |||
| 01: Grid is being normal. | |||
| 2, 3, 4 | Binary | 1: Grid agent is able to control DCV. | |
| 0: Grid agent is not able to control DCV. | |||
| 5, 6 | Binary | 1: Battery agent is able to control DCV. | |
| 0: Battery agent is not able to control DCV. | |||
| 7 | Binary | 1: WPGS agent is able to control DCV. | |
| 0: WPGS agent is not able to control DCV. | |||
| 8, 9 | Binary | 1: Load power is greater than wind power (). | |
| 0: Load power is smaller than wind power (). | |||
| 10 | Double | Load power |
| Unit | Parameter | Symbol | Value | |
|---|---|---|---|---|
| Grid operator | Maximum power supplied from grid to DCMG | 2 kW | ||
| Maximum power injected to grid from DCMG | 2 kW | |||
| Grid agent | Grid voltage | 220 V | ||
| Grid frequency | 60 Hz | |||
| Frequency for SCCM | 20 Hz | |||
| Transformer | T | 380/220 V | ||
| Local controller: Digital signal processor (DSP) TMS320F28335 | - | - | ||
| WPGS agent | Induction machine | Rated power | 3 kW | |
| Rated voltage | 380 V | |||
| Rated speed | 1425 min−1 | |||
| Power factor | cos | 0.85 | ||
| Permanent magnet synchronous generator (PMSG) | Stator resistance | 0.64 Ω | ||
| dq-axis inductance | 0.82 mH | |||
| Number of pole pairs | 6 | |||
| Inertia | 0.111 kgm2 | |||
| Flux linkage | 0.18 Wb | |||
| Rated power | 3 kW | |||
| Maximum speed | 3200 rpm | |||
| Voltage constant | 147 V/Krpm | |||
| Predefined level for frequency detection in grid recovery identification algorithm | N | 11 | ||
| Local controller: DSP TMS320F28335 | - | - | ||
| Battery agent | Maximum discharging power | 2 kW | ||
| Maximum voltage | 265 V | |||
| Maximum SOC | 90 % | |||
| Minimum SOC | 10 % | |||
| Rated capacity | C | 30 Ah | ||
| Predefined level for frequency detection in grid recovery identification algorithm | N | 11 | ||
| Local controller: DSP TMS320F28335 | - | - | ||
| Load agent | Power of load 1 | 0.5 kW | ||
| Power of load 2 | 1 kW | |||
| Power of load 3 | 2 kW | |||
| Priority level: load 1 > load 2 > load 3 | - | - | ||
| Local controller: DSP TMS320F28335 | - | - | ||
| DC-link | Nominal voltage | 400 V | ||
| Maximum DCV used for grid fault | 420 V | |||
| First threshold level for DCV used for grid fault | 370 V | |||
| Second threshold level for DCV used for grid fault | 390 V | |||
| Minimum DCV used for grid fault | 360 V | |||
| Maximum DCV used for grid recover | 410 V | |||
| Minimum DCV used for grid recover | 390 V | |||
| Capacitance | 4 mF | |||
| Operation Conditions | Time (s) | |
|---|---|---|
| 1 | Load 3 is switched in. | 1 |
| 2 | Wind power gradually decreases from 0.5 kW to 0. | 1.5 |
| 3 | Wind power increases from 0 to 2 kW. | 2 |
| 4 | Wind power increases from 2 kW to 4 kW. | 2.5 |
| 5 | Load 2 and load 3 are switched out. | 3 |
| 6 | Battery fault occurs. | 3.5 |
| Operation Conditions | Time (s) | |
|---|---|---|
| 1 | Grid fault occurs. | 1 |
| 2 | Wind power decreases from 2 kW to 1 kW. | 1.5 |
| 3 | Battery SOC reaches the minimum level. | 2 |
| 4 | Wind power increases from 1 kW to 2 kW. | 2.5 |
| 5 | Load 2 is reconnected. | 3 |
| 6 | Grid is recovered. | 3.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, T.V.; Kim, K.-H. An Improved Power Management Strategy for MAS-Based Distributed Control of DC Microgrid under Communication Network Problems. Sustainability 2020, 12, 122. https://doi.org/10.3390/su12010122
Nguyen TV, Kim K-H. An Improved Power Management Strategy for MAS-Based Distributed Control of DC Microgrid under Communication Network Problems. Sustainability. 2020; 12(1):122. https://doi.org/10.3390/su12010122
Chicago/Turabian StyleNguyen, Thanh Van, and Kyeong-Hwa Kim. 2020. "An Improved Power Management Strategy for MAS-Based Distributed Control of DC Microgrid under Communication Network Problems" Sustainability 12, no. 1: 122. https://doi.org/10.3390/su12010122
APA StyleNguyen, T. V., & Kim, K.-H. (2020). An Improved Power Management Strategy for MAS-Based Distributed Control of DC Microgrid under Communication Network Problems. Sustainability, 12(1), 122. https://doi.org/10.3390/su12010122






