Optimal Placement of TCSC for Congestion Management and Power Loss Reduction Using Multi-Objective Genetic Algorithm
Abstract
1. Introduction
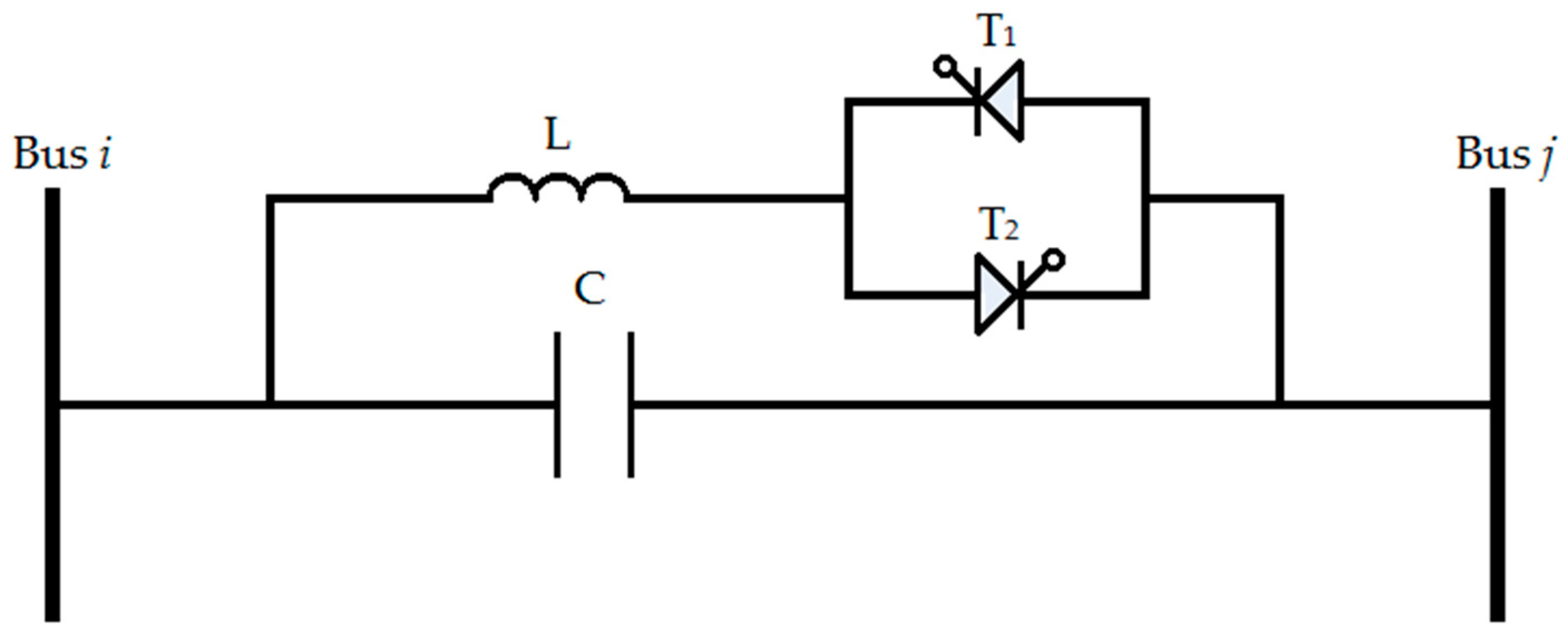
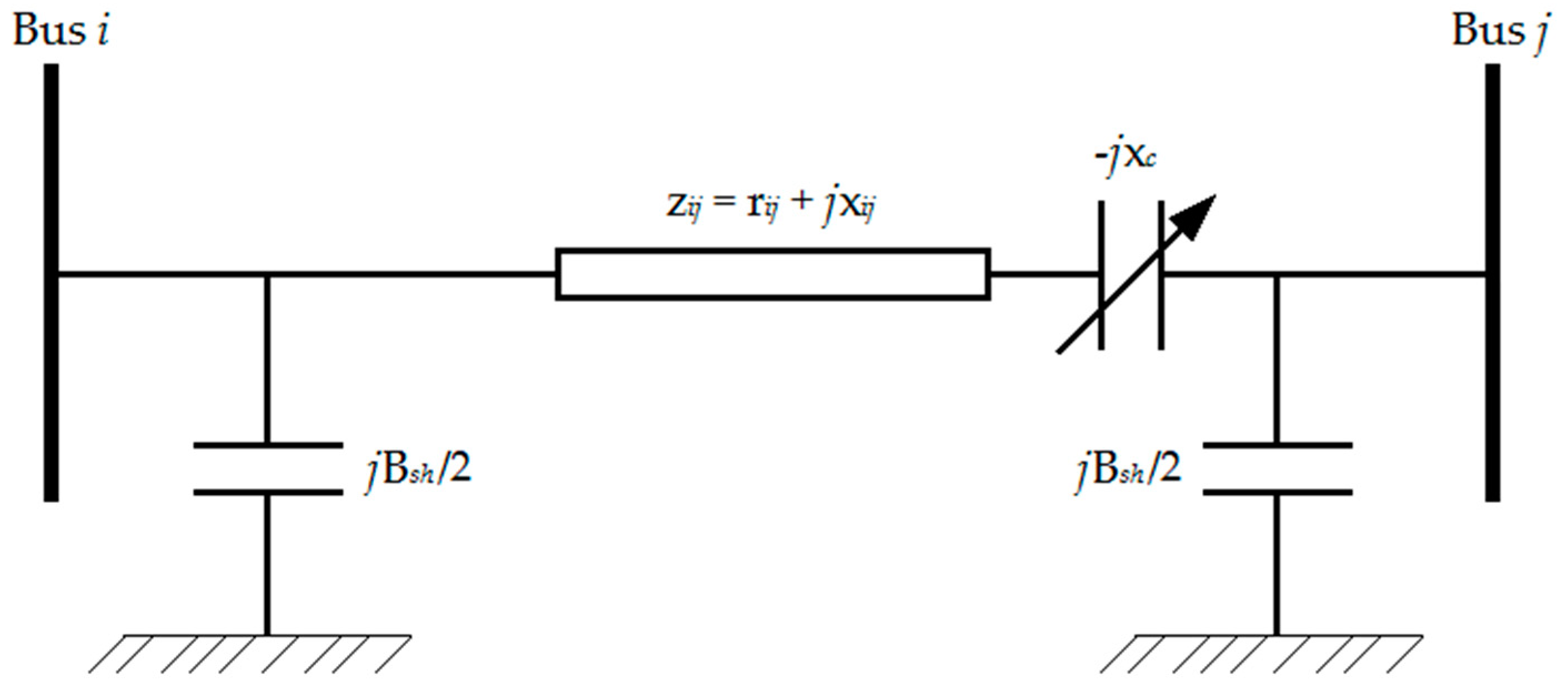
2. Structure and Model of the TCSC
3. Power Congestion Index of Transmission Lines
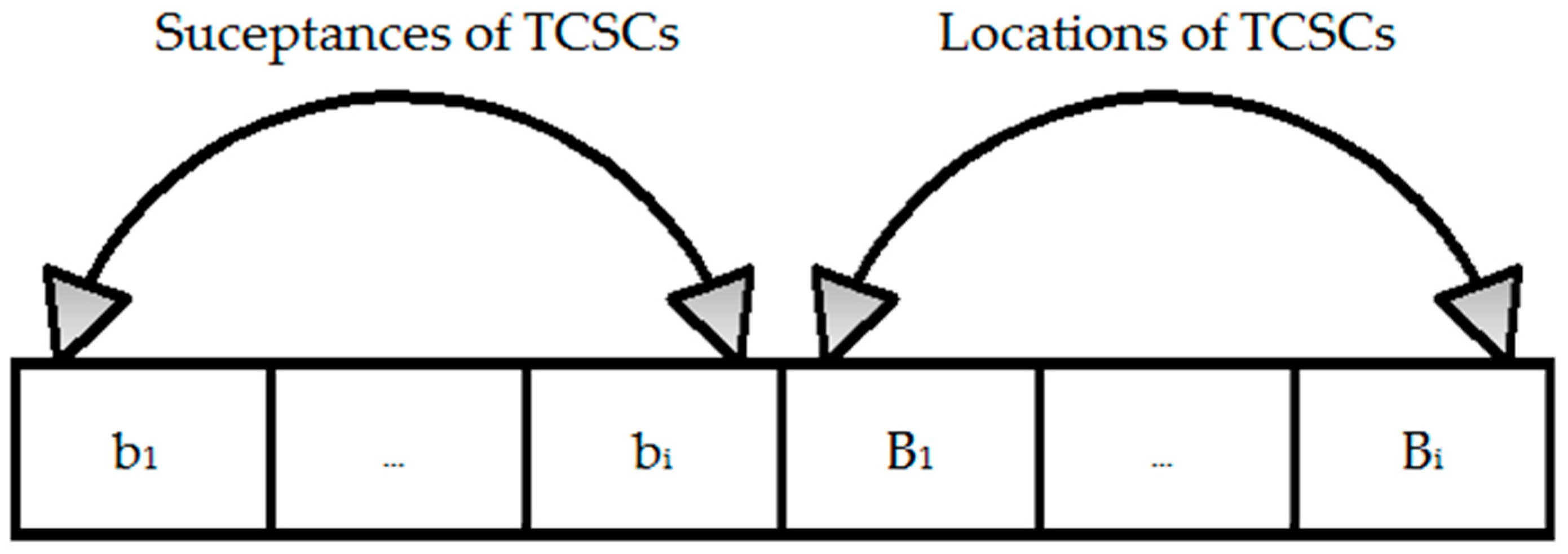
4. Proposed Multi-Objective Genetic Algorithm (MOGA)
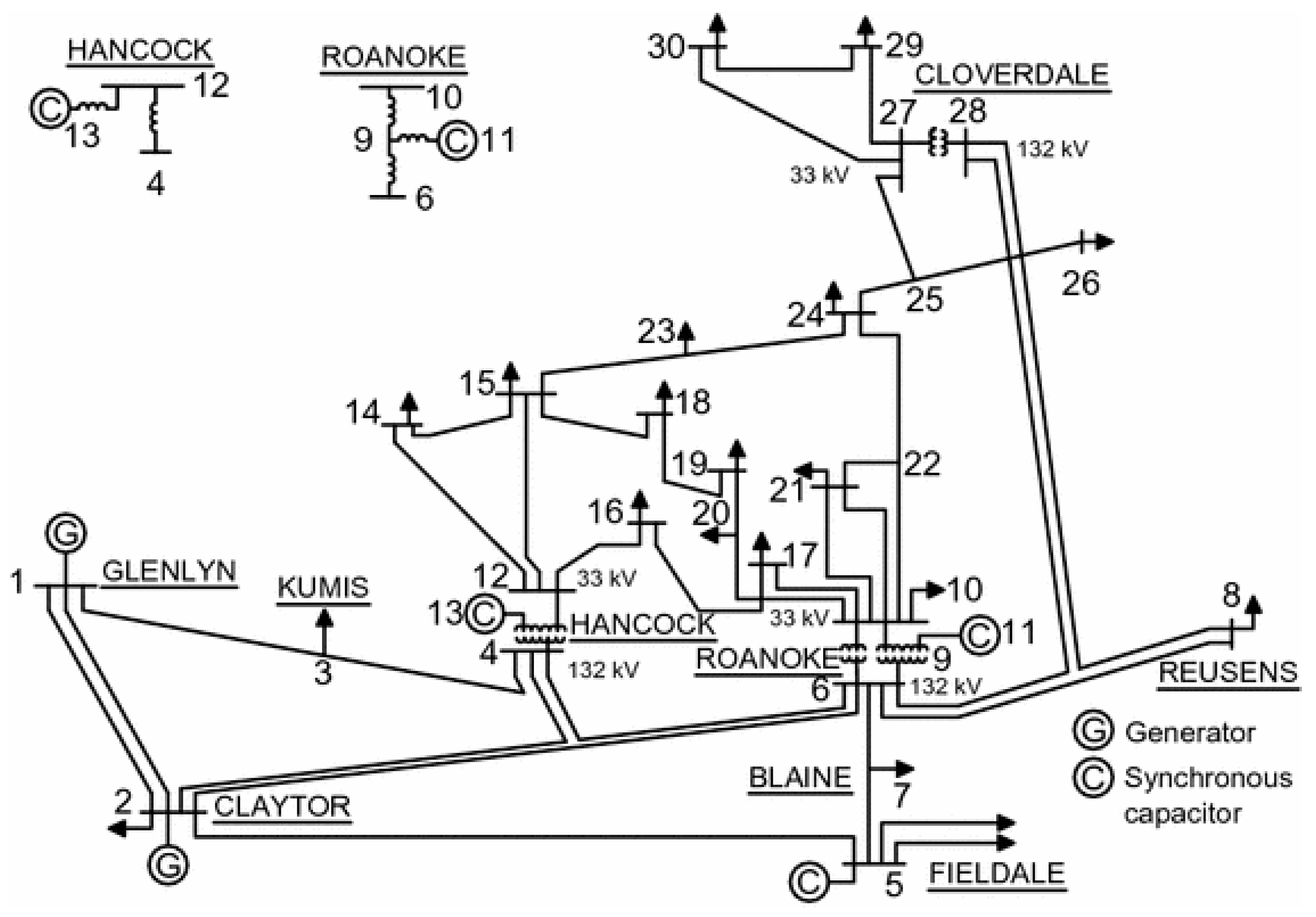
5. Simulation Results and Discussions
5.1. Simulation Results
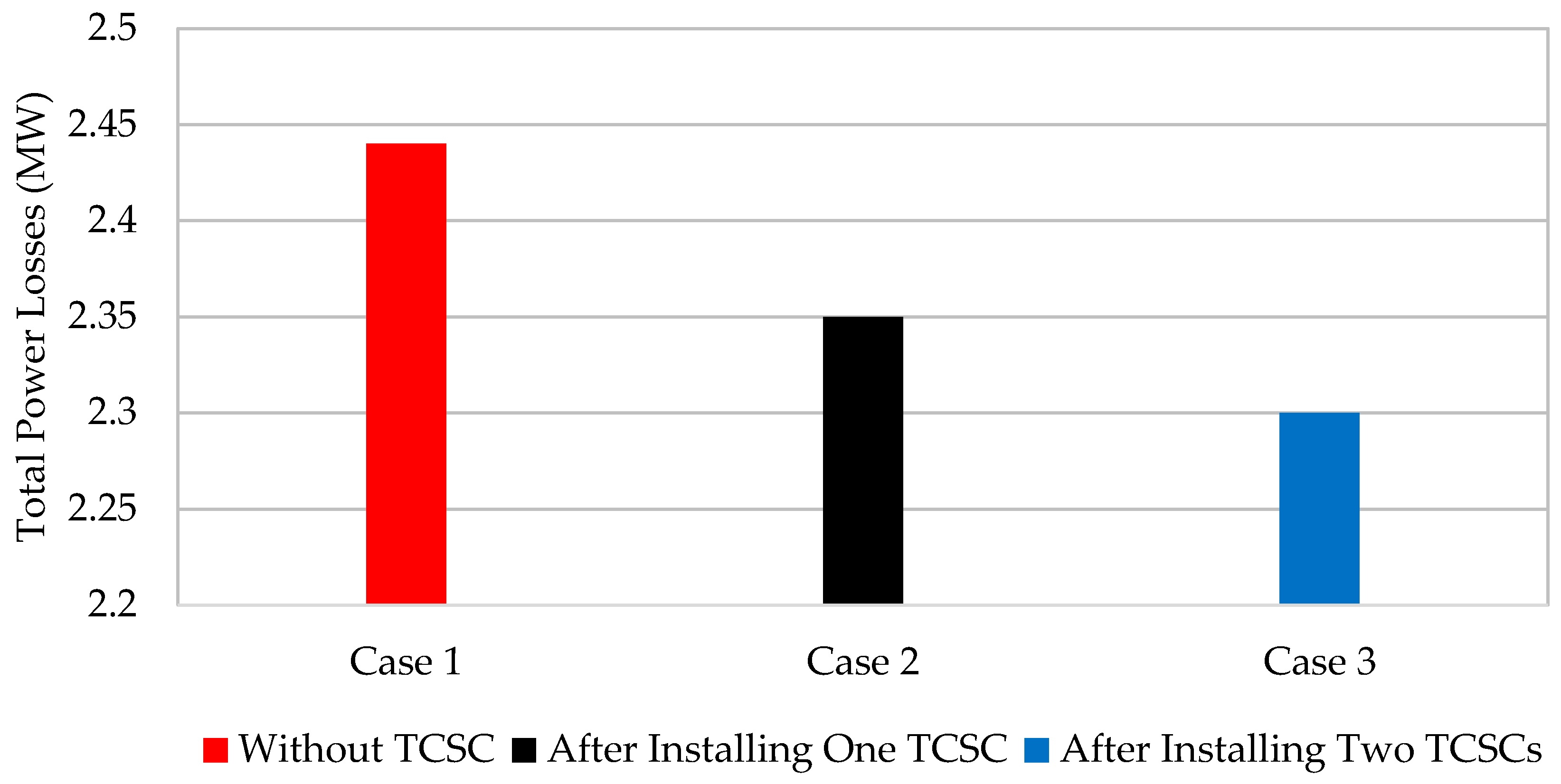
5.1.1. Installation of One TCSC
5.1.2. Installation of Two TCSCs
5.1.3. Optimizing the Congestion Index with One TCSC
5.1.4. Optimizing the Congestion Index with Two TCSCs
5.1.5. Comparison of the Impact of TCSC Installation on the Congestion Index
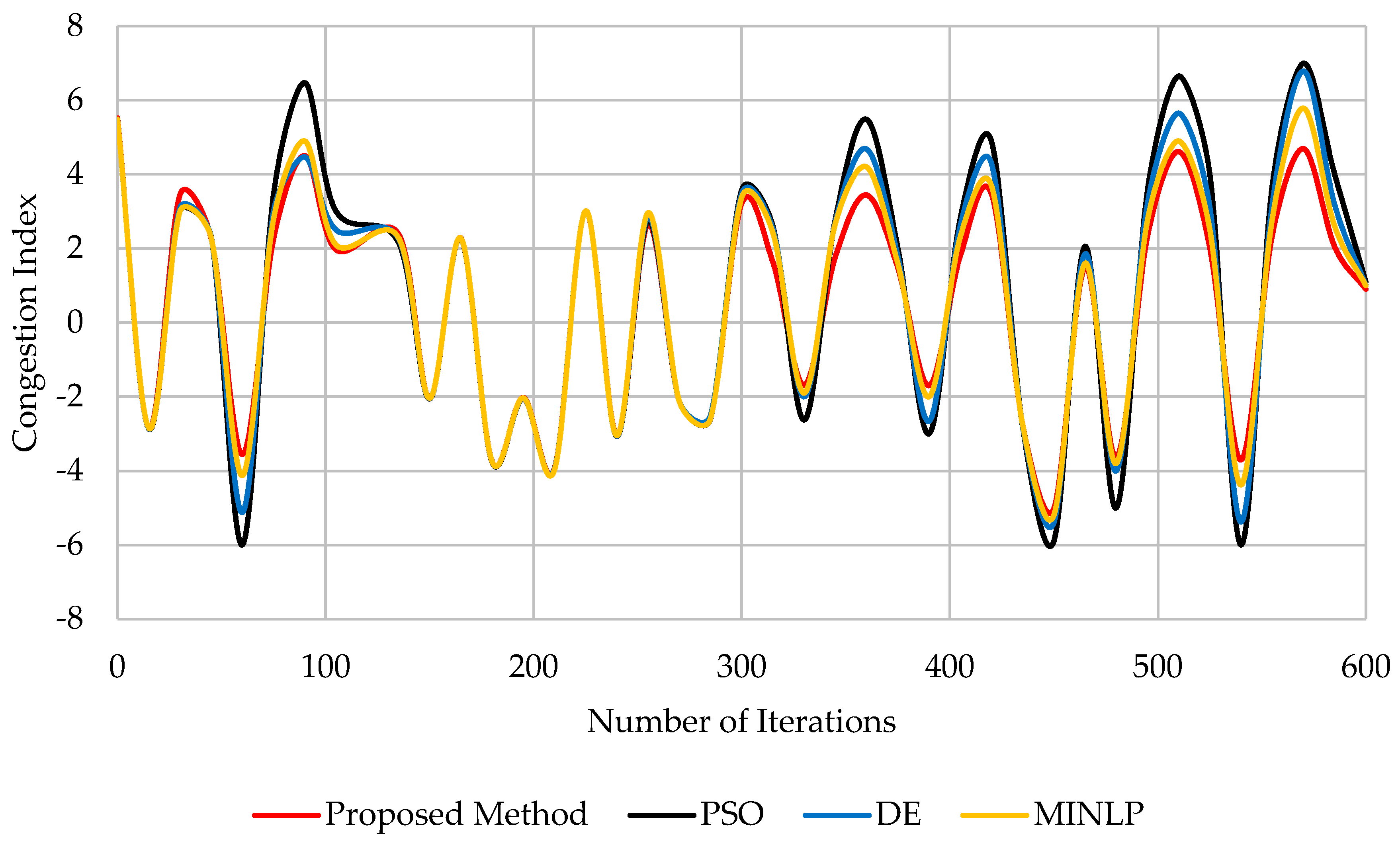
5.2. Performance Evaluation Using Different Heuristic Techniques
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Besharat, H.; Taher, S.A. Congestion management by determining optimal location of TCSC in deregulated power systems. Int. J. Electr. Power Energy Syst. 2008, 30. [Google Scholar] [CrossRef]
- Rajderkar, V.P.; Chandrakar, V.K. Comparison of series FACTS devices via optimal location in a power system for congestion management. In Proceedings of the Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 27–31 March 2009. [Google Scholar]
- Mandala, M.; Gupta, C.P. Congestion management by optimal placement of facts device. In Proceedings of the Joint International Conference on Power Electronics, Drives and Energy Systems and 2010 Power India, New Delhi, India, 20–23 December 2010. [Google Scholar]
- Hosseinipoor, N.; Nabavi, S.M.H. Optimal locating and sizing of TCSC using genetic algorithm for congestion management in deregualted power markets. In Proceedings of the 9th International Conference on Environment and Electrical Engineering, Prague, Czech Republic, 16–19 May 2010. [Google Scholar]
- Yousefi, A.; Nguyan, T.T.; Zareipour, H.; Malik, O.P. Congestion management using demand response and FACTS devices. Int. J. Electr. Power Energy Syst. 2012, 37. [Google Scholar] [CrossRef]
- Kumar, A.; Srivastava, S.C.; Singh, S.N. A zonal congestion management approach using AC transmission congestion distribution factors. Electr. Power Syst. Res. 2004. [Google Scholar] [CrossRef]
- Mori, H.; Goto, Y. A parallel tabu search based method for determining optimal allocation of FACTS in power systems. In Proceedings of the International Conference on Power System Technology, Perth, Australia, 4–7 December 2000. [Google Scholar]
- Singh, S.N.; David, A.K. Congestion management by optimising FACTS device location. In Proceedings of the International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, London, UK, 4–7 April 2000. [Google Scholar]
- Gerbex, S.; Cherkaoui, R.; Germond, A.J. Optimal location of multi-type FACTS devices in a power system by means of genetic algorithms. IEEE Trans. Power Syst. 2001, 16. [Google Scholar] [CrossRef]
- Kumar, A.; Sekhar, C. Congestion management with FACTS devices in deregulated electricity markets ensuring loadability limit. Int. J. Electr. Power Energy Syst. 2013. [Google Scholar] [CrossRef]
- Vetrivel, K.; Mohan, G.; Rao, K.U.; Bhat, S.H. Optimal placement and control of TCSC for transmission congestion management. In Proceedings of the International Conference on Computation of Power, Energy, Information and Communication (ICCPEIC), Chennai, India, 16–17 April 2014. [Google Scholar]
- Choudekar, P.; Sinha, S.K.; Siddiqui, A. Transmission line efficiency improvement and congestion management under critical contingency condition by optimal placement of TCSC. In Proceedings of the 7th India International Conference on Power Electronics (IICPE), Patiala, India, 17–19 November 2016. [Google Scholar]
- Surya, R.; Janarthanan, N.; Balamurugan, S. A novel technique for congestion management in transmission system by real power flow control. In Proceedings of the International Conference on Intelligent Computing, Instrumentation and Control Technologies (ICICICT), Kannur, India, 6–7 July 2017. [Google Scholar]
- Retnamony, R.; Raglend, I.J. Congestion management is to enhance the transient stability in a deregulated power system using FACTS devices. In Proceedings of the International Conference on Control, Instrumentation, Communication and Computational Technologies (ICCICCT), Kumaracoil, India, 18–19 December 2015. [Google Scholar]
- Dawn, S.; Tiwari, P.K.; Gope, S.; Goswami, A.K.; Kumar, P. An active power spot price based approach for congestion management by optimal allocation of TCSC in competitive power market. In Proceedings of the IEEE Region 10 Conference (TENCON), Singapore, Singapore, 22–25 November 2016. [Google Scholar]
- Kulkarni, P.P.; Ghawghawe, N.D. Optimal placement and parameter setting of tcsc in power transmission system to increase the power transfer capability. In Proceedings of the International Conference on Energy Systems and Applications, Pune, India, 30 October–1 November 2015. [Google Scholar]
- Ziaee, O.; Choobineh, F.F. Optimal location-allocation of TCSC devices on a transmission network. IEEE Trans. Power Syst. 2017, 32. [Google Scholar] [CrossRef]
- Khatavkar, V.; Namjoshi, M.; Dharme, A. Congestion management in deregulated electricity market using FACTS and multi-objective optimization. In Proceedings of the Indian Control Conference (ICC), Hyderabad, India, 4–6 January 2016. [Google Scholar]
- Shchetinin, D.; Hug, G. Optimal TCSC allocation in a power system for risk minimization. In Proceedings of the North American Power Symposium (NAPS), Pullman, WA, USA, 7–9 September 2014. [Google Scholar]
- Siddiqui, A.S.; Khan, M.T.; Iqbal, F. A novel approach to determine optimal location of TCSC for congestion management. In Proceedings of the 6th IEEE Power India International Conference (PIICON), Delhi, India, 5–7 December 2014. [Google Scholar]
- Tang, W.; Pan, W.; Zhang, K.; Liu, C. Study of the location of TCSC for improving ATC considering N-1 security constraints. In Proceedings of the 26th Chinese Control and Decision Conference (CCDC), Changsha, China, 31 May–2 June 2014. [Google Scholar]
- Sarwar, M.; Khan, M.T.; Siddiqui, A.S.; Quadri, I.A. An approach to locate TCSC optimally for congestion management in deregulated electricity market. In Proceedings of the 7th India International Conference on Power Electronics (IICPE), Patiala, India, 17–19 November 2016. [Google Scholar]
- Sharma, A.; Jain, S. Locating series FACTS devices for managing transmission congestion in deregulated power market. In Proceedings of the 7th India International Conference on Power Electronics (IICPE), Patiala, India, 17–19 November 2016. [Google Scholar]
- Gitizadeh, M.; Khalilnezhad, H. Power system loss reduction through TCSC economic installation considering switching loss. In Proceedings of the 45th International Universities Power Engineering Conference (UPEC), Cardiff, Wales, UK, 31 August–3 September 2010. [Google Scholar]
- Baghaee, H.R.; Kaviani, A.K.; Mirsalim, M.; Gharehpetian, G.B. Short circuit level and loss reduction by allocating TCSC and UPFC using particle swarm optimization. In Proceedings of the 19th Iranian Conference on Electrical Engineering, Tehran, Iran, 17–19 May 2011. [Google Scholar]
- Hridya, K.R.; Mini, V.; Visakhan, R.; Kurian, A.A. Analysis of voltage stability enhancement of a grid and loss reduction using series FACTS controllers. In Proceedings of the International Conference on Power, Instrumentation, Control and Computing (PICC), Thrissur, India, 9–11 December 2015. [Google Scholar]
- Manganuri, Y.; Choudekar, P.; Abhishek; Asija, D.; Ruchira. Optimal location of TCSC using sensitivity and stability indices for reduction in losses and improving the voltage profile. In Proceedings of the 1st International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 4–6 July 2016. [Google Scholar]
- Moslemi, R.; Shayanfar, H.A. Optimal location for series FACTS devices to transient stability constrained congestion management. In Proceedings of the 10th International Conference on Environment and Electrical Engineering, Rome, Italy, 8–11 May 2011. [Google Scholar]
- Reddy, S.S.; Kumari, M.S.; Sydulu, M. Congestion management in deregulated power system by optimal choice and allocation of FACTS controllers using multi-objective genetic algorithm. IEEE PES 2010. [Google Scholar] [CrossRef]
- Abou-Ghazala, A. Optimal capacitor placement in distribution systems feeding nonlinear loads. In Proceedings of the IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003. [Google Scholar]
- Mohammadi, F.; Zheng, C. Stability analysis of electric power system. In Proceedings of the 4th National Conference on Technology in Electrical and Computer Engineering, Tehran, Iran, 27 December 2018. [Google Scholar]
- Mohammadi, F.; Nazri, G.-A.; Saif, M. A bidirectional power charging control strategy for plug-in hybrid electric vehicles. Sustainability 2019, 11, 4317. [Google Scholar] [CrossRef]
- Mohammadi, F.; Nazri, G.-A.; Saif, M. An improved mixed AC/DC power flow algorithm in hybrid AC/DC grids with MT-HVDC systems. Appl. Sci. 2020, 10, 297. [Google Scholar] [CrossRef]
- Khanabadi, M.; Ghasemi, H. Transmission congestion management through optimal transmission switching. In Proceedings of the IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011. [Google Scholar]
- Christie, R. Power Systems Test Case Archive; UW Power Systems Test Case Archive: Seattle, WA, USA, 1993. [Google Scholar]
- Zimmerman, R.D.; Murillo-Sanchez, C.E.; Thomas, R.J. MATPOWER: Steady-state operations, planning and analysis tools for power systems research and education. IEEE Trans. Power Syst. 2011, 26. [Google Scholar] [CrossRef]
- Mohammadi, F.; Nazri, G.-A.; Saif, M. A fast fault detection and identification approach in power distribution systems. In Proceedings of the 5th International Conference on Power Generation Systems and Renewable Energy Technologies (PGSRET 2019), Istanbul, Turkey, 26–27 August 2019. [Google Scholar]
- Karimi, H.; Ghasemi, R.; Mohammadi, F. Adaptive neural observer-based nonsingular terminal sliding mode controller design for a class of nonlinear systems. In Proceedings of the 6th International Conference on Control, Instrumentation, and Automation (ICCIA 2019), Kordestan, Iran, 30–31 October 2019. [Google Scholar]
- Tavoosi, J.; Mohammadi, F. Design a new intelligent control for a class of nonlinear systems. In Proceedings of the 6th International Conference on Control, Instrumentation, and Automation (ICCIA 2019), Kordestan, Iran, 30–31 October 2019. [Google Scholar]








| Without TCSC | With Installing One TCSC | With Installing Two TCSCs |
|---|---|---|
| 5.6782 | 5.5209 | 5.4876 |
| 3.4496 | 3.4496 | 2.9298 |
| −6.1228 | −3.5560 | −3.5882 |
| 4.5056 | 1.9668 | 1.9282 |
| −2.0359 | −2.0359 | −1.9552 |
| −2.0222 | −2.0222 | −1.8619 |
| 3.0062 | 3.0062 | 1.4983 |
| −2.1218 | −2.1218 | −2.2608 |
| 3.2135 | 3.2135 | 2.6835 |
| −3.6272 | −1.6807 | −1.8361 |
| 3.0220 | 1.4799 | 1.4364 |
| 3.4788 | 1.7925 | 1.7634 |
| −2.7393 | −5.0217 | −5.0954 |
| −6.2709 | −3.6420 | −3.0750 |
| 4.1085 | 2.1043 | 1.9749 |
| 4.6944 | 2.3643 | 2.3378 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, T.T.; Mohammadi, F. Optimal Placement of TCSC for Congestion Management and Power Loss Reduction Using Multi-Objective Genetic Algorithm. Sustainability 2020, 12, 2813. https://doi.org/10.3390/su12072813
Nguyen TT, Mohammadi F. Optimal Placement of TCSC for Congestion Management and Power Loss Reduction Using Multi-Objective Genetic Algorithm. Sustainability. 2020; 12(7):2813. https://doi.org/10.3390/su12072813
Chicago/Turabian StyleNguyen, Thang Trung, and Fazel Mohammadi. 2020. "Optimal Placement of TCSC for Congestion Management and Power Loss Reduction Using Multi-Objective Genetic Algorithm" Sustainability 12, no. 7: 2813. https://doi.org/10.3390/su12072813
APA StyleNguyen, T. T., & Mohammadi, F. (2020). Optimal Placement of TCSC for Congestion Management and Power Loss Reduction Using Multi-Objective Genetic Algorithm. Sustainability, 12(7), 2813. https://doi.org/10.3390/su12072813





