1. Introduction
As a safer, greener, faster, and more punctual tool, subways have become a widely accepted means of public travel [
1]. In this paper, a “subway” refers to urban rail transit that has exclusive right of way—whether on the ground, underground, or elevated—as defined in [
2]. In the urban and suburban areas of Beijing, tens of millions passengers were transported by subway every day in 2018 [
3]. The Beijing subway has been continually expanding its network by investing in new stations and lines. During the study period, there were a total of 14 operation lines, 174 stations, and 370 sections in 2011. At the end of 2017, there were 20 operation lines, 291 stations, and 658 sections in total. Moreover, the passenger traffic increased from 2.193 billion in 2011 to 3.778 billion in 2017 [
3].
The rapid expansion of the network scale and rapid increase in passenger flow have brought a series of challenges to efficient subway operation. To minimize costs, subway systems are often designed to operate at short intervals and to carry passengers close to maximum capacity of trains [
4] with little redundancy. This renders them sensitive to various disruptions [
1]. Owing to the typical complexity of a subway network, when a disruption occurs at one station, it can easily cause knock-on delays [
4,
5] at other related stations. Knock-on delay here refers to that if a train breaks down, this will cause late on subsequent trains as defined in reference [
4]. The dependent subway system will fail or function at a low-level service [
4]. In the first half of 2019, a total of 709 disturbance cases occurred. There were 1622 trains that were at least 2 min late, as reported by the Beijing Metro network control centre, Beijing Municipal Commission of Transport, in 2019. The same problems have been reported in other international cities; for example, in Japan, where the number of subway accidents in Tokyo, along with the impact of these disruptions on society, has been increasing [
6].
It is questionable whether passengers should suffer from the negative impacts of disruptions while enjoying the high-level commuter services provided by subways. System theory asserts that the function of a networked system is determined by the system structure [
7]. It is challenging to determine an appropriate optimization strategy which reduces the negative impacts of disruption in a subway network. This is partly owing to the lack of an effective understanding of the influence of the network topological attributes on the performance of networked transport systems. Although numerous studies have suggested that the topological characteristics, such as the degree, betweenness, and clustering, of stations play an important role in serviceability under disruptions [
8,
9], their results have not been verified by empirical data. To fill this research gap, this study aims to explore the associations between the topological characteristics and disruption impact in a subway network using service disruption data.
It is often perceived that the topological characteristics of a subway system significantly affect its resilience under service disruptions [
8]. However, perception may not always be the reality. Clarifying these issues is crucial for at least two reasons: Firstly, it is helpful to improve the serviceability management level of transportation agencies, in order to improve understanding of the impact of the network structure on system performance. Secondly, the research results may enable traffic planners to gain an improved understanding of the different topological structures characteristics of service reliability. These will subsequently facilitate the development of network strategies to improve transport services and further enhance system resilience. To the best of our knowledge, this study is the first of its kind to provide an analysis, using empirical evidence, in order to demonstrate the correlation between the topological characteristics and extent of damage in a subway network. The remainder of this paper is organized as follows: In
Section 2, a literature review of the impact of topological characteristics on disruption in general is presented and the drawbacks of the current research are discussed. The methods employed in the analysis are presented in
Section 3. In
Section 4, the Beijing subway is taken as a case study. A complete description of the data, including the service disruption data set (recorded from 2011 to 2017) and the network structure, which represents the underlying space in which these disruptions occurred, is presented. In
Section 5, the results of the correlation and regression analyses between the topological characteristics and service disruption impacts are presented and discussed. The conclusions, along with the implications of our findings and directions for further research, are outlined in
Section 6.
2. Literature Review
In recent years, an increasing number of researchers have used scientific network indicators to test the serviceability of subway networks [
7,
10,
11]. The impacts of disruption on the serviceability of subway networks are often quantified by graph theory and complex network indicators, such as a decrease in the operational efficiency of the subway network following failure of a station or section [
7]. In studies relating to transport and territory, the impact is generally measured in terms of accessibility or serviceability indicators, such as the proportion of delayed passengers [
12], the proportion of cut-off passengers [
12,
13], or the time loss when passengers select alternative routes that are not optimal [
13].
Disruption has been simulated by complete closure of a station or track section [
13] which is passed by several lines with a high degree (an indicator used to measure the number of times a station is passed by subway lines) [
14], high betweenness (an indicator used to measure the role that a station or section plays as a key bridge in all shortest paths in a network) [
12], high closeness (an indicator used to measure how easily a station is reached from other stations) [
15], and high clustering (characterized by redundant tracks between neighbours) [
9]. Stations passing by more than three lines have been proven to be not as vulnerable to targeted attacks [
14]. This finding contradicted the results of [
9], who demonstrated that stations with high degree and high closeness tend to exhibit increased vulnerability. Moreover, stations with high betweenness were found to tend to reduce the impact of service disruption [
9]. However, it has been proven that stations with higher betweenness and degree are more vulnerable to disruptions [
14]. Stations with high clustering tend to provide higher levels of protection against disruptions [
9]. Furthermore, the addition of edges to a network can improve network resilience [
2]. Links on the branch, which exhibit limited redundancy, have been proved to be particularly vulnerable to disruptions [
16]. In contrast, stations in the central parts of the network exhibit lower vulnerability to disruptions.
According to the overall characteristics of network structure, the mass rapid transport (MRT) network has been proven to be a highly efficient transportation system on a global scale; however, it is not fault-tolerant [
17]. Moreover, it has been found that subway networks provide robustness against random attacks and are more vulnerable to targeted attacks [
18]. When a subway network is more heterogeneous, it is more vulnerable to targeted attacks [
7]. With increasing network size, a subway network tends to become more clustered while the scaling factor settles at a relatively high value [
10]. A high cluster coefficient and low scale factor are preferable for subway network robustness. The robustness in the case of disturbance becomes stronger with the network complexity [
12,
14]. Likewise, the resilience quantified by the connectivity decreases with an increase in the network span, but increases with the degree of stations [
8].
Based on the above literature review, it can be concluded that the existing findings are inconsistent. These studies were conducted using failure scenarios and numerical simulations, and the multi-platform characteristics of the transfer stations were always overlooked. Furthermore, these findings have not been verified using empirical data. The majority of empirical investigations into the impact analysis under service disruptions within a transportation context has paid little attention to subways [
19]. From an empirical perspective, only the relationship between the transfer station and delay duration has been analysed [
19]. These authors found, by utilizing accelerated failure time hazard models, that the delay duration was shorter at transfer stations than at non-transfer stations. Although several researchers have focused on service disruption from an empirical analysis perspective [
20,
21,
22,
23], they have not paid attention to the influence of the topological characteristics and the impact of transit service disruptions. Moreover, the delay duration has been widely used as a quantification tool for the resilience of subway systems under disruption. However, certain disruptions, such as train malfunctions, have resulted in the complete closure of stations, although the duration is short. Moreover, in some cases (e.g., track failure), although the duration is long, the result is lower train speeds in the segment. The results of a train cancellation are generally larger than that when there is no train cancellation [
22]. Therefore, the delay duration is not an effective indicator to reflect the impact of disruption on transport services.
It can be observed, from the literature review, that the existing studies on public transport disruption are far from sufficient, in terms of considering topological factors from an empirical perspective. Therefore, the aim of this study is to verify the relationship between the topological factors and the impacts of transit service disruption in subway systems on the empirical level.
6. Conclusions
In this paper, we presented a correlation analysis of the topological characteristics of a subway network with number of affected trains and delay duration. In contrast to studies based on simulation and graph theoretic methods, we used the data of 392 actual service disruptions that occurred in the Beijing subway network from 2011 to 2017. The Spearman rank correlation coefficient was used to analyse the correlations among the complex attributes of the holistic network, the complex attributes of local stations, and the service disruption. This enabled not only clarification of the relationships, but also an assessment of the possible means of optimizing the planning of subway networks. The information provided by the research results may aid scholars in identifying the shortcomings of several hypotheses in theoretical research. Moreover, this information can be provided to aid the preparation of planners and managers, in order to mitigate the impact of accidents on the network by planning new routes or expanding existing routes to reduce vulnerability and critical factors.
From a complex network theory perspective, the evolution of a subway network does not definitely increase the network complexity while improving its convenience to passengers. Up to 2017, the main objective of the Beijing subway extension was to expand its coverage areas. At this stage, the Beijing subway is expanding its network mainly by constructing new stations to the edges along radial lines, rather than by adding tracks between existing stations to increase the network density. Nonetheless, the expansion of new stations will generate substantially more non-transfer stations than transfer stations. An increase in transfer stations may decrease the heterogeneity of the network. From a mathematical perspective, an increasing scaling factor is demonstrated. The rapid increase in the number of stations leads to a lack of connectivity between existing stations, which eventually results in an increasing length of the shortest path of the network and a decrease in the clustering. This is the reason that the scale-free feature of the network grows, but the small-world feature of the network does not improve significantly. Only at a later stage, in which the evolution of the network is based on the construction of tracks to connect old stations, will both the scale-free and small-world complexity attributes increase simultaneously.
Additionally, although the number of affected trains increases with an increase of the scaling factor, the negative impact is absorbed by the high clustering characteristic of the subway network. At a developed stage, in which the network evolves by constructing tracks among old stations, both the scale-free and small-world complexity attributes increase simultaneously. This means that, if the subway network is extended by adding tracks between existing stations, the vulnerability caused by an increase of the scale-free features can be absorbed by improving the small-world features of the network. These results demonstrate subway network expansion will not result in a paradox between convenience and vulnerability from an actual data perspective.
Meanwhile, the number of affected trains is a valuable indicator to quantify the relationship with service delivery level under disruption and topological characterise of MRT network structure than delay duration, according to our empirical result. This is because of the two dependent variables under service disruption: only the number of affected trains exhibited correlation with the independent variables, while the delay duration exhibited no correlation. The service disruption duration cannot reflect the actual negative effect on the transport service. That is because certain disruptions that last for a long time may only affect a few trains. However, certain disruptions with very short durations ultimately cause the delay of more trains. In most transportation-related studies, the delay duration or delay time-superimposed passenger flow is generally used to quantify the impact of disruptions.
The conclusion of most studies—that subway networks are more vulnerable to targeted attacks than to random attacks—was not supported by our empirical data from service delivery perspective. In such studies, targeted attacks were simulated in numerous manners, such as deleting stations with higher degree, betweenness, or clustering. The results of our empirical analysis demonstrated no significant relationship between transfer and non-transfer stations. The station betweenness also showed no significant difference in the number of affected trains. In theoretical studies, the platforms and tracks of transfer stations were assumed to be unique. This assumption induces the conclusion that, once an incident occurs at the transfer station, the platform and tracks will be occupied; which means that all trains planning to pass this station will be affected by travelling at a lower speed or being cancelled. However, in actual operations, the platforms and tracks are not unique: different lines occupy different platforms and tracks. An incident on one platform does not necessarily affect the normal operation of trains on other platforms. Therefore, there was no significant difference in the number of affected trains at different station degrees. Furthermore, the irrelevancy of transfer stations serves as a reminder to establish the problem of multi-platform transfer in metro transfer stations correctly when conducting research based on simulation methods, rather than all lines of a transfer station sharing the same platform.
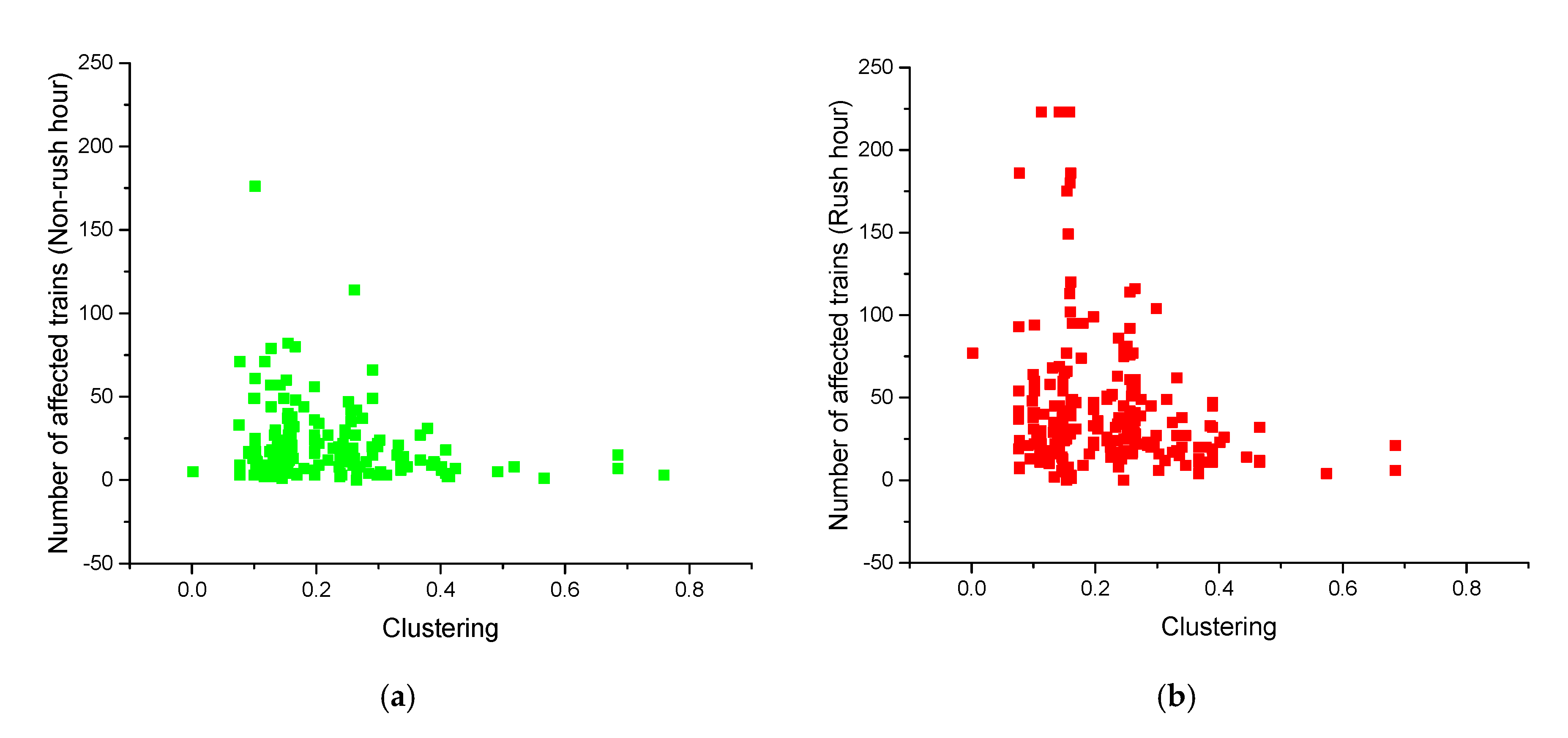
Moreover, the negative correlation between the clustering and number of affected trains indicates that the impact on the subway service disruption occurring at stations with high clustering was smaller than that at stations with low clustering. In practice, increasing the construction of tracks between existing stations can improve the clustering coefficient of the stations. Higher clustering tends to provide protection against service disruption for stations by means of alternative tracks. For example, in the Beijing subway network, the airport line has four stations in total: Dongzhimen station, Sanyuanqiao station, T2 station, and T3 station. Sanyuanqiao station, T2 station, and T3 station are all connected by tracks, forming a triple. Therefore, the clustering values of T2 and T3 are greater than 0.6. If a disruption occurs at the T3 station, T2 can be reached directly from Sanyuanqiao station, thereby providing a highly significant protective effect. Additionally, station lines within 16 stations or more than 20 stations can be planned to improve the resilience of the subway service under disruptions. This finding is consistent with [
8], that networks with a higher diameter are often sparser and contain less redundant connections. However, when the diameter is sufficiently large, service disruptions occurring at the edge of the network have a limited radiation capacity, which will reduce the impact.
Last of all, we want to note several drawbacks of the study. Firstly, using of ‘number of affected trains’ as indicator for disruption impacts is from transport service delivery perspective. When a disruption happened, providers of the transport service or manager of transport service can know how the planned service delivery level is affected by ‘number of affected trains’. The actual passenger capacity or density of trains is not considered in this indicator. Although we have separated the analysis into rush hour and non-rush hour group, actual passenger capacity or density of trains may be different in city centre line and suburban line. How many passengers affected due to disruptions cannot be known by ‘number of affected trains’. Researchers had used AFC data to evaluate disruption impact on passengers. On one hand, affected passenger has delay effect and escape effect. The delayed effect refers to that affected passengers will be reflected on the AFC data after the disruption is over. The escape effect means that some of affected passengers will leave MRT system and cannot be reflected by the AFC data. Therefore, if AFC data are to be used as a tool for disruption impact assessment, the time duration selected for AFC data is very critical, which will directly change results. On the other hand, even if the appropriate time duration is selected to extract the AFC data, only the number of passengers actually served can be known. If we want to know how many passengers are affected by the disruption, simulation method is needed to support the calculation of the number of passengers that should be provided transport service. Therefore, the results also depend on the accuracy of the simulation data of passenger flow.
Secondly, the length of shortest path was calculated by the number of transfers and number of stations passed in this study. This makes the shortest path length between stations will only increase if adding a new station between existing stations when extend subway network. The Beijing subway network was not a whole connected in 2011 and 2012. It became a whole connected network till to 2013. Since 2013, there were 30,450 connected pairs existing in those 174 stations. The average shortest path length of the 30,450 OD pairs was increased from 15.9713 in 2013 to 16.6098 in 2014. That was because new stations had been added between existing stations. Whereas the reverse is true if the length of shortest path would calculate the geodesic link length; whilst using link travel times might increase the shortest path length somewhat if the dwell times result in longer journey times for through passengers. In the future study, the appropriate way to calculated the shortest path should be used according to the purpose of the research.
Thirdly, some of disruptions was the result of domino effect of another disruption, while the domino effect was not considered here. Such a disposition, may let space correlation information be missed. Therefore, in the future study, the disruptions should be considered as chains or even formulate into networks. The factors related with spatial, such as geographical, economic, and demographic attributes and so on should be taken into account when carrying out spatial autocorrelation analysis. It is really an interesting question whether there are spatial autocorrelation characteristics of subway disruption incidents.
From the perspective of prediction analysis, the regression analysis results showed that using only topological features cannot demonstrate a good interpretation of the disruption impact. Therefore, in the future, we need to consider not only the topological characteristics, but also the factors from GIS information, operations, passenger flow, and the cause of disruptions in the regression analysis.