Compressive Shear Strength of Reinforced Concrete Walls at High Ductility Levels
Abstract
:1. Introduction
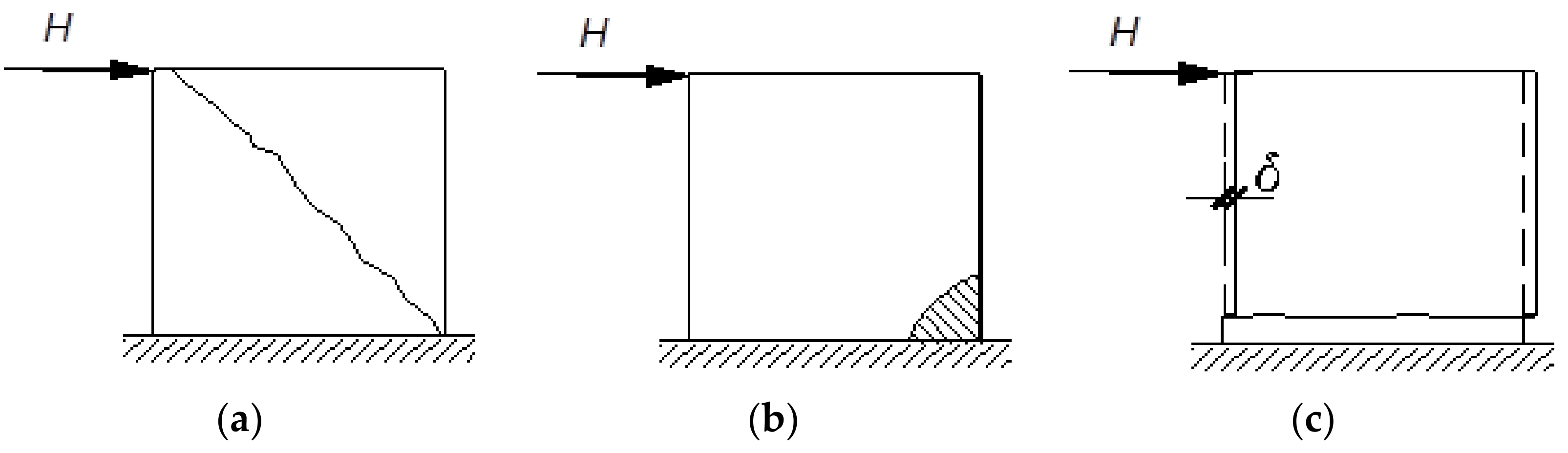
2. Methods of Determining Shear Strength
2.1. EN 1998-1 Provisions
- αcw coefficient of normal force influence,
- bw breadth of a wall,
- h height of a wall cross section,
- ν1 influence of cracks on strength ν1 = 0.6 × (1 − fck/250),
- fcd design compressive strength of concrete and
2.2. EN 1998-3 Provisions
- μθpl plastic rotation ductility factor μθpl = μθ – 1,
- μθ rotation ductility factor,
- N axial force,
- Ac cross section area of concrete,
- ρtot total vertical reinforcement ratio and
- Ls/h ratio of shear span to cross section height.
2.3. Fib Model Code 2010 Provisions
2.4. Comparison of EN 1998-1 and EN 1998-3 Provisions
- T1 fundamental period of the structure in a given direction and
- TC corner period dependent on the soil.
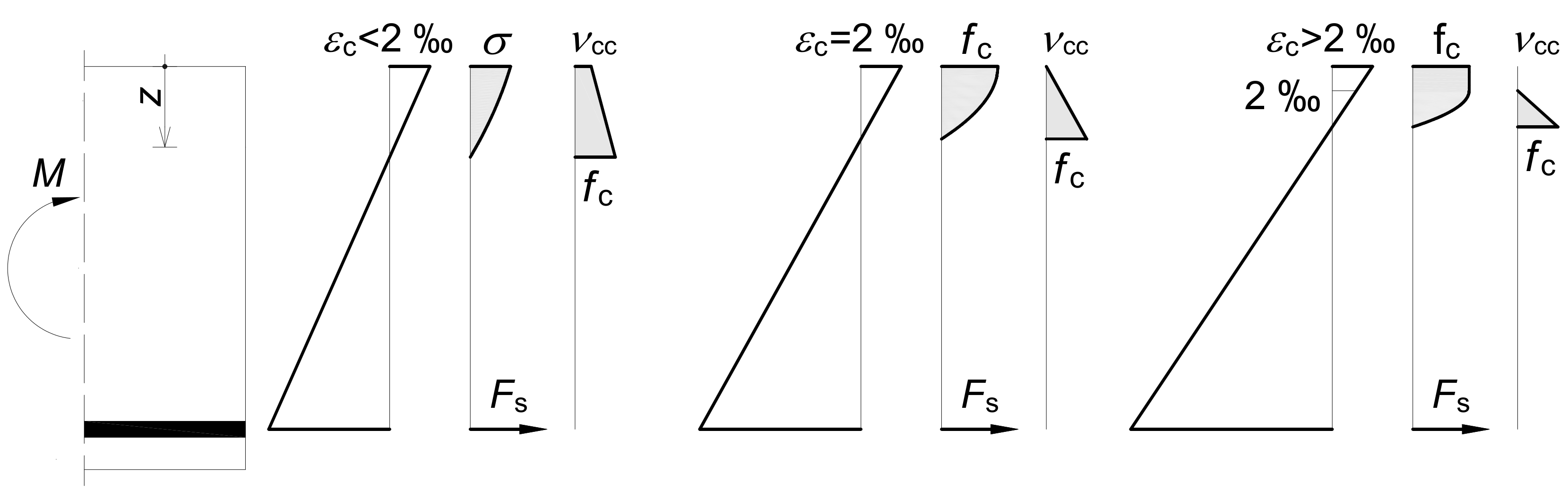
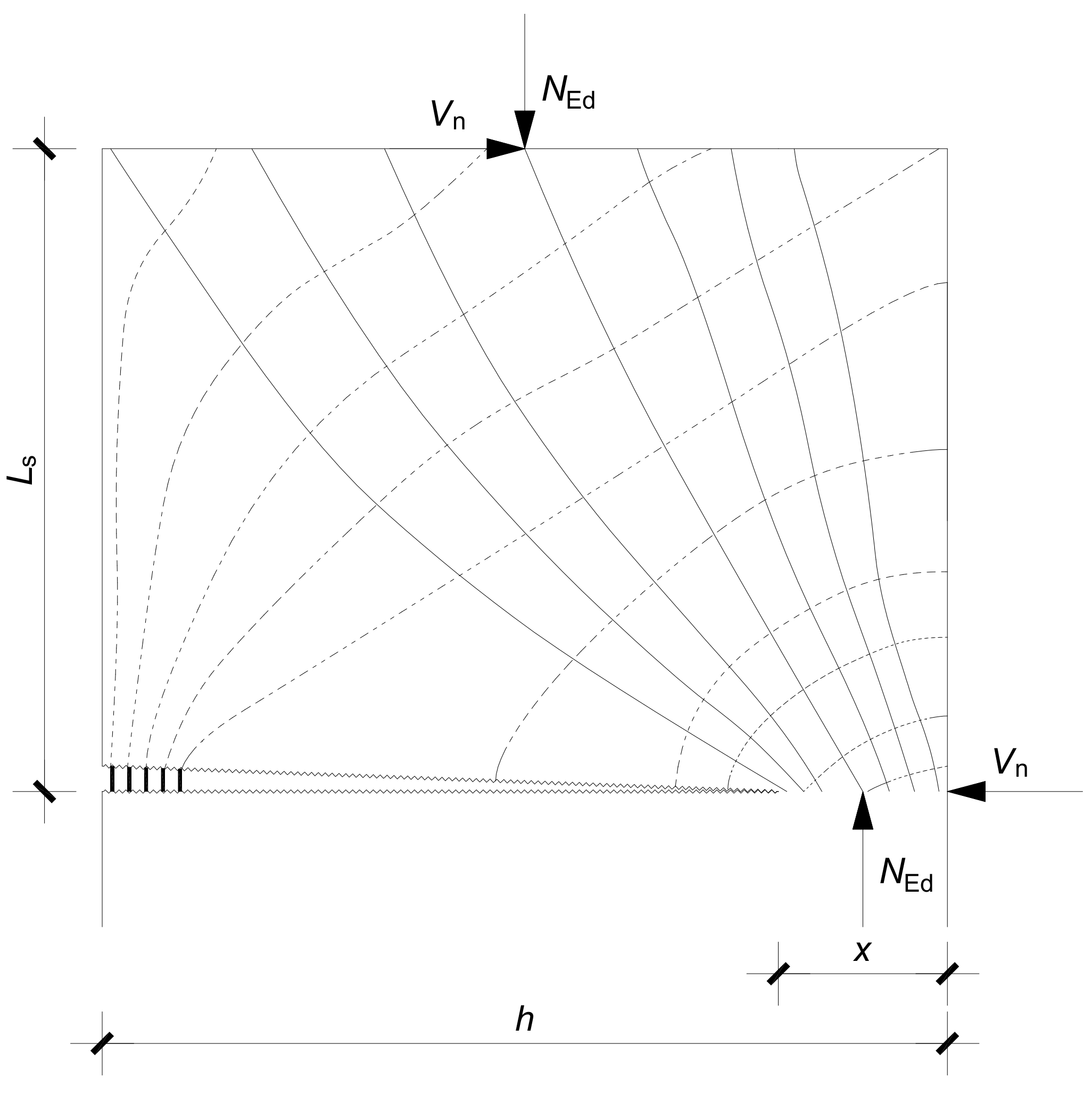
2.5. Analytical Model of Compressive Shear Strength
- fc compression strength of concrete and
- σ (z) normal stress at a point z due to the bending moment and axial force.
3. Results
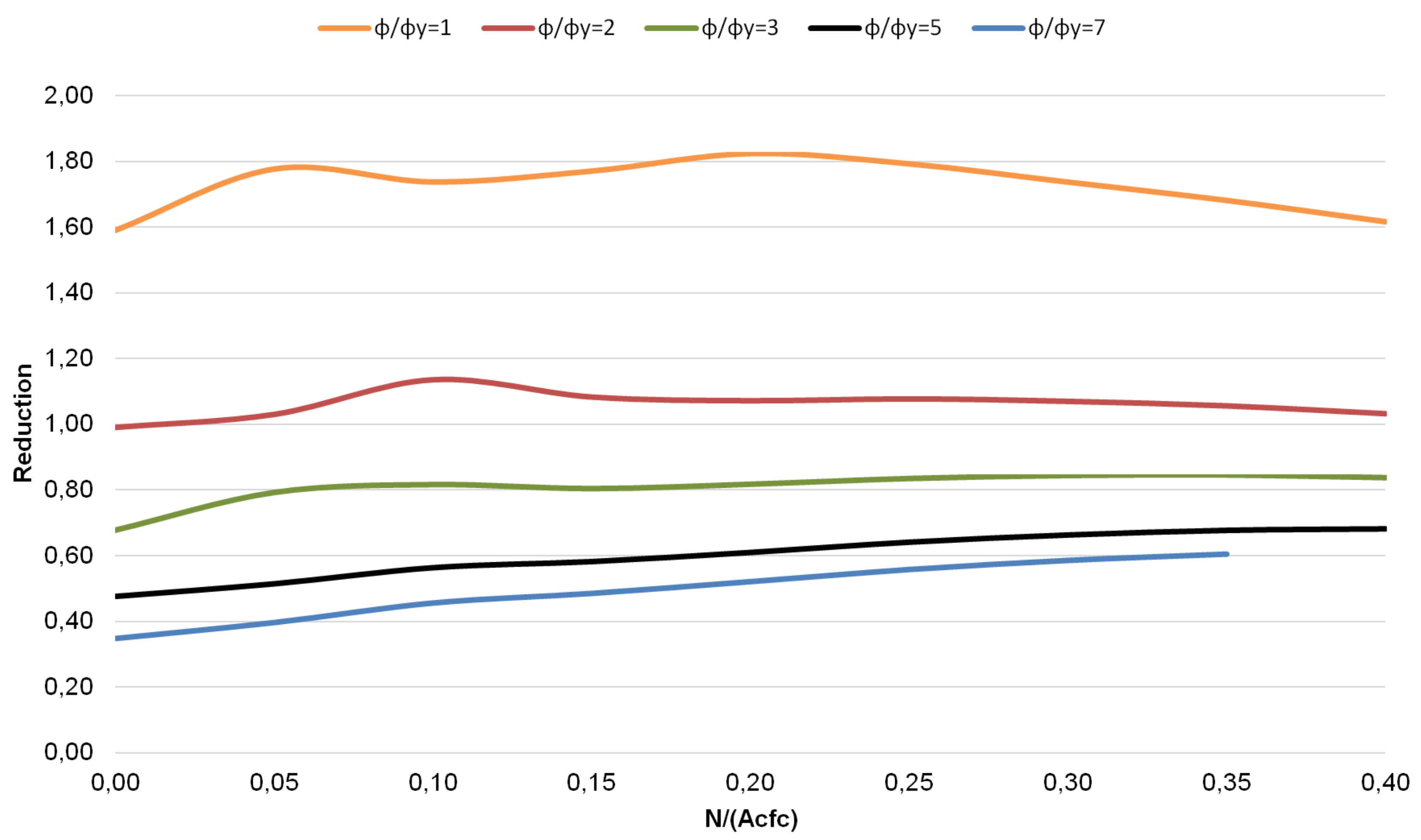
3.1. Influence of Axial Force
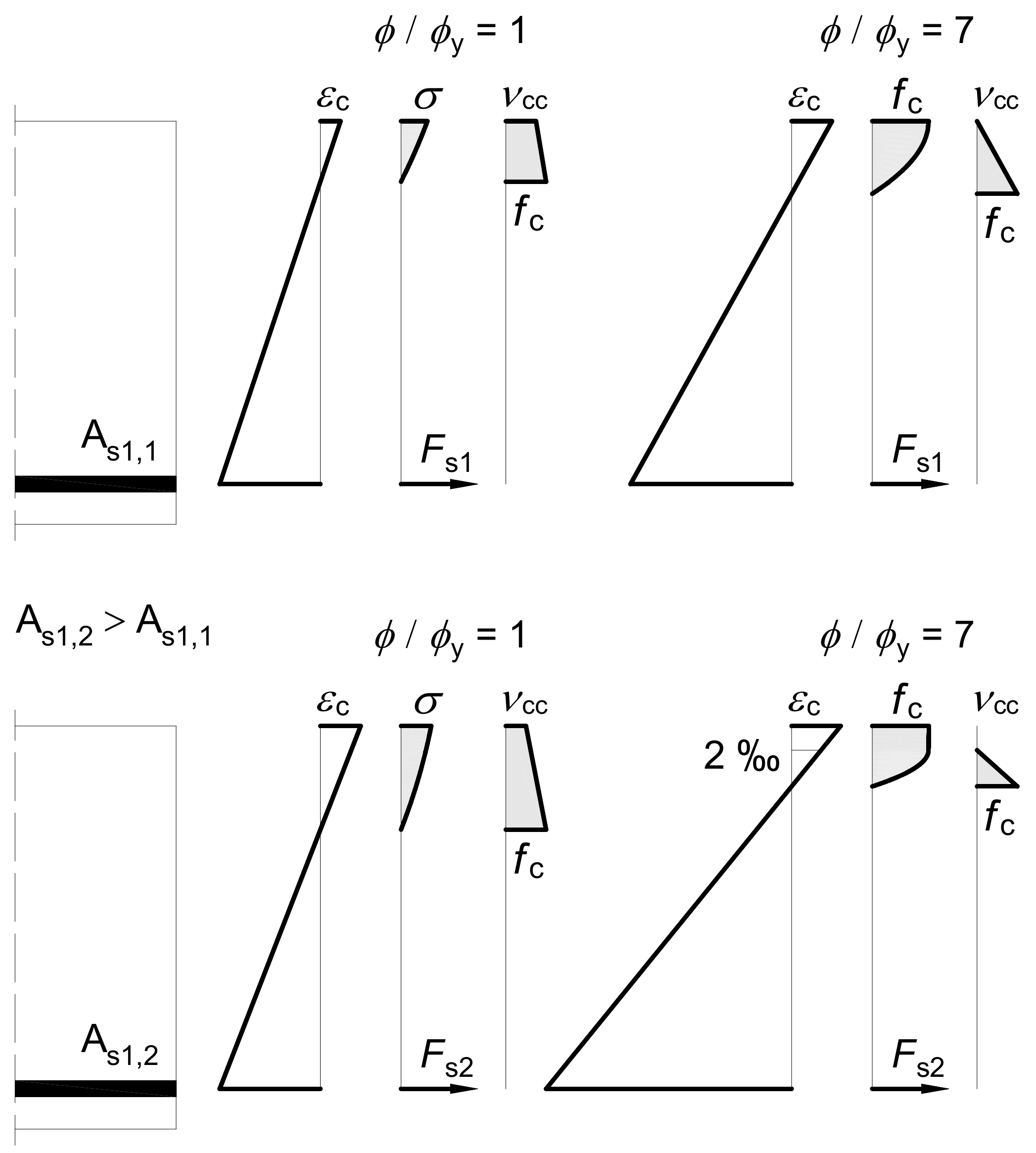
3.2. Influence of the Amount of Longitudinal Reinforcement
3.3. Influence of the Value of Ultimate Curvature
3.4. Influence of the Reinforcement Arrangement
3.5. Adjusting the Analytic Procedure with the Existing Code
4. Discussion
5. Conclusions
- Axial force significantly influences compressive shear strength, which is increased by compressive force.
- The longitudinal reinforcement ratio slightly influences compressive shear strength at high curvatures. There is an upper limit to the influence of the reinforcement.
- The ultimate curvature of a section has no influence on compressive shear strength at a specific curvature, but does influence compressive shear strength at an ultimate curvature.
- The reinforcement arrangement inside a section does not influence compressive shear strength at a specific curvature, but does influence the ductility and stiffness of the element.
- The reduction of compressive shear strength is recommended for medium-ductility structures.
- The reduction of compressive shear strength is not correlated with the dynamic nature of the response.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Paulay, T.; Priestley, M.J.N. Seismic Design of Reinforced Concrete and Masonry Buildings, 1st ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1992; p. 744. [Google Scholar]
- Penelis, G.G.; Penelis, G.G. Concrete Buildings in Seismic Regions, 1st ed.; Taylor & Francis: Boca Raton, FL, USA, 2014; p. 826. [Google Scholar]
- Eurocode 8: Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings; EN 1998-1; CEN: Brussels, Belgium, 2004.
- Eurocode 8: Design of Structures for Earthquake Resistance—Part 3: Assessment and Retrofitting of Buildings; EN 1998-3; CEN: Brussels, Belgium, 2004.
- Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings; EN 1992-1-1; CEN: Brussels, Belgium, 2004.
- Grammatikou, S.; Biskinis, D.E.; Fardis, M.N. Strength, deformation capacity and failure modes of RC walls under cyclic loading. Bull. Earthq. Eng. 2015, 11, 3277–3300. [Google Scholar] [CrossRef]
- Biskinis, D.E.; Roupakias, G.K.; Fardis, M.N. Degradation of Shear Strength of Reinforced Concrete Members with Inelastic Cyclic Displacements. ACI Struct. J. 2004, 101, 773–783. [Google Scholar]
- Biskinis, D.E.; Fardis, M.N. Cyclic shear resistance model for Eurocode 8 consistent with the second-generation Eurocode 2. Bull. Earthq. Eng. 2020, 18, 2891–2915. [Google Scholar] [CrossRef]
- Designers Guide to EN 1998-1 and EN 1998-5; Gulvanessian, H. (Ed.) Thomas Telford: London, UK, 2005; p. 279. [Google Scholar]
- Model Code 2010; fib Bulletin 56; FIB: Lausanne, Switzerland, 2010; Volume 2.
- Park, H.G.; Yu, E.J.; Choi, K.K. Shear-strength degradation model for RC columns subjected to cyclic loading. Eng. Struct. 2012, 34, 187–197. [Google Scholar] [CrossRef]
- Sezen, H.; Moehle, J.P. Shear Strength Model for Lightly Reinforced Concrete Columns. J. Struct. Eng. 2004, 130, 1692–1703. [Google Scholar] [CrossRef]
- Priestley, M.J.N.; Verma, R.; Xiao, Y. Seismic shear strength of reinforced concrete columns. J. Struct. Eng. 1994, 120, 2310–2329. [Google Scholar] [CrossRef]
- Ang, B.G.; Priestley, M.J.N.; Paulay, T. Seismic Shear Strength of Circular Reinforced Concrete Columns. Struct. J. 1989, 86, 45–59. [Google Scholar]
- Li, Y.; Hwang, S.J. Prediction of Lateral Load Displacement Curves for Reinforced Concrete Short Columns Failed in Shear. J. Struct. Eng. 2017, 143, 04016164. [Google Scholar] [CrossRef]
- Pan, Z.; Li, B. Truss-Arch Model for Shear Strength of Shear-Critical Reinforced Concrete Columns. J. Struct. Eng. 2013, 139, 548–560. [Google Scholar] [CrossRef]
- Fu, L.; Nakamura, H.; Furuhashi, H.; Yamamoto, Y.; Miura, T. Mechanism of shear strength degradation of a reinforced concrete column subjected to cyclic loading. Struct. Concr. 2017, 18, 177–188. [Google Scholar] [CrossRef]
- Hua, J.; Eberhard, M.O.; Lowes, L.N.; Gu, X. Modes, Mechanisms, and Likelihood of Seismic Shear Failure in Rectangular Reinforced Concrete Columns. J. Struct. Eng. 2019, 145, 04019096. [Google Scholar] [CrossRef]
- Terzioglu, T.; Orakcal, K.; Massone, L.M. Cyclic lateral load behavior of squat reinforced concrete walls. Eng. Struct. 2018, 160, 147–160. [Google Scholar] [CrossRef]
- Ni, X.; Cao, S.; Liang, S.; Li, Y.; Liu, Y. High-strength bar reinforced concrete walls: Cyclic loading test and strength prediction. Eng. Struct. 2019, 198, 109508. [Google Scholar] [CrossRef]
- Chen, X.L.; Fu, J.P.; Hao, X.; Yang, H.; Zhang, D.Y. Seismic behavior of reinforced concrete squat walls with high strength reinforcements: An experimental study. Struct. Concr. 2019, 20, 911–931. [Google Scholar] [CrossRef]
- Baek, J.W.; Park, H.G.; Shin, H.M.; Yim, S.J. Cyclic Loading Test for Reinforced Concrete Walls (Aspect Ratio 2.0) with Grade 550 MPa (80 ksi) Shear Reinforcing Bars. ACI Struct. J. 2017, 114, 673–686. [Google Scholar] [CrossRef]
- Baek, J.W.; Park, H.G.; Lee, J.H.; Bang, C.J. Cyclic Loading Test for Walls of Aspect Ratio 1.0 and 0.5 with Grade 550 MPa (80 ksi) Shear Reinforcing Bars. ACI Struct. J. 2017, 114, 969–982. [Google Scholar] [CrossRef]
- Salonikios, T.N. Analytical Prediction of the Inelastic Response of RC Walls with Low Aspect Ratio. J. Struct. Eng. 2007, 133, 844–854. [Google Scholar] [CrossRef]
- Rutenberg, A. Seismic shear forces on RC walls: Review and bibliography. Bull. Earthq. Eng. 2013, 11, 1727–1751. [Google Scholar] [CrossRef]
- Rejec, K.; Isaković, T.; Fischinger, M. Seismic shear force magnification in RC cantilever structural walls, designed according to Eurocode 8. Bull. Earthq. Eng. 2012, 10, 567–586. [Google Scholar] [CrossRef]
- Yathon, J.S. Seismic Shear Demand in Reinforced Concrete Cantilever Walls. Ph.D. Thesis, The University of British Columbia, Vancouver, BC, Canada, April 2011. [Google Scholar]
- Rivera, J.P.; Whittaker, A.S. Damage and Peak Shear Strength of Low-Aspect-Ratio Reinforced Concrete Shear Walls. J. Struct. Eng. 2019, 145, 04019141. [Google Scholar] [CrossRef]
- Building Code Requirements for Structural Concrete; ACI 318-14; ACI: Farmington Hills, MI, USA, 2011.
- Standard Specifications for Concrete Structures “Design”; JSCE No. 15; JSCE: Tokyo, Japan, 2007.
- Concrete Structures Standard—Part 1—The Design of Concrete Structures; NZS 3101-1; SNZ: Wellington, New Zealand, 2006.
- Chen, W.F. Plasticity in Reinforced Concrete, 1st ed.; McGraw-Hill: New York, NY, USA, 1982; p. 474. [Google Scholar]
- Kišiček, T.; Sorić, Z. Bending moment-curvature diagram for reinforced-concrete girders. Građevinar 2003, 55, 207–215. [Google Scholar]



| μθpl | Reduction |
|---|---|
| 0 | 1.00 |
| 1 | 0.94 |
| 2 | 0.88 |
| 3 | 0.82 |
| 4 | 0.76 |
| ≥5 | 0.70 |
| Concrete Class | Reduction ν |
|---|---|
| C20/25 | 0.28 |
| C25/30 | 0.27 |
| C30/37 | 0.26 |
| C35/45 | 0.25 |
| C45/55 | 0.25 |
| C50/60 | 0.24 |
| Concrete Class | τRd,minEN-3 | τRd,maxEN-3 | VRd,minEN-1/ (bw × z) | VRd,maxEN-1 /(bw × z) | Rmin | Rmax> Ls/h = 1 | Rmax Ls/h ≥ 1 |
|---|---|---|---|---|---|---|---|
| C20/25 | 2.42 | 5.70 | 3.68 | 4.60 | 0.66 | 1.24 | 0.93 |
| C25/30 | 2.71 | 6.37 | 4.50 | 5.63 | 0.60 | 1.13 | 0.85 |
| C30/37 | 2.96 | 6.98 | 5.28 | 6.60 | 0.56 | 1.06 | 0.79 |
| C35/45 | 3.20 | 7.54 | 6.02 | 7.53 | 0.53 | 1.00 | 0.75 |
| C40/50 | 3.42 | 8.06 | 6.72 | 8.40 | 0.51 | 0.96 | 0.72 |
| C45/55 | 3.63 | 8.55 | 7.38 | 9.23 | 0.49 | 0.93 | 0.70 |
| C50/60 | 3.83 | 9.01 | 8.00 | 10,00 | 0.48 | 0.90 | 0.68 |
| Parameter | h [m] | Ls/h | h/bw | fc [MPa] | N/(Ac ∙ fc) | ρtot [%] |
|---|---|---|---|---|---|---|
| average value | 1.38 | 1.6 | 12.6 | 32.9 | 0.08 | 1.4 |
| μϕ | R2 | R3 | R4 | R5 | R6 | R7 | R8 | R9 | R10 | Ru |
|---|---|---|---|---|---|---|---|---|---|---|
| 8 | 1.03 | 0.74 | 0.59 | 0.50 | 0.44 | 0.40 | 0.37 | - | - | 0.37 |
| 9 | 1.03 | 0.74 | 0.59 | 0.50 | 0.44 | 0.40 | 0.37 | 0.35 | - | 0.35 |
| 10 | 1.04 | 0.74 | 0.59 | 0.50 | 0.44 | 0.40 | 0.37 | 0.35 | 0.33 | 0.33 |
| 11 | 1.04 | 0.74 | 0.59 | 0.50 | 0.45 | 0.40 | 0.37 | 0.35 | 0.33 | 0.31 |
| 12 | 1.04 | 0.74 | 0.59 | 0.50 | 0.45 | 0.40 | 0.37 | 0.35 | 0.33 | 0.30 |
| 13 | 1.04 | 0.74 | 0.59 | 0.51 | 0.45 | 0.40 | 0.37 | 0.35 | 0.33 | 0.29 |
| 14 | 1.04 | 0.75 | 0.60 | 0.51 | 0.45 | 0.41 | 0.37 | 0.35 | 0.33 | 0.28 |
| 15 | 1.10 | 0.80 | 0.64 | 0.54 | 0.48 | 0.43 | 0.40 | 0.37 | 0.35 | 0.28 |
| 16 | 1.13 | 0.87 | 0.69 | 0.58 | 0.51 | 0.46 | 0.42 | 0.39 | 0.37 | 0.29 |
| r | R7 |
|---|---|
| 0.0 | 0.41 |
| 0.5 | 0.40 |
| 1.0 | 0.40 |
| 1.5 | 0.40 |
| 2.0 | 0.39 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kišiček, T.; Renić, T.; Lazarević, D.; Hafner, I. Compressive Shear Strength of Reinforced Concrete Walls at High Ductility Levels. Sustainability 2020, 12, 4434. https://doi.org/10.3390/su12114434
Kišiček T, Renić T, Lazarević D, Hafner I. Compressive Shear Strength of Reinforced Concrete Walls at High Ductility Levels. Sustainability. 2020; 12(11):4434. https://doi.org/10.3390/su12114434
Chicago/Turabian StyleKišiček, Tomislav, Tvrtko Renić, Damir Lazarević, and Ivan Hafner. 2020. "Compressive Shear Strength of Reinforced Concrete Walls at High Ductility Levels" Sustainability 12, no. 11: 4434. https://doi.org/10.3390/su12114434
APA StyleKišiček, T., Renić, T., Lazarević, D., & Hafner, I. (2020). Compressive Shear Strength of Reinforced Concrete Walls at High Ductility Levels. Sustainability, 12(11), 4434. https://doi.org/10.3390/su12114434






