Experimental Air Impingement Crossflow Comparison and Theoretical Application to Photovoltaic Efficiency Improvement

Abstract

The photovoltaic cell temperature is a key factor in solar energy harvesting. Solar radiation raises temperature on the cell, lowering its peak efficiency. Air jet impingement is a high heat transfer rate system and has been previously used to cool the back surface of photovoltaic modules and cells. In this work, an experimental comparison of the cooling performance of two different air jet impingement crossflow schemes was performed. Crossflow is defined as the air mass interacting with a certain jet modifying its movement. This leads to a change in its heat exchange capabilities and is related with the inlet-outlet arrangement of the fluid. In this work, zero and minimum crossflow schemes were compared. The main contribution of this work considered the consumption of the flow supplying devices to determine the most suitable system. The best configuration increased the net power output of the cell by 6.60%. These results show that air impingement cooling can play a role in increasing photovoltaic profitability. In terms of uniformity, on small impingement plates with a low number of nozzles, the advantages expected from the zero crossflow configuration did not stand out.

1. Introduction

Solar photovoltaic $PV$ energy is a renewable energy source with great projection [1] and a wide adoption of this technology could lead to an abundant and inexpensive power source. This is the power source with the largest installed capacity during 2017, beating the sum of the new nuclear and fossil fuel power plants and doubling wind energy [2]. Over the years, the drop of cell cost associated with manufacturing partially explains this success. However, in the foreseeable stagnation of this factor [3], increased cell efficiency and systems can be the key to sustaining this growth and achieving the ambitious global sustainability goals.

Photovoltaic cells directly convert incident solar radiation into usable electrical energy. The efficiency of a photovoltaic system is defined as the fraction of usable electrical energy that has been converted from the incident energy. Efficiency is influenced by several factors, such as cell material [4], manufacturing process [5], or environmental conditions [6]. This last factor is of great importance, since the irradiance, environmental temperature, weather conditions, or presence of dust or dirt can influence the temperature of the cell, leading to variations in its efficiency. This led to researchers like Ali et al. [7] to develop models that determine the parameters that define a $PV$ cell efficiency in real time.

An increase in the temperature of the cell leads to a reduction of the band gap of the semiconductor. The consequence is a decrease in the open circuit generated voltage $V_{oc}$. This change in the properties of the material leads to a greater absorption of energy, since the percentage of light capable of rising load carriers from the valence band to the conduction band is higher. This results in an increase in the short-circuit current $I_{sc}$ [8]. The combination of these effects causes a reduction on the output power and therefore in efficiency [9]. This aspect causes a displacement of the maximum power point of the system. The research in innovative maximum power point tracker (MPPT) algorithms seeks to give a solution to this problem by optimizing the production of the power generation systems [10].

Depending on the cell type and construction or the conditions in which it has been characterized [11,12,13], the efficiency can decrease by about 0.45% when the temperature increases by one degree. Thus, part of the research and engineering related to this energy source focuses on the thermal management of these devices. In addition, as Sharma et al. [14] indicated in their research, the application of cooling in photovoltaic panels can have an effect on the panel’s lifetime. The lifetime would be increased, bringing environmental and economic benefits to the users and owners of this technology.

Several methods have been used for this, such as radiative cooling, natural or forced convection, microchannels, or impingement. This last system is the one that has been investigated in this work. Zhu et al. [15] investigated the potential for radiation into outer space by taking advantage of the atmospheric transparency window placing a sheet over the photovoltaic cell. This passive mode not only allows the temperature of the cell to be lowered by up to 13 °C but also maintains and even increases the energy absorption of the cell. Another way of cooling the cells, or in this case photovoltaic panels, is proposed by Amelia et al. [16], where the effect of including one or more fans on the back of these panels to improve performance in hot climates is experimentally analyzed. The results are compared with a panel under natural convection conditions. The thermal distribution of each panel is analyzed by thermography and the results show that the output power increases as the temperature decreases. In their conclusions they indicate, without quantitatively analyzing, that the increase in the number of fans is a disadvantage since they require electrical power, thus affecting the net performance of the installation. Another form of forced convection was used by Radwan et al. [17] in their research using microchannels. A fluid containing nanoparticles is circulated through these channels to cool a low concentrated photovoltaic-thermal system. Moreover, within the forced convection systems but separated by its nature is the impingement cooling. This last method is the one that has been investigated in this work. Hasan et al. [18] performed a similar work to that of Radwan, but instead used fluid impingement as a cooling technique for a commercial size solar panel. Their results show output power increases of up to 62.5%.

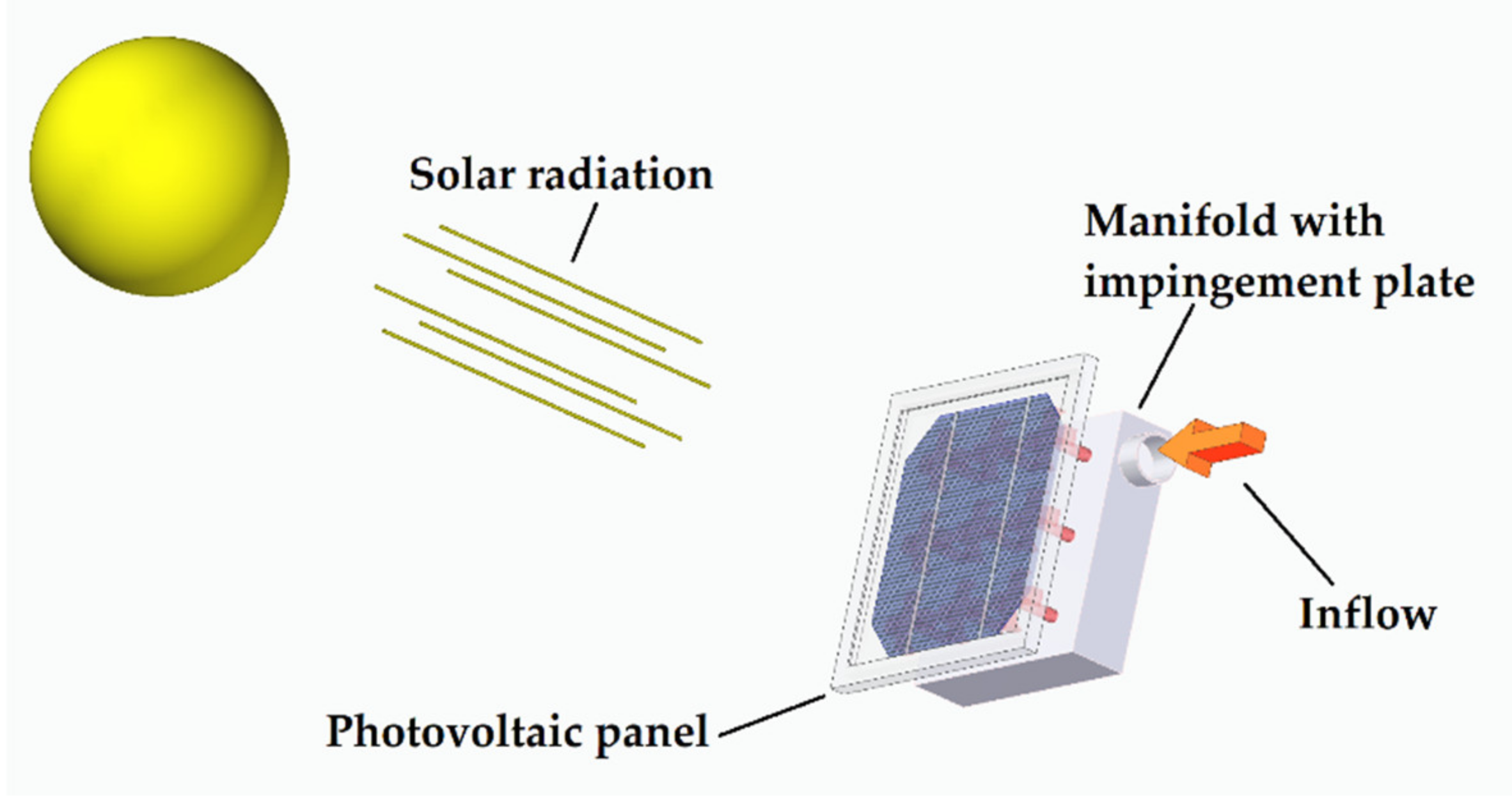
Air jet impingement systems have proven to be a very efficient way of heat transfer, allowing them to be applied in several industries [19,20]. This technology is based on the impact of a fluid, injected from one or several nozzles, on the surface to be cooled. These nozzles are usually normal to the target plate, but other angles of incidence have been experimentally tested [21]. Figure 1 represents the basic system of study of this work. It shows a solar panel exposed to the incidence of solar rays. In the rear side, a cooling fluid is introduced in a manifold and exits through a series of nozzles that form jets. These jets impinge the back of the $PV$ assembly, creating a forced convection heat transfer system. In Figure 2, the basic parameters of a single impinging jet are shown. The nozzle diameter ($D)$, its distance to the target plate ($z),$ and the thickness of the impingement plate ($e)$, are also shown. In practical applications it is usual to use nozzle arrays placed into a plate to achieve a high heat transfer rate distributed over the entire exchange surface. The crossflow scheme is defined by the spent air crosses the space between the impingement and target plates. Depending on the available air outlets crossflow is named as minimum, medium, maximum, or zero, as sketched in Figure 3. In this figure, another main parameter of an impingement system is shown, nozzle-to-nozzle spacing ($S)$. In the same figure, the outlet of the air from the impingement zone is indicated by arrows, except for the zero crossflow case. In this case, the air outlet is indicated by the colored nozzles and normal to the view.

In the present paper, the research focused on evaluating the minimum and zero crossflow configurations. Other configurations were discarded because medium crossflow offered very similar results to minimum, while maximum crossflow suffered from a lack of uniformity, which is an undesirable characteristic. In the first configuration, the impinging air exchanged heat after forming a jet through the nozzles and escaped through the sides of the system, parallel to the target plate. However, in the case of zero crossflow, the air passed through another array of nozzles in the impingement plate, leading to a chamber in which would release into the atmosphere. These outlet nozzles were located between the inlet nozzles, so that the air, after hitting the target plate and exchanging heat, escaped with little travel through the plate. In the case of minimum crossflow, the air reached the sides of the impingement plate with varying distance, depending on the location of the nozzle through which the jet flowed. This means that the configurations with higher crossflow presented less uniformity in heat transfer [23]. However, the pumping power required for the air to flow through the impingement plate was twice as high [24].

The use of air impingement as a thermal management technique was previously used in the field of $PV$ energy. Bahaidarah [25] investigated the feasibility of cooling $PV$ panels with impingement in the Middle East, achieving temperature drops of up to 12 °C and maximum harvesting improvements of around 50%. Lee and Vafai [26] compared microchannels and impingement, concluding that while the first system requires low flow and causes high pressure drop, the opposite occurs in the impingement. The uniformity in the heat transfer of an impingement system in a zero crossflow configuration allows more homogeneous thermal distribution in the cell or photovoltaic panel to be cooled [24,27] and therefore operates in better conditions [28].

The objectives of this research were, firstly, to experimentally validate a refrigeration evaluation system by air jet impingement for the improvement of photovoltaic systems. In addition, we sought to compare the cooling capacity of two air jet impingement crossflow configurations experimentally and theoretically evaluate their implications in the efficiency of a photovoltaic system. Regarding this feature, we analyzed the uniformity advantages of the zero crossflow configuration of large photovoltaic panels, examining if they were applicable to smaller units that served as a power supply to low power devices. Unlike other studies, part of the innovation and contribution of the present study is the consideration of the net power increase when comparing cases. For this purpose, the hydraulic power required to project the jets was taken into account, especially when compared to the total increase in electrical power harvested.

2. Materials and Methods

2.1. Experimental Setup

A test bench was designed to evaluate the heat transfer capacity of an air jet impingement system with two crossflow configurations. Figure 4 shows a section of the parts that constitute the impingement system, with the plenum, impingement plate, and target plate. The air was introduced through the upper orifice (1) of the plenum box. A diffuser (2) guaranteed a uniform distribution of the air and a uniform outlet through the nozzles. The function of the plenum box (3) was to stabilize the air so that it could be considered a static pressurized air storage. From this chamber, the air passed through the inlet nozzles (5), which form the impingement plate (4), in both cases forming the jets that impacted the heat exchange surface of the target plate (6). This piece was electrically heated by means of two electrodes located at its ends (8). Subsequently, the air left the system laterally (7) in the case of minimum crossflow or through the outlet nozzles in the case of zero crossflow. There was a side opening (9) for the measurement of the static pressure in the chamber. This setup allowed a quick change between crossflow configurations for testing. The number of nozzles, layout, and other parameters are shown below in

Table 1. Impingement plate geometrical parameters.

Parameter	Unit	Minimum Crossflow	Zero Crossflow–Inlet/Outlet
D	mm	5	5/5
Array dimension	-	3 × 3	3 × 3/2 × 2
S/D	-	6.66	6.66
e/D	-	0.71429	2.85714/0.71429
z/D	-	3	3
Lips	-	Sharp	Sharp

. The selected number of nozzles was chosen for two reasons. First, a configuration where jet interactions could be seen was chosen. In addition, the area affected by each jet was as large as possible so that the resolution of the camera could accurately capture the thermal gradients. That was why a 3 × 3 rectangular grid was chosen for the 100 mm × 100 mm target plate, which corresponded to the length ($L)$ and width ($W)$. Figure 5 shows in detail the impingement plates used in this study and displays examples of the path of air through them.

The target plate consisted of a thin mica insulating sheet of 350 μm thickness covered with a 50 μm thick electrically conductive layer. The conducting layer was an electric paint of Bare Conductive brand, where joule heating took place when applying a voltage. This paint was applied using screen painting 43T mesh to ensure a uniform thickness. Its relatively high electrical surface resistivity, 50 Ω/Square, allowed to heat the target plate at low potential compared to others [29,30,31]. The electrical current came from an AC power grid with potential regulated with an autotransformer.

Air was supplied using the compressed air connection of the laboratory, whilst the volumetric flow rate was determined using an SMC PFMB7501 digital flow switch, with a working range from 5 to 500 L/min, which was in the optimum range for this study. Static pressure in the plenum was measured with a PCE-P01 pressure meter. Air temperature was measured with a type-T thermocouple inserted through a hole at the plenum entrance and connected to an Amprobe TMD-56 logging thermometer. Electric current and potential measurements were recorded using a Fluke 115 multimeter. In Figure 6 a schematic of the setup is shown.

The cooling capacity of each assembly was evaluated using infrared thermography with an OPTRIS PI400 camera. The camera was located behind the target plate pointing to the electric conductive layer. The postprocessing of the thermographic images was performed using a MATLAB script where the methodology applied by Cocchi et al. [29] was employed. Due to the lower thickness of the target plate of this study and the low thermal conductivity of the mica sheet, a simplification was done over that model, neglecting the planar heat conduction. In Figure 7, a sketch of the explained above is shown. The calibration process of the thermographic camera was carried out using thermocouples placed in contact with the surface.

The thermal load applied to the target plate was regulated with the autotransformer. The voltage applied to the plate was 50V AC 50 Hz, which led to a dissipated power of 21.5 W. To determine the range of volumetric flow of the study, which was limited by the sensitivity of the instruments and the higher flow restriction caused by the zero crossflow impingement plate, a preliminary study was made. With steps between different levels of approximately 50 L/min, five experiments were conducted for each impingement plate, increasing the flow approximately from 50 L/min to 250 L/min. A natural convection case (0 L/min) was not considered for two reasons. The first reason was that, at the applied power levels, the temperature reached without flow compromises the integrity of the target plate. The increase in temperature caused the detachment of the electrodes and permanent deterioration of the electrical conductive paint. Secondly, the presence of a plenum prevented the contact of the back side with the external surrounding air, impeding natural convection cooling. This system required lower voltages than other systems based on metallic sheets [29], although it was suitable only for a temperature range lower than 90–100 °C based on previous prototypes destruction.

The result of the postprocessed thermal images obtained in the experiments is the Nusselt Number (Nu) distribution over the target plate, which allowed for a later estimation for an impingement system of similar dimensions. This non-dimensional number related the convective heat transfer coefficient with the conductive heat transfer coefficient, giving a perspective on how effective a convective cooling system was.

2.2. Photovoltaic Efficiency Estimation Model

In order to estimate the efficiency of a photovoltaic module, a finite difference 1D steady state thermal load model was used. This model simulated the heating of a solar module under a certain irradiance and environmental conditions. This model was based on the model developed by Hammami et al. [32].

A theoretical $PV$ module matching the dimensions of the previously tested target plate was considered, 100 × 100 mm. This area was fully covered by the photovoltaic cell and composed of the layers and materials described in

Table 2. Layers and materials considered for the solar thermal load model.

Layer Number	Material	Thickness [mm]
1	Glass	4
2	Ethylene Vinyl Acetate (EVA)	0.4
3	Silicon $PV$ cell	0.4
4	Ethylene Vinyl Acetate (EVA)	0.4
5	Backsheet	0.3

.

The internal heat flow inside the 1D finite difference steady state implicit model was similar to the one shown in Figure 7, except for the heat generation that took place due to the solar loads and the power that left the systems inside the $PV$ cell as incident solar radiation was converted into electric power. In Figure 8, a conventional natural convection cooling $PV$ system (a) with thermal flows is shown and compared with an impingement cooling system (b).

The operating temperatures were solved by applying the following thermal balance with the employed 1D thermal model:

$$G_{n}A-P_{pv}-Q_{tot}=0$$

(1)

where $G_n$ is the radiation flux W/m² incident on the module, $A$ is the area, $P_{pv}$ is the transformed electrical power, and $Q_{tot}$ the addition of all convective and conductive thermal losses. This term, which comprised all the heat flows represented in Figure 8b, included the convective heat transfer determined experimentally with the setup presented in Section 2.1. The conversion efficiency ${\eta }_{PV}$ of the $PV$ cell was then calculated with the cell average temperature $T_c$ and, assuming a linear decrease with temperature, the following model, with coefficients taken from Mbewe et al. [11].

$${\eta }_{PV}=a\left(1-b{T}_c\right)$$

(2)

The boundary conditions applied to this model to evaluate the performance of the solar cell under natural and forced convection are in

Table 3. Solar 1D model boundary conditions.

	Natural Convection	Forced Convection
Tilt angle (°)	45
Air temperature (°C)	20
Ground temperature (°C)	20
Irradiance (W/m2)	1000
Wind speed (m/s)	1
Rear convection	Analytical plate at specified angle	Nusselt number obtained from experiments

.

3. Results

This research was divided into the following sections to make it easier to understand. First, the influence of the crossflow configuration on the hydraulic characteristic curve of the installation was evaluated. Due to the resulting airflow, a temperature distribution was produced, which is examined below. Once the thermal distribution and the air flow were known, the heat transfer that took place in the plate was calculated by obtaining the Nusselt number, so that the results could be extrapolated to other cases. Finally, the capability of a cooling system such as the one studied for increasing the harvesting efficiency of a solar cell was analyzed.

3.1. Hydraulic Response of the System

The configurations evaluated in this paper differed in the way that air escaped from the heat exchange zone. While in the case of minimum crossflow, the air escaped parallel to the impingement plate; in the case of zero crossflow, the air escaped perpendicularly to the plate through other holes. This last configuration caused the flow used in the cooling of the component to pass twice through a constriction, which meant that the pressure losses generated in a system were larger.

Figure 9 shows the characteristic curves of each of the configurations at the five flow rates tested. It is clear how the zero crossflow plate obtained higher pressure drop values over the entire range studied than those obtained in the minimum crossflow configuration.

These curves were adjusted to equations of the form $y=a{x}^2$ as they were characteristic curves and the pressure had a quadratic dependence with respect to the flow that crossed the obstruction, in this case, the impingement plate. The (0,0) point also was considered in the fitting. The equation that models the pressure loss in the evaluated plates is:

$$\Delta p=\frac{8\rho }{N^2{\pi }^2{C}_d^2{D}^4}{Q}^2$$

(3)

where $\Delta p$ and $Q$ are the pressure drop and volumetric flow. The density of the fluid $\rho$ at the testing conditions is 1.2027 $kg/m^3$. The number of nozzles $N$ and their diameter $D$ are the same of Table 1. Pressure drop data is fitted to the equation using $C_d$ as fitting coefficient, and the results are shown in

Table 4. Fitting coefficient and determination coefficient for the pressure drop versus flow curve

	${\mathit{C}}_{\mathit{d}}$	${\mathit{R}}^2$
Zero Crossflow	0.369	0.994
Minimum Crossflow	0.723	0.999

, including the goodness of the fitting represented by the determination coefficient $R^2$.

The nozzles and plate of the minimum crossflow case of this study have the same ratio of thickness and diameter $e/D$ as in the study developed by Royne [33]. The resulting discharge coefficient value of 0.723 for the minimum crossflow case was higher than the 0.582 obtained in that research work using the same fitting technique, although it was among the theoretical limits for the discharge coefficient for a single plate pass, 0.570–0.990. For the zero crossflow scheme, the discharge coefficient represented the equivalent of the two passes through the impingement plate of nine and four nozzles. Therefore, the fitting coefficient lay outside of the mentioned bounds. To get an appropriate value for each nozzle array properly, it would be necessary to place an additional pressure sensor in the heat exchange zone.

3.2. Thermal Distribution and Heat Transfer

Tested impingement plates generated a thermal distribution over the target plate by extracting heat from the impingement of the jets. First, Figure 10 shows the thermal distribution in the measurement area of the images taken with the infrared camera. These images were processed in a way that allowed us to show the temperature of the impact side of the jets applying the methodology described in Section 2.1.

In these images, the first thing that can be clearly distinguished is the location of the jets that cooled the plate by means of their impact; concentric temperature gradients formed with respect to the location of each nozzle. There was no difference in shape due to the crossflow effect, so at first glance it is not possible to distinguish which impingement plate an image belongs.

As for the temperature levels of each case, it appreciated for the whole range of flows studied. The minimum crossflow impingement plate obtained lower values in the centers of the jets.

By comparing each flow level, it can be seen how the temperatures on the sides of the target plate were higher in the case of zero crossflow, achieving in all cases the maximum temperature. This effect is related to the outflow of the air from the heat exchange zone. While in the case of minimum crossflow, the air outlet was located at the extremes of the plate, in the case of minimum crossflow it was located in four holes inside the plate, leaving an area with lower cooling.

The cooling of the impingement plate and lowering of the temperatures were the consequence of the heat transfer that took place in the impingement of the air jets. One way to evaluate that heat transfer was through the Nusselt Number, which indicated the efficiency of a convective cooling system. This dimensionless number, Equation (4), measured the increase in heat transfer on the surface over which a fluid was circulating compared to the transfer that would occur only by conduction. The terms of this equation defined the heat transfer coefficient $h$, a characteristic length of the system $L_C$, and the thermal conductivity of the fluid $k$.

$$Nu=\frac{h{L}_C}{k}$$

(4)

For this case, the characteristic length of the system is defined using the following relationship involving its length $L$ and width $W$. This widens the range of application in the mathematical model presented in Section 2.2, allowing the use of cells or panels with different aspect ratios and in different positions.

$$L_C=\frac{LW}{2L+2W}$$

(5)

In order to compare quantitatively the Nusselt number distribution along the target plate, six measurement lines were used. Three of these lines were vertical and three of them horizontal, as sketched in Figure 11, covering the full surface crossing all nozzle center locations.

The following graphs, Figure 12, represent the measurement lines on the surface of the target plate for each of the tested cases. Since the number of curves is high and in order to facilitate understanding, graphs were generated to show the average of these lines $\mu$ together with their standard deviation $\sigma$.

The plots from Figure 12 show that the Nusselt number in all the investigated flow rates was higher in the case of minimum crossflow, as it was expected due to the lower temperatures obtained by the thermographic camera. This can be observed when comparing the maximum values, located at nozzle centers for the same flow rate. It can also be seen how the standard deviation was higher in the case of minimum crossflow, thus it can be said that the uniformity in cooling was higher in the case of zero crossflow. The Nusselt Number curves obtained at low flow rates reached very similar values for both configurations. However, as the circulating flow increased, the differences were accentuated when comparing the profiles of the same flow. A clearer distinction in the heat transfer peaks that overlapped with the nozzle locations were made. The minimum values of each measuring line, located in the separation of the area of influence of each jet, did not vary greatly.

Figure 13 compares the average Nusselt number of each case tested with (a) the Reynolds number and (b) the pressure drop in each flow. When comparing the Nusselt Number with the Reynolds number, it can be observed that, for both cross-flow configurations, the values obtained increased throughout the Reynolds range studied. The values were higher throughout the range for the minimum crossflow case. The gap between both cases became significant from the third flow rate studied. For the first two cases, the Nusselt Number of the minimum crossflow was 1.1–1.2 times higher than zero crossflow. However, from then on, this difference increased to values between 1.5 and 1.6 times higher. This difference was caused by an increase in the slope of the curve of the minimum crossflow case. The plot was for both cases monotonically increasing. This indicates that, for the range studied, there was no fluid dynamic phenomenon that generated local maximums or minimums in heat transfer. When comparing the number of Nusselt obtained with the pressure drop caused in the hydraulic system, it was observed that both curves had a steeper slope in the cases tested with lower flow, reducing it as the flow increased. It can be concluded that the minimum crossflow cases achieved higher heat transfer rates than zero crossflow cases with lower pressure drops all over the studied range.

3.3. Effect of Cooling on the Efficiency of a Photovoltaic Cell

Once the heat transfer values for the selected impingement plates were determined for an operating flow range between 50 and 250 L/min, the effect of using a cooling system of this type on the efficiency of a photovoltaic cell was evaluated. The combination of these data with the algorithm adapted to this case described in Section 2 made it possible to compare both systems from the point of view of energy harvesting and the overall efficiency of a combined system.

The following tables contains the numerical results of the combination of the solar harvesting prediction model and the experimentally obtained heat transfer due to air impingement. The results compare the power output of a $PV$ panel under the simulated conditions indicated in Section 2.2 with the power output of an air jet impingement cooled panel. In order to achieve this increase in harvested electrical power $\Delta P_{EL}$, it was necessary to pump air through the impingement plate, which had an associated energetic cost. The power input $P_{INP}$ required to supply air at a given pressure and flow is determined by Equation (6). This was the result of the hydraulic provided by centrifugal blowers and their efficiency ${\eta }_B$, which took a typical value of 60% at the optimum point of operation.

$$P_{INP}=\frac{\Delta p·Q}{{\eta }_B}$$

(6)

Table 5. Power balance chart for zero crossflow cooled $PV$ cell and comparison with base (natural convection) case.

Re	∆PEL [W]	PINP (EST) [W]	ΔPNET [W]	%ΔP [-]
1587	0.117	0.198	−0.081	−5.87%
3205	0.130	1.488	−1.358	−97.90%
4729	0.134	4.391	−4.257	−306.85%
6316	0.137	9.417	−9.280	−668.97%
7872	0.139	18.061	−17.922	−1291.98%

Power balance chart for zero crossflow cooled $PV$ cell and comparison with base (natural convection) case. It shows the data for the zero crossflow case.

Table 6. Power balance chart for minimum crossflow cooled $PV$ cell and comparison with base (natural convection) case.

Re	∆PEL [W]	PINP (EST) [W]	ΔPNET [W]	%ΔP [-]
1556	0.119	0.028	0.092	6.60%
3111	0.133	0.278	−0.144	−10.41%
4636	0.141	0.952	−0.811	−58.48%
6285	0.143	2.244	−2.101	−151.47%
7809	0.145	4.462	−4.318	−311.24%

Power balance chart for minimum crossflow cooled $PV$ cell and comparison with base (natural convection) case. It shows the data for the minimum crossflow case. The total $\Delta P_{NET}$ and percentual $\%\Delta P$ power variation of the cooled systems was compared with a cell cooled by natural convection and no power input.

The harvested power variation increased as airflow and Re increased and the cell temperature lowered for both cases. The difference crossflow schemes was between 1.7% and 4.3% higher for the minimum crossflow case. However, the power input required to pump air and lower the cell temperature was three to six times higher in the zero crossflow case. This imbalance in the harvested and input power made that only one of the tested points of both cases reach a positive net power variation $\Delta P_{NET}$. This increase was of 0.092 W for the tested $PV$ panel under the studied conditions, which represented an improvement of 6.60% over the natural convection case power output.

Figure 14 shows the increase in electrical energy due to cooling as compared to the power required to obtain this temperature drop via air impulsion. The efficiency limit curve (green color) shows the boundary that the power required to pump air for cooling equaled the increase in harvested power. If a value is located at the right of the green curve, it means that the power required to pump air was higher than the increase in harvested power, giving a lower net power output. In contrary, if a value lies at the left of the efficiency limit, the opposite occurs, meaning that the net power output was higher than in natural convection case. Looking at the curves of each crossflow configuration, it can be noticed that the minimum crossflow was the only one that had a point on the left side of the efficiency limit curve. Thus, the value that remains in that region was the only one among the studied combinations of flow and crossflow configurations that would make the system increase its overall efficiency. At that point, the energy obtained by cooling the cell was higher than the energy used for such cooling, with a net increase in the generated power of 6.60%. The zero crossflow configuration did not have any value that allowed for a net increase of the collected power.

4. Discussion

From the hydraulic point of view, the response of the two impingement plates tested was expected, obtaining higher pressure drops in the case of zero crossflow due to the double crossing of the fluid through the plate.

As far as the value of the discharge coefficient was concerned, a higher value than expected was obtained, having designed the minimum crossflow plate with the same value $e/D$ as the one used by Royne [33]. This variation in the $C_D$ was due to the following factors. First, the fluid used in that case was water, so viscosity could be a determining parameter in the fluid dynamics as it passed through the hole. Secondly, in the array used in the mentioned study, only four nozzles were used, so the existing crossflow may impact the jets. Finally, it may be due to a small difference in the nozzle-to-plate distance $z/D$, of 3.57 for that study. However, the difference seemed to be too small to have such relevant results.

Regarding the temperature distribution of Figure 10, there were no characteristic features on the thermal maps indicating the connection with any crossflow scheme. The reason for this may be that the array of nozzles chosen in this study (i.e., nine nozzles) was too few nozzles for the effects of the crossflow to be appreciable, especially at the ends of the target plate. The only remarkable feature was that, at the ends of the zero crossflow plate, higher temperature values were appreciated. This makes sense since these zones, located away from the air outlet nozzles, were prone to find low fluid velocities and recirculation zones that did not promote efficient heat transfer. This seems to indicate that the uniformity benefits attributed to a zero crossflow plate were not reflected in arrays with a low number of nozzles.

Concerning the heat transfer that took place, it was remarkable that, for the first flow rates tested (50 L/min and 100 L/min), the appreciable differences both in the Nusselt profiles (Figure 12) and in the average (Figure 13a) were not high. However, from this value, the differences in heat transfer became more pronounced between 100 L/min and 150 L/min, recovering a proportional trend from then onwards. The explanation of this phenomenon could be related to the evacuation of hot air. At low flow rates, fountain regions located at the place of the interaction point of four inlet jets were not strong enough to block the evacuation of hot air coming from the exterior zones. These fountain regions were located just below the outlet nozzles and, as flow rate increased, blocked the outlet nozzles, leading to the recirculation of hot air at the perimeter of the plate.

Finally, regarding the effect on the harvesting efficiency of a photovoltaic cell, the use of air impingement was capable of effectively reducing the temperature of the cell, according to the 1D model used for the heat transfer coefficients that were obtained experimentally. The increase in harvested power, considering the power needed to pump air and create cooling jets, reached a maximum of 6.60% increase for the best case. For a typical 300 W peak power module, assuming linearity in the pumping requirement for that area, an extra power of 18 W could be produced. The estimations of the electrical power required to cool the cell resulted in only one evaluated case that increased the overall efficiency of the system using air impingement. This case had the lowest flow rate for the minimum crossflow case. In the case of lower zero crossflow flow, the power consumed by the system was very close to that needed to produce an increase in the net power generated.

Considering the results, the study of low flows rates seemed necessary to find the maximum efficiency that could be reached with the impingement design of minimum crossflow tested, as well as the possibility that the design of zero crossflow could provide positive values of variation in the overall efficiency. The efficiency of the system could also be improved using air jet impingement plate optimization algorithms such as the one developed by Martínez-Filgueira et al. [34]. This multi-objective algorithm could determine the optimum nozzle number, diameter, and other interest parameters, depending on the requirements. For this case, the optimization should minimize the cell temperature while minimizing the required pumping power.

5. Conclusions

In this work, two different air jet impingement plates were evaluated to determine if the net harvesting efficiency of a photovoltaic cell could be improved by reducing its operating temperature.

A zero crossflow scheme was shown to require three to six times higher electrical pumping power than a minimum crossflow scheme, according to results Table 5 and Table 6 to provide the same flow rate.

The theoretical advantages of higher uniformity in a zero crossflow scheme were not evident in this case, probably due to the small size of the target plate and the low number of nozzles. Maximum temperature values were located at the perimeter for this arrangement. However, the effects of crossflow could not be be ignored, since it dramatically increased heat transfer in the case of minimum crossflow from the middle of the tested flow range. For these cases, the variation between peaks of Nusselt number at the same flow rate was slightly less than 1.9 times higher.

For a better understanding of the applicability of air jet impingement when cooling real solar installations, arrays of larger size and number of nozzles should be tested. In this way, it would also be checked if the advantages of uniformity in the case of zero crossflow could lead to a higher efficiency at some operating point compared to the minimum crossflow case. The reduction of perimetral area affected by recirculation could overcome the higher pumping requirement with the expected higher uniformity.

As final conclusion, it can be said that the theoretical analysis of cooling on a photovoltaic cell shows that it was possible to increase the net harvesting efficiency as well as the power produced by up to 6.60%. This increase in generated power cold make investments in photovoltaic energy more profitable. In addition, it could reduce the environmental impact of these facilities by requiring fewer modules to reach the same power output and helping to extend their service life.

This study was conducted in a range where only one point has proven successful to increase harvesting. For future cases, it would be convenient to adapt the flow rate range by making a pre-study of the area that may be of most interest. In the upcoming research, we will start from geometries previously optimized by means of algorithms. The effect of the weighting of the optimization parameters on the final geometry and heat transfer will be analyzed simultaneously.