Improved Predictive Control for an Asymmetric Multilevel Converter for Photovoltaic Energy
Abstract
:1. Introduction
2. The Proposed Solution
2.1. Converter Modulation
2.2. AC Link Dynamic Model
2.3. DC Link Dynamic Model
2.4. Predictive Algorithm
2.4.1. Stability and Robustness Assessment
2.4.2. Mitigation of Undesired Commutations
2.5. Zero State Equalization
2.6. Control Strategy
3. Simulation Results
3.1. Transient State Analysis
3.2. Steady State Analysis
4. Experimental Implementation
4.1. Commutation Elimination in the HPC
4.2. Discrete Master Control
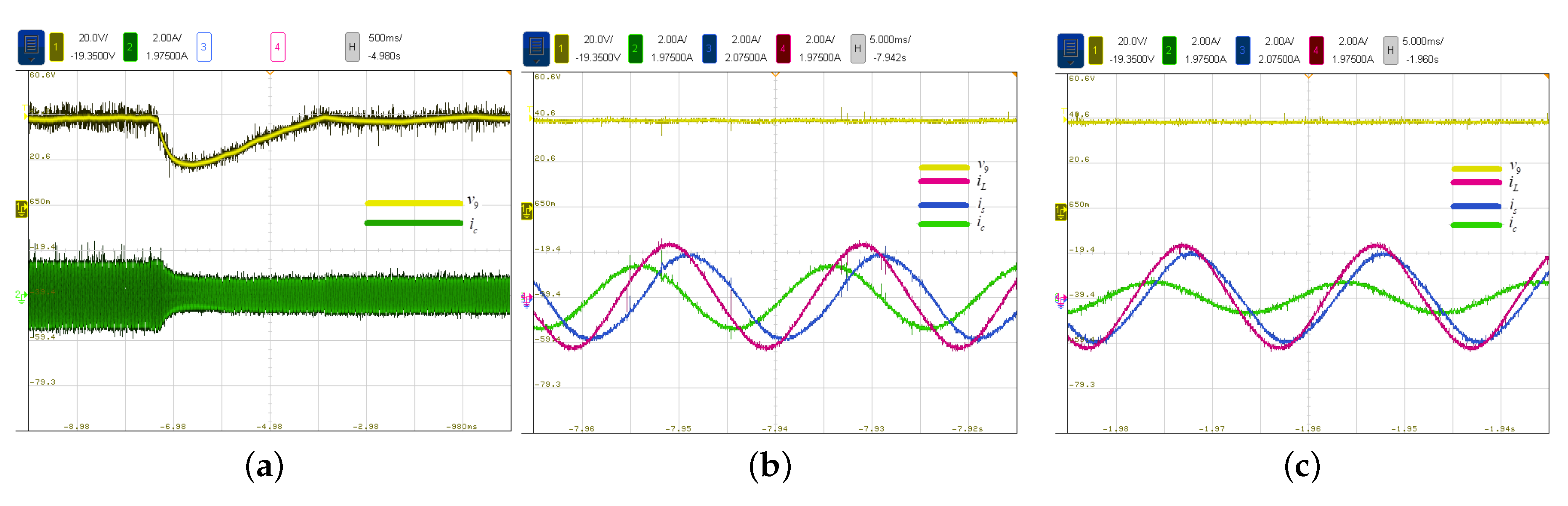
4.3. Result Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| IEEE | Institute of Electrical and Electronics Engineers |
| AC | Alternating Current |
| MPPT | Maximum Power Point Tracker |
| DC | Direct Current |
| PWM | Pulse Width Modulation |
| APOD | Alternative Phase Opposition Disposition Pulse Width Modulation |
| POD | Phase Opposition Disposition Pulse Width Modulation |
| LS-PWM | Level Shifted Pulse Width Modulation |
| ACMLI | Asymmetric Cascade Multi-level Inverter |
| NPC | Neutral Point Clamped |
| CHB | Cascade H-Bridge |
| MMC | Modular Multilevel Converter |
| AMC | Asymmetric Multilevel Converter |
| PV | Photovoltaic |
| SVM | Space Vector Modulation |
| MPC | Modulated Model Predictive Control |
| PI | Proportional Integrative |
| PR | Proportional Resonant |
| THD | Total Harmonic Distortion |
| DSP | Digital Signal Processing |
| FPGA | Field-Programmable Gate Array |
| HPC | High-Power Cell |
| MPC | Medium-Power Cell |
| LPC | Low-Power Cell |
| MOSFET | Metal-Oxide-Semiconductor Field-Effect Transistor |
References
- Renewable Capacity Highlights. Available online: https://www.irena.org/ (accessed on 29 July 2020).
- Global Energy System Based on 100% Renewable Energy. Available online: http://energywatchgroup.org/new-study-global-energy-system-based-100-renewable-energy (accessed on 29 July 2020).
- Beránek, V.; Olšan, T.; Libra, M.; Poulek, V.; Sedlacek, J.; Dang, M.Q.; Tyukhov, I. New Monitoring System for Photovoltaic Power Plants’ Management. Energies 2018, 11, 2495. [Google Scholar] [CrossRef] [Green Version]
- Franquelo, L.G.; Rodriguez, J.; Leon, J.I.; Kouro, S.; Portillo, R.; Prats, M.A.M. The age of multilevel converters arrives. IEEE Ind. Electron. Mag. 2008, 2, 28–39. [Google Scholar] [CrossRef] [Green Version]
- Kouro, S.; Leon, J.I.; Vinnikov, D.; Franquelo, L.G. Grid-Connected Photovoltaic Systems: An Overview of Recent Research and Emerging PV Converter Technology. IEEE Ind. Electron. Mag. 2015, 9, 47–61. [Google Scholar] [CrossRef]
- Kouro, S.; Malinowski, M.; Gopakumar, K.; Pou, J.; Franquelo, L.G.; Wu, B.; Rodriguez, J.; Perez, M.A.; Leon, J.I. Recent Advances and Industrial Applications of Multilevel Converters. IEEE Trans. Ind. Electron. 2010, 57, 2553–2580. [Google Scholar] [CrossRef]
- Rodriguez, J.; Bernet, S.; Wu, B.; Pontt, J.O.; Kouro, S. Multilevel Voltage-Source-Converter Topologies for Industrial Medium-Voltage Drives. IEEE Trans. Ind. Electron. 2007, 54, 2930–2945. [Google Scholar] [CrossRef]
- Pereda, J.; Dixon, J. Cascaded Multilevel Converters: Optimal Asymmetries and Floating Capacitor Control. IEEE Trans. Ind. Electron. 2013, 60, 4784–4793. [Google Scholar] [CrossRef]
- Yenes, A.; Muñoz, D.; Pereda, J. Optimal asymmetry for cascaded multilevel converter with cross-connected half-bridges. In Proceedings of the IECON 2015—41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 1795–1800. [Google Scholar] [CrossRef]
- Chattopadhyay, S.K.; Chakraborty, C. Performance of Three-Phase Asymmetric Cascaded Bridge (16:4:1) Multilevel Inverter. IEEE Trans. Ind. Electron. 2015, 62, 5983–5992. [Google Scholar] [CrossRef]
- Gonzalez, S.A.; Valla, M.I.; Christiansen, C.F. Five-level cascade asymmetric multilevel converter. IET Power Electron. 2010, 3, 120–128. [Google Scholar] [CrossRef]
- Buccella, C.; Cimoroni, M.G.; Cecati, C. General Formula for SHE Problem Solution. Energies 2020, 13, 3740. [Google Scholar] [CrossRef]
- Briz, F.; Lopez, M.; Rodriguez, A.; Arias, M. Modular Power Electronic Transformers: Modular Multilevel Converter Versus Cascaded H-Bridge Solutions. IEEE Ind. Electron. Mag. 2016, 10, 6–19. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, T.; Mao, W.; Tan, D.; Chang, L. Multilevel Inverters for Grid-Connected Photovoltaic Applications: Examining Emerging Trends. IEEE Power Electron. Mag. 2018, 5, 32–41. [Google Scholar] [CrossRef]
- Leon, J.I.; Vazquez, S.; Kouro, S.; Franquelo, L.G.; Carrasco, J.M.; Rodriguez, J. Unidimensional Modulation Technique for Cascaded Multilevel Converters. IEEE Trans. Ind. Electron. 2009, 56, 2981–2986. [Google Scholar] [CrossRef]
- Bohari, A.A.; Goh, H.H.; Tonni, A.K.; Lee, S.S.; Sim, S.Y.; Goh, K.C.; Lim, C.S.; Luo, Y.C. Predictive Direct Power Control for Dual-Active-Bridge Multilevel Inverter Based on Conservative Power Theory. Energies 2020, 13, 2951. [Google Scholar] [CrossRef]
- Kamani, P.L.; Mulla, M.A. Middle-Level SHE Pulse-Amplitude Modulation for Cascaded Multilevel Inverters. IEEE Trans. Ind. Electron. 2018, 65, 2828–2833. [Google Scholar] [CrossRef]
- Ding, K.; Cheng, K.W.E.; Zou, Y.P. Analysis of an asymmetric modulation method for cascaded multilevel inverters. IET Power Electron. 2012, 5, 74–85. [Google Scholar] [CrossRef]
- Edpuganti, A.; Rathore, A.K. A Survey of Low Switching Frequency Modulation Techniques for Medium-Voltage Multilevel Converters. IEEE Trans. Ind. Appl. 2015, 51, 4212–4228. [Google Scholar] [CrossRef]
- Muñoz, J.; Gaisse, P.; Baier, C.; Rivera, M.; Gregor, R.; Zanchetta, P. Asymmetric multilevel topology for photovoltaic energy injection to microgrids. In Proceedings of the 2016 IEEE 17th Workshop on Control and Modeling for Power Electronics (COMPEL), Trondheim, Norway, 27–30 June 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Muñoz, J.; Gaisse, P.; Cadena, F.; Baier, C.; Aliaga, R.; Troncoso, J. Proportional resonant controller for a 27-level asymmetric multilevel STATCOM. In Proceedings of the 2017 CHILEAN Conference on Electrical, Electronics Engineering, Information and Communication Technologies (CHILECON), Pucon, Chile, 18–20 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Ogata, K. Ingeniería de Control Moderna; Pearson: Madrid, Spain, 2010. [Google Scholar]
- Muñoz, J.; Gaisse, P.; Cadena, F.; Rivera, M.; Baier, C.; Restrepo, C. Model predictive control for a 27-level asymmetric multilevel STATic COMpensator. In Proceedings of the 2017 IEEE Southern Power Electronics Conference (SPEC), Puerto Varas, Chile, 4–7 December 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Villalón, A.; Rivera, M.; Salgueiro, Y.; Muñoz, J.; Dragičević, T.; Blaabjerg, F. Predictive control for microgrid applications: A review study. Energies 2020, 13, 2454. [Google Scholar] [CrossRef]
- Geyer, T. Computationally efficient model predictive direct torque control. IEEE Trans. Power Electron. 2011, 26, 2804–2816. [Google Scholar] [CrossRef]
- Rodriguez, J.; Kazmierkowski, M.P.; Espinoza, J.R.; Zanchetta, P.; Abu-Rub, H.; Young, H.A.; Rojas, C.A. State of the Art of Finite Control Set Model Predictive Control in Power Electronics. IEEE Trans. Ind. Inform. 2013, 9, 1003–1016. [Google Scholar] [CrossRef]
- Perez, M.A.; Cortes, P.; Rodriguez, J. Predictive Control Algorithm Technique for Multilevel Asymmetric Cascaded H-Bridge Inverters. IEEE Trans. Ind. Electron. 2008, 55, 4354–4361. [Google Scholar] [CrossRef]
- Muñoz, J.; Soto, B.; Villalón, A.; Rivera, M.; Cossutta, P.; Aguirre, M. Predictive Control of a 27-level Asymmetric Multilevel Current Source Inverter. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I CPS Europe), Palermo, Italy, 12–15 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Chattopadhyay, S.K.; Chakraborty, C. Three-Phase Hybrid Cascaded Multilevel Inverter Using Topological Modules with 1:7 Ratio of Asymmetry. IEEE J. Emerg. Sel. Top. Power Electron. 2018. [Google Scholar] [CrossRef]
- Vargas, R.A.; Figueroa, A.; DeLeon, S.E.; Aguayo, J.; Hernandez, L.; Rodriguez, M.A. Analysis of Minimum Modulation for the 9-Level Multilevel Inverter in Asymmetric Structure. IEEE Lat. Am. Trans. 2015, 13, 2851–2858. [Google Scholar] [CrossRef]
- Silva, P.; Muñoz, J.; Aliaga, R.; Gaisse, P.; Restrepo, C.; Fernández, M. On the DC/DC converters for cascaded asymmetric multilevel inverters aimed to inject photovoltaic energy into microgrids. In Proceedings of the 2016 IEEE 2nd Annual Southern Power Electronics Conference (SPEC), Auckland, New Zealand, 5–8 December 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Rodriguez-Rodríguez, J.; Venegas-Rebollar, V.; Moreno-Goytia, E. Single DC-Sourced 9-level DC/AC Topology as Transformerless Power Interface for Renewable Sources. Energies 2015, 8, 1273–1290. [Google Scholar] [CrossRef] [Green Version]
- Sánchez, G.; Murillo, M.; Genzelis, L.; Deniz, N.; Giovanini, L. MPC for nonlinear systems: A comparative review of discretization methods. In Proceedings of the 2017 XVII Workshop on Information Processing and Control (RPIC), Mar del Plata, Argentina, 20–22 September 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Rawlings, J.B.; Mayne, D.Q.; Diehl, M.M. (Eds.) Model Predictive Control: Theory, Computation, and Design, 2nd ed.; Nob Hill Publishing: Madison, WI, USA, 2017; ISBN 9780975937730. [Google Scholar]
- Rivera, M.; Kouro, S.; Rodriguez, J.; Wu, B.; Espinoza, J. Predictive control of a current source converter operating with low switching frequency. In Proceedings of the IECON 2012—38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 674–679. [Google Scholar] [CrossRef]
- Langella, R.; Testa, A.; Alii, E. IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems; IEEE: Piscataway Township, NJ, USA, 2014. [Google Scholar] [CrossRef]
- Moran, L.A.; Fernandez, L.; Dixon, J.W.; Wallace, R. A simple and low-cost control strategy for active power filters connected in cascade. IEEE Trans. Ind. Electron. 1997, 44, 621–629. [Google Scholar] [CrossRef]
- Colak, I.; Kabalci, E.; Keven, G. Comparision of multi-carrier techniques in seven-level asymmetric cascade multilevel inverter. In Proceedings of the 4th International Conference on Power Engineering, Energy and Electrical Drives, Istanbul, Turkey, 13–17 May 2013; pp. 1619–1624. [Google Scholar]
- Sujitha, N.; Krithiga, S. Hybrid carrier based space vector modulation for PV fed asymmetric cascaded multilevel inverter. In Proceedings of the 2015 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Kochi, India, 10–13 August 2015; pp. 1058–1064. [Google Scholar]
- Kumar, S.; Pal, Y. A Three-Phase Asymmetric Multilevel Inverter for Standalone PV Systems. In Proceedings of the 2019 6th International Conference on Signal Processing and Integrated Networks (SPIN), Uttar Pradesh, India, 7–8 March 2019; pp. 357–361. [Google Scholar]
- Boobalan, S.; Dhanasekaran, R. Hybrid topology of asymmetric cascaded multilevel inverter with renewable energy sources. In Proceedings of the 2014 IEEE International Conference on Advanced Communications, Control and Computing Technologies, Ramanathapuram, India, 8–10 May 2014; pp. 1046–1051. [Google Scholar] [CrossRef]
- Mishra, N.; Kant, P.; Singh, B. An Asymmetric Seven Level Multilevel Converter for Grid Integrated Systems. In Proceedings of the 2018 8th IEEE India International Conference on Power Electronics (IICPE), Jaipur, India, 13–15 December 2018; pp. 1–6. [Google Scholar]
- Shankar, J.G.; Belwin Edward, J. A 15-level asymmetric cascaded H bridge multilevel inverter with less number of switches for photo voltaic system. In Proceedings of the 2016 International Conference on Circuit, Power and Computing Technologies (ICCPCT), Nagercoil, India, 18–19 March 2016; pp. 1–10. [Google Scholar]
- Vasquez, M.; Pontt, J.; Olivares, M.; Vargas, J. Model Predictive Control for an Asymmetric Multilevel Converter with Two Floating Cells per Phase. In Proceedings of the 2015 17th European Conference on Power Electronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015; pp. 1–10. [Google Scholar] [CrossRef]
- Vásquez, M.; Pontt, J.; Vargas, J. Predictive control of an asymmetric cascaded multilevel inverter with a single DC source. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Wien, Austria, 10–13 November 2013; pp. 6305–6310. [Google Scholar]
- Zaouche, K.; Benmerabet, S.M.; Talha, A.; Berkouk, E.M. Finite-Set Model Predictive Control of an Asymmetric Cascaded H-bridge photovoltaic inverter. Appl. Surf. Sci. 2019, 474, 102–110. [Google Scholar] [CrossRef]













| State | HPC | MPC | LPC | Converter Voltage |
|---|---|---|---|---|
| 1 | − V9 − V3 − V1 | |||
| 2 | 0 | − V9 − V3 | ||
| 3 | 1 | − V9 − V3 + V1 | ||
| 4 | 0 | − V9 − V1 | ||
| 5 | 0 | 0 | − V9 | |
| 6 | 0 | 1 | − V9 + V1 | |
| 7 | 1 | − V9 + V3 − V1 | ||
| 8 | 1 | 0 | − V9 + V3 | |
| 9 | 1 | 1 | − V9 + V3 + V1 | |
| 10 | 0 | − V3 − V1 | ||
| 11 | 0 | 0 | − V3 | |
| 12 | 0 | 1 | − V3 + V1 | |
| 13 | 0 | 0 | − V1 | |
| 14 | 0 | 0 | 0 | 0 |
| 15 | 0 | 0 | 1 | V1 |
| 16 | 0 | 1 | + V3 − V1 | |
| 17 | 0 | 1 | 0 | + V3 |
| 18 | 0 | 1 | 1 | + V3 + V1 |
| 19 | 1 | + V9 − V3 − V1 | ||
| 20 | 1 | 0 | + V9 − V3 | |
| 21 | 1 | 1 | + V9 − V3 + V1 | |
| 22 | 1 | 0 | + V9 − V1 | |
| 23 | 1 | 0 | 0 | + V9 |
| 24 | 1 | 0 | 1 | + V9 + V1 |
| 25 | 1 | 1 | + V9 + V3 − V1 | |
| 26 | 1 | 1 | 0 | + V9 + V3 |
| 27 | 1 | 1 | 1 | + V9 + V3 + V1 |
| Element | Description | Value |
|---|---|---|
| Converter resistance | 10 Ω | |
| Converter inductance | ||
| Grid voltage | ||
| Converter voltage | ||
| C | High-power cell (HPC) capacitor | |
| HPC direct current (DC) Reference | ||
| System frequency | ||
| Sampling time |
| 1 | … | 9 | 10 | … | 18 | 19 | … | 27 | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | … | 0 | 1 | … | 1 | 1 | … | 1 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |||
| 9 | 0 | … | 0 | 1 | … | 1 | 1 | … | 1 |
| 10 | 1 | … | 1 | 0 | … | 0 | 1 | … | 1 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |||
| 18 | 1 | … | 1 | 0 | … | 0 | 1 | … | 1 |
| 19 | 1 | … | 1 | 1 | … | 1 | 0 | … | 0 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |||
| 27 | 1 | … | 1 | 1 | … | 1 | 0 | … | 0 |
| THD | Simulation | Experimental |
|---|---|---|
| Article | Topology | Modulation | Type | Application | Control | ||
|---|---|---|---|---|---|---|---|
| [38] | 7-level ACMLI | POD-PWM (4 kHz) | Sim | - | - | 1.12% | 14.83% |
| [38] | 7-level ACMLI | APOD-PWM (4 kHz) | Sim | - | - | 1.05% | 15.2% |
| [39] | 7-level asymmetric cascaded multilevel inverter | Hybrid carrier-based space vector modulation technique (HCBSVM) | Sim | PV | - | - | 3.71% |
| [41] | Cascaded 63-level asymmetrical multilevel inverter | Staircase | Sim | Ren. Energy | - | - | 3.85% |
| [40] | 5-level asymmetric cascaded multilevel inverter | Phase-shifted PWM | Sim | PV | - | - | 5.22% |
| [40] | 5-level asymmetric cascaded multilevel inverter | Level shifted PWM | Sim | PV | - | - | 3.84% |
| [43] | 15-level asymmetrical cascaded H-bridge multilevel inverter | PD-PWM (2 kHz) | Sim | PV | - | - | 6.03% |
| [44] | Asymmetric multilevel converter, composed of a two-level inverter and two floating cells per phase | Space vector | Sim | - | Predictive control | 0.55% | 4.9% |
| [45] | Asymmetric cascaded multilevel inverter with a single DC source | Space vector | Sim | - | Space vector control and predictive control | 1.5% | 12.9% |
| [46] | 15-level asymmetrical cascaded H-bridge multilevel inverter | - | Sim | PV | FS-MPC | <1% | - |
| [42] | 7-level asymmetric cascaded multilevel inverter | LS-PWM (1kHz) | Prot | PV | PI | 2.2% | 13.3% |
| [10] | 16:4:1 Asymmetric multilevel inverter | Space vectors with asymmetrical -staircase | Prot | - | - | - | <4% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaisse, P.; Muñoz, J.; Villalón, A.; Aliaga, R. Improved Predictive Control for an Asymmetric Multilevel Converter for Photovoltaic Energy. Sustainability 2020, 12, 6204. https://doi.org/10.3390/su12156204
Gaisse P, Muñoz J, Villalón A, Aliaga R. Improved Predictive Control for an Asymmetric Multilevel Converter for Photovoltaic Energy. Sustainability. 2020; 12(15):6204. https://doi.org/10.3390/su12156204
Chicago/Turabian StyleGaisse, Patricio, Javier Muñoz, Ariel Villalón, and Rodrigo Aliaga. 2020. "Improved Predictive Control for an Asymmetric Multilevel Converter for Photovoltaic Energy" Sustainability 12, no. 15: 6204. https://doi.org/10.3390/su12156204
APA StyleGaisse, P., Muñoz, J., Villalón, A., & Aliaga, R. (2020). Improved Predictive Control for an Asymmetric Multilevel Converter for Photovoltaic Energy. Sustainability, 12(15), 6204. https://doi.org/10.3390/su12156204






