Research on the Influence of a High-Speed Railway on the Spatial Structure of the Western Urban Agglomeration Based on Fractal Theory—Taking the Chengdu–Chongqing Urban Agglomeration as an Example

Abstract

By shortening the transportation time between cities, high-speed rail shortens the spatial distance between cities and exerts a far-reaching influence on urban agglomerations’ spatial structures. In order to explore the influence of high-speed rail on the spatial reconstruction of an urban agglomeration in western China, this paper employs fractal theory to compare and analyze the spatial structure evolution of the Chengdu–Chongqing urban agglomeration in western China before and after the opening of a high-speed railway. The results show that after the completion of the high-speed railway, the intercity accessibility is improved. The Chengdu–Chongqing urban agglomeration’s spatial distribution shows a decreasing density from the central city to the surrounding areas. Furthermore, the urban system presents a trend of an agglomeration distribution. Therefore, strengthening the construction of high-speed rail channels between primary and medium-sized cities, as well as accelerating the construction of intercity railway networks and rapid transportation systems based on high-speed rail cities, would help develop urban agglomerations in western China.

1. Introduction

In recent years, infrastructure construction mainly based on the high-speed railway has led to urban form transformation. In the great transformation from the ordinary railway era to the high-speed railway era, the urban form has undergone important changes both in the urban agglomeration and in the urban interior [1]. According to the space–time compression theory, the change of high-speed railway speed will affect the spatial–temporal relationship of the urban network, which has an important influence on the regional spatial reconstruction. According to this theory, in Europe in the second half of the 20th century, the EU invested a lot to promote the construction of transnational and trans-regional high-speed rail. Studies have confirmed that high-speed railways can improve different nodes’ accessibility, reducing the time and space distances between Asia and Europe [2]. Scholars believe that high-speed rail links many cities together to create a new area or corridor with higher inter-regional accessibility [3]. Besides, studies have also focused on the negative impact of high-speed rail construction. While absolute accessibility and mobility have improved, the relative accessibility of some regions and cities has decreased. Studies have shown that the primary beneficiaries of constructing the high-speed railway in Europe in the 20th century are the urban agglomerations covered by the high-speed railway network [4]. The accessibility improvement brought by the construction of high-speed railway attracts more people to move out of big cities’ core area to the periphery of urban agglomerations. It promotes the more even distribution of the population [5]. The peripheral areas outside the high-speed rail network (such as Spain and Portugal), if they are not effectively connected to the high-speed rail network, will not benefit from the urban agglomeration’s spreading effect and will be further marginalized [6,7]. Other scholars believe that the polarization and equilibrium effects of constructing the high-speed rail network on the reshaping of regional and urban temporal and spatial relationships exist simultaneously. The evaluation of these two effects should consider the differences in the specific research areas and research scales. On the macro-scale, the construction of high-speed rail makes the regional spatial distribution more balanced. While on the micro-scale, the two effects of equilibrium and polarization exist simultaneously [8].

With the rapid development of China’s high-speed railway, the network of high-speed railway has changed the traffic location and external relations of the cities with high-speed railway stations [9,10], increasing the adsorption capacity of the central cities [11], and weakening the influence of spatial location on urban accessibility [12,13,14,15]. Furthermore, the evolution of urban spatial form along the high-speed railway has a profound impact. Due to the centripetal distribution of the high-speed rail network and the influence of spatial correlation, the urban internal traffic structure and urban spatial structure are more optimized. [16,17]. Moreover, the high-speed railway and various transportation modes’ intermodal transport have brought an unprecedented population and economic flow under the market economy mechanism. The substantial links provided by the transportation infrastructure strengthen the communication within and between cities, and the city develops from an isolated monomer to an urban agglomeration [1]. The spatial reconstruction caused by high-speed rail at the urban agglomerations and metropolitan circles has also become a research focus [18]. Sheng studied the influence of high-speed rail and expressways on urban scale distribution using the rank-size rule [19]. Lu studied the spatial structure of the Beijing–Tianjin–Hebei urban agglomeration using the gravity model that introduced the time distance of high-speed railway [20]. The results showed that its spatial economic trend was very similar to the high-speed railway route map. Wang analyzed the linkage pattern and space–time evolvement of the Beijing–Tianjin–Hebei urban agglomeration based on population flow, and the author verified the heterogeneous effect of the opening of a high-speed railway on the spatial pattern of the urban agglomeration [21]. However, most current studies focus on the more mature urban agglomerations in eastern China and pay less attention to the developing western urban agglomerations. In order to promote the development of a western urban agglomeration more effectively, this paper studies the spatial reconstruction of the western urban agglomeration from the perspective of high-speed railway construction. This paper analyzes the spatial structure change after the high-speed railway opening in the western typical urban agglomeration (the Chengdu–Chongqing urban agglomeration). With the concept of "transportation first in city development" [1], the paper explores ways to promote the spatial structure optimization of the western urban agglomeration from the perspective of high-speed rail planning and construction.

Some advanced methods were proposed to study the evolution of the urban agglomerations’ spatial structure under the influence of high-speed rail construction. Among them, Euclidean geometry has played an important role in the expression and description of urban forms. However, its limitations are obvious in the face of a large number of complex and irregular events (things and phenomena) in real cities [22]. Therefore, Mandelbrot creatively proposed the concepts of fractal and fractal dimension and established a new science—"fractal geometry" [23,24]. It is regarded as the language of nature and the fourth-generation language of geography [25,26], which provides a new mathematical tool for revealing the law of urban self-organization evolution [27,28]. The combination of fractal geometry and urban science has given birth to a new and important research direction: fractal city research [29]. Traditional urban fractal characteristics research is based on the premise of a unified transportation mode. It analyzes based on the spatial distance network structure, ignoring specific traffic modes’ impact on the urban spatial structure [30,31,32]. This study studies the fractal characteristics of the urban agglomeration spatial structure from the perspective of spatial and temporal differences caused by different traffic modes before and after the completion of high-speed rail. Due to the reduction in traffic time after the opening of high-speed rail, the connection between cities will be strengthened. Therefore, it is more scientific to study the urban agglomeration spatial structure’s fractal characteristics using traffic time distance instead of spatial distance [33].

This article aims to explore the impact of high-speed rail on the spatial reconstruction of western urban agglomerations. First, Zipf’s law is combined with fractal theory to analyze the rank-size structure of the Chengdu–Chongqing urban agglomeration, the Guanzhong Plain urban agglomeration, the Lanzhou–Xining(Lan-Xi) urban agglomeration, and the Hohhot–Baotou–Ordos–Yulin (HBOY) urban agglomeration. Then, based on these, we take the Chengdu–Chongqing urban agglomeration as an example, and analyze the spatial cohesion and spatial correlation of the urban agglomeration before and after the opening of the high-speed rail using the aggregation dimension and correlation dimension in the fractal, to reveal the changes in the spatial structure of the Chengdu–Chongqing urban agglomeration. The research results will provide scientific reference for the western region to formulate a reasonable high-speed rail construction plan and promote the urban agglomeration scale and structure optimization.

2. Methods and Data

In order to test the evolution of the spatial structure of urban agglomerations in western China during the period of the rapid development of the western railway, four urban agglomerations in western China were selected as the research areas: they are the Chengdu–Chongqing urban agglomeration, the Guanzhong Plain urban agglomeration, the Lanzhou–Xining (Lan-Xi) urban agglomeration, and the Hohhot–Baotou–Ordos–Yulin (HBOY) urban agglomeration. In February 2010, the Zhengzhou–Xi’an high-speed railway, the first high-speed rail with a maximum speed of 350 km per hour in the central and western regions, was completed and put into operation, marking the beginning of the era of high-speed rail in the western region. Therefore, when studying the western urban agglomeration’s rank-size structure, 2010–2017 was selected as the research time limit. To further explore the impact of high-speed rail on the spatial structure of urban agglomerations, the Chengdu–Chongqing urban agglomeration, which has the fastest high-speed rail network construction and the most mature development among the western urban agglomerations, was taken as an example. Fractal theory was used to study the spatial cohesion and spatial correlation of the urban agglomeration after completing the Chengdu–Chongqing high-speed rail.

2.1. Method

2.1.1. Fractal Model of Urban Scale Sequence Structure

The rank-size structure of the urban system has fractal characteristics. The most basic method to determine the urban system’s rank-size structure is the Hausdorff fractal dimension [22]. In previous studies, many scholars combined the Hausdorff dimension with Zipf’s law and selected the urban population as an indicator, making the data collection and calculation process easier [34]. The Hausdorff dimension’s basic idea is to give an object’s measure its volume through a set of measurement scales, r, and the measurement result must be a value related to r, denoted as N(r). Obviously, the smaller the scale of the r, the larger the measurement result (N(r)); the larger the scale of the r, the smaller the measurement result (N(r)). Generally, the relationship between N(r) and r is expressed as [35]:

$$N\left(r\right)=C{r}^{-D}$$

(1)

Among them, the constant D is usually called the Hausdorff fractal dimension, and C is a constant. Taking the logarithm of both ends of the above formula, the following can be obtained:

$$lnN\left(r\right)=lnC-Dlnr$$

(2)

A series of point pairs (r, N(r)) can be formed by the scale r and the corresponding measurement result N(r), and the linear regression obtains the fractal dimension D.

The formula of Zipf’s law is

$$P\left(r\right)=P_1{r}^{-q}$$

(3)

which can be transformed into

$$lnP\left(r\right)=ln{P}_1-qlnr$$

(4)

Among them, r represents the city sequence; P(r) represents the population of the j-th city; P₁ represents the population of the primary city; and q represents the Zidf dimension. Chen (1999) proved Formula (3) is equivalent to Formula (1), and D =1/q [35]. D in different intervals represents different meanings. If D > 1, it means that the urban population is evenly distributed in the city, the number of medium-sized cities is more, and the city size is centralized distribution. If D < 1, it indicates that the urban population distribution is uneven, the primary city is in an obvious monopoly position, and the city size is distributed in a decentralized way. The case of D = 1 is too ideal and will not be discussed here.

2.1.2. Correlation Model of Urban Spatial Structure

The correlation dimension can simulate the correlation characteristics among the important nodes in an urban agglomeration. The specific model is as follows:

$$C\left(r\right)=\frac{1}{N^2}{{\displaystyle \sum }}_i^N{{\displaystyle \sum }}_j^{n}H\left(r-d_{ij}\right),\left(i\ne j\right)$$

(5)

$$H\left(r-d_{ij}\right)=\{\begin{array}{c}1, d_{ij}\le r\\ 0, d_{ij}>r\end{array}$$

(6)

In order to facilitate the actual calculation, Formula (5) is often changed into

$$C\left(r\right)={{\displaystyle \sum }}_{i,j=1}^{N}H\left(r-d_{ij}\right),\left(i=j\right)$$

(7)

If the relationship between C(r) and r is satisfied, then

$$C\left(r\right)\propto r^D$$

(8)

The fractal characteristics of the system is

$$lnC\left(r\right)=A+Dlnr$$

(9)

Among them, A is a constant; H is the Heaviside function; r is the spatial scale; N is the number of cities in the urban agglomeration; and d_ij refers to the distance between the node cities. When d_ij represents the Euclidean distance, D reflects the spatial distribution characteristics of the urban system. When d_ij represents the actual traffic mileage, D reflects the connectivity characteristics of the transportation network between the inner cities in the urban system. If the correlation fractal dimension D value is between 0 and 2, the smaller the value, the higher the urban space distribution concentration, and the stronger the city spatial correlation. D tending towards 0 means the cities’ spatial distribution is highly concentrated in the primary city; D tending towards 2 means that the cities are evenly distributed in the urban agglomeration space [36].

Suppose the fractal dimension D′ calculated based on actual traffic mileage is closer to the fractal dimension D calculated based on the Euclidean distance. In that case, it indicates that the connectivity between the cities within the urban agglomeration is better [37]; that is, the closer the network accessibility ρ is to 1, the better the accessibility between the cities. The calculation formula of the network accessibility is

$$\rho =\frac{D^{\prime }}{D}$$

(10)

2.1.3. Agglomeration Model of Urban Spatial Structure

It is assumed that the urban agglomerations surrounding cities gather around the central city in a cohesive state and follow some self-similar law [38]. Since the value of r will affect the fractal dimension, the average radius is used instead of r. There are

$$R_s=\langle {(\frac{1}{S}{{\displaystyle \sum }}_{i=1}^S{r}_i^2)}^{\frac{1}{2}}\rangle$$

(11)

$$R_s\propto S^{\frac{1}{D}}$$

(12)

Among them, R_s is the average radius; r_i is the distance from the i th city to the central city; S represents the number of cities in the circle with r as the radius; and D is the fractal dimension of the agglomeration. If D > 2, it indicates that the distribution of the urban agglomeration elements is funneled discrete, and the density decreases from the periphery to the city center, which is abnormal. If D = 2, it indicates that the urban agglomeration elements change uniformly along the urban radius. If D < 2, it indicates that the urban agglomeration elements present an increasing trend from the surrounding cities to the center, and the distribution of the urban agglomeration elements is in a concentrated state [39].

2.2. Data

In this paper, the urban population data are taken as samples to calculate the rank-size structure of the urban agglomeration. The data mainly come from (1) the statistical yearbooks of the relevant provinces, cities, and autonomous regions in Western China; (2) China’s urban statistical yearbook; and (3) the statistical annual report of national economic and social development.

When calculating the correlation dimension and the aggregation dimension of the urban spatial structure, it is introduced to use the traffic time distance to replace the traditional geographic space measurement distance [34]. The main modes of transportation in the Chengdu–Chongqing urban agglomeration are expressways, ordinary railways, high-speed railways, and aviation. As aviation is mostly used between long-distance cities, it is not considered. The specific calculation formula for the traffic time distance with or without high-speed rail is

$$T_1=\sqrt{b·p}, T_2=\sqrt[3]{b·p·g}$$

(13)

Among them, T₁ and T₂ respectively represent the traffic time distance between the cities before and after the completion of the high-speed rail; b, p, and g respectively represent the traffic time between the cities using expressways, ordinary railways, and high-speed railways. The traffic time data of ordinary railways and high-speed railways between the cities are obtained from the China Railway Customer Service Center website’s train schedule. When two cities have direct high-speed railways or ordinary railways, the shortest time is used as the traffic distance. In the absence of direct railways, first calculate the time required to use ordinary railways or high-speed railways to reach the transit city closest to the destination, plus the highway traffic distance from the transit city to the destination city.

3. Results

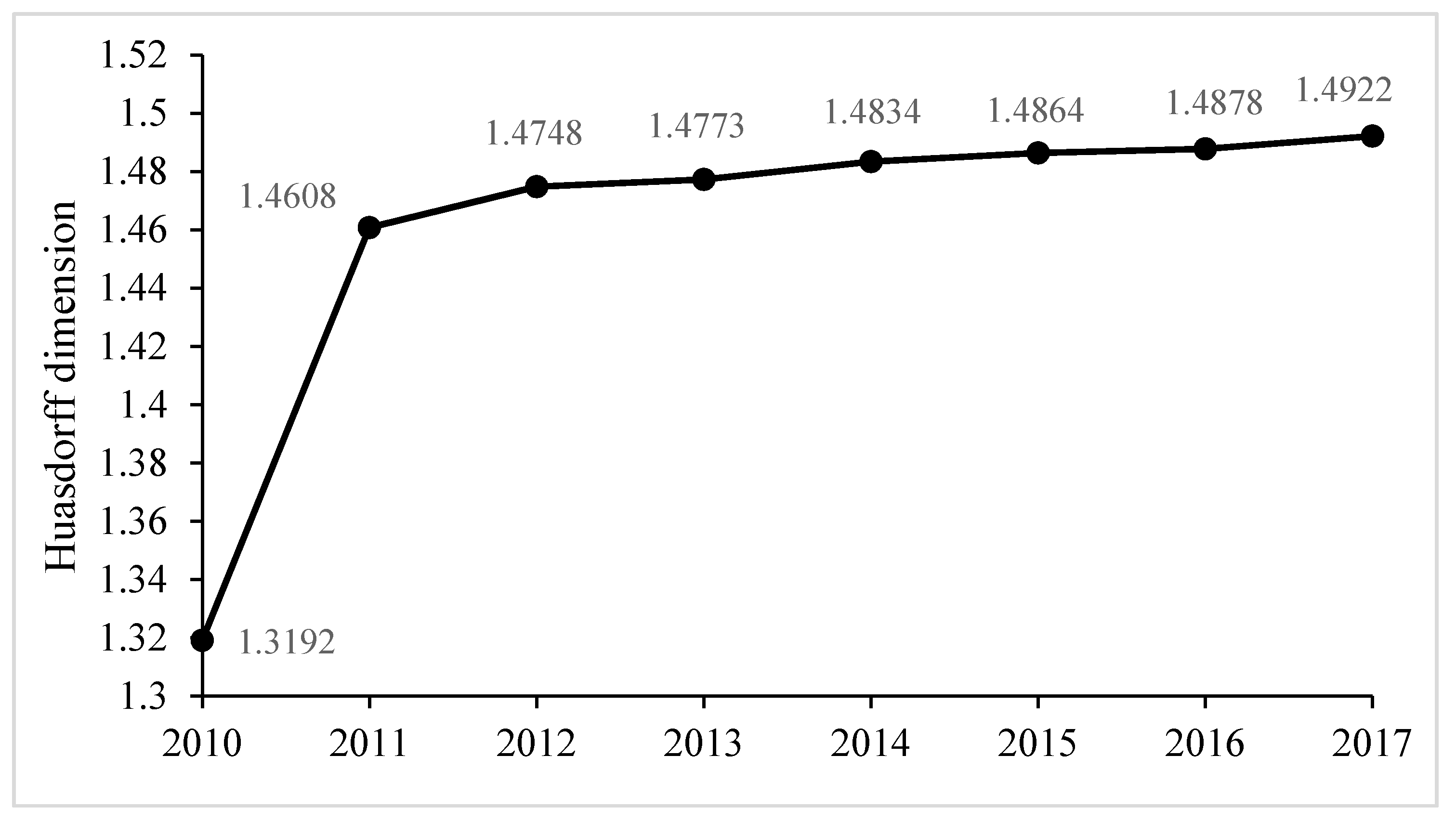
3.1. The Rank-Size Structure of Urban Agglomerations in the Western Region

We used Formula (3) to nonlinearly regress the population data of each urban agglomeration in Western China from 2010 to 2017, and summarized the Hausdorff dimension of each urban agglomeration in Figure 1.

The trend in the Hausdorff dimension of each urban agglomeration from 2010 to 2017 in the figure is displayed with different-colored broken lines. It is important to note that the reference axis of the line graph of the HBOY urban agglomeration in the picture is the secondary axis (the secondary axis is indicated in yellow). The figure shows that the Hausdorff dimension of Chengdu–Chongqing urban agglomeration and HBOY urban agglomeration constantly changes during the period, and is always greater than the equilibrium value 1, showing a typical "rank-size" spatial structure. Besides, the Chengdu–Chongqing high-speed rail was completed and put into operation at the end of 2015. It can be seen from the figure that after one year of operation, the Hausdorff dimension of the Chengdu–Chongqing urban agglomeration has dropped significantly and tends to the ideal value 1. Although the fractal dimension of the spatial structure of Lan-Xi urban agglomeration and Guanzhong Plain Urban Agglomeration showed a gradual increase trend from 2010 to 2017, it was still less than the equilibrium value of 1, showing a "primacy" spatial structure.

To clarify the rank-size structure changes of the four urban agglomerations in the western region from 2010 to 2017, the average value of the fractal dimensions of the four urban agglomerations was obtained to depict the changing trend, shown in Figure 2.

As shown in the figure, the mean value of the fractal dimension increased significantly from 2010 to 2011, and then showed a stable upward trend from 2011 to 2017. Generally speaking, the fractal dimension gradually increased from 2010 to 2017. That means the overall spatial structure of the western urban agglomeration tends to be agglomerative. The population growth rate of the small and medium-sized cities is far greater than that of the primary city.

The urban agglomeration space has an obvious scale-free area, so the spatial structure shows obvious fractal characteristics [16]. The superposition of different traffic network levels not only changes the fractal characteristics of the urban traffic networks but also affects the urban spatial structure at the global level.

3.2. The Spatial Structure of the Chengdu–Chongqing Urban Agglomeration

The Chengdu–Chongqing urban agglomeration is the area with the best economic foundation and the strongest economic strength in the western region. The urban system is relatively sound, with 113 towns per 10000 square kilometers, much higher than other areas in the west, and has huge potential for future development. Moreover, its high-speed rail network construction is highly valued and actively supported by the state, and it has an absolute advantage in the western urban agglomeration. Therefore, we further study its spatial structure by using fractal theory.

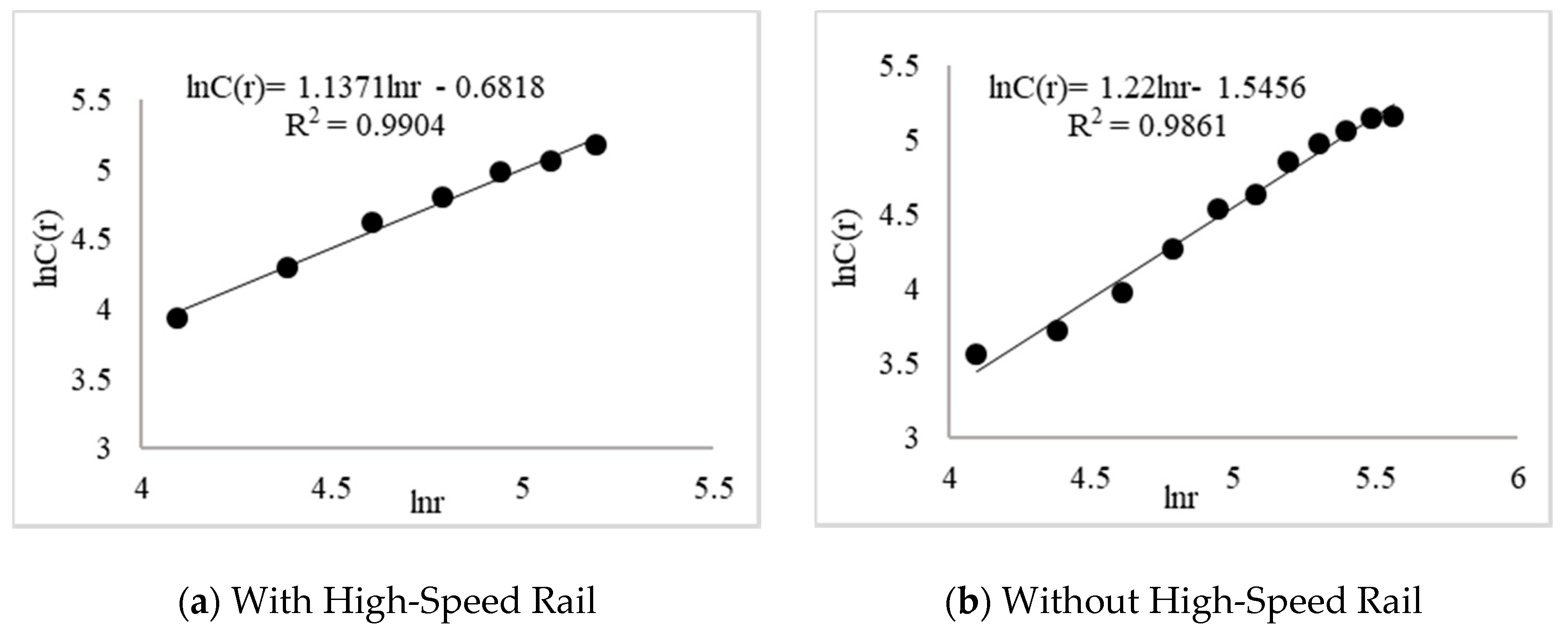
3.2.1. The Spatial Structure Correlation of the Chengdu–Chongqing Urban Agglomeration

According to the development plan of the Chengdu–Chongqing urban agglomeration, 15 important cities were selected to study. To clearly demonstrate the current high-speed rail traffic between these cities, we have drawn a schematic diagram of the high-speed rail links between them, as shown in Figure 3.

To compare the transformation of spatial structure correlation of the Chengdu–Chongqing urban agglomeration with or without high-speed rail, we used Formula (13) to calculate the traffic time distance of these cities in these two cases and to integrate the results into

Table 1. Traffic distance matrix between cities with or without high-speed rail.

	Chengdu	Chongqing	Mianyang	Leshan	Suining	Neijiang	Nanchong	Zigong	Ziyang	Deyang	Meishan	Guang’an	Dazhou	Wanzhou	Hechuan
Chengdu	0	174	107	110	85	282	111	362	146	47	72	202	195	385	166
Chongqing	77	0	259	313	122	195	98	195	222	291	270	77	150	317	33
Mianyang	36	135	0	237	171	204	138	228	185	42	165	185	282	346	201
Leshan	46	164	102	0	178	118	220	108	106	179	75	245	361	421	224
Suining	56	70	148	131	0	101	43	125	103	137	150	84	136	451	80
Neijiang	40	42	94	121	107	0	136	46	68	164	128	150	284	331	137
Nanchong	88	69	126	175	34	144	0	170	139	172	186	85	81	396	62
Zigong	86	91	228	108	419	46	370	0	93	187	121	175	310	360	157
Ziyang	25	62	79	104	82	20	111	165	0	106	77	165	280	339	166
Deyang	23	127	17	111	80	76	115	187	57	0	171	223	283	364	211
Meishan	32	143	81	19	108	99	282	121	69	86	0	228	394	393	218
Guang’an	127	66	171	201	68	134	46	175	170	175	180	0	140	262	76
Dazhou	155	127	85	249	115	220	84	310	257	211	394	70	0	266	185
Wanzhou	198	90	246	282	179	157	172	360	185	228	246	237	374	0	237
Hechuan	100	25	201	224	50	88	48	157	109	211	133	92	125	124	0

. In order to save space, the table integrates the non-zero elements of the traffic time distance matrix in the two types of situations; that is, the upper triangle of the matrix in the table is the traffic time distance without high-speed rail, and the lower triangle of the matrix is the traffic time distance with high-speed rail. In the calculation, the zero elements of the two matrices should be supplemented. The data processing methods of the two cases are the same. Take the high-speed railway distance as an example. The total distance points, in this case, are N² = 15 × 15, to build a 15 × 15 matrix, and take the step size Δr = 20 as the scale r, and get r = 420, 400, …, 20. Then the number of points C(r) of the cities within the range of r will change with r. The composition of point column (r, C(r)) is shown in

Table 2. Scale r of the distance matrix of the high-speed railway and its correlation function C(r).

Number	1	2	3	4	5	6	7	8	9	10	11
r	20	40	60	80	100	120	140	160	180	200	220
C(r)	21	35	51	73	101	121	145	157	177	183	193
Number	12	13	14	15	16	17	18	19	20	21
r	240	260	280	300	320	340	360	380	400	420
C(r)	201	209	209	213	215	215	217	221	223	225

.

Based on the data in Table 2, a double logarithmic coordinate map (only the selected scale-free section images) is obtained. It can be seen that the urban spatial correlation dimension D₁ is 1.1371 with high-speed rail. Similarly, the urban spatial correlation dimension D₂ is 1.22 without high-speed rail.

It can be seen from Figure 4 that D₁ < D₂. In view of the correlation dimension’s nature, the completion of high-speed rail will improve the spatial distribution of the Chengdu–Chongqing urban agglomeration to the primary city. It can be seen from Figure 5 that the fractal dimension under the Euclidean distance of the Chengdu–Chongqing urban agglomeration is 1.1517. Using Formula (10), it can be calculated that the network accessibility after the completion of the high-speed railway is 0.9873 and that before the completion of the high-speed railway it is 1.0593. After the completion of high-speed rail, the network accessibility is closer to 1, which indicates that the accessibility of the Chengdu–Chongqing urban agglomeration has improved.

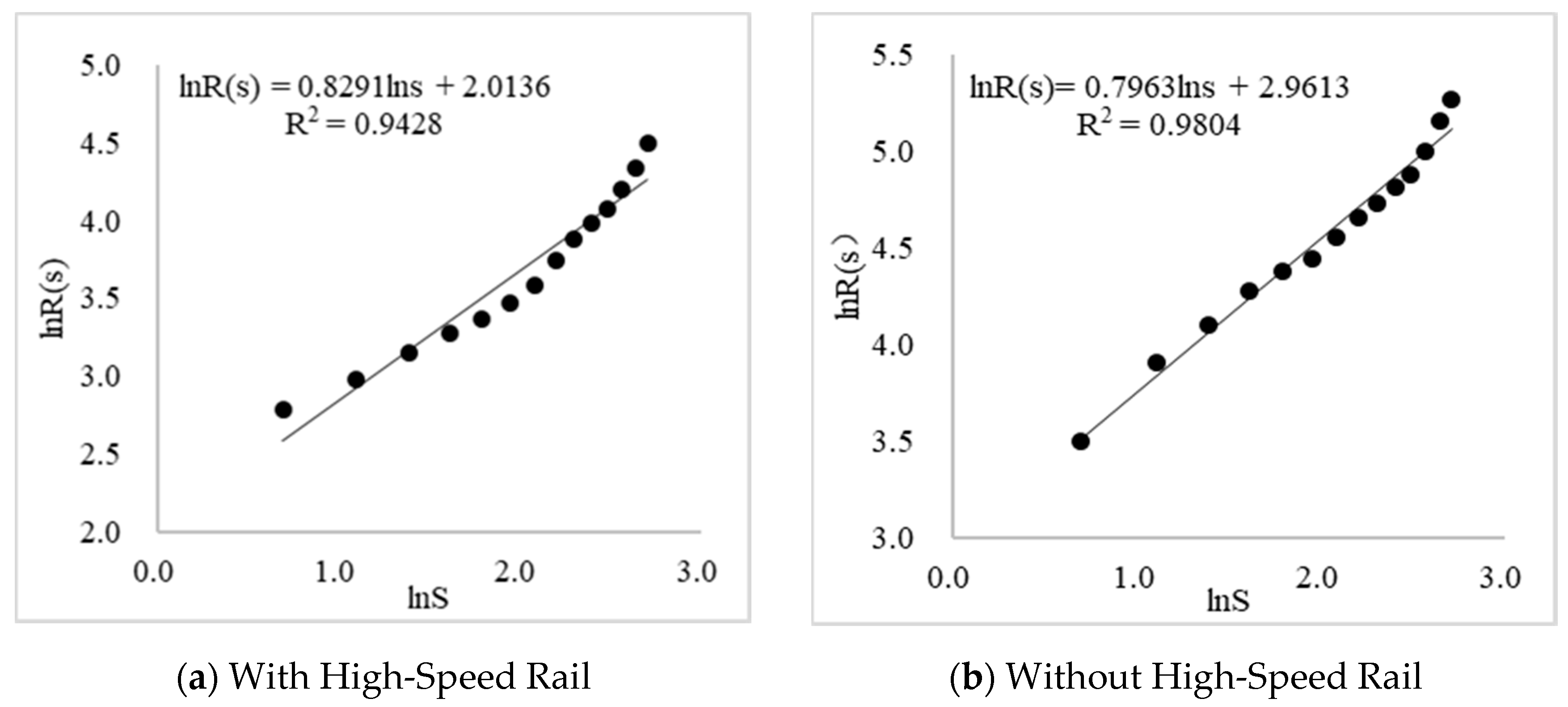
3.2.2. The Agglomeration of the Spatial Structure of the Chengdu–Chongqing Urban Agglomeration

In this section, we take Chengdu as the central city to study the spatial structure agglomeration of the Chengdu–Chongqing urban agglomeration. According to the agglomeration dimension model, the results are shown in

Table 3. The average radius of cities with or without high-speed rail.

With High-Speed Rail				Without High-Speed Rail
City Name	Distance from Chengdu	Number of Cities	Average Radius	City Name	Distance from Chengdu	Number of Cities	Average Radius
	ri	S	Rs		ri	S	Rs
Chengdu	0	1	0.00	Chengdu	0	1	0.00
Deyang	23	2	16.26	Deyang	47	2	33.23
Ziyang	25	3	19.61	Meishan	72	3	49.64
Meishan	32	4	23.33	Suining	85	4	60.45
Mianyang	36	5	26.36	Mianyang	107	5	72.20
Neijiang	40	6	29.08	Leshan	110	6	79.76
Leshan	46	7	32.05	Nanchong	111	7	84.93
Suining	56	8	35.93	Ziyang	146	8	94.74
Chongqing	77	9	42.50	Hechuan	166	9	105.07
Zigong	86	10	48.63	Chongqing	174	10	113.86
Nanchong	88	11	53.42	Dazhou	195	11	123.46
Hechuan	100	12	58.73	Guang’an	202	12	131.80
Guang’an	127	13	66.52	Neijiang	282	13	148.84
Dazhou	155	14	76.32	Zigong	362	14	173.01
Wanzhou	198	15	89.72	Wanzhou	385	15	194.47

.

According to Table 3, the double logarithmic coordinate diagram is obtained as follows in Figure 6:

It can be seen from the figure that the spatial agglomeration dimension of the Chengdu–Chongqing urban agglomeration with high-speed rail is 1.2061, and the agglomeration dimension without high-speed rail is 1.2558. After the opening of the high-speed railway, the spatial agglomeration dimension is smaller. This indicates that the radiation capacity of the core cities is enhanced after the opening of high-speed rail. The spatial distribution density of the Chengdu–Chongqing urban agglomeration along the central city decreases gradually, and the degree of agglomeration gradually increases.

4. Conclusions and Discussion

Many scholars in the world have studied the impact of high-speed rail construction on urban structure. They found that high-speed rail in Europe improves the accessibility between cities, and the population migrates from the core area of the urban agglomeration to its peripheral areas. This article studies the impact of high-speed rail on the Chengdu–Chongqing urban agglomeration based on fractal theory. The research results confirm the findings that high-speed rail construction does help improve cities’ accessibility. We also found that the opening of high-speed rail has enhanced the degree of spatial agglomeration of the urban agglomerations through a comparative analysis. Populations and resources flowed from the core cities to surrounding cities through high-speed rail, which promoted the spatial structure of the Chengdu–Chongqing urban agglomeration to develop toward the “rank-size” type. However, not all the western urban agglomerations’ spatial structures have reached the "rank-size" type. Therefore, this article combines the urban agglomeration development plan and proposes the following suggestions for the optimization of the spatial structure of the western urban agglomeration from the perspective of high-speed rail network construction.

(1)

Through the research on the spatial structure of the western urban agglomeration, the results show that the Hausdorff dimension of the Lan–Xi urban agglomeration and Guanzhong Plain urban agglomeration is less than 1. The primary city is in a prominent monopoly position, and the spatial structure is an unbalanced "primacy” type. For such urban agglomerations, it is suggested that the leading role of the primary city should be actively used in the construction of high-speed rail by means of "point-line-surface". Specifically, strengthening the construction of high-speed rail channels between the primary and medium-sized cities promotes the flow of the industry, population, and resources of the primary city to the medium-sized city, and then cultivate the regional secondary central city. Finally, it promotes the spatial structure of the urban agglomeration to develop toward the “rank-size” type.

(2)

By comparing the traffic distance matrix between the cities and the average radius of the cities with or without high-speed rail, it was found that the traffic time distance and average radius show an apparent downward trend after the opening of high-speed rail. This indicates that the opening of high-speed rail is indeed conducive to improve the internal correlation and agglomeration degree of urban agglomerations. Therefore, to promote the economic restructuring and spatial pattern reconstruction of an urban agglomeration, we should take the Chengdu–Chongqing urban agglomeration as a reference. Specifically, speeding up the construction of intercity railway networks and rapid transportation systems based on high-speed rail cities. With the convenience of high-speed rail networks, we can promote the exchange and cooperation of excellent industries between high-speed rail cities and non-high-speed rail cities, further accelerating the formation of an urban agglomeration pattern with high-speed rail as the link.

(3)

It was found from the development planning documents of the four urban agglomerations that different areas of the same province are divided into different urban agglomerations. This means that the linkage development among the western urban agglomerations needs to strengthen the cooperation between the urban agglomerations. The Chengdu–Chongqing high-speed railway and Xi’an–Chengdu high-speed railway connect the Chengdu–Chongqing urban agglomeration, which is the key to the National Southwest open channel strategy, and to the Guanzhong Plain Urban Agglomeration, which is the strategic hub of the Northwest Open Channel. It connects Xi’an, Chongqing, and Chengdu, which are the fastest developing cities in western China. Furthermore, it promotes the in-depth exchange of human resources, information, resources, science, and technology between Sichuan, Chongqing, and northwest China. Therefore, it is urgent to speed up the construction of a high-speed rail network in western China to promote urban agglomeration in western China.