Hybrid Wind–PV Frequency Control Strategy under Variable Weather Conditions in Isolated Power Systems

Abstract

Over the last two decades, variable renewable energy technologies (i.e., variable-speed wind turbines (VSWTs) and photovoltaic (PV) power plants) have gradually replaced conventional generation units. However, these renewable generators are connected to the grid through power converters decoupled from the grid and do not provide any rotational inertia, subsequently decreasing the overall power system’s inertia. Moreover, the variable and stochastic nature of wind speed and solar irradiation may lead to large frequency deviations, especially in isolated power systems. This paper proposes a hybrid wind–PV frequency control strategy for isolated power systems with high renewable energy source integration under variable weather conditions. A new PV controller monitoring the VSWTs’ rotational speed deviation is presented in order to modify the PV-generated power accordingly and improve the rotational speed deviations of VSWTs. The power systems modeled include thermal, hydro-power, VSWT, and PV power plants, with generation mixes in line with future European scenarios. The hybrid wind–PV strategy is compared to three other frequency strategies already presented in the specific literature, and gets better results in terms of frequency deviation (reducing the mean squared error between 20% and 95%). Additionally, the rotational speed deviation of VSWTs is also reduced with the proposed approach, providing the same mean squared error as the case in which VSWTs do not participate in frequency control. However, this hybrid strategy requires up to a 30% reduction in the PV-generated energy. Extensive detailing of results and discussion can be also found in the paper.

1. Introduction

Over the last two decades, power systems’ generation has slowly been changing, replacing conventional generation units (mainly based on the fossil and nuclear fuels) with variable renewable energy sources (vRESs) [1]. This transition has been supported by several aspects, including environmental concern (especially greenhouse gas emissions) and the aim of decreasing the energy dependence of third countries [2,3,4]. vRES refers to variable-speed wind turbines (VSWTs) and photovoltaic (PV) power plants, which have a stochastic behavior due to their dependence on weather conditions [5]. Together with this point, vRESs are connected to the grid through power inverters decoupled from the grid and, hence, do not inherently provide any inertial or frequency response under power imbalances [6]. Consequently, the high penetration levels of vRESs will substantially challenge the supply security and reliability of future power systems, thus requiring more flexibility to maintain the balance between generation and demand [7,8,9]. Moreover, this real-time power balance is required for a stable grid frequency [10].

As an attempt to improve the frequency response of power systems with high vRES integration, several frequency control techniques have been proposed for such generation units in the specific literature [11,12]. In fact, they are usually classified as depicted in Figure 1. Together with these strategies, energy storage systems (i.e., batteries, flywheels, and supercapacitors) have also been considered as suitable options to maintain grid stability [13,14]. With regard to PV power plants, as they are static elements without any rotating parts, they do not have any stored kinetic energy [15]. Therefore, their synchronous inertia constant is nearly zero ($H_{PV}\approx 0$) [16]. Consequently, they can only provide frequency response based on de-loading strategies. The de-loading technique implies the reduction of the supplied active power under normal operation conditions, going towards the right part of the P–V curve (refer to Figure 2). In this way, when grid frequency is lower than its nominal value, the PV installations can slightly decrease their voltage (from $V_{del}$ to $V_{MPP}$, see Figure 2) and subsequently increase the corresponding generated power [17]. The $\Delta V$ decrease is usually estimated based on the grid frequency deviation $\Delta f$ through a proportional or proportional–integral controller. Similarly to PV power plants, VSWTs can also provide frequency response using the de-loading technique. In this case, it is performed by pitching the blades or over-speeding the rotor [18]. De-loading strategies imply a reduction of the electrical power generated (both for PV and VSWTs) and, subsequently, a considerable decrease in the benefits for their owners [19]. As VSWTs have some stored kinetic energy due to their blades, drive train, and the electrical generator, some authors affirm that VSWTs’ inertia constant $H_{WT}$ is in line with those of conventional power plants, but it is hidden from the power system point of view due to the power converter [20,21]. Consequently, together with the de-loading approach, VSWTs can provide such rotational inertia to the grid through different inertial response strategies. These strategies require at least one supplementary control loop to be included in the power controller [22]. Under frequency deviation conditions, the frequency control loop(s) will provide an additional input to the VSWTs, aiming to temporarily increase their active power generation. With this type of controller, VSWTs can always generate their maximum active power according to each wind speed value, in contrast to the de-loading technique, in which they slightly curtailed certain amounts of power. As a result, inertial response approaches are preferable to the de-loading technique, since the wind resource is better used [23]. However, inertial response approaches are limited by the VSWTs’ speed governor, which prevents the rotational speed of the VSWTs from decreasing below the minimum allowed value [24].

Table 1. PV frequency control proposals.

Ref.	Type of Control	PV Integration (%)	$\Delta \mathit{P}$ (%)	Year
[40]	De-loading	9	5	2012
[41]	De-loading	9	5	2012
[42]	De-loading	16	–	2013
[43]	De-loading	22	8.1	2014
[44]	De-loading	23–48	50	2017
[45]	De-loading	10–20–30	10	2019
[46]	De-loading	10	10	2019

and

Table 2. Variable-speed wind turbine (VSWT) frequency control proposals.

Ref.	Type of Control	VSWT Integration (%)	$\Delta \mathit{P}$ (%)	Year
[47]	De-loading (pitch)	—	—	2016
[48]	Droop	11, 29.5	15	2013
[49]	Hidden-inertia emulation	20	8.3	2015
[50]	Hidden-inertia emulation	—	10	2016
[51]	Hidden-inertia emulation	—	10	2019
[52]	Fast power reserve	20	10	2015
[53]	Fast power reserve	16.7–33	16.7	2016
[54]	Fast power reserve	5–45	2.5–10	2018

summarize different vRES frequency control strategies proposed in the specific literature over the last years, including the type of control, PV/VSWT integration level, and the power imbalance ($\Delta P$) that causes the frequency deviation. As can be seen in Table 1 and Table 2, these frequency control strategies are usually analyzed under severe power imbalances (up to 50%). However, in isolated power systems with high wind–PV integration, the variability of wind speed and solar irradiation commonly causes large deviations in the system frequency [25]. Indeed, these fluctuations pose stress on the power system operation, as transmission and distribution system operators (TSOs/DSOs) deal with not only unmanageable demand, but also uncontrollable generation [26]. Consequently, there is an acute need to improve the frequency response of isolated power systems with high vRES integration, especially under typical variable meteorological changes. In fact, over the last decade, some studies have already focused on this topic. However, most of the works proposed are based on including energy storage systems [27,28,29,30,31,32,33,34], demand response [35], and electric vehicles [36], or using independent frequency controllers for VSWT and PV power plants [37,38,39].

In contrast to the previous studies, this paper proposes a hybrid wind–PV frequency control strategy in which the VSWTs’ rotational speed deviation is the proportional–integral (PI) controller input of the PV frequency response strategy. Similar approaches have been previously proposed by the authors, but by linking the rotational speed deviation of VSWTs to hydro-power plants instead of PV power plants [55]. The main contributions of this paper can be summarized as:

• A new hybrid wind–PV frequency control strategy is proposed. VSWTs include the hidden-inertia emulation technique, whereas PV power plants use the de-loading approach. The novelty of the hybrid control is that the PV frequency controller receives the VSWTs’ rotational speed deviation as an input instead of the grid frequency deviation.
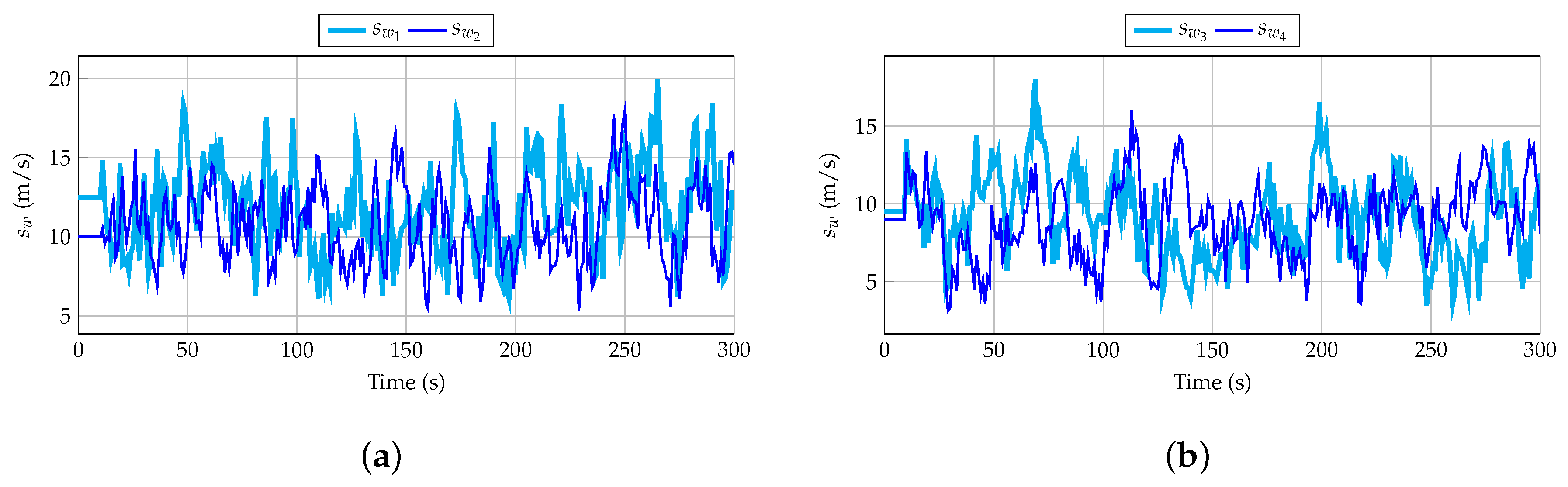
• The proposed controller is tested on an isolated power system consisting of thermal, hydro-power, VSWT, and PV power plants under six different scenarios. Frequency deviations are the result of the variability of both wind speed and solar irradiation, synthetically estimated (wind speed) and based on real measured values (solar irradiation).
• The frequency response is compared to three different frequency strategies: $\left(i\right)$ conventional power plants; $\left(ii\right)$ conventional power plants and wind power plants; and $\left(iii\right)$ conventional power plants, wind power plants, and PV power plants with frequency deviation as input. Minor frequency oscillations were obtained with the hybrid wind–PV frequency strategy in terms of minimum and maximum frequency deviations and mean squared error (MSE) of frequency, as well as in terms of minimum and maximum rotational speed of the VSWTs and MSE of their rotational speed deviation.

The rest of the paper is organized as follows: The models used for the simulations are described in Section 2; the methodology followed to carry out this study is presented in Section 3; in Section 4, the results of the study are shown and analyzed; finally, Section 5 presents the main conclusions of the paper.

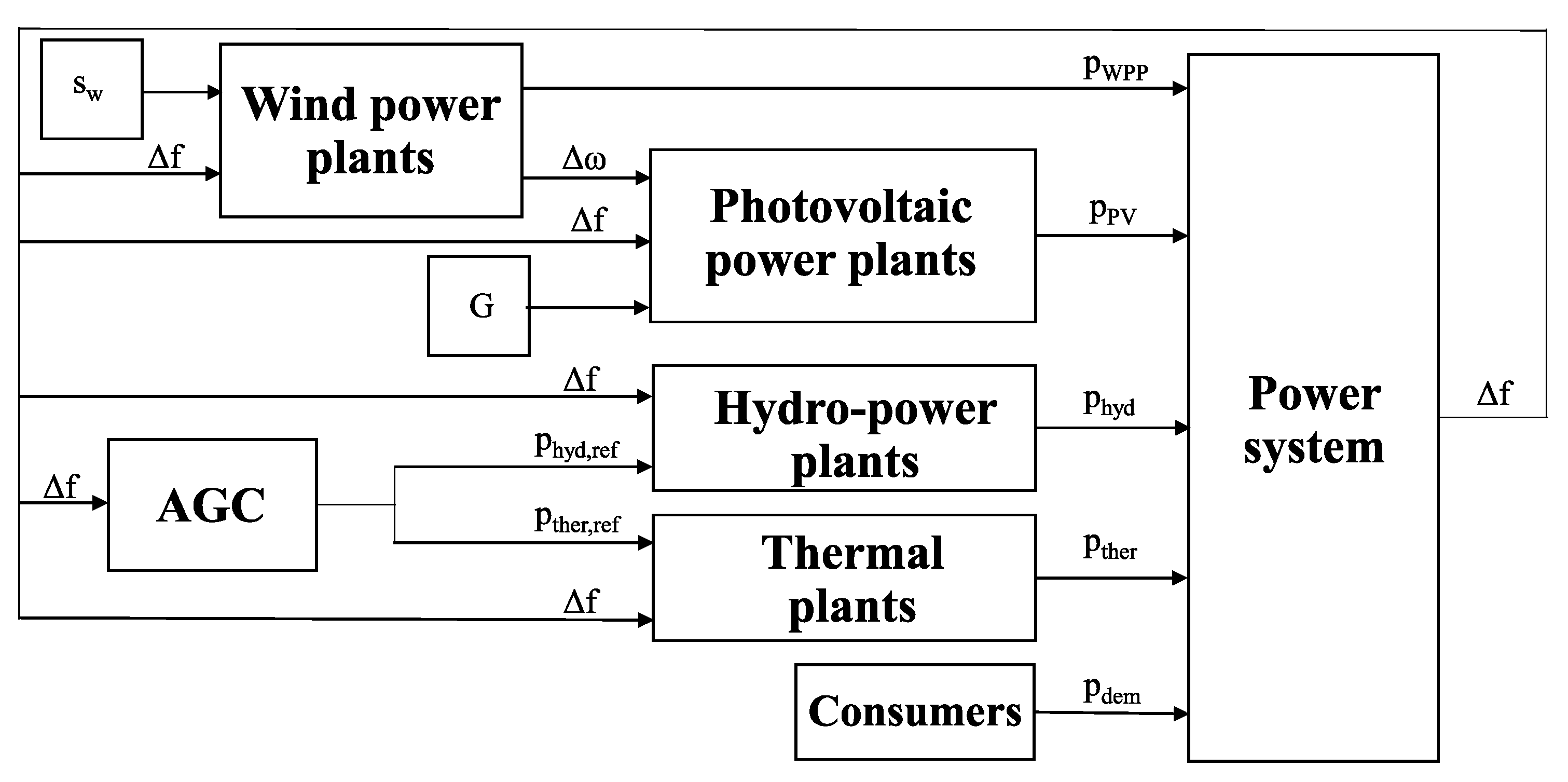
2. Proposed System Modeling

A mathematical simulation model is used to analyze the proposed hybrid wind–PV frequency controller. This power system and, consequently, the model implemented in Matlab/Simulink includes conventional generators (hydro-power and thermal power plants), PV power plants, and VSWTs as well as the power demand, as shown in Figure 3. The frequency control is in line with current European requirements (primary and secondary controls), as will be presented in Section 3. In the following subsections, the main components of the proposed model are described in detail.

2.1. Power System and System Inertia

The power system is modeled considering an aggregated inertial model as proposed in [56]. This formulation has been previously used to model the Irish isolated power system [57] and El Hierro isolated power system [58], among others. Grid frequency variations are the result of the imbalance between the power generation and the corresponding demand (see Equation (1)):

$$f{\displaystyle \frac{df}{dt}}={\displaystyle \frac{1}{2H_{eq}}}(p_w+p_{PV}+p_{hyd}+p_{ther}-p_{dem}-D_{net}\Delta f),$$

(1)

where $p_w$, $p_{PV}$, $p_{hyd}$, and $p_{ther}$ represent the power supplied by VSWT, PV, hydro-power, and thermal power plants, respectively; $p_{dem}$ is the total power demand; and $D_{net}$ is the consumer load sensitivity factor to frequency variations. System inertia ($H_{eq}$) is estimated as [59]:

$$H_{eq}=H_{hyd}+H_{ther},$$

(2)

where $H_{hyd}$ and $H_{ther}$ are the hydro-power and thermal power plants’ inertia constants, respectively. The VSWT and PV power plants are connected to the grid through power converters and, therefore, do not inherently provide synchronous inertia to the grid, as already discussed in Section 1.

2.2. Conventional Power Plants

The conventional power plants (CPPs) considered in this paper are reheat thermal and hydro-power plants. Both of them are modeled following the transfer functions proposed in [60]. Thermal power plants’ transfer function, shown in Figure 4a, provides the power variations of these power plants from the frequency deviation ($\Delta f$) and the automatic generation control (AGC) power reference ($p_{ther,ref}$). Figure 4b shows the transfer function to model the hydro-power plant, including the conduits’ dynamics. The generated power $p_{hyd}$ also depends on the frequency deviation $\Delta f$ and the power reference signal provided by the AGC ($p_{hydr,ref}$). The parameters for both models in Figure 4 are listed in Table 3.

2.3. Wind Power Plants

Four different wind power plants (WPPs) are considered by modeling each WPP with an aggregated wind turbine. Therefore, one equivalent wind turbine is then simulated by multiplying the corresponding generated power by the number of VSWTs of such a WPP [61]. The VSWT model includes the wind power model, which determines the power extracted from the wind speed; the blade pitch control to regulate the wind input torque; the torque maximum power point (MPP) tracking control, which restores the optimal rotor speed after a rotational speed deviation; and the frequency controller, which is discussed in Section 3.2. Further information with regard to the VSWT model can be found in [62]. The one-mass rotor mechanical model is used for simulations, and is acceptable when the voltage is assumed to be constant [63,64]:

$${\omega }_{WT}={\displaystyle \frac{p_{mt}-p_W}{2H_{WT}s}}.$$

(3)

The reference rotational speed ${\omega }_{ref}$ is determined from the measured power $p_{ef}$, which is the active generated power $p_W$ after a delay $T_f$:

$${\omega }_{ref}=-0.67\times p_{ef}^2+1.42\times p_{ef}+0.51.$$

(4)

The VSWT model is represented in Figure 5. The values of the different parameters are listed in Table 3.

2.4. PV Power Plant

Four different PV power plants are also considered. They are modeled following the diode equation, where the output current $I_{PV}$ is given by [65,66]:

$$I_{PV}=N_P\times I_{ph}-N_P\times I_{rs}\times \left[\exp \left({\displaystyle \frac{q}{k_B\times T_C\times A}}\times {\displaystyle \frac{V_{PV}}{N_s}}\right)-1\right].$$

(5)

$N_s$ is the number of cells in series, $N_P$ is the number of strings in parallel, $I_{ph}$ is the photo-current, q is the electron charge, $k_B$ is Boltzmann’s constant, $T_C$ is the temperature of the cell, A is the diode ideality factor, and $V_{PV}$ is the PV voltage. The photo-current $I_{ph}$ is calculated by:

$$I_{ph}=[I_{sc}+k_I(T_C-T_{STC})]\times G,$$

(6)

where $I_{sc}$ is the PV cell’s short-circuit current, $k_I$ is the short-circuit current temperature coefficient of the PV cell, $T_{STC}$ is the temperature under Standard Test Conditions (STC), and G is the solar irradiation. The PV cell’s reverse saturation current $I_{rs}$ follows Equation (7), where $I_{r,ref}$ is the reverse saturation current at $T_{STC}$, and $E_G$ is the band-gap energy of the PV cell’s material:

$$I_{rs}=I_{r,ref}\times {\left({\displaystyle \frac{T_C}{T_{STC}}}\right)}^3\times \exp \left[{\displaystyle \frac{q\times E_G}{k_B\times A}}\times \left({\displaystyle \frac{1}{T_{STC}}}-{\displaystyle \frac{1}{T_C}}\right)\right].$$

(7)

The voltage at the MPP ($V_{MPP}$) for a given irradiation G and cell temperature $T_C$ is estimated depending on its value at STC and a correction factor ${\alpha }_V$:

$$V_{MPP}=V_{MPP,STC}\times \left({\displaystyle \frac{\ln \left(G\right)}{\ln \left(1000\right)}}\right)\times (1+{\alpha }_V\times (T_C-T_{STC})).$$

(8)

By multiplying the PV voltage $V_{PV}$ by the output PV current $I_{PV}$, the active power of the PV generator is then estimated. In the case that the PV voltage corresponds to the MPP voltage $V_{MPP}$, the output power of the PV power plants would be the maximum available active power under such G and $T_C$ conditions. The values of the different parameters considered are listed in Table 3.

Table 3. Power plant parameters [60,62,66].

Thermal		Hydro-Power		VSWTs		PV
Parameter	Value	Parameter	Value	Parameter	Value	Parameter	Value
$R_{ther}$	$0.05$	$R_{hyd}$	$0.05$	$T_f$	5	$k_I$	$0.0017$
$T_g$	$0.2$	$T_g$	$0.2$	$T_{con}$	$0.02$	$I_{r,ref}$	$1.2\times {10}^{-7}$
$T_{CH}$	$0.3$	$T_R$	5	$v_{WT}$	1	${\alpha }_v$	$-5.53\times {10}^{-3}$
$F_{HP}$	$0.3$	$R_T$	$0.38$	$K_{pt}$	1	q	$1.602\times {10}^{-19}$
$T_{RH}$	7	$R_P$	$0.05$	$K_{it}$	$0.2$	$k_B$	$1.38\times {10}^{-23}$
$H_{ther}$	5	$T_w$	1			A	$1.92$
		$H_{hydro}$	$3.3$			$I_{sc}$	$8.03$
						$E_g$	$1.12$

Table 3. Power plant parameters [60,62,66].

Thermal		Hydro-Power		VSWTs		PV
Parameter	Value	Parameter	Value	Parameter	Value	Parameter	Value
$R_{ther}$	$0.05$	$R_{hyd}$	$0.05$	$T_f$	5	$k_I$	$0.0017$
$T_g$	$0.2$	$T_g$	$0.2$	$T_{con}$	$0.02$	$I_{r,ref}$	$1.2\times {10}^{-7}$
$T_{CH}$	$0.3$	$T_R$	5	$v_{WT}$	1	${\alpha }_v$	$-5.53\times {10}^{-3}$
$F_{HP}$	$0.3$	$R_T$	$0.38$	$K_{pt}$	1	q	$1.602\times {10}^{-19}$
$T_{RH}$	7	$R_P$	$0.05$	$K_{it}$	$0.2$	$k_B$	$1.38\times {10}^{-23}$
$H_{ther}$	5	$T_w$	1			A	$1.92$
		$H_{hydro}$	$3.3$			$I_{sc}$	$8.03$
						$E_g$	$1.12$

3. Methodology

Frequency control strategies focus on minimizing grid frequency variations due to generation–demand mismatches [67]. With this aim, generation units must increase/decrease their generation to equal the total power demand (plus the power system losses) [68]. In the following subsections, frequency controls for CPPs, VSWTs, and PV power plants are described.

3.1. Frequency Control in Conventional Power Plants

CPPs based on synchronous generators inherently release or absorb kinetic energy as a natural inertial response to frequency deviations. In Europe, frequency control with CPPs has a hierarchical structure, usually organized in primary control (frequency containment reserves), secondary control (frequency restoration reserves), and tertiary control (replacement reserves) [69]. Primary frequency control (PFC) is automatically activated by the generator units some seconds after the power imbalance. The CPP power response is proportional to the frequency deviation $\Delta f$, following Equation (9), in which R is the droop characteristic [70,71]:

$$\Delta p=-{\displaystyle \frac{\Delta f}{R}}.$$

(9)

According to the European network of transmission system operators for electricity (ENTSO-E), R should range between 2% and 12%, with a dead-band between 10 and 30 mHz in which the PFC is not activated [72]. For this work, R is considered as 5% for both thermal and hydro-power plants, and the dead-band is established at 30 mHz. Subsequent to the PFC action, there is still some remaining frequency deviation due to the power imbalance. The secondary frequency control is then required to completely remove this frequency deviation [73,74]. In fact, this secondary frequency control is in charge of modifying the power generation set-point accordingly [75]. The AGC coordinates the effort’s dispatch among the different CPPs of the secondary frequency control. In this paper, the equivalent total secondary regulation effort ($\Delta RR$) is determined by:

$$\Delta RR=-\Delta f\times K_f,$$

(10)

where $K_f$ is estimated following the ENTSO-E’s recommendations [76]. This $\Delta RR$ is distributed between the thermal and hydro-power plants depending on their participation factors ($K_{u,i}$), determined according to the droop of each power plant [77]:

$$\Delta p_{i,ref}=\frac{1}{T_{u,i}}\int \Delta RR\times K_{u,i}dt=\frac{-1}{T_{u,i}}\times K_{u,i}\times K_f\times \int \Delta fdt,$$

(11)

where i represents $hyd$ or $ther$, and $K_{u,hyd}+K_{u,ther}=1$.

3.2. VSWT Frequency Control Strategy

Among the three different inertial response strategies for VSWTs (refer to Figure 1), the hidden-inertia emulation technique is selected for this work. The hidden-inertia emulation technique is based on a proportional–derivative ($PD$) control loop, with $\Delta f$ as input. This $PD$ controller provides an additional power proportional to the frequency deviation and its derivative value:

$$\Delta p_{FC}=K_d\times {\displaystyle \frac{d\Delta f}{dt}}+K_p\times \Delta f.$$

(12)

The derivative part represents the inertial control loop (emulating the hidden-inertia of the VSWTs). These inertial (derivative) and proportional control loops allow that some of the kinetic energy stored in the rotating masses of the VSWTs (i.e., rotor, drive train, and electrical generator) is released to provide a fast frequency response from the power converter’s capability. This $\Delta p_{FC}$ signal is added to the power reference output depending on the wind speed.

3.3. PV Frequency Control Strategy

The de-loading technique is used for PV frequency control. This strategy curtails a certain amount of active power, working the PV power plant on a de-loaded voltage value ($V_{del}$) on the right side of the MPP voltage ($V_{MPP}$), as shown in Figure 2. Note that $V_{del}>V_{MPP}$. In the following subsections, the traditional de-loading strategy and the proposed hybrid wind–PV frequency control approach are analyzed.

3.3.1. Conventional De-Loaded PV Frequency Control Strategy

To provide frequency response, the PV power plant usually works at the de-loaded voltage $V_{del}$. In the case of frequency reduction, the PV voltage should be also reduced, moving towards $V_{MPP}$ to increase its generated active power. The strategies previously proposed in the specific literature include a proportional (P) or proportional–integral ($PI$) controller, with the frequency deviation ($\Delta f$) as an input of such a controller [40,41,42,43]. Frequency deviation ($\Delta f$) passes through the corresponding control loop (P or $PI$), giving an additional voltage $\Delta V$ (refer to Figure 6). The modified PV voltage is then determined as:

$$V_{PV}=V_{del}-\Delta V.$$

(13)

This $V_{PV}$ is used in Equation (5) to determine the PV current, $I_{PV}$, which is the corresponding PV active power:

$$P_{PV}=I_{PV}\times V_{PV}.$$

(14)

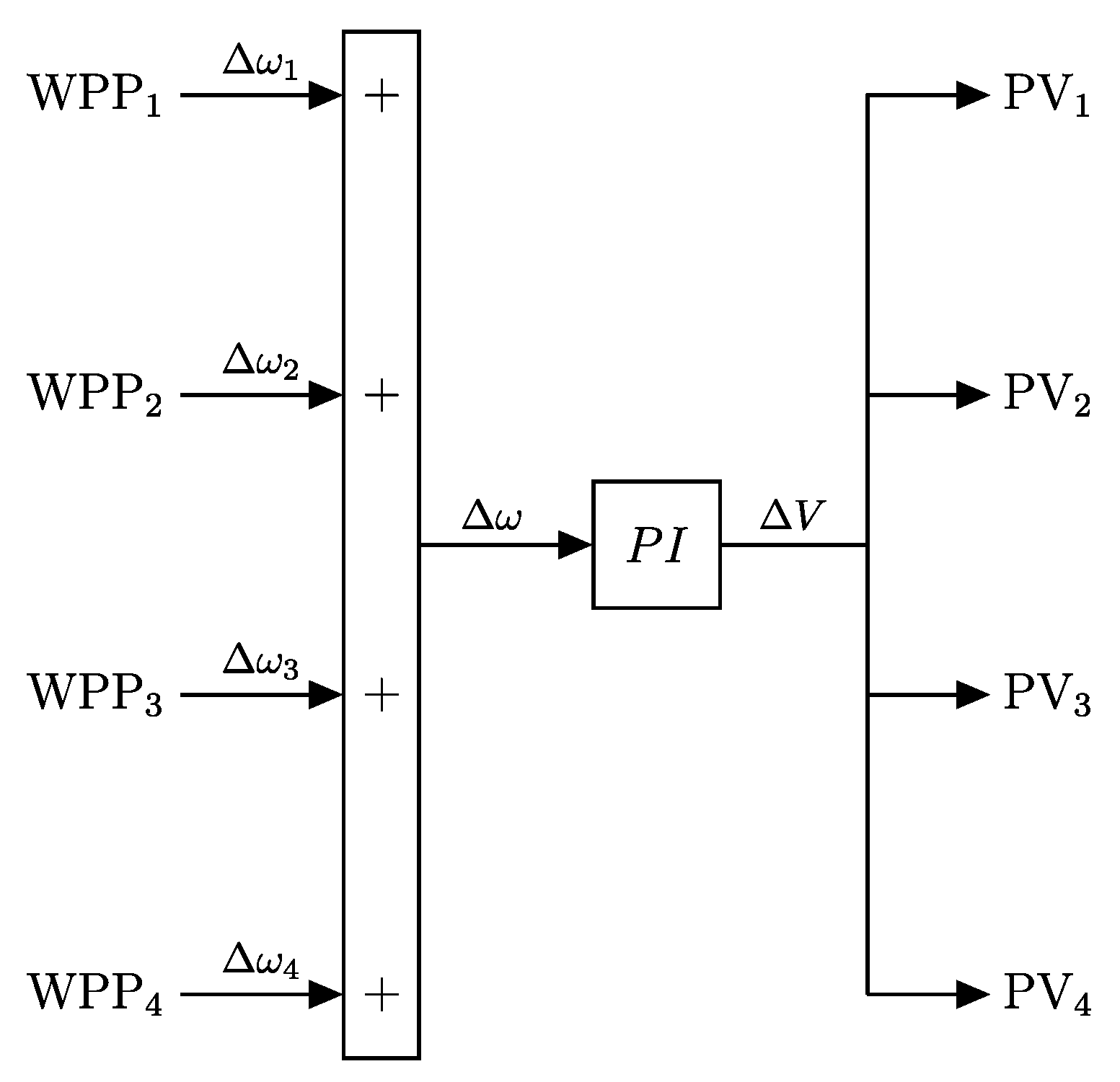
3.3.2. Hybrid Wind–PV Frequency Control

In this work, and in contrast to previous studies, the authors propose the use of the VSWT rotational speed deviation $\Delta \omega$ as an input for the de-loaded PV frequency controller. Due to the VSWTs’ hidden-inertia frequency controller, the rotational speed ${\omega }_j$ of each WPP deviates from the reference value ${\omega }_{ref,j}$, following Equation (15):

$$\Delta {\omega }_j={\omega }_j-{\omega }_{ref,j},$$

(15)

where ${\omega }_{ref,j}$ is calculated from Equation (4). The global $\Delta \omega$ sent to the PV power plants is the sum of the $\Delta {\omega }_j$ of each WPP:

$$\Delta \omega =\sum _{j=1}^4\Delta {\omega }_j.$$

(16)

This global $\Delta \omega$ will pass through the $PI$ controller, obtaining the value of $\Delta V$ of Equation (13). An overview of the hybrid wind–PV frequency control approach is shown in Figure 7. By using $\Delta \omega$ as an input, PV power plants modify their generated power according to this rotational speed deviation, improving the VSWTs’ rotational speed control and subsequently increasing the inertial control performance of the VSWTs.

4. Results

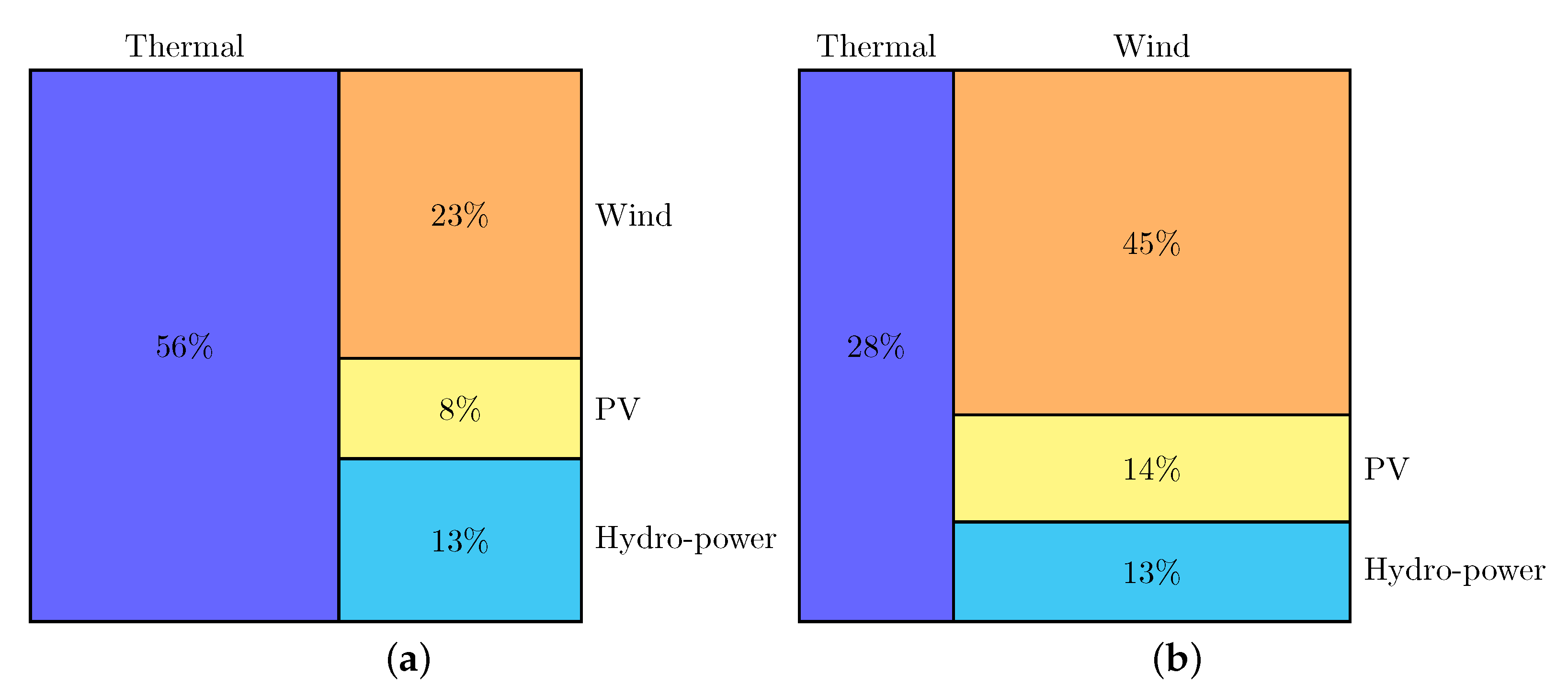
4.1. Scenarios under Consideration

The Ten-Year Network Development Plan (TYNDP) 2020 Scenario Report is used to propose the generation mix under consideration [78]. National trend scenarios are taken into account by the authors, which account for both the supply and demand data collected from the European electricity TSOs. Figure 8 shows the generation mix considered in this paper following [78] for the years 2025 and 2040.

Three different electricity demand values (i.e., valley, mean, and peak periods) are also studied based on the Gran Canaria isolated power system (Spain). This power system has been extensively described in [79]. Consequently, by combining the two generation mixes and the three different demand values, six scenarios are under analysis. Power demand is assumed as constant during the simulations, as the timeframe under analysis is 5 min (300 s). As presented in

Table 4. Time interval where demand is considered as constant for different transmission system operators (TSOs).

TSO	Location	Time (min)	Website
ENMAX	Canada	15	[80]
ERGON	Australia	15	[81]
RTE	France	15	[82]
REE	Spain	10	[83]
IESO	Canada	5	[84]
CAISO	California	5	[85]
TEPCO	Japan	5	[86]
TRANSPOWER	New Zealand	5	[87]

, this assumption is in line with most TSOs.

Wind speed and solar irradiation present some oscillations during the simulation time intervals. These variations cause certain frequency deviations from the nominal value (50 Hz). Real measured values of solar irradiation from a PV power plant in Albacete (Spain) are used for simulation purposes. In addition, synthetic wind speeds estimated from the methodology detailed in [88] are also included in the scenarios. Such synthetic wind speeds have been statistically compared to real measured wind speed series, obtaining similar values.

As mentioned in Section 2, four different WPPs and PV power plants are considered:

$$p_{WPP}=\sum _{j=1}^4{p}_{WPP,j},$$

(17)

$$p_{PV}=\sum _{k=1}^4{p}_{PV,k}.$$

(18)

A heterogeneous distribution of wind- and PV-generated power is estimated to give more realistic simulations, considering that WPP${}_1$ and PV${}_1$ account for 50% of the total $p_{WPP}$ and $p_{PV}$; WPP${}_2$ and PV${}_2$ are 25% of the total $p_{WPP}$ and $p_{PV}$; and WPP${}_3=$ WPP${}_4$ and PV${}_3=$ PV${}_4$ are 12.5% of the total $p_{WPP}$ and $p_{PV}$, respectively. The wind speed values $s_w$ and solar irradiation G for each WPP and PV power plant are depicted in Figure 9 and Figure 10.

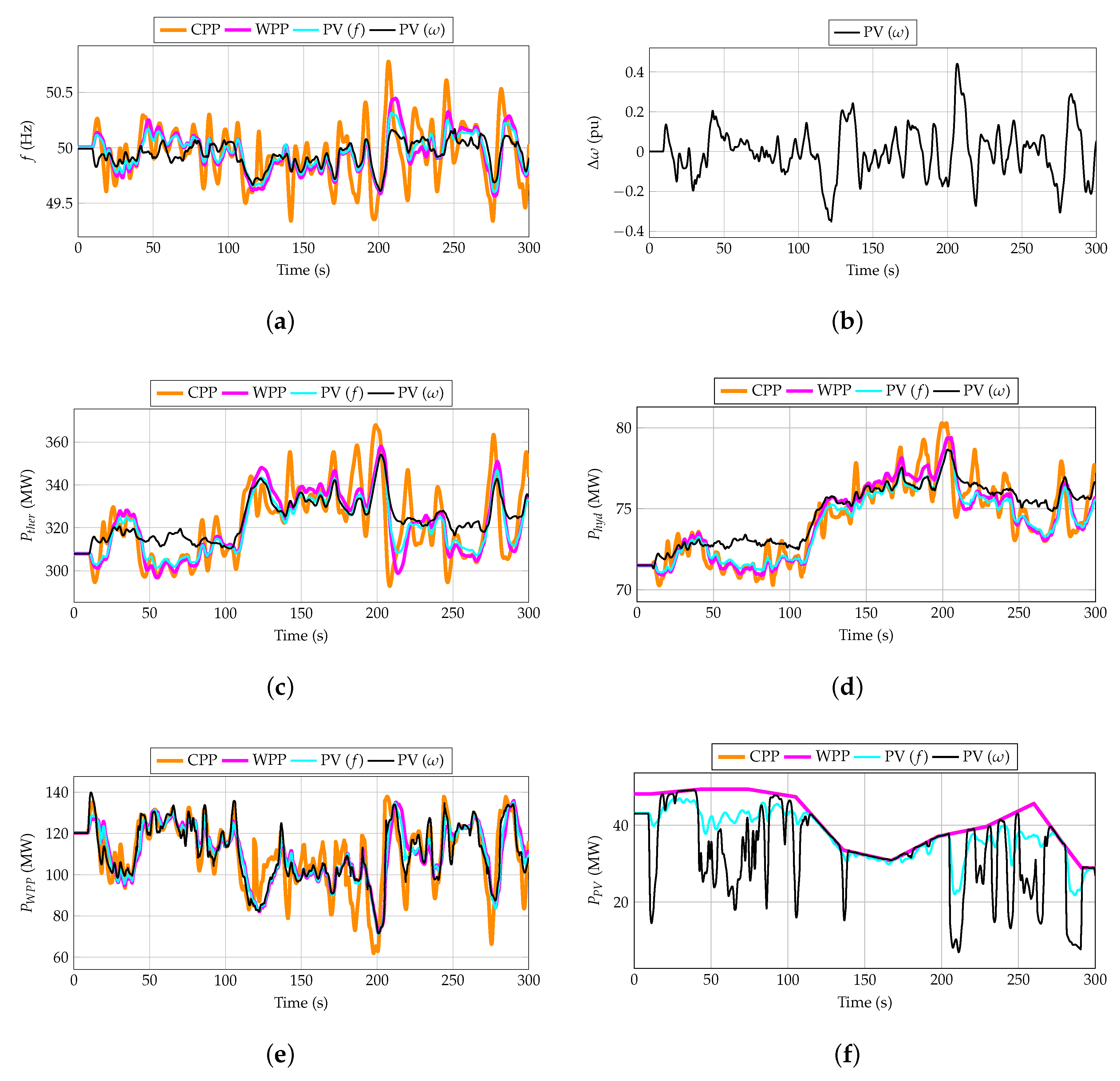
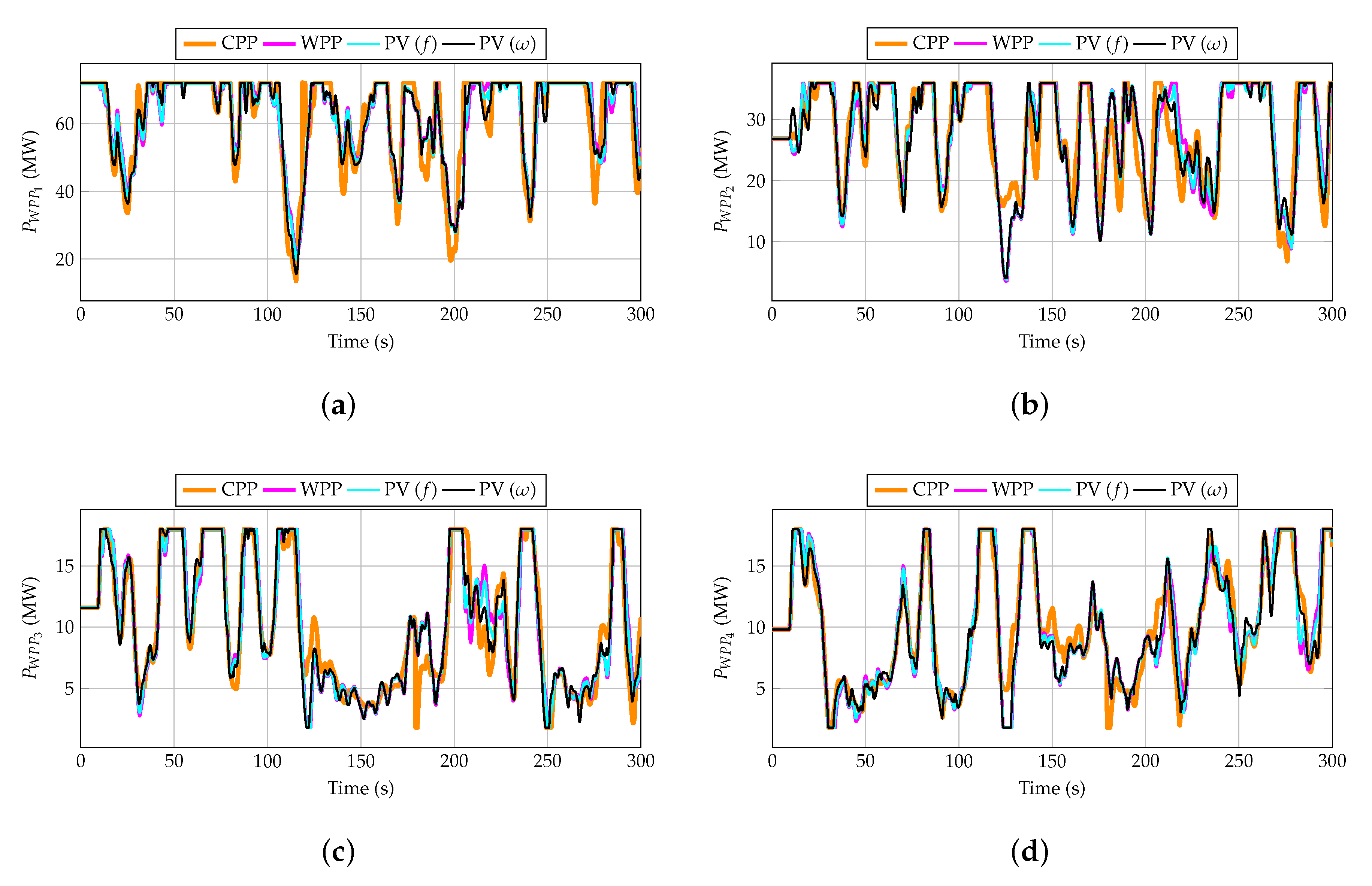
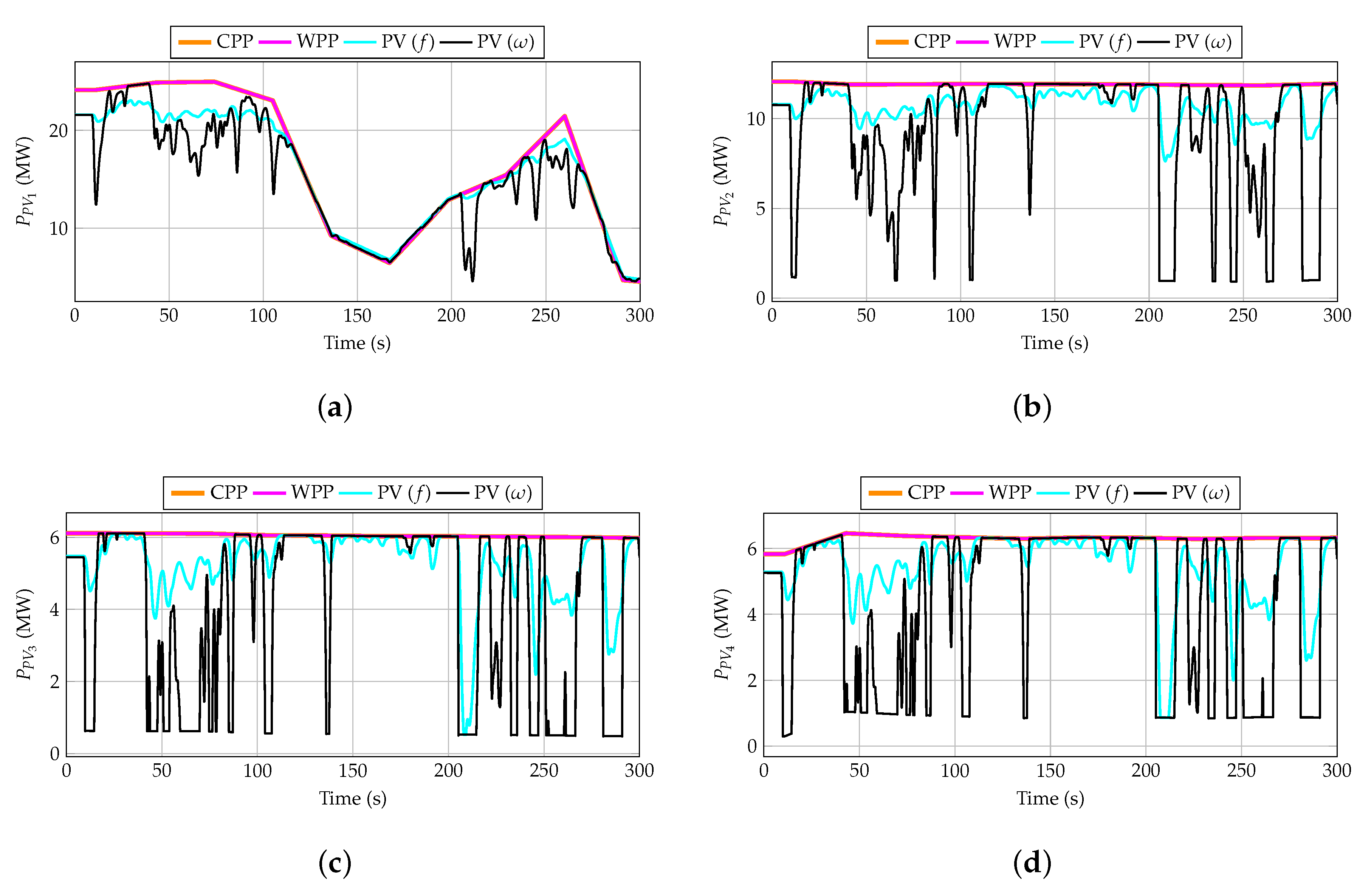
4.2. Simulation Results

The six scenarios presented in Section 4.1 were simulated in a Matlab/Simulink environment. A fixed step with the ode3 (Bogcki-Shampine) solver and a step size of ${10}^{-2}$ s was used. The Matlab version was r2016a. Four different frequency control strategies were compared:

• Frequency control is only provided by conventional power plants (referred to as CPP).
• Frequency control is provided by conventional power plants and WPPs with a hidden-inertia emulation technique (referred to as WPP).
• Frequency control is provided by conventional power plants, WPPs with a hidden-inertia emulation technique, and PV power plants with 10% de-loading and a P controller with $\Delta f$ as input (referred to as PV (f)).
• Frequency control is provided by conventional power plants, WPPs with a hidden-inertia emulation technique, and PV power plants with 10% de-loading and a $PI$ controller with $\Delta \omega$ of the VSWTs as input (referred to as PV (ω)), which is the hybrid wind–PV frequency strategy proposed in this paper.

In each simulation, the authors considered different criteria to compare the frequency control strategies under consideration. Specifically, the parameters taken into account are the following: the minimum and maximum frequency values, the MSE of the grid frequency, the PV-generated energy, the MSE of the thermal and hydro-power plants with respect to their initial assigned power, the minimum and maximum values of the rotational speed of each WPP, and the MSE of the rotational speed of each WPP with respect to their reference value (${\omega }_{ref}$) for each wind speed.

Table 5. Simulation results: frequency, PV electrical energy, and the conventional power plants’ mean square error (MSE).

Scenario	Load (MW)	250		400		550
	Year	2025	2040	2025	2040	2025	2040
$f_{min}$ (Hz)	CPP	49.28	44.89	49.31	46.24	49.34	45.74
	WPP	49.54	48.49	49.55	48.59	49.57	48.63
	PV (f)	49.58	48.88	49.61	48.85	49.60	49.00
	PV ($\omega$)	49.58	48.94	49.61	48.87	49.61	49.20
$f_{max}$ (Hz)	CPP	50.85	54.30	50.84	54.16	50.78	54.08
	WPP	50.47	50.74	50.47	50.71	50.45	50.72
	PV (f)	50.26	50.41	50.29	50.48	50.32	50.48
	PV ($\omega$)	50.23	50.25	50.18	50.23	50.17	50.54
$MS{E}_f$ (Hz${}^2$)	CPP	0.072	1.481	0.069	1.123	0.063	1.154
	WPP	0.035	0.243	0.034	0.216	0.032	0.203
	PV (f)	0.019	0.108	0.021	0.111	0.023	0.104
	PV ($\omega$)	0.015	0.087	0.014	0.082	0.015	0.085
$E_{PV}$ (MWh)	CPP	1.536	2.878	2.636	4.645	3.424	5.955
	WPP	1.536	2.878	2.636	4.645	3.424	5.955
	PV (f)	1.269	2.391	2.251	3.930	3.096	5.010
	PV ($\omega$)	1.072	2.186	1.962	3.610	2.740	4.091
$MS{E}_{P_{ther}}$ (MW${}^2$)	CPP	105.4	198.7	258.1	515.6	442.0	932.0
	WPP	83.40	171.8	206.3	442.2	370.9	795.8
	PV (f)	56.98	128.2	143.9	320.5	290.7	555.3
	PV ($\omega$)	73.62	150.3	170.5	359.4	328.7	773.7
$MS{E}_{P_{hyd}}$ (MW${}^2$)	CPP	2.931	41.51	7.272	97.38	12.51	177.1
	WPP	2.579	31.51	6.426	74.60	11.69	130.8
	PV (f)	2.029	20.28	4.939	49.68	9.798	81.92
	PV ($\omega$)	3.021	26.07	7.021	61.54	13.19	127.3

,

Table 6. Simulation results: rotational speed of WPP${}_1$.

Scenario	Load (MW)	250		400		550
	Year	2025	2040	2025	2040	2025	2040
${\omega }_{1,min}$ (pu)	CPP	1.067	1.067	1.067	1.067	1.067	1.067
	WPP	1.000	0.971	1.003	0.983	1.005	0.976
	PV (f)	1.024	1.000	1.019	1.001	1.016	0.995
	PV ($\omega$)	1.030	1.000	1.033	1.026	1.030	0.995
${\omega }_{1,max}$ (pu)	CPP	1.359	1.359	1.359	1.359	1.359	1.359
	WPP	1.394	1.405	1.391	1.409	1.389	1.408
	PV (f)	1.381	1.399	1.385	1.405	1.385	1.403
	PV ($\omega$)	1.372	1.370	1.377	1.376	1.379	1.403
$MS{E}_{{\omega }_1}$, $\times {10}^{-3}$ (pu${}^2$)	CPP	3.631	2.649	2.649	2.649	2.479	2.649
	WPP	4.406	6.485	4.081	5.582	4.098	5.966
	PV (f)	3.738	4.956	3.613	4.517	3.770	4.892
	PV ($\omega$)	3.631	4.551	3.497	3.985	3.589	5.075

,

Table 7. Simulation results: rotational speed of WPP${}_2$.

Scenario	Load (MW)	250		400		550
	Year	2025	2040	2025	2040	2025	2040
${\omega }_{2,min}$ (pu)	CPP	1.052	1.052	1.052	1.052	1.038	1.052
	WPP	1.011	0.885	1.014	0.945	1.015	0.919
	PV (f)	1.037	0.906	1.032	0.966	1.027	0.938
	PV ($\omega$)	1.043	0.891	1.041	0.945	1.040	0.926
${\omega }_{2,max}$ (pu)	CPP	1.327	1.327	1.327	1.327	1.327	1.327
	WPP	1.407	1.385	1.406	1.389	1.404	1.389
	PV (f)	1.393	1.393	1.396	1.390	1.399	1.391
	PV ($\omega$)	1.348	1.373	1.355	1.376	1.360	1.403
$MS{E}_{{\omega }_2}$, $\times {10}^{-3}$ (pu${}^2$)	CPP	3.037	3.037	3.037	3.037	3.517	3.037
	WPP	5.455	9.638	5.470	8.692	5.268	8.902
	PV (f)	4.485	7.363	4.663	7.191	4.718	7.317
	PV ($\omega$)	3.765	6.432	3.948	6.138	4.031	7.117

,

Table 8. Simulation results: rotational speed of WPP${}_3$.

Scenario	Load (MW)	250		400		550
	Year	2025	2040	2025	2040	2025	2040
${\omega }_{3,min}$ (pu)	CPP	0.917	0.917	0.917	0.917	0.766	0.917
	WPP	0.915	0.885	0.912	0.894	0.914	0.891
	PV (f)	0.917	0.902	0.914	0.917	0.915	0.912
	PV ($\omega$)	0.922	0.917	0.919	0.925	0.919	0.916
${\omega }_{3,max}$ (pu)	CPP	1.345	1.345	1.345	1.345	1.366	1.345
	WPP	1.410	1.410	1.408	1.413	1.406	1.412
	PV (f)	1.386	1.414	1.390	1.410	1.395	1.414
	PV ($\omega$)	1.352	1.383	1.367	1.380	1.369	1.401
$MS{E}_{{\omega }_3}$, $\times {10}^{-3}$ (pu${}^2$)	CPP	11.778	11.778	11.778	11.778	24.351	11.778
	WPP	13.636	15.890	13.653	15.304	13.572	15.314
	PV (f)	12.912	14.462	13.120	14.287	13.230	14.492
	PV ($\omega$)	11.394	12.575	11.650	12.774	11.803	13.708

and

Table 9. Simulation results: rotational speed of WPP${}_4$.

Scenario	Load (MW)	250		400		550
	Year	2025	2040	2025	2040	2025	2040
${\omega }_{4,min}$ (pu)	CPP	0.925	0.925	0.925	0.925	0.925	0.925
	WPP	0.946	0.817	0.947	0.865	0.945	0.848
	PV (f)	0.933	0.847	0.936	0.871	0.938	0.874
	PV ($\omega$)	0.924	0.866	0.925	0.879	0.926	0.895
${\omega }_{4,max}$ (pu)	CPP	1.332	1.332	1.332	1.332	1.323	1.332
	WPP	1.376	1.455	1.377	1.431	1.373	1.443
	PV (f)	1.366	1.438	1.370	1.437	1.368	1.433
	PV ($\omega$)	1.356	1.440	1.361	1.436	1.361	1.427
$MS{E}_{{\omega }_4}$, $\times {10}^{-3}$ (pu${}^2$)	CPP	8.601	8.601	8.601	8.601	11.235	8.601
	WPP	9.380	13.266	9.593	12.791	9.485	12.584
	PV (f)	9.113	11.317	9.300	11.347	9.276	11.096
	PV ($\omega$)	8.820	10.696	8.846	10.446	8.854	11.237

show the results of the parameters for the six scenarios simulated under the different frequency control strategies. The PV-generated energy is determined by multiplying the active power $P_{PV}$ by the time interval under analysis (5 min).

With respect to the frequency deviations, the proposed hybrid wind–PV technique results in the maximum $f_{min}$ and the minimum $f_{max}$ values. This means that smaller frequency deviations are obtained, which is also shown in the MSE. In fact:

• A reduction of the MSE between 75% and 95% is obtained when the proposed hybrid wind–PV frequency strategy is used, in contrast to the CPP approach.
• A reduction of the MSE between 50% and 65% is obtained when the proposed hybrid wind–PV frequency strategy is used, in contrast to the WPP approach.
• A reduction of the MSE between 20% and 35% is obtained when the proposed hybrid wind–PV frequency strategy is used, in contrast to the PV(f) approach.

Moreover, the authors would like to highlight that similar results are obtained for the three different power demand scenarios in terms of minimum and maximum frequency deviations, together with the MSE of frequency. Consequently, it can be affirmed that this study is scalable to other isolated power systems, and similar results will be obtained independently of the demand as long as the generation mixes are similar to those considered here, which are in line with future European renewable energy integration roadmaps. It is important to remark that, for the 2025 scenario, frequency deviations are nearly within the acceptable range proposed by the ENTSO-E, i.e., $\pm 800$ mHz [89], even if the vRESs do not participate in frequency control. However, as vRESs massively replace CPPs, frequency response will be substantially deteriorated. In fact, minimum and maximum frequency values under 45 Hz and over 54 Hz, respectively, are obtained if only CPPs are considered for frequency control response for year 2040. This means that, in the medium term, it is a crucial need that vRESs participate in frequency control to avoid such negative effects due to important (and negative) frequency oscillations.

Focusing on the PV-generated energy, the hybrid wind–PV technique gets the minimum values, mainly due to the initial 10% power de-loading and the action based on the $\Delta \omega$ that comes from VSWTs. Specifically:

• Considering the CPP and WPP strategies, the PV power plants work on their MPP and, subsequently, their generated energy is the maximum among the four strategies (and the same for both cases).
• Considering the PV(f) strategy, the PV power plants are de-loaded by 10%. A reduction between 10% and 20% of the PV-generated energy is then obtained in comparison to the CPP and WPP strategies.
• A reduction between 20% and 30% of the PV-generated energy is obtained by using the proposed hybrid wind–PV control compared to the CPP and WPP strategies.

Therefore, the hybrid wind–PV strategy implies an additional PV energy reduction of up to 10% in comparison to a conventional PV frequency control strategy. This aspect should be subsequently evaluated by the PV installation operators. Indeed, their benefits should be partially reduced if TSOs/DSOs do not reward them for providing frequency control services.

With regard to the conventional power plants, including any frequency strategy of vRESs reduces the contribution of thermal and hydro-power to the frequency response. The MSE between the power generated by them and their initial assigned value is thus reduced:

• Comparing the CPP and WPP strategies, the use of VSWTs for frequency control reduces the MSE of thermal power plants by between 14%–20%, with a reduction between 12%–24% for hydro-power plants.
• Comparing the CPP and PV(f) strategies, including a conventional de-loading frequency control strategy for PV power plants reduces the MSE of thermal power plants by between 35%–46%, with a reduction between 31%–51% for hydro-power plants.
• Comparing the CPP and PV($\omega$) strategies, using the hybrid wind–PV control approach reduces the MSE of thermal power plants between 24%–30%, with a reduction between 5%–35% for hydro-power plants. Moreover, there are some cases in which the MSE of the hydro-power plant is slightly increased.

The PV(f) strategy is then the best technique from the point of view of the MSE of conventional power plants.

Finally, focusing on the rotational speed of WPPs (Table 6, Table 7, Table 8 and Table 9):

• The CPP strategy has the smallest variations of rotational speeds. This is due to the fact that such rotational speed variations are only the result of wind speed changes.
• The WPP strategy has the largest variations of rotational speed values. In fact, both the minimum/maximum values of ${\omega }_j$ are obtained with this technique, even though they are small variations of around 5%–10%. Consequently, the maximum MSE is obtained with the WPP strategy. In some cases, the MSE result is three times higher than the value obtained with the CPP approach. Naturally, the speed deviations with this strategy are the result of both the wind speed changes and the hidden-inertia frequency control approach.
• The PV(f) technique slightly improves the minimum/maximum rotational speed values and the MSE (if comparing to the WPP strategy). However, these values are still worse than with the CPP approach.
• The PV($\omega$) strategy reduces the minimum and maximum values of the rotational speed even more, and, consequently, reduces the MSE (if comparing to the WPP and PV(f) strategies). In fact, there are some cases in which the MSE is quite similar for both the CPP and PV($\omega$) techniques.

It can be affirmed that the PV($\omega$) technique is the best overall frequency control strategy, as frequency deviations are reduced and the rotational speed variations of the WPPs are closer to their reference values. Nevertheless, this frequency control solution implies certain reductions in PV-generated energy that should be analyzed by the PV installation operators to compensate for possible decreases in benefits. In Figure 11, the frequency evolution, active power of the four generation units, and $\Delta \omega$ input for the $PI$ controller of PV power plants for the hybrid wind–PV strategy are presented for the 550 MW load and 2025 year scenario. As can be seen, when CPPs are only considered for frequency control, there are severe frequency oscillations, which are reduced by including vRESs into the frequency control. As was discussed, among the three different vRES frequency control strategies, the proposed hybrid wind–PV technique reduces frequency oscillations, together with lower fluctuations in both thermal and hydro-power generation units. Even though CPPs oscillate less than with the other approaches, they are working further than their initially assigned values, as demonstrated with the MSE of Table 5. Similar output wind power values are determined for the three vRES strategies, as the same $PD$ constants are assumed. This response is also less oscillatory than the case in which only CPPs are responding under imbalance conditions. Finally, the PV output power is equal if only the CPP or WPP strategies are considered, as PV active power only changes due to the variations in the solar irradiation G. When the de-loading technique is implemented, the PV power plants include a curtailed 10% active power (from 50 to 45 MW, approximately). Moreover, note that considering the $\Delta \omega$ as input significantly reduces the PV-generated power and, consequently, the generated energy (refer to Table 5), but the frequency deviations are also reduced in comparison to the PV(f) strategy. In Figure 12 and Figure 13, the active power of the four WPP and PV power plants are shown, respectively.

Figure 14 depicts the frequency evolution, active power of the four generation units, and $\Delta \omega$ input for the $PI$ controller of PV power plants for the hybrid wind–PV strategy, corresponding to the 250 MW demand and year 2040 scenario. These results are similar to the previous simulations depicted in Figure 11. In this case, when only CPPs participate in frequency control, the frequency oscillations are higher due to the reduced synchronous inertia of the power system. Grid frequency oscillations are drastically reduced by including vRESs into the frequency response, especially with the proposed hybrid wind–PV solution. Similar active wind power is obtained if they also participate in frequency regulation, providing lower oscillations than the case in which only CPPs are considered. When PV power plants include the de-loading technique, a 10% power reduction is required (from 38 to 34 MW, approximately). When the PV installations receive the $\Delta \omega$ as an input, their active power is reduced accordingly, in line with the generated energy shown in Table 5.

4.3. Limitations and Further Work

This paper tests the benefits of introducing a hybrid wind–PV frequency controller that is able to monitor not only frequency deviations, but also VSWTs’ rotational speed deviations from their optimal reference values. This generalization allows conclusions to be drawn in a high casuistry of scenarios, but it makes it necessary to neglect or simplify some aspects without losing accuracy. These simplifications are:

• Thermal units are supposed to work at the same operating point, considering a single equivalent turbine. In addition, only one thermal power plant technology is assumed (reheat thermal). Hydro-power plants are modeled analogously (including only one kind of hydro turbine). Finally, each wind power plant is modeled as one equivalent VSWT.
• The initial assigned power (generation programming) of each one of the generation units was not obtained with technical–economic criteria (unit commitment), nor were their PFC reserves and secondary control action. Once each generation unit is individually modeled, it is reasonable to assign an initial power to each unit according to both technical and economic criteria.
• To obtain each vRES penetration level, the ENTSO-E recommendations for interconnected power systems were followed by the authors. However, isolated power systems can have different vRES integration levels. However, this hypothesis is assumed to give generality to the present study.
• As described in Section 2, power line dynamics are neglected, as well as the communication lines between the wind and PV power plants for the proposed hybrid wind–PV controller set-up.

As the results and conclusions of this study can be considered as positive, the next step proposed by the authors is to analyze the impact of establishment in some specific isolated power systems, such as one of the existing ones in the Canary archipelago, in the Aegean islands, or in the Azores archipelago. Since those power systems are well known, it is reasonable to individually introduce each generation unit into the dynamic model. Additionally, current and future renewable energy penetration as well as real wind speed and irradiation data can be used for future simulations. Once the locations of both wind and PV power plants are known, the influence of the communication time on the control actions can be also analyzed. The corresponding time delays with the measurement of errors and the transmission of control signals between wind and PV power plants would then be included in the model. Likewise, this proposal will be able to optimize the power system’s operation by associating the control of some specific wind power plants to certain geographically neighboring PV power plants.

5. Conclusions

This paper proposes a hybrid wind–PV frequency control approach for isolated power systems with high vRES integration under variable weather conditions. The proposed controller consists of VSWTs that include a hidden-inertia emulation technique and PV power plants working with a de-load power of 10%. The input of the PV frequency control is the rotational speed deviation of the VSWTs, in contrast to previous studies where the frequency deviation is the input of the de-loaded PV controller. In this way, the PV power plants modify their generated power by following the rotational speed deviation of the VSWTs, reducing the deviation of such rotational speeds, and, consequently, minimizing the frequency deviations under power imbalances. The proposed hybrid frequency approach is compared to three different frequency strategies: $\left(i\right)$ conventional power plants, $\left(ii\right)$ conventional power plants and wind power plants, and $\left(iii\right)$ conventional power plants, wind power plants, and PV power plants with grid frequency as input. The results show that frequency oscillations are drastically reduced by including the proposed hybrid controller. In fact, the mean squared error of frequency variations is reduced by up to 95% in comparison to the case in which only conventional power plants are controlling the frequency variations. Severe reductions are also found when comparing the hybrid wind–PV strategy to the other two strategies in which vRESs participate in frequency control (between 20% and 65%). The rotational speed deviation of the VSWTs also decreases with the hybrid wind–PV frequency approach, even getting the same mean squared error as when VSWTs do not participate in frequency control. However, the energy generated by the PV power plants decreases by between 20% and 30% when using the proposed approach, and should be subsequently analyzed by the transmission/distribution operators to guarantee some additional benefits for the owners of such generation units. Based on the results, the authors also wish to remark on the importance of vRESs participating in frequency control in the near future in order to avoid significant frequency deviations that will occur if these sources keep replacing conventional power plants without providing any frequency response. Consequently, hybrid frequency control strategies in line with this work should be proposed and analyzed to minimize frequency variations linked to a massive vRES integration.