The impact of car-sharing on car-use is defined as the change in km travelled by car per week as a driver. This includes distances travelled by a respondent’s own car, a shared car, and cars that are borrowed from friends and family.
The implication of the conceptual framework is that the impact of car-sharing on the distance travelled by car will be different for the LAUs and HAUs. To avoid violation of SUTVA, the effect of car-sharing on transport demand has been estimated separately for HAUs and LAUs.
2.5.1. Higher Access Users (HAUs)
For HAUs with no cars in the household, the impact of car-sharing on car-use is directly observed, since without car-sharing, these users would not have access to a car. Therefore, the impact on car-use for these users is the distance travelled by shared cars. However, for HAUs with cars in the household, the direct effect cannot be measured in the same way: it cannot be ruled out that, without car-sharing, such a user would postpone a journey until a household car became available; in other words, the use of shared cars may replace some private car-use, rather than replacing other modes or used to make additional journeys. The impact of car-sharing on car-use for this group could be estimated using the same method used for LAUs; however, due to the small sample size of HAUs and the representative control group, it is not possible to use methods robust to unconfoundedness. Instead, we make use of a question in the survey in which car-sharing users are asked how they would replace car-sharing journeys if they were no longer car-sharing members (i.e., self-assessed counterfactual). For example, if a user travels 100 km by car-sharing in a typical week, and estimates that 25% of journeys currently made by car-sharing would be replaced with a private car, then the counterfactual estimate of car-use is 25 km, and the corresponding impact of car-sharing on car-use is an increase of (100–25) 75 km.
2.5.2. Lower Access Users (LAUs)
In order to estimate the counterfactual distance travelled by car for LAUs, we make use of a quasi-experimental method to ensure unconfoundedness. Applied to this context, the unconfoundedness assumption relies on there being no factors that affect both participation in car-sharing and car-use. To ensure that uncounfoundedness is not violated, we compare the outcomes of users to non-users while adjusting for factors that may affect both participation and outcome using regression. There are four stages to this process:
Pre-screen the treatment group to include only those who are classed as “Active” LAUs
Pre-screen the control group to include only users who are similar to the treatment group
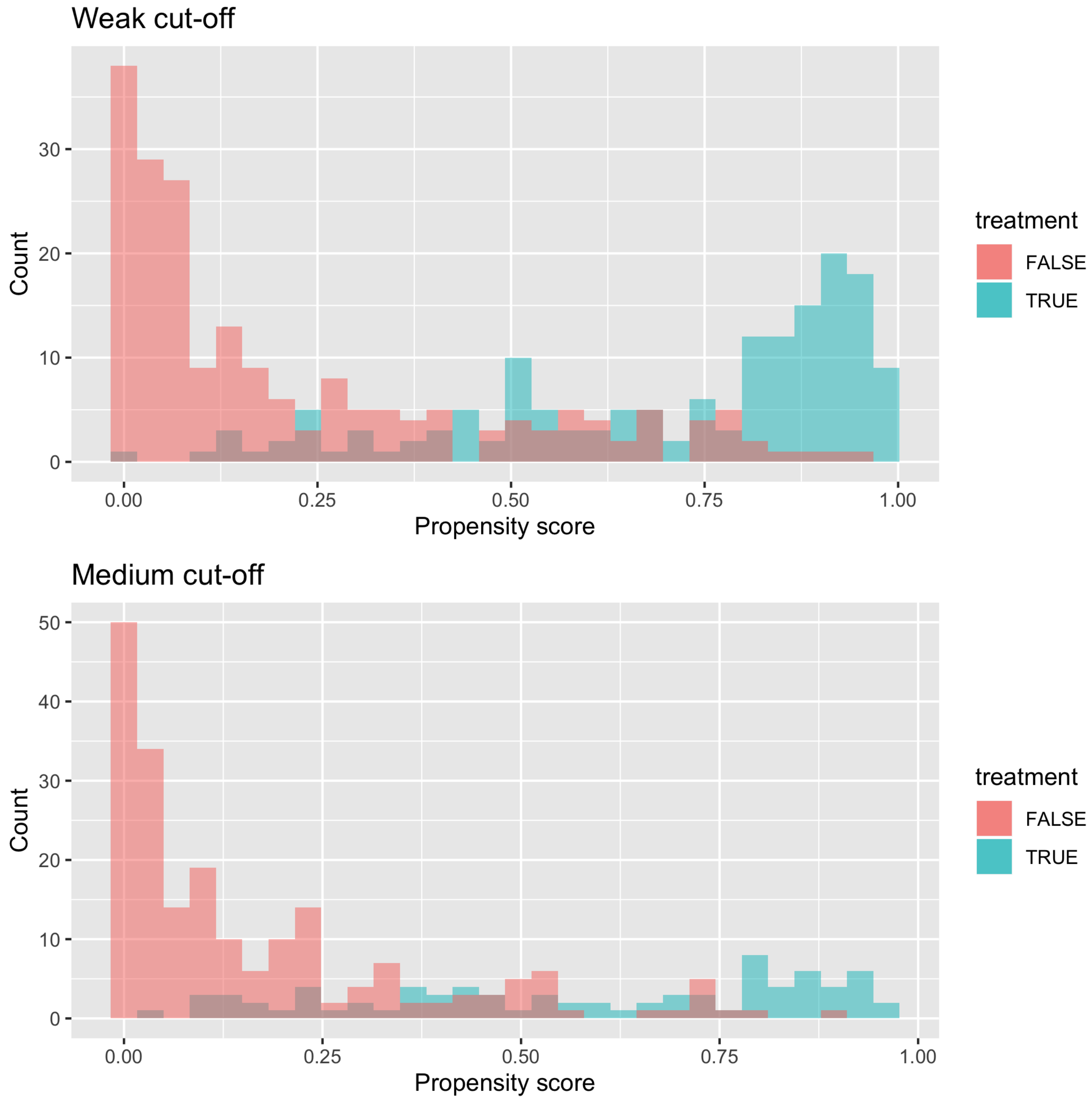
Pre-screen both the treatment and control group using propensity score matching to reduce model dependence
Use regressions to control for observed differences between the treatment and control groups (see
Section 2.5.3).
The treatment group only contain users who have been affected by car-sharing, that is, active users. The estimated effect is therefore the average treatment effect on the treated (ATT), as opposed to the average treatment effect (ATE), which considers those who may join but are not affected by car-sharing. Active users were judged to be those who travel at least some amount of km per week using car-sharing, or whose car-ownership has been affected by car-sharing (i.e., this includes those who do not use car-sharing at all in a typical week, but who still own fewer cars because of car-sharing).
The control group was pre-screened to exclude observations who showed no interest in car-sharing, determined by answers to the DCE and the respondent’s own assessment. Specifically, non-users were filtered to include only those who chose car-sharing four or more times in the DCE (out of eight), and who showed a willingness to join car-sharing now or in the future. Furthermore, each non-car-sharing user was asked following the DCE whether they considered the scenario where they were replacing an existing car or choosing an additional car. Thus, for each member of the control group, we were additionally able to understand whether they envisaged car-sharing as replacing a private car or using it as an additional vehicle, mirroring the designation of car-sharing users as LAUs or HAUs.
A final stage of pre-screening based on matching methodology was also implemented in a set of models to increase the internal validity of the estimates. There is a threat to internal validity if the distributions of each control variable for treatment and control groups do not overlap [
29], i.e., there are observations of treated or control units for whom there is no similar comparison. Estimates of the treatment effect thus rely on extrapolation of the regression results, leading to dependence on the correct specification of the subsequent regression model [
27,
29] (pp. 309–336). The degree of overlap of each control variable can be determined by comparing the distributions of each variable for treatment and control groups. However, in order to reduce the dimensionality and complexity of this, it is common to use a single composite variable known as the propensity score. We calculated the propensity score by fitting a binomial logit regression with treatment (car-sharing membership) as the dependent variable and all the control variables which are hypothesised to determine both car-sharing membership and outcomes (car-use and car-ownership). This propensity score can be thought of as an estimate of the probability of an observation being a member of car-sharing. Each treatment unit is then matched to a control unit using nearest neighbour matching. For the most robust model, any observations in the control or treatment group with a propensity score that is out-with the range of the propensity score of the other group were discarded. The matching was performed using the
MatchIt package [
30] for R [
31].
The major threat to external validity, that is, that the results can be generalised to other (geographical) contexts, is the non-random sample. This has been captured to some extent by a sensitivity analysis where the over representation of p2p users is considered.
2.5.3. Zero-Inflated Negative Binomial Regressions
To control for any remaining differences between LAU car-sharing users and non-users, we regress the total km driven on a set of control variables that may also affect both car-sharing membership and distance driven by car. Since the dependent variable is bounded by zero, and exhibits large dispersion, we make use of negative binomial regression. The negative binomial distribution (NB) is a variant of the Poisson distribution, both of which are used for count data, in which the dependent variable consists of positive integers only; the NB, however allows for data that is more heavily skewed by relaxing the restriction of a Poisson regression that the variance must be equal to the mean. In this case, the data exhibits a positive skew, with a variance much larger than the mean.
Additionally, the dependent variable contains a significant number of zeros, indicating that the respondent does not use a car at all. This is particularly the case for car-sharing users who have given up a car because of car-sharing and consequently no longer drive. While both Poisson and NB regressions allow for zeros in the dependent variable, the number of zeros predicted by the models is often underestimated [
32]. Since these zeros are both prevalent in the data and meaningful, underestimating their frequency could lead to biased results; thus we make-use of zero-inflated negative binomial (ZINB) regressions.
In ZINB models, the dependent variable is modelled as the outcome of two different processes: one that determines whether an observation would be zero, and another that estimates the outcome for all non-zero observations. A binomial logit model is used to estimate the probability that the dependent variable (total distance travelled by car) is equal to zero, while a negative binomial model (using the log link function) is used to estimate the distance travelled by car. The ZINB models were estimated in R v3.6.1 [
31] using the
zeroinfl [
33] function from the
pscl package [
34].
To estimate the treatment effect based on these regressions, we make use of the average predicted valued method described by Albert et al. [
35], except we only calculated the counterfactual for treatment observations, and ignore controls (following the desire to estimate the ATT rather than the ATE). The process is straightforward:
Calculate the fitted values for each observation
Estimate the counterfactual by calculating fitted values for the treatment group, but ignoring the effect of the treatment variables.
The mean difference between the two calculated effects across all treated observations gives the ATT.
More formally, the expected value of the total distance travelled by car per week for a respondent is:
where
is the combined distance travelled by private car (i.e., cars owned by the respondent), shared cars and cars borrowed from friends and family,
is a vector of control variables (see below), and
and
are the estimated treatment regression coefficients for the logit and the NB model respectively.
and
represent the regression coefficients for the control variables. Car-sharing membership is represented by a vector,
, which includes a dummy variable indicating membership as well as a set of other dummies corresponding to different types of car-sharing, that is, free-floating car-sharing, whether the user provides their own car for others to use, and for the sensitivity analysis, whether the respondent uses p2p car-sharing more often than b2c car-sharing. The treatment vector also contains interactions with the counterfactual number of cars in the household (
), the intuition being that the impact of car-sharing is also affected by how many cars remain (the variable
is not interacted with
, since only those who have a car in the household (hhpcars.pre.cs = 2) are able to share, thus the interaction is redundant). The counterfactual number of cars, instead of the observed number, is used to avoid endogeneity bias in the results, that is, using a variable that is itself affected by car-sharing. To calculate the variable, we assume that each LAUt car-sharing user has one fewer cars in the household as a result of car-sharing.
The average treatment effect,
is then estimated by:
where
j represents the subset of treatment observations, and
J its total. This equation is equivalent to the mean difference between the observed distance travelled and the counterfactual.
Control Variables
The choice of control variables is crucial to establish causal inference in a regression model. Not including relevant variables violates unconfoundedness, leading to biased estimators of the effect of car-sharing. However, using control variables that are likely to be affected by treatment, that is, joining car-sharing, will also lead to a biased estimators. Thus, the selection of control variables in this model is based on the following criteria:
- (1)
the variable should have a plausible causal influence on the dependent variable (i.e., distance travelled by car)
- (2)
the variable should have a plausible causal influence on the treatment variable (i.e., the decision to join car-sharing)
- (3)
the variable should not be affected by the treatment (i.e., the decision to join car-sharing)
In general, to avoid violation of the third criteria, it is recommended to only use variables that are fixed, deterministic, or measured pre-treatment [
36]. For example, age is deterministic, and thus is not affected by car-sharing, although it may affect whether someone joins car-sharing. However, it is not possible to measure pre-treatment variables in cross-sectional studies such as this. Instead, all control variables must meet the criteria through plausible justification. For example, the number of children in a household is not expected to be affected by the decision to join car-sharing, but it may affect both car-use (the dependent variable) and the decision to join car-sharing, and hence it is included as a control variable. We also included three variables that reflect answers to statements on different aspects of mobility, answers to which could be given on a five-point likert scale. Given the criteria above, we assume that these attitudes are not affected by joining car-sharing, but are instead stable attitudes that are independent of car-sharing.
Details of all the control variables are given in
Table 6.
Some of the control variables contained missing values, mostly because the respondent chose not to answer. For attitude questions (i.e., Q36_1N, Q36_3N, Q36_7N), missing values were coded as “neutral”: we assume that if the user chose not to answer the question, then he/she does not have a strong opinion. For the “environment” variable, values were imputed based on how others in the same postcode answered. If there was no clear majority for one choice, then the population density was used to judge which value was most appropriate. Finally, for gender, both missing values and those who chose not to reveal their gender were replaced at random.
In the regression models with smaller samples (i.e., medium and strong cut-off samples), some of the control variables had to be dropped in order for the regression models to be estimated. The procedure for dealing with this was first to try to identify and then drop the variable causing the issue. This was mainly due to a lack of variance in the variable, or because of high correlation with other variables in the model. If no variable could be identified, then variables that were insignificant based on the p-values of regressions of the larger samples were removed.
2.5.4. Stable Unit Treatment Value Assumption (SUTVA)
In the potential outcome framework, a key assumption is the SUTVA, made up of two parts: that those who receive the treatment (car-sharing) do not affect whether others receive the treatment, and that each unit receives the same treatment [
27](p.10). In this case study, we must therefore assume that one person joining car-sharing does not affect another unit’s outcome. While more users would lead to more use of shared cars, and perhaps less shared car availability, we assume that this effect is not large. It is also likely that car-sharing providers adapt the number of shared cars provided to match demand. The second part of the SUTVA, however, is perhaps more problematic. The treatment “being a member of car-sharing” is not stable when we consider the different types of treatment available: car-sharing may be a round-trip system or a free-floating system, different car-sharing systems may have different cost structures, the cars used by different companies may be more or less appealing to each user, and outcomes may depend on the business model (e.g., peer-to-peer vs business-to-consumer). Of most concern is perhaps the difference between free-floating and round-trip systems, since there is evidence in other studies that these systems are used in different ways [
37]; however, this is less problematic in this case due to the few respondents who use free-floating car-sharing systems. Other aspects that may violate the SUTVA is the difference between p2p and b2c car-sharing, and, as a p2p car-sharer, providing your own car to other users. To account for both membership of free-floating car-sharing and p2p car-sharing, and those who share there own car, we introduced variables that control for these differences in the regression (the variables
cs.ff,
p2p, and
csprovider respectively). The results of the p2p model are discussed in the sensitivity analysis (
Section 3.6). The results of free-floating members or those who share their own car are not highlighted here due to the small number of these users in the survey.