New Computational Artificial Intelligence Models for Generating Synthetic Formation Bulk Density Logs While Drilling
Abstract
1. Introduction
2. Data Analysis and Processing
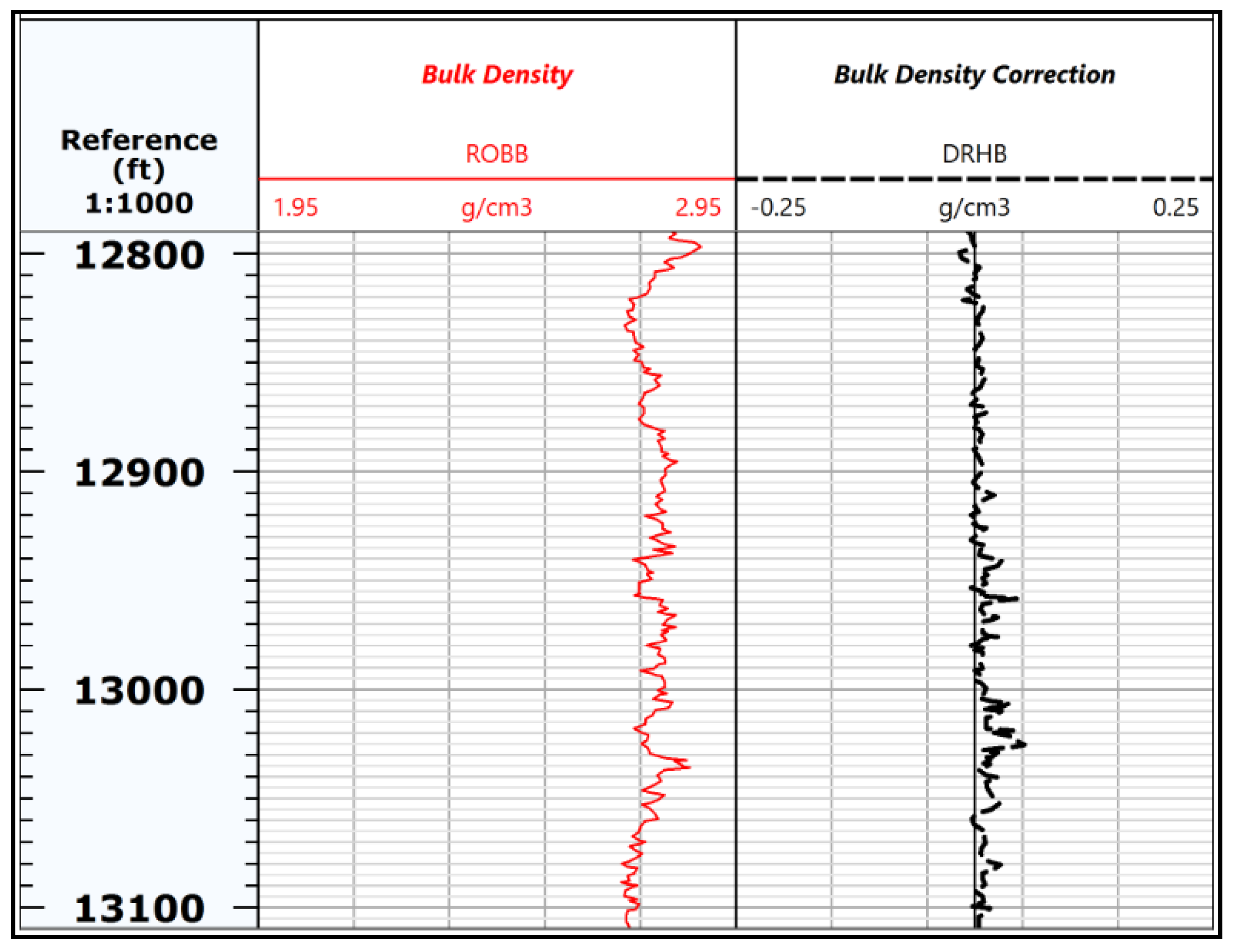
2.1. Data Description
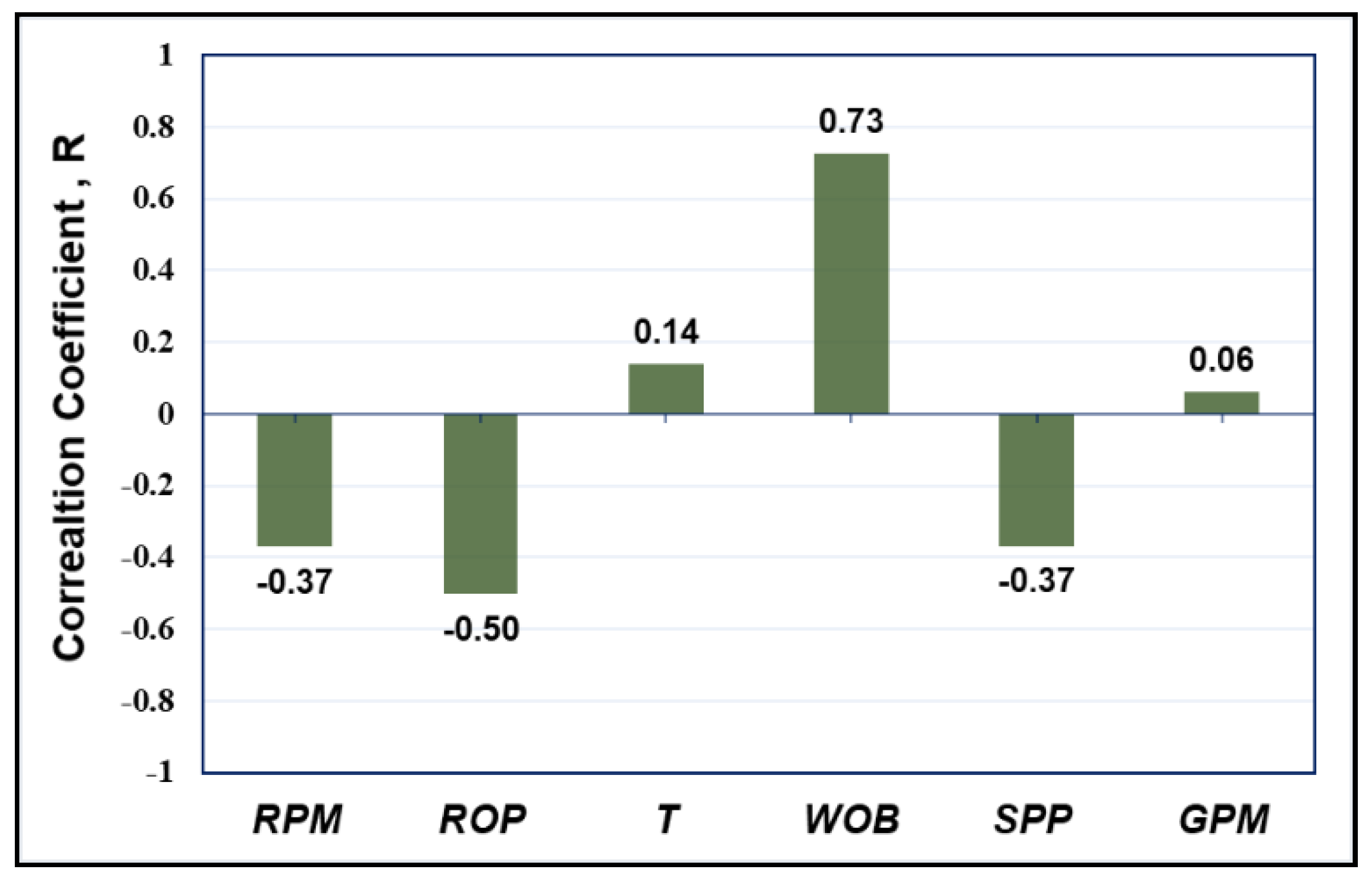
2.2. Relative Importance of the Input(s) to the Output
2.3. Data Processing
3. RHOB Model Development
3.1. Adaptive Network-Based Fuzzy Interference Systems (ANFIS)
Building the RHOB Model Using ANFIS
3.2. Functional Networks (FN)
Building the RHOB Model using an FN
3.3. Support Vector Machines
Building the RHOB Model Using SVM
4. Model Validation
5. Conclusions
- (1)
- The ANFIS-based model outperformed the FN- and SVM-based models in terms of the accuracy of the RHOB predictions, with an AAPE of 0.81% between the predicted and actual RHOB values, as compared to 0.95% and 1.13% for the FN- and SVM-based models, respectively.
- (2)
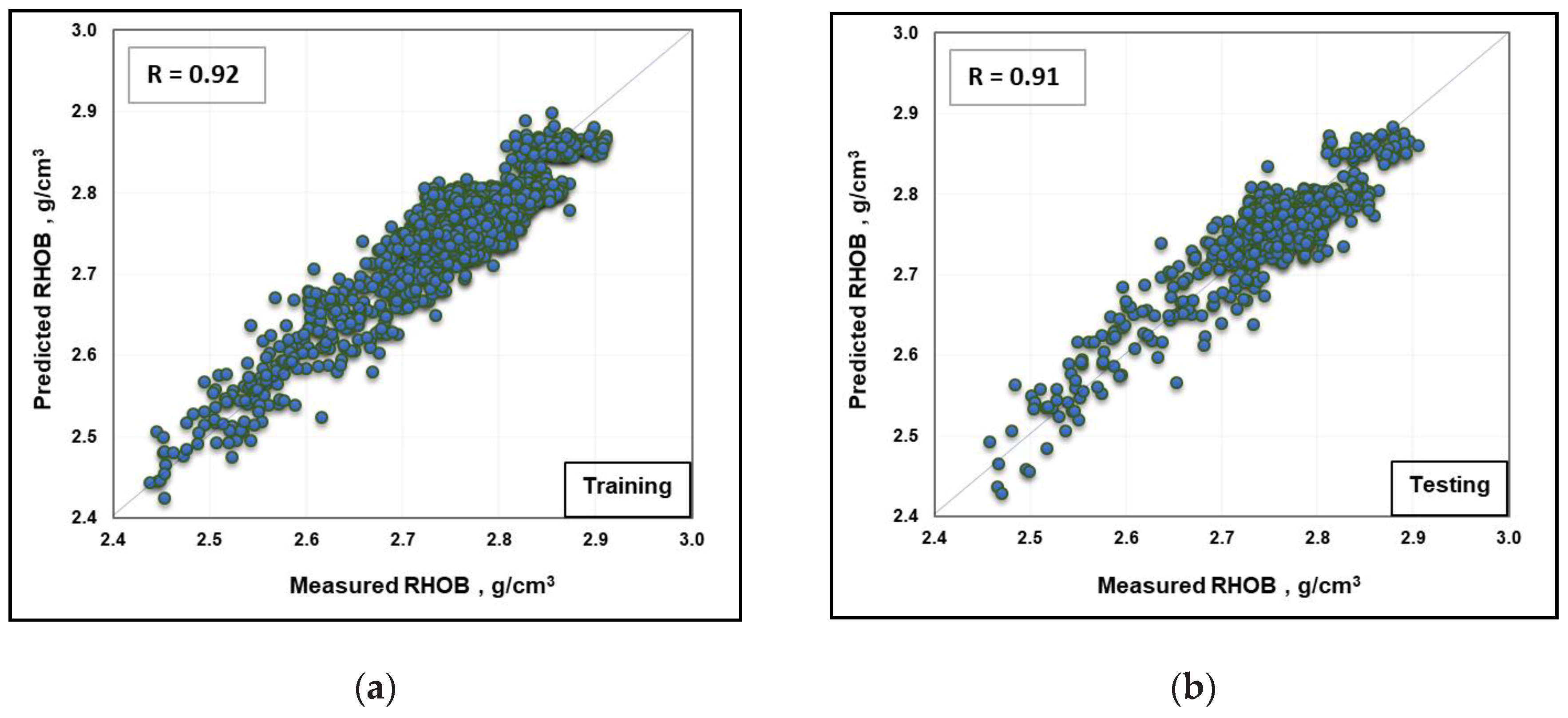
- The optimized ANFIS model is capable of predicting RHOB values to a high level of accuracy, as indicated by its R of 0.93 and AAPE of 0.81% between the predicted and measured RHOB values.
- (3)
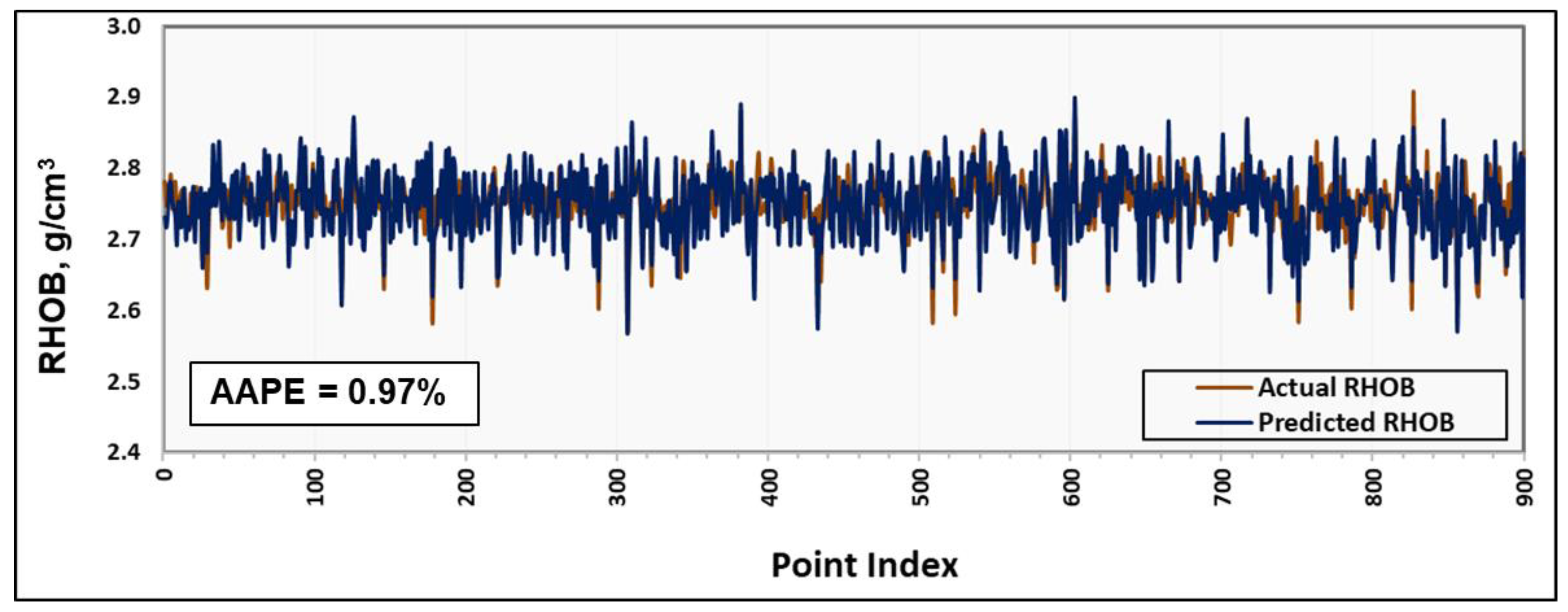
- The validation process for the ANFIS-based model (using field data from another well) confirmed its outstanding prediction performance, as indicated by an AAPE of 0.97% between the predicted and actual RHOB values.
- (4)
- The developed ANFIS-based model can be used to predict RHOB values with reliably high accuracy, especially in wells where the well logging data are not available or are partially absent.
- (5)
- RHOB predictions that are obtained during drilling using the developed ANFIS-based model will assist in assessing the formations being drilled, and, in turn, avoid interruptions such as kicks and the loss of circulation when identifying the zones causing these issues.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| AAPE | Average absolute percentage error |
| AI | Artificial Intelligence |
| ANFIS | Adaptive network-based fuzzy interference system |
| BE | Backward elimination |
| BF | Backward–forward |
| ES | Exhaustive search |
| FB | Forward–backward |
| FN | Function network |
| FS | Forward selection |
| MSE | Mean square error |
| R | Correlation coefficient |
| ROP | Rate of penetration |
| RPM | Rotating speed in revolution per minute |
| SPP | Standpipe pressure |
| SVM | Support vector machine |
| T | Torque |
| WOB | Weight on bit |
Appendix A
References
- Ellis, D. Formation porosity estimation from density logs. Petrophysics 2003, 44, 306–316. [Google Scholar]
- Rolon, L.; Mohaghegh, S.D.; Ameri, S.; Gaskari, R.; McDaniel, B. Using artificial neural networks to generate synthetic well logs. J. Nat. Gas Sci. Eng. 2009, 1, 118–133. [Google Scholar] [CrossRef]
- Wraight, P.D.; Evans, M.; Marienbach, E.; Rhein-Knudsen, E.; Best, D. Combination formation density and neutron porosity measurements while drilling. In Proceedings of the SPWLA 30th Annual Logging Symposium, Denver, CO, USA, 11–14 June 1989; Society of Petrophysicists and Well-Log Analysts Inc.: Houston, TX, USA, 1989. [Google Scholar]
- Bassiouni, Z. Theory, Measurement, and Interpretation of Well Logs; SPE Textbook Series; Society of Petroleum Engineers: Houston, TX, USA, 1994; Volume 4, p. 372. [Google Scholar]
- Gatens, J.M.; Harrison, C.W.; Lancaster, D.E.; Guidry, F.K. In-Situ Stress Tests and Acoustic Logs Determine Mechanical Properties and Stress Profiles in the Devonian Shales. SPE Form. Eval. 1990, 5, 248–254. [Google Scholar] [CrossRef]
- Reichel, N.; Evans, M.; Allioli, F.; Mauborgne, M.L.; Nicoletti, L.; Haranger, F.; Laporte, N.; Stoller, C.; Cretoiu, V.; El Hehiawy, E.; et al. Neutron-Gamma Density (NGD): Principles, field test results and log quality control of a radioisotope-free bulk density measurement. In Proceedings of the SPWLA 53rd Annual Logging Symposium, Cartagena, CO, USA, 16–20 June 2012; Society of Petrophysicists and Well-Log Analysts Inc.: Houston, TX, USA, 2012. [Google Scholar]
- Wahl, J.S.; Tittman, J.; Johnstone, C.W. The dual spacing formation density log. J. Pet. Technol. 1964, 16, 1–411. [Google Scholar] [CrossRef]
- Alger, R.P.; Raymer, L.L. Formation Density Log Applications in Liquid-Filled Holes. J. Pet. Technol. 1963, 15, 321–332. [Google Scholar] [CrossRef]
- Spross, R.; Burnett, T.; Freeman, J.; Jones, D.; Paske, W.; Zannoni, S. Formation Density Measurement While Drilling. In Proceedings of the SPWLA 34th Annual Logging Symposium, Calgary, AB, Canada, 13–16 June 1993. [Google Scholar]
- Falconer, I.G.; Burgess, T.M.; Sheppard, M.C. Separating Bit and Lithology Effects from Drilling Mechanics Data. In Proceedings of the SPE/IADC Drilling Conference, Dallas, TX, USA, 28 February–2 March 1988. [Google Scholar] [CrossRef]
- Jackson, C.E.; Heysse, D.R. 1994, Improving Formation Evaluation by Resolving Differences Between LWD and Wireline Log Data. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 25–28 September 1994. [Google Scholar] [CrossRef]
- Xu, H.; Li, X.; Li, Y.; Lei, Z.; Sui, S. A Calculation of Cuttings Lag Time for Foam Drilling. Pet. Explor. Dev. 2009, 36, 503–507. [Google Scholar]
- Zhang, D.; Chen, Y.; Meng, J. Synthetic well logs generation via Recurrent Neural Networks. Pet. Explor. Dev. 2018, 45, 598–607. [Google Scholar] [CrossRef]
- Gowida, A.; Elkatatny, S.; Abdulraheem, A. Application of Artificial Neural Network to Predict Formation Bulk Density While Drilling. Petrophysics 2019, 60, 660–674. [Google Scholar] [CrossRef]
- González, J.W.; Valdez, R.; Torres, J.; Medina, F. Identification of Zones of Abnormal Pressures and Determination of the Mechanical Properties of the Rock through Pseudo-Sonic and Pseudo-Density Logs in Conventional and Unconventional Reservoirs. In Proceedings of the SPE Argentina Exploration and Production of Unconventional Resources Symposium, Neuquen, Argentina, 14–16 August 2018. [Google Scholar] [CrossRef]
- Bourgoyne, A.T., Jr.; Millheim, K.K.; Chenevert, M.E.; Young, F.S., Jr. Applied Drilling Engineering; Society of Petroleum Engineers Inc.: Houston, TX, USA, 1986; Volume 2. [Google Scholar]
- Mensa-Wilmot, G.; Calhoun, B.; Perrin, V.P. Formation drillability-definition, quantification and contributions to bit performance evaluation. In Proceedings of the SPE/IADC Middle East Drilling Technology Conference, Abu Dhabi, UAE, 8–10 November 1999; Society of Petroleum Engineers: Houston, TX, USA, 1999. [Google Scholar]
- Hemphill, T.; Bern, P.; Rojas, J.; Ravi, K. Field Validatio of Drillpipe Rotation Effects on Equivalent Circulatin Density. In Proceedings of the SPE Annua Technical Conference and Exhibition, Anaheim, CA, USA, 11–14 November 2007. [Google Scholar] [CrossRef]
- Ellis, D.V.; Singer, J.M. Well Logging for Earth Scientists, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2007; ISBN 978-1-4020-3738-2. [Google Scholar] [CrossRef]
- Jang, J.S.; Sun, C.T. Neuro-fuzzy modeling and control. Proc. IEEE 1995, 83, 378–406. [Google Scholar] [CrossRef]
- Walia, N.; Singh, H.; Sharma, A. ANFIS: Adaptive neuro fuzzy inference system—A survey. Int. J. Comput. Appl. 2015, 123, 32–38. [Google Scholar] [CrossRef]
- Jang, J.S. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Jang, J.S. Input selection for ANFIS learning. In Proceedings of the IEEE 5th International Fuzzy Systems, New Orleans, LA, USA, 11 September 1996; pp. 1493–1499. [Google Scholar]
- Aghli, G.; Moussavi-Harami, R.; Mortazavi, S.; Mohammadian, R. Evaluation of new method for estimation of fracture parameters using conventional petrophysical logs and ANFIS in the carbonate heterogeneous reservoirs. J. Pet. Sci. Eng. 2019, 172, 1092–1102. [Google Scholar] [CrossRef]
- Ja’fari, A.; Kadkhodaie-Ilkhchi, A.; Sharghi, Y.; Ghanavati, K. Fracture density estimation from petrophysical log data using the adaptive neuro-fuzzy inference system. J. Geophys. Eng. 2012, 9, 105–114. [Google Scholar] [CrossRef]
- Ahmed, A.; Elkatatny, S.; Ali, A.; Abdulraheem, A. Comparative analysis of artificial intelligence techniques for formation pressure prediction while drilling. Arab. J. Geosci. 2019, 12, 592. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Elkatatny, S.; Abdulraheem, A.; Mahmoud, M. Application of Artificial Intelligence Techniques in Estimating Oil Recovery Factor for Water Derive Sandy Reservoirs. In Proceedings of the SPE Kuwait Oil & Gas Show and Conference, Kuwait City, Kuwait, 15–18 October 2017; Society of Petroleum Engineers: Houston, TX, USA, 2017. [Google Scholar]
- Castillo, E.; Gutiérrez, J.M.; Hadi, A.S.; Lacruz, B. Some Applications of Functional Networks in Statistics and Engineering. Technometrics 2001, 43, 10–24. [Google Scholar] [CrossRef]
- Anifowose, F.; Labadin, J.; Abdulraheem, A. A least-square-driven functional networks type-2 fuzzy logic hybrid model for efficient petroleum reservoir properties prediction. Neural Comput. Appl. 2013, 23, 179–190. [Google Scholar] [CrossRef]
- Castillo, E.; Cobo, A.; Gutierrez, J.A.; Pruneda, R.E. Functional Networks with Applications: A Neural-Based Paradigm; Springer Science & Business Media: New York, NY, USA, 2012; Volume 473. [Google Scholar]
- Castillo, E.; Hadi, A.S. Functional networks. In Wiley StatsRef: Statistics Reference Online; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Cobo, A.; Gutierrez, J.M.; Pruneda, E. Functional Networks: A New Network-Based Methodology. Comput. Civ. Infrastruct. Eng. 2000, 15, 90–106. [Google Scholar] [CrossRef]
- Castillo, E.; Cobo, A.; Gutiérrez, J.M.; Pruneda, R.E. Functional Networks with Applications; Springer: Boston, MA, USA, 1999. [Google Scholar] [CrossRef]
- Ahmed, A.; Khalid, M. An intelligent framework for short-term multi-step wind speed forecasting based on Functional Networks. Appl. Energy 2018, 225, 902–911. [Google Scholar] [CrossRef]
- Bello, O.; Asafa, T. A functional networks softsensor for flowing bottomhole pressures and temperatures in multiphase production wells. In Proceedings of the SPE Intelligent Energy Conference & Exhibition, Utrecht, The Netherlands, 1–3 April 2014; Society of Petroleum Engineers: Houston, TX, USA, 2014. [Google Scholar]
- Mahmoud, A.A.A.; Elkatatny, S.; Mahmoud, M.; Abouelresh, M.; Abdulraheem, A.; Ali, A. Determination of the total organic carbon (TOC) based on conventional well logs using artificial neural network. Int. J. Coal Geol. 2017, 179, 72–80. [Google Scholar] [CrossRef]
- Tariq, Z.; Abdulraheem, A.; Mahmoud, M.; Ahmed, A. A Rigorous Data-Driven Approach to Predict Poisson’s Ratio of Carbonate Rocks Using a Functional Network. Petrophysics 2018, 59, 761–777. [Google Scholar]
- Nooruddin, H.A.; Anifowose, F.; Abdulraheem, A. Applying artificial intelligence techniques to develop permeability predictive models using mercury injection capillary-pressure data. In Proceedings of the SPE Saudi Arabia Section Technical Symposium and Exhibition, Al-Khobar, Saudi Arabia, 19–22 May 2013; Society of Petroleum Engineers: Houston, TX, USA, 2013. [Google Scholar]
- El-Sebakhy, E.A.; Hadi, A.S.; Faisal, K.A. Iterative least squares functional networks classifier. IEEE Trans. Neural Netw. 2007, 18, 844–850. [Google Scholar] [CrossRef] [PubMed]
- Anifowose, F.; Labadin, J.; Abdulraheem, A. Improving the prediction of petroleum reservoir characterization with a stacked generalization ensemble model of support vector machines. Appl. Soft Comput. 2015, 26, 483–496. [Google Scholar] [CrossRef]
- Anifowose, F.; Adeniye, S.; Abdulraheem, A.; Al-Shuhail, A. Integrating seismic and log data for improved petroleum reservoir properties estimation using non-linear feature-selection based hybrid computational intelligence models. J. Pet. Sci. Eng. 2016, 145, 230–237. [Google Scholar] [CrossRef]
- Anifowose, F.A.; Labadin, J.; Abdulraheem, A. Ensemble model of non-linear feature selection-based extreme learning machine for improved natural gas reservoir characterization. J. Nat. Gas Sci. Eng. 2015, 26, 1561–1572. [Google Scholar] [CrossRef]
- Tariq, Z.; Mahmoud, M.; Abdulraheem, A. Core log integration: A hybrid intelligent data-driven solution to improve elastic parameter prediction. Neural Comput. Appl. 2019, 31, 1–21. [Google Scholar] [CrossRef]




| Parameter | Value | |
|---|---|---|
| Geometry | Hole Size | 6″ |
| TVD | 10,500 ft | |
| Dip Angle | ||
| Drilling Fluid | Type | Oil-Based Mud (80/20 ratio) |
| Mud Weight | 69–71 pcf | |
| Solid Content | 4% | |
| Lithology | Mainly Carbonate |
| Parameter | RPM | ROP (ft/h) | T (kIb ft) | WOB (klb) | SPP (psi) | GPM | RHOB (g/cm3) |
|---|---|---|---|---|---|---|---|
| Min. | 58.497 | 5.812 | 1.033 | 4.604 | 2393.772 | 195.111 | 2.438 |
| Max. | 135.90 | 65.89 | 8.02 | 35.33 | 3483.93 | 305.24 | 2.91 |
| Mean | 104.71 | 29.83 | 4.77 | 18.52 | 3044.19 | 264.81 | 2.75 |
| Mode | 99.91 | 18.15 | 4.83 | 21.52 | 2935.41 | 265.73 | 2.74 |
| Range | 77.40 | 60.09 | 6.99 | 30.72 | 1090.16 | 110.12 | 0.47 |
| Skewness | −0.64 | 0.42 | −0.46 | −1.12 | −0.30 | −4.18 | −1.29 |
| Radius | R_Train | R_Test | AAPE_Train | AAPE_Test |
|---|---|---|---|---|
| 0.2 | 0.95 | 0.93 | 0.71 | 0.81 |
| 0.3 | 0.94 | 0.93 | 0.79 | 0.86 |
| 0.4 | 0.92 | 0.91 | 0.91 | 0.92 |
| 0.5 | 0.91 | 0.89 | 0.94 | 0.99 |
| 0.6 | 0.92 | 0.90 | 0.92 | 0.97 |
| 0.7 | 0.90 | 0.88 | 1.00 | 1.05 |
| 0.8 | 0.90 | 0.89 | 1.00 | 1.05 |
| 0.9 | 0.88 | 0.87 | 1.02 | 1.07 |
| Method | R_Train | R_Test | AAPE_Train | AAPE_Test |
|---|---|---|---|---|
| ES | 0.90 | 0.88 | 1.01 | 1.06 |
| FS | 0.91 | 0.90 | 0.95 | 1.01 |
| BE | 0.90 | 0.89 | 1.02 | 1.06 |
| FE | 0.92 | 0.91 | 0.90 | 0.95 |
| BF | 0.87 | 0.86 | 1.11 | 1.13 |
| Parameter | Value |
|---|---|
| Kernel function | Gaussian |
| Kernel option | 7 |
| Lambda | 1 × 10−7 |
| Epsilon | 0.01 |
| Verbose | 1 |
| C | 1000 |
| Radius | R_Train | R_Test | AAPE_Train | AAPE_Test | MSE_Train | MSE_Test |
|---|---|---|---|---|---|---|
| ANFIS | 0.95 | 0.93 | 0.71 | 0.81 | 0.0006 | 0.0008 |
| FN | 0.92 | 0.91 | 0.90 | 0.95 | 0.0009 | 0.0010 |
| SVM | 0.92 | 0.80 | 0.97 | 1.3 | 0.0012 | 0.0023 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gowida, A.; Elkatatny, S.; Al-Afnan, S.; Abdulraheem, A. New Computational Artificial Intelligence Models for Generating Synthetic Formation Bulk Density Logs While Drilling. Sustainability 2020, 12, 686. https://doi.org/10.3390/su12020686
Gowida A, Elkatatny S, Al-Afnan S, Abdulraheem A. New Computational Artificial Intelligence Models for Generating Synthetic Formation Bulk Density Logs While Drilling. Sustainability. 2020; 12(2):686. https://doi.org/10.3390/su12020686
Chicago/Turabian StyleGowida, Ahmed, Salaheldin Elkatatny, Saad Al-Afnan, and Abdulazeez Abdulraheem. 2020. "New Computational Artificial Intelligence Models for Generating Synthetic Formation Bulk Density Logs While Drilling" Sustainability 12, no. 2: 686. https://doi.org/10.3390/su12020686
APA StyleGowida, A., Elkatatny, S., Al-Afnan, S., & Abdulraheem, A. (2020). New Computational Artificial Intelligence Models for Generating Synthetic Formation Bulk Density Logs While Drilling. Sustainability, 12(2), 686. https://doi.org/10.3390/su12020686






