Prediction of the Rate of Penetration while Drilling Horizontal Carbonate Reservoirs Using the Self-Adaptive Artificial Neural Networks Technique
Abstract
1. Introduction
1.1. Linear Regression-Based Correlations for Rate of Penetration Estimation
1.2. Application of Artificial Intelligence for Rate of Penetration Estimation
2. Methods
2.1. Data Preparation
2.2. Training the ANN Model
2.3. Testing and Validation of the Developed ANN-Based Correlation
2.4. Evaluation Criteria
3. Results and Discussion
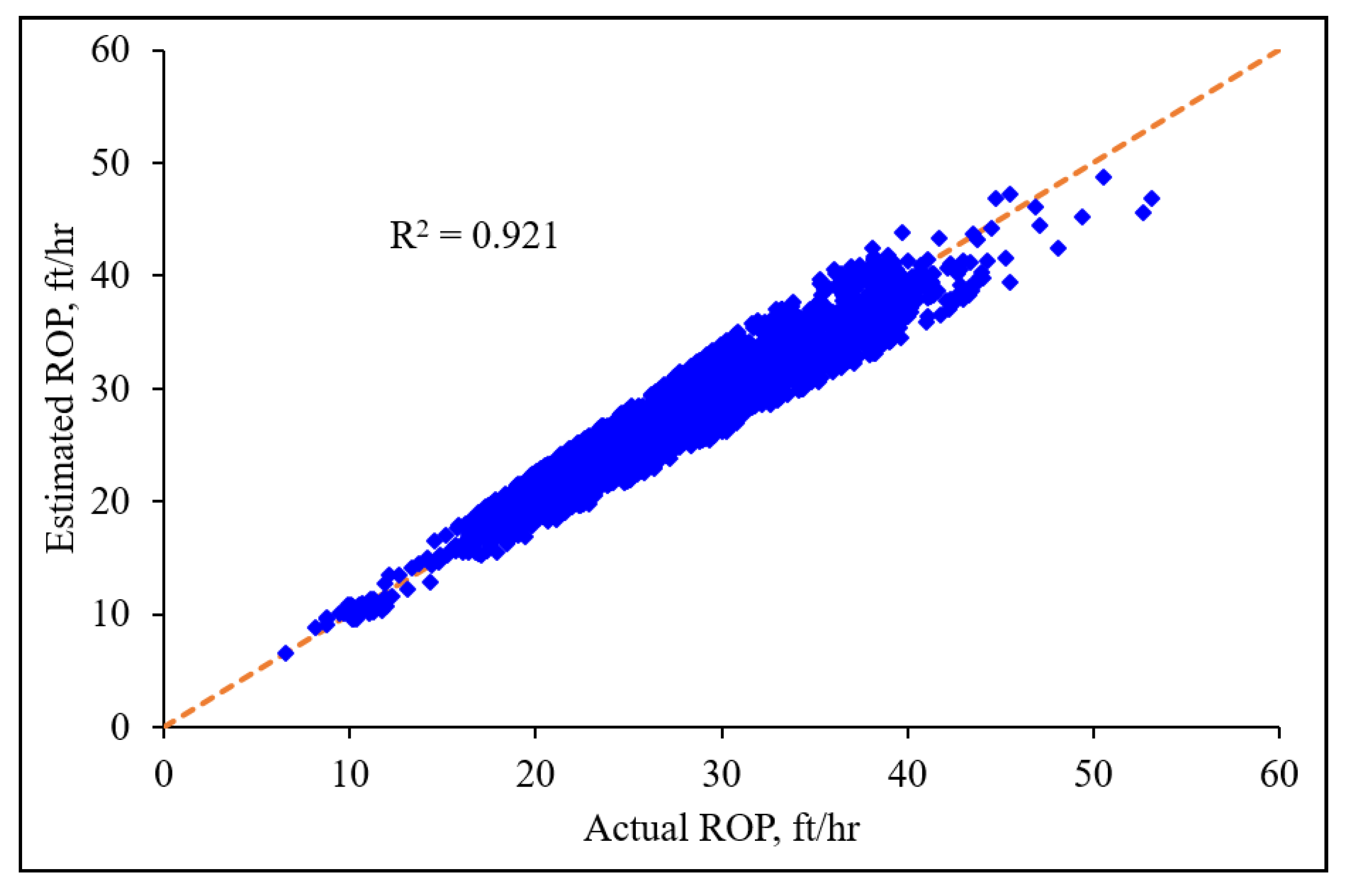
3.1. Training the ANN model
3.2. Developing the ANN-Based Correlation
3.3. Testing the Developed ANN-Based Correlation
3.4. Validation of the Developed ANN-Based Empirical Correlation
3.5. Comparison of the Predictability of the Developed ANN-Based Empirical Correlation with Available Correlations
4. Conclusions
- The optimized ANN model predicted the ROP for the training dataset (3000 data points) with an AAPE of 5.12% and a correlation coefficient (R) of 0.960;
- The developed correlation predicted the ROP for the testing dataset (531 data points) with AAPE and R values of 5.80% and 0.951, respectively;
- The developed ROP correlation outperformed a recently developed empirical correlation for estimating ROP in directional wells (the Osgouei model), which predicted the ROP for the validation data with a high AAPE and a low R of 14.60% and 0.629, respectively;
- The developed correlation predicted ROP for the validation dataset of Well-B (3600 data points) with an AAPE of only 5.26% and a high R of 0.956.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| AAPE | Average Absolute Percentage Error |
| AI | Artificial Intelligence |
| ANN | Artificial Neural Network |
| DE | Differential Evolution |
| DR | Deep Resistivity |
| ECD | Equivalent Circulation Density |
| GPM | Pumping Rate |
| GR | Gamma Ray |
| logsig | log-sigmoid |
| MW | Mud Density |
| PV | Plastic Viscosity |
| R | Correlation Coefficient |
| R2 | Coefficient of Determination |
| RHOB | Formation Bulk Density |
| ROP | Rate of Penetration |
| RPM | Rotation Speed |
| SaDE | Self-Adaptive Differential Evolution |
| SPP | Standpipe Pressure |
| SVM | Support Vector Machine |
| T | Torque |
| trainbfg | BFGS Quasi-Newton Backpropagation |
| WOB | Weight-on-Bit |
References
- Lyons, W.C.; Plisga, G.J. Standard Handbook of Petroleum and Natural Gas. Engineering, 2nd ed.; Gulf Professional Publishing: Woburn, MA, USA, 2004; ISBN 10: 0750677856. [Google Scholar]
- Barbosa, L.F.F.M.; Nascimento, A.; Mathias, M.H.; de Carvalho, J.A., Jr. Machine learning methods applied to drilling rate of penetration prediction and optimization-A review. J. Pet. Sci. Eng. 2019, 183, 106332. [Google Scholar] [CrossRef]
- Hossain, M.E.; Al-Majed, A.A. Fundamentals of Sustainable Drilling Engineering, 1st ed.; Wiley-Scrivener: Austin, TX, USA, 2015; ISBN 10: 0470878177. [Google Scholar]
- Eren, T.; Ozbayoglu, M.E. Real time optimization of drilling parameters during drilling operations. In Proceedings of the SPE Oil and Gas India Conference and Exhibition, Mumbai, India, 20–22 January 2010. SPE-129126-MS. [Google Scholar] [CrossRef]
- Payette, G.S.; Spivey, B.J.; Wang, L.; Bailey, J.R.; Sanderson, D.; Kong, R.; Pawson, M.; Eddy, A. Real-time well-site based surveillance and optimization platform for drilling: Technology, basic workflows and field results. In Proceedings of the SPE/IADC Drilling Conference and Exhibition, The Hague, The Netherlands, 14–16 March 2017. SPE-184615-MS. [Google Scholar] [CrossRef]
- Osgouei, R.E. Rate of Penetration Estimation Model for Directional and Horizontal Wells. Master’s Thesis, Middle East Technical University, Ankara, Turkey, 2007. [Google Scholar]
- Soares, C.; Daigle, H.; Gray, K. Evaluation of PDC bit ROP models and the effect of rock strength on model coefficients. J. Nat. Gas Sci. Eng. 2016, 34, 1225–1236. [Google Scholar] [CrossRef]
- Soares, C.; Gray, K. Real-time predictive capabilities of analytical and machine learning rate of penetration (ROP) models. J. Pet. Sci. Eng. 2019, 172, 934–959. [Google Scholar] [CrossRef]
- Mitchell, R.F.; Miska, S.Z. Fundamentals of Drilling Engineering; Society of Petroleum Engineers: Richardson, TX, USA, 2011; ASIN: B01L0O8WJA. [Google Scholar]
- Hegde, C.; Daigle, H.; Millwater, H.; Gray, K. Analysis of Rate of Penetration (ROP) Prediction in Drilling Using Physics-Based and Data-Driven Models. J. Pet. Sci. Eng. 2017, 159, 295–306. [Google Scholar] [CrossRef]
- Maurer, W. The “perfect-cleaning” theory of rotary drilling. J. Pet. Technol. 1962, 14, 1270–1274. [Google Scholar] [CrossRef]
- Bingham, M.G. A New Approach to Interpreting Rock Drillability; Petroleum Publishing Co.: Tulsa, OK, USA, 1965. [Google Scholar]
- Bourgoyne, A.; Young, F.S. A multiple regression approach to optimal drilling and abnormal pressure detection. Soc. Pet. Eng. J. 1974, 14, 371–384. [Google Scholar] [CrossRef]
- Mahmoud, A.A.; Elzenary, M.; Elkatatny, S. New Hybrid Hole Cleaning Model for Vertical and Deviated Wells. J. Energy Resour. Technol. 2020, 142, 034501. [Google Scholar] [CrossRef]
- Hag Elsafi, S. Artificial Neural Networks (ANNs) for flood forecasting at Dongola Station in the River Nile, Sudan. Alex. Eng. J. 2014, 53, 655–662. [Google Scholar] [CrossRef]
- Babikir, H.A.; Abd Elaziz, M.; Elsheikh, A.H.; Showaib, E.A.; Elhadary, M.; Wu, D.; Liu, Y. Noise prediction of axial piston pump based on different valve materials using a modified artificial neural network model. Alex. Eng. J. 2019, 58, 1077–1087. [Google Scholar] [CrossRef]
- Nayak, S.C.; Misra, B.B.; Behera, H.S. Artificial chemical reaction optimization based neural net for virtual data position exploration for efficient financial time series forecasting. Ain Shams Eng. J. 2018, 9, 1731–1744. [Google Scholar] [CrossRef]
- Jana, G.C.; Swetapadma, A.; Pattnaik, P.K. Enhancing the performance of motor imagery classification to design a robust brain computer interface using feed forward back-propagation neural network. Ain Shams Eng. J. 2018, 9, 2871–2878. [Google Scholar] [CrossRef]
- Abdelwahed, M.F.; Mohamed, A.E.; Saleh, M.A. Solving the motion planning problem using learning experience through case-based reasoning and machine learning algorithms. Ain Shams Eng. J. 2019, in press. [Google Scholar] [CrossRef]
- Abd Elrehim, M.Z.; Eid, M.A.; Sayed, M.G. Structural optimization of concrete arch bridges using Genetic Algorithms. Ain Shams Eng. J. 2019, 10, 507–516. [Google Scholar] [CrossRef]
- Arehart, R.A. Drill-bit diagnosis with neural networks. SPE Comput. Appl. 1990, 2, 24–28. [Google Scholar] [CrossRef]
- Abdelgawad, K.; Elkatatny, S.; Moussa, T.; Mahmoud, M.; Patil, S. Real Time Determination of Rheological Properties of Spud Drilling Fluids Using a Hybrid Artificial Intelligence Technique. J. Energy Resour. Technol. 2018. [Google Scholar] [CrossRef]
- Elkatatny, S.M. Real Time Prediction of Rheological Parameters of KCl Water-Based Drilling Fluid Using Artificial Neural Networks. Arab. J. Sci. Eng. 2017, 42, 1655–1665. [Google Scholar] [CrossRef]
- Ren, X.; Hou, J.; Song, S.; Liu, Y.; Chen, D.; Wang, X.; Dou, L. Lithology identification using well logs: A method by integrating artificial neural networks and sedimentary patterns. J. Pet. Sci. Eng. 2019, 182, 106336. [Google Scholar] [CrossRef]
- Mahmoud, A.A.; Elkatatny, S.; Ali, A.; Abouelresh, M.; Abdulraheem, A. Evaluation of the Total Organic Carbon (TOC) Using Different Artificial Intelligence Techniques. Sustainability 2019, 11, 5643. [Google Scholar] [CrossRef]
- Mahmoud, A.A.; Elkatatny, S.; Abdulraheem, A.; Mahmoud, M.; Ibrahim, O.; Ali, A. New Technique to Determine the Total Organic Carbon Based on Well Logs Using Artificial Neural Network (White Box). In Proceedings of the 2017 SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition, Dammam, Saudi Arabia, 24–27 April 2017. SPE-188016-MS. [Google Scholar] [CrossRef]
- Mahmoud, A.A.; Elkatatny, S.; Ali, A.; Abouelresh, M.; Abdulraheem, A. New Robust Model to Evaluate the Total Organic Carbon Using Fuzzy Logic. In Proceedings of the SPE Kuwait Oil & Gas Show and Conference, Mishref, Kuwait, 13–16 October 2019. SPE-198130-MS. [Google Scholar] [CrossRef]
- Mahmoud, A.A.; Elkatatny, S.; Mahmoud, M.; Abouelresh, M.; Abdulraheem, A.; Ali, A. Determination of the total organic carbon (TOC) based on conventional well logs using artificial neural network. Int. J. Coal Geol. 2017, 179, 72–80. [Google Scholar] [CrossRef]
- Mahmoud, A.A.; Elkatatny, S.; Abouelresh, M.; Abdulraheem, A.; Ali, A. Estimation of the Total Organic Carbon Using Functional Neural Networks and Support Vector Machine. In Proceedings of the 12th International Petroleum Technology Conference and Exhibition, Dhahran, Saudi Arabia, 13–15 January 2020. IPTC-19659-MS. [Google Scholar] [CrossRef]
- Mahmoud, A.A.; Elkatatny, S.; Chen, W.; Abdulraheem, A. Estimation of Oil Recovery Factor for Water Drive Sandy Reservoirs through Applications of Artificial Intelligence. Energies 2019, 12, 3671. [Google Scholar] [CrossRef]
- Mahmoud, A.A.; Elkatatny, S.; Abdulraheem, A.; Mahmoud, M. Application of Artificial Intelligence Techniques in Estimating Oil Recovery Factor for Water Drive Sandy Reservoirs. In Proceedings of the 2017 SPE Kuwait Oil & Gas Show and Conference, Kuwait City, Kuwait, 15–18 October 2017. SPE-187621-MS. [Google Scholar] [CrossRef]
- Ahmed, A.S.; Mahmoud, A.A.; Elkatatny, S. Fracture Pressure Prediction Using Radial Basis Function. In Proceedings of the AADE National Technical Conference and Exhibition, Denver, CO, USA, 9–10 April 2019. AADE-19-NTCE-061. [Google Scholar]
- Ahmed, A.S.; Mahmoud, A.A.; Elkatatny, S.; Mahmoud, M.; Abdulraheem, A. Prediction of Pore and Fracture Pressures Using Support Vector Machine. In Proceedings of the 2019 International Petroleum Technology Conference, Beijing, China, 26–28 March 2019. IPTC-19523-MS. [Google Scholar] [CrossRef]
- Mahmoud, A.A.; Elkatatny, S.; Ali, A.; Moussa, T. Estimation of Static Young’s Modulus for Sandstone Formation Using Artificial Neural Networks. Energies 2019, 12, 2125. [Google Scholar] [CrossRef]
- Mahmoud, A.A.; Elkatatny, S.; Ali, A.; Moussa, T. A Self-adaptive Artificial Neural Network Technique to Estimate Static Young’s Modulus Based on Well Logs. In Proceedings of the Oman Petroleum & Energy Show, Muscat, Oman, 9–11 March 2020. SPE-200139-MS. [Google Scholar] [CrossRef]
- Elkatatny, S.; Tariq, Z.; Mahmoud, M.; Abdulraheem, A.; Mohamed, I. An integrated approach for estimating static Young’s modulus using artificial intelligence tools. Neural Comput. Appl. 2019, 31, 4123. [Google Scholar] [CrossRef]
- Elkatatny, S.; Tariq, Z.; Mahmoud, M.; Abdulraheem, A. New insights into porosity determination using artificial intelligence techniques for carbonate reservoirs. Petroleum 2018, 4, 408–418. [Google Scholar] [CrossRef]
- Elkatatny, S.; Aloosh, R.; Tariq, Z.; Mahmoud, M.; Abdulraheem, A. Development of a New Correlation for Bubble Point Pressure in Oil Reservoirs using Artificial Intelligence Technique. In Proceedings of the SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition, Dammam, Saudi Arabia, 24–27 April 2017. [Google Scholar] [CrossRef]
- Elkatatny, S.; Al-AbdulJabbar, A.; Mahmoud, A.A. New Robust Model to Estimate the Formation Tops in Real-Time Using Artificial Neural Networks (ANN). Petrophysics 2019, 60, 825–837. [Google Scholar] [CrossRef]
- Bilgesu, H.; Tetrick, L.; Altmis, U.; Mohaghegh, S.; Ameri, S. A new approach for the prediction of rate of penetration (ROP) values. In Proceedings of the SPE Eastern Regional Meeting, Lexington, Kentucky, 22–24 October 1997. SPE-39231-MS. [Google Scholar] [CrossRef]
- Amar, K.; Ibrahim, A. Rate of penetration prediction and optimization using advances in artificial neural networks, a comparative study. In Proceedings of the 4th International Joint Conference on Computational Intelligence, Barcelona, Spain, 5–7 October 2012; pp. 647–652. [Google Scholar] [CrossRef]
- Mantha, B.; Samuel, R. ROP Optimization Using Artificial Intelligence Techniques with Statistical Regression Coupling. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dubai, UAE, 26–28 September 2016. SPE-181382-MS. [Google Scholar] [CrossRef]
- Elkatatny, S. New Approach to Optimize the Rate of Penetration Using Artificial Neural Network. Arab. J. Sci. Eng. 2018, 43, 6297–6304. [Google Scholar] [CrossRef]
- Ahmed, A.S.; Salaheldin, E.; Abdulraheem, A.; Mahmoud, M.; Ali, A.Z.; Mohamed, I.M. Prediction of Rate of Penetration of Deep and Tight Formation Using Support Vector Machine. In Proceedings of the SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition, Dammam, Saudi Arabia, 23–26 April 2018. SPE-192316-MS. [Google Scholar] [CrossRef]
- Monjezi, M.; Dehghani, H. Evaluation of effect of blasting pattern parameters on back break using neural networks. Int. J. Rock Mech. Min. Sci. 2008, 45, 1446–1453. [Google Scholar] [CrossRef]
- Angelini, E.; Ludovici, A. CDS Evaluation Model with Neural Networks. J. Serv. Sci. Manag. 2009, 2, 15. [Google Scholar] [CrossRef][Green Version]
- Gurney, K. An Introduction to Neural Networks; UCL Press Limited: London, UK, 1997; ISBN 0-203-45151-1. [Google Scholar]
- Omran, M.G.H.; Salman, A.; Engelbrecht, A.P. Self-adaptive Differential Evolution. In Computational Intelligence and Security; CIS 2005; Lecture Notes in Computer Science; Hao, Y., Liu, J., Wang, Y., Cheung, Y.-M., Yin, H., Jiao, L., Ma, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3801. [Google Scholar]
- Al-Anazi, A.F.; Gates, I.D. A support vector machine algorithm to classify lithofacies and model permeability in heterogeneous reservoirs. Eng. Geol. 2010, 114, 267–277. [Google Scholar] [CrossRef]
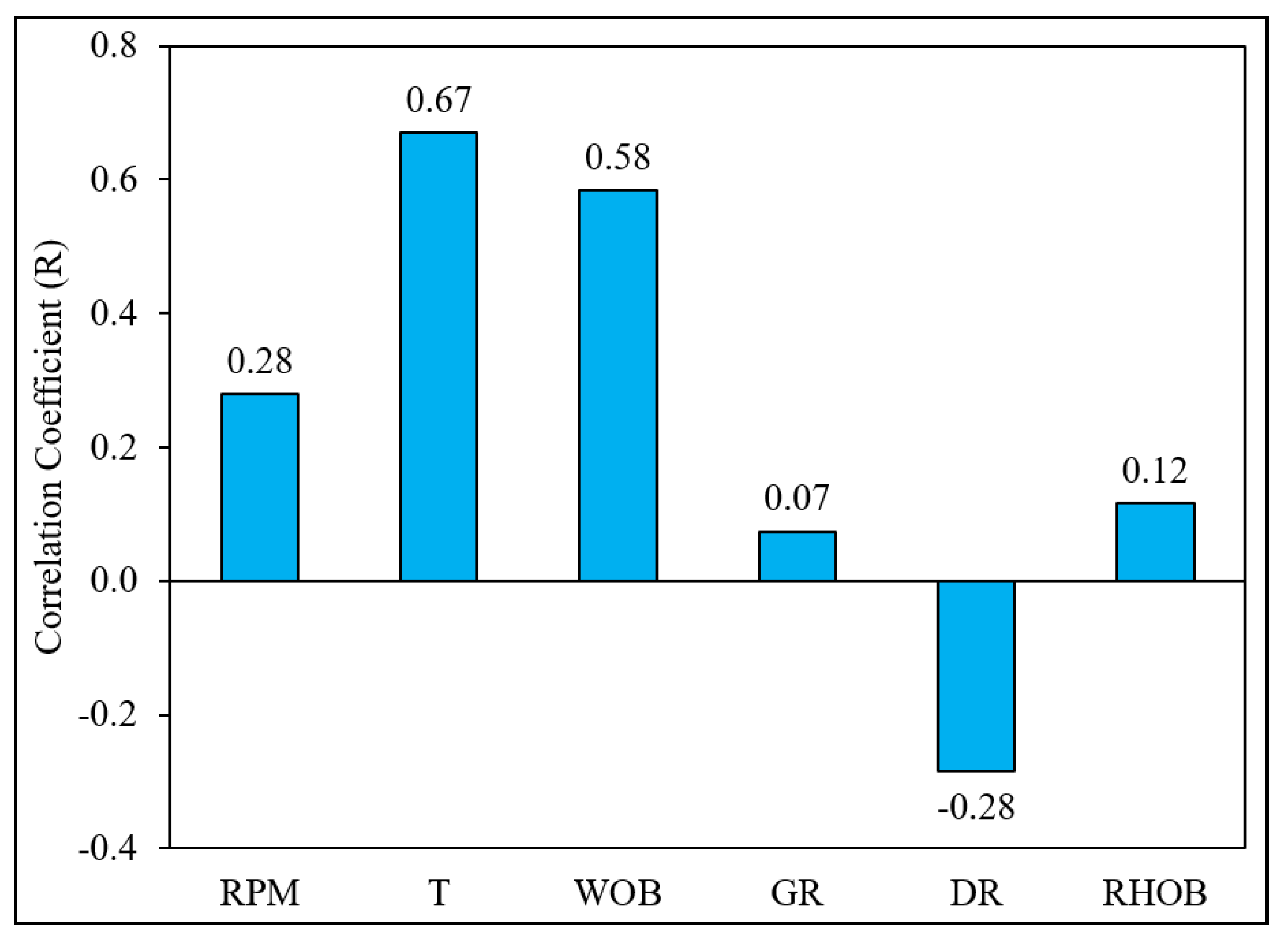








| Statistical Parameters | RPM (rpm) | T (kft.lbf) | WOB (klbf) | GR (API) | DR (Ω.m) | RHOB (g/cm3) | ROP (ft/hr) |
|---|---|---|---|---|---|---|---|
| Minimum | 59.8 | 3.06 | 5.55 | 8.80 | 0.64 | 2.13 | 59.8 |
| Maximum | 132 | 7.81 | 24.3 | 69.5 | 965 | 3.02 | 132 |
| Range | 72.2 | 4.75 | 18.8 | 60.7 | 963.9 | 0.89 | 72.2 |
| Standard Deviation | 17.5 | 0.75 | 2.64 | 8.5 | 212.4 | 0.16 | 17.5 |
| Sample Variance | 306 | 0.57 | 6.99 | 72.9 | 45114 | 0.02 | 306 |
| Kurtosis | −1.14 | 0.16 | 1.55 | 1.96 | 6.09 | −0.87 | −1.14 |
| Skewness | −0.49 | −0.44 | −0.94 | 1.27 | 2.49 | −0.10 | −0.49 |
| Parameter | Value |
|---|---|
| Training function | trainbfg |
| Transfer function | logsig |
| Number of hidden layers | 1 |
| Number of neurons | 26 |
| i | w1i,1 | w1i,2 | w1i,3 | w1i,4 | w1i,5 | w1i,6 | b1i | w2i |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.472 | −1.869 | 3.127 | −1.312 | 0.232 | −0.621 | 6.431 | 0.190 |
| 2 | −0.778 | −3.454 | 1.887 | 6.725 | −2.769 | −6.941 | −5.566 | −0.299 |
| 3 | 3.037 | −4.214 | −2.902 | −5.927 | 1.752 | −0.969 | −4.733 | 0.396 |
| 4 | 3.279 | 2.073 | −4.944 | 2.953 | −0.896 | 6.679 | −5.680 | −0.654 |
| 5 | −1.167 | 0.034 | 1.637 | −4.192 | −0.988 | −3.395 | 2.298 | −1.056 |
| 6 | −5.614 | 0.971 | −4.185 | −2.940 | −0.165 | 2.019 | 3.522 | 0.418 |
| 7 | 4.712 | 1.857 | 2.161 | 3.803 | −1.979 | −0.936 | −3.041 | 0.859 |
| 8 | −0.795 | 0.183 | 0.660 | −4.797 | −13.842 | 1.330 | −14.488 | −0.945 |
| 9 | 3.732 | −4.144 | −3.459 | −1.063 | 3.321 | −3.952 | −1.752 | −0.451 |
| 10 | 0.502 | −10.524 | 5.801 | 1.869 | −0.852 | −6.240 | −3.857 | 0.294 |
| 11 | −0.317 | −5.318 | 6.544 | 3.210 | 1.360 | 0.461 | 1.090 | −0.326 |
| 12 | 4.212 | 0.773 | 0.592 | 1.958 | 1.470 | 2.034 | −0.118 | −0.388 |
| 13 | 2.910 | 0.433 | 3.394 | 0.904 | −1.510 | 0.177 | −0.756 | 0.195 |
| 14 | −3.365 | −6.367 | −1.462 | 3.218 | −5.920 | 4.702 | −1.646 | 0.416 |
| 15 | −2.423 | 3.326 | 0.483 | −3.764 | −3.841 | −4.881 | 0.170 | −0.324 |
| 16 | 2.190 | 5.445 | 0.414 | −2.546 | 0.930 | −2.493 | −1.045 | 0.704 |
| 17 | −1.443 | 2.033 | 8.548 | 4.160 | 3.550 | 9.202 | −0.189 | 0.176 |
| 18 | 1.699 | −0.890 | −0.025 | −0.947 | −2.317 | 3.959 | −0.119 | −0.379 |
| 19 | −2.209 | 3.899 | −4.020 | −7.417 | 1.532 | 1.539 | −2.022 | 0.738 |
| 20 | −1.240 | 2.891 | −3.411 | −8.762 | 1.554 | 0.939 | −3.210 | −0.762 |
| 21 | 3.398 | −3.788 | −4.602 | 1.518 | −1.239 | 0.043 | −0.422 | −0.048 |
| 22 | 1.904 | −1.289 | 6.963 | −1.661 | 0.961 | −3.726 | −4.547 | 0.378 |
| 23 | −3.985 | 1.949 | −2.266 | 1.458 | 0.686 | 2.434 | −4.530 | −1.069 |
| 24 | −0.462 | −1.879 | 0.058 | 3.565 | 1.033 | −2.105 | −4.423 | 0.795 |
| 25 | −0.804 | 0.043 | 0.667 | −3.192 | −10.184 | 1.230 | −11.419 | 1.249 |
| 26 | −5.700 | −2.821 | −1.045 | 1.765 | 2.478 | −3.574 | −6.170 | −0.580 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-AbdulJabbar, A.; Elkatatny, S.; Abdulhamid Mahmoud, A.; Moussa, T.; Al-Shehri, D.; Abughaban, M.; Al-Yami, A. Prediction of the Rate of Penetration while Drilling Horizontal Carbonate Reservoirs Using the Self-Adaptive Artificial Neural Networks Technique. Sustainability 2020, 12, 1376. https://doi.org/10.3390/su12041376
Al-AbdulJabbar A, Elkatatny S, Abdulhamid Mahmoud A, Moussa T, Al-Shehri D, Abughaban M, Al-Yami A. Prediction of the Rate of Penetration while Drilling Horizontal Carbonate Reservoirs Using the Self-Adaptive Artificial Neural Networks Technique. Sustainability. 2020; 12(4):1376. https://doi.org/10.3390/su12041376
Chicago/Turabian StyleAl-AbdulJabbar, Ahmad, Salaheldin Elkatatny, Ahmed Abdulhamid Mahmoud, Tamer Moussa, Dhafer Al-Shehri, Mahmoud Abughaban, and Abdullah Al-Yami. 2020. "Prediction of the Rate of Penetration while Drilling Horizontal Carbonate Reservoirs Using the Self-Adaptive Artificial Neural Networks Technique" Sustainability 12, no. 4: 1376. https://doi.org/10.3390/su12041376
APA StyleAl-AbdulJabbar, A., Elkatatny, S., Abdulhamid Mahmoud, A., Moussa, T., Al-Shehri, D., Abughaban, M., & Al-Yami, A. (2020). Prediction of the Rate of Penetration while Drilling Horizontal Carbonate Reservoirs Using the Self-Adaptive Artificial Neural Networks Technique. Sustainability, 12(4), 1376. https://doi.org/10.3390/su12041376






