Requirement-Oriented Engineering Characteristic Identification for a Sustainable Product–Service System: A Multi-Method Approach

Abstract

Product–service systems (PSSs) have great potential for competitiveness and sustainability. Customers’ requirements cannot be directly used in the design of a PSS. Accurate identification of customer requirements, especially hidden requirements in the product life cycle, and transformation of customer requirements into specific engineering characteristics for PSS design are urgent problems. This study proposed a systematic and whole-process framework employing specific identification processes and methods, as well as a big data analysis. A set of refined and integrated methods were used to better identify customer requirements and to transform the customer requirements into specific engineering characteristics more accurately and efficiently. We also used customers’ online review data—a huge information resource to be explored—and big data technology to improve the requirement information identification process. A case study was implemented to verify our methodology. We obtained the engineering characteristics of a smartphone PSS matching the customer requirements as well as the exact importance rankings of customer requirements and engineering characteristics. The analysis results revealed that the proposed methodology allowed PSS designers to assess the PSS requirements more specifically and accurately by providing an intuitive evaluation of the role and importance of the requirements, engineering characteristics, and their mutual interactions that were hidden or indirect.

1. Introduction

Sustainability has become one of the critical factors for long-term business success [1]. For a product–service system (PSS), sustainability is often seen as both a driver and a result [2]. On the one hand, under the current situation of environment and resources, modern industrial production requires higher efficiency, which implies using the right resources the right way [3]. PSS has been proved to be one of the most effective instruments to improve resource efficiency [4,5,6]. On the other hand, a PSS proposes a value detached from the product, which can extend the product life cycle, achieve better environmental performance, reduce material consumption, and change consumption patterns [7,8,9]. PSSs provide an integration of tangible products and intangible services that are more focused on consumers’ true desires [10,11,12]. In addition to the possibility of improving customer satisfaction and enterprise competitiveness in the market [13,14], this integration leads to the partial separation of value from material consumption. This shows a potential contribution of PSSs to sustainability [11,15]. The concept of the PSS seeks to replace personal ownership and excess material consumption with alternative utilization options [16].

A PSS is designed to focus on how to deliver the desired utility or function to increase customer value [17,18]. As compared with physical product design, PSS design is more concerned about value in use [19]. Effective PSS design requires a deep understanding of target customers [20,21]. In particular, to achieve sustainability, addressing current behavior is more important than encouraging behavioral change in customers [22]. Therefore, customer requirement analysis is crucial in PSS design [23,24]. Customer requirements and customer satisfaction are related to both products and services, and it is quite important to identify the key parameters from a broad perspective in PSS design. Nevertheless, research on requirement handling for PSSs is not yet a highly developed domain [25], especially with respect to how to accurately identify specific customer requirements and how to translate customer requirements into engineering characteristics for PSS design. Engineering characteristics of a PSS include product-related engineering characteristics and service-related engineering characteristics [26]. Rating the importance of engineering characteristics greatly affects the attainment of an optimal PSS planning. To accomplish this goal, this study proposes a two-phased multi-method approach by integrating a series of methods and techniques to improve the performances of classical Kano and QFD (Quality Function Deployment).

The remainder of this paper is organized as follows. The related works are reviewed in the following section. The proposed approach is presented under “Methodology”. An example to validate the proposed approach is discussed under “Case Study”. Finally, the conclusions and future research directions are presented under “Conclusions and Future Research”.

2. Related Works

Providing products alone is insufficient in terms of maintaining the competitiveness of companies [27]. The global market has experienced a shift from products to an increased importance of services [28] to satisfy the burgeoning individualized and personalized customer demand [29]. Under this circumstance, service-oriented manufacturing (SOM) was derived from the integration of servitization and the conventional manufacturing industry in the past decades [30,31,32,33,34]. The SOM strategy helps manufacturing enterprises to extend their reach ever closer to the customers and their requirements [35]. SOM extends the principles of the value chain and value creation of enterprises and customers by bundling tangible products and relevant intangible services [36], and the interaction between products and services leads to the in-depth participation of customers in the development and manufacturing processes [24]. Paying more attention to customer demand and customer value is one of the most important characteristics of SOM, which is different from traditional manufacturing. SOM has some similar concepts, including service-based manufacturing [37] and service-enhanced manufacturing [38].

A PSS is a combination of products, services, networks of players, and supporting infrastructure [32,39] that are jointly capable of fulfilling specific customer requirements in an economical and sustainable manner [12,24]. A PSS is an important component of servitization, and the basic idea of a PSS is to sell solutions that provide the capability to satisfy individual customer needs and enhance the competitiveness of manufacturers [40,41,42,43]. Many researchers have investigated the implementation of PSSs in industry [6,44,45,46] by involving the aspects of product life cycle [47] and sustainable production [48] and business models [49], among others [4,29,43,50,51,52,53]. A PSS is a business model focusing on providing a set of products and services that are designed to be economically, socially, and environmentally sustainable, with the final aim of fulfilling customers’ needs [54,55,56]. There are many problems at the input end of the PSS that remain unclear. When implementing a PSS solution, customers’ perception of the values associated with a PSS need to be investigated more accurately [57,58,59], and more attention should be directed towards enhancing the definition and interactions among the PSS components [60,61]. Understanding the customer requirements is one of the most important ways to reduce the fuzziness in the early development of PSSs. More importantly, the way of translating customer requirements into engineering characteristics for PSS design is the main link affecting the effectiveness of a PSS system.

QFD is a classical method in the field of customer requirement analysis, and is mainly used for transforming customer requirements into engineering characteristics [62]. The QFD method is a complex system with an input, process, and output. It is a multi-level deductive analysis method that translates customers’ requirements into design requirements (engineering characteristics), so it is market-oriented [63]. In the QFD methodology, house of quality (HoQ) is an intuitive binary matrix expansion chart that is used for defining the relationship between customer desires and the firm/product capabilities. It has been widely adopted for conceptual design, process planning, and project management, among others [64,65]. Customer requirements are inputs of the QFD model. The successful implementation of the QFD method needs to start with accurate identification of customer demand. Different customer survey methods have been adopted in QFD to collect customer requirements and to measure their degrees of importance [66,67,68,69,70]. Research on the integration of QFD with other methods has also been conducted [71,72,73,74,75]. Although the QFD model has achieved good results in enterprise practice, it has a problem of low accuracy in the customer requirement analysis. If the demand information is not accurate enough, it can make the follow-up process go in the wrong direction, eventually leading to the failure of the product or service design. The Kano model is an insightful way of understanding, categorizing, and prioritizing customer requirements. It explores the nature of customer requirements and facilitates effective analysis of them [76]. In view of the advantages of the Kano model in the acquisition of customer requirements [77], it is commonly used to categorize customer requirements into different types to facilitate better understanding of the customers’ needs and customer satisfaction. Compared with that in QFD, the relationship between customer requirements and customer satisfaction in the Kano model is not specified quantitatively. Integrating the Kano model with QFD for might help to make up for their shortcomings and help PSS designers to analyze customer requirements more precisely. In addition, a series of methods and techniques, such as data mining and a fuzzy analytic hierarchy process, are also used to improve the outputs of the Kano and QFD model.

3. Methodology

This study aimed to identify customer requirements and to translate them into specific engineering characteristics for PSS design. The proposed approach consists of two stages. We used an improved Kano model to identify, classify, and rank the customer requirements. Then, we used an improved QFD model to transform the customer requirements into specific engineering characteristics and to rank the importance of the indicators.

3.1. Refined Kano Model for Identifying Customer Requirements

Customer requirement analysis is important in the development of a PSS, and requirement classification is one of the primary tasks of requirement analysis. The Kano model posits that the key product or service attributes are related to customer satisfaction. This model analyzes the nature of the product or service attributes and provides a better understanding of customer requirements by classifying these attributes into different categories (A: Attractive Quality, O: One-dimensional Quality, M: Must-be Quality, I: Indifferent Quality, R: Reverse Quality) [78,79]. To understand and identify the customer requirements more accurately and to focus on the factors of customer satisfaction and customer value promotion, this study screened the five categories of requirements [80] of the original Kano model in examining the customer requirements of the PSS. We only retained the two categories of O and A: the requirements that customers are very concerned about and that are positively related to customer satisfaction, as well as the requirements that can surprise customers and create a huge customer value. As servitization is an upgrade and innovation based on the traditional manufacturing industry, it emphasizes active service through the perception of customer needs and behavior. We generally assume that enterprises that take the initiative to explore servitization already have a good level in dealing with the M, I, and R requirements. Moreover, the design and development of a PSS is the key to tapping the requirements of categories O and A.

Before creating the Kano questionnaire design, we additionally analyzed customers’ online reviews using big data technologies. The development of the Internet and information technology has provided more convenient channels for customers to share their product evaluations online [81]. Online reviews greatly affect customers’ purchasing decisions, and they are one of the most important forms of online word-of-mouth communication [82]. Consumers’ online comments contain abundant information that can be used as a reference by researchers. Traditional methods (such as questionnaire surveys) for capturing customer requirements are well developed and have numerous advantages, but they are usually time-consuming, expensive, and not easily able to access a large scale of opinions. The development and application of big data technologies provide convenient tools for the analysis and processing of massive amounts of information. Therefore, to ensure the accuracy, objectivity, and comprehensiveness of the Kano questionnaire design, we collected and analyzed online customer reviews to identify the customer requirements, which are one of the improvements of the Kano model in this study. Then, we designed more pertinent questionnaires according to the preliminarily identified requirements, scopes, and labels to obtain more accurate customer requirements and classification through the questionnaire survey and data analysis.

Aside from the requirement classification, requirement prioritization is also a necessary step to ensure the success of requirement analysis. This refers to assigning importance weights to different PSS requirements that affect the target values to be set for the design requirements [25]. The original Kano model only categorizes customer requirements and preliminarily evaluates the importance of each category according to the characteristics of the five categories. To deal with the vagueness, uncertainty, and diversity in decision-making, we use the fuzzy analytic hierarchy process (FAHP) to improve the importance rankings of the requirements of the traditional Kano model. We combine the opinions of industry experts and the subjective judgments of customers to obtain more accurately quantified customer requirement weights and to prepare for the input of the follow-up QFD model. The improvement of the importance rankings of customer requirements is one of the improvements of the Kano model in this study.

Summary: The main content of this section is the identification and weight rankings of the customer requirements based on the improved Kano model. The improvements of the Kano model are mainly embodied in the following: (1) screening of the Kano model’s original requirement categories according to the characteristics of a PSS, (2) analyzing customers’ online reviews based on big data and data mining technologies and making a primary selection of customer requirements to better design and implement a follow-up questionnaire survey, and (3) using the FAHP to obtain a more accurate weight ranking of customer requirements.

3.2. Refined QFD for Matching Specific Engineering Characteristics

QFD is a multipurpose tool for quality planning, continuous product improvement, and decision-making [83]. It offers a systematic framework to convert customer expectations into design characteristics [84]. It is used to understand customers’ needs and the conversion of such needs into proxy attributes and product specifications. QFD is commonly used by expressing the correlation matrix between customer requirements and product–service design in the form of an HoQ [85]. Considering the characteristics of SOM and PSS design, this study constructed the HoQ for a product and service, respectively; that is, it separated the logistics and service flow of a PSS to provide new design perspectives and suggestions for the design of SOM systems.

The corresponding relationship between customer requirements and engineering characteristics was obtained by studying the literature, industry production materials, enterprise annual report information, and interviews with relevant industry practitioners. The corresponding relationship is the foundation of building the ceiling of the HoQ. The specific relationships between customer requirements and engineering characteristics, as well as their respective weights, were obtained through expert scoring, which is the basis for building the rooms. The product HoQ model was established on the basis of the importance ratings obtained by the improved Kano model and the autocorrelation matrix of the engineering characteristics obtained by experts’ scoring. The method used to construct the service HoQ is consistent with the above method. Note that under the background of SOM, the concept of service has greatly expanded. The service activities of manufacturing enterprises are not limited to after-sales service, but encompass the service of the whole life cycle. Therefore, customer requirements may involve both products and services at the same time, and identification of which parts are achieved through the characteristics of the product process and which parts are achieved through the service process is necessary.

Experts scored the relevance of requirements of engineering characteristics and obtained a fuzzy set of scoring semantics. We introduced triangular fuzzy numbers to represent the inaccurate expert semantics. Thus, the weight of the engineering characteristics of the QFD output was also expressed in the form of triangular fuzzy numbers, which are fuzzy outputs of the inaccurate inputs. In this study, another improvement of the QFD method is the optimization of the fuzzy output. We introduced the concept of the possibility degree of triangular fuzzy numbers to optimize the output results. The ranking vectors of the triangular fuzzy number vectors for the product and service engineering characteristics were calculated to obtain the importance rankings of the engineering characteristics.

Summary: The main content of this section is the identification of the engineering characteristics matching the customer requirements and the attainment of the importance rankings of these engineering characteristics based on the improved QFD model. The improvements of the QFD model are mainly embodied in the following: (1) the construction of two HoQ models for a product and service, respectively, from the perspective of PSS design, (2) the integration of the Kano model into QFD to evaluate customer requirements more precisely, and (3) the improvement of the fuzzy output of the QFD model using the FAHP to obtain a more accurate index weight and importance ranking.

4. Case Study

To demonstrate the application of the proposed approach, a case study associated with the design of a smartphone PSS is introduced in this section.

4.1. Preliminary Identification of Customer Requirements

We retained two categories of the Kano model requirements: category O (e.g., camera and internal memory) and category A (e.g., beautiful appearance). The collection and analysis of the customer online comment data required the assistance of data mining technology. In this part, we used the user comment block of Tmall (https://www.tmall.com) for demonstration because this block displays real online user reviews supported by data mining technology. The content of each product comment was analyzed and filtered to generate different evaluation tags. Figure 1 shows a comment tag for the Huawei P30 Pro.

As shown in the figure, seven tags are screened out from the evaluation of 16,891 items. The number in brackets at the end of each tag indicates the number of comments related to the tag. The customer requirements represented by red labels belong to categories O and A in the Kano model. The green label reflects the customer complaints and dissatisfaction, which can be regarded as reverse demand and are not included in the statistical scope of this study. By collecting and analyzing the comment tags of the top 20 smartphone models being sold, we classified these tags semantically and obtained the top 12 customer demand classification tags as the initial customer requirements. These original labels have the characteristics of being colloquial, incomplete, and ambiguous, and they cannot be directly used to define customer requirements. The next step is to collect more accurate customer requirements and further categorize them using a traditional questionnaire investigation. The importance of this part is to delimit a relatively vague scope for further clarification and refinement of customer requirements. It is equivalent to a preliminary and efficient market survey, which can help us better define the framework of customer requirement identification and improve the subsequent questionnaire investigation.

4.2. Traditional Questionnaire Research

According to the Kano model and analytic hierarchy process, we further supplemented, refined, extracted, and classified the primary screened customer requirements and then stratified them into ‘pre-sale’, ‘product’, ‘after-sale’, and ‘brand value’. The specific hierarchical structure and settings of the questions are illustrated in Figure 2.

Our questionnaires were released online through the Questionnaire Star platform (https://www.wjx.cn), and 224 valid answers were collected. Questionnaire Star is a professional online questionnaire, survey, evaluation, and voting platform that focuses on providing users with a powerful and humanized online design of questionnaires and data collection services. Compared with traditional questionnaire survey methods, Questionnaire Star has the obvious advantages of being fast, easy to use, and low cost. It is widely used by a large number of enterprises and individuals. By August 2019, 44.34 million users had provided 3.087 billion replies through Questionnaire Star. We used the SPSS 23.0 software to analyze and process the collected data. An invalid sample analysis was conducted, and samples with more than 90% of the same options were eliminated. Then, the outliers were detected and eliminated. After filtering out the invalid samples, Cronbach reliability analysis was performed to calculate the corrected item–total correlation (CITC) and Cronbach’s α coefficient for each question. Cronbach’s α was 0.913, which shows a good reliability of the data. Cronbach’s α if item deleted was not higher, which means that every question in the questionnaire could be retained. Each CITC value was higher than 0.4, and most CITC values were higher than 0.5, indicating a good correlation between each item and a good reliability level.

4.3. Weight Assessment of Customer Requirements

Based on the identification of the customer requirements in the previous section, a hierarchical structure model of customer requirements was established. The first layer is the target layer, that is, the customer perceived requirements. The second level defines the four types of requirements in chronological order and is represented by the character F. The third level is the index level, which is deepened and expanded on the basis of the second level, and is specific to 20 specific indicators. The hierarchical structure is shown in Figure 3. We used the FAHP method to improve the demand hierarchy of the traditional Kano model and combine the opinions of the industry experts with the subjective judgments of customers to obtain the more accurate weights of the customer requirements. The importance of each index was compared by the experts. The evaluation results are expressed by nine scales (0.1–0.9). Among them, 0.5 indicates that two indexes are equally important, 0.9 indicates that one index is extremely important compared with another one, and 0.1–0.4 indicates converse comparison. If index $a_i$ is compared with index $a_j$, and the judgment result $r_{ij}$ is obtained, then the result of $a_j$ compared with $a_i$ is $1-r_{ij}$. The judgment matrix obtained by pairwise comparison is as follows [86]:

$$R=\left(\begin{array}{ccc}{r}_{11}& \dots & r_{1n}\\ ⋮& r_{ii}& ⋮\\ r_{n1}& \dots & r_{nn}\end{array}\right).$$

(1)

We interviewed experienced practitioners from the mobile phone industry. The interviewees, who comprised 15 experts in the field, included salesmen from smartphone dealers and marketing staff from the mobile phone manufacturers. The forms of interviews included face-to-face conversations, WeChat (WeChat data report 2018: WeChat is the most widely used instant messaging application in China; as of September 2018, WeChat has covered more than 96% of smartphones in China, and the total number of active accounts has reached 1.082 billion (https://support.weixin.qq.com/cgi-bin/mmsupport-bin/getopendays)) communication, and e-mail consultation. The judgment matrix corresponding to each expert was obtained. In this study, 15 expert judgment matrices were processed using the arithmetic average, and a decimal number was reserved to obtain the preliminary fuzzy judgment matrix.

The consistency of the fuzzy judgment matrix reflects the consistency of the people’s thinking and judgment. However, in practical decision analysis, the constructed fuzzy judgment matrices are usually inconsistent because of the complexity of the problem and the prejudices people may have. Therefore, transforming the obtained inconsistent matrices into consistent matrices is necessary. This study referred to Reference [87] for the consistency judgment of matrices and for constructing the fuzzy consistent judgment matrices. The judgment matrix of the first level is F, and the judgment matrices of the second level are $F_1,F_2,F_3,F_4$, respectively. Among the five matrices we obtained, all were inconsistent matrices except for matrix $F_4$. Thus, these fuzzy inconsistent matrices needed to be adjusted to become fuzzy consistent matrices. The adjusted fuzzy consistent judgment matrices are as follows:

$$\begin{gathered} F=\left[\begin{array}{c}\begin{array}{ccc}0.5& 0.1& 0.4\\ 0.9& 0.5& 0.8\\ 0.6& 0.2& 0.5\end{array}\begin{array}{c} 0.5\\ 0.9\\ 0.6\end{array}\\ \begin{array}{cc}0.5& 0.1\end{array}\begin{array}{cc}0.4& 0.5\end{array}\end{array}\right] \\ {F}_1=\left[\begin{array}{c}\begin{array}{ccc}0.5& 0.2& 0.3\\ 0.8& 0.5& 0.6\\ 0.7& 0.4& 0.5\end{array}\begin{array}{c}0.4 \\ 0.7 \\ 0.6 \end{array}\begin{array}{c}0.4\\ 0.7\\ 0.6\end{array}\\ \begin{array}{ccc}0.6& 0.3& 0.4\end{array}\begin{array}{cc}0.5& 0.5\end{array}\\ \begin{array}{ccc}0.6& 0.3& 0.4\end{array}\begin{array}{cc}0.5& 0.5\end{array}\end{array}\right] \\ {F}_2=\left[\begin{array}{c}\begin{array}{ccccccccc}0.5& 0.3& 0.5& 0.3& 0.3& 0.5& 0.6& 0.7& 0.7\\ 0.7& 0.5& 0.7& 0.5& 0.5& 0.7& 0.8& 0.9& 0.9\\ 0.5& 0.3& 0.5& 0.3& 0.3& 0.5& 0.6& 0.7& 0.7\\ 0.7& 0.5& 0.7& 0.5& 0.5& 0.7& 0.8& 0.9& 0.9\\ 0.7& 0.5& 0.7& 0.5& 0.5& 0.7& 0.8& 0.9& 0.9\\ 0.5& 0.3& 0.5& 0.3& 0.3& 0.5& 0.6& 0.7& 0.7\\ 0.4& 0.2& 0.4& 0.2& 0.2& 0.4& 0.5& 0.6& 0.6\\ 0.3& 0.31& 0.3& 0.1& 0.1& 0.3& 0.4& 0.5& 0.5\\ 0.3& 0.31& 0.3& 0.1& 0.1& 0.3& 0.4& 0.5& 0.5\end{array}\end{array}\right] \\ {F}_3=\left[\begin{array}{c}\begin{array}{ccc}0.5& 0.6& 0.4\\ 0.4& 0.5& 0.3\\ 0.6& 0.7& 0.5\end{array}\begin{array}{c}0.3\\ 0.2\\ 0.4\end{array}\\ \begin{array}{cc}0.7& 0.8\end{array}\begin{array}{cc}0.6& 0.5\end{array}\end{array}\right],F_4=\left[\begin{array}{cc}0.5& 0.7\\ 0.3& 0.5\end{array}\right] \end{gathered}$$

Assuming that there are n primary requirements, the weight ranking vector is

$$W_1=\left(w_1,w_2,\dots ,w_n\right),$$

where the value of $w_i$ is

$$w_i=\frac{1}{n}-\frac{1}{2\alpha }+\frac{{{\displaystyle \sum }}_{k=1}^n{r}_{ij}}{n\alpha },{{\displaystyle \sum }}_{i=1}^n{w}_i=1,$$

(2)

where $\alpha$ is an index factor indicating the difference in importance degree, and its value range satisfies $\alpha \ge \left(n-1\right)/2$. The greater the value is, the less attention is paid to the difference in the importance degree between the indicators. To provide a better reference for designers, this study defines $\alpha =\left(n-1\right)/2$. Please refer to Reference [88] for a more detailed introduction to the weight calculation method.

After obtaining the fuzzy judgment matrix, the weight ranking vector was calculated using Equation (2). $W_1=\left(0.16,0.45,0.23,0.16\right)$ was obtained by calculating the matrix F. $F_1$, $F_2$, $F_3$, and $F_4$ were calculated in turn:

$$\begin{gathered} W_{11}=(0.13,0.28,0.23,0.18,0.18) \\ {W}_{12}=(0.11,0.16,0.11,0.16,0.16,0.11,0.09,0.05,0.05) \\ {W}_{13}=(0.22,0.15,0.28,0.35),W_{14}=(0.7,0.3). \end{gathered}$$

The weights of the secondary requirements needed to be adjusted according to the weights of the primary requirements. The calculation formula is as follows:

$$W_{Fj}=w_1\ast w_{ij}.$$

(3)

All the weights of the requirements were obtained based on expert scoring. Combining the data collected by the questionnaire research and the results of the experts’ scoring, the requirement weights were processed through a fuzzy comprehensive evaluation.

For the secondary requirements, the final weight ranking was obtained using Equation (3):

$$W_F=(0.0208,0.0448,0.0368,0.0288,0.0288,0.0495,0.072,0.0495,0.0072,0.0072,0.0495,0.0405,0.0225,0.0225,0.0506,0.0345,0.0644,0.0805,0.112,0.048).$$

By multiplying the weight of each evaluation index by the relative membership value of the corresponding evaluation index of each scheme, the comprehensive index value ($z_i$) of the fuzzy evaluation was obtained. Then, $z_i$ was standardized so that

$$Z=\left(z_1,z_2,\cdots ,z_n\right),{\displaystyle \sum }_{i=1}^n{z}_i=1.$$

Then, the final weight vector of each requirement was obtained:

$$W=Z\left(z_1,z_2,\cdots ,z_n\right).$$

The questionnaire on the customer requirements was normalized. The results of the membership degree are as follows (

Table 1. Scoring results of the questionnaire.

Requirement	$C_1$	$C_2$	$C_3$	$C_4$	$C_5$	$C_6$	$C_7$	$C_8$	$C_9$	$C_{10}$
Weight	0.6575	0.6621	0.6758	0.4703	0.6658	0.8420	0.9087	0.8685	0.8758	0.9352
Requirement	$C_{11}$	$C_{12}$	$C_{13}$	$C_{14}$	$C_{15}$	$C_{16}$	$C_{17}$	$C_{18}$	$C_{19}$	$C_{20}$
Weight	0.9114	0.8502	0.8776	0.7763	0.8447	0.6192	0.8210	0.8320	0.7078	0.6320

). C represents the customer requirements.

According to $W=Z\left(z_1,z_2,\cdots ,z_n\right)$, the final weight ranking vector was calculated as follows: W = (0.0173, 0.0375, 0.0314, 0.0171, 0.0242, 0.0526, 0.0826, 0.0543, 0.0797, 0.0850, 0.0570, 0.0435, 0.0249, 0.0221, 0.0540, 0.0270, 0.0668, 0.0846, 0.1001, 0.0383).

4.4. Output of the Engineering Characteristics

In the process of transforming customer requirements into engineering characteristics, a hierarchical structure was established. Each layer was connected by the input and output of the HoQ model to obtain a hierarchical decomposition structure. Based on the results of the identification of the customer requirements through the improved Kano model in the previous section combined with the literature review, annual reports of enterprises, and interviews with industry practitioners, we established the following corresponding relationships between the customer requirements and the engineering characteristics (

Table 2. Corresponding relationships between the customer requirements and the engineering characteristics.

Customer Requirement	Engineering Characteristic
$C_1:$ Diversified purchasing channels	None
$C_2:$ Preferential activities	None
$C_3:$ Logistical efficiency of a non-physical store purchase	Product packaging
$C_4:$ Customization	Packaging and appearance
$C_5:$ Pre-purchase guidance and experience	None
$C_6:$ Satisfactory sizes and weights	Size and material of the phone
$C_7:$ Reliable and indestructible hardware	Hardware quality indices
$C_8:$ Satisfactory appearance	Aesthetic design
$C_9:$ Long duration	Battery capacity and power consumption level
$C_{10}:$ Smooth operating system	Operating system components and indicators
$C_{11}:$ Satisfactory screen performance	Screen material and design
$C_{12}:$ Satisfactory photography and camera function	Camera pixel and capture function design
$C_{13}:$ Easy and comfortable human–machine interaction interface	Aesthetic and operating system design
$C_{14}:$ Excellent applications and expansion functions	Software design and development
$C_{15}:$ High efficiency of refund and exchange process	None
$C_{16}:$ Product use guidance and question answering service	Software design and development
$C_{17}:$ Satisfactory product repair service	None
$C_{18}:$ Follow-up tracking and maintenance	Software design and development
$C_{19}:$ Brand construction and cultural propaganda with identity	None
$C_{20}:$ Excellent peripheral products	Relevant product development

).

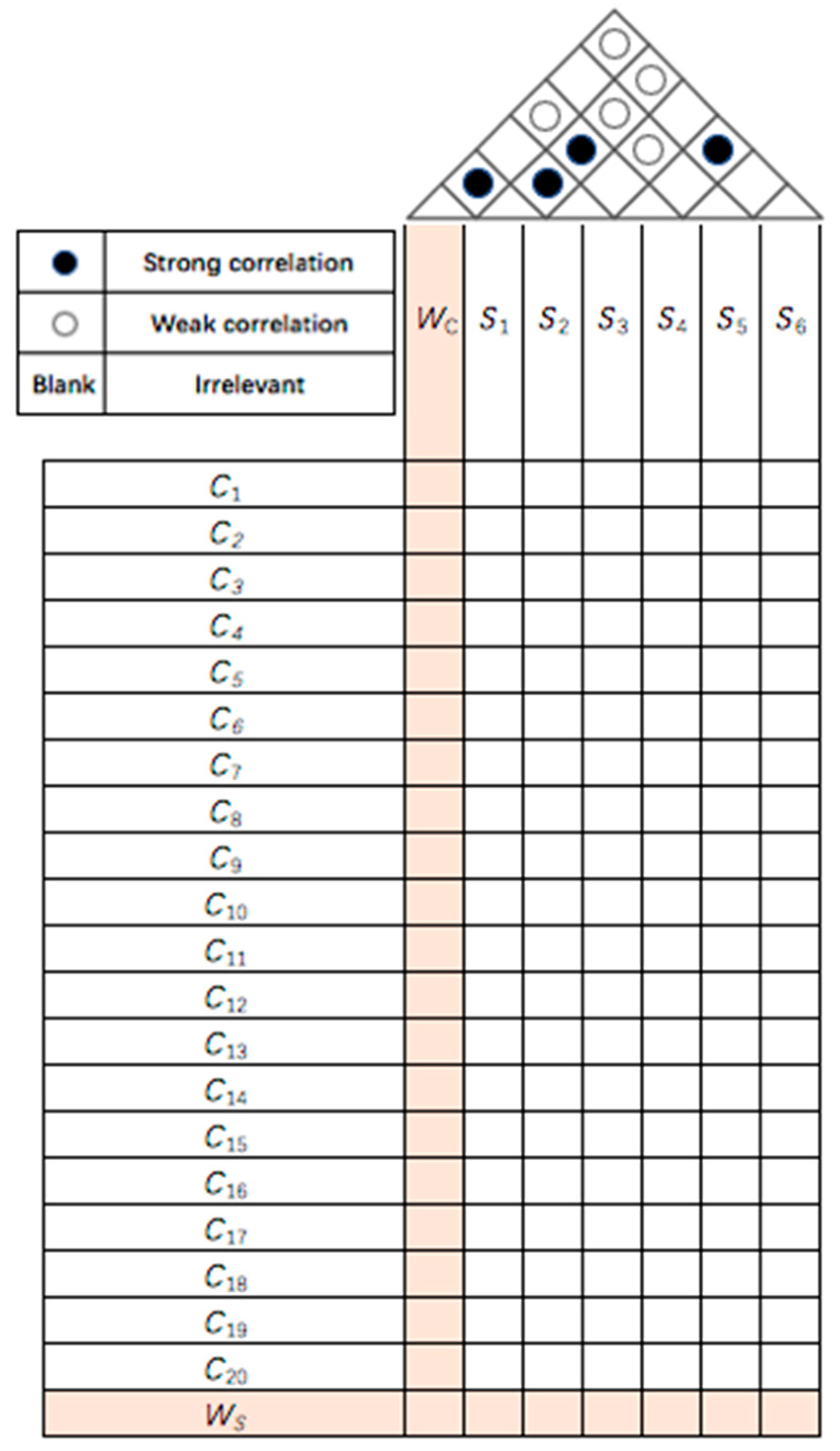
In this study, the relationship matrix was determined by the experts’ scores. The experts estimated the correlation between the customer requirements and the engineering characteristics based on experience. The experts’ semantic representation was classified into four levels: strong correlation, general correlation, weak correlation, and irrelevance. We invited 12 practitioners with professional knowledge who have been in the mobile phone industry for a long time to interview them and record the information we needed. According to the actual situation of expert scoring, we used the mode to obtain the final judgment matrix and used triangular fuzzy numbers to deal with the inaccurate semantic expression of the experts. We set the score of the semantic fuzzy set to U = {SP, P, WP, M}. SP denotes a strong correlation, and its triangular fuzzy numbers are (0.6, 0.8, 1); P denotes a general correlation, and its triangular fuzzy numbers are (0.4, 0.6, 0.8); WP denotes a weak correlation, and its triangular fuzzy numbers are (0.2, 0.4, 0.6); M denotes irrelevance, and its triangular fuzzy numbers are (0, 0, 0). The correlation matrix of the customer requirements and product specifications is presented in

Table 3. Corresponding relationships between the customer requirements and the engineering characteristics.

T		${\mathit{T}}_1$	${\mathit{T}}_2$	${\mathit{T}}_3$	${\mathit{T}}_4$	${\mathit{T}}_5$	${\mathit{T}}_6$	${\mathit{T}}_7$	${\mathit{T}}_8$	${\mathit{T}}_9$	${\mathit{T}}_{10}$	${\mathit{T}}_{11}$	${\mathit{T}}_{12}$	${\mathit{T}}_{13}$	${\mathit{T}}_{14}$
C	${\mathit{W}}_{\mathit{c}}$
$C_1$	0.0173	M	M	M	M	M	M	M	M	M	M	M	M	M	WP
$C_2$	0.0375	M	M	M	M	M	M	M	M	M	M	M	M	M	P
$C_3$	0.0314	WP	M	M	M	M	M	M	M	M	M	M	M	M	M
$C_4$	0.0171	SP	P	M	M	M	P	M	M	M	M	M	M	M	M
$C_5$	0.0242	WP	M	M	M	M	M	M	M	M	M	M	M	P	M
$C_6$	0.0526	P	SP	SP	P	WP	SP	SP	SP	WP	M	WP	WP	P	WP
$C_7$	0.0826	M	SP	P	SP	SP	WP	P	WP	P	M	WP	WP	M	M
$C_8$	0.0543	WP	P	P	P	WP	SP	M	M	M	WP	M	M	M	WP
$C_9$	0.0797	M	M	SP	SP	P	M	SP	SP	P	WP	M	M	WP	M
$C_{10}$	0.085	M	M	M	M	P	M	M	P	SP	SP	M	M	P	M
$C_{11}$	0.057	M	M	WP	SP	M	M	WP	P	WP	M	M	WP	WP	M
$C_{12}$	0.0435	M	M	M	M	P	P	M	M	P	M	SP	SP	P	M
$C_{13}$	0.0249	M	M	M	WP	M	SP	M	M	M	WP	M	M	SP	M
$C_{14}$	0.0221	M	M	M	M	WP	WP	M	M	P	P	M	M	SP	P
$C_{15}$	0.054	M	M	M	M	M	M	M	M	M	M	M	M	M	M
$C_{16}$	0.027	M	M	M	M	M	M	M	M	M	M	M	M	P	M
$C_{17}$	0.0668	M	M	M	M	WP	M	M	M	M	M	M	M	M	WP
$C_{18}$	0.0846	M	M	M	M	M	M	M	M	M	M	M	M	P	WP
$C_{19}$	0.1001	WP	M	M	M	M	P	M	M	M	M	M	M	WP	P
$C_{20}$	0.0383	M	M	M	M	M	M	M	M	M	M	M	M	WP	SP
$W_T$

C: Customer requirement, $T_7$: Battery capacity. $W_c$: Weight of requirement, $T_8$: Power consumption level. T: Product-related engineering characteristics, $T_9$: CPU processor. $T_1$: Product packaging, $T_{10}$: Operating system. $T_2$: Packaging and appearance, $T_{11}$: Camera pixel. $T_3$: Size and material, $T_{12}$: Capture function. $T_4$: Screen material and design, $T_{13}$: Software development. $T_5$: Hardware quality indices, $T_{14}$: Relevant product development. $T_6$: Aesthetic design, $W_T:$ Weight of engineering characteristic.

.

The weights of the customer requirements were confirmed by the Kano model. According to QFD theory, the weight of the engineering characteristic WT is calculated by the customer requirement vector and the correlation matrix of the customer requirements and engineering characteristics. The calculation formula is as follows:

$$W_T=W_c\times R^T.$$

(4)

The correlation matrix is given in its abbreviated form. The improved weights of the product-related engineering characteristics are as follows:

$$W_T=W_c\times R_1^T=\left[\begin{array}{c}0.0173\\ 0.0375\\ 0.0314\\ \dots \\ 0.1001\\ 0.383\end{array}\right]\left[\begin{array}{c}\begin{array}{ccc}(0,0,0)& (0,0,0)& (0.2,0.4,0.6)\\ (0,0,0)& (0,0,0)& (0,0,0)\\ (0,0,0)& (0,0,0)& (0,0,0)\end{array}\begin{array}{ccc}\dots & (0.2,0.4,0.6)& (0,0,0)\\ \dots & (0,0,0)& (0,0,0)\\ \dots & (0,0,0)& (0,0,0)\end{array}\\ \begin{array}{ccc}⋮& ⋮& ⋮\\ (0,0,0)& (0,0,0)& (0,0,0)\\ (0.2,0.4,0.6)& (0.4,0.6,0.8)& (0,0,0)\end{array}\begin{array}{ccc}\ddots & ⋮& ⋮\\ \dots & (0.4,0.6,0.8)& (0.4,0.6,0.8)\\ \cdots & (0.4,0.6,0.8)& (0.6,0.8,1)\end{array}\end{array}\right]$$

=[(0.0733,0.1292,0.1852),(0.1097,0.1510,0.1923),(0.1455,0.2108,0.2760),(0.1793,0.2495,0.3198),(0.1720,0.2693,0.3666),(0.1643,0.2437,0.3232),(0.1238,0.1782,0.2326),(0.1527,0.2241,0.2955),(0.1641,0.2326,0.3171),(0.0916,0.1448,0.1980),(0.0531,0.0889,0.1246),(0.0645,0.1117,0.1588),(0.2100,0.3378,0.4656),(0.1420,0.2367,0.3314)]

Through the above process, the corresponding weights of the product-related engineering characteristics were obtained (

Table 4. Weights of the product-related engineering characteristics.

Engineering Characteristic	Fuzzy Weight	Engineering Characteristic	Fuzzy Weight
$T_1$	(0.0733, 0.1292, 0.1852)	$T_8$	(0.1527, 0.2241, 0.2955)
$T_2$	(0.1097, 0.1510, 0.1923)	$T_9$	(0.1641, 0.2326, 0.3171)
$T_3$	(0.1455, 0.2108, 0.2760)	$T_{10}$	(0.0916, 0.1448, 0.1980)
$T_4$	(0.1793, 0.2495, 0.3198)	$T_{11}$	(0.0531, 0.0889, 0.1246)
$T_5$	(0.1720, 0.2693, 0.3666)	$T_{12}$	(0.0645, 0.1117, 0.1588)
$T_6$	(0.1643, 0.2437, 0.3232)	$T_{13}$	(0.2100, 0.3378, 0.4656)
$T_7$	(0.1238, 0.1782, 0.2326)	$T_{14}$	(0.1420, 0.2367, 0.3314)

). The results can be used as a reference for better consideration of customer requirements in product design.

According to the weight of the customer requirements confirmed by the Kano model and the correlation matrix of the customer requirements and product specifications given by the experts, the HoQ model of the product-related engineering characteristics is illustrated in Figure 3.

Similarly, this study established the corresponding relationship between the customer requirements and the service-related engineering characteristics. According to the expert scores and triangular fuzzy numbers, we obtained the correlation matrix of the customer requirements and service-related engineering characteristics. The HoQ model of the service process was established. See Figure 4 for details.

According to QFD theory, the weight of the service-related engineering characteristics was calculated by the following formula: $W_s=W_c\times R^T$.

The weights of the service-related engineering characteristics are as follows:

$$W_T=W_c\times R^T=\left[\begin{array}{c}0.0173\\ 0.0375\\ 0.0314\\ ⋮\\ 0.1001\\ 0.383\end{array}\right]\left[\begin{array}{c}\begin{array}{ccc}(0,0,0)& (0,0,0)& (0.2,0.4,0.6)\\ (0.6,0.8,1)& (0.4,0.6,0.8)& (0.2,0.4,0.6)\\ (0.4,0.6,0.8)& (0.2,0.4,0.6)& (0.6,0.8,1)\end{array}\begin{array}{ccc}\cdots & (0.2,0.4,0.6)& (0.4,0.6,0.8)\\ \cdots & (0.2,0.4,0.6)& (0.2,0.4,0.6)\\ \cdots & (0,0,0)& (0,0,0)\end{array}\\ \begin{array}{ccc}(0.4,0.6,0.8)& (0.6,0.8,1)& (0,0,0)\\ (0.6,0.8,1)& (0.4,0.6,0.8)& (0.2,0.4,0.6)\\ (0.2,0.4,0.6)& (0.2,0.4,0.6)& (0,0,0)\end{array}\begin{array}{ccc}\cdots & (0.6,0.8,1)& (0.6,0.8,1)\\ \cdots & (0,0,0)& (0.2,0.4,0.6)\\ \cdots & (0.2,0.4,0.6)& (0,0,0)\end{array}\end{array}\right]$$

=[(0.4435,0.6218,0.8000),(0.2828,0.4302,0.5777),(0.1126,0.1574,0.2022),(0.2188,0.3216,0.4244),(0.0851,0.1341,0.1832),(0.1208,0.1862,0.2516)]

The corresponding weights of the service-related engineering characteristics were obtained, as shown in

Table 5. Weights of the service-related engineering characteristics.

Engineering Characteristic	Fuzzy Weight
$S_1:$ Technological service	(0.4435, 0.6218, 0.8000)
$S_2:$ Information service	(0.2828, 0.4302, 0.5777)
$S_3:$ Logistical service	(0.1126, 0.1574, 0.2022)
$S_4:$ Consulting and business service	(0.2188, 0.3216, 0.4244)
$S_5:$ Financial and insurance service	(0.0851, 0.1341, 0.1832)
$S_6:$ Human resource service	(0.1208, 0.1862, 0.2516)

. S represents the service-related engineering characteristics.

4.5. Importance Ranking of the Engineering Characteristics

We used the concept of possibility degree of the triangular fuzzy numbers to optimize the fuzzy output of the QFD model. Specifically, the ranking vectors of the triangular fuzzy number vectors of the product- and service-related engineering characteristics were calculated, respectively, to obtain the rankings of all indicators.

Assume the triangular fuzzy number $a=\left(a^L,a^M,a^U\right),b=\left(b^L,b^M,b^U\right)$, and thus

$$\begin{gathered} p\left(a\ge b\right)=\lambda \frac{min\left\{a^M-a^L+b^M-b^L,max\left(a^M-b^L,0\right)\right\}}{a^M-a^L+b^M-b^L} \\ \left(1-\lambda \right)\frac{max\left\{a^U-a^M+b^U-b^M,max\left(a^U-b^M,0\right)\right\}}{a^U-a^M+b^U-b^M} \end{gathered}$$

is called the possibility degree of $a\ge b$.

The value of $\lambda$ depends on the decision-maker’s risk attitude. When $\lambda$ > 0.5, the decision-maker has a high-risk preference; when $\lambda$ = 0.5, the decision-maker is risk-neutral; and when $\lambda$ < 0.5, the decision-maker has a low-risk preference. In this study, we took $\lambda$ = 0.5. By calculating the possibility degrees of the triangular fuzzy numbers, the possibility degree matrix of the triangular fuzzy numbers can be established. The possibility degree matrix P is a complementary matrix, and element P_ij denotes the possibility degree of index i relative to index j.

The calculation formula of the ranking vector $\omega ={\left({\omega }_1,{\omega }_2,\cdots ,{\omega }_n\right)}^T$ based on the fuzzy complementary judgment matrix is as follows [89]:

$${\omega }_i=\frac{{{\displaystyle \sum }}_{j=1}^n{p}_{ij}+\frac{n}{2}-1}{n\left(n-1\right)},i\in N,$$

(5)

where $p_{ij}=P\left(Z_i\ge Z_j\right)$.

The weights of the product-related engineering characteristics obtained in the previous section were substituted into Equation (5) to calculate the possibility degree matrix of all indicators. For layout reasons, only the abbreviated form of the matrix is given here.

$$P_T=\left[\begin{array}{c}\begin{array}{ccc}0.5& 0.6000& 0.5\\ 0.4000& 0.5& 0.5258\\ 0.5& 0.4742& 0.5\end{array}\begin{array}{ccc}\dots & 0.5& 0.5\\ \dots & 0.5& 0.5331\\ \dots & 0.5021& 0.7150\end{array}\\ \begin{array}{ccc}⋮& ⋮& ⋮\\ 0.5& 0.5& 0.4979\\ 0.5& 0.4669& 0.2850\end{array}\begin{array}{ccc}\ddots & ⋮& ⋮\\ \dots & 0.5& 0.9544\\ \cdots & 0.0456& 0.5\end{array}\end{array}\right]$$

The ranking vector of the product-related engineering characteristics is as follows: ${\omega }_T=$(0.0712,0.1102,0.1488,0.1751,0.1701,0.1623,0.1211,0.1533,0.1627,0.0897,0.0521,0.0638,0.218,0.1405)^T.

Similarly, the ranking vectors of the service-related engineering characteristics can be calculated, and the result is as follows:

$$\begin{gathered} P_S=\left[\begin{array}{c}\begin{array}{ccc}0.5000& 0.0677& 0.9408\\ 0.9323& 0.5000& 0.5928\\ 0.0592& 0.4072& 0.5000\end{array}\begin{array}{ccc}0.3512& 0.9648& 0.7599\\ 0.9340& 0.6282& 0.6464\\ 0.5000& 0.8854& 0.6601\end{array}\\ \begin{array}{ccc}0.6488& 0.0660& 0.5000\\ 0.0352& 0.3718& 0.1146\\ 0.2401& 0.3536& 0.3399\end{array}\begin{array}{ccc}0.5000& 0.4556& 0.2081\\ 0.5444& 0.5000& 0.5581\\ 0.7919& 0.4419& 0.5000\end{array}\end{array}\right] \\ {\omega }_T=(0.4417,0.2806,0.1107,0.2164,0.0812,0.1188{)}^{\mathrm{T}}. \end{gathered}$$

From the ranking vector of the product-related engineering characteristics, the order of importance of the technical indicators for smartphone products from high to low is as follows based on the perspective of customer requirements: software development, hardware quality, related product development, aesthetic design, screen material and design, CPU processor, power consumption level, size and material, battery capacity, operating system, packaging and appearance, capture function, camera pixels, and product packaging. In the design of the service process, the order of importance of the engineering characteristics according to the customers is as follows: technological service, information service, consulting and business service, human resource service, logistical services, and financial insurance services. The specific rankings and weights are presented in

Table 6. Rankings of the product-related engineering characteristics.

Importance Ranking	Engineering Characteristic	Importance Weight
1	$T_{13}$: Software development	0.2186
2	$T_5$: Hardware quality	0.1751
3	$T_{14}$: Relevant product development	0.1701
4	$T_6$: Aesthetic design	0.1627
5	$T_4$: Screen material and design	0.1623
6	$T_9$: CPU processor	0.1533
7	$T_8$: Power consumption level	0.1488
8	$T_3$: Size and material	0.1405
9	$T_7$: Battery capacity	0.1211
10	$T_{10}$: Operating system	0.1102
11	$T_2$: Packaging and appearance	0.0897
12	$T_{12}$: Capture function	0.0712
13	$T_{11}$: Camera pixel	0.0638
14	$T_1$: Product packaging	0.0521

and

Table 7. Rankings of the service-related engineering characteristics.

Importance Ranking	Engineering Characteristic	Importance Weight
1	$S_1:$ Technological service	0.4417
2	$S_2:$ Information service	0.2806
3	$S_4:$ Consulting and business service	0.2164
4	$S_6:$ Human resource service	0.1188
5	$S_3:$ Logistical service	0.1107
6	$S_5:$ Financial and insurance service	0.0812

.

Since the life cycle of smartphones is becoming shorter, users are demanding new and improved smartphone features for updated smartphones, but it is not easy to know which features are the most important to users. By quantifying the indexes indicated by customers, it is possible to smell something different or find some new discoveries about what really matters to customers. For example, people attach great importance to the software and hardware quality of smartphone products, while the product packaging is actually the least valued by customers. This is consistent with our previous knowledge. However, when it comes to services, some characteristics (logistical service and financial and insurance service) may be not as important as product managers and system designers thought. The importance weights and rankings of customer requirements are evaluated so they can be selected by designers. Since the importance weights of engineering characteristics are also provided, this helps guide designers and product managers to allocate resources reasonably and develop their products and services for maximum customer satisfaction.

Moreover, the shift from traditional product design to PSS design can be difficult for inexperienced managers and practitioners, leading to the risk that they may unintentionally opt for solutions that might reduce customers’ satisfaction. In other words, the methodology can be utilized in the development and design of PSSs. This facilitates continuous feedback, which can enable engineers to better manage the PSS development activities by verifying the inputs and outputs of each step. For enterprise, it can reduce the effort used for unimportant engineering characteristics, reduce mistakes and neglect in decision-making, mitigate the need for additional resources at later stages of the PSS development process (redesigning or reassessing the solution’s characteristics), and save the costs in product and service development. In addition, the developed product can help to achieve the desired quality and better meet customer requirements.

5. Conclusions and Future Research

Customers’ requirements cannot be directly used in the design of PSSs, and they need to be converted into a form that PSS designers can understand [90]. The conversion of customer requirements into specific engineering characteristics is important for PSS design. Although many researchers have made diligent efforts in PSS design and development, much remains to be done.

We truly acknowledge that using merely a series of integrated and improved methods to transform customer requirements into engineering characteristics is not particularly novel. However, a systematic and whole-process framework employing specific identification processes and methods, as well as a big data analysis, has not been found in previous works. The proposed framework would provide PSS designers and later researchers with some inspirations with a standardized process reference from the capture of the primary requirements to the identification of the final engineering characteristics. It is hoped that this study can trigger more exploration in this important and interesting field.

One limitation of this study is that we chose the risk preference $\lambda =0.5$ for the calculation. That is, we assumed that the decision-makers are risk-neutral, a situation that could differ from the actual one. For the design of PSSs in different industries, evaluating the risk preferences of decision-makers in depth is necessary for more accurate ranking results of the indices. Our study provides practical insights of the smartphone industry in the context of e-commerce, which can be considered exploratory. The methodology and procedure can be used to define new research questions and hypotheses. However, the proposed procedure, like any other novel approach, should be carried out in different contexts and industries to refine it, as well as to check its validity and applicability. The integration of methods also needs to be rechecked with respect to its assumptions and applicability through further studies. These cross-validations can be valuable for theory development and for practitioners in the PSS field.

A future research direction also lies in studying a more systematic process and more efficient methods and tools for PSS requirement management. A point of concern is PSS requirement management with the support of big data technology. Customer demand is ever changing and difficult to identify, especially during the process of servitization. Capturing and tracking the changes in customers’ needs in the traditional way is difficult. The development of big data technology makes it possible to analyze big data in different stages of the PSS life cycle. A large amount of structured and unstructured data can be obtained in the product operation stage, which can help us to better understand users’ behavioral characteristics and preferences. We attempted to use big data analysis in the stage of customer requirement identification and online customer comment data to screen and identify customer requirements. However, the application potential of big data technologies in PSS design remains to be explored. Data mining and prediction are expected to make requirement identification and trend prediction more accurate and even achieve dynamic forecasting.