Default Behaviors of Contractors under Surety Bond in Construction Industry Based on Evolutionary Game Model
Abstract
:1. Introduction
2. Literature Review
2.1. Default Risk in Construction Industry
2.2. Surety Bond in Construction Industry
2.3. Evolutionary Game Analysis in Construction Industry
2.4. Summary of the Literature Review
3. Problem Description and Assumptions
3.1. Problem Description
3.2. Model Assumptions
4. Static Model
4.1. Static Model Description
4.2. Static Model Analysis
4.2.1. Static Model under Low-Penalty Unconditional Bond
4.2.2. Static Model under High-Penalty Conditional Bond
5. Dynamic Model
5.1. Dynamic Model Description
5.2. Dynamic Model Analysis
5.2.1. Dynamic Model under Low-penalty Unconditional Bond
5.2.2. Dynamic Model under High-Penalty Conditional Bond
6. Numerical Simulation
6.1. Case Assumption
6.2. Simulation
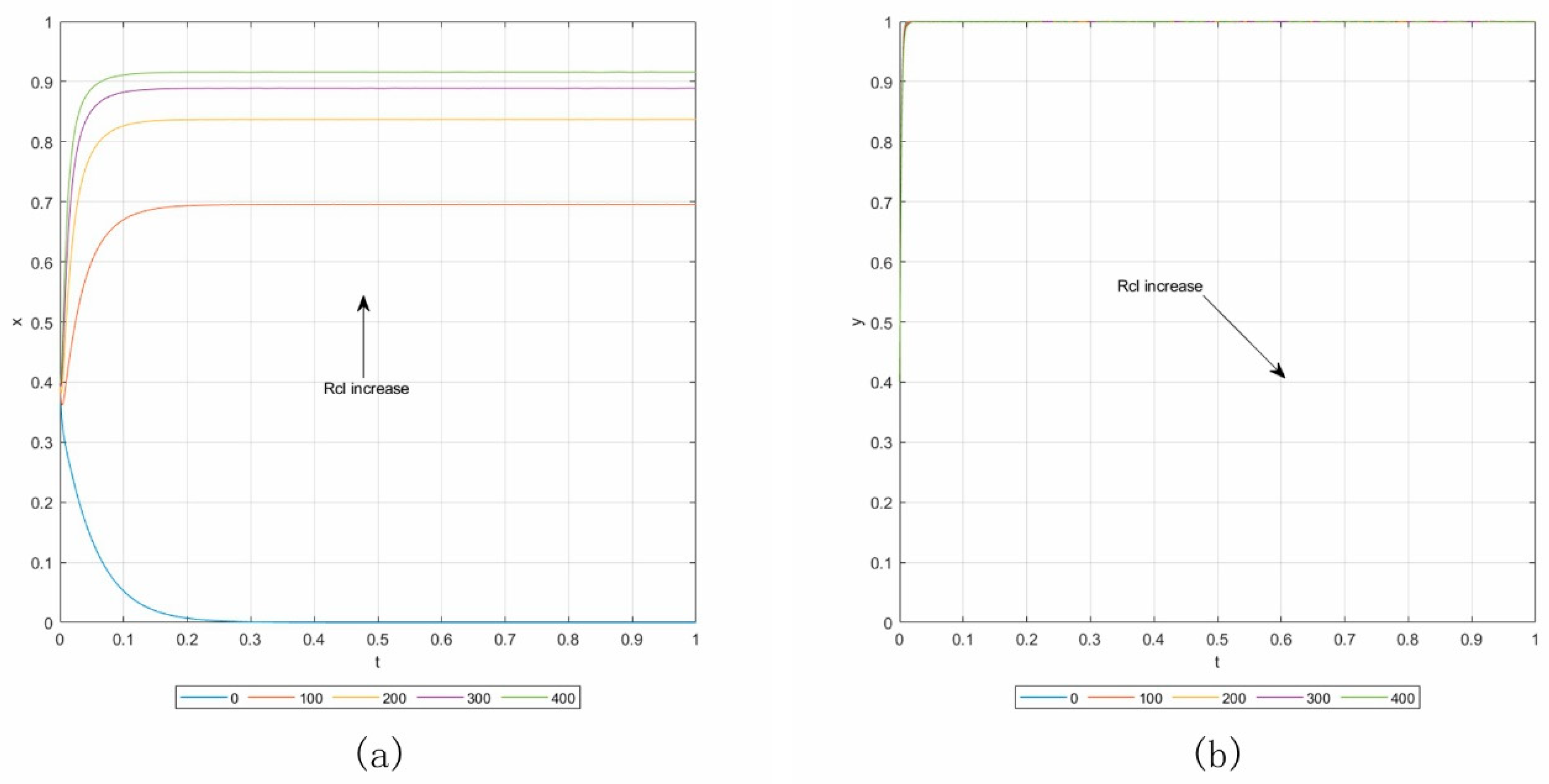
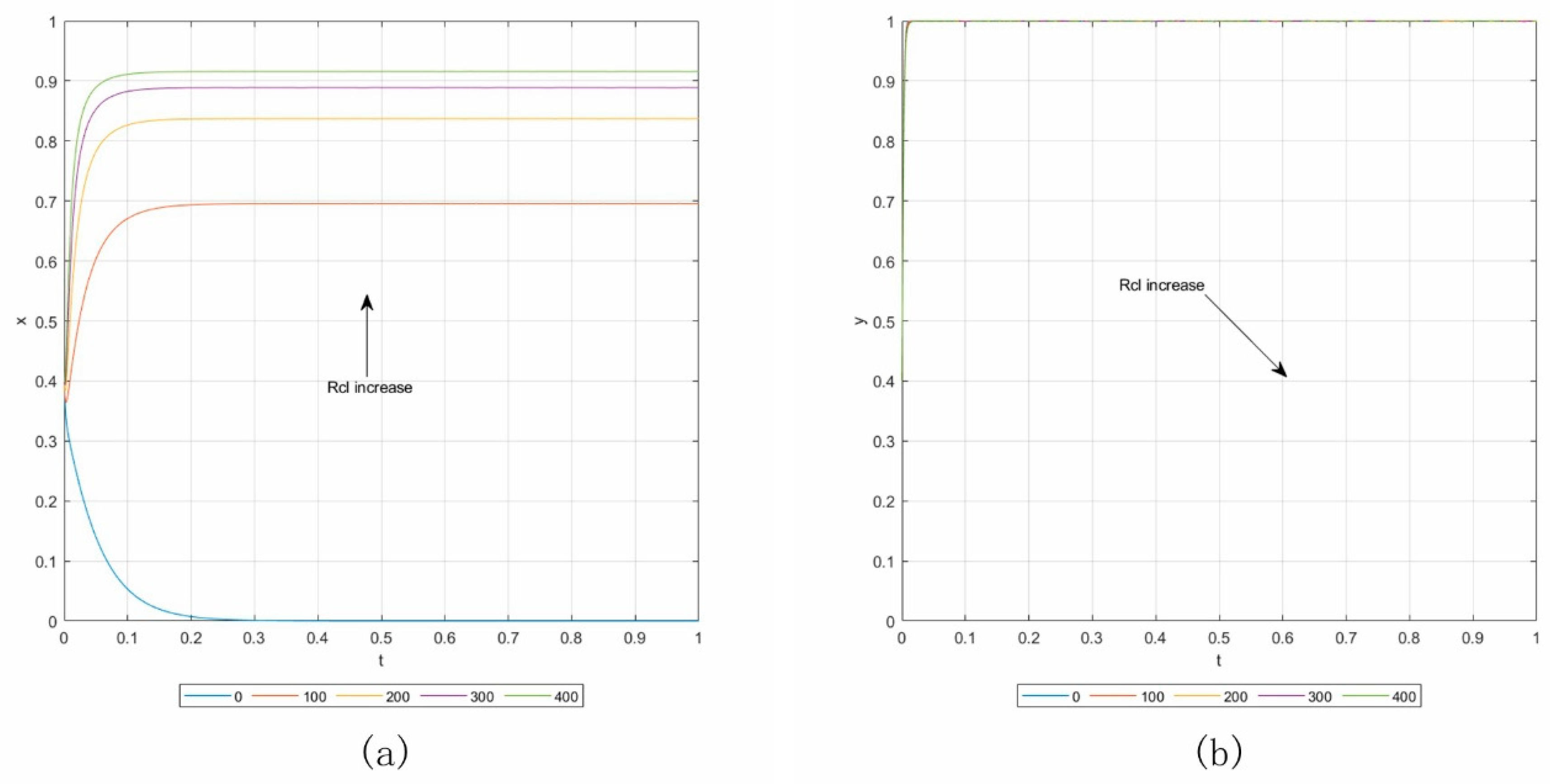
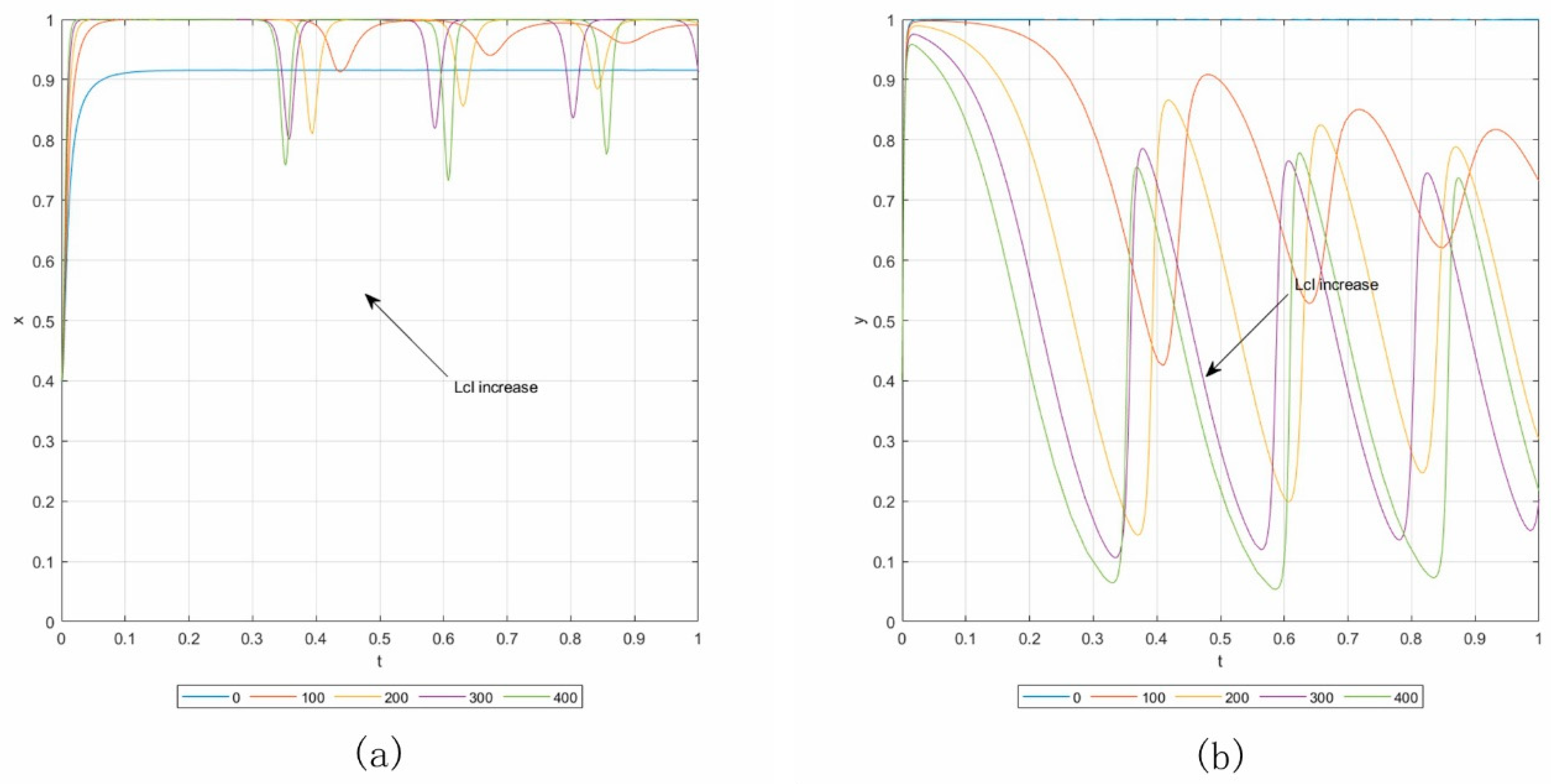
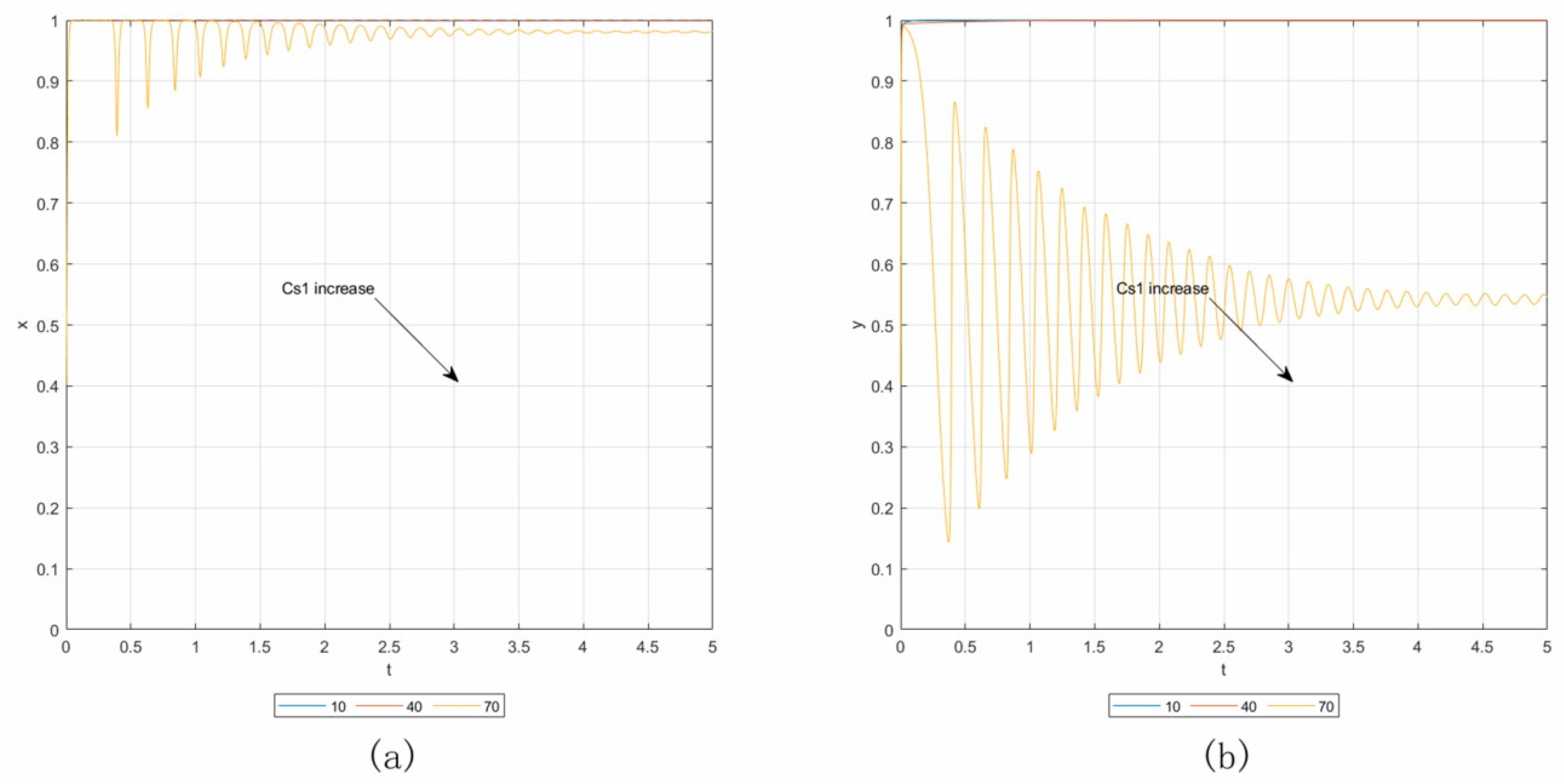
6.3. Influence Analysis of Parameters
7. Discussions
- 1.
- Low-penalty unconditional bond
- 2.
- High-penalty conditional bond
- 3.
- Comparison
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Chava, S.; Jarrow, R.A. Bankruptcy prediction with industry effects. Rev. Finance 2004, 8, 537–569. [Google Scholar] [CrossRef]
- Tserng, H.P.; Lin, G.-F.; Tsai, L.K.; Chen, P.-C. An enforced support vector machine model for construction contractor default prediction. Autom. Constr. 2011, 20, 1242–1249. [Google Scholar] [CrossRef]
- Cruz, C.O.; Marques, R.C. Using probabilistic methods to estimate the public sector comparator. Comput. Civ. Infrastruct. Eng. 2012, 27, 782–800. [Google Scholar] [CrossRef]
- Horta, I.M.; Camanho, A.S. Company failure prediction in the construction industry. Expert Syst. Appl. 2013, 40, 6253–6257. [Google Scholar] [CrossRef]
- Tserng, H.P.; Ngo, T.L.; Chen, P.C.; Tran, L.Q. A grey system theory-based default prediction model for construction firms. Comput. Civ. Infrastruct. Eng. 2014, 30, 120–134. [Google Scholar] [CrossRef]
- Wu, W.-W. Beyond business failure prediction. Expert Syst. Appl. 2010, 37, 2371–2376. [Google Scholar] [CrossRef]
- Kangari, R.; Farid, F.; Elgharib, H.M. Financial performance analysis for construction industry. J. Constr. Eng. Manag. 1992, 118, 349–361. [Google Scholar] [CrossRef]
- Russell, J.S.; Zhai, H. Predicting contractor failure using stochastic dynamics of economic and financial variables. J. Constr. Eng. Manag. 1996, 122, 183–191. [Google Scholar] [CrossRef] [Green Version]
- Ng, S.T.; Wong, J.M.; Zhang, J. Applying Z-score model to distinguish insolvent construction companies in China. Habitat Int. 2011, 35, 599–607. [Google Scholar] [CrossRef]
- Tserng, H.P.; Chen, P.-C.; Huang, W.-H.; Lei, M.C.; Tran, Q.H. Prediction of default probability for construction firms using the logit model. J. Civ. Eng. Manag. 2014, 20, 247–255. [Google Scholar] [CrossRef] [Green Version]
- Cheng, M.-Y.; Hoang, N.-D.; Limanto, L.; Wu, Y.-W. A novel hybrid intelligent approach for contractor default status prediction. Knowl.-Based Syst. 2014, 71, 314–321. [Google Scholar] [CrossRef]
- Choi, H.; Son, H.; Kim, C. Predicting financial distress of contractors in the construction industry using ensemble learning. Expert Syst. Appl. 2018, 110, 1–10. [Google Scholar] [CrossRef]
- You, J.; Chen, Y.; Wang, W.; Shi, C. Uncertainty, opportunistic behavior, and governance in construction projects: The efficacy of contracts. Int. J. Proj. Manag. 2018, 36, 795–807. [Google Scholar] [CrossRef]
- Nasir, M.K.; Hadikusumo, B.H.W. System dynamics model of contractual relationships between owner and contractor in construction projects. J. Manag. Eng. 2019, 35, 04018052. [Google Scholar] [CrossRef]
- Zhang, L.; Qian, Q. How mediated power affects opportunism in owner–contractor relationships: The role of risk perceptions. Int. J. Proj. Manag. 2017, 35, 516–529. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, X.; Li, Y. Exploring the factors inducing contractors’ unethical behavior: Case of China. J. Prof. Issues Eng. Educ. Pr. 2017, 143, 04016023. [Google Scholar] [CrossRef]
- Lu, W.; Zhang, L.; Zhang, L. Effect of contract completeness on contractors’ opportunistic behavior and the moderating role of interdependence. J. Constr. Eng. Manag. 2016, 142, 04016004. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, S.; Gao, Y.; Ding, X. Contractual governance: Effects of risk allocation on contractors’ cooperative behavior in construction projects. J. Constr. Eng. Manag. 2016, 142, 04016005. [Google Scholar] [CrossRef]
- Kangari, R.; Bakheet, M. Construction surety bonding. J. Constr. Eng. Manag. 2001, 127, 232–238. [Google Scholar] [CrossRef]
- Awad, A.; Fayek, A.R. Adaptive learning of contractor default prediction model for surety bonding. J. Constr. Eng. Manag. 2013, 139, 694–704. [Google Scholar] [CrossRef]
- Deng, X.; Ding, S.; Tian, Q. Reasons underlying a mandatory high penalty construction contract bonding system. J. Constr. Eng. Manag. 2004, 130, 67–74. [Google Scholar] [CrossRef]
- Eaglestone, F.N.; Smyth, C. Insurance under the ICE Contract; Godwin: London, UK, 1985. [Google Scholar]
- Russell, J.S. Surety Bonds for Construction Contracts; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2000. [Google Scholar]
- Winston, S.; Ichniowski, T. Procurement: Miller act reforms approved by house. Eng. Newsrev. 1999, 243, 11. [Google Scholar]
- Bayraktar, M.E.; Hastak, M. Scoring approach to construction bond underwriting. J. Constr. Eng. Manag. 2010, 136, 957–967. [Google Scholar] [CrossRef]
- Marsh, K.; Fayek, A.R. SuretyAssist: Fuzzy expert system to assist surety underwriters in evaluating construction contractors for bonding. J. Constr. Eng. Manag. 2010, 136, 1219–1226. [Google Scholar] [CrossRef]
- Awad, A.; Fayek, A.R. A decision support system for contractor prequalification for surety bonding. Autom. Constr. 2012, 21, 89–98. [Google Scholar] [CrossRef]
- El-Mashaleh, M.S.; Horta, I.M. Evaluating contractors for bonding: DEA decision making model for surety underwriters. J. Manag. Eng. 2016, 32, 04015020. [Google Scholar] [CrossRef]
- Al-Sobiei, O.S.; Arditi, D.; Polat, G. Managing owner’s risk of contractor default. J. Constr. Eng. Manag. 2005, 131, 973–978. [Google Scholar] [CrossRef]
- Nash, J. Non-cooperative games. Ann. Math. 1951, 54, 286–295. [Google Scholar] [CrossRef]
- Smith, J.M.; Price, G.R. The logic of animal conflict. Nat. Cell Biol. 1973, 246, 15–18. [Google Scholar] [CrossRef]
- Smith, J.M. The theory of games and the evolution of animal conflicts. J. Theor. Biol. 1974, 47, 209–221. [Google Scholar] [CrossRef] [Green Version]
- Taylor, P.D.; Jonker, L.B. Evolutionary stable strategies and game dynamics. Math. Biosci. 1978, 40, 145–156. [Google Scholar] [CrossRef]
- Bester, H.; Güth, W. Is altruism evolutionarily stable? J. Econ. Behav. Organ. 1998, 34, 193–209. [Google Scholar] [CrossRef] [Green Version]
- Dufwenberg, M.; Güth, W. Indirect evolution vs. strategic delegation: A comparison of two approaches to explaining economic institutions. Eur. J. Political-Econ. 1999, 15, 281–295. [Google Scholar] [CrossRef]
- Naini, S.G.J.; Aliahmadi, A.R.; Jafari-Eskandari, M. Designing a mixed performance measurement system for environmental supply chain management using evolutionary game theory and balanced scorecard: A case study of an auto industry supply chain. Resour. Conserv. Recycl. 2011, 55, 593–603. [Google Scholar] [CrossRef]
- Wang, G.; Xue, Y.; Skibniewski, M.J.; Song, J.; Lu, H. Analysis of private investors conduct strategies by governments supervising public-private partnership projects in the new media era. Sustainability 2018, 10, 4723. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Li, Z.; Jiang, L.; Wu, G.; Cheng, D. Enhanced cooperation among stakeholders in PPP mega-infrastructure projects: A China study. Sustainability 2018, 10, 2791. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; Fang, M.; Shi, Q.; Wang, P.; Li, Q. Contractor cooperation mechanism and evolution of the green supply chain in mega projects. Sustainability 2018, 10, 4306. [Google Scholar] [CrossRef] [Green Version]
- Hao, C.; Du, Q.; Huang, Y.; Shao, L.; Yan, Y. Evolutionary game analysis on knowledge-sharing behavior in the construction supply chain. Sustainability 2019, 11, 5319. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Tang, W.; Shen, W.; Wang, T. Enhancing risk management by partnering in international EPC projects: Perspective from evolutionary game in chinese construction companies. Sustainability 2019, 11, 5332. [Google Scholar] [CrossRef] [Green Version]
- Zheng, L.; Lu, W.; Chen, K.; Chau, K.W.; Niu, Y. Benefit sharing for BIM implementation: Tackling the moral hazard dilemma in inter-firm cooperation. Int. J. Proj. Manag. 2017, 35, 393–405. [Google Scholar] [CrossRef] [Green Version]
- Du, Y.; Zhou, H.; Yuan, Y.; Xue, H. Exploring the moral hazard evolutionary mechanism for bim implementation in an integrated project team. Sustainability 2019, 11, 5719. [Google Scholar] [CrossRef] [Green Version]
- Jide, S.; Xincheng, W.; Liangfa, S. Research on the mobility behaviour of Chinese construction workers based on evolutionary game theory. Econ. Res. 2018, 31, 1–14. [Google Scholar] [CrossRef]
- Pi, Z.; Gao, X.; Chen, L.; Liu, J. The new path to improve construction safety performance in China: An evolutionary game theoretic approach. Int. J. Environ. Res. Public Heal. 2019, 16, 2443. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, Y.; Zhu, D.; Zhou, L. A game theory analysis of promoting the spongy city construction at the building and community scale. Habitat Int. 2019, 86, 91–100. [Google Scholar] [CrossRef]
- Chen, J.; Hua, C.; Liu, C. Considerations for better construction and demolition waste management: Identifying the decision behaviors of contractors and government departments through a game theory decision-making model. J. Clean. Prod. 2019, 212, 190–199. [Google Scholar] [CrossRef]
- Jide, S.; Xincheng, W.; Liangfa, S. Chinese construction workers’ behaviour towards attending vocational skills trainings: Evolutionary game theory with government participation. J. Differ. Equ. Appl. 2016, 23, 468–485. [Google Scholar] [CrossRef]
- Shi, Q.; Zhu, J.; Li, Q. Cooperative evolutionary game and applications in construction supplier tendency. Complexity 2018, 2018, 8401813. [Google Scholar] [CrossRef]
- Xu, X.; Li, Z.; Wang, J.; Huang, W. Collaboration between designers and contractors to improve building energy performance. J. Clean. Prod. 2019, 219, 20–32. [Google Scholar] [CrossRef]
- Pan, Y.; Deng, X.; Maqbool, R.; Niu, W. Insurance crisis, legal environment, and the sustainability of professional liability insurance market in the construction industry: Based on the US market. Adv. Civ. Eng. 2019, 2019, 1614868. [Google Scholar] [CrossRef] [Green Version]
- Friedman, D. Evolutionary games in economics. Econ. J. Econ. Soc. 1991, 59, 637. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Hu, Z.-H. Using evolutionary game theory to study governments and manufacturers’ behavioral strategies under various carbon taxes and subsidies. J. Clean. Prod. 2018, 201, 123–141. [Google Scholar] [CrossRef]
- Fang, Y.; Chen, L.; Mei, S.; Wei, W.; Huang, S.; Liu, F. Coal or electricity? An evolutionary game approach to investigate fuel choices of urban heat supply systems. Energy 2019, 181, 107–122. [Google Scholar] [CrossRef]








| Variables | Descriptions | Variables | Descriptions |
| x | The proportion of contractors adopting “not default” strategy | y | The proportion of owners adopting “surety bond” strategy |
| Parameters | Descriptions | Parameters | Descriptions |
| Rof | The owners’ revenue from the construction projects if the contractors adopt “not default” strategy | Cof | The owners’ cost on the construction projects if the contractors adopt “not default” strategy |
| Rou | The owners’ revenue from the construction projects if the contractors adopt “default” strategy | Cou | The owners’ cost on the construction projects if the contractors adopt “default” strategy |
| Rcf | The contractors’ revenue from the construction projects if they adopt “not default” strategy | Ccf | The contractors’ cost on the construction projects if they adopt “not default” strategy |
| Rcu | The contractors’ revenue from the construction projects if they adopt “default” strategy | Ccu | The contractors’ cost on the construction projects if they adopt “default” strategy |
| Rcl | The contractors’ long-term revenue from the good reputation in surety bond institutions | Lcl | The contractors’ long-term loss from the poor reputation in surety bond institutions |
| P1 | The contractors’ punishment for default under high-penalty conditional bond | Lou | The owners’ loss resulting from the default of the contractors |
| P2 | The contractors’ punishment for default under low-penalty unconditional bonds | Cs1 | The owners’ cost on the high-penalty conditional bond |
| P3 | The contractors’ reimbursement due to default under high-penalty conditional bond | Cs2 | The owners’ cost on the low-penalty unconditional bond |
| ΔP4 | The bid price reduction under high-penalty conditional bond |
| Contractors | Owners | |
|---|---|---|
| Surety Bond (y) | Not Surety Bond (1 − y) | |
| not default (x) | C11, O11 | C12, O12 |
| default (1 − x) | C21, O21 | C22, O22 |
| Utility | Calculation | Utility | Calculation |
|---|---|---|---|
| C11 | Rcf + Rcl − Ccf | O11 | Rof − Cof − Cs2 |
| C12 | Rcf − Ccf | O12 | Rof − Cof |
| C21 | Rcu − Ccu − P2− Lcl | O21 | Rou + P2 − Cou − Cs2 − Lou |
| C22 | Rcu − Ccu | O22 | Rou − Cou − Lou |
| Variables | Descriptions | Variables | Descriptions |
|---|---|---|---|
| C11 | Rcf + Rcl − Ccf − ΔP4 | O11 | Rof − Cof − Cs1+ ΔP4 |
| C12 | Rcf − Ccf | O12 | Rof − Cof |
| C21 | Rcu − Ccu − P3− P1− Lcl − ΔP4 | O21 | Rof + P1− Cou − Cs1+ ΔP4 |
| C22 | Rcu − Ccu | O22 | Rou − Cou − Lou |
| Equilibrium Points | Rcl + P2+ Lcl < Ccf + Rcu − Rcf − Ccu | Rcl + P2+ Lcl > Ccf + Rcu − Rcf − Ccu | ||||
|---|---|---|---|---|---|---|
| detJ1 | trJ1 | State | detJ1 | trJ1 | State | |
| (0, 0) | − | ± | Saddle point | − | ± | Saddle point |
| (0, 1) | + | − | ESS | − | ± | Saddle point |
| (1, 0) | − | ± | Saddle point | − | ± | Saddle point |
| (1, 1) | + | + | Instability point | − | ± | Saddle point |
| (x1, y1) | / | / | / | + | 0 | Central point |
| Equilibrium Points | Rcl + P3+ P1+ Lcl < Ccf + Rcu − Rcf − Ccu | |||||
| Cs1< ΔP4 | Cs1> ΔP4 | |||||
| detJ2 | trJ2 | State | detJ2 | trJ2 | State | |
| (0, 0) | − | ± | Saddle point | − | ± | Saddle point |
| (0, 1) | + | − | ESS | + | − | ESS |
| (1, 0) | + | + | Instability point | − | ± | Saddle point |
| (1, 1) | − | ± | Saddle point | + | + | Instability point |
| Equilibrium Points | Rcl + P3+ P1+ Lcl > Ccf + Rcu − Rcf − Ccu | |||||
| Cs1< ΔP4 | Cs1> ΔP4 | |||||
| detJ2 | trJ2 | State | detJ2 | trJ2 | State | |
| (0, 0) | − | ± | Saddle point | − | ± | Saddle point |
| (0, 1) | − | ± | Saddle point | − | ± | Saddle point |
| (1, 0) | + | + | Instability point | − | ± | Saddle point |
| (1, 1) | + | − | ESS | − | ± | Saddle point |
| (x2, y2) | / | / | / | + | 0 | Central point |
| Utility | Calculation | Utility | Calculation |
|---|---|---|---|
| C11 | Rcf + Rcl(1 − x) − Ccf | O11 | Rof − Cof − Cs2(1 − qx) |
| C12 | Rcf − Ccf | O12 | Rof − Cof |
| C21 | Rcu − Ccu − P2(1 − nx) − Lcl ∗ x | O21 | Rou + P2(1 − nx) − Cou − Cs2(1 − qx) − Lou |
| C22 | Rcu − Ccu | O22 | Rou − Cou − Lou |
| Variables | Descriptions | Variables | Descriptions |
|---|---|---|---|
| C11 | Rcf + Rcl(1 − x) − Ccf − ΔP4 | O11 | Rof −Cof −Cs1(1 − px) + ΔP4 |
| C12 | Rcf −Ccf | O12 | Rof −Cof |
| C21 | Rcu −Ccu −P3−P1(1 − mx) − Lcl*x − ΔP4 | O21 | Rof + P1(1 − mx) − Cou − Cs1(1 − px) + ΔP4 |
| C22 | Rcu −Ccu | O22 | Rou −Cou −Lou |
| Variables | Descriptions | Variables | Descriptions |
| x | The proportion of contractors adopting “not default” strategy | y | The proportion of owners adopting “surety bond” strategy |
| Parameters | Descriptions | Parameters | Descriptions |
| Rof | The owners’ revenue from the construction projects if the contractors adopt “not default” strategy | Cof | The owners’ cost on the construction projects if the contractors adopt “not default” strategy |
| Rou | The owners’ revenue from the construction projects if the contractors adopt “default” strategy | Cou | The owners’ cost on the construction projects if the contractors adopt “default” strategy |
| Rcf | The contractors’ revenue from the construction projects if they adopt “not default” strategy | Ccf | The contractors’ cost on the construction projects if they adopt “not default” strategy |
| Rcu | The contractors’ revenue from the construction projects if they adopt “default” strategy | Ccu | The contractors’ cost on the construction projects if they adopt “default” strategy |
| Rcl(1 − x) | The contractors’ dynamic long-term revenue from the good reputation in surety bond institutions | Lcl ∗ x | The contractors’ dynamic long-term loss from the poor reputation in surety bond institutions |
| P1(1 − mx), m ∈ [0, 1] | The contractors’ dynamic punishment for default under high-penalty conditional bond | Lou | The owners’ loss resulting from the default of the contractors |
| P2(1 − nx), n ∈ [0, 1] | The contractors’ dynamic punishment for default under low-penalty unconditional bond | Cs1(1 − px), p ∈ [0, 1] | The owners’ dynamic cost on the high-penalty conditional bond |
| P3 | The contractors’ reimbursement due to default under high-penalty conditional bond | Cs2(1 − qx), q ∈ [0, 1] | The owners’ dynamic cost on the low-penalty unconditional bond |
| ΔP4 | The bid price reduction under high-penalty conditional bond |
| Equilibrium Points | P2+ Rcl < Ccf + Rcu − Rcf − Ccu | ||||||
| P2(1 − n) + Lcl < Ccf + Rcu − Rcf − Ccu | P2(1 − n) + Lcl > Ccf + Rcu − Rcf − Ccu | ||||||
| detJ3 | trJ3 | State | detJ3 | trJ3 | State | Special Condition | |
| (0, 0) | − | ± | Saddle point | − | ± | Saddle point | / |
| (0, 1) | + | − | ESS | + | − | ESS | / |
| (1, 0) | − | ± | Saddle point | − | ± | Saddle point | / |
| (1, 1) | + | + | Instability point | − | ± | Saddle point | / |
| (x3, y3) | / | / | / | + | + | Central point | x4 ∈ [0, 1] y3 ∈ [0, 1] |
| (x4, 1) | / | / | / | − | ± | Saddle point | x4 ∈ [0, 1] y3 ∈ [0, 1] |
| (x4, 1) | / | / | / | + | + | Instability point | x4 ∈ [0, 1] y3 ∉ [0, 1] |
| Equilibrium Points | P2+ Rcl > Ccf + Rcu − Rcf − Ccu | ||||||
| P2(1 − n) + Lcl < Ccf + Rcu − Rcf − Ccu | P2(1 − n) + Lcl > Ccf + Rcu − Rcf − Ccu | ||||||
| detJ3 | trJ3 | State | detJ3 | trJ3 | State | Special Condition | |
| (0, 0) | − | ± | Saddle point | − | ± | Saddle point | / |
| (0, 1) | − | ± | Saddle point | − | ± | Saddle point | / |
| (1, 0) | − | ± | Saddle point | − | ± | Saddle point | / |
| (1, 1) | + | + | Instability point | − | ± | Saddle point | / |
| (x3, y3) | + | − | Asymptotic stable point | + | − | Asymptotic stable point | x4 ∈ [0, 1] y3 ∈ [0, 1] Lcl − Rcl2 − Pn < 0 |
| (x3, y3) | / | / | / | + | + | Central point | x4 ∈ [0, 1] y3 ∈ [0, 1] Lcl − Rcl 2 − Pn > 0 |
| (x4, 1) | − | ± | Saddle point | / | / | / | x4 ∈ [0, 1] y3 ∈ [0, 1] |
| (x4, 1) | + | − | ESS | / | / | / | x4 ∈ [0, 1] y3 ∉ [0, 1] |
| Equilibrium Points | P3+ P1+ Rcl < Ccf + Rcu − Rcf − Ccu P3+ P1(1 − m) + Lcl < Ccf + Rcu − Rcf − Ccu | ||||||
| Cs1(1 − p) < ΔP4 | Cs1(1 − p) > ΔP4 | ||||||
| detJ4 | trJ4 | State | detJ4 | trJ4 | State | Special Condition | |
| (0, 0) | − | ± | Saddle point | − | ± | Saddle point | / |
| (0, 1) | + | − | ESS | + | − | ESS | / |
| (1, 0) | + | + | Instability point | − | ± | Saddle point | / |
| (1, 1) | − | ± | Saddle point | + | + | Instability point | / |
| Equilibrium Points | P3+ P1+ Rcl < Ccf + Rcu − Rcf − Ccu P3+ P1(1 − m) + Lcl > Ccf + Rcu − Rcf − Ccu | ||||||
| Cs1(1 − p) < ΔP4 | Cs1(1 − p) > ΔP4 | ||||||
| detJ4 | trJ4 | State | detJ4 | trJ4 | State | Special Condition | |
| (0, 0) | − | ± | Saddle point | − | ± | Saddle point | / |
| (0, 1) | + | − | ESS | + | − | ESS | / |
| (1, 0) | + | + | Instability point | - | ± | Saddle point | / |
| (1, 1) | + | − | ESS | − | ± | Saddle point | / |
| (x5, y5) | / | / | / | + | + | Central point | x6 ∈ [0, 1] y5 ∈ [0, 1] |
| (x6, 1) | − | ± | Saddle point | − | ± | Saddle point | x6 ∈ [0, 1] y5 ∈ [0, 1] |
| (x6, 1) | − | ± | Saddle point | + | + | Instability point | x6 ∈ [0, 1] y5 ∉ [0, 1] |
| Equilibrium Points | P3+ P1+ Rcl > Ccf + Rcu − Rcf − Ccu P3+ P1(1 − m) + Lcl < Ccf + Rcu − Rcf − Ccu | ||||||
| Cs1(1 − p) < ΔP4 | Cs1(1 − p) > ΔP4 | ||||||
| detJ4 | trJ4 | State | detJ4 | trJ4 | State | Special Condition | |
| (0, 0) | − | ± | Saddle point | − | ± | Saddle point | / |
| (0, 1) | − | ± | Saddle point | − | ± | Saddle point | / |
| (1, 0) | + | + | Instability point | − | ± | Saddle point | / |
| (1, 1) | − | ± | Saddle point | + | + | Instability point | / |
| (x5, y5) | / | / | / | + | − | Asymptotic stable point | x6 ∈ [0, 1] y5 ∈ [0, 1] |
| (x6, 1) | + | − | ESS | − | ± | Saddle point | x6 ∈ [0, 1] y5 ∈ [0, 1] |
| (x6, 1) | + | − | ESS | + | − | ESS | x6 ∈ [0, 1] y5 ∉ [0, 1] |
| Equilibrium Points | P3+ P1+ Rcl > Ccf + Rcu − Rcf − Ccu P3+ P1(1 − m) + Lcl > Ccf + Rcu − Rcf − Ccu | ||||||
| Cs1(1 − p) < ΔP4 | Cs1(1 − p) > ΔP4 | ||||||
| detJ4 | trJ4 | State | detJ4 | trJ4 | State | Special Condition | |
| (0, 0) | − | ± | Saddle point | − | ± | Saddle point | / |
| (0, 1) | − | ± | Saddle point | − | ± | Saddle point | / |
| (1, 0) | + | + | Instability point | − | ± | Saddle point | / |
| (1, 1) | + | − | ESS | − | ± | Saddle point | / |
| (x5, y5) | / | / | / | + | − | Asymptotic stable point | Lcl − Rcl − P1m < 0 |
| (x5, y5) | / | / | / | + | + | Central point | Lcl − Rcl − P1m > 0 |
| Variables | Values (Million Dollars) | Variables | Values (Million Dollars) |
| Rcf | 1000 | Ccf | 900 |
| Rcu | 900 | Ccu | 600 |
| Rof | 1100 | P3 | 150 |
| Rou | 300 | Lou | 200 |
| ΔP4 | 30 | P1 | 30 |
| P2 | 110 | Cs2 | 50 |
| Parameters | Values | Parameters | Values |
| p | 0.3 | m | 0.5 |
| q | 0.3 | n | 0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, J.; Deng, X.; Maqbool, R.; Rashid, Y.; Ashfaq, S. Default Behaviors of Contractors under Surety Bond in Construction Industry Based on Evolutionary Game Model. Sustainability 2020, 12, 9162. https://doi.org/10.3390/su12219162
Jing J, Deng X, Maqbool R, Rashid Y, Ashfaq S. Default Behaviors of Contractors under Surety Bond in Construction Industry Based on Evolutionary Game Model. Sustainability. 2020; 12(21):9162. https://doi.org/10.3390/su12219162
Chicago/Turabian StyleJing, Jiabao, Xiaomei Deng, Rashid Maqbool, Yahya Rashid, and Saleha Ashfaq. 2020. "Default Behaviors of Contractors under Surety Bond in Construction Industry Based on Evolutionary Game Model" Sustainability 12, no. 21: 9162. https://doi.org/10.3390/su12219162
APA StyleJing, J., Deng, X., Maqbool, R., Rashid, Y., & Ashfaq, S. (2020). Default Behaviors of Contractors under Surety Bond in Construction Industry Based on Evolutionary Game Model. Sustainability, 12(21), 9162. https://doi.org/10.3390/su12219162





