Tree Ecosystem Services, for Everyone? A Compositional Analysis Approach to Assess the Distribution of Urban Trees as an Indicator of Environmental Justice
Abstract
1. Introduction
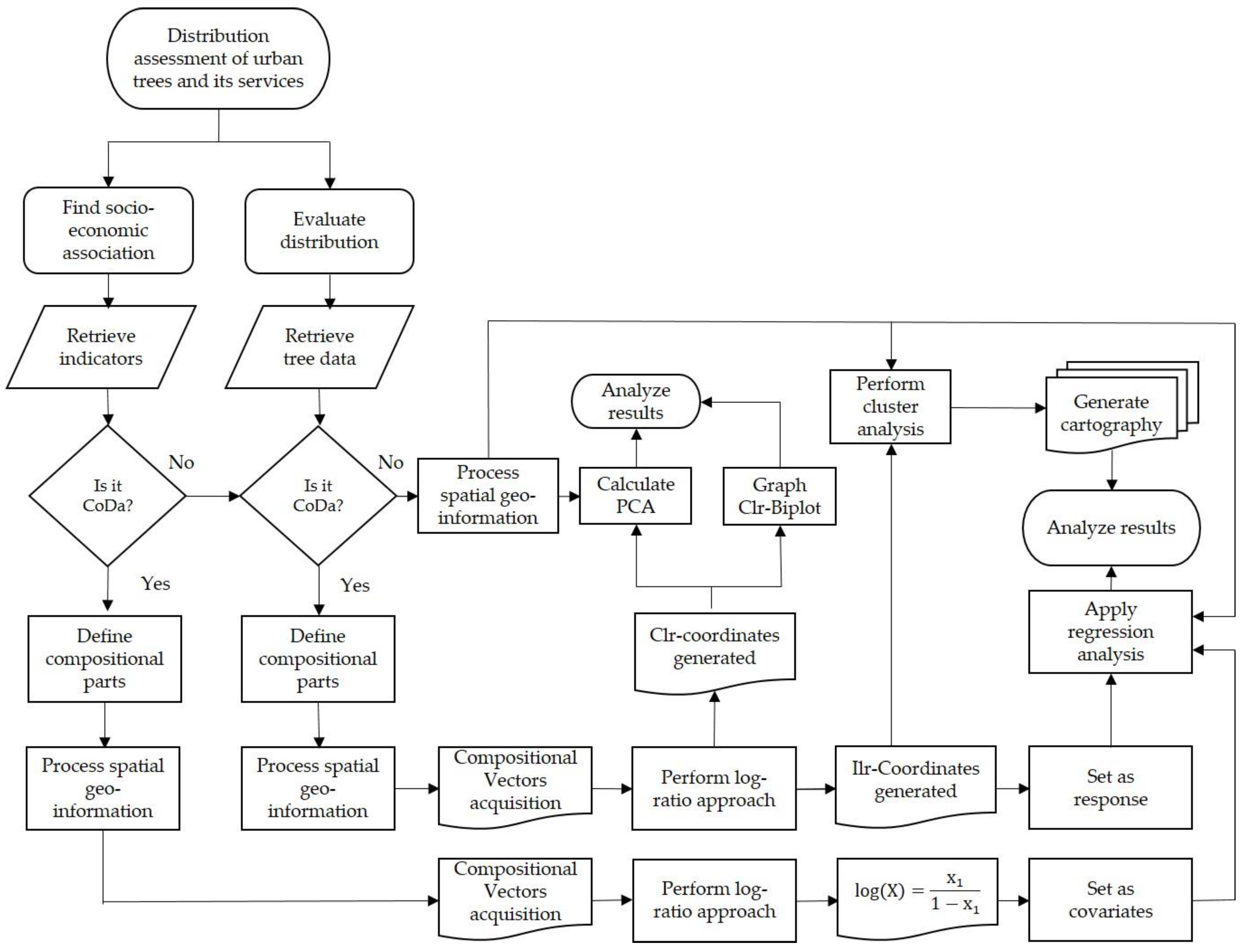
2. Materials and Methods
2.1. Case Study Description: Guadalajara, Jalisco, Mexico
2.2. Datasets
2.3. A Compositional Data Analysis Approach
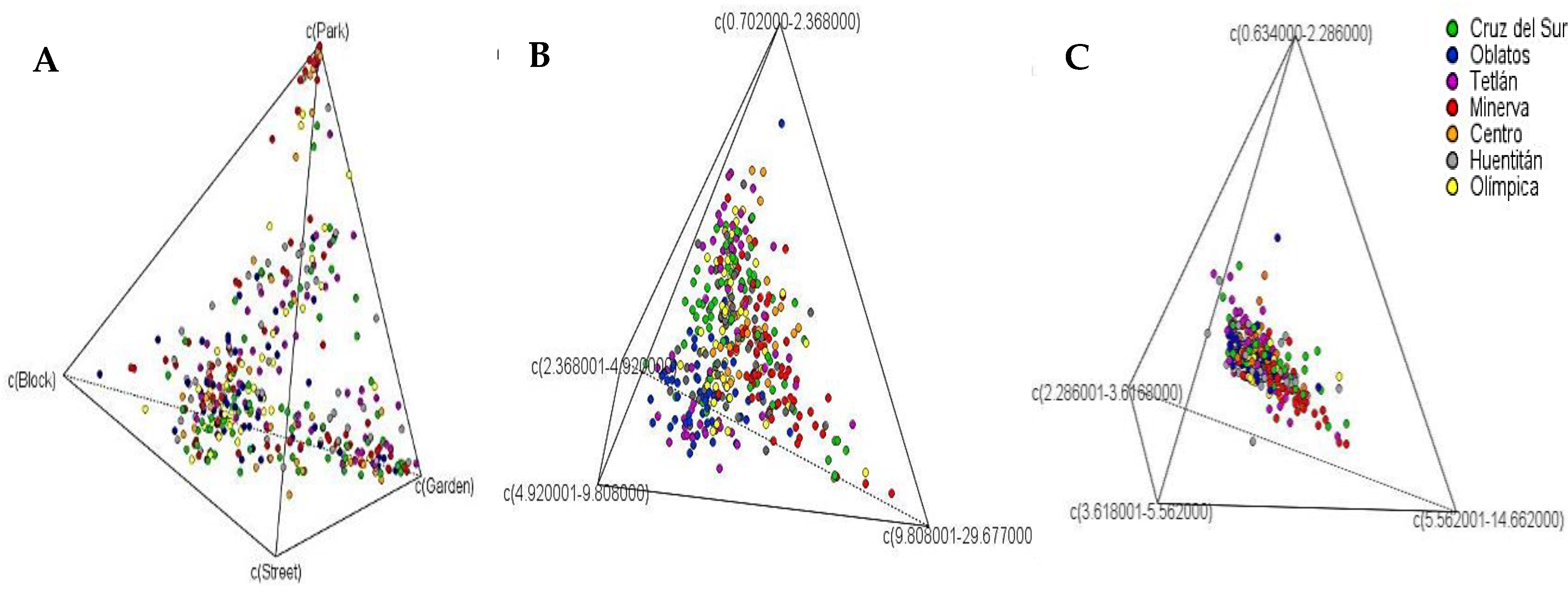
2.4. Simplex Visualization
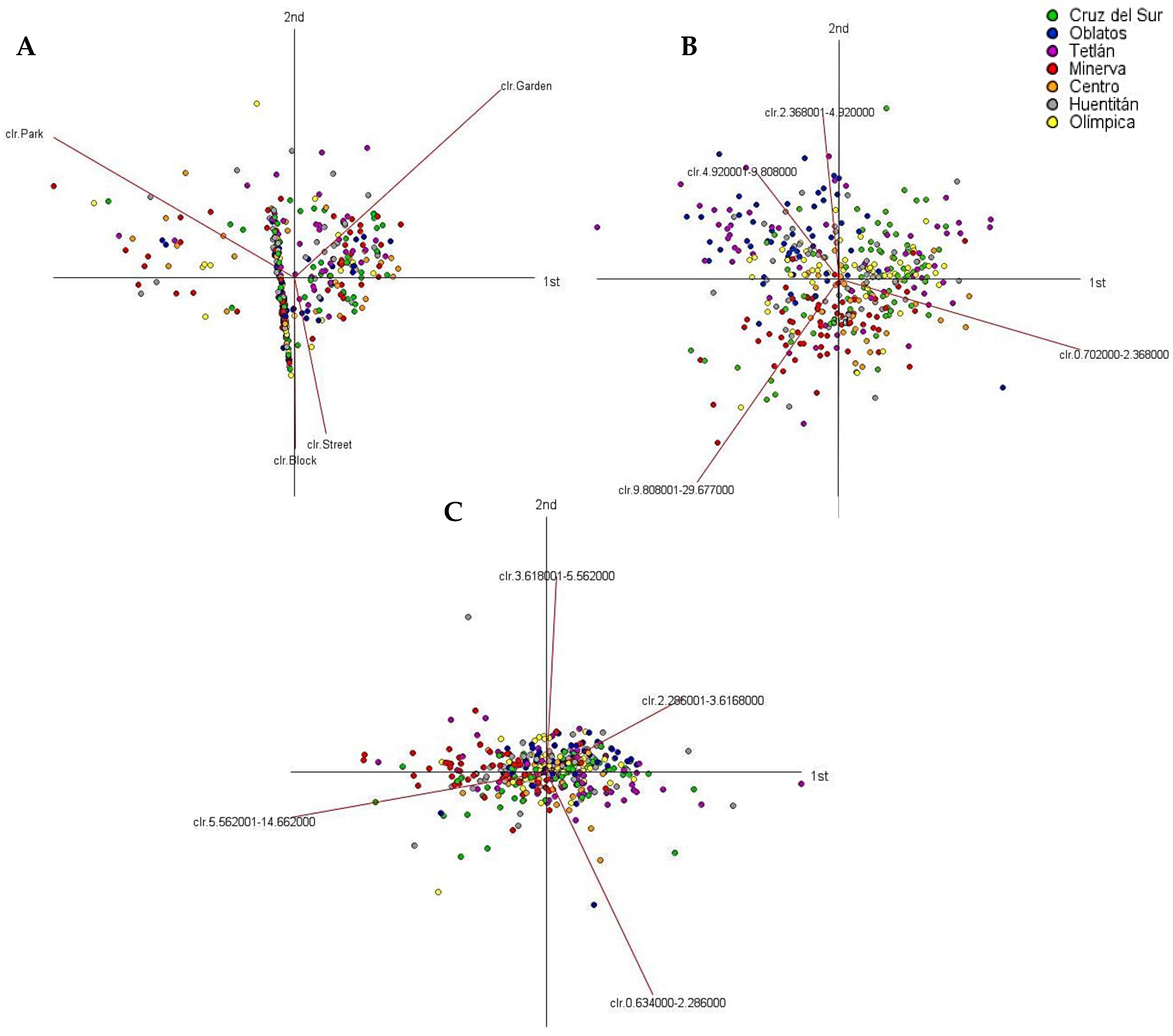
2.5. Principal Component Analysis
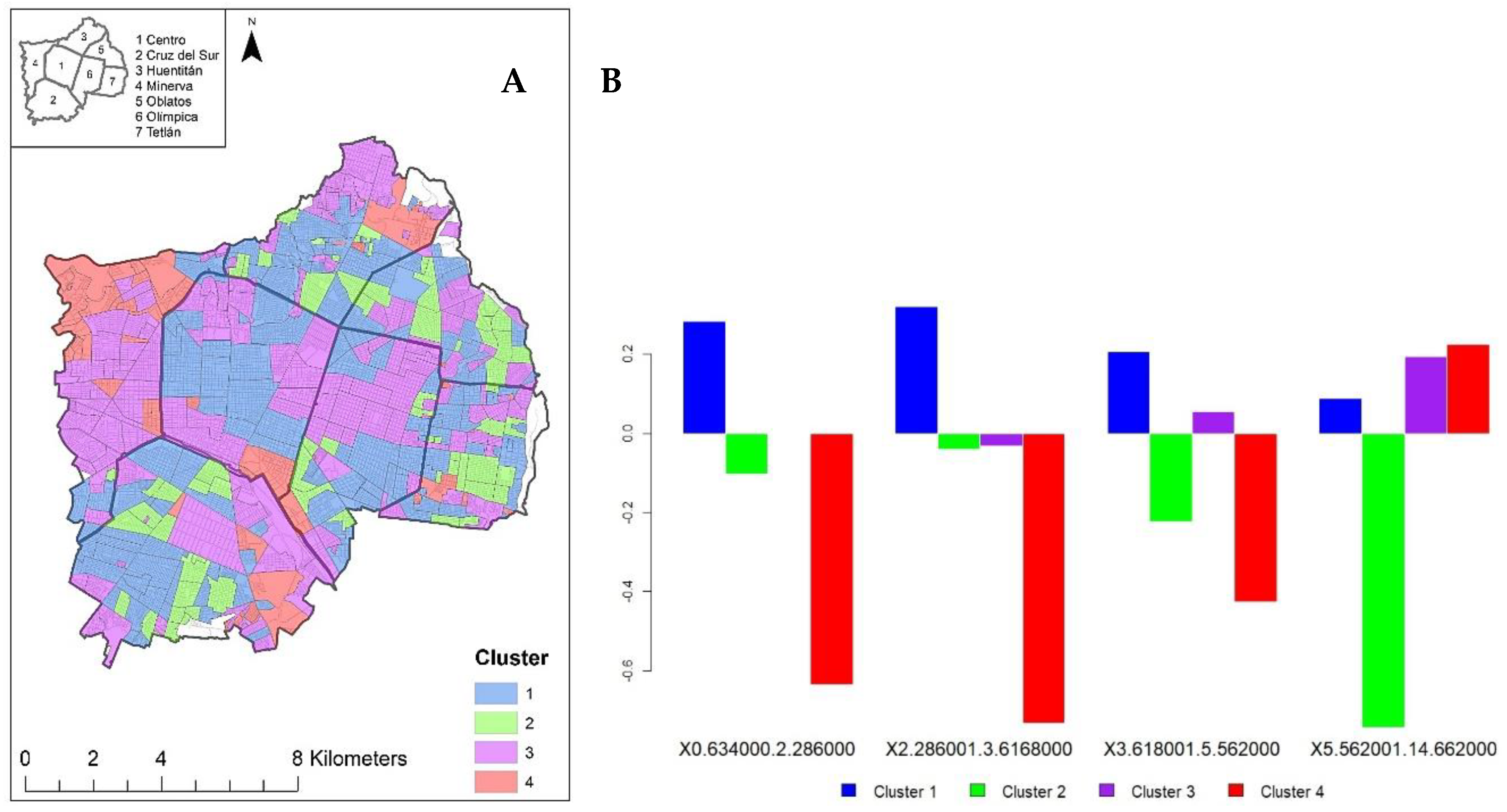
2.6. Cluster Analysis
2.7. Linear Regression
3. Results
3.1. Assessing the Distribution of Urban Trees in Guadalajara
3.2. Characterizing the Neighborhoods of Guadalajara
3.3. Who Is Benefitting from Urban Trees Ecosystem Services in Guadalajara?
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Greenwalt, J.; Raasakka, N.; Alverson, K. Building Urban Resilience to Address Urbanization and Climate Change. In Resilience; Zommers, Z., Alverson, K., Eds.; Elsevier Inc.: Amsterdam, The Netherlands, 2018; pp. 151–164. ISBN 9780128118917. [Google Scholar]
- Liang, L.; Wang, Z.; Li, J. The effect of urbanization on environmental pollution in rapidly developing urban agglomerations. J. Clean. Prod. 2019, 237, 117649. [Google Scholar] [CrossRef]
- Grimm, N.B.; Faeth, S.H.; Golubiewski, N.E.; Redman, C.L.; Wu, J.; Bai, X.; Briggs, J.M. Global change and the ecology of cities. Science 2008, 319, 756–760. [Google Scholar] [CrossRef] [PubMed]
- Cai, W.; Liu, C.; Zhang, C.; Ma, M.; Rao, W.; Li, W.; He, K.; Gao, M. Developing the ecological compensation criterion of industrial solid waste based on emergy for sustainable development. Energy 2018, 157, 940–948. [Google Scholar] [CrossRef]
- Rahmasary, A.N.; Robert, S.; Chang, I.S.; Jing, W.; Park, J.; Bluemling, B.; Koop, S.; van Leeuwen, K. Overcoming the Challenges of Water, Waste and Climate Change in Asian Cities. Environ. Manage. 2019, 63, 520–535. [Google Scholar] [CrossRef]
- Nedved, M.; Jansz, J. Waste water pollution control in the Australian mining industry. J. Clean. Prod. 2006, 14, 1118–1120. [Google Scholar] [CrossRef]
- Hassan Rashid, M.A.U.; Manzoor, M.M.; Mukhtar, S. Urbanization and its effects on water resources: An exploratory analysis. Asian J. Water, Environ. Pollut. 2018, 15, 67–74. [Google Scholar] [CrossRef]
- Lin, B.; Zhu, J. Changes in urban air quality during urbanization in China. J. Clean. Prod. 2018, 188, 312–321. [Google Scholar] [CrossRef]
- Ponce, P.; Alvarado, R. Air pollution, output, FDI, trade openness, and urbanization: Evidence using DOLS and PDOLS cointegration techniques and causality. Environ. Sci. Pollut. Res. 2019, 26, 19843–19858. [Google Scholar] [CrossRef]
- Hodgkins, G.A.; Dudley, R.W.; Archfield, S.A.; Renard, B. Effects of climate, regulation, and urbanization on historical flood trends in the United States. J. Hydrol. 2019, 573, 697–709. [Google Scholar] [CrossRef]
- Huang, G. A Revisit to Impact of Urbanization on Flooding. In Urban Planning and Water-Related Disaster Management; Huang, G., Shen, Z., Eds.; Springer: Cham, Germany; pp. 43–56. ISBN 978-3-319-90172-5.
- Li, G.; Zhang, X.; Mirzaei, P.A.; Zhang, J.; Zhao, Z. Urban heat island effect of a typical valley city in China: Responds to the global warming and rapid urbanization. Sustain. Cities Soc. 2018, 38, 736–745. [Google Scholar] [CrossRef]
- Goddard, I.L.M.; Tett, S.F.B. How much has urbanisation affected United Kingdom temperatures? Atmos. Sci. Lett. 2019, 20, 1–6. [Google Scholar] [CrossRef]
- Lafortezza, R.; Sanesi, G. Nature-based solutions: Settling the issue of sustainable urbanization. Environ. Res. 2019, 394–398. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.; Qian, J.; Tao, Y.; Hu, F.; Ou, W. Evaluating spatial priority of urban green infrastructure for urban sustainability in areas of rapid urbanization: A case study of Pukou in China. Sustainability 2018, 10, 327. [Google Scholar] [CrossRef]
- United Nations Sustainable Development Goals. Available online: https://sustainabledevelopment.un.org/?menu=1300 (accessed on 5 July 2019).
- De Sousa, S.; Panagopoulos, T. Environmental Justice in Accessibility to Green. Land 2018, 7, 1–23. [Google Scholar]
- Wolch, J.R.; Byrne, J.; Newell, J.P. Urban green space, public health, and environmental justice: The challenge of making cities ‘just green enough’. Landsc. Urban Plan. 2014, 125, 234–244. [Google Scholar] [CrossRef]
- Cole, H.V.S.; Triguero-mas, M.; Connolly, J.J.T.; Anguelovski, I. Determining the health bene fi ts of green space: Does gentri fi cation matter? Health Place 2019, 57, 1–11. [Google Scholar] [CrossRef]
- Russo, A.; J Escobedo, F.; Zerbe, S. Quantifying the local-scale ecosystem services provided by urban treed streetscapes in Bolzano, Italy. AIMS Environ. Sci. 2016, 3, 58–76. [Google Scholar] [CrossRef]
- Ziter, C.D.; Pedersen, E.J.; Kucharik, C.J.; Turner, M.G. Scale-dependent interactions between tree canopy cover and impervious surfaces reduce daytime urban heat during summer. Proc. Natl. Acad. Sci. USA 2019, 1–6. [Google Scholar] [CrossRef]
- Duncan, J.M.A.; Boruff, B.; Saunders, A.; Sun, Q.; Hurley, J.; Amati, M. Science of the Total Environment Turning down the heat: An enhanced understanding of the relationship between urban vegetation and surface temperature at the city scale. Sci. Total Environ. 2019, 656, 118–128. [Google Scholar] [CrossRef]
- Zhang, B.; Xie, G.; Zhang, C.; Zhang, J. The economic benefits of rainwater-runoff reduction by urban green spaces: A case study in Beijing, China. J. Environ. Manage. 2012, 100, 65–71. [Google Scholar] [CrossRef]
- Oke, T.R.; Crowther, J.M.; Mcnaughton, K.G.; Monteith, J.L.; Gardiner, B. The Micrometeorology of the Urban Forest [ and Discussion ]. Philos. Trans. R. Soc. B 1989, 324, 335–349. [Google Scholar]
- Kercher, G.J. Anglin 22 Benefits of Urban Street Trees. Available online: https://www.pleasanthilliowa.org/DocumentCenter/View/511/22-Benefits-of-Urban-Street-Trees?bidId= (accessed on 20 July 2019).
- De Carvalho, R.M.; Szlafsztein, C.F. Urban vegetation loss and ecosystem services: The influence on climate regulation and noise and air pollution. Environ. Pollut. 2019. [Google Scholar] [CrossRef] [PubMed]
- Guo, T.; Morgenroth, J.; Conway, T. To plant, remove, or retain: Understanding property owner decisions about trees during redevelopment. Landsc. Urban Plan. 2019, 190, 103601. [Google Scholar] [CrossRef]
- Sander, H.; Polasky, S.; Haight, R.G. The value of urban tree cover: A hedonic property price model in Ramsey and Dakota. Ecol. Econ. 2010, 69, 1646–1656. [Google Scholar] [CrossRef]
- Burley, B.A. Green infrastructure and violence: Do new street trees mitigate violent crime? Health Place 2018, 54, 43–49. [Google Scholar] [CrossRef]
- Wolf, K.L. Freeway roadside management: The urban forest beyond the white line. J. Arboric. 2003, 29, 127–136. [Google Scholar]
- Wolf, K.L. Business District Streetscapes, Trees, and Consumer Response. J. For. 2001, 103, 396–400. [Google Scholar]
- Kweon, B.; Sullivan, W.C.; Wiley, A.R. Green common spaces and the social integration of inner-city older adults. Environ. Behav. 1998, 832–858. [Google Scholar] [CrossRef]
- Takano, T.; Nakamura, K.; Watanabe, M. Urban residential environments and senior citizens’ longevity in megacity areas: The importance of walkable green spaces. J. Epidemiol. Community Health 2002. [Google Scholar] [CrossRef]
- Kardan, O.; Gozdyra, P.; Misic, B.; Moola, F.; Palmer, L.J.; Paus, T. Neighborhood greenspace and health in a large urban center. Sci. Rep. 2015, 5, 11610. [Google Scholar] [CrossRef]
- Anguelovski, I.; Connolly, J.J.T.; Masip, L.; Pearsall, H.; Anguelovski, I.; Connolly, J.J.T.; Masip, L.; Pearsall, H.; Anguelovski, I. Assessing green gentrification in historically disenfranchised neighborhoods: A longitudinal and spatial analysis of Barcelona Barcelona. Urban Geogr. 2017, 39, 458–491. [Google Scholar] [CrossRef]
- Gould, K.A.; Lewis, T.L. Green Gentrification. Urban Sustainability and the Struggle for Environmental Justice, 1st ed.; Agyeman, J., Patel, Z., Eds.; Routledge.Taylor & Francis Group: New York, NY, USA, 2017; ISBN 978-1-138-92016-3. [Google Scholar]
- Anguelovski, I.; Irazábal-Zurita, C.; Connolly, J.J.T. Grabbed Urban Landscapes: Socio-spatial Tensions in Green Infrastructure Planning in Medellín. Int. J. Urban Reg. Res. 2019, 43, 133–156. [Google Scholar] [CrossRef]
- Checker, M. Wiped Out by the “Greenwave”: Environmental Gentrification and the Paradoxical Politics of Urban Sustainability. City Soc. 2011, 23, 210–229. [Google Scholar] [CrossRef]
- Schwarz, K.; Fragkias, M.; Boone, C.G.; Zhou, W.; McHale, M.; Grove, J.M.; O’Neil-Dunne, J.; McFadden, J.P.; Buckley, G.L.; Childers, D.; et al. Trees grow on money: Urban tree canopy cover and environmental justice. PLoS ONE 2015, 10, e0122051. [Google Scholar] [CrossRef]
- Byrne, J.; Wolch, J. Nature, race, and parks: Past research and future directions for geographic research. Prog. Hum. Geogr. 2009, 33, 743–765. [Google Scholar] [CrossRef]
- Carmichael, C.E.; McDonough, M.H. Community Stories: Explaining Resistance to Street Tree-Planting Programs in Detroit, Michigan, USA. Soc. Nat. Resour. 2019, 32, 588–605. [Google Scholar] [CrossRef]
- Baró, F.; Calderón-Argelich, A.; Langemeyer, J.; Connolly, J.J.T. Under one canopy? Assessing the distributional environmental justice implications of street tree benefits in Barcelona. Environ. Sci. Policy 2019, 102, 54–64. [Google Scholar] [CrossRef]
- Park, Y.M.; Kwan, M.P. Multi-contextual segregation and environmental justice research: Toward fine-scale spatiotemporal approaches. Int. J. Environ. Res. Public Health 2017, 14, 1205. [Google Scholar]
- Landry, S.M.; Chakraborty, J. Street trees and equity: Evaluating the spatial distribution of an urban amenity. Environ. Plan. 2009, 41, 2651–2671. [Google Scholar] [CrossRef]
- Maroko, A.R.; Maantay, J.A.; Sohler, N.L.; Grady, K.L.; Arno, P.S. The complexities of measuring access to parks and physical activity sites in New York City: A quantitative and qualitative approach. Int. J. Health Geogr. 2009, 23, 1–23. [Google Scholar] [CrossRef]
- Coen, S.E.; Ross, N.A. Exploring the material basis for health: Characteristics of parks in Montreal neighborhoods with contrasting health outcomes. Health Place 2006, 12, 361–371. [Google Scholar] [CrossRef] [PubMed]
- Lewis, T.L. Global Civil Society and the distribution of environmental goods: Funding for environmental NGO’s in Ecuador. In Inequalities, Environmental Beyond Borders. Local Perspectives on Global Injustices; Joann, C., Agyeman, J., Eds.; The MIT Press: Cambridge, MA, USA, 2011; pp. 88–104. ISBN 9780262015516. [Google Scholar]
- Gould, K.A.; Lewis, T.L. From Green Gentrification to Resilience Gentrification: An Example from Brooklyn 1. City Community 2018, 12–15. [Google Scholar] [CrossRef]
- Scopelliti, M.; Carrus, G.; Adinolfi, C.; Suarez, G.; Colangelo, G.; Lafortezza, R. Staying in touch with nature and well-being in different income groups: The experience of urban parks in Bogotá. Landsc. Urban PLa 2016, 148, 139–148. [Google Scholar] [CrossRef]
- Zhou, X.; Kim, J. Social disparities in tree canopy and park accessibility: A case study of six cities in Illinois using GIS and remote sensing. Urban For. Urban Green. 2013, 12, 88–97. [Google Scholar] [CrossRef]
- Chuang, W.-C.; Boone, C.G.; Locke, D.H.; Grove, J.M.; Whitmer, A.L.; Geoffrey, B.; Zhang, S. Tree canopy Change and neighborhood stability: A Comparative Analysis of Washington, DC and Baltimore, MD. Urban For. Urban Green. 2017, 27, 363–372. [Google Scholar] [CrossRef]
- Krafft, J.; Fryd, O. Spatiotemporal patterns of tree canopy cover and socioeconomics in Melbourne. Urban For. Urban Green. 2016, 15, 45–52. [Google Scholar] [CrossRef]
- Hernández, H.J.; Villaseñor, N.R. Twelve-year change in tree diversity and spatial segregation in the Mediterranean city of Santiago, Chile. Urban For. Urban Green. 2018, 29, 10–18. [Google Scholar] [CrossRef]
- Wang, H.; Qiu, F. Spatial disparities in neighborhood public tree coverage: Do modes of transportation matter? Urban For. Urban Green. 2018, 29, 58–67. [Google Scholar] [CrossRef]
- Cole, H.V.S.; Lamarca, M.G.; Connolly, J.J.T.; Anguelovski, I.; Hospital, I. Are green cities healthy and equitable? Unpacking the relationship between health, green space and gentrification. Epidemiol Community Heal. 2017, 71, 1118–1121. [Google Scholar] [CrossRef]
- Mills, J.R.; Cunningham, P.; Donovan, G.H. Urban forests and social inequality in the Pacific Northwest. Urban For. Urban Green. 2016, 16, 188–196. [Google Scholar] [CrossRef]
- Pawlowsky-Glahn, V.; Egozcue, J.J. Compositional data and their analysis: An introduction. In Compositional Data Anlaysis in the Geosciences. From Theory to Practice; Buccianti, A., Mateu-Figueras, G., Paw, Eds.; The Geological Society: London, UK, 2006; pp. 1–10. ISBN 1-86239-205-6. [Google Scholar]
- Filzmoser, P.; Hron, K.; Templ, M. Applied Compositional Data Analysis, 1st ed.; Diggle, P., Gather Ursula, Z.S., Eds.; Springer Series in Statistics: Cham, Switzerland, 2018; ISBN 978-3-319-96420-1. [Google Scholar]
- Marcillo-Delgado, J.C.; Ortego, M.I.; Pérez-Foguet, A. A compositional approach for modelling SDG7 indicators: Case study applied to electricity access. Renew. Sustain. Energy Rev. 2019, 107, 388–398. [Google Scholar] [CrossRef]
- IMEPLAN. Area metropolitana de Guadalajara, Expansión urbana, Análisis y prospectiva: 1970–2045, 1st ed.; Orozco, A., Shalisko, V., Rodríguez, M., Hernández, D., Morfín, J., Chávez, R., Eds.; Editoriales e Industrias Creativas de México SA de CV: Guadalajara, Mexico, 2015; Volume 1. [Google Scholar]
- Government of Guadalajara. Plan Municipal de Desarrollo y Gobernanza 2018–2021; Government of Guadalajara: Guadalajara, Mexico, 2018.
- Government of Guadalajara. Plan Municipal de Desarrollo Guadalajara 2015–2018, 500 Visión 2042; Government of Guadalajara: Guadalajara, Mexico, 2016; Volume II.
- Government of Guadalajara. Online Mapping Service of the Government of Guadalajara. Available online: https://mapa.guadalajara.gob.mx/ (accessed on 1 May 2019).
- ESRI ArcMap, version 10.2.2, ArcGIS Desktop. Eris: Redlands, CA, USA, 2013.
- ESRI Natural Ruptures (Jenks). Available online: https://pro.arcgis.com/es/pro-app/help/mapping/layer-properties/data-classification-methods.htm (accessed on 1 August 2019).
- Government of Guadalajara GeoGDL. Available online: https://mapa.guadalajara.gob.mx/geomap (accessed on 5 June 2019).
- INEGI Cartografía geoestadística urbana, Cierre del Censo de Población y Vivienda 2010. Guadalajara. Available online: https://www.inegi.org.mx/app/biblioteca/ficha.html?upc=702825588335 (accessed on 25 January 2020).
- INEGI Sistema para la Consulta de Información Censal 2010. Available online: http://gaia.inegi.org.mx/scince2/viewer.html (accessed on 1 May 2019).
- UN-Habitat. Planning and Design for Sustainable Urban Mobility. Global Report on Human Settlements, 1st ed.; Routledge: Abingdon, UK, 2013; ISBN 9780415723183. [Google Scholar]
- INEGI Principales resultados por AGEB y manzana urbana. Instituto Nacional de Estadística Geografía e Informática. Censo Población y Vivienda 2010, 1–19.
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2014. [Google Scholar]
- RStudio Team. RStudio: Integrated Development Environment for R; R Foundation for Statistical Computing: Vienna, Austria, 2016. [Google Scholar]
- Comas-Cufí, M.; Thió-Henestrosa, S. CoDaPack 2.0: A stand-alone, multi-platform compositional software. In Proceedings of the CoDaWork’11: 4th International Workshop on Compositional Data Analysis, Sant Feliu de Guíxols, Spain, 9–13 May 2011. [Google Scholar]
- Egozcue, J.J. Reply to “On the Harker vriation diagrams;...” by J.A. Cortés. Math. Geosci. 2009, 41, 829–834. [Google Scholar] [CrossRef]
- Pawlowsky-Glahn, V.; Egozcue, J.J.; Tolosana-Delgado, R. Modeling and Analysis of Compositional Data, 1st ed.; John Wiley & Sons: London, UK, 2015; ISBN 9783540773405. [Google Scholar]
- Pearson, K. Mathematical Contributions to the Theory of Evolution.—On a Form of Spurious Correlation Which May Arise When Indices Are Used in the Measurement of Organs. Proc. R. Soc. London 1896, 60, 489–498. [Google Scholar]
- Chayes, F. Ratio Correlation: A Manual for Students of Petrology and Geochemistry; University of Chicago Press: Chicago, IL, USA, 1971. [Google Scholar]
- Aitchison, J. The Statistical Analysis of Geochemical Compositions. Math. Geol. 1984, 16, 15–18. [Google Scholar] [CrossRef]
- Aitchison, J. The Statistical Analysis of Compositional Data. Monographs on Satistics and Applied Probability, Chapman & Hall Ltd, Ed.; 1st ed.; Springer: London, UK, 1986; ISBN 978-0412280603. [Google Scholar]
- Rock, N.M.S. Lecture Notes in Earth Sciences; Bhattacharji, S., Friedmand, G.M., Neugebauer, H.J., SeilacherAdolf, Eds.; Springer-Verlag New York Inc.: Nedlands, Western Australia, 1988. [Google Scholar]
- Rollinson, H.R. Another look at the constant sum problem in geochemistry. Mineral. Mag. 1992, 56, 469–475. [Google Scholar] [CrossRef]
- Martín-Fernández, J.A.; Palarea-Albaladejo, J.; Olea, R.A. Dealing with Zeros. In Compositional Data Anlaysis: Theory and Applications; Pawlowsky-Glahn, V., Buccianti, A., Eds.; Wiley: Hoboken, NJ, USA, 2011; pp. 43–58. [Google Scholar]
- Egozcue, J.J.; Pawlowsky-Glahn, V.; Mateu-Figueras, G.; Barceló-Vidal, C. Isometric Logratio Transformations for Compositional Data Analysis. Math. Geol. 2003, 35, 279–300. [Google Scholar] [CrossRef]
- O’Sullivan, D.; Unwin, D. Reducing the number of variables: Principal Component Analysis. In Geographic Information Analysis; John Wiley & Sons, Ed.; Wiley: Hoboken, NJ, USA, 2002; pp. 343–355. ISBN 0471211761, 9780471211761. [Google Scholar]
- Gabriel, K.R. The Biplot Graphic Display of Matrices with application to Principal Component Analysis. Biometrika 1971, 58, 453–467. [Google Scholar] [CrossRef]
- Aitchison, J. The one-hour course in compositional data analysis or compositional data analysis is simple. In Proceedings of the IAMG’97—The 3rd Annual Conference of the International Association for Mathematical Geology, Barcelona, Spain, 22–27 September 1997. [Google Scholar]
- Daunis-i-Estadella, J.; Thió-Henestrosa, S.; Mateu-Figueras, G. Computers & Geosciences Including supplementary elements in a compositional biplot. Comput. Geosci. 2011, 37, 696–701. [Google Scholar]
- Murtagh, F.; Legendre, P. Ward’s Hierarchical Agglomerative Clustering Method: Which Algorithms Implement Ward’s Criterion? J. Classif. 2014, 31, 274–295. [Google Scholar] [CrossRef]
- Egozcue, J.J.; Pawlowsky-Glahn, V. Groups of Parts and Their Balances in Compositional Data Analysis. Math. Geol. 2005, 37, 795–828. [Google Scholar] [CrossRef]
- Roy, S.; Byrne, J.; Pickering, C. A systematic quantitative review of urban tree benefits, costs, and assessment methods across cities in different climatic zones. Urban For. Urban Green. 2012, 11, 351–363. [Google Scholar] [CrossRef]
- López, E. La cuadrícula en el desarrollo de la ciudad hispanoamericana. Guadalajara, México; Universidad de Guadalajara. Instituto Tecnológico y de Estudios Superiores de Occidente: Guadalajara, Mexico, 2001. [Google Scholar]
- Cabrales, L.F.; Canosa, E. Segregación residencial y fragmentación urbana: Los fraccionamientos cerrados en Guadalajara. Espiral 2001, VII, 223–253. [Google Scholar] [CrossRef]
- Brandis-García, D.; Mas-Hernández, R. Propiedad inmueble, morfología urbana y precios del suelo en Guadalajara (siglo XIX). Tiempos de América 1997, 1, 57–69. [Google Scholar]
- Cabrales, L.F.; Chong, M.A. Divide y venderás: Promoción inmobiliaria del barrio de Artesanos de Guadalajara, 1898–1908. Scr. Nov. Rev. Electrónica Geogr. y Ciencias Soc. 2006, X, 741–798. [Google Scholar]
- Aguilar, A.G.; Escamilla, I.H. Segregación urbana y espacios de exclusión. Ejemplos de México y América Latina; Universidad Nacional Autónoma de México, UNAM. MAPorrúa: Mexico City, Mexico, 2015; ISBN 978-607-401-963-6. [Google Scholar]
- Cobos, E.P. La ciudad capitalista en el patrón neoliberal de acumulación en América Latina TT—The capitalist city in the neoliberal pattern of accumulation in Latin America. Cad. Metrópole 2014, 16, 37–60. [Google Scholar] [CrossRef]
- Guevara, T. Abordajes teóricos sobre las transformaciones sociales, económicas y territoriales en las ciudades latinoamericanas contemporáneas. Eure 2015, 41, 5–24. [Google Scholar] [CrossRef]
- Marrufo, R.M.; Bass, S. Segregación socioespacial y servicios de salud en Ciudad Juáres. In Segregación Urbana y Espacios de Exclusión; Ejemplos de México y América Latina; Aguilar, A.G., Escamilla, H.I., Eds.; Universidad Nacional Autónoma de México.Miguel Ángel Porrúa: Mexico City, Mexico, 2015; pp. 139–162. [Google Scholar]
- Moreno, O. Insustentabilidad de la vida, segregación social y pobreza urbana: Efectos de las políticas de vivienda en la era del ultraliberalismo. In Segregación Urbana y Espacios de Exclusión; Ejemplos de México y América Latina; Aguilar, A.G., Escamilla, H.I., Eds.; Universidad Nacional Autónoma de México.Miguel Ángel Porrúa: Mexico City, Mexico, 2015; pp. 307–328. [Google Scholar]
- González-Rodriguez, S.M. Las políticas urbanas de inclusión socio-espacial de la zona nor-oriente de la ciudad de Guadalajara, algunas reflexiones. Periodo 2010–2012. In Proceedings of the International Conference Virtual City and Territory. "9° Congresso Città e Territorio Virtuale, Rome, Italy, 2–4 October 2013; pp. 1470–1484. [Google Scholar]
- Danford, R.S.; Strohbach, M.W.; Ryan, R.; Nicolson, C.; Warren, P.S. What does it take to achieve equitable urban tree canopy distribution? A Boston case study. Cities Environ. 2014, 7, 1–20. [Google Scholar]




| Abbreviation | Definition |
|---|---|
| VPH_AU | Private households with an automobile |
| VPH_PC | Private households with a computer |
| VPH_CE | Private households with a cellphone |
| VPH_IN | Private households with Internet service |
| By Location Type | |||
| 1 Street | 2 Block | 3 Park | 4 Garden |
| By Height [m] | |||
| Int1 = 0.70–2.36 | Int2 = 2.36–4.92 | Int3 = 4.92–9.80 | Int4 = 9.80–29.67 |
| By Diameter [m] | |||
| Int1 = 0.63–2.28 | Int2 = 2.28–3.61 | Int3 = 3.61–5.56 | Int4 = 5.56–14.66 |
| By Location Type | ||||
| Order | X1 | X2 | X3 | X4 |
| (Street) | (Block) | (Park) | (Garden) | |
| 1 | +1 | +1 | −1 | −1 |
| 2 | +1 | −1 | 0 | 0 |
| 3 | 0 | 0 | +1 | −1 |
| By Height | ||||
| Order | X1 (Int1) | X2 (Int2) | X3 (Int3) | X4 (Int4) |
| 1 | −1 | −1 | +1 | +1 |
| 2 | 0 | 0 | −1 | +1 |
| 3 | −1 | +1 | 0 | 0 |
| By Diameter | ||||
| Order | X1 (Int1) | X2 (Int2) | X3 (Int3) | X4 (Int4) |
| 1 | −1 | −1 | +1 | +1 |
| 2 | 0 | 0 | −1 | +1 |
| 3 | −1 | +1 | 0 | 0 |
| Covariates m | Definition |
|---|---|
| RelVPH_AU | Log-ratio of private households with an automobile, divided by those without. |
| RelVPH_PC | Log-ratio of private households with a computer, divided by those without. |
| RelVPH_CE | Log-ratio of private households with a cellphone, divided by those without. |
| RelVPH_IN | Log-ratio of private households with internet service, divided by those without. |
| Model | - | β | t | p |
| RelVPH_AU | - | 0.483 | 1.876 | ns |
| RelVPH_PC | - | −0.846 | −1.073 | ns |
| RelVPH_CE | - | −0.909 | −2.818 | 0.005 |
| RelVPH_IN | - | 0.223 | 0.337 | ns |
| Model | - | β | t | p |
| RelVPH_AU | - | 0.366 | 2.486 | 0.013 |
| RelVPH_PC | - | 0.360 | 0.797 | ns |
| RelVPH_CE | - | −0.425 | −2.301 | 0.021 |
| RelVPH_IN | - | −0.558 | −1.472 | ns |
| Model | - | β | t | p |
| RelVPH_AU | - | 0.167 | 0.522 | ns |
| RelVPH_PC | - | −0.476 | −0.484 | ns |
| RelVPH_CE | - | −0.284 | −0.707 | ns |
| RelVPH_IN | - | 0.195 | 0.237 | ns |
| Model fit | R | R2 | F | p |
| 0.078 | 0.069 | 8.31 | 0.000 | |
| 0.026 | 0.016 | 2.65 | 0.032 | |
| 0.008 | −0.001 | 0.873 | ns |
| Model | - | β | t | p |
| RelVPH_AU | - | −0.069 | −0.538 | ns |
| RelVPH_PC | - | −0.753 | −1.899 | 0.05 |
| RelVPH_CE | - | 0.179 | 1.108 | ns |
| RelVPH_IN | - | 0.618 | 1.857 | ns |
| Model | - | β | t | p |
| RelVPH_AU | - | −0.671 | −7.386 | 0.000 |
| RelVPH_PC | - | 0.465 | 1.673 | ns |
| RelVPH_CE | - | 0.002 | 0.025 | ns |
| RelVPH_IN | - | 0.410 | 1.755 | ns |
| Model | - | β | T | p |
| RelVPH_AU | - | 0.391 | 3.643 | 0.000 |
| RelVPH_PC | - | −0.294 | −0.894 | ns |
| RelVPH_CE | - | 0.240 | 1.786 | ns |
| RelVPH_IN | - | −0.371 | −1.347 | ns |
| Model fit | R | R2 | F | p |
| 0.011 | 0.001 | 1.145 | ns | |
| 0.322 | 0.315 | 46.32 | 0.000 | |
| 0.200 | 0.191 | 24.4 | 0.000 |
| Model | - | β | t | p |
| RelVPH_AU | - | −0.071 | −1.029 | ns |
| RelVPH_PC | - | −0.361 | −1.699 | ns |
| RelVPH_CE | - | −0.032 | −0.375 | ns |
| RelVPH_IN | - | 0.492 | 2.762 | 0.006 |
| Model | - | β | t | p |
| RelVPH_AU | - | −0.243 | −4.409 | 0.000 |
| RelVPH_PC | - | −0.206 | −1.219 | ns |
| RelVPH_CE | - | −0.005 | −0.084 | ns |
| RelVPH_IN | - | 0.441 | 3.106 | 0.002 |
| Model | - | β | t | p |
| RelVPH_AU | - | 0.039 | 1.261 | ns |
| RelVPH_PC | - | −0.023 | −0.238 | ns |
| RelVPH_CE | - | 0.062 | 1.583 | ns |
| RelVPH_IN | - | −0.012 | −0.155 | ns |
| Model fit | R | R2 | F | p |
| 0.094 | 0.084 | 10.14 | 0.000 | |
| 0.131 | 0.122 | 14.70 | 0.000 | |
| 0.024 | 0.014 | 2.40 | 0.049 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cruz-Sandoval, M.; Ortego, M.I.; Roca, E. Tree Ecosystem Services, for Everyone? A Compositional Analysis Approach to Assess the Distribution of Urban Trees as an Indicator of Environmental Justice. Sustainability 2020, 12, 1215. https://doi.org/10.3390/su12031215
Cruz-Sandoval M, Ortego MI, Roca E. Tree Ecosystem Services, for Everyone? A Compositional Analysis Approach to Assess the Distribution of Urban Trees as an Indicator of Environmental Justice. Sustainability. 2020; 12(3):1215. https://doi.org/10.3390/su12031215
Chicago/Turabian StyleCruz-Sandoval, Marco, María Isabel Ortego, and Elisabet Roca. 2020. "Tree Ecosystem Services, for Everyone? A Compositional Analysis Approach to Assess the Distribution of Urban Trees as an Indicator of Environmental Justice" Sustainability 12, no. 3: 1215. https://doi.org/10.3390/su12031215
APA StyleCruz-Sandoval, M., Ortego, M. I., & Roca, E. (2020). Tree Ecosystem Services, for Everyone? A Compositional Analysis Approach to Assess the Distribution of Urban Trees as an Indicator of Environmental Justice. Sustainability, 12(3), 1215. https://doi.org/10.3390/su12031215






