Development of an Optimal Model for the Xiluodu-Xiangjiaba Cascade Reservoir System Considering the Downstream Environmental Flow
Abstract
1. Introduction
2. Materials and Methods
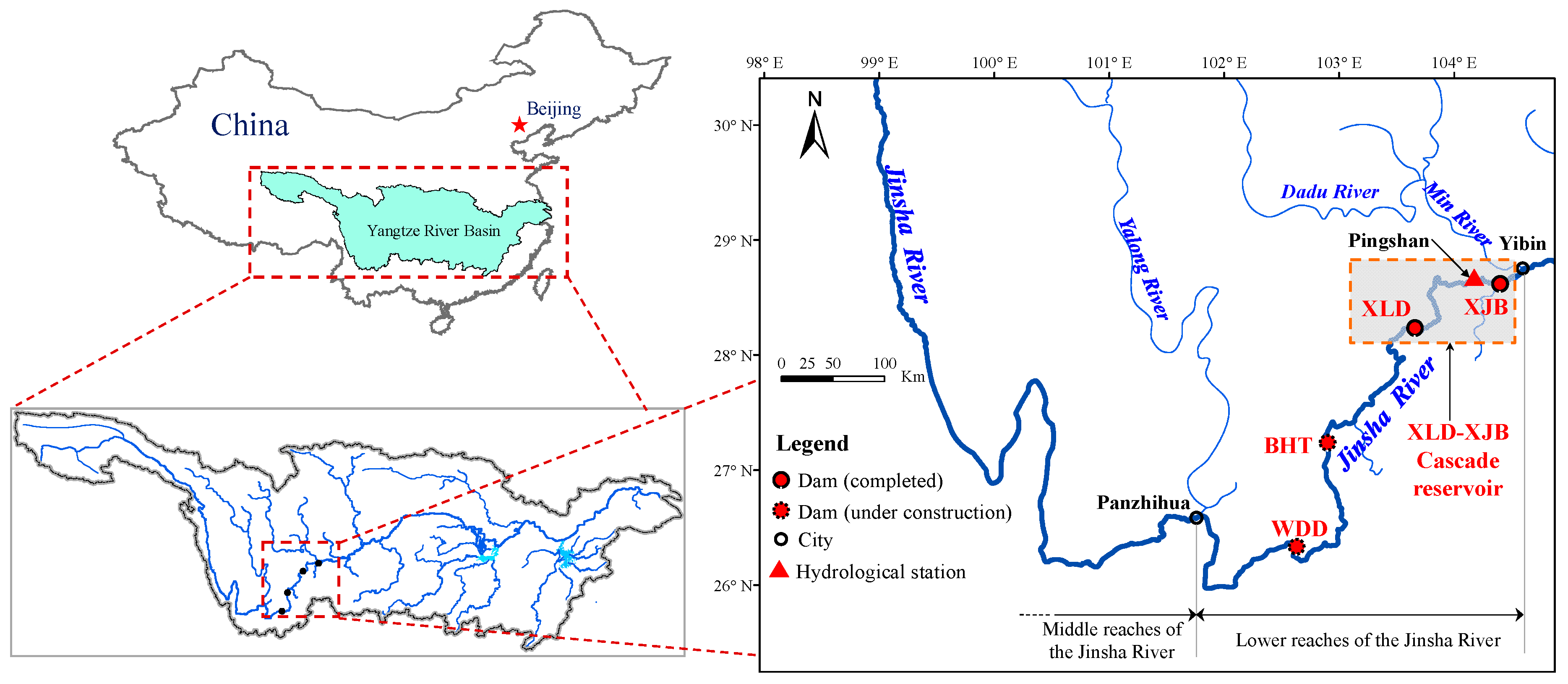
2.1. Study Area
2.2. Model Establishment
2.2.1. Objective Functions
2.2.2. Constraint Conditions
2.2.3. Penalty Functions
2.3. Model Solution
2.3.1. Fast Nondominated Sorting
2.3.2. Distribution Retention Method
2.3.3. Adaptive Elite Retention Strategy
2.3.4. Parameter Setting
3. Results and Discussion
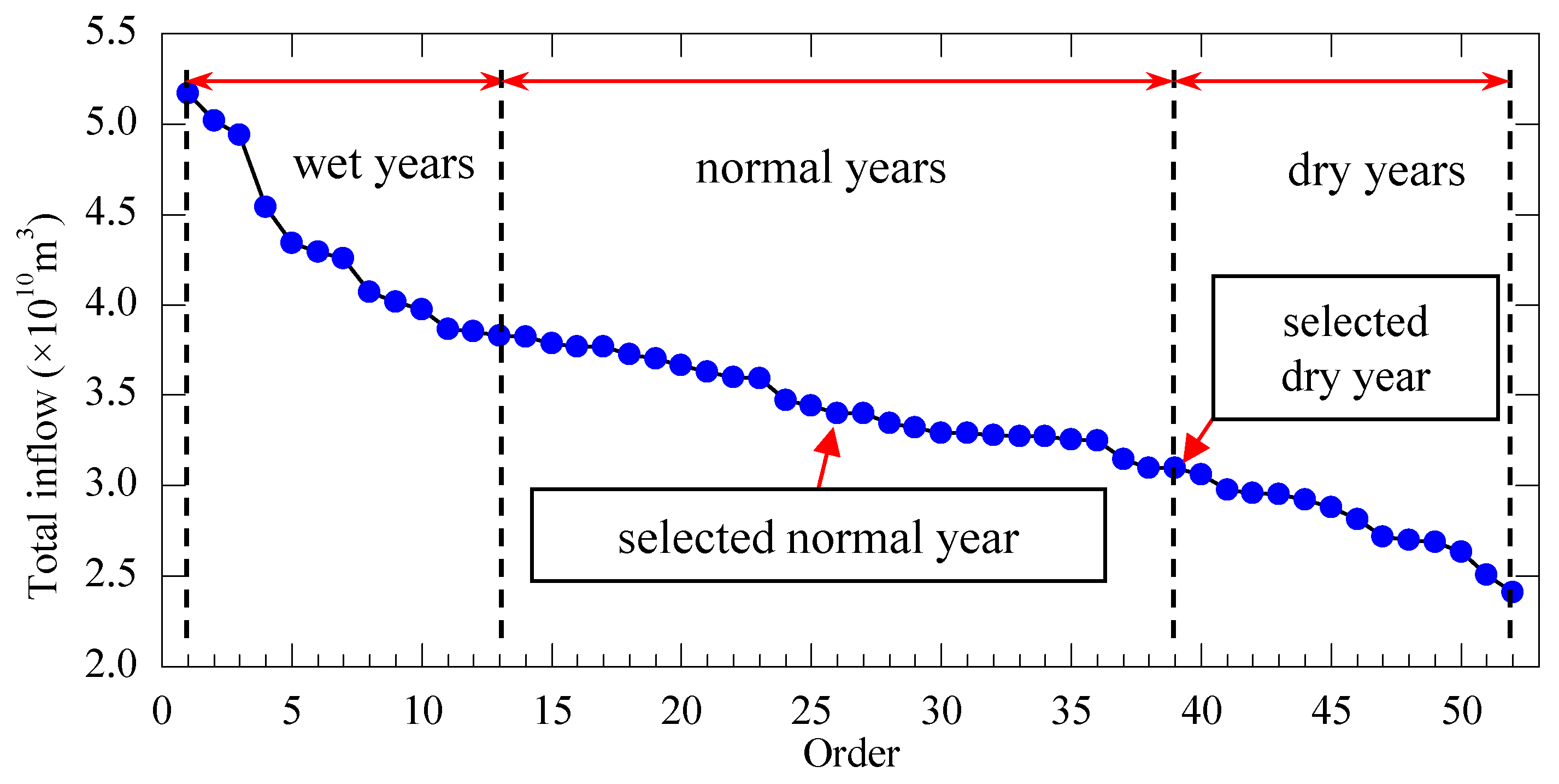
3.1. Optimization Period and Typical Years
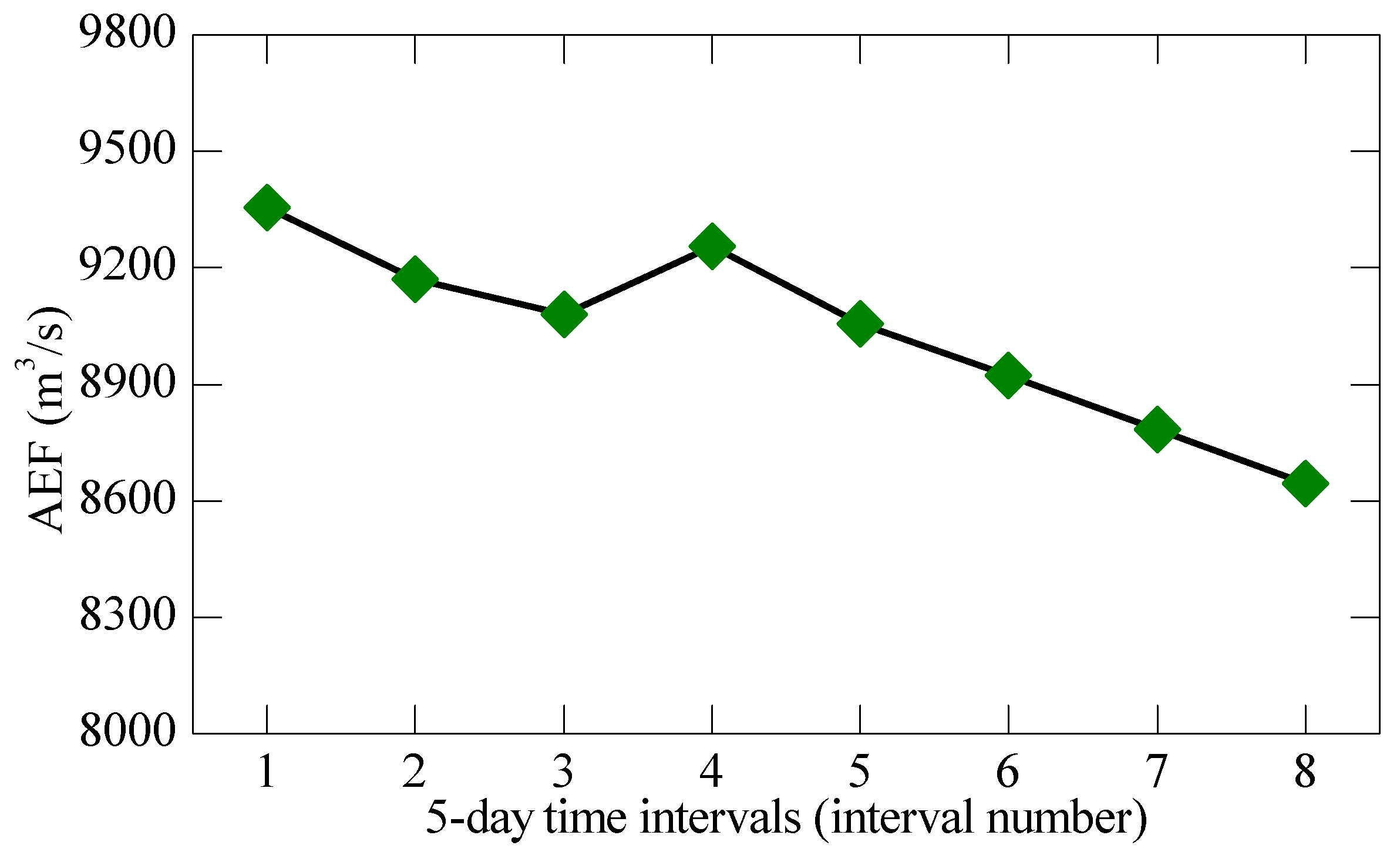
3.2. Determination of the Appropriate Environmental Flow
3.3. Optimization Results
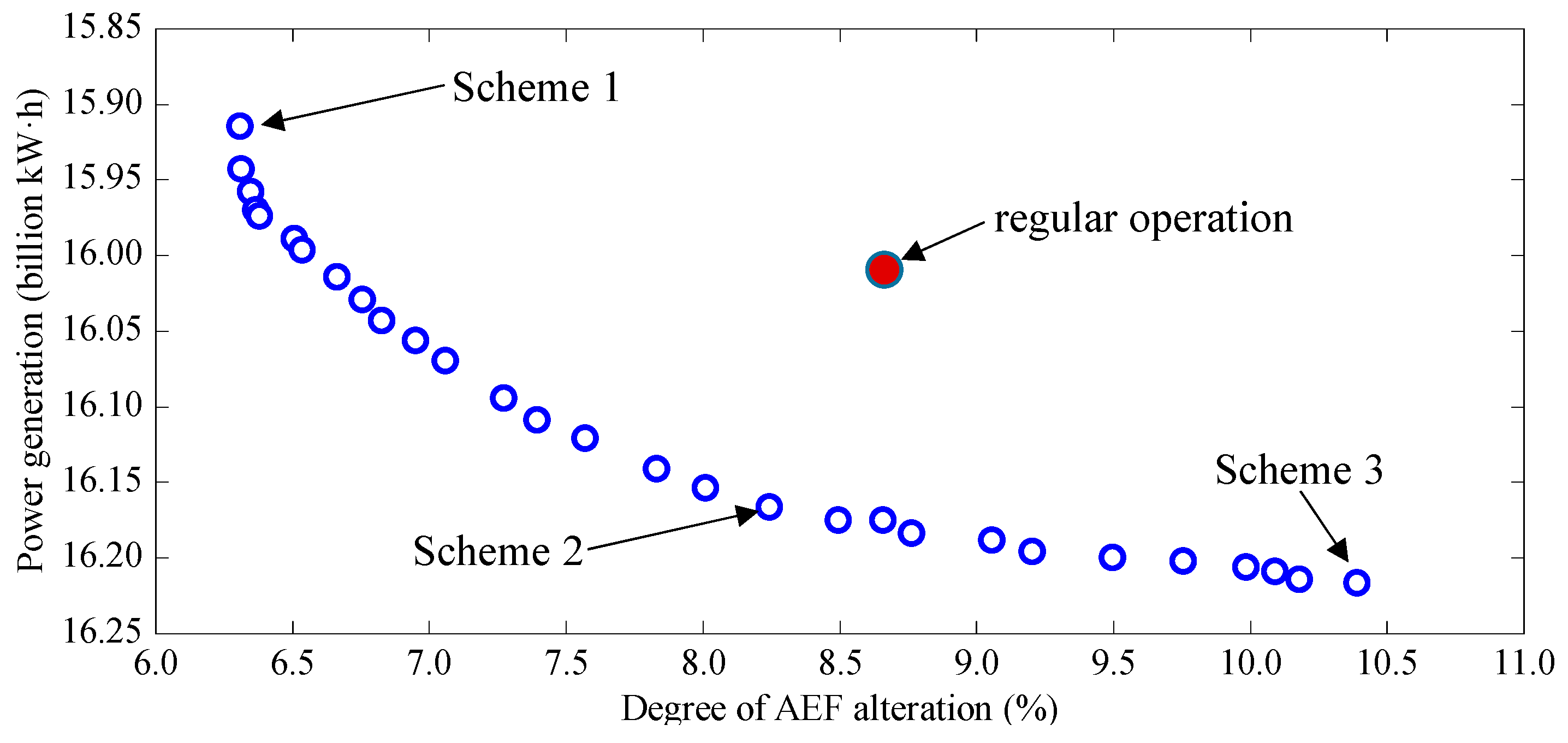
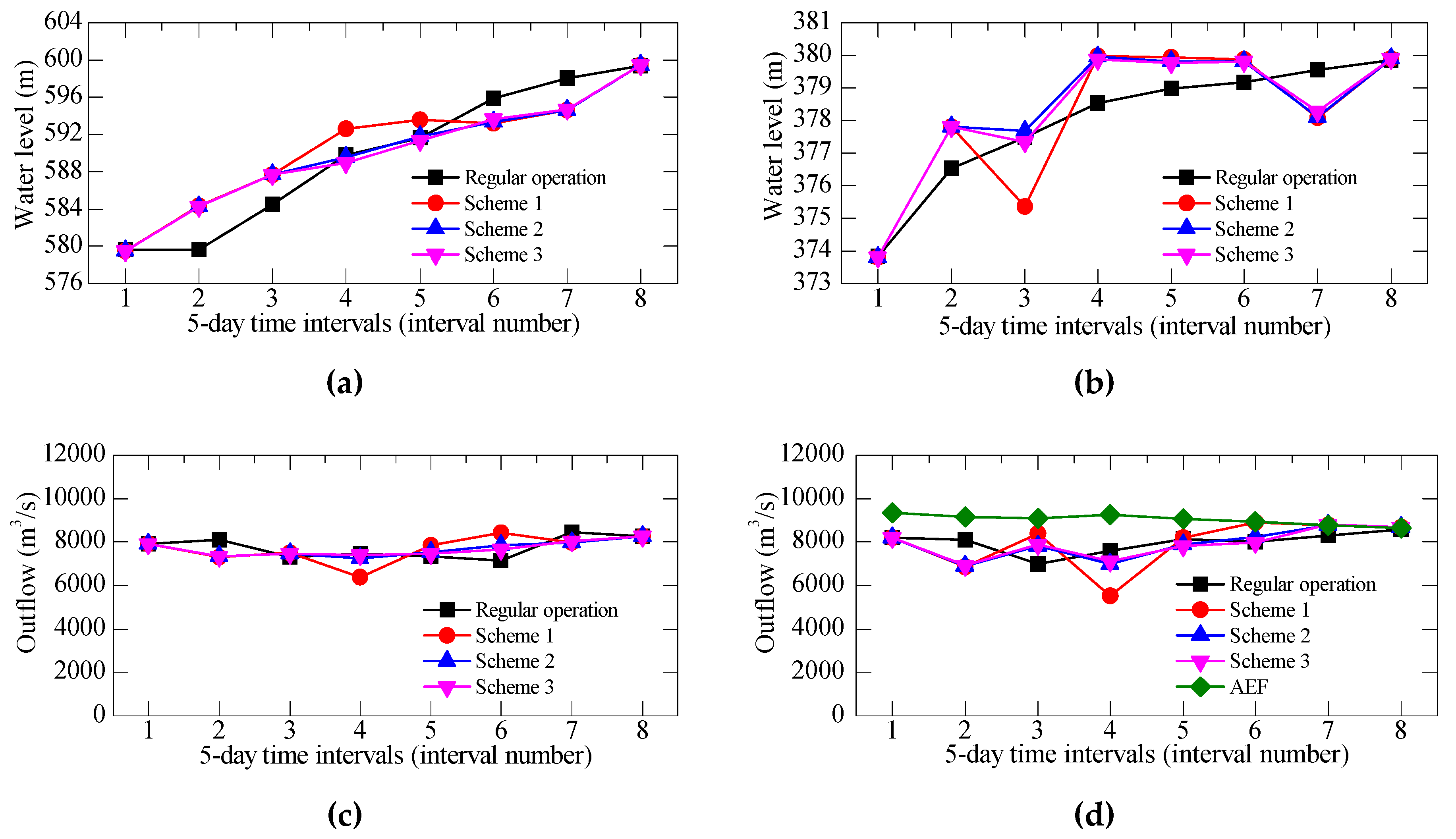
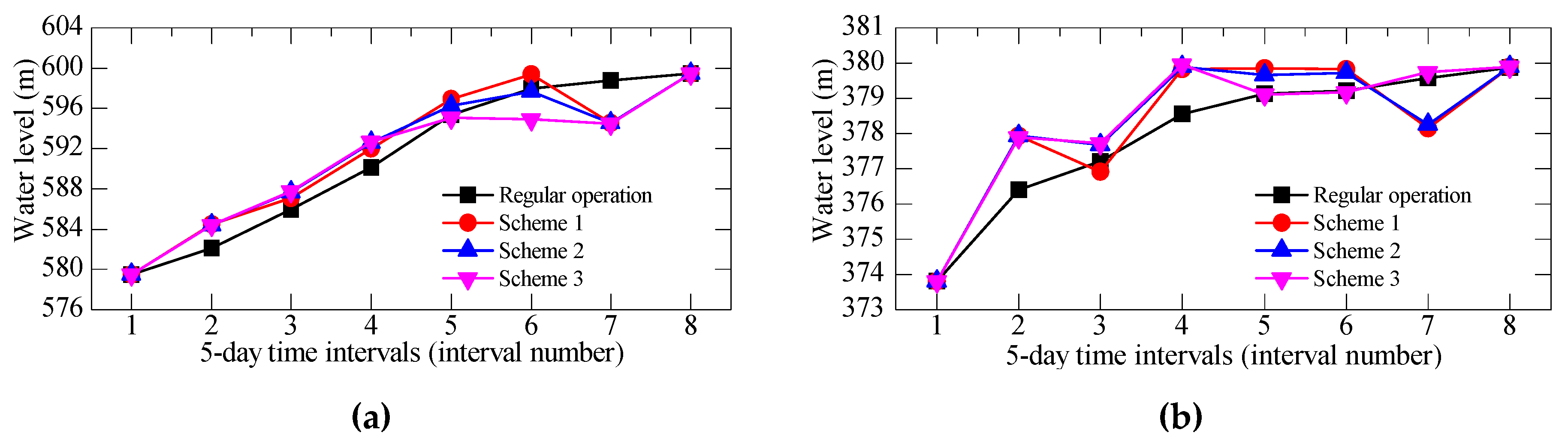
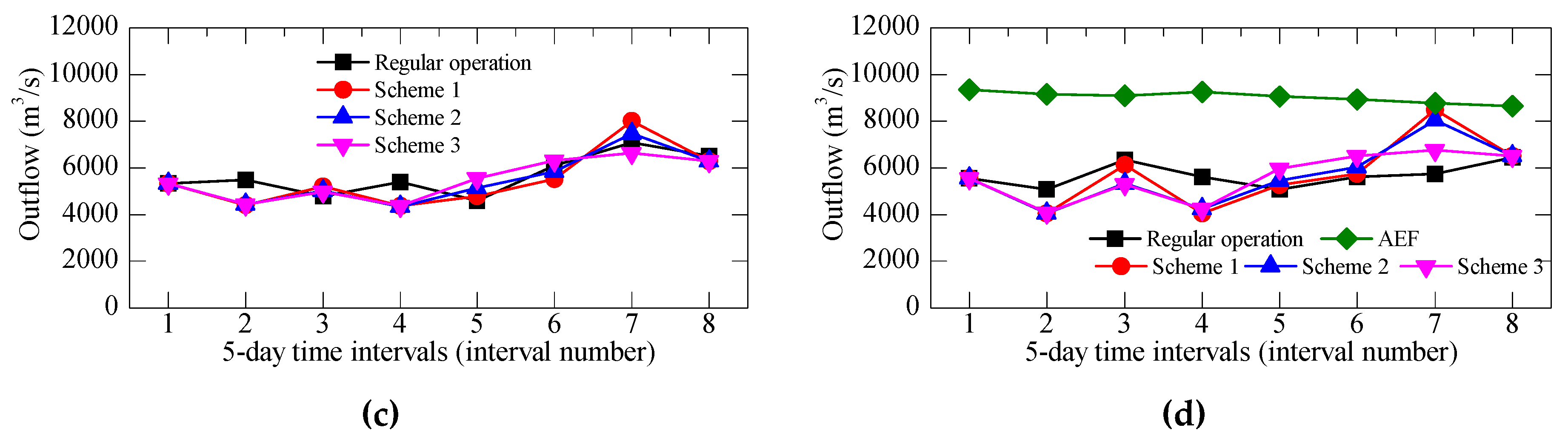
3.3.1. Optimization Results for a Normal Year
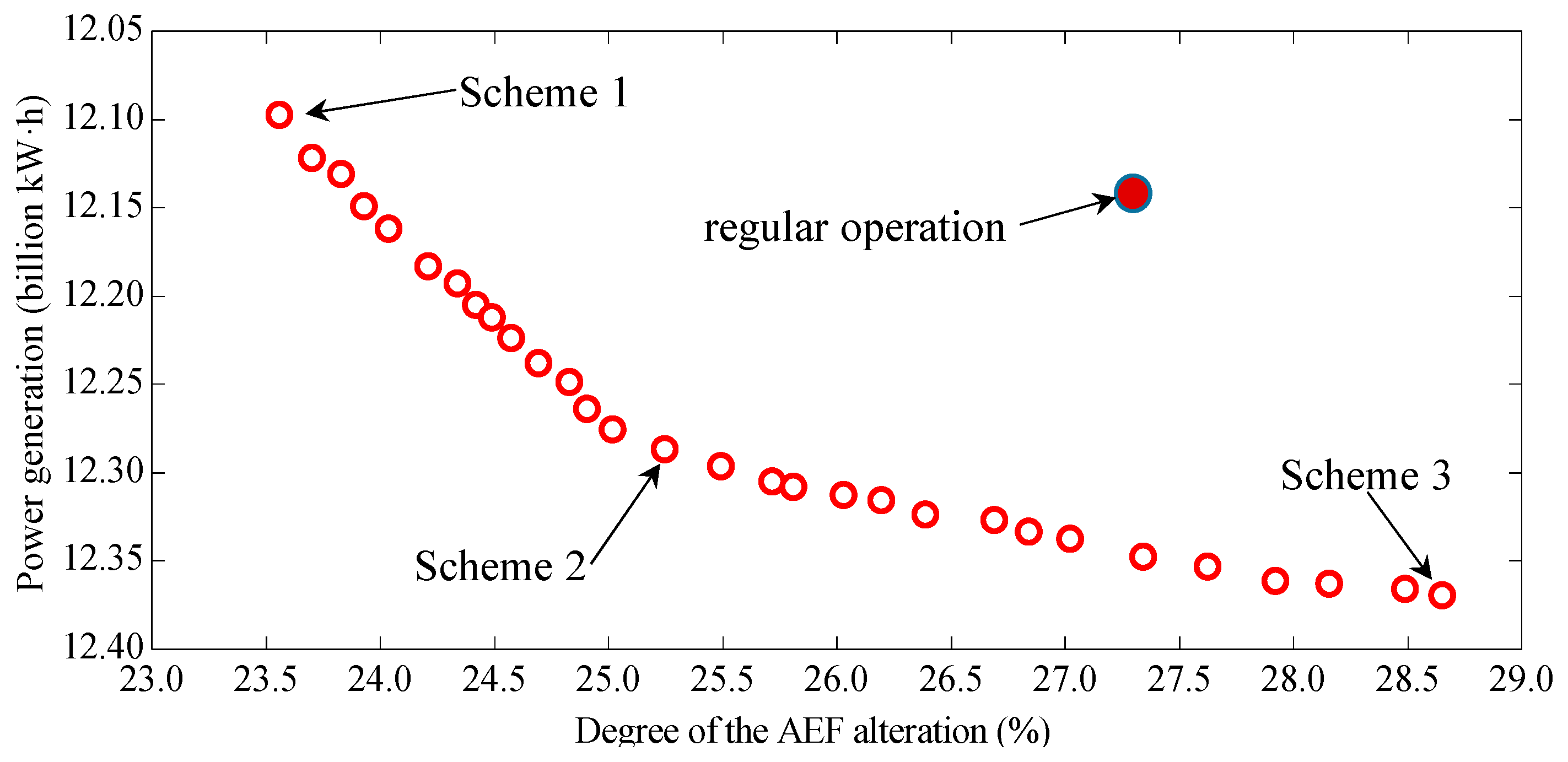
3.3.2. Optimization Results for a Dry Year
3.4. Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zarei, A.; Mousavi, S.F.; Gordji, M.E.; Karami, H. Optimal Reservoir Operation Using Bat and Particle Swarm Algorithm and Game Theory Based on Optimal Water Allocation among Consumers. Water Resour. Manag. 2019, 33, 3071–3093. [Google Scholar] [CrossRef]
- Bilgili, M.; Bilirgen, H.; Ozbek, A.; Ekinci, F.; Demirdelen, T. The role of hydropower installations for sustainable energy development in Turkey and the world. Renew. Energy 2018, 126, 755–764. [Google Scholar] [CrossRef]
- Xu, B.; Ma, Y.F.; Zhong, P.A.; Yu, Z.B.; Zhang, J.Y.; Zhu, F.L. Bargaining Model of Synergistic Revenue Allocation for the Joint Operations of a Multi-Stakeholder Cascade Reservoir System. Water Resour. Manag. 2018, 32, 4625–4642. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T. China’s large-scale hydropower system: Operation characteristics, modeling challenge and dimensionality reduction possibilities. Renew. Energy 2019, 136, 805–818. [Google Scholar] [CrossRef]
- Zhou, Y.L.; Guo, S.L.; Chang, F.J.; Xu, C.Y. Boosting hydropower output of mega cascade reservoirs using an evolutionary algorithm with successive approximation. Appl. Energy 2018, 228, 1726–1739. [Google Scholar] [CrossRef]
- Neto, R.M.; Nocko, H.R.; Ostrensky, A. Environmental characterization and impacts of fish farming in the cascade reservoirs of the Paranapanema River, Brazil. Aquac. Environ. Interact. 2015, 6, 255–272. [Google Scholar]
- Yazdi, J.; Moridi, A. Multi-Objective Differential Evolution for Design of Cascade Hydropower Reservoir Systems. Water Resour. Manag. 2018, 32, 4779–4791. [Google Scholar] [CrossRef]
- Khorshidi, M.S.; Nikoo, M.R.; Sadegh, M.; Nematollahi, B. A Multi-Objective Risk-Based Game Theoretic Approach to Reservoir Operation Policy in Potential Future Drought Condition. Water Resour. Manag. 2019, 33, 1999–2014. [Google Scholar] [CrossRef]
- Graham, E.B.; Stegen, J.C.; Huang, M.; Chen, X.Y.; Scheibe, T.D. Subsurface biogeochemistry is a missing link between ecology and hydrology in dam-impacted river corridors. Sci. Total Environ. 2019, 657, 435–445. [Google Scholar] [CrossRef]
- Anindito, Y.; Haas, J.; Olivares, M.; Nowak, W.; Kern, J. A new solution to mitigate hydropeaking? Batteries versus re-regulation reservoirs. J. Clean Prod. 2019, 210, 477–489. [Google Scholar] [CrossRef]
- Al-Jawad, J.Y.; Alsaffar, H.M.; Bertram, D.; Kalin, R.M. Optimum socio-environmental flows approach for reservoir operation strategy using many-objectives evolutionary optimization algorithm. Sci. Total Environ. 2019, 651, 1877–1891. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Qiao, Y.; Schineider, M.; Chang, J.B.; Mutzner, R.; Fluixa-Sanmartin, J.; Yang, Z.; Fu, R.; Chen, X.J.; Cai, L.; et al. Using a hierarchical model framework to assess climate change and hydropower operation impacts on the habitat of an imperiled fish in the Jinsha River, China. Sci. Total Environ. 2019, 646, 1624–1638. [Google Scholar] [CrossRef] [PubMed]
- He, D.; Dai, Q.; Tang, H.; Yang, Z. Length-weight relationships for three fish species from the middle and lower reaches of the Jinsha River, China. J. Appl. Ichthyol. 2018, 34, 760–761. [Google Scholar] [CrossRef]
- Shao, K.; Que, Y.F.; Xiong, M.H.; Li, W.T.; Yu, D.; Shi, F. Length-weight and length-length relationships of thirteen fish species from the lower Jinsha River, southwest China. J. Appl. Ichthyol. 2018, 34, 774–776. [Google Scholar] [CrossRef]
- Zhang, P.; Cai, L.; Yang, Z.; Chen, X.J.; Qiao, Y.; Chang, J.B. Evaluation of fish habitat suitability using a coupled ecohydraulic model: Habitat model selection and prediction. River Res. Appl. 2018, 34, 937–947. [Google Scholar] [CrossRef]
- Li, G.N.; Sun, S.K.; Liu, H.T.; Zheng, T.G. Optimizing the entrance location for a fish pass facility with limited attraction flow in a large river—A case study of the Jinsha River, China. Can. J. Civ. Eng. 2019, 46, 847–857. [Google Scholar] [CrossRef]
- Luo, D.N.; Lin, P.; Li, Q.B.; Zheng, D.; Liu, H.Y. Effect of the impounding process on the overall stability of a high arch dam: A case study of the Xiluodu dam, China. Arab. J. Geosci. 2015, 8, 9023–9041. [Google Scholar] [CrossRef]
- Zhu, T.B.; Yang, D.G. Length-weight relationships of two fish species from the middle reaches of the Jinsha River, China. J. Appl. Ichthyol. 2016, 32, 747–748. [Google Scholar] [CrossRef]
- Morrison, R.R.; Stone, M.C. Evaluating the impacts of environmental flow alternatives on reservoir and recreational operations using system dynamics modeling. J. Am. Water Resour. Assoc. 2015, 51, 33–46. [Google Scholar] [CrossRef]
- Karakoyun, Y.; Donmez, A.H.; Yumurtaci, Z. Comparison of environmental flow assessment methods with a case study on a runoff river-type hydropower plant using hydrological methods. Environ. Monit. Assess. 2018, 190, 1–15. [Google Scholar] [CrossRef]
- Rashid, M.U.; Latif, A.; Azmat, M. Optimizing Irrigation Deficit of Multipurpose Cascade Reservoirs. Water Resour. Manag. 2018, 32, 1675–1687. [Google Scholar] [CrossRef]
- King, A.J.; Gawne, B.; Beesley, L.; Koehn, J.D.; Nielsen, D.L.; Price, A. Improving Ecological Response Monitoring of Environmental Flows. Environ. Manag. 2015, 55, 991–1005. [Google Scholar] [CrossRef] [PubMed]
- Giraldo, M.A.; Dark, S.; Pendleton, P.; Stein, E.D.; Mazor, R.; Andreas, J. Environmental predictors of stream flow in semi-arid watersheds for biological assessments. Ecol. Indic. 2019, 104, 429–438. [Google Scholar] [CrossRef]
- Dupuis, J.R.; Cullingham, C.I.; Nielsen, S.E.; Sperling, F.A.H. Environmental effects on gene flow in a species complex of vagile, hilltopping butterflies. Biol. J. Linnean Soc. 2019, 127, 417–428. [Google Scholar] [CrossRef]
- Zhang, H.X.; Chang, J.X.; Gao, C.; Wu, H.S.; Wang, Y.M.; Lei, K.X.; Long, R.H.; Zhang, L.P. Cascade hydropower plants operation considering comprehensive ecological water demands. Energy Conv. Manag. 2019, 180, 119–133. [Google Scholar] [CrossRef]
- Takada, A.; Hiramatsu, K.; Trieu, N.A.; Harada, M.; Tabata, T. Development of an optimizing method for the operation rule curves of a multipurpose reservoir in a Southeast Asian watershed. Paddy Water Environ. 2019, 17, 195–202. [Google Scholar] [CrossRef]
- Sichilalu, S.; Wamalwa, F.; Akinlabi, E.T. Optimal control of wind-hydrokinetic pumpback hydropower plant constrained with ecological water flows. Renew. Energy 2019, 138, 54–69. [Google Scholar] [CrossRef]
- Stuart, I.; Sharpe, C.; Stanislawski, K.; Parker, A.; Mallen-Cooper, M. From an irrigation system to an ecological asset: Adding environmental flows establishes recovery of a threatened fish species. Mar. Freshw. Res. 2019, 70, 1295–1306. [Google Scholar] [CrossRef]
- Lu, P.; Zhou, J.Z.; Wang, C.; Qiao, Q.; Mo, L. Short-term hydro generation scheduling of Xiluodu and Xiangjiaba cascade hydropower stations using improved binary-real coded bee colony optimization algorithm. Energy Conv. Manag. 2015, 91, 19–31. [Google Scholar] [CrossRef]
- Geressu, R.T.; Harou, J.J. Reservoir system expansion scheduling under conflicting interests. Environ. Modell. Softw. 2019, 118, 201–210. [Google Scholar] [CrossRef]
- Yassin, F.; Razavi, S.; Elshamy, M.; Davison, B.; Sapriza-Azuri, G.; Wheater, H. Representation and improved parameterization of reservoir operation in hydrological and land-surface models. Hydrol. Earth Syst. Sci. 2019, 23, 3735–3764. [Google Scholar] [CrossRef]
- Fallah-Mehdipour, E.; Bozorg-Haddad, O.; Loaiciga, H.A. Calculation of multi-objective optimal tradeoffs between environmental flows and hydropower generation. Environ. Earth Sci. 2018, 77, 1–10. [Google Scholar] [CrossRef]
- Carmignani, J.R.; Roy, A.H. Ecological impacts of winter water level drawdowns on lake littoral zones: A review. Aquat. Sci. 2017, 79, 803–824. [Google Scholar] [CrossRef]
- Xie, M.F.; Zhou, J.Z.; Li, C.L.; Zhu, S. Long-term generation scheduling of Xiluodu and Xiangjiaba cascade hydro plants considering monthly streamflow forecasting error. Energy Conv. Manag. 2015, 105, 368–376. [Google Scholar] [CrossRef]
- Shen, J.J.; Zhang, X.F.; Wang, J.; Cao, R.; Wang, S.; Zhang, J.H. Optimal Operation of Interprovincial Hydropower System Including Xiluodu and Local Plants in Multiple Recipient Regions. Energies 2019, 12, 144. [Google Scholar] [CrossRef]
- Kamodkar, R.U.; Regulwar, D.G. Optimal multiobjective reservoir operation with fuzzy decision variables and resources: A compromise approach. J. Hydro-Environ. Res. 2014, 8, 428–440. [Google Scholar] [CrossRef]
- Shahhosseini, H.R.; Farsi, M.; Eini, S. Multi-objective optimization of industrial membrane SMR to produce syngas for Fischer-Tropsch production using NSGA-II and decision makings. J. Nat. Gas Sci. Eng. 2016, 32, 222–238. [Google Scholar] [CrossRef]
- Navabi, S.; Khaninezhad, R.; Jafarpour, B. A unified formulation for generalized oilfield development optimization. Comput. Geosci. 2017, 21, 47–74. [Google Scholar] [CrossRef]
- Prakash, O.; Srinivasan, K.; Sudheer, K.P. Adaptive multi-objective simulation-optimization framework for dynamic flood control operation in a river-reservoir system. Hydrol. Res. 2015, 46, 893–911. [Google Scholar] [CrossRef]
- Peng, S.T.; Li, T.; Zhao, J.L.; Lv, S.P.; Tan, G.Z.; Dong, M.M.; Zhang, H.C. Towards energy and material efficient laser cladding process: Modeling and optimization using a hybrid TS-GEP algorithm and the NSGA-II. J. Clean Prod. 2019, 227, 58–69. [Google Scholar] [CrossRef]
- Mann, G.W.; Eckels, S. Multi-objective heat transfer optimization of 2D helical micro-fins using NSGA-II. Int. J. Heat Mass Transf. 2019, 132, 1250–1261. [Google Scholar] [CrossRef]
- Jadidi, A.; Menezes, R.; de Souza, N.; de Castro Lima, A.C. Short-Term Electric Power Demand Forecasting Using NSGA II-ANFIS Model. Energies 2019, 12, 1891. [Google Scholar] [CrossRef]
- Grantham, T.E.; Zimmerman, J.K.H.; Carah, J.K.; Howard, J.K. Stream flow modeling tools inform environmental water policy in California. Calif. Agric. 2019, 73, 33–39. [Google Scholar] [CrossRef]
- Zhao, C.S.; Yang, S.T.; Liu, J.G.; Liu, C.M.; Hao, F.H.; Wang, Z.G.; Zhang, H.T.; Song, J.X.; Mitrovic, S.M.; Lim, R.P. Linking fish tolerance to water quality criteria for the assessment of environmental flows: A practical method for streamflow regulation and pollution control. Water Res. 2018, 141, 96–108. [Google Scholar] [CrossRef]
- Ceola, S.; Pugliese, A.; Ventura, M.; Galeati, G.; Montanari, A.; Castellarin, A. Hydro-power production and fish habitat suitability: Assessing impact and effectiveness of ecological flows at regional scale. Adv. Water Resour. 2018, 116, 29–39. [Google Scholar] [CrossRef]
- Theodoropoulos, C.; Skoulikidis, N.; Rutschmann, P.; Stamou, A. Ecosystem-based environmental flow assessment in a Greek regulated river with the use of 2D hydrodynamic habitat modelling. River Res. Appl. 2018, 34, 538–547. [Google Scholar] [CrossRef]
- Ksiazek, L.; Wos, A.; Florek, J.; Wyrebek, M.; Mlynski, D.; Walega, A. Combined use of the hydraulic and hydrological methods to calculate the environmental flow: Wisloka river, Poland: Case study. Environ. Monit. Assess. 2019, 191, 1–17. [Google Scholar] [CrossRef]
- Mishra, S.K.; Amrit, K.; Pandey, R.P. Correlation between Tennant method and Standardized Precipitation Index for predicting environmental flow condition using rainfall in Godavari Basin. Paddy Water Environ. 2019, 17, 515–521. [Google Scholar] [CrossRef]
- Windfeld, E.J.; Ford, J.D.; Berrang-Ford, L.; McDowell, G. How do community-level climate change vulnerability assessments treat future vulnerability and integrate diverse datasets? A review of the literature. Environ. Rev. 2019, 27, 427–434. [Google Scholar] [CrossRef]
- El-Jabi, N.; Caissie, D. Characterization of natural and environmental flows in New Brunswick, Canada. River Res. Appl. 2019, 35, 14–24. [Google Scholar] [CrossRef]
- Vietz, G.J.; Lintern, A.; Webb, J.A.; Straccione, D. River Bank Erosion and the Influence of Environmental Flow Management. Environ. Manag. 2018, 61, 454–468. [Google Scholar] [CrossRef] [PubMed]
- Johnson, J.A.; Sivakumar, K.; Rosenfeld, J. Ecological flow requirement for fishes of Godavari river: Flow estimation using the PHABSIM method. Curr. Sci. 2017, 113, 2187–2193. [Google Scholar] [CrossRef]



| Parameter | Xiluodu Reservoir | Xiangjiaba Reservoir |
|---|---|---|
| Height of dam (m) | 285.5 | 162.0 |
| Dead water level (m) | 540.0 | 370.0 |
| Normal water level (m) | 600.0 | 380.0 |
| Flood limit water level (m) | 560.0 | 370.0 |
| Installed capacity (MW) | 12600 | 6000 |
| Minimum output (MW) | 6650 | 2000 |
| Maximum output (MW) | 12600 | 6000 |
| Total capacity (108 m3) | 126.7 | 51.6 |
| Minimum outflow (m3/s) | 1500 | 1500 |
| Scheme | Objective | Power Generation (Billion kW·h) | Degree of AEF Alteration (%) |
|---|---|---|---|
| Scheme 1 | Minimizing the degree of AEF alteration | 15.912 | 9.11% |
| Scheme 2 | Unbiased | 16.153 | 11.01% |
| Scheme 3 | Maximizing the power generation | 16.217 | 13.39% |
| Reference scheme | Regular operation | 16.011 | 11.76% |
| Scheme | Objective | Power Generation (billion kW·h) | Degree of the AEF Alteration (%) |
|---|---|---|---|
| Scheme 1 | Minimizing the degree of AEF alteration | 12.098 | 23.56% |
| Scheme 2 | Unbiased | 12.287 | 25.25% |
| Scheme 3 | Maximizing the power generation | 12.370 | 28.65% |
| Reference scheme | Regular operation | 12.156 | 27.30% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, L.; Dai, H.; Liu, H.; Wang, Y.; Guo, J.; Cai, Z.; Mi, C. Development of an Optimal Model for the Xiluodu-Xiangjiaba Cascade Reservoir System Considering the Downstream Environmental Flow. Sustainability 2020, 12, 966. https://doi.org/10.3390/su12030966
Dai L, Dai H, Liu H, Wang Y, Guo J, Cai Z, Mi C. Development of an Optimal Model for the Xiluodu-Xiangjiaba Cascade Reservoir System Considering the Downstream Environmental Flow. Sustainability. 2020; 12(3):966. https://doi.org/10.3390/su12030966
Chicago/Turabian StyleDai, Lingquan, Huichao Dai, Haibo Liu, Yu Wang, Jiali Guo, Zhuosen Cai, and Chenxi Mi. 2020. "Development of an Optimal Model for the Xiluodu-Xiangjiaba Cascade Reservoir System Considering the Downstream Environmental Flow" Sustainability 12, no. 3: 966. https://doi.org/10.3390/su12030966
APA StyleDai, L., Dai, H., Liu, H., Wang, Y., Guo, J., Cai, Z., & Mi, C. (2020). Development of an Optimal Model for the Xiluodu-Xiangjiaba Cascade Reservoir System Considering the Downstream Environmental Flow. Sustainability, 12(3), 966. https://doi.org/10.3390/su12030966






