Extreme Learning Machine Based Prediction of Soil Shear Strength: A Sensitivity Analysis Using Monte Carlo Simulations and Feature Backward Elimination
Abstract
1. Introduction
2. Methodology
2.1. Data Collection and Preparation
2.2. Extreme ML-Based Modeling
2.3. Backward Elimination-Based Sensitivity Analysis
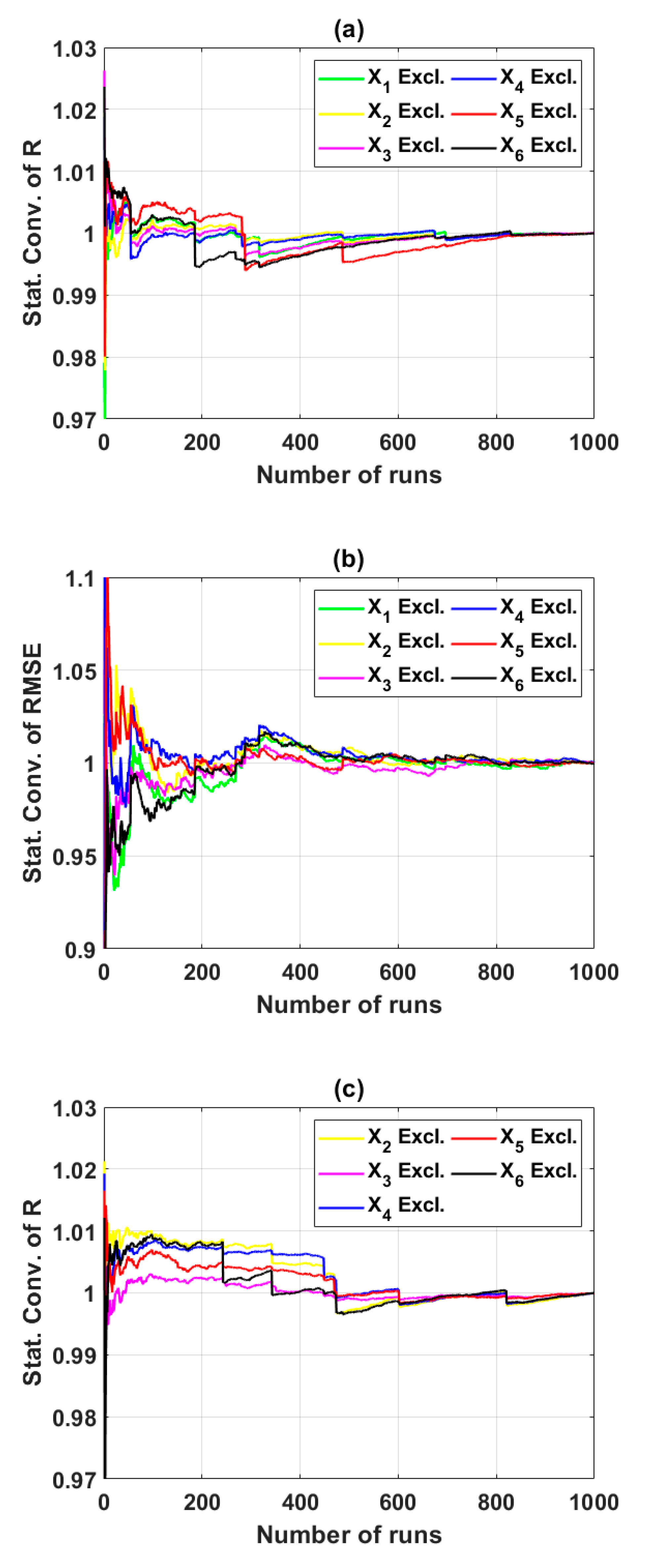
2.4. Monte Carlo Simulations
2.5. Performance Evaluation
3. Results
3.1. Validation of ELM with Various Number of Neurons
3.2. Sensitivity Analysis Using Backward Elimination and Monte Carlo Simulations
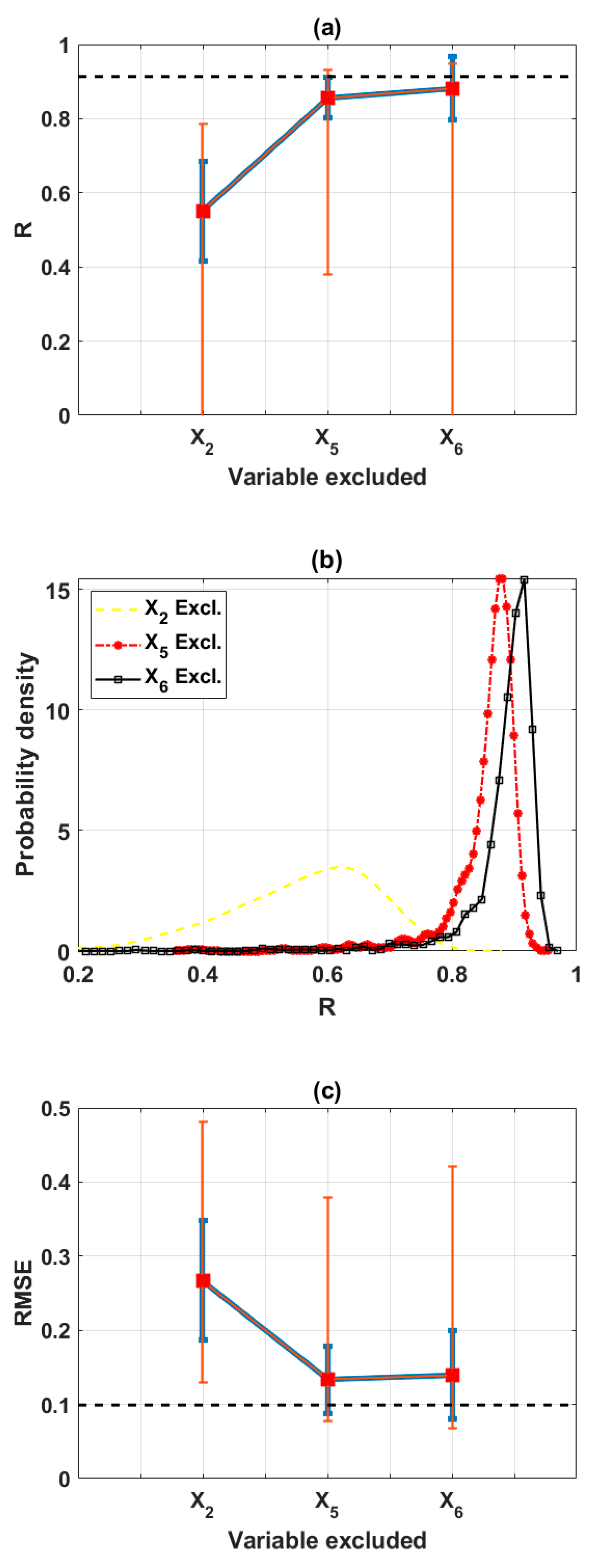
3.2.1. Reduction of the Input Space from 6 to 5 Variables (Scenario 1)
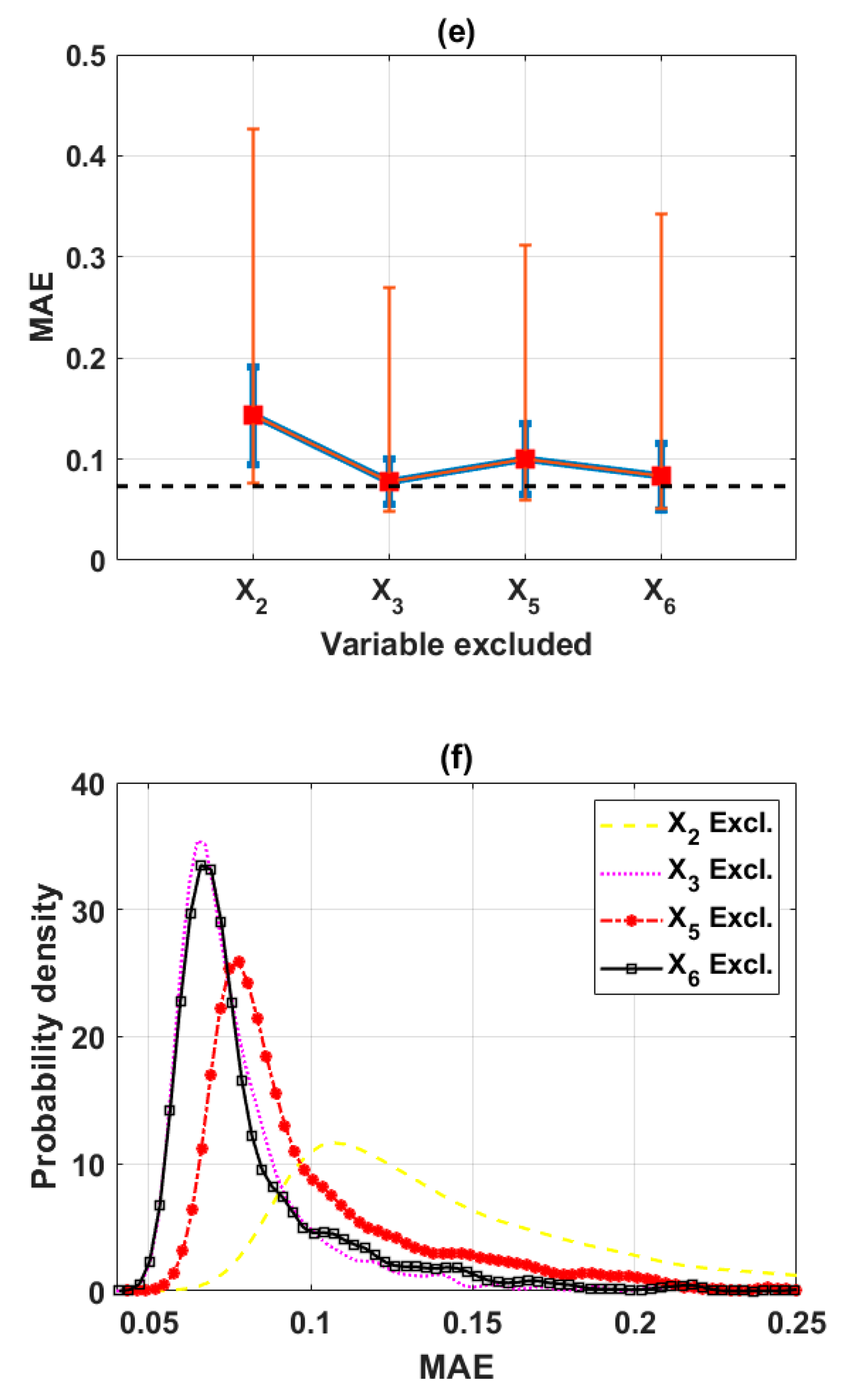
3.2.2. Reduction of the Input Space from Five to Four Variables (Scenario 2)
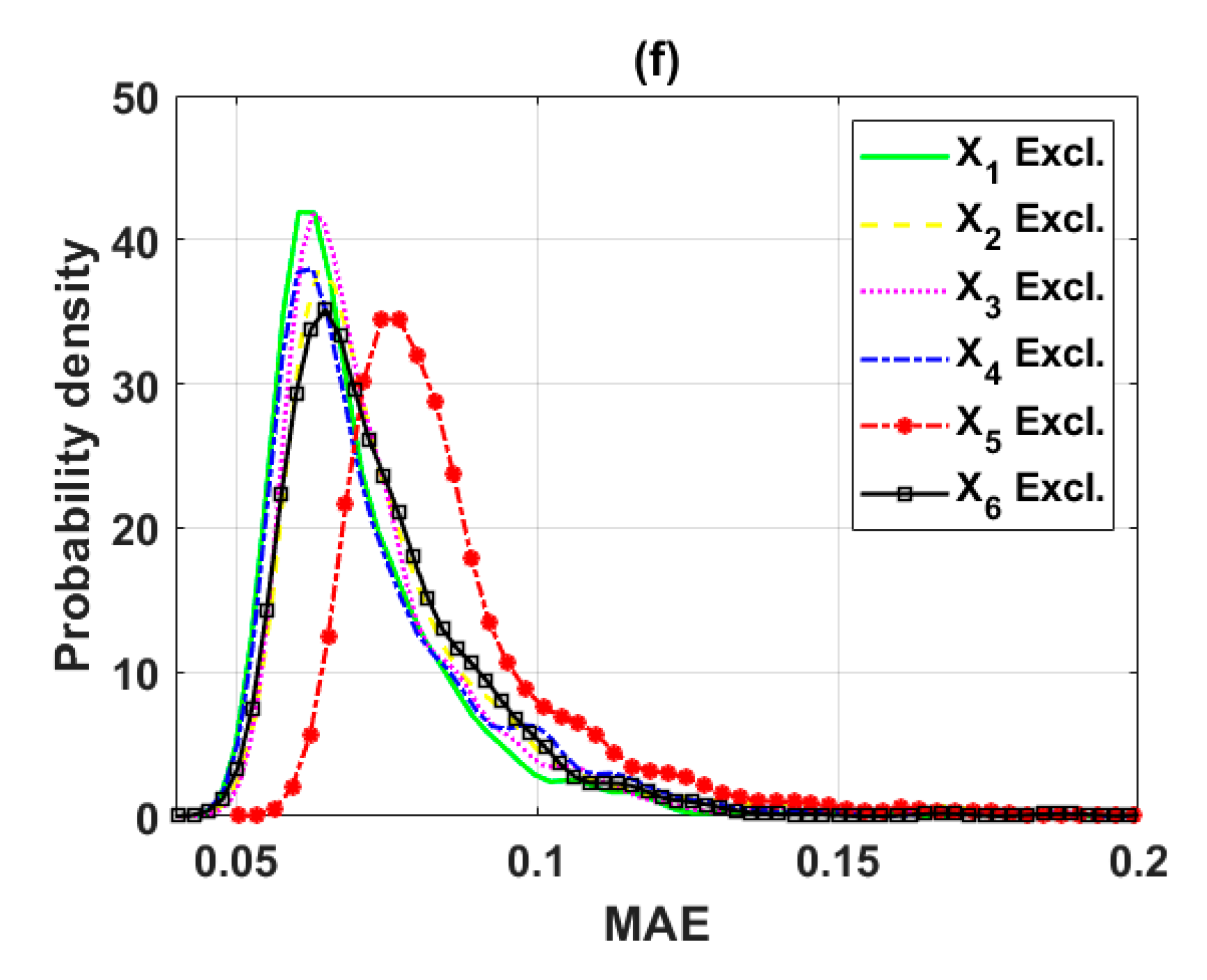
3.2.3. Reduction of the Input Space from Four to Three Variables (Scenario 3)
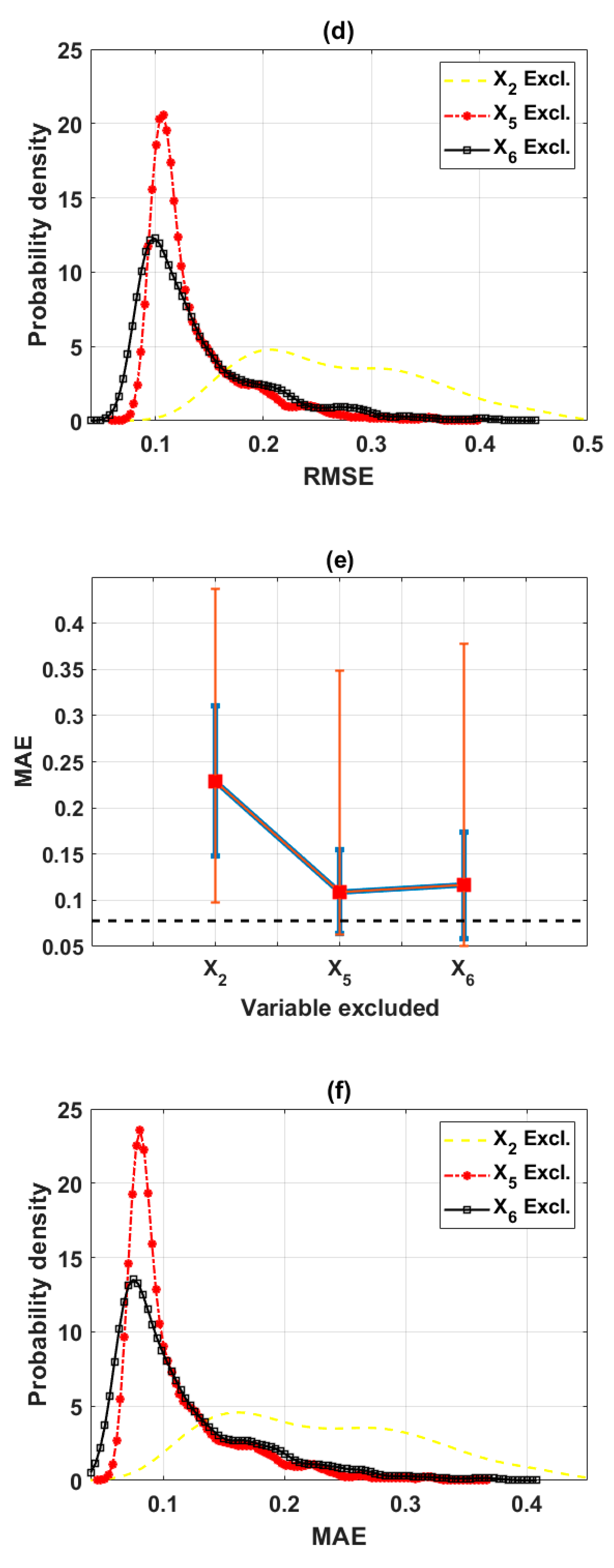
3.2.4. Final Input Space with Three Variables (Scenario 4)
4. Discussions
4.1. Performance of ELM in Predicting the Shear Strength of Soil
4.2. Reliability of the Predicted Results by Monte Carlo Approach
4.3. Backward Elimination Criteria-Based Sensitivity Analysis
4.4. Importance of Input Factors for Prediction of Soil Shear Strength
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tien Bui, D.; Hoang, N.-D.; Nhu, V.-H. A swarm intelligence-based machine learning approach for predicting soil shear strength for road construction: A case study at Trung Luong National Expressway Project (Vietnam). Eng. Comput. 2019, 35, 955–965. [Google Scholar] [CrossRef]
- Garven, E.A.; Vanapalli, S.K. Evaluation of Empirical Procedures for Predicting the Shear Strength of Unsaturated Soils. In Proceedings of the Fourth International Conference on Unsaturated Soils, Carefree, AZ, USA, 2–6 April 2006; pp. 2570–2592. [Google Scholar]
- Sheng, D.; Zhou, A.; Fredlund, D.G. Shear Strength Criteria for Unsaturated Soils. Geotech. Geol. Eng. 2011, 29, 145–159. [Google Scholar] [CrossRef]
- Vanapalli, S.K.; Fredlund, D.G. Comparison of Different Procedures to Predict Unsaturated Soil Shear Strength. In Advances in Unsaturated Geotechnics; American Society of Civil Engineers: Reston, VA, USA, 2000; pp. 195–209. [Google Scholar]
- Al Aqtash, U.; Bandini, P. Prediction of unsaturated shear strength of an adobe soil from the soil–water characteristic curve. Constr. Build. Mater. 2015, 98, 892–899. [Google Scholar] [CrossRef]
- Pham, B.T.; Son, L.H.; Hoang, T.-A.; Nguyen, D.-M.; Tien Bui, D. Prediction of shear strength of soft soil using machine learning methods. CATENA 2018, 166, 181–191. [Google Scholar] [CrossRef]
- Moayedi, H.; Tien Bui, D.; Dounis, A.; Kok Foong, L.; Kalantar, B. Novel Nature-Inspired Hybrids of Neural Computing for Estimating Soil Shear Strength. Appl. Sci. 2019, 9, 4643. [Google Scholar] [CrossRef]
- Nhu, V.-H.; Hoang, N.-D.; Duong, V.-B.; Vu, H.-D.; Tien Bui, D. A hybrid computational intelligence approach for predicting soil shear strength for urban housing construction: A case study at Vinhomes Imperia project, Hai Phong city (Vietnam). Eng. Comput. 2019. [Google Scholar] [CrossRef]
- Das, S.; Samui, P.; Khan, S.; Sivakugan, N. Machine learning techniques applied to prediction of residual strength of clay. Open Geosci. 2011, 3, 449–461. [Google Scholar] [CrossRef]
- Nguyen, M.D.; Pham, B.T.; Tuyen, T.T.; Hai Yen, H.P.; Prakash, I.; Vu, T.T.; Chapi, K.; Shirzadi, A.; Shahabi, H.; Dou, J.; et al. Development of an Artificial Intelligence Approach for Prediction of Consolidation Coefficient of Soft Soil: A Sensitivity Analysis. Open Constr. Build. Technol. J. 2019, 13, 178–188. [Google Scholar] [CrossRef]
- Pham, B.T.; Nguyen, M.D.; Dao, D.V.; Prakash, I.; Ly, H.-B.; Le, T.-T.; Ho, L.S.; Nguyen, K.T.; Ngo, T.Q.; Hoang, V.; et al. Development of artificial intelligence models for the prediction of Compression Coefficient of soil: An application of Monte Carlo sensitivity analysis. Sci. Total Environ. 2019, 679, 172–184. [Google Scholar] [CrossRef]
- Asteris, P.G.; Ashrafian, A.; Rezaie-Balf, M. Prediction of the compressive strength of self-compacting concrete using surrogate models. Comput. Concr. 2019, 24, 137–150. [Google Scholar]
- Qi, C.; Ly, H.-B.; Chen, Q.; Le, T.-T.; Le, V.M.; Pham, B.T. Flocculation-dewatering prediction of fine mineral tailings using a hybrid machine learning approach. Chemosphere 2019, 244, 125450. [Google Scholar] [CrossRef]
- Ly, H.-B.; Monteiro, E.; Le, T.-T.; Le, V.M.; Dal, M.; Regnier, G.; Pham, B.T. Prediction and Sensitivity Analysis of Bubble Dissolution Time in 3D Selective Laser Sintering Using Ensemble Decision Trees. Materials 2019, 12, 1544. [Google Scholar] [CrossRef]
- Le, L.M.; Ly, H.-B.; Pham, B.T.; Le, V.M.; Pham, T.A.; Nguyen, D.-H.; Tran, X.-T.; Le, T.-T. Hybrid Artificial Intelligence Approaches for Predicting Buckling Damage of Steel Columns Under Axial Compression. Materials 2019, 12, 1670. [Google Scholar] [CrossRef] [PubMed]
- Khosravi, K.; Shahabi, H.; Pham, B.T.; Adamawoski, J.; Shirzadi, A.; Pradhan, B.; Dou, J.; Ly, H.-B.; Gróf, G.; Ho, H.L. A Comparative Assessment of Flood Susceptibility Modeling Using Multi-Criteria Decision-Making Analysis and Machine Learning Methods. J. Hydrol. 2019, 573, 311–323. [Google Scholar] [CrossRef]
- Qi, C.; Tang, X.; Dong, X.; Chen, Q.; Fourie, A.; Liu, E. Towards Intelligent Mining for Backfill: A genetic programming-based method for strength forecasting of cemented paste backfill. Miner. Eng. 2019, 133, 69–79. [Google Scholar] [CrossRef]
- Ly, H.-B.; Le, L.M.; Phi, L.V.; Phan, V.-H.; Tran, V.Q.; Pham, B.T.; Le, T.-T.; Derrible, S. Development of an AI Model to Measure Traffic Air Pollution from Multisensor and Weather Data. Sensors 2019, 19, 4941. [Google Scholar] [CrossRef]
- Pham, B.T.; Jaafari, A.; Prakash, I.; Singh, S.K.; Quoc, N.K.; Bui, D.T. Hybrid computational intelligence models for groundwater potential mapping. CATENA 2019, 182, 104101. [Google Scholar] [CrossRef]
- Ly, H.-B.; Le, L.M.; Duong, H.T.; Nguyen, T.C.; Pham, T.A.; Le, T.-T.; Le, V.M.; Nguyen-Ngoc, L.; Pham, B.T. Hybrid Artificial Intelligence Approaches for Predicting Critical Buckling Load of Structural Members under Compression Considering the Influence of Initial Geometric Imperfections. Appl. Sci. 2019, 9, 2258. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: A new learning scheme of feedforward neural networks. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks (IEEE Cat. No.04CH37541), Budapest, Hungary, 25–29 July 2004; Volume 2, pp. 985–990. [Google Scholar]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Kumar, V.; Minz, S. Feature selection: A literature review. Smart Comput. Rev. 2014, 4, 211–229. [Google Scholar] [CrossRef]
- Jović, A.; Brkić, K.; Bogunović, N. A review of feature selection methods with applications. In Proceedings of the 2015 38th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 25–29 May 2015; pp. 1200–1205. [Google Scholar]
- Christian, S. (Ed.) Stochastic Models of Uncertainties in Computational Mechanics; Amer Society of Civil Engineers: Reston, VA, USA, 2012; ISBN 978-0-7844-1223-7. [Google Scholar]
- Nguyen, H.-L.; Pham, B.T.; Son, L.H.; Thang, N.T.; Ly, H.-B.; Le, T.-T.; Ho, L.S.; Le, T.-H.; Tien Bui, D. Adaptive Network Based Fuzzy Inference System with Meta-Heuristic Optimizations for International Roughness Index Prediction. Appl. Sci. 2019, 9, 4715. [Google Scholar] [CrossRef]
- Nguyen, H.-L.; Le, T.-H.; Pham, C.-T.; Le, T.-T.; Ho, L.S.; Le, V.M.; Pham, B.T.; Ly, H.-B. Development of Hybrid Artificial Intelligence Approaches and a Support Vector Machine Algorithm for Predicting the Marshall Parameters of Stone Matrix Asphalt. Appl. Sci. 2019, 9, 3172. [Google Scholar] [CrossRef]
- Guilleminot, J.; Dolbow, J.E. Data-driven enhancement of fracture paths in random composites. Mech. Res. Commun. 2020, 103, 103443. [Google Scholar] [CrossRef]
- Wang, H.; Guilleminot, J.; Soize, C. Modeling uncertainties in molecular dynamics simulations using a stochastic reduced-order basis. Comput. Methods Appl. Mech. Eng. 2019, 354, 37–55. [Google Scholar] [CrossRef]
- Wang, X.; Yang, Z.; Jivkov, A.P. Monte Carlo simulations of mesoscale fracture of concrete with random aggregates and pores: A size effect study. Constr. Build. Mater. 2015, 80, 262–272. [Google Scholar] [CrossRef]
- Jaskulski, R.; Wiliński, P. Probabilistic Analysis of Shear Resistance Assured by Concrete Compression. Proced. Eng. 2017, 172, 449–456. [Google Scholar] [CrossRef]
- Ly, H.-B.; Desceliers, C.; Le, L.M.; Le, T.-T.; Pham, B.T.; Nguyen-Ngoc, L.; Doan, V.T.; Le, M. Quantification of Uncertainties on the Critical Buckling Load of Columns under Axial Compression with Uncertain Random Materials. Materials 2019, 12, 1828. [Google Scholar] [CrossRef]
- Mordechai, S. Applications of Monte Carlo Method in Science and Engineering; IntechOpen: London, UK, 2011; ISBN 978-953-307-691-1. [Google Scholar]
- Guilleminot, J.; Soize, C. Generalized stochastic approach for constitutive equation in linear elasticity: A random matrix model. Int. J. Numer. Methods Eng. 2012, 90, 613–635. [Google Scholar] [CrossRef]
- Soize, C. Uncertainty Quantification: An Accelerated Course with Advanced Applications in Computational Engineering; Interdisciplinary Applied Mathematics; Springer International Publishing: Berlin, Germany, 2017; ISBN 978-3-319-54338-3. [Google Scholar]
- Cunha, A.; Nasser, R.; Sampaio, R.; Lopes, H.; Breitman, K. Uncertainty quantification through the Monte Carlo method in a cloud computing setting. Comput. Phys. Commun. 2014, 185, 1355–1363. [Google Scholar] [CrossRef]
- Le, T.T.; Guilleminot, J.; Soize, C. Stochastic continuum modeling of random interphases from atomistic simulations. Application to a polymer nanocomposite. Comput. Methods Appl. Mech. Eng. 2016, 303, 430–449. [Google Scholar] [CrossRef]
- Soize, C.; Desceliers, C.; Guilleminot, J.; Le, T.T.; Nguyen, M.T.; Perrin, G.; Allain, J.M.; Gharbi, H.; Duhamel, D.; Funfschilling, C. Stochastic representations and statistical inverse identification for uncertainty quantification in computational mechanics. In Proceedings of the Uncecomp 2015 1st Eccomas Thematic Conference on Uncertainty Quantification in Computational Sciences and Engineering, Crete Island, Greece, 25–27 May 2015; pp. 1–26. [Google Scholar]
- Guilleminot, J.; Le, T.T.; Soize, C. Stochastic framework for modeling the linear apparent behavior of complex materials: Application to random porous materials with interphases. Acta Mech. Sin. 2013, 29, 773–782. [Google Scholar] [CrossRef]
- Staber, B.; Guilleminot, J.; Soize, C.; Michopoulos, J.; Iliopoulos, A. Stochastic modeling and identification of a hyperelastic constitutive model for laminated composites. Comput. Methods Appl. Mech. Eng. 2019, 347, 425–444. [Google Scholar] [CrossRef]
- Dao, D.V.; Trinh, S.H.; Ly, H.-B.; Pham, B.T. Prediction of Compressive Strength of Geopolymer Concrete Using Entirely Steel Slag Aggregates: Novel Hybrid Artificial Intelligence Approaches. Appl. Sci. 2019, 9, 1113. [Google Scholar] [CrossRef]
- Ly, H.-B.; Pham, B.T.; Dao, D.V.; Le, V.M.; Le, L.M.; Le, T.-T. Improvement of ANFIS Model for Prediction of Compressive Strength of Manufactured Sand Concrete. Appl. Sci. 2019, 9, 3841. [Google Scholar] [CrossRef]
- Ly, H.-B.; Le, T.-T.; Le, L.M.; Tran, V.Q.; Le, V.M.; Vu, H.-L.T.; Nguyen, Q.H.; Pham, B.T. Development of Hybrid Machine Learning Models for Predicting the Critical Buckling Load of I-Shaped Cellular Beams. Appl. Sci. 2019, 9, 5458. [Google Scholar] [CrossRef]
- Miche, Y.; Van Heeswijk, M.; Bas, P.; Simula, O.; Lendasse, A. TROP-ELM: A double-regularized ELM using LARS and Tikhonov regularization. Neurocomputing 2011, 74, 2413–2421. [Google Scholar] [CrossRef]
- Dao, D.V.; Ly, H.-B.; Trinh, S.H.; Le, T.-T.; Pham, B.T. Artificial Intelligence Approaches for Prediction of Compressive Strength of Geopolymer Concrete. Materials 2019, 12, 983. [Google Scholar] [CrossRef]
- Cokca, E.; Erol, O.; Armangil, F. Effects of compaction moisture content on the shear strength of an unsaturated clay. Geotech. Geol. Eng. 2004, 22, 285. [Google Scholar] [CrossRef]
- Spoor, G.; Godwin, R.J. Soil Deformation and Shear Strength Characteristics of Some Clay Soils at Different Moisture Contents. J. Soil Sci. 1979, 30, 483–498. [Google Scholar] [CrossRef]
- Calder, M.; Kolberg, M.; Magill, E.H.; Reiff-Marganiec, S. Feature interaction: A critical review and considered forecast. Comput. Netw. 2003, 41, 115–141. [Google Scholar] [CrossRef]



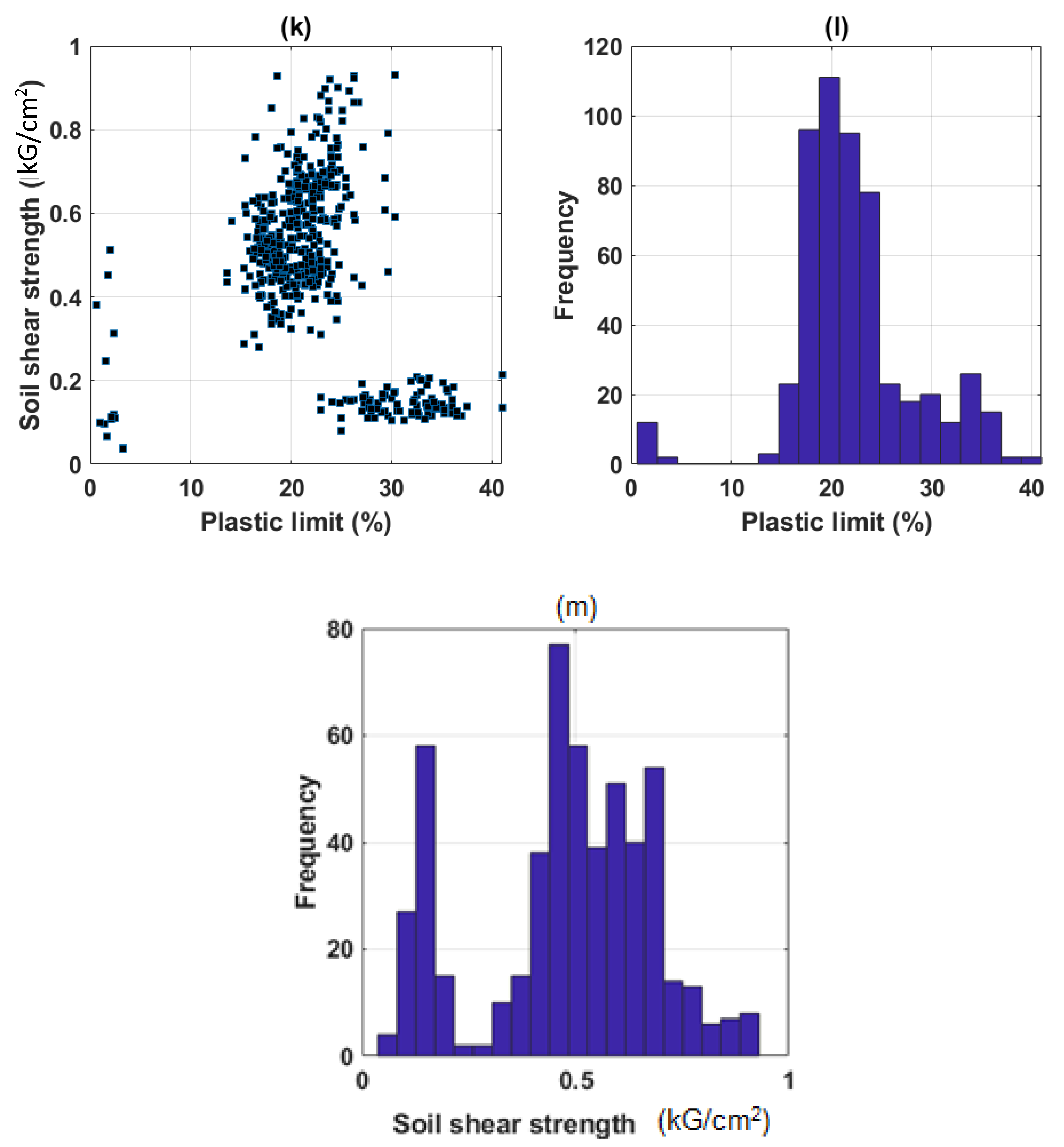











| Parameter | Clay | Moisture Content | Specific Gravity | Void Ratio | Liquid Limit | Plastic Limit | Soil Shear Strength |
|---|---|---|---|---|---|---|---|
| Unit | mm | % | - | - | % | % | kG/cm2 |
| Coding | X1 | X2 | X3 | X4 | X5 | X6 | Y |
| Min (α) | 0.2000 | 0.7200 | 0.0100 | 0.0210 | 0.7000 | 0.6000 | 0.0368 |
| Average | 33.2467 | 31.8336 | 2.6142 | 0.9142 | 42.3649 | 22.1678 | 0.4791 |
| Median | 33.2000 | 26.5500 | 2.6900 | 0.7870 | 42.5000 | 21.4000 | 0.4964 |
| Max (β) | 77.6000 | 75.1400 | 2.7500 | 2.0890 | 74.9000 | 41.0000 | 0.9307 |
| SD* | 16.1388 | 15.2671 | 0.4271 | 0.3935 | 13.2635 | 6.1376 | 0.2036 |
| Q25 | 20.7000 | 23.6100 | 2.6700 | 0.7090 | 33.5000 | 18.7000 | 0.3978 |
| Q50 | 33.2000 | 26.5500 | 2.6900 | 0.7870 | 42.5000 | 21.4000 | 0.4964 |
| Q75 | 47.4000 | 30.9700 | 2.7100 | 0.8850 | 50.4000 | 24.3000 | 0.6287 |
| Excluded | X1 | X2 | X3 | X4 | X5 | X6 | Full | Decide |
|---|---|---|---|---|---|---|---|---|
| Mean (R) | 0.9203 | 0.9121 | 0.9136 | 0.9191 | 0.8858 | 0.9167 | 0.9218 | X1 |
| Max (R) | 0.9581 | 0.9504 | 0.9502 | 0.9604 | 0.9302 | 0.9552 | - | X4 |
| Mean (RMSE) | 0.0925 | 0.0968 | 0.0944 | 0.0941 | 0.1080 | 0.0961 | 0.1082 | X1 |
| Min (RMSE) | 0.0675 | 0.0662 | 0.0639 | 0.0641 | 0.0797 | 0.0652 | - | X3 |
| Mean (MAE) | 0.0722 | 0.0762 | 0.0740 | 0.0743 | 0.0867 | 0.0753 | 0.0857 | X1 |
| Min (MAE) | 0.0506 | 0.0500 | 0.0489 | 0.0502 | 0.0601 | 0.0482 | - | X6 |
| Excluded | X2 | X3 | X4 | X5 | X6 | Full | Decide |
|---|---|---|---|---|---|---|---|
| Mean (R) | 0.9089 | 0.9149 | 0.9188 | 0.8868 | 0.9113 | 0.9203 | X4 |
| Max (R) | 0.9528 | 0.9503 | 0.9533 | 0.9333 | 0.9503 | - | X4 |
| Mean (RMSE) | 0.0957 | 0.0969 | 0.0931 | 0.1083 | 0.1002 | 0.0925 | X4 |
| Min (RMSE) | 0.0694 | 0.0683 | 0.0644 | 0.0772 | 0.0650 | - | X4 |
| Mean (MAE) | 0.0751 | 0.0760 | 0.0732 | 0.0861 | 0.0793 | 0.0722 | X4 |
| Min (MAE) | 0.0508 | 0.0507 | 0.0495 | 0.0593 | 0.0511 | - | X4 |
| Excluded | X2 | X3 | X5 | X6 | Full | Decide |
|---|---|---|---|---|---|---|
| Mean (R) | 0.7985 | 0.9138 | 0.8897 | 0.9164 | 0.9188 | X6 |
| Max (R) | 0.8864 | 0.9574 | 0.9360 | 0.9535 | - | X3 |
| Mean (RMSE) | 0.1722 | 0.0993 | 0.1219 | 0.1031 | 0.0931 | X3 |
| Min (RMSE) | 0.0990 | 0.0633 | 0.0792 | 0.0670 | - | X3 |
| Mean (MAE) | 0.1429 | 0.0778 | 0.1002 | 0.0827 | 0.0732 | X3 |
| Min (MAE) | 0.0758 | 0.0480 | 0.0591 | 0.0516 | - | X3 |
| Excluded | X2 | X5 | X6 | Full | Decide |
|---|---|---|---|---|---|
| Mean(R) | 0.5499 | 0.8571 | 0.8815 | 0.9138 | X6 |
| Max(R) | 0.7851 | 0.9322 | 0.9481 | - | X6 |
| Mean(RMSE) | 0.2673 | 0.1334 | 0.1397 | 0.0993 | X5 |
| Min(RMSE) | 0.1296 | 0.0782 | 0.0684 | - | X6 |
| Mean(MAE) | 0.2291 | 0.1093 | 0.1162 | 0.0778 | X5 |
| Min(MAE) | 0.0979 | 0.0627 | 0.0509 | - | X6 |
| Order of Importance | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Scenario 1 | X1 | X4 | X3 | X6 | X2 | X5 |
| Scenario 2 | X4 | X2 | X3 | X6 | X5 | - |
| Scenario 3 | X3 | X6 | X5 | X2 | - | - |
| Scenario 4 | X5 | X6 | X2 | - | - | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, B.T.; Nguyen-Thoi, T.; Ly, H.-B.; Nguyen, M.D.; Al-Ansari, N.; Tran, V.-Q.; Le, T.-T. Extreme Learning Machine Based Prediction of Soil Shear Strength: A Sensitivity Analysis Using Monte Carlo Simulations and Feature Backward Elimination. Sustainability 2020, 12, 2339. https://doi.org/10.3390/su12062339
Pham BT, Nguyen-Thoi T, Ly H-B, Nguyen MD, Al-Ansari N, Tran V-Q, Le T-T. Extreme Learning Machine Based Prediction of Soil Shear Strength: A Sensitivity Analysis Using Monte Carlo Simulations and Feature Backward Elimination. Sustainability. 2020; 12(6):2339. https://doi.org/10.3390/su12062339
Chicago/Turabian StylePham, Binh Thai, Trung Nguyen-Thoi, Hai-Bang Ly, Manh Duc Nguyen, Nadhir Al-Ansari, Van-Quan Tran, and Tien-Thinh Le. 2020. "Extreme Learning Machine Based Prediction of Soil Shear Strength: A Sensitivity Analysis Using Monte Carlo Simulations and Feature Backward Elimination" Sustainability 12, no. 6: 2339. https://doi.org/10.3390/su12062339
APA StylePham, B. T., Nguyen-Thoi, T., Ly, H.-B., Nguyen, M. D., Al-Ansari, N., Tran, V.-Q., & Le, T.-T. (2020). Extreme Learning Machine Based Prediction of Soil Shear Strength: A Sensitivity Analysis Using Monte Carlo Simulations and Feature Backward Elimination. Sustainability, 12(6), 2339. https://doi.org/10.3390/su12062339









