China’s Carbon Pricing Based on Heterogeneous Tail Distribution
Abstract
1. Introduction
2. Literature Review
2.1. Carbon Pricing based on Historical Carbon Price Data
2.2. Factors Influencing Carbon Price
- (1)
- Macroeconomy: The smooth and robust expansion of the macroeconomy has an obvious impact on the carbon emissions trading market. Carbon prices fluctuate considerably with the macroeconomy [4]. The increasing macroeconomy, especially the development of industrial economy, helps to increase the price of carbon emissions trading rights [5]. Conversely, carbon price falls substantially when the macroeconomy slows [6]. Stock prices, as an important indicator of macroeconomic situations, show a positive correlation with carbon prices [7].
- (2)
- Similar products: Carbon prices in different regions have the same properties and show a strong correlation; thus, they can interfere with one another [8]. As a participant in clean development mechanism (CDM) projects, China’s regional carbon emissions trading price is also affected by international carbon price mechanisms, such as the certification emission reduction (CER) and the European Union Allowance (EUA).
- (3)
- Energy price: Fossil fuel combustion is key human activity affecting GHG emissions [9]. An increase in fossil energy prices increases carbon trading prices [10]. Coal consumption is the largest source of carbon dioxide emissions, which determines the demand for carbon emission quotas and is regarded as the most important determinant of carbon pricing. Oil price plays a leading role in the trend of energy price changes; so, the impact of oil price on the carbon pricing is also important.
- (4)
- Exchange rate: As a participant in CDM projects, China faces an exchange rate volatility risk [11]. The most common settlement currency in international carbon trading is the Euro; thus, any changes in the exchange rate directly affect the carbon price.
- (5)
- Policy adjustment and information disclosure: Politics affects climate change policy, further influencing carbon trading prices. Policies can affect carbon prices, mainly due to, besides the commodity property, carbon markets having obvious political properties [12]. The carbon emissions trading market directly reflects mutual coordination between the government and the market regulations [13]. Government regulation plays a primary role because the carbon market system is not perfect in its early stages; therefore, policy adjustment and information disclosure are fundamental causes of carbon price fluctuations. Policy changes by the government weakly positively impact carbon prices. For example, the announcement of the national quota allocation plan has had a significant positive effect on the carbon price income, indicating a long-lasting pre-event effect [14].
2.3. Heterogeneous Distribution of Carbon Price
- (1)
- Is the new APT-SSAEPD-GA model more accurate for China’s carbon pricing?
- (2)
- What causes China’s carbon price to have fat and heterogeneous tails?
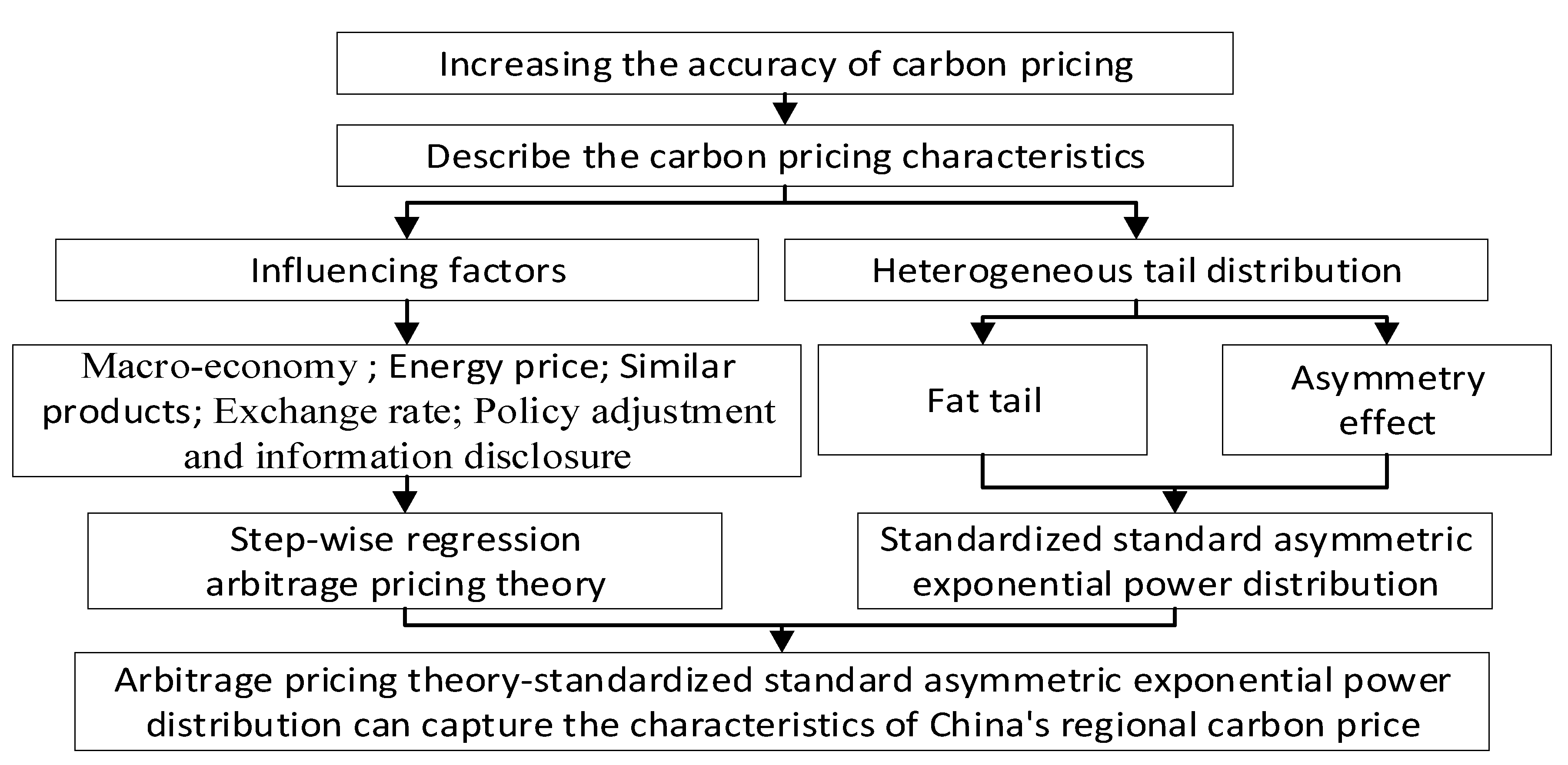
3. Methodology
3.1. Construction of Arbitrage Pricing Theory-Standardized Standard Asymmetric Exponential Power Distribution Model
3.1.1. Asymmetric Exponential Power Distribution
3.1.2. Standard Asymmetric Exponential Power Distribution (SAEPD)
3.1.3. Standardized Standard Asymmetric Exponential Power Distribution
3.2. Linear Programming Algorithm Selection and Optimization
4. Results
4.1. Data
4.2. Selection of Influencing Factors
4.3. Estimation Results
4.3.1. Parameters Estimation of China’s Carbon Pricing
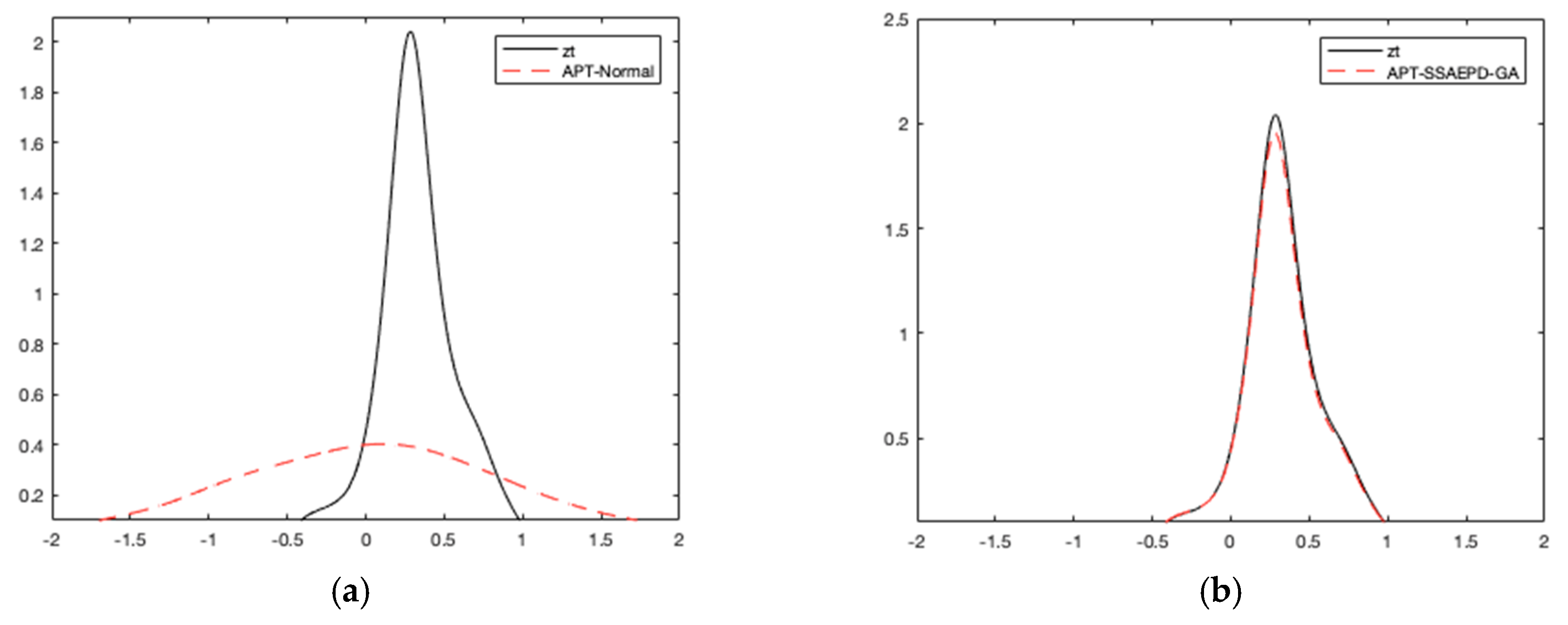
4.3.2. Residual Comparison of China’s Carbon Pricing
4.4. Robustness Test
4.5. Discussion
4.5.1. Influencing Factors and Carbon Price Mechanism
Macroeconomy
Similar Products
Energy Price
Exchange Rate
4.5.2. Heterogeneous Tail Distribution
Non-normal Distribution of Carbon Price Return
Heterogeneous Tail Distribution of Carbon Price Return
5. Conclusions
5.1. Conclusions
5.2. Policy Implications
5.3. Future Studies and Limitation
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nie, L.; Wang, W.J. Study on the game price game of carbon emission in China. Price Theory Pract. 2014, 5, 38–40. [Google Scholar]
- Zhang, C.; Yang, X. China’s regional carbon price forecasting based on Grey-Markov model. Stat. Decis. 2016, 9, 92–95. [Google Scholar]
- Zhu, B.; Wang, P.; Wei, Y. Multi scale analysis on the influence factors of carbon price based on EMD. Econ. Perspect. 2012, 6, 92–97. [Google Scholar]
- Hintermann, B.; Peterson, S.; Rickels, W. Price and Market Behavior in Phase II of the EU ETS: A Review of the Literature. Rev. Environ. Econ. Policy 2014, 110, 1381–1394. [Google Scholar]
- Hai, X.H. Research on Carbon Dioxide Price of EU ETS based on MSVAR. J. Financ. Econ. Theory 2017, 6, 37–46. [Google Scholar]
- Christiansen, A.C.; Arvanitakis, A.; Tangen, K.; Hasselknippe, H. Price determinants in the EU emissions trading scheme. Clim. Policy 2005, 5, 15–30. [Google Scholar] [CrossRef]
- Lutz, B.J.; Pigorsch, U.; Rotfuß, W. Nonlinearity in cap-and-trade systems: The EUA price and its fundamentals. Energy Econ. 2013, 40, 222–232. [Google Scholar] [CrossRef]
- Mansanet-Bataller, M.; Chevallier, J.; Hervé-Mignucci, M.; Alberola, E. EUA and sCER phase II price drivers: Unveiling the reasons for the existence of the EUA–sCER spread. Energy Policy 2011, 39, 1056–1069. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, K.; Wei, Y.; Liu, L. International Carbon Market and Its Impacts on CO2 Emission Abatement. In Energy Economics: CO2 Emissions in China; Springer: Berlin/Heidelberg, Germany, 2011; pp. 231–299. [Google Scholar]
- Hammoudeh, S.; Nguyen, D.K.; Sousa, R.M. What explains the short-term dynamics of the prices of CO2 emissions? Energy Econ. 2014, 46, 122–135. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, Y.; Zhang, T. The Integrated Measurement about Carbon Finance Market Risk of Commercial Banks Based on Copula Model. Chin. J. Manag. Sci. 2015, 23, 61–69. [Google Scholar]
- Zhang, Y.J.; Huang, Y.S. The multi-frequency correlation between EUA and sCER futures prices: Evidence from the EMD approach. Fractal 2015, 23, 1–18. [Google Scholar] [CrossRef]
- Zhang, Y.J. Research on carbon emission trading mechanisms: Current status and future possibilities. Int. J. Glob. Energy Issues 2016, 39, 89–107. [Google Scholar] [CrossRef]
- Jia, J.J.; Xu, J.H.; Fan, Y. Impact of Pivotal Announcement Event on Carbon Price in European Union Emission Trading Scheme. Bull. Chin. Acad. Sci. 2018, 32, 1347–1355. [Google Scholar]
- Tzang, S.W.; Wang, C.W.; Yu, M.T. Systematic risk and volatility skew. Int. Rev. Econ. Financ. 2016, 43, 72–87. [Google Scholar] [CrossRef]
- Sanin, M.E.; Violante, F.; Mansanet-Bataller, M. Understanding volatility dynamics in the EU-ETS market. Energy Policy 2015, 82, 21–331. [Google Scholar]
- Montagnoli, A.; Vries, F.P.D. Carbon trading thickness and market efficiency. Energy Econ. 2010, 32, 1331–1336. [Google Scholar] [CrossRef]
- Dutta, A. Modeling and Forecasting the Volatility of Carbon Emission Market: The Role of Outliers, Time-varying Jumps and Oil Price Risk. J. Clean Prod. 2017, 172, 2773–2781. [Google Scholar] [CrossRef]
- Benz, E.A.; Trück, S. Modeling the Price Dynamics of Co2 Emission Allowances. Energy Econ. 2009, 31, 4–15. [Google Scholar] [CrossRef]
- Zhu, D.; Zinde-Walsh, V. Properties and estimation of asymmetric exponential power distribution. J. Econ. 2007, 148, 86–99. [Google Scholar] [CrossRef]
- Zhu, J.Y.; Li, L.L. Analysis of the CDS Correlation Based on a New VAR-GARCH Model with SSAEPD Margins. China Financ. Rev. Int. Conf. 2015, 26, 37–62. [Google Scholar]
- Tong, X.; Li, X.; Tong, L.; Jiang, X. Spatial spillover and the influencing factors relating to provincial carbon emissions in china based on the spatial panel data model. Sustainability 2018, 10, 4739. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, H.W.; Zikhali, P.; Lv, Y.K. Carbon Emissions in China: A Spatial Econometric Analysis, at the Regional Level. Sustainability 2014, 6, 6005–6023. [Google Scholar] [CrossRef]

| Shenzhen Allowance 2013 (SZA 2013) | Shenzhen Allowance 2014 (SZA 2014) | Shenzhen Allowance 2015 (SZA 2015) | Shenzhen Allowance 2016 (SZA 2016) | Shenzhen Allowance 2017 (SZA 2017) | Shenzhen Allowance 2018 (SZA 2018) | |
|---|---|---|---|---|---|---|
| Mean | −0.0023 | −0.0020 | −0.0020 | −0.0025 | −0.0022 | −0.0024 |
| Maximum | 0.2598 | 0.0961 | 0.1906 | 0.0965 | 0.0962 | 0.1280 |
| Minimum | −0.1056 | −0.1061 | −0.1762 | −0.2100 | −0.3157 | −0.1379 |
| SD | 0.0374 | 0.05297 | 0.0546 | 0.0764 | 0.0638 | 0.0478 |
| Skewness | 0.5017 | −0.2068 | −0.1738 | −0.1261 | −0.5702 | −0.2759 |
| Kurtosis | 13.7309 | 3.5895 | 3.8157 | 1.8198 | 4.3431 | 4.5366 |
| Jarque–Bera | 1989.2080 | 8.8815 | 13.4619 | 24.942 | 53.1667 | 45.6535 |
| Probability | 0.00 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 |
| Factors | Index |
|---|---|
| International economic development | Standard and Poor’s 500 Composite Stock Price Index (S&P 500) |
| Domestic economic development | China Securities Index 300 (CSI300) |
| Similar product | Certification emission reduction (CER) European Union allowance (EUA) |
| SZA 2013 | |
| SZA 2014 | |
| SZA 2015 | |
| SZA 2016 SZA 2017 | |
| Fujian carbon price | |
| Tianjin carbon price Beijing carbon price Hubei carbon price Guangdong carbon price Shanghai carbon price Chongqing carbon price Shenzhen carbon price | |
| Energy price | Coal price |
| Oil price | |
| Exchange rate | Euro against Chinese Yuan |
| Influencing Factor | Coefficient |
|---|---|
| SZA 2015 | 0.1512 *** |
| SZA 2017 | 0.1091 *** |
| SZA 2013 | 0.1732 *** |
| Fujian carbon price | −0.1151 *** |
| CSI 300 | 0.4012 ** |
| Tianjin carbon price | 0.3073 ** |
| Euro against Chinese Yuan | −0.7108 * |
| Shanghai carbon price | −0.0448 * |
| Coal | −0.2922 * |
| Factors | Arbitrage Pricing Theory-Normal (APT-Normal) | Arbitrage Pricing Theory-Standardized Standard Asymmetric Exponential Power Distribution-Interior Point (APT-SSAEPD-IP) | Arbitrage Pricing Theory-Standardized Standard Asymmetric Exponential Power Distribution-Genetic Algorithm (APT-SSAEPD-GA) |
|---|---|---|---|
| SZA 2015 | 0.1503 | 0.1700 | 0.1967 |
| SZA 2017 | 0.1077 | 0.1058 | 0.3584 |
| SZA 2013 | 0.1705 | 0.9935 | 0.9991 |
| Fujian carbon price | −0.1167 | −0.1913 | −0.2101 |
| CSI 300 | 0.4035 | 0.6980 | 0.7631 |
| Tianjin carbon price | 0.3157 | 0.3159 | 0.4098 |
| Euro against Chinese Yuan | −0.7096 | −1.0300 | −1.1124 |
| Shanghai carbon price | −0.0453 | −0.0423 | −0.0710 |
| Coal | −0.3318 | −0.4470 | −0.5212 |
| α | 0.5 | 0.6448 | 0.7009 |
| p1 | 2 | 0.7975 | 0.9792 |
| p2 | 2 | 0.2622 | 0.2912 |
| Akaike information criterion (AIC) | −3.3165 | −4.9775 | −5.7251 |
| Schwarz criterion (SC) | −3.2187 | −4.9678 | −5.7153 |
| Factors | APT-Normal | APT-SSAEPD-IP | APT-SSAEPD-GA |
|---|---|---|---|
| SZA 2015 | −0.0897 | −0.3709 | −0.4903 |
| SZA 2014 | 0.0666 | 0.0904 | −0.1507 |
| Guangdong carbon price | 0.0948 | 0.2033 | 0.2180 |
| SZA 2013 | −0.0539 | −0.1521 | −0.1713 |
| CER | 0.0597 | 0.0873 | 0.0967 |
| Euro against Chinese Yuan | −0.4215 | −0.7017 | −0.8144 |
| SZA 2017 | 0.0212 | 0.0406 | 0.0637 |
| EUA | 0.0374 | 0.1549 | −0.2501 |
| α | 0.5 | 0.4190 | 0.4225 |
| p1 | 2 | 0.4760 | 0.4761 |
| p2 | 2 | 1.1537 | 1.2842 |
| AIC | −3.9132 | −4.0214 | −4.9468 |
| SC | −3.8252 | −4.0116 | −4.9371 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Zhang, C.; Yang, Y.; Wu, Y.; Yun, P.; Wagan, Z.A. China’s Carbon Pricing Based on Heterogeneous Tail Distribution. Sustainability 2020, 12, 2754. https://doi.org/10.3390/su12072754
Yang X, Zhang C, Yang Y, Wu Y, Yun P, Wagan ZA. China’s Carbon Pricing Based on Heterogeneous Tail Distribution. Sustainability. 2020; 12(7):2754. https://doi.org/10.3390/su12072754
Chicago/Turabian StyleYang, Xianzi, Chen Zhang, Yu Yang, Yaqi Wu, Po Yun, and Zulfiqar Ali Wagan. 2020. "China’s Carbon Pricing Based on Heterogeneous Tail Distribution" Sustainability 12, no. 7: 2754. https://doi.org/10.3390/su12072754
APA StyleYang, X., Zhang, C., Yang, Y., Wu, Y., Yun, P., & Wagan, Z. A. (2020). China’s Carbon Pricing Based on Heterogeneous Tail Distribution. Sustainability, 12(7), 2754. https://doi.org/10.3390/su12072754





