Application and Comparison of Multiple Models on Agricultural Sustainability Assessments: A Case Study of the Yangtze River Delta Urban Agglomeration, China
Abstract
:1. Introduction
2. Materials and Methods
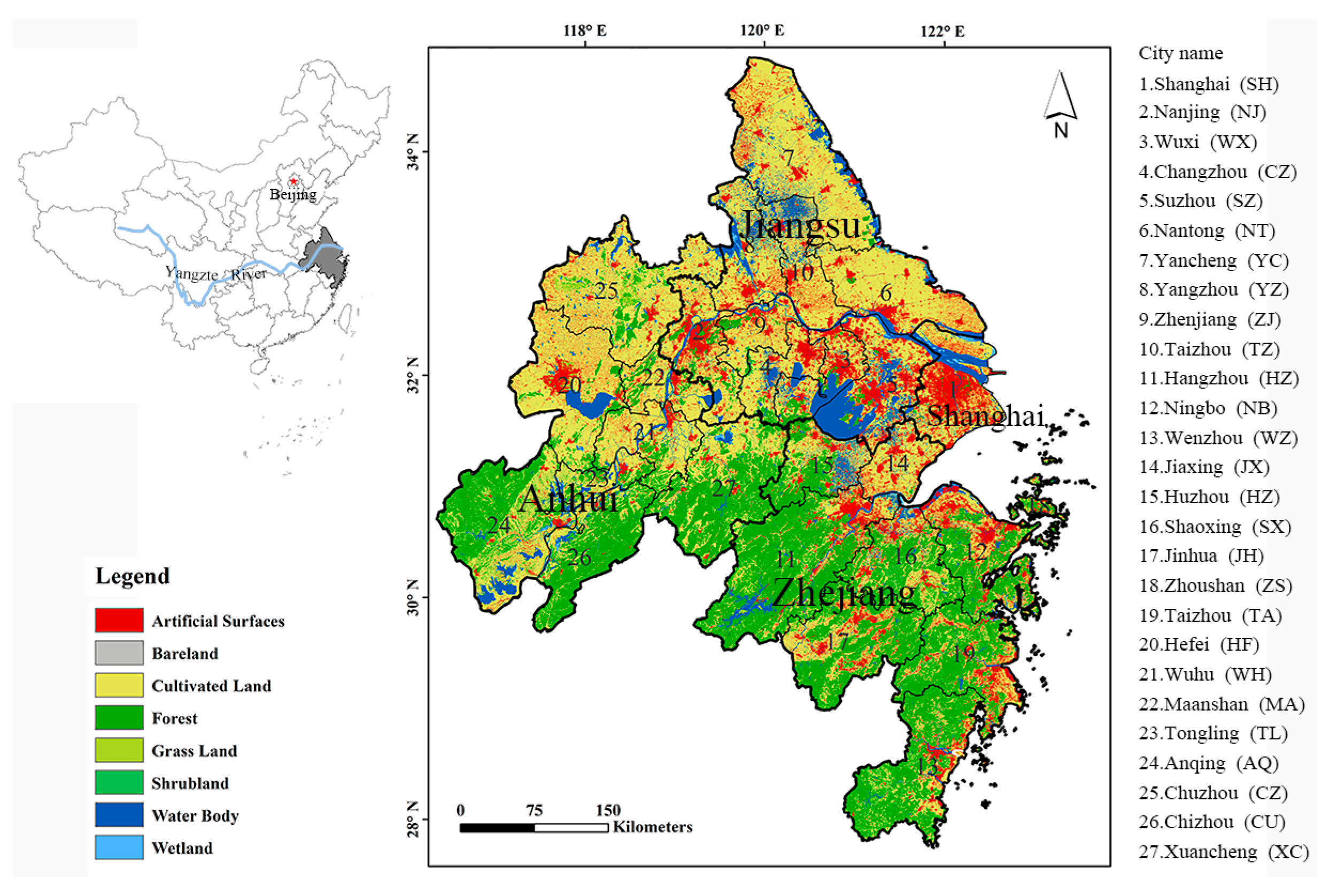
2.1. Study Area
2.2. Model Description and Data Preparation
2.2.1. DPSIR Model
2.2.2. EF Model
2.2.3. EMA Model
2.2.4. Results Comparison Analysis
3. Results
3.1. DPSIR Model
3.2. EF Model
3.3. EMA Model
3.4. Comparison of the Three Models
4. Discussion
4.1. Comparative Analysis with the Literature
4.2. Uncertainty Analysis of the Three Models
4.3. Adaptability Analysis of the Three Models
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shah, S.M.; Liu, G.; Yang, Q.; Wang, X.; Casazza, M.; Agostinho, F.; Lombardi, G.V.; Giannetti, B.F. Emergy-based valuation of agriculture ecosystem services and dis-services. J. Clean. Prod. 2019, 239, 1–7. [Google Scholar] [CrossRef]
- Tilman, D.; Cassman, K.G.; Matson, P.A.; Naylor, R.; Polasky, S. Agricultural sustainability and intensive production practices. Nature 2002, 418, 671–677. [Google Scholar] [CrossRef] [PubMed]
- Tilman, D.; Balzer, C.; Hill, A.; Befort, B.L. Global food demand and the sustainable intensification of agriculture. Proc. Natl. Acad. Sci. USA 2011, 108, 20260–20264. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Godfray, H.C.J.; Beddington, J.R.; Crute, I.R.; Haddad, L.; Lawrence, D.; Muir, J.F.; Pretty, J.; Robinson, S.; Thomas, S.M.; Toulmin, C. Food security: The challenge of feeding 9 billion people. Science 2010, 327, 812–818. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Q.; Ma, Z.; Ma, Q.; Liu, M.; Yuan, X.; Mu, R.; Zuo, J.; Zhang, J.; Wang, S. Comprehensive evaluation and optimization of agricultural system: An emergy approach. Ecol. Indic. 2019, 107, 1–8. [Google Scholar] [CrossRef]
- Jia, H. Agriculture: Science and technology safeguard sustainability. Natl. Sci. Rev. 2019, 6, 595–600. [Google Scholar] [CrossRef]
- Quintero-Angel, M.; González-Acevedo, A. Tendencies and challenges for the assessment of agricultural sustainability. Agric. Ecosyst. Environ. 2018, 254, 273–281. [Google Scholar] [CrossRef]
- Binder, C.R.; Feola, G.; Steinberger, J.K. Considering the normative, systemic and procedural dimensions in indicator-based sustainability assessments in agriculture. Environ. Impact Assess. Rev. 2010, 30, 71–81. [Google Scholar] [CrossRef]
- Soldi, A.; Meza, M.J.A.; Guareschi, M.; Donati, M.; Ortiz, A.I. Sustainability Assessment of Agricultural Systems in Paraguay: A Comparative Study Using FAO’s SAFA Framework. Sustainability. 2019, 11, 3745. [Google Scholar] [CrossRef] [Green Version]
- Calleros-Islas, A. Sustainability assessment. An adaptive low-input tool applied to the management of agroecosystems in México. Ecol. Indic. 2019, 105, 386–397. [Google Scholar] [CrossRef]
- Van Cauwenbergh, N.; Biala, K.; Bielders, C.; Brouckaert, V.; Franchois, L.; Cidad, V.G.; Hermy, M.; Mathijs, E.; Muys, B.; Reijnders, J.; et al. SAFE—A hierarchical framework for assessing the sustainability of agricultural systems. Agric. Ecosyst. Environ. 2007, 120, 229–242. [Google Scholar] [CrossRef]
- OECD. Environmental Indicators—Development, Measurement and Use; Organisation of Economic Co-operation and Development: Paris, France, 2003. [Google Scholar]
- Niemeijer, D.; De Groot, R.S. Framing environmental indicators: Moving from causal chains to causal networks. Environ. Dev. Sustain. 2006, 10, 89–106. [Google Scholar] [CrossRef]
- Wen, S.; Wen, X.; An, Y. Analysis of Sustainability of the Dryland Farming with Limited Irrigation Based on DPSIR Model in Tongxin, Ningxia Hui Autonomous Region. Res. Soil Water Conserv. 2011, 18, 231–236. [Google Scholar]
- Binimelis, R.; Monterroso, I.; Rodríguez-Labajos, B. Catalan agriculture and genetically modified organisms (GMOs)—An application of DPSIR model. Ecol. Econ. 2010, 69, 55–62. [Google Scholar] [CrossRef]
- Chen, W.; Geng, Y.; Dong, H.; Tian, X.; Zhong, S.; Wu, Q.; Xu, Y.; Zhang, Q.; Li, S. An emergy accounting based regional sustainability evaluation: A case of Qinghai in China. Ecol. Indic. 2018, 88, 152–160. [Google Scholar] [CrossRef]
- Odum, H.T. Emergy and Decision Making; John Wiley: New York, NY, USA, 1996. [Google Scholar]
- Scienceman, D.M. Letters to the editor: Emergy definition. Ecol. Eng. 1997, 9, 209–212. [Google Scholar]
- Skaf, L.; Buonocore, E.; Dumontet, S.; Capone, R.; Franzese, P.P. Food security and sustainable agriculture in Lebanon: An environmental accounting framework. J. Clean. Prod. 2019, 209, 1025–1032. [Google Scholar] [CrossRef]
- Zhao, H.; Zhai, X.; Guo, L.; Liu, K.; Huang, D.; Yang, Y.; Li, J.; Xie, S.; Zhang, C.; Tang, S.; et al. Assessing the efficiency and sustainability of wheat production systems in different climate zones in China using emergy analysis. J. Clean. Prod. 2019, 235, 724–732. [Google Scholar] [CrossRef]
- Wackernagel, M. Our Ecological Footprint: Reducing Human Impact on the Earth; New Society Publishers: Gabriola Island, BC, Canada, 1996. [Google Scholar]
- Passeri, N.; Borucke, M.; Blasi, E.; Franco, S.; Lazarus, E. The influence of farming technique on cropland: A new approach for the Ecological Footprint. Ecol. Indic. 2013, 29, 1–5. [Google Scholar] [CrossRef]
- Passeri, N.; Blasi, E.; Franco, S.; Martella, A.; Pancino, B.; Cicatiello, C. The environmental sustainability of national cropping systems: From assessment to policy impact evaluation. Land Use Policy 2016, 57, 305–312. [Google Scholar] [CrossRef]
- Li, M.; Zhou, Y.; Wang, Y.; Singh, V.P.; Li, Z.; Li, Y. An ecological footprint approach for cropland use sustainability based on multi-objective optimization modelling. J. Environ. Manag. 2020, 273, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Hao, J.; Chen, A.; Wang, N. Supply and demand banlance of ecological carrying capacitu in provincial arable land of China. J. China Agric. Univ. 2019, 24, 146–155. [Google Scholar]
- Shi, K.; Diao, C.; Sun, X.; Zuo, T. Ecological balance between supply and demand in Chongqing City based on cultivated land ecological footprint method. Acta Ecol. Sin. 2013, 33, 1872–1880. [Google Scholar] [CrossRef]
- Liu, M.; Li, W.; Xie, G. Estimation of China ecological footprint production coefficient based on net primary productivity. Chin. Acad. Sci. 2010, 29, 592–597. [Google Scholar]
- Wang, C.; Zhang, S.; Yan, W.; Wang, R.; Liu, J.; Wang, Y. Evaluating renewable natural resources flow and net primary productivity with a GIS-Emergy approach: A case study of Hokkaido, Japan. Sci. Rep. 2016, 6, 1–7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, Y.C.; Huang, S.L.; Budd, W.W. Assessing the environmental impacts of high-altitude agriculture in Taiwan: A Driver-Pressure-State-Impact-Response (DPSIR) framework and spatial emergy synthesis. Ecol. Indic. 2013, 32, 42–50. [Google Scholar] [CrossRef]
- Zhao, S.; Li, Z.; Li, W. A modified method of ecological footprint calculation and its application. Ecol. Model. 2004, 185, 65–75. [Google Scholar] [CrossRef]
- Talukder, B.; Blay-Palmer, A.; Hipel, K.W.; VanLoon, G.W. Elimination method of multi-criteria decision analysis (MCDA): A simple methodological approach for assessing agricultural sustainability. Sustainability 2017, 9, 287. [Google Scholar] [CrossRef] [Green Version]
- De Olde, E.M.; Moller, H.; Marchand, F.; McDowell, R.W.; MacLeod, C.J.; Sautier, M.; Halloy, S.; Barber, A.; Benge, J.; Bockstaller, C.; et al. When experts disagree: The need to rethink indicator selection for assessing sustainability of agriculture. Environ. Dev. Sustain. 2017, 19, 1327–1342. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Sun, Y.; Wu, J. Environmental warning system based on the DPSIR model: A practical and concise method for environmental assessment. Sustainability 2018, 10, 1728. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Wang, X.; Qu, L.; Li, S.; Lin, Y.; Yao, R.; Zhou, X.; Li, J. Land use/cover predictions incorporating ecological security for the Yangtze River Delta region, China. Ecol. Indic. 2020, 119, 1–11. [Google Scholar] [CrossRef]
- Wang, Y.; Ding, Q.; Zhuang, D. An eco-city evaluation method based on spatial analysis technology: A case study of Jiangsu Province, China. Ecol. Indic. 2015, 58, 37–46. [Google Scholar] [CrossRef]
- Hoang, H.T.T.; Truong, Q.H.; Nguyen, A.T.; Hens, L. Multicriteria evaluation of tourism potential in the central highlands of vietnam: Combining geographic information system (GIS), analytic hierarchy process (AHP) and principal component analysis (PCA). Sustainability 2018, 10, 3097. [Google Scholar] [CrossRef] [Green Version]
- Delgado, A.; Romero, I. Environmental conflict analysis using an integrated grey clustering and entropy-weight method: A case study of a mining project in Peru. Environ. Model. Softw. 2016, 77, 108–121. [Google Scholar] [CrossRef]
- Li, S.; Wei, H.; Ni, X.; Gu, Y.W.; Li, C. Evaluation of urban human settlement quality in Ningxia based on AHP and the entropy method. Chin. J. Appl. Ecol. 2014, 25, 2700–2708. [Google Scholar]
- Simmons, C.; Lewis, K.; Barrett, J. Two feet-two approaches: A component based model of ecological footprinting. Ecol. Econ. 2000, 32, 375–380. [Google Scholar]
- Liu, Y.; Ma, Y. Progress and outlook of agricultural ecological footprints. Chin. J. Eco-Agric. 2019, 27, 1115–1123. [Google Scholar]
- Liu, G.; Yang, Z. Emergy Theory and Practice: Ecological Economic Accounting and Urban Green Management; Science Press: Beijing, China, 2018; pp. 363–372. [Google Scholar]
- Brown, M.T.; Ulgiati, S. Emergy assessment of global renewable sources. Ecol. Model. 2015, 339, 148–156. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Fu, X.; Zheng, D. Emergy analysis for evaluating sustainability of Chinese economy. J. Nat. Resour. 2001, 4, 287–294. [Google Scholar]
- Duan, Y.; Liu, Y.; Liu, X.; Wang, H. Identification of polycentric urban structure of central chongqing using points of interest big data. J. Nat. Resour. 2018, 33, 788–800. [Google Scholar]
- Yang, Q. The Research of Gansu Agricultural Ecosystem Sustainable Development on the Base of Emergy Theory and Model of Ecological Footprint; Gansu Agricultural University: Gansu, China, 2013. [Google Scholar]
- Yuan, H. Research of Regional Sustainable DeveloPment Based on the Emergy Theory and Eeological Footprint Model-Taking Wanzhou District of Chongqing as an Example. Master’s Thesis, Southwest University, Chongqing, China, 2011. [Google Scholar]
- Nakajima, E.S.; Ortega, E. Carrying capacity using emergy and a new calculation of the ecological footprint. Ecol. Indic. 2016, 60, 1200–1207. [Google Scholar] [CrossRef]
- Siche, J.; Agostinho, F.; Ortega, E.; Romeiro, A. Sustainability of nations by indices: Comparative study between environmental sustainability index, ecological footprint and the emergy performance indices. Ecol. Econ. 2008, 66, 628–637. [Google Scholar] [CrossRef]
- Agostinho, F.; Pereira, L. Support area as an indicator of environmental load: Comparison between embodied energy, ecological footprint, and emergy accounting methods. Ecol. Indic. 2013, 24, 494–503. [Google Scholar] [CrossRef]
- Kharrazi, A.; Kraines, S.; Hoang, L.; Yarime, M. Advancing quantification methods of sustainability: A critical examination emergy, exergy, ecological footprint, and ecological information-based approaches. Ecol. Indic. 2014, 37, 81–89. [Google Scholar] [CrossRef]
- Hou, Y.; Zhou, S.; Burkhard, B.; Müller, F. Socioeconomic influences on biodiversity, ecosystem services and human well-being: A quantitative application of the DPSIR model in Jiangsu, China. Sci. Total. Environ. 2014, 490, 1012–1028. [Google Scholar] [CrossRef]
- Cao, J.; Li, H.; Yang, J.; Zhang, Q. Comparison of sustainable development status in Hubei Provice based on traditional ecological footprint method and emerfy ecological footprint method. J. Hubei Univ. (Nat. Sci.) 2011, 33, 313–317. [Google Scholar]
- Amaral, L.P.; Martins, N.; Gouveia, J.B. A review of emergy theory, its application and latest developments. Renew. Sustain. Energy Rev. 2016, 54, 882–890. [Google Scholar] [CrossRef]
- Zhang, L.; Bao, B.; Yang, S. Spatial exploratory analysis of agricultural sustainable development in China. Econ. Geogr. 2019, 39, 159–164. [Google Scholar]
- Luo, Q.; Tang, Q.; Liu, Y.; Gao, M.; Ma, L. Construction of index system evaluating agricultural sustainable development in China. Chin. Agric. Sci. Bull. 2017, 33, 158–164. [Google Scholar]
- Agricultural Modernization Process and Development Level of Huzhou Rank First for 5 Consecutive Years in Zhejiang Province. Available online: https://m.sohu.com/a/270519176_167432 (accessed on 23 October 2018).
- Yang, D.; Jiang, H. Food security of main grain sales regions in China-based on a gap in balance between grain supply and demand. J. Agric. Sci. Technol. 2017, 19, 1–9. [Google Scholar]
- Mili, S.; Martínez-Vega, J. Accounting for regional heterogeneity of agricultural sustainability in Spain. Sustainability 2019, 11, 299. [Google Scholar] [CrossRef] [Green Version]
- Hubeau, M.; Marchand, F.; Coteur, I.; Mondelaers, K.; Debruyne, L.; Van Huylenbroeck, G. A new agri-food systems sustainability approach to identify shared transformation pathways towards sustainability. Ecol. Econ. 2017, 131, 12. [Google Scholar] [CrossRef]









| Target Layer | Criterion Layer | Indicator Layer | Combined Weight | |
|---|---|---|---|---|
| Agricultural sustainability assessment of the YRDUA | Driver (D) | 1 | Natural population growth rate (%) | 0.0247 |
| 2 | Urbanization level (%) | 0.0298 | ||
| 3 | Disposable income between urban and rural residents (%) | 0.0354 | ||
| 4 | Per capita grain possession (kg) | 0.0343 | ||
| Pressure (P) | 5 | Level of fertilizer use (kg ha−1) | 0.0510 | |
| 6 | Consumption of pesticides (kg ha−1) | 0.0583 | ||
| 7 | Plastics film for agricultural use (kg ha−1) | 0.0546 | ||
| 8 | Agricultural water consumption (m3 ha−1) | 0.0440 | ||
| 9 | Electricity consumption of per unit of agricultural added value (Kwh yuan−1) | 0.0354 | ||
| State (S) | 10 | Per capita area of cultivated land (ha per−1) | 0.0282 | |
| 11 | Multiple cropping index (%) | 0.0399 | ||
| 12 | Area ratio of high and medium quality of cultivated land (%) | 0.0641 | ||
| 13 | Effective utilization coefficient of irrigation water (%) | 0.0361 | ||
| 14 | Forest coverage rate of city (%) | 0.0423 | ||
| Impact (I) | 15 | Grain production of per unit area of cultivated land (kg ha−1) | 0.0412 | |
| 16 | Agricultural added value of per unit area of cultivated land (yuan ha−1) | 0.0447 | ||
| 17 | Agricultural value added of per labor (yuan per−1) | 0.0515 | ||
| 18 | Farmland abandonment (%) | 0.0331 | ||
| Response (R) | 19 | Total power of agricultural machinery (Kw ha−1) | 0.0307 | |
| 20 | Rate of cultivated land using water-saving irrigation (%) | 0.0469 | ||
| 21 | Application of facility agriculture (%) | 0.0536 | ||
| 22 | Level of large-scale modern agriculture (%) | 0.0454 | ||
| 23 | Quality of agricultural labor (%) | 0.0412 | ||
| 24 | Proportion of R&D investment in agriculture (%) | 0.0335 | ||
| Criterion Layer | Driving Layer | Pressure Layer | State Layer | Impact Layer | Response Layer | |
|---|---|---|---|---|---|---|
| 5 | 4 | 5 | 5 | 4 | 6 | |
| 1.12 | 0.89 | 1.12 | 1.12 | 0.89 | 1.26 | |
| 0.004 | 0.003 | 0.012 | 0.074 | 0.009 | 0.038 |
| Types | Agroecosystem Ecological Carrying Situation | EI |
|---|---|---|
| Agroecosystem ecological affluent | Affluent | 1.1 < EI |
| Agroecosystem ecological balance | Balance | 1 < EI ≤ 1.1 |
| Deficit | 0.9 < EI ≤ 1.0 | |
| Agroecosystem ecological deficit | Overload | 0.7 < EI ≤ 0.9 |
| Severe overload | EI ≤ 0.7 |
| Items | Unit | UEV (sej/unit) | References for UEV |
|---|---|---|---|
| Global Tripartite | |||
| 1 Solar emergy | j | 1.00 × 100 | (Odum, 1996) |
| 2 Earth cycle emergy | j | 4.90 × 103 | (Odum, 1996) |
| Sum of Tripartite | |||
| Secondary and Tertiary Sources | |||
| 3 Rain chemical emergy | j | 2.31 × 104 | (Odum, 1996) |
| 4 Rain geopotential emergy | j | 1.33 × 104 | (Odum, 1996) |
| 5 Wind emergy | j | 1.24 × 103 | (Odum, 1996) |
| Largest of 2nd and 3rd | |||
| Renewable Input (R, locally available) | |||
| Nonrenewable Input (N0, locally available) | |||
| 6 Topsoil losses | j | 9.40 × 104 | (Brown and Bardi, 2001) |
| Purchased Renewable Resources (FR) | |||
| 7 Human labor (10%) | sej/h | 5.72 × 1013 | (Liu, 2018) |
| 8 Irrigating water | sej/kg | 2.13 × 104 | (Liu, 2018) |
| 9 Seed | g | 9.07 × 108 | Coppola(2009) |
| Subtotal | |||
| Purchased Nonrenewable Resources (FN) | |||
| 10 Human labor (90%) | sej/h | 5.72 × 1013 | (Liu, 2018) |
| 11 Electricity | j | 2.21 × 105 | (Liu, 2018) |
| 12 Nitrogen fertilizer | g | 4.83 × 109 | (Odum, 1996) |
| 13 Phosphate fertilizer | g | 4.95 × 109 | (Odum, 1996) |
| 14 Potash fertilizer | g | 1.40 × 109 | (Odum, 1996) |
| 15 Compound fertilizer | g | 3.56 × 109 | (Odum, 1996) |
| 16 Plastic sheeting | g | 4.83 × 108 | (Brown and Bardi, 2001) |
| 17 Diesel | j | 8.38 × 104 | (Odum, 1996) |
| 18 Pesticide | g | 2.03 × 109 | Lan et al., 2002 |
| 19 Capital investment | ¥ | 9.23 × 1011 | Zhao et al. (2019) |
| Subtotal | |||
| Output (E) | |||
| 21 Paddy rice | j | 4.56 × 104 | Lan et al., 2002 |
| 22 Corn | j | 2.70 × 104 | Ulgiati et al. (1993) |
| 23 Wheat | j | 6.80 × 104 | Lu et al. (2010) |
| 24 Soybean | j | 8.30 × 104 | Ulgiati et al. (1993) |
| 25 Potato | j | 8.30 × 104 | Lu et al. (2010) |
| 26 Peanut | j | 8.60 × 104 | Ulgiati et al. (1993) |
| 27 Rapeseed | j | 8.60 × 104 | Ulgiati et al. (1993) |
| 29 Cotton | j | 1.90 × 104 | Ulgiati et al. (1993) |
| 30 Vegetables | j | 2.70 × 104 | Lu et al. (2010) |
| Subtotal | |||
| Wastes Emergy (W) | |||
| 31 Rice straw | j | 4.96 × 104 | Sui et al. (2006) |
| 32 Corn stalk | j | 4.96 × 104 | Sui et al. (2006) |
| 33 Wheat stem | j | 4.96 × 104 | Sui et al. (2006) |
| 34 Soybean stem | j | 4.96 × 104 | Sui et al. (2006) |
| 35 Rape stem | j | 4.96 × 104 | Sui et al. (2006) |
| Subtotal |
| Emergy Indicators | Evaluation Expression | Meaning |
|---|---|---|
| Local renewable environmental resources | R | Renewable emergy flows from local resources, such as sunlight, rain, wind, and so on |
| Local nonrenewable environmental resources | N0 | Slow-renewable resources used in a nonrenewable manner such as soil |
| Purchased renewable resources | FR | Renewable resources and service from artificial input |
| Purchased nonrenewable resources | FN | Nonrenewable resources from artificial input |
| Total energy input | U = R + N0 + FR + FN | Emergy flows of total input |
| Total energy output | Y = E + W | Total energy of products |
| Emergy yield ratio | EYR = Y/(FR + FN) | A measure of ecological benefits of agricultural system |
| Environmental loading ration | ELR = (N0 + FN)/(R + FR) | A measure of the potential stress of the agricultural system on the local environment |
| Emergy sustainability index | ESI = EYR/ELR | A measure of the sustainability of the production system |
| DPSIR Model | EF Model | EMA Model | |
|---|---|---|---|
| DPSIR model | 1.00 | - | - |
| EF model | 0.71 (P < 0.01) | 1.00 | - |
| EMA model | 0.25 (P = 0.902 > 0.05) | −0.28 (P = 0.151 > 0.05) | 1.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, X.; Zhang, D.; Li, C.; Li, Y.; Huang, J.; Wang, X. Application and Comparison of Multiple Models on Agricultural Sustainability Assessments: A Case Study of the Yangtze River Delta Urban Agglomeration, China. Sustainability 2021, 13, 121. https://doi.org/10.3390/su13010121
Geng X, Zhang D, Li C, Li Y, Huang J, Wang X. Application and Comparison of Multiple Models on Agricultural Sustainability Assessments: A Case Study of the Yangtze River Delta Urban Agglomeration, China. Sustainability. 2021; 13(1):121. https://doi.org/10.3390/su13010121
Chicago/Turabian StyleGeng, Xiaolei, Dou Zhang, Chengwei Li, Yanyao Li, Jingling Huang, and Xiangrong Wang. 2021. "Application and Comparison of Multiple Models on Agricultural Sustainability Assessments: A Case Study of the Yangtze River Delta Urban Agglomeration, China" Sustainability 13, no. 1: 121. https://doi.org/10.3390/su13010121





