S235JRC+C Steel Response Analysis Subjected to Uniaxial Stress Tests in the Area of High Temperatures and Material Fatigue
Abstract
:1. Introduction
2. Data Relevant for Research
Material
3. Results and Discussion
3.1. Tensile Engineering Stress-Strain Diagrams and Mechanical Properties Versus Temperature
- the chemical composition of the test material specified in this paper as well as chemical composition of the material specified in [11] is within the limits set by the EN standard.
- the values of the tested mechanical properties of steel S235JRC + C shown in this paper and those shown for the material S235JRC in [11], differ from each other.
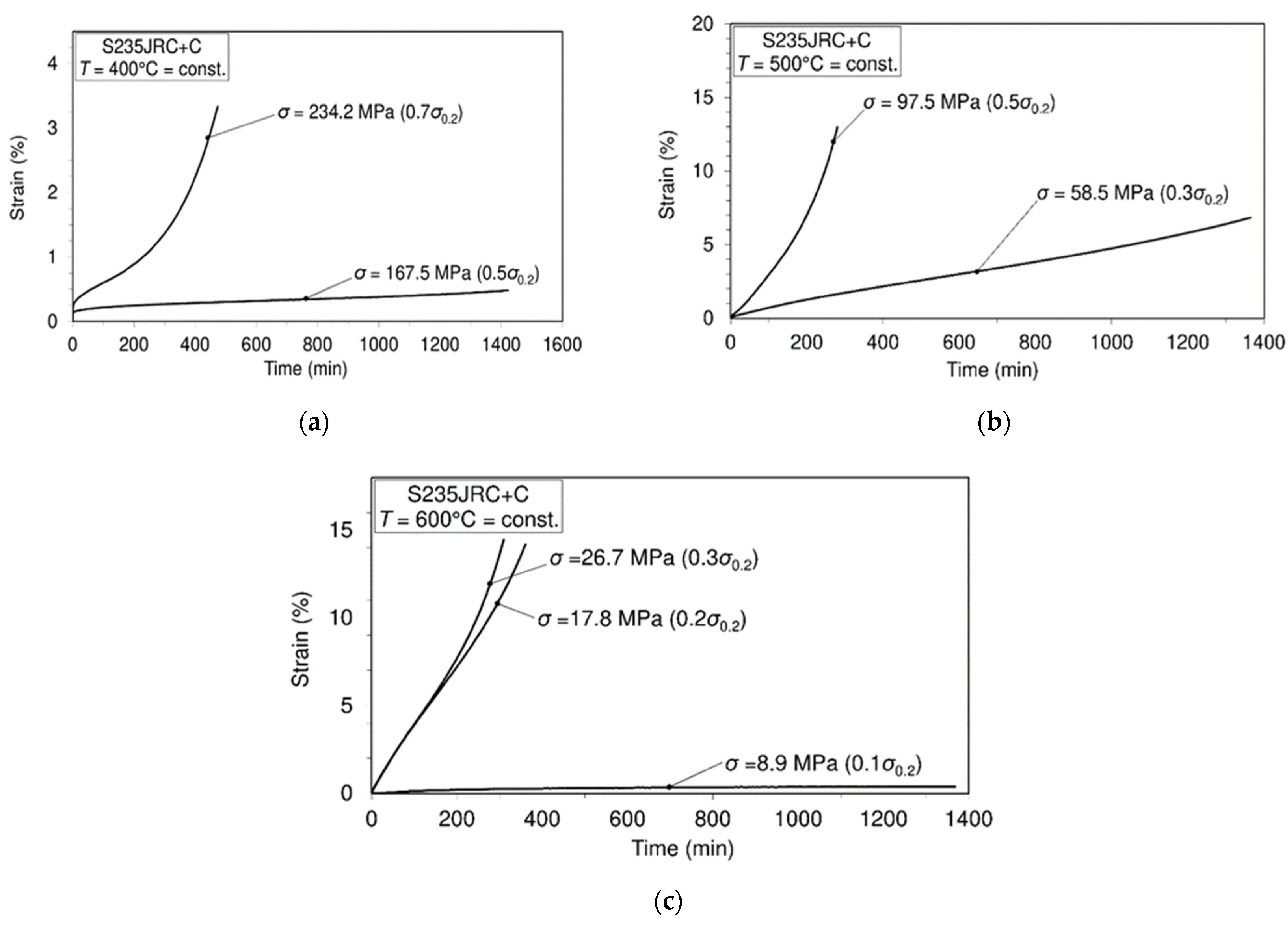
3.2. Tensile Short Time Creep Tests
3.3. Uniaxial Fully Reversed Mechanical High-Cyclic Fatigue Tests Performed on Unnotched Specimens
3.3.1. Stress-Life (S-N) Diagram
3.3.2. Fatigue Limit Calculation
- , the coefficient for the one sided tolerance limit for a normal distribution, and
- , the estimated standard deviation of the fatigue strength that can be calculated as:
- for = 200 + 5 × (7/4 − 1/2) = 206.25 MPa,or, this item can be obtained as (Table 4):
- for = (200 + 205 + 210 + 205 + 210 + 205 + 210)/7 = 206.43 MPa, whose amount is similar to previously obtained one.Now, based on Equation (3), it is:
- for = 1.62 × 5 × (0.1875 + 0.029) = 1.754 MPa.Finally, fatigue limit is (Equation (1)):
- for = 206.25 − 2.333 × 1.754 = 202.16 MPa.
3.4. A Brief Review of the Microstructure Analysis of the Tested Material
4. Conclusions
- Mechanical behavior of material at room and high temperatures is presented in the form of engineering stress-strain diagrams and tabular with numerical values of mechanical properties.
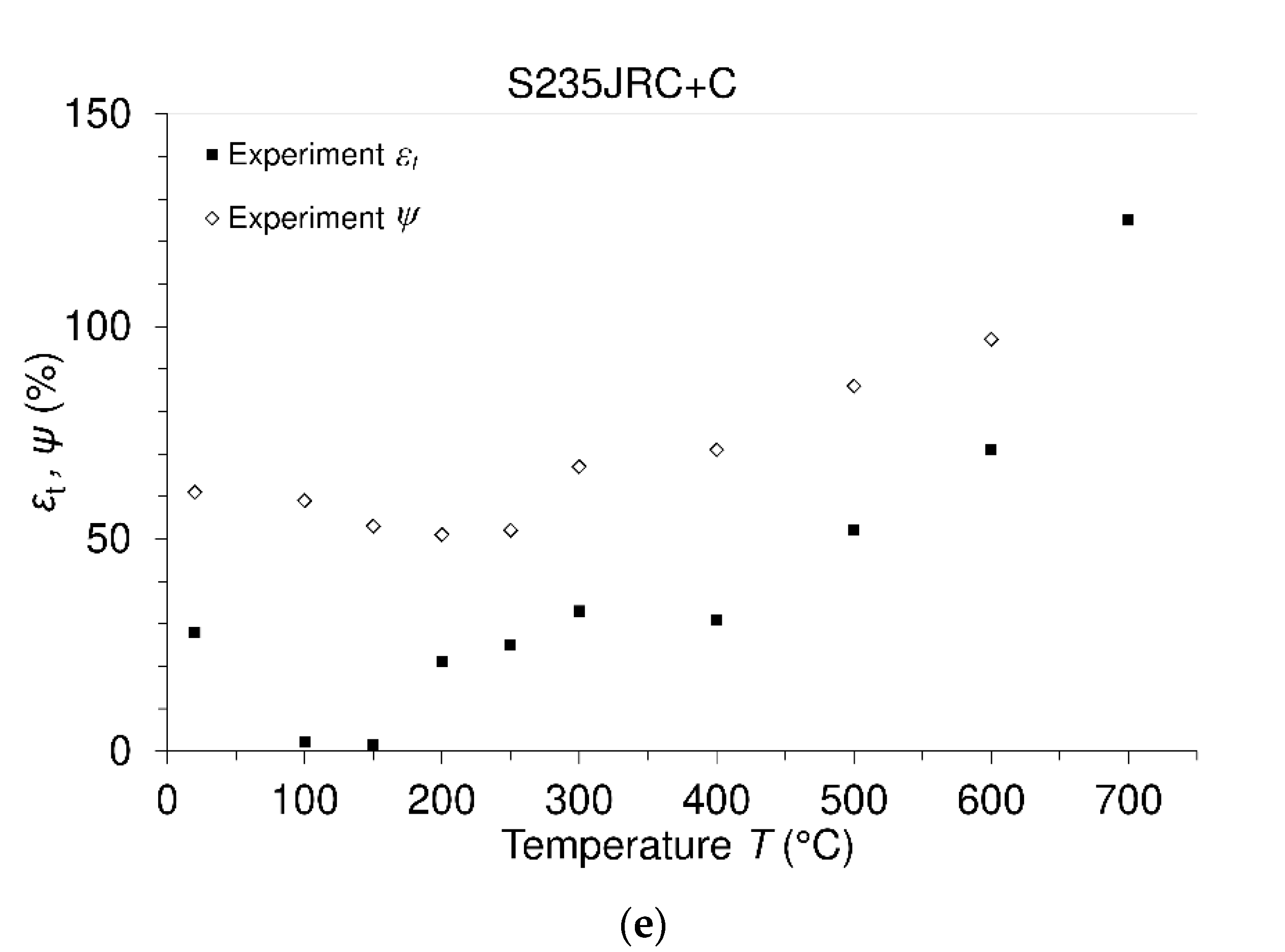
- It was found experimentally that the value of ultimate tensile strength of steel S235JRC + C, based on this study, occurs at a temperature of 200 °C. This fact is visible from Table 2.
- Creep behavior of S235JRC steel is presented and analyzed. It was found that this steel can be treated as creep resistant only at temperature of 400 °C and applied stress not exceeding 50% of the yield stress corresponding to this temperature.
- Fatigue behavior related to fully reversed uniaxial mechanical fatigue is presented in the form of stress-life( diagram.
- Fatigue (endurance) limit calculation procedure using modified staircase method is also given and fatigue limit is determined.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Ashby, M.F. Materials Selection inMechanical Design, 4th ed.; Butterwortg—Heinemann: New York, NY, USA, 2011. [Google Scholar]
- Bathe, K.J. Finite Element Procedures in Engineering Analysis; Prentice–Hall, Inc.: Hoboken, NJ, USA, 1982. [Google Scholar]
- Dowling, N.E. Mechanical Behavior of Materials, 4th ed.; Pearson: New York, NY, USA, 2013. [Google Scholar]
- Brnic, J.; Turkalj, G.; Canadija, M.; Lanc, D.; Krscanski, S.; Brcic, M.; Li, Q.; Niu, J. Mechanical properties, short timecCreep, and fatigue of an austenitic steel. Materials 2016, 9, 298. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brnic, J.; Turkalj, G.; Canadija, M.; Krscanski, S.; Brcic, M.; Lanc, D. Deformation behavior and material properties ofaAustenitic heat-resistant steel X15CrNiSi25-20 subjected to high temperatures and creep. Mater. Des. 2015, 69, 219–229. [Google Scholar] [CrossRef]
- Boresi, A.P.; Schmidt, R.J.; Sidebottom, O.M. Advanced Mechanics of Materials, 5th ed.; Joh Wily & Sons: New York, NY, USA, 1993. [Google Scholar]
- Raghavan, V. Materials Science and Engineering; Prentice-Hall of India: New Delhi, India, 2004. [Google Scholar]
- Stegemann, R.; Cabeza, S.; Lyamkin, V.; Bruno, G.; Pittner, A.; Wimpory, R.; Boin, M.; Kreutzbruck, M. Residual stress characterization of steel TIG welds by neutron diffraction and by residual magnetic stray field mappings. J. Mag. Mag. Mater. 2017, 426, 580–587. [Google Scholar] [CrossRef]
- Mróz, K.P.; Bigos, A.; Kucharski, S.; Doliński, K.; Mikułowski, G.; Bltowska-Lehman, E.; Nolbrzak, P. Failure modes of coatings on steels Substrate. Bull. Pol. Acad. Sci. Te. 2016, 64, 249–256. [Google Scholar] [CrossRef] [Green Version]
- Mroz, K.P.; Bigos, A.; Kucharski, S.; Dolinski, K.; Bełtowska-Lehman, E. Ni-W electrodeposited coatings on low carbon steel substrate: Fatigue observations. J. Mater. Eng. Perform. 2014, 2310, 3459–3466. [Google Scholar] [CrossRef] [Green Version]
- Tsonev, V.; Nikolov, N.; Marcheva, Y. Influence of plastic deformation of S235JR steel rods on their mechanical properties and corrosion behavior in NaCl solution. In Proceedings of the MATEC Web of Conference, Sozopol, Bulgaria, 15–17 September 2018. [Google Scholar] [CrossRef]
- Tsonev, V.; Kuzmanov, N.; Borisov, B.; Penkov, K. System for materials testing at static loading. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Plovdiv, Bulgaria, 16–18 May 2019. [Google Scholar] [CrossRef]
- Ferro, A.C.; Calado, L. Fracture of a galvanized steel U-bolt sirrup of an overhead electrical transport line. Procedia Struct. Integr. 2016, 1, 249–256. [Google Scholar] [CrossRef] [Green Version]
- Jurkovič, M.; Kalina, T.; Zgutova, K.; Neslušan, M.; Pitonak, M. Analysis of magnetic anisotropy and non-homogeneity of S235 ship structure steel after plastic straining by the use of barkhausen noise. Materials 2020, 13, 4588. [Google Scholar] [CrossRef] [PubMed]
- ISO 12107:2012 (E). Metallic Materials—Fatigue Testing—Statistical Planning and Analysis of Data; ISO Copyright office: Geneva, Switzerland, 2012. [Google Scholar]
- Annual Book of ASTM Standards. Metals—Mechanical Testing; Elevated and Low-Temperature Tests; Metallography, ASTM International: Baltimore, MD, USA, 2015; Volume 3. [Google Scholar]
- Roth, J.T. Elevated Temperature Mechanical Properties of Line Pipe Steels. Master’s Thesis, Colorado School of Mines, Golden, CO, USA, 2015. [Google Scholar]
- Brnic, J.; Krscanski, S.; Lanc, D.; Brcic, M.; Turkalj, G.; Canadija, M.; Niu, J. Analysis of the mechanical behavior, creep resistance and uniaxial fatigue strength of martensitic steel X46Cr13. Materials 2017, 10, 388. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, K.; Chen, W.; Ye, J.; Jiang, J.; Chen, W.; Liu, B.; Xu, C. Experimental investigation on the creep behavior of G550 cold –formed steel at elevated temperature. Structures 2021, 31, 49–56. [Google Scholar] [CrossRef]
- Suresh, S. Fatigue of Materials, 2nd ed.; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Correia, J.A.F.O.; da Silva, A.L.L.; Xin, H.; Lesiuk, G.; Zhu, S.-P.; de Jesus, A.M.P.; Fernandes, A.A. Fatigue performance prediction od S235 base steel plates in the riveted connections. Structures 2021, 30, 745–755. [Google Scholar] [CrossRef]
- Sabih, A.; Nemes, J.A. Internal ductile failure mechanisms in steel cold heading process. J. Mater. Process. Technol. 2009, 209, 94292–94311. [Google Scholar] [CrossRef]
- Cherolis, N.E. Facets on fatigue fractures. Microsc. Microanal. 2013, 19 (Suppl. S2), 1838. [Google Scholar] [CrossRef] [Green Version]
- Balos, S.; Rajnovic, D.; Sidjanin, L.; Savkovic, B.; Kovac, P.; Janjatovic, P. Tensile and fatigue properties, machinability and machined surface roughness of Al-Si-Cu alloys. Rev. Mater. 2019, 24, e12456. [Google Scholar] [CrossRef]
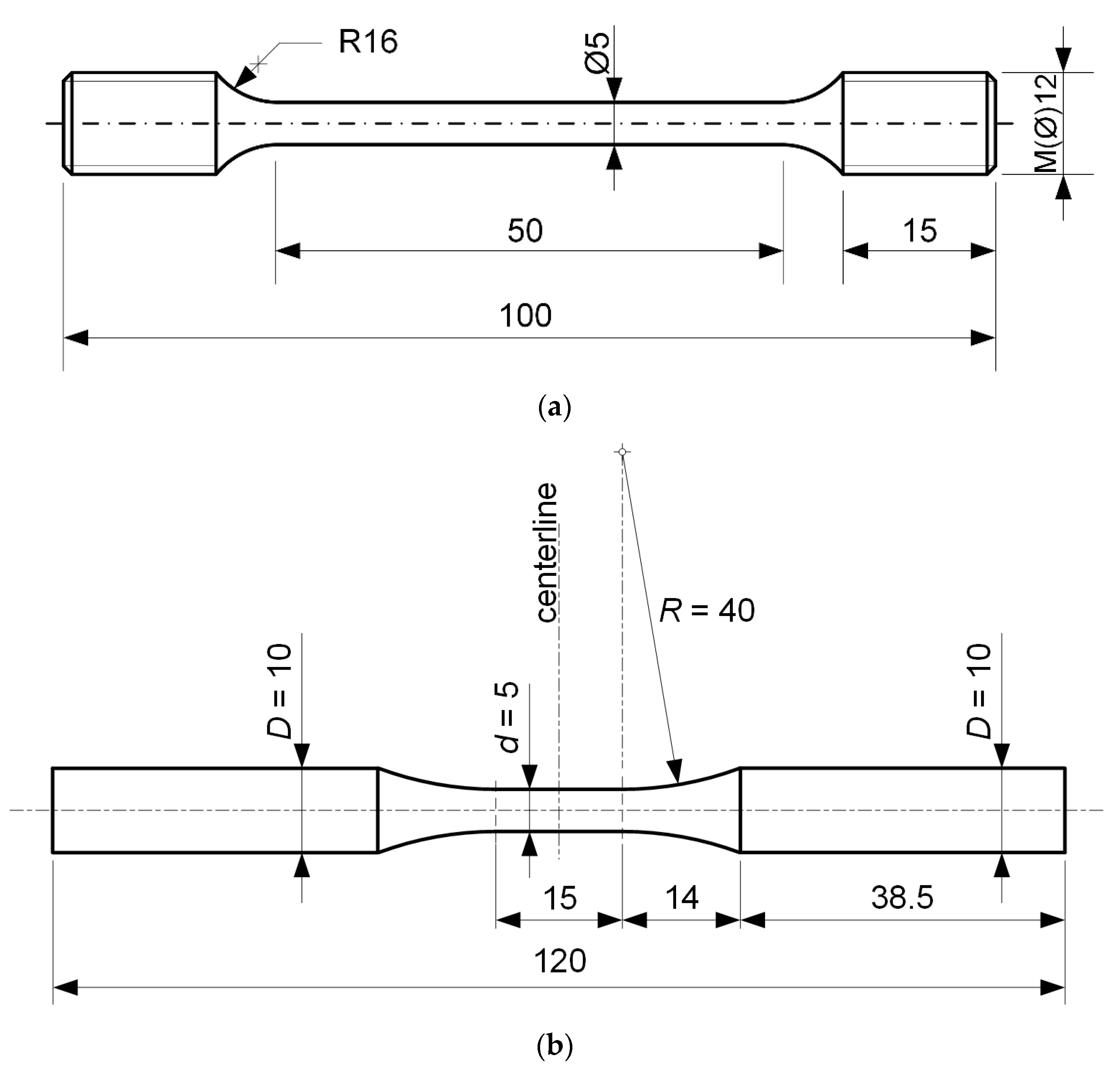






| Tested Material Mass (%) | |||||||
|---|---|---|---|---|---|---|---|
| C | Si | Mn | P | S | Cr | Ni | Mo |
| 0.162 | 0.237 | 0.534 | 0.011 | 0.012 | 0.158 | 0.028 | 0.009 |
| Cu | Al | W | Sn | Nb | Co | Rest | |
| 0.039 | 0.027 | 0.003 | 0.008 | 0.003 | 0.002 | 98.767 | |
| Classification: Unalloyed high-quality structural steel/steel for construction industry | |||||||
| Chemical composition (Certified Labor. “Metris”, Pula) | |||||||
| Temp. T (°C) | Ultimate Tensile Strength Yield Strength | Reduction Factor
| Total Strain | ||||||
|---|---|---|---|---|---|---|---|---|---|
(MPa) | (MPa) | Ratio | E (GPa) | εt (%) | ψ (%) | ||||
| 20 | 534 | 488 | 0.93 | 196 | 1 | 1 | 1 | 28 | 61 |
| 100 | 500 | 463 | 0.93 | 194 | 0.94 | 0.95 | 0.99 | 2.3 | 59 |
| 150 | 524 | 467 | 0.89 | 191 | 0.94 | 0.95 | 0.89 | 1.6 | 53 |
| 200 | 565 | 475 | 0.84 | 186 | 1.01 | 0.96 | 0.66 | 21 | 51 |
| 250 | 561 | 459 | 082 | 182 | 1.007 | 0.93 | 0.87 | 25 | 52 |
| 300 | 518 | 424 | 0.82 | 174 | 0.93 | 0.86 | 0.81 | 33 | 67 |
| 400 | 379 | 335 | 0.88 | 153 | 0.68 | 0.68 | 0.819 | 31 | 71 |
| 500 | 204 | 195 | 0.94 | 124 | 0.481 | 0.39 | 0.71 | 52 | 86 |
| 600 | 103 | 89 | 0.96 | 85 | 0.37 | 0.29 | 0.4 | 71 | 97 |
| 700 | 67 | 47 | 0.7 | 43 | 0.12 | 0.1 | 0.2 | 125 | ---- |
| Chemical Composition (%) | C | Si | Mn | P | S | Cr | Cu | Properties | ||
|---|---|---|---|---|---|---|---|---|---|---|
| σm | σ0.2 | (GPa) | ||||||||
| EN 10277-2-2008; S235JRC/1.0122; (max) | 0.17 | - | 1.4 | 0.04 | 0.04 | - | 0.55 | Specimen: 16–40 mm, (+C) | ||
| 390–730 | 260 | - | ||||||||
| S235JRC + C (This paper)/cold drawn | 0.162 | 0.237 | 0.534 | 0.011 | 0.012 | 0.158 | 0.039 | 534 | 488 | 196 |
| S235JRC, Ref. [11])/cold drawn | 0.08 | 0.2 | 0.08 | 0.027 | 0.027 | 0.1 | 0.55 | 609 | 559 | 208 |
| Low-Carbon (Plain) Steels | AISI 1008 (1.0204) Ref. [17] | AISI 1020 (1.0402) Ref. [17] | S235JRC + C (1.0122) (This Study) |
|---|---|---|---|
| Ultimate tensile strength at T = 200 °C (considered as maximum) MPa;/= / | 400 | 550 | 565 |
| Stress max (MPa) | Specimen | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 210 | ♦ | ♦ | ♦ | ||||
| 205 | ○ | ♦ | ○ | ||||
| 200 | ○ | ||||||
| Stress /MPa | Stress level, i | fi | ifi | i2fi |
| 210 | 2 | 3 | 6 | 12 |
| 205 | 1 | 1 | 1 | 1 |
| 200 | 0 | 0 | 0 | 0 |
| 4 | 7 | 13 | ||
| Formula | Tested material: |
| 7 | |
| 13 | |
| 4 | |
| 0.1875 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brnic, J.; Brcic, M.; Balos, S.; Vukelic, G.; Krscanski, S.; Milutinovic, M.; Dramicanin, M. S235JRC+C Steel Response Analysis Subjected to Uniaxial Stress Tests in the Area of High Temperatures and Material Fatigue. Sustainability 2021, 13, 5675. https://doi.org/10.3390/su13105675
Brnic J, Brcic M, Balos S, Vukelic G, Krscanski S, Milutinovic M, Dramicanin M. S235JRC+C Steel Response Analysis Subjected to Uniaxial Stress Tests in the Area of High Temperatures and Material Fatigue. Sustainability. 2021; 13(10):5675. https://doi.org/10.3390/su13105675
Chicago/Turabian StyleBrnic, Josip, Marino Brcic, Sebastian Balos, Goran Vukelic, Sanjin Krscanski, Mladomir Milutinovic, and Miroslav Dramicanin. 2021. "S235JRC+C Steel Response Analysis Subjected to Uniaxial Stress Tests in the Area of High Temperatures and Material Fatigue" Sustainability 13, no. 10: 5675. https://doi.org/10.3390/su13105675



.JPG)






