Probabilistic Seismic Demand Analysis of Soil Nail Wall Structures Using Bayesian Linear Regression Approach
Abstract
:1. Introduction
2. Numerical Modeling and Verification
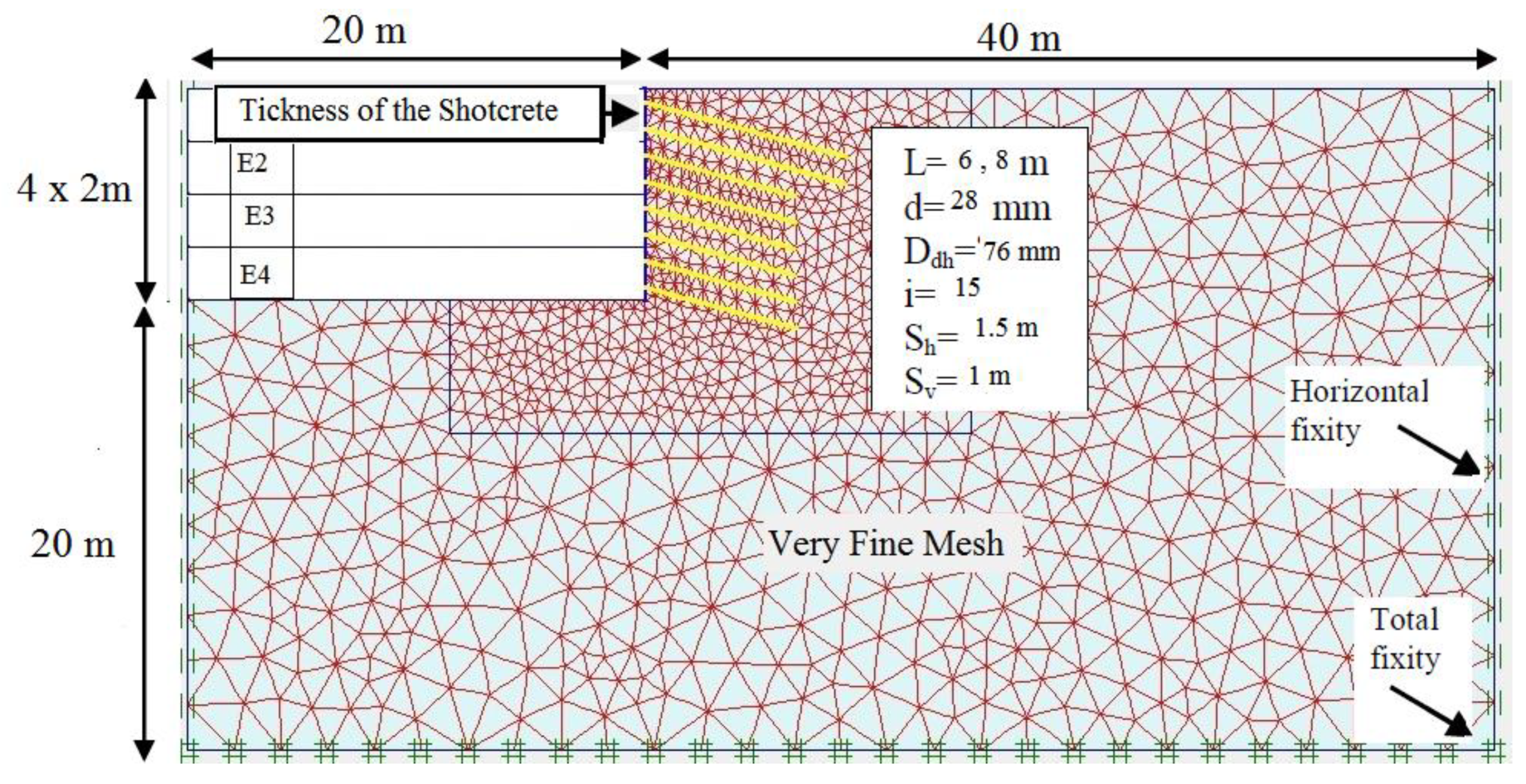
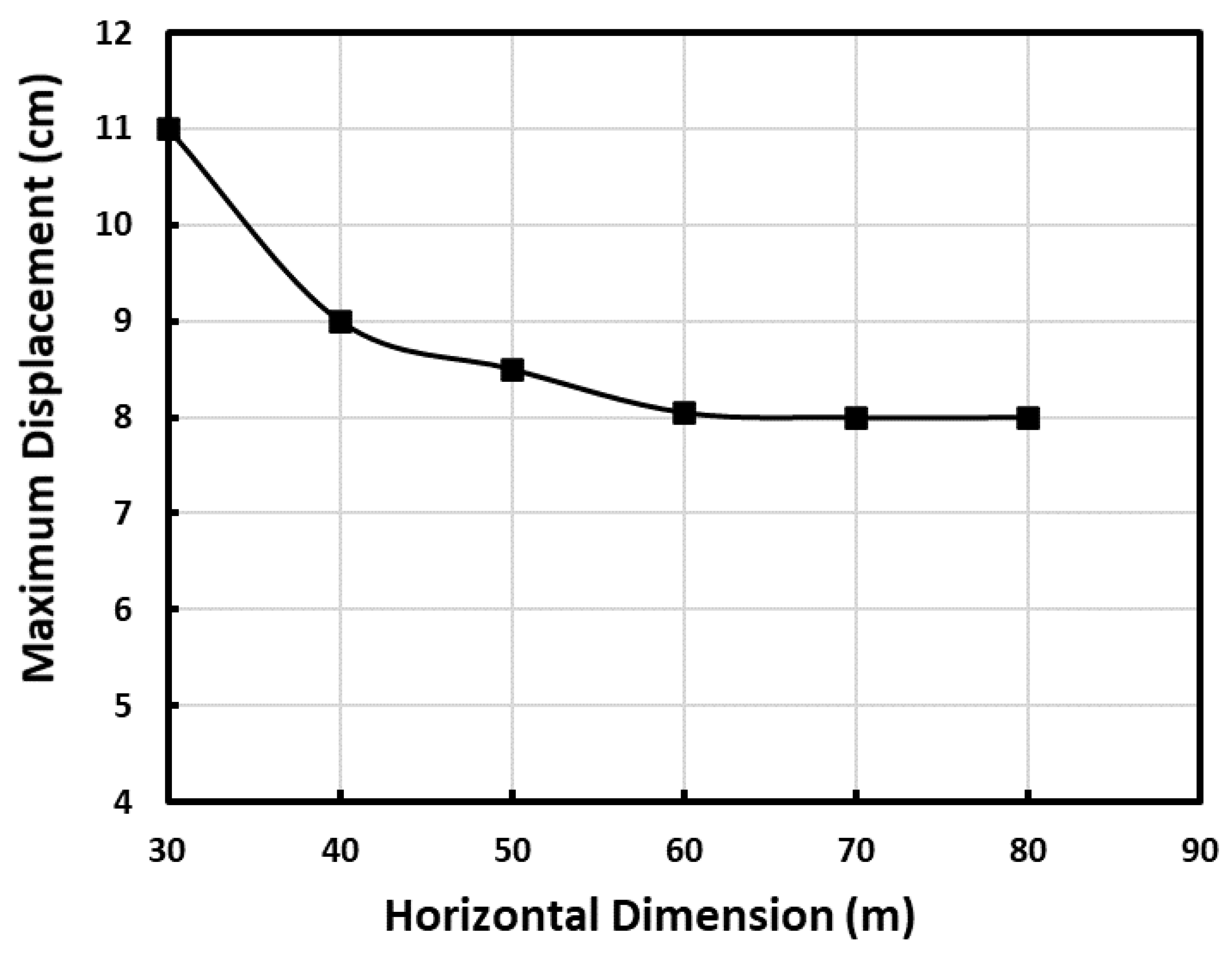
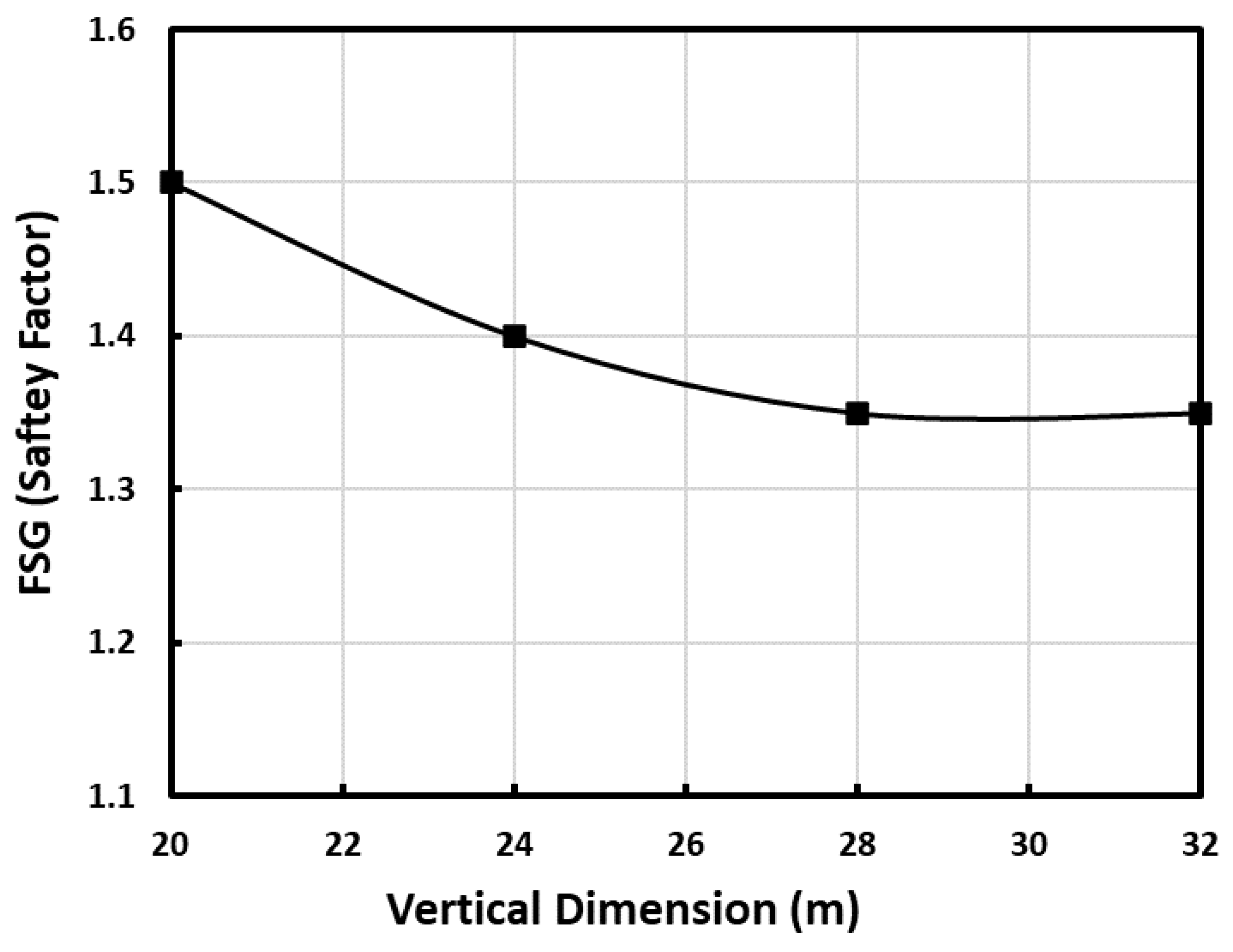
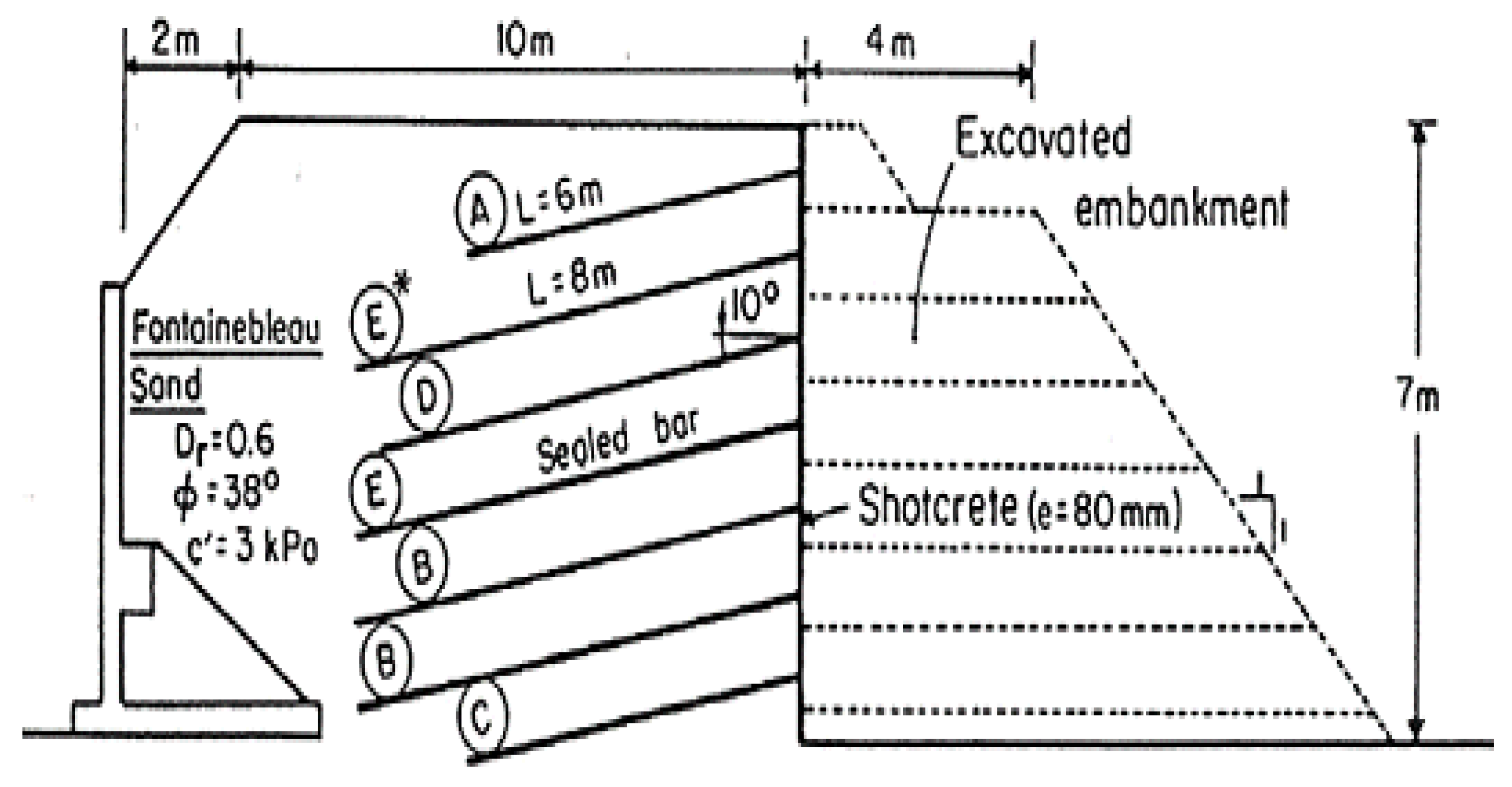
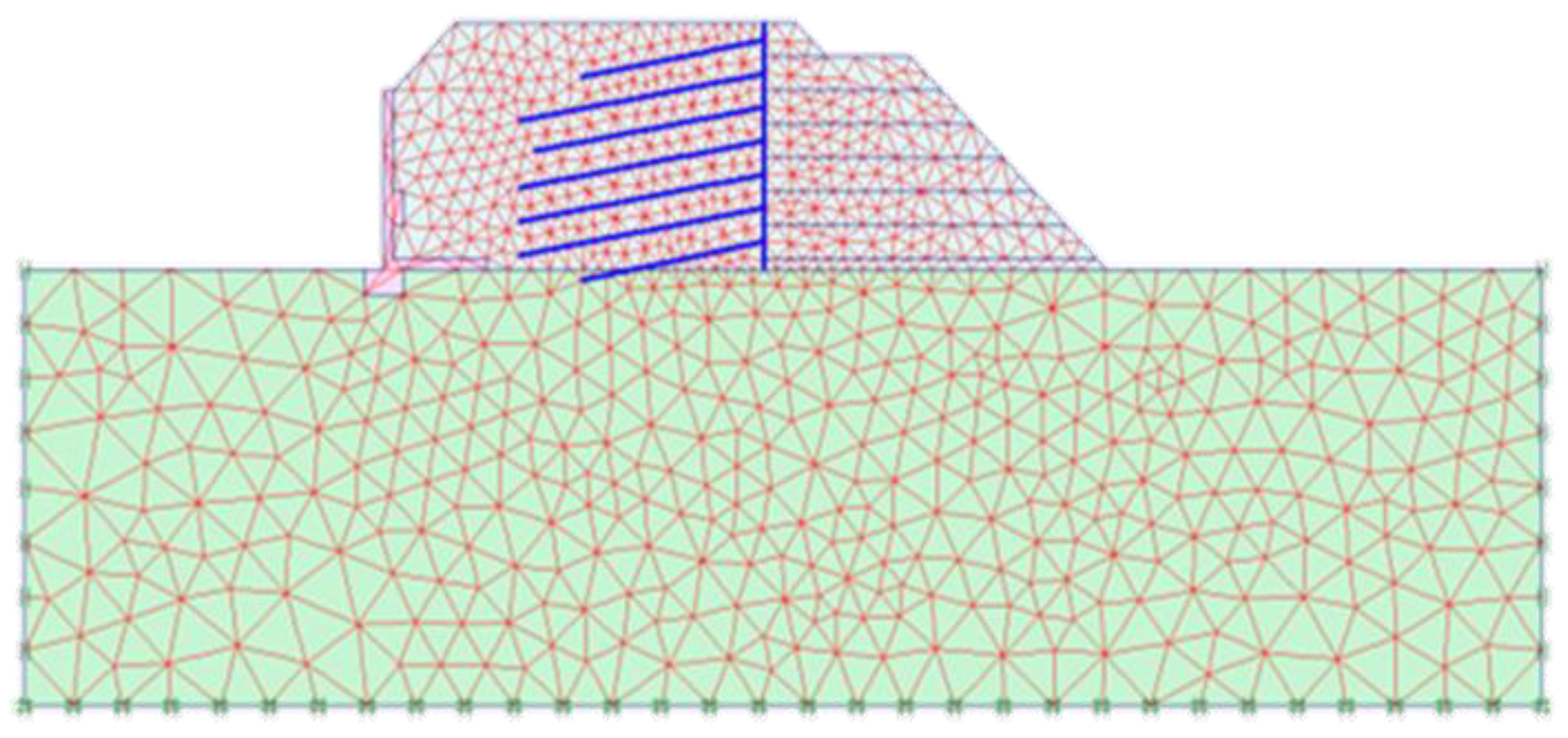
2.1. Numerical Modeling
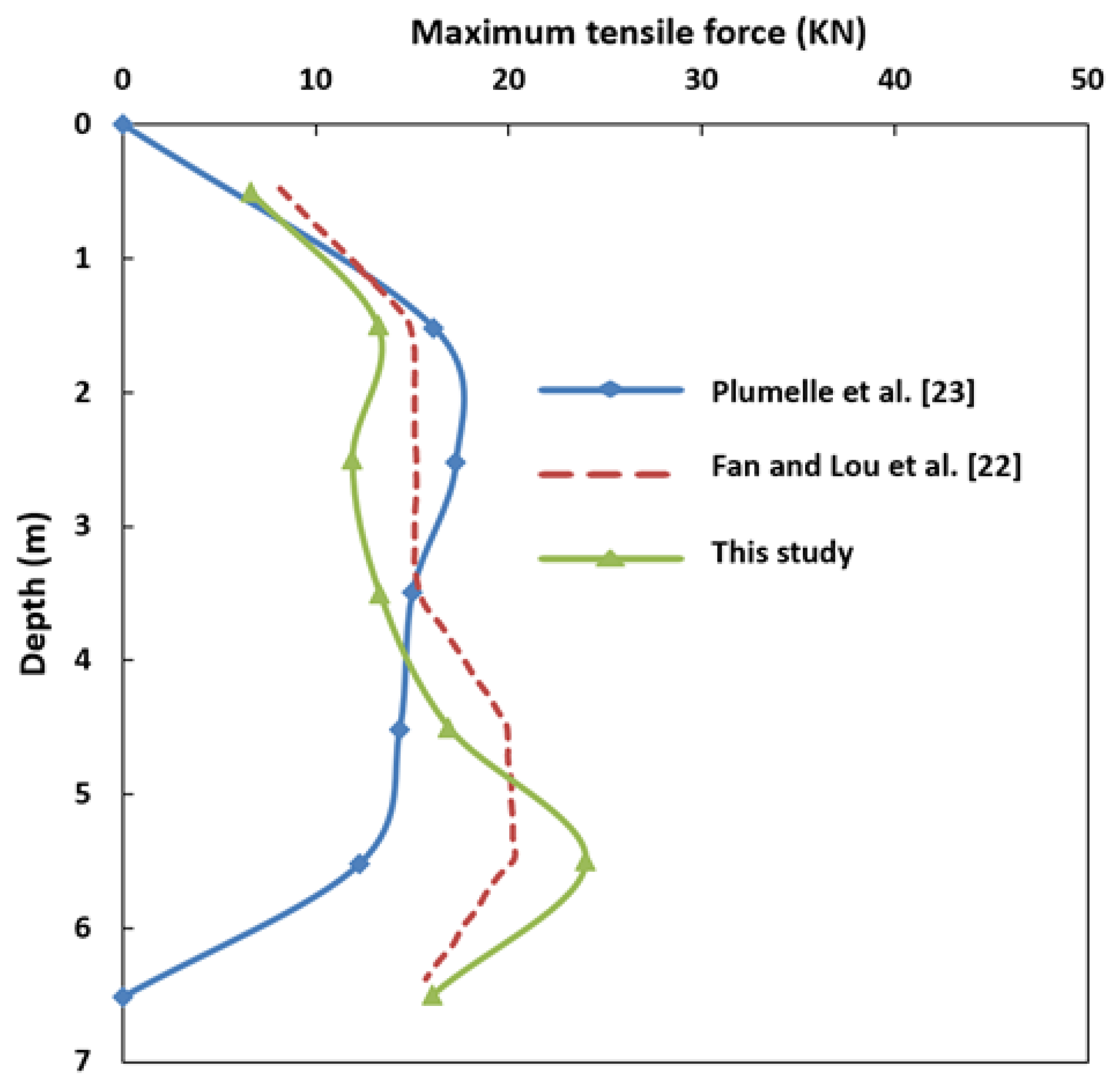
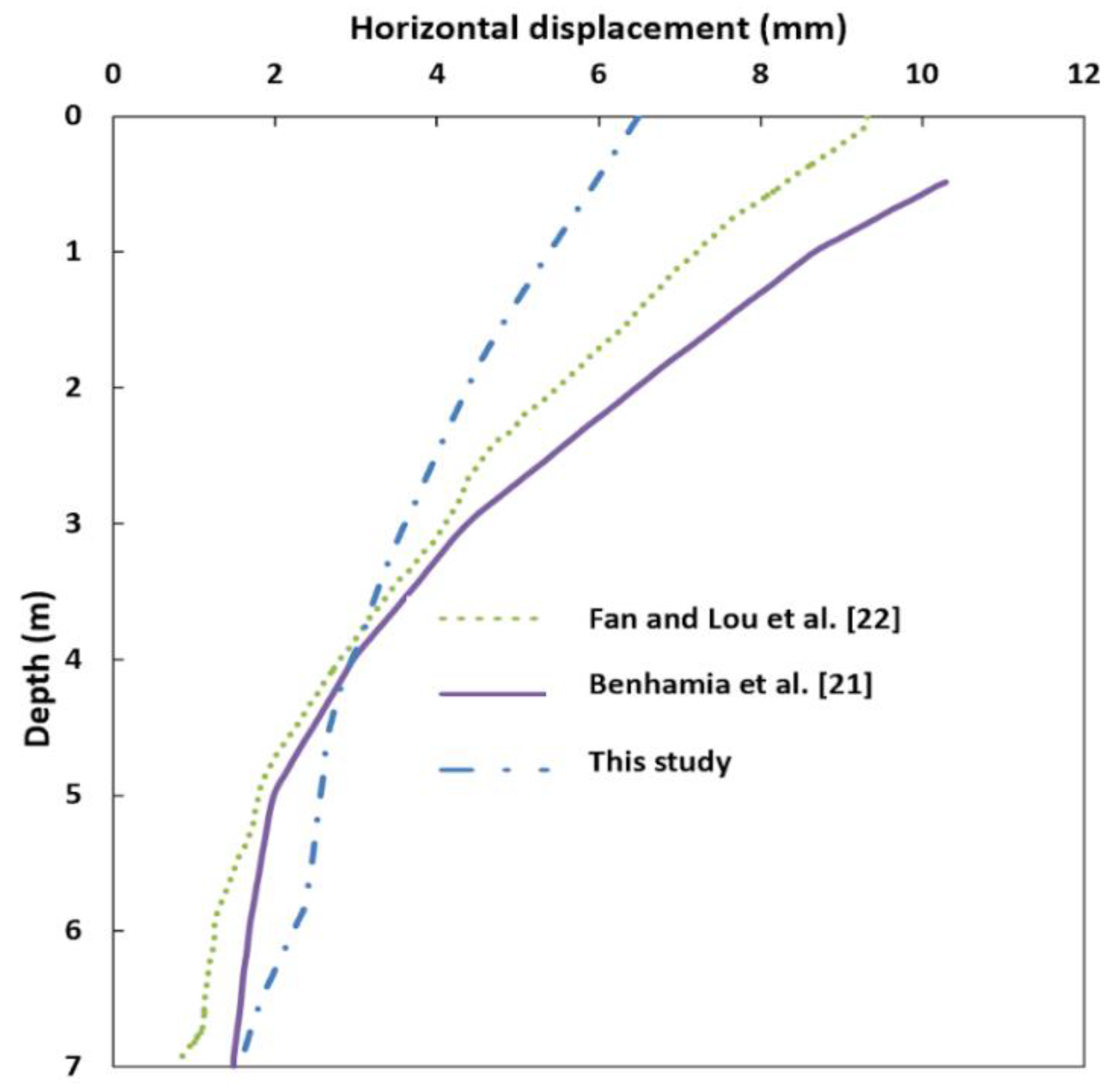
2.2. Model Verification
- The number of parameters: The existence of various materials in this research (soil, shotcrete, nail) has led to a large number of parameters being required to model this issue. Nineteen parameters are needed to model this problem, and due to insufficient material test information in different locations of the test, the probability of error in numerical simulation is increased.
- Behavioral model: Due to inherent uncertainties in the field tests, exact modeling of the soil and materials is not possible.
- Error in test data collection: Uncertainties always accompany the installation of sensors and monitor the behavior in the test.
3. Soil Modeling and Material Properties
3.1. Mohr-Coulomb Model (MC)
3.2. Hardening Soil Model (HS)
3.3. The Hardening Soil Model with Stiffness Effect from Small Strains (HSS)
3.4. Nail Correspondence Parameters
3.5. Overall Procedure of Numerical Modeling
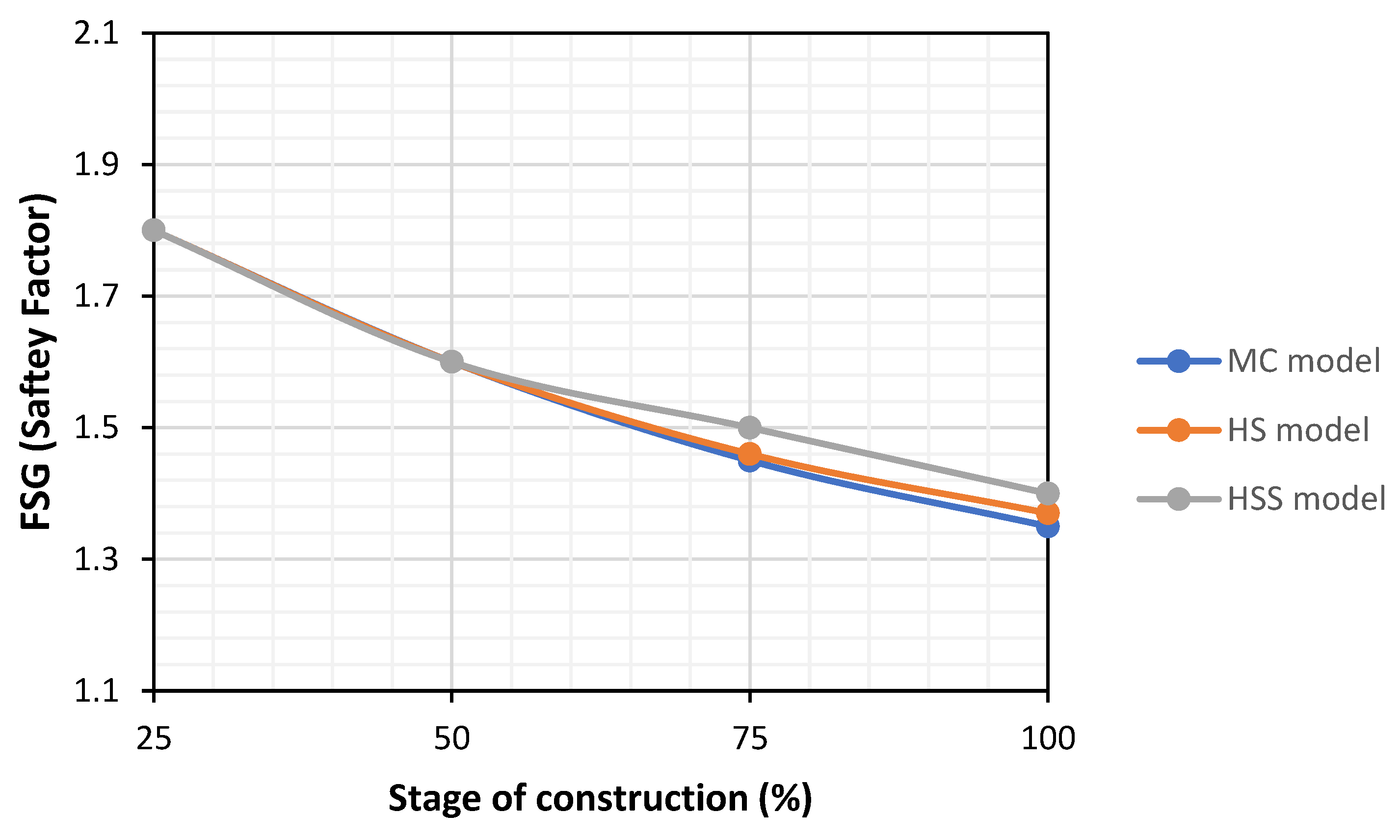
3.6. The Effect of Behavioral Models on Global Stability
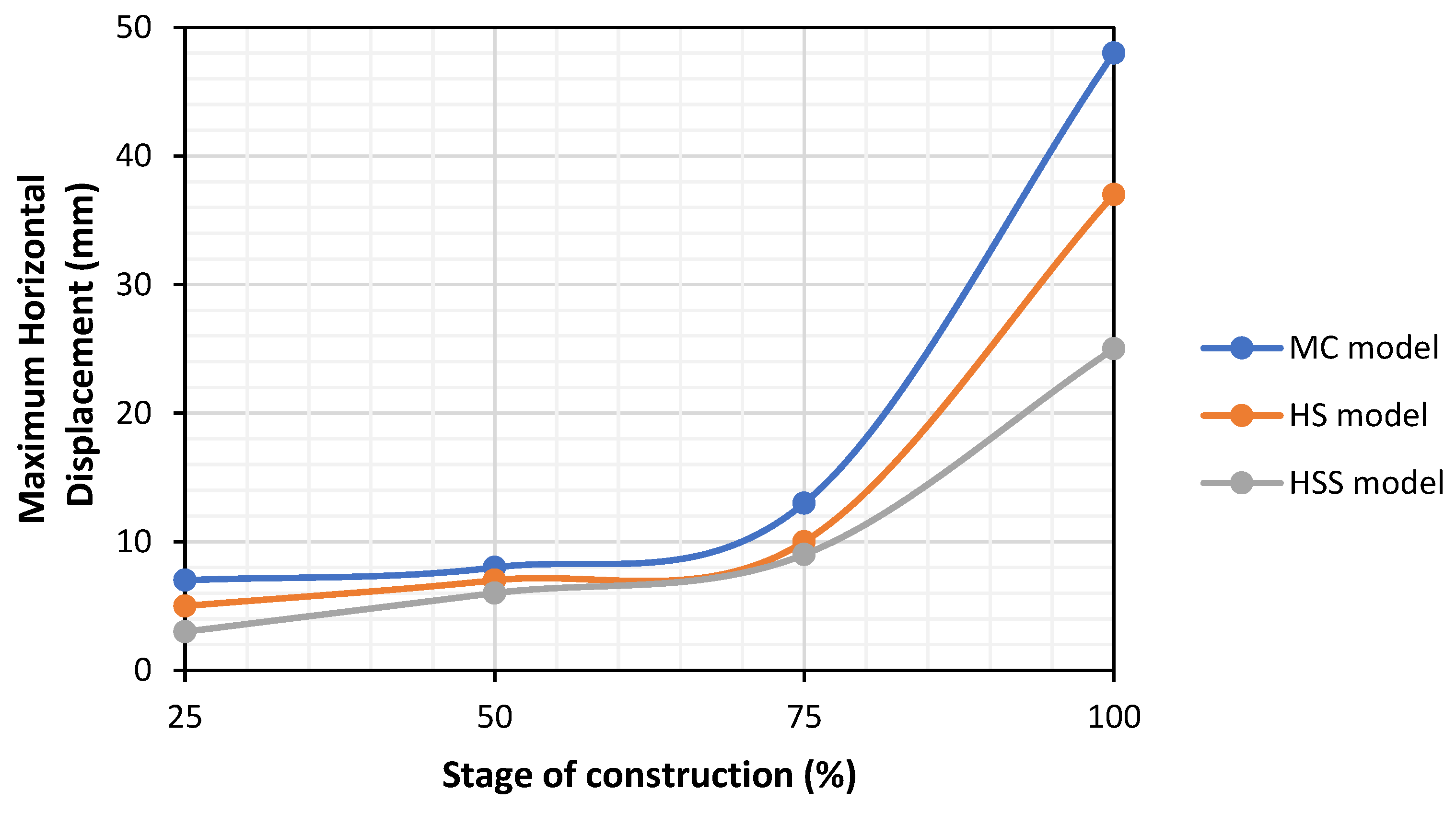
3.7. The Effect of Modeling Approach on the Maximum Horizontal Displacement of the Soil Nailed Wall System
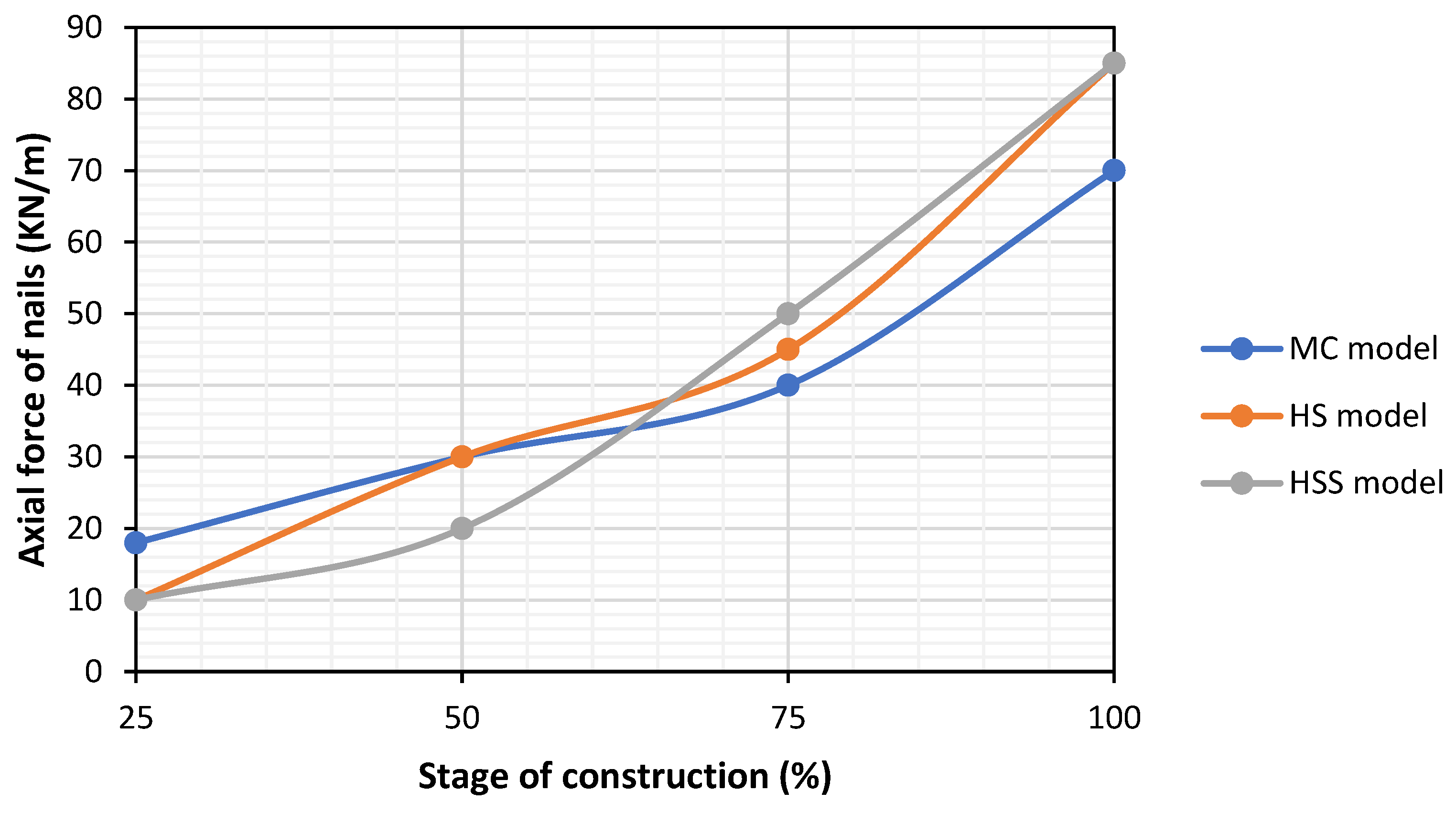
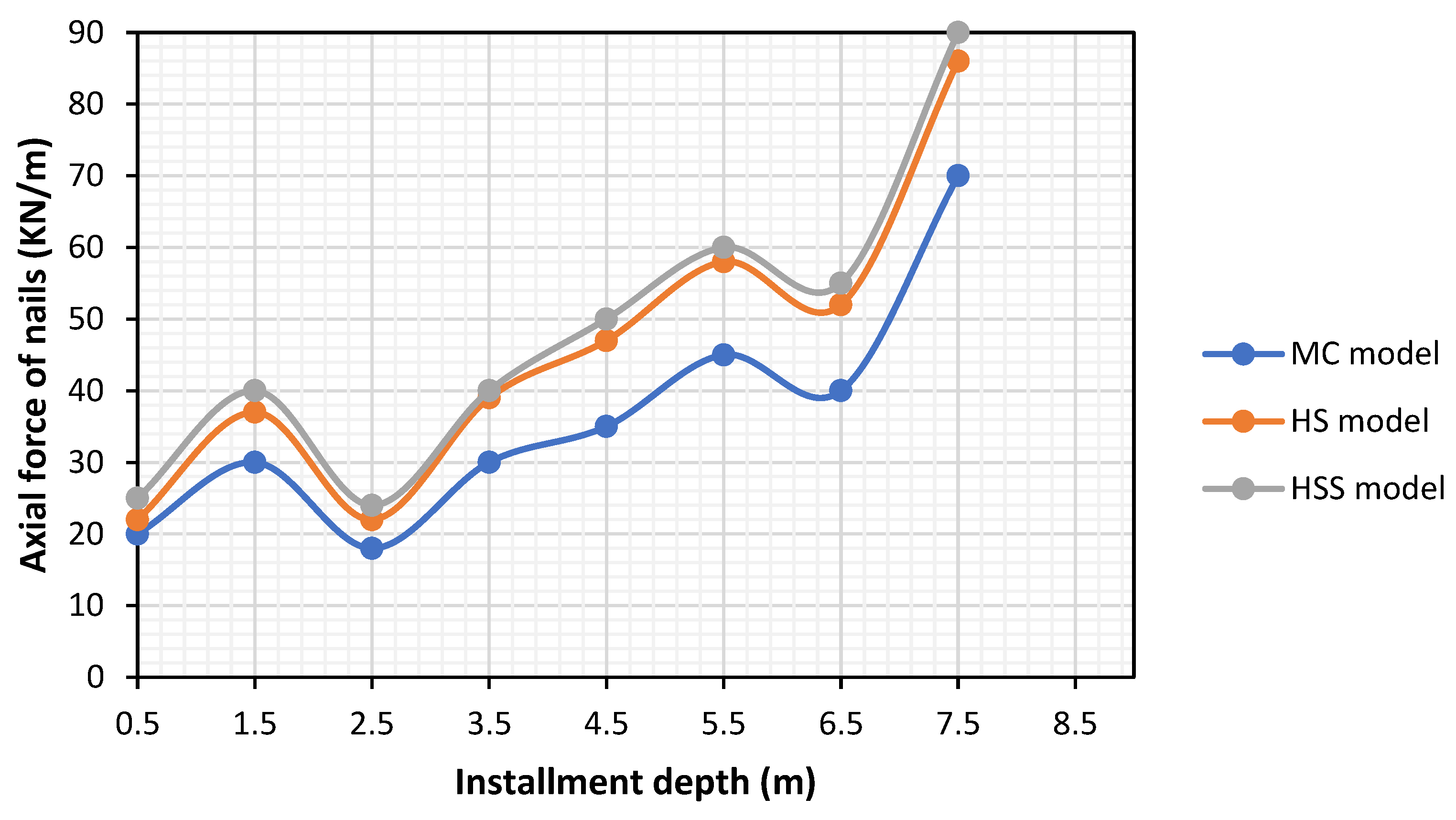
3.8. The Effect of Behavioral Models on Axial Forces Generated in the Nails
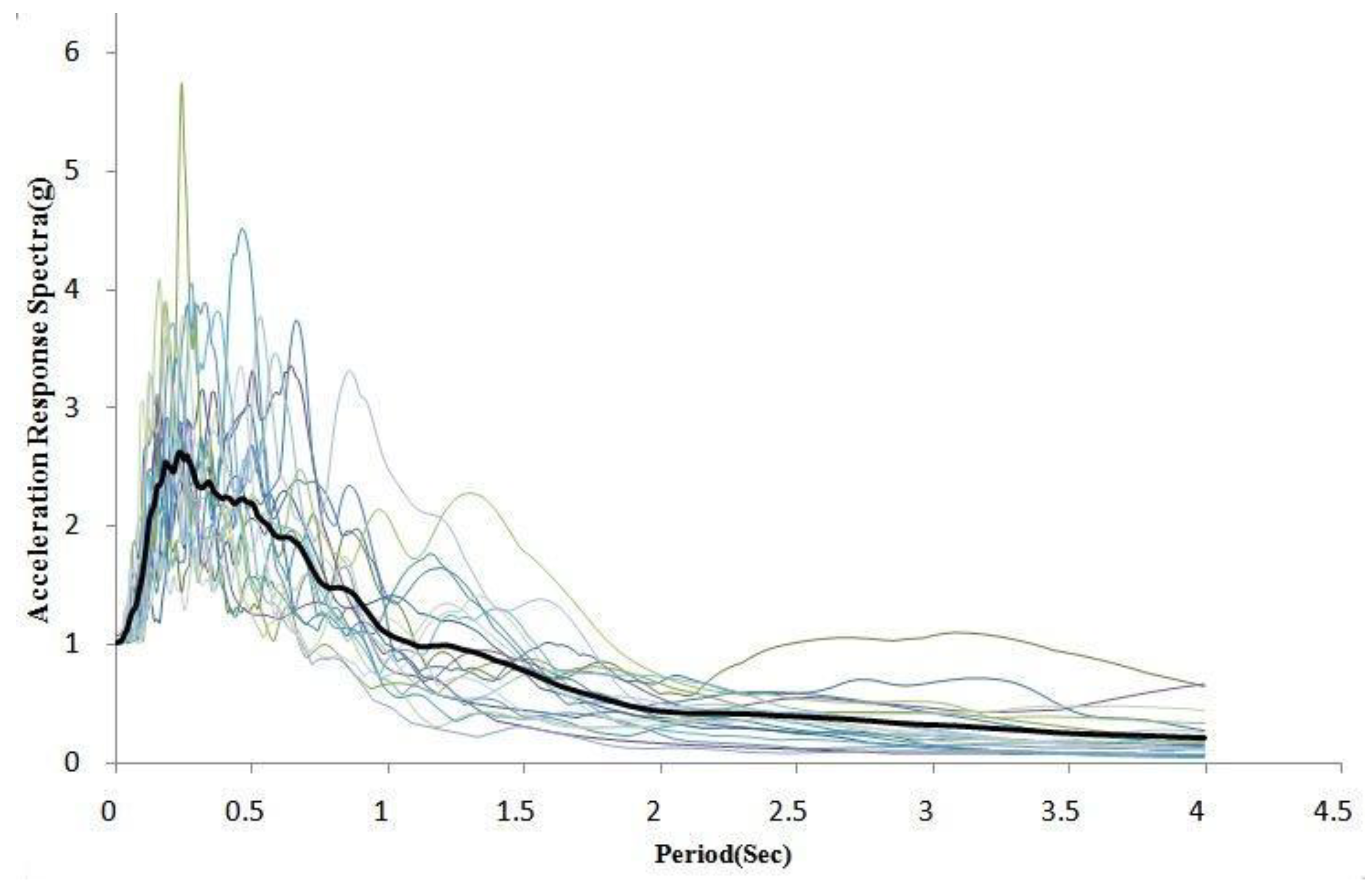
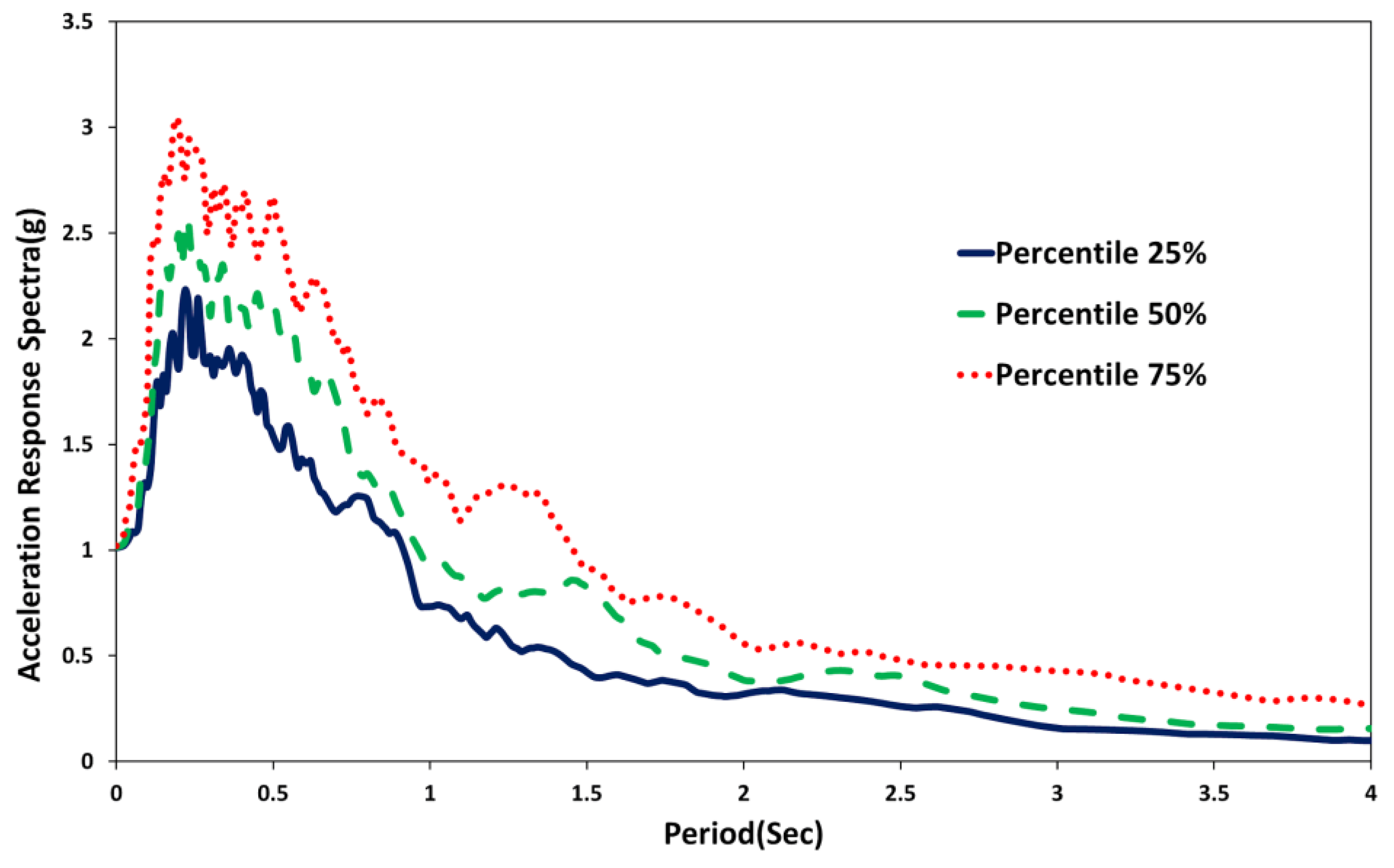
4. Seismic Ground Motion Records
- (a)
- Magnitude > 6.5
- (b)
- Distance from source to site >10 km (average of Joyner-Boore and Campbell distances) [31]
- (c)
- Peak Ground Acceleration (PGA) > 0.2 g and Peak Ground Velocity (PGV) > 15 cm/s
- (d)
- Soil shear wave velocity, in upper 30 m of soil, greater than 180 m/s
- (e)
- Lowest useable frequency <0.25 Hz, to ensure that the low-frequency content was not removed by the ground motion filtering process
- (f)
- Strike-slip and thrust faults (consistent with California)
- (g)
- No consideration of spectral shape
- (h)
- No consideration of station housing, but PEER-NGA records were selected to be “free-field”
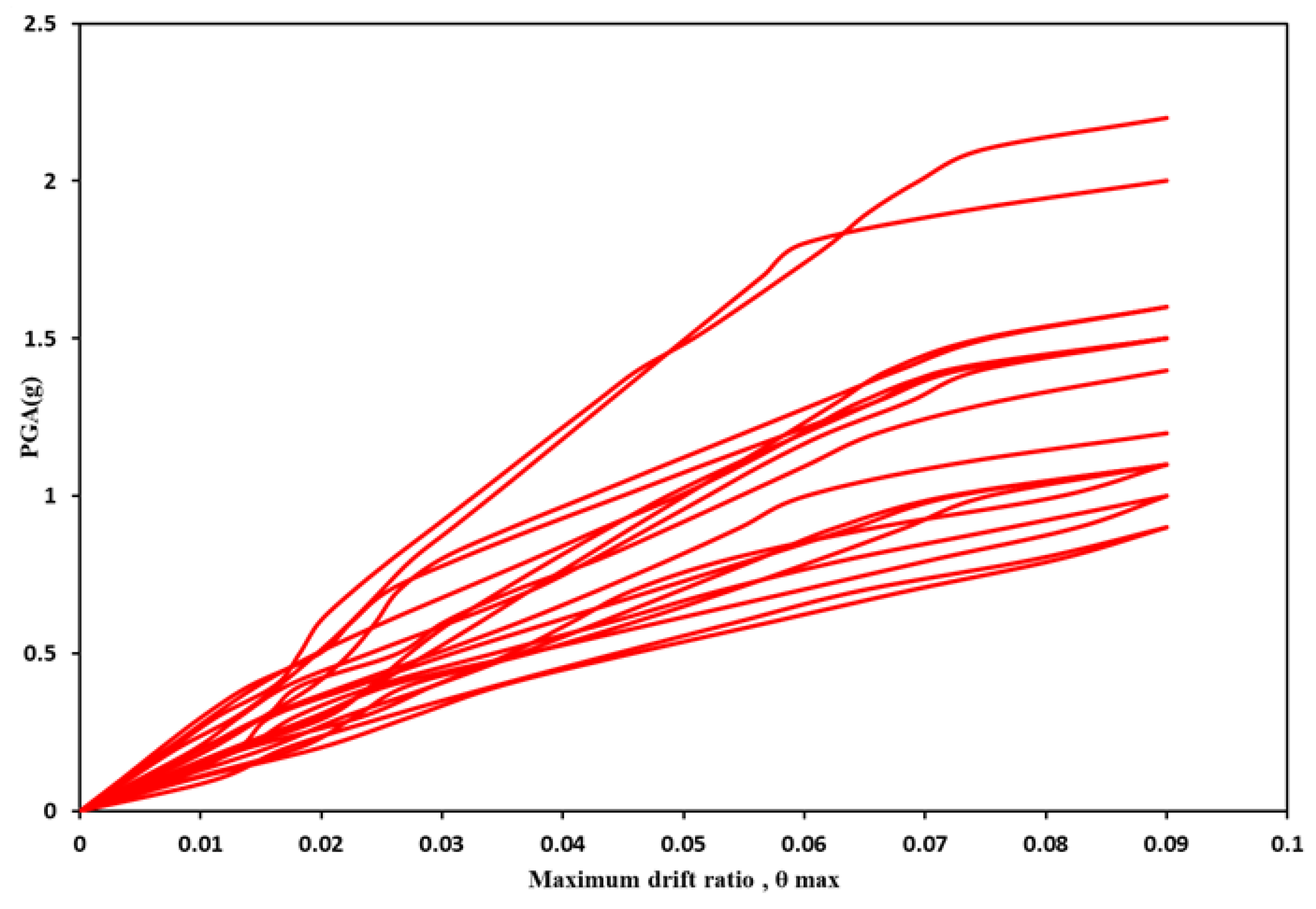
5. Incremental Dynamic Analysis (IDA) and Fragility Curves
5.1. Incremental Dynamic Analysis (IDA)
Intensity Measures (IM) and Damage States (DS)
5.2. Fragility Function Methodology
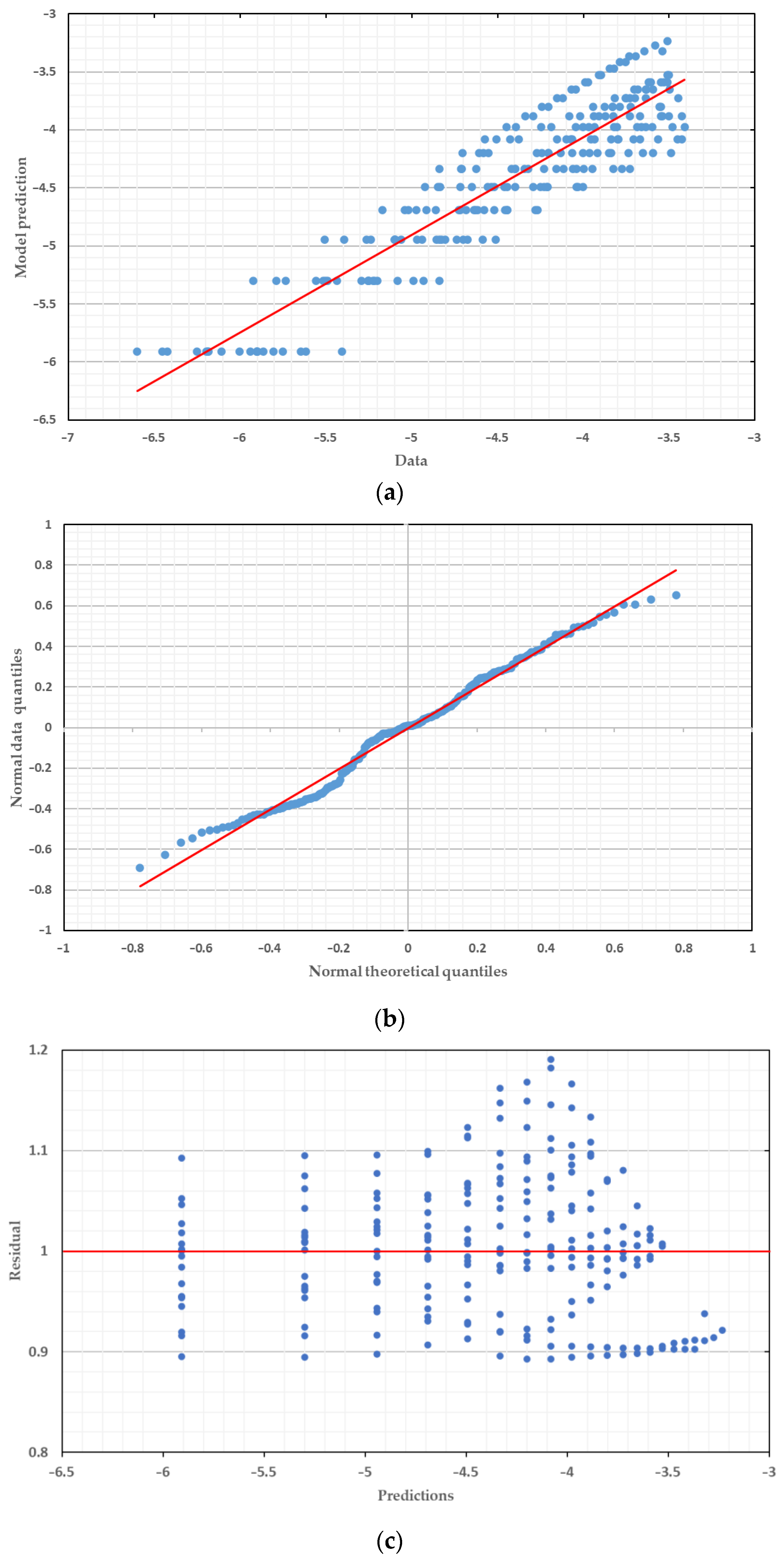
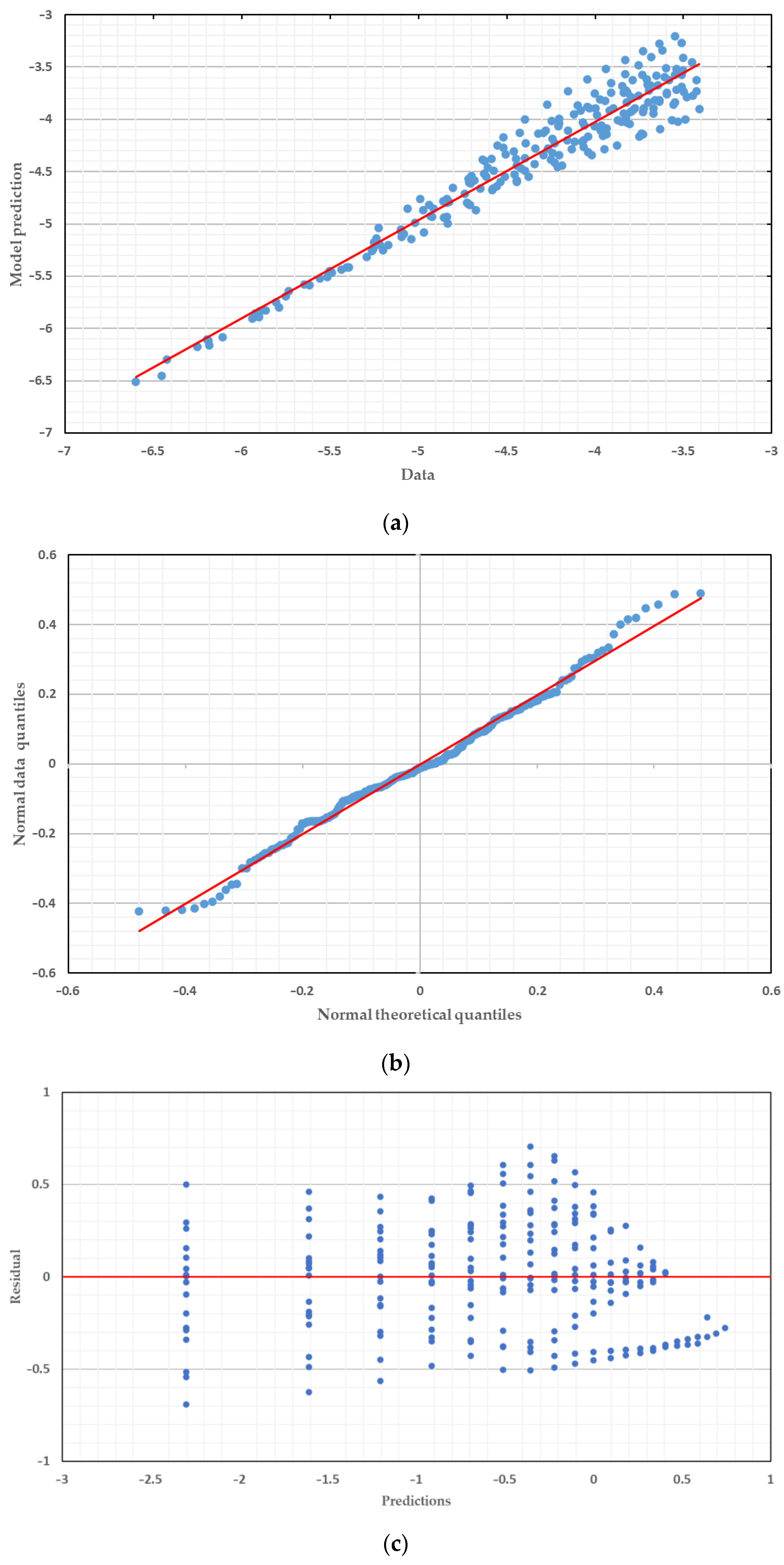
6. Bayesian Statistical Inference
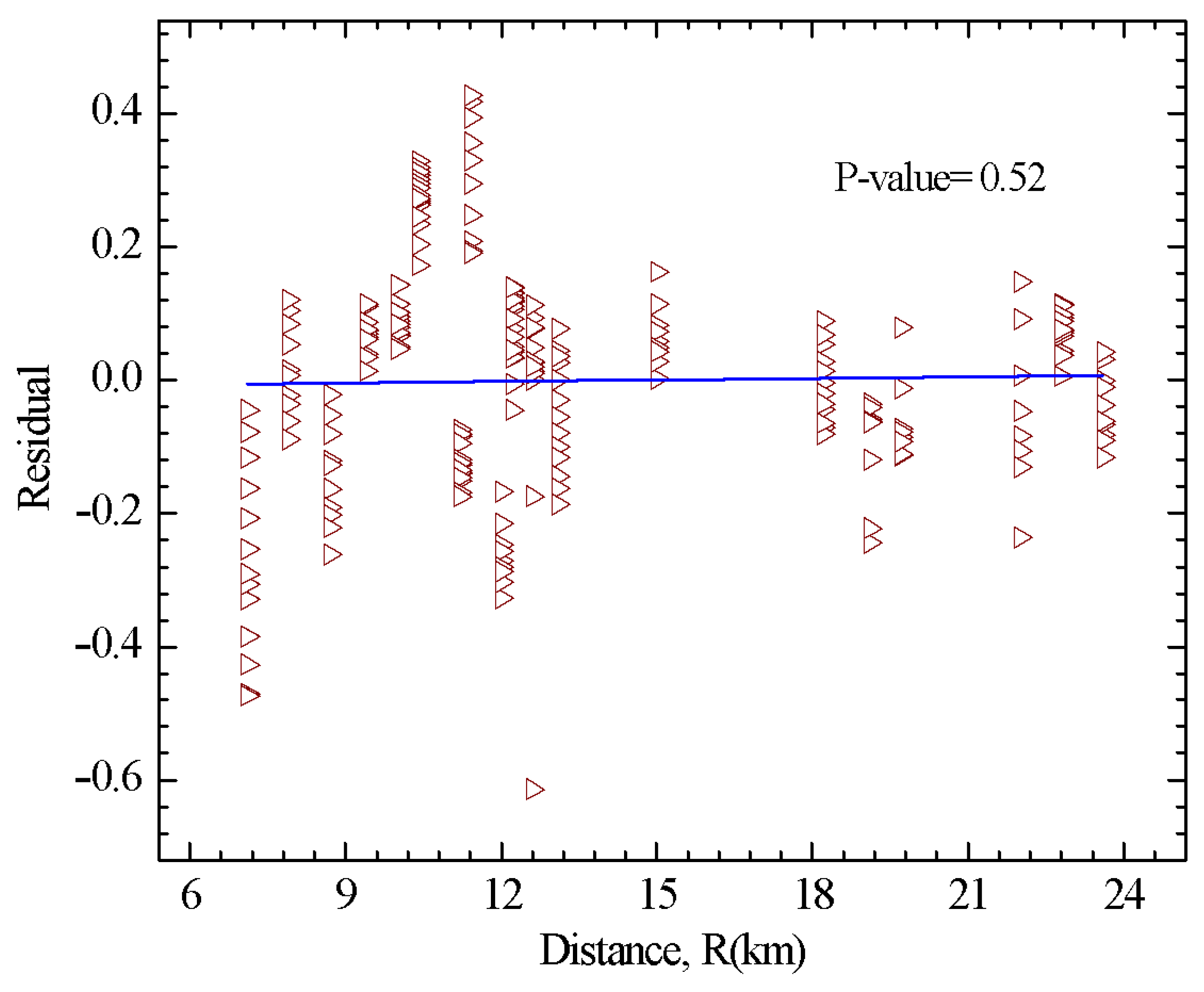
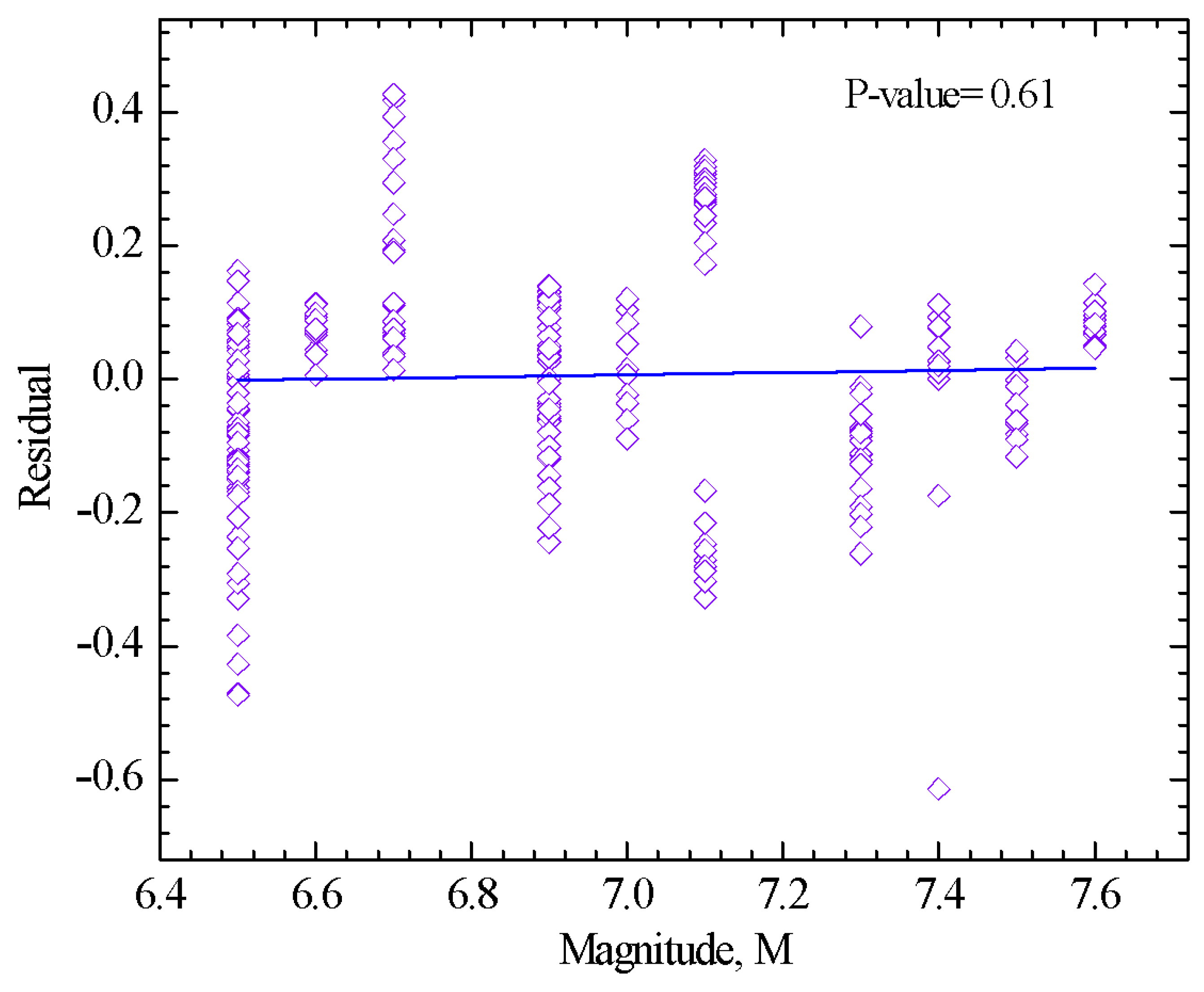
6.1. Efficiency of an Intensity Measure (IM)
6.2. Sufficiency of an Intensity Measure (IM)
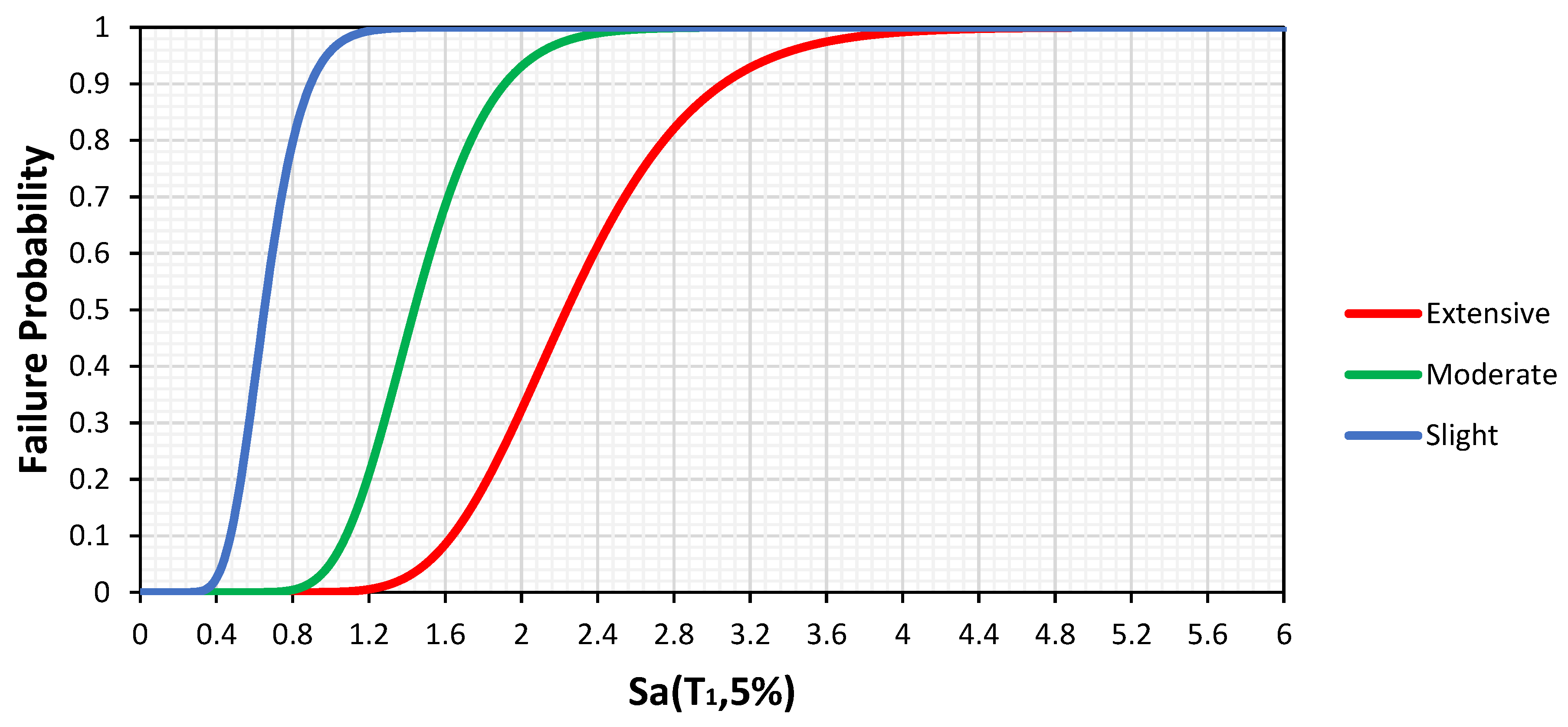
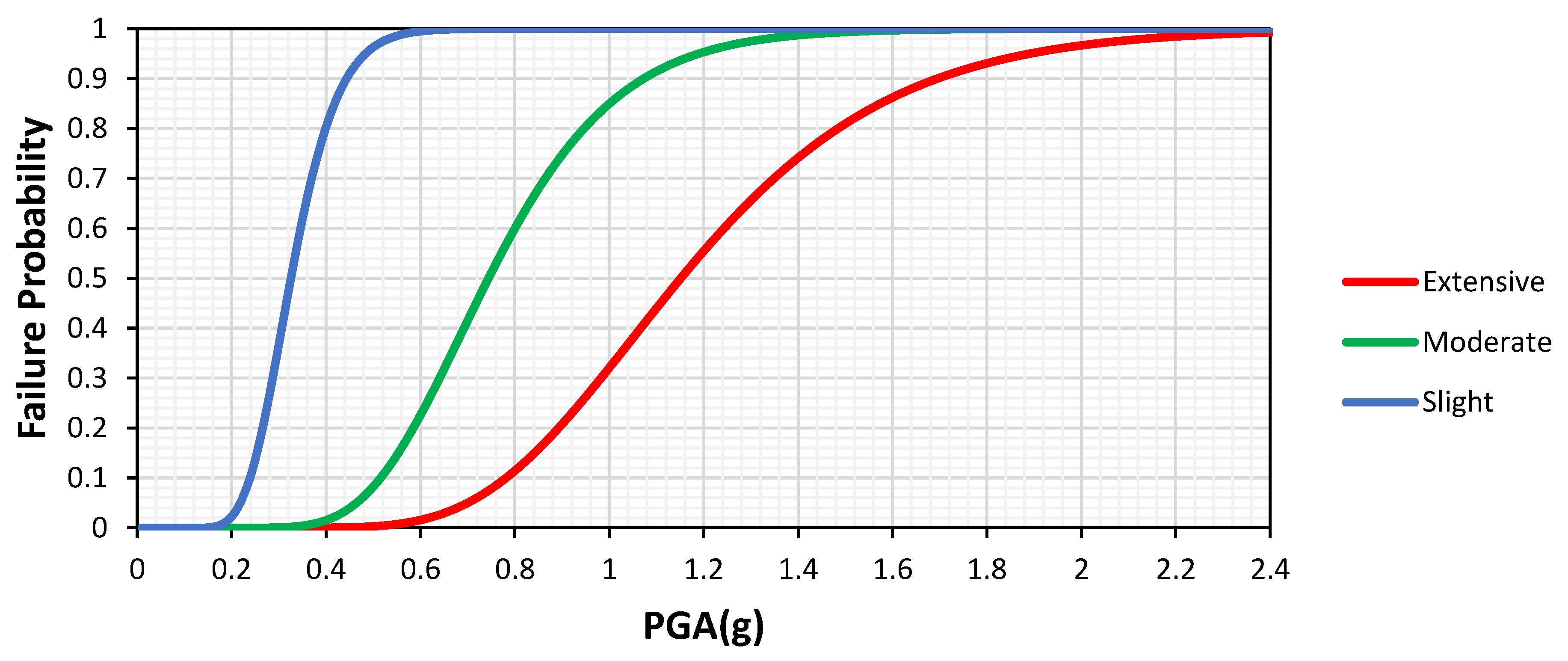
7. Fragility Analysis Results
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Basoz, N.; Kiremidjian, A.S. Evaluation of Bridge Damage Data from the Loma Prieta and Northridge, California Earthquakes; Multidisciplinary Center for Earthquake Engineering Research: Buffalo, NY, USA, 1998. [Google Scholar]
- Shinozuka, M.; Banerjee, S.; Kim, S.H. Fragility Considerations in Highway Bridge Design (No. MCEER-07-0023); Multidisciplinary Center for Earthquake Engineering Research: Buffalo, NY, USA, 2007. [Google Scholar]
- Shinozuka, M.; Feng, M.Q.; Lee, J.; Naganuma, T. Statistical analysis of fragility curves. J. Eng. Mech. 2000, 126, 1224–1231. [Google Scholar] [CrossRef] [Green Version]
- Ardakani, A.; Bayat, M.; Javanmard, M. Numerical modeling of soil nail walls considering Mohr Coulomb, hardening soil and hardening soil with small-strain stiffness effect models. Geomech. Eng. 2014, 6, 391–401. [Google Scholar] [CrossRef]
- Chu, L.M.; Yin, J.H. A Laboratory Device to Test the Pull out Behavior of Soil Nails. Geotech. Test. J. 2015, 28, 499–513. [Google Scholar] [CrossRef]
- Chu, L.M.; Yin, J.H. Comparison of Interface Shear Strength of Soil Nails Measured by Both Direct Shear Box Tests and Pull-Out Tests. J. Geotech. Geoenvironmental Eng. 2005, 131, 1097–1107. [Google Scholar] [CrossRef]
- Bayat, M.; Daneshjoo, F.; Nisticò, N. The effect of different intensity measures and earthquake directions on the seismic assessment of skewed highway bridges. Earthq. Eng. Eng. Vib. 2017, 16, 165–179. [Google Scholar] [CrossRef]
- Shome, N.; Cornell, C.A.; Bassurro, P.; Carballo, J.E. Earthquakes, records, and nonlinear responses. Earthq. Spectra 1998, 14, 469–500. [Google Scholar] [CrossRef]
- ATC. Earthquake Damage Evaluation Data for California; ATC-13; Applied Technology Council: Redwood City, CA, USA, 1985. [Google Scholar]
- FEMA. Earthquake Model. HAZUS-MH MR1: Technical Manual; Federal Emergency Management Agency: Washington, DC, USA, 2003.
- Shome, N. Probabilistic Seismic Demand Analysis of Non-linear Structures. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1999. [Google Scholar]
- Tothong, P.; Luco, N. Probabilistic seismic demand analysis using advanced ground motion intensity measures. Earthq. Eng. Struct. Dyn. 2007, 36, 1837. [Google Scholar] [CrossRef]
- Padgett, J.E.; Nielson, B.G.; DesRoches, R. Selection of optimal intensity measures in probabilistic seismic demand models of highway bridge portfolios. Earthq. Eng. Struct. Dyn. 2008, 37, 711–726. [Google Scholar] [CrossRef]
- Bayat, M.; Daneshjoo, F.; Nisticò, N. A novel proficient and sufficient intensity measure for probabilistic analysis of skewed highway bridges. Struct. Eng. Mech. 2015, 55, 1177–1202. [Google Scholar] [CrossRef]
- Baker, J.W.; Allin Cornell, C. A vector-valued ground motion intensity measure consisting of spectral acceleration and epsilon. Earthq. Eng. Struct. Dyn. 2005, 34, 1193–1217. [Google Scholar] [CrossRef]
- Luco, N.; Cornell, A.C. Structure-specific scalar intensity measures for near-source and ordinary earthquake ground motions. Earthq. Spectra 2007, 23, 357–392. [Google Scholar] [CrossRef] [Green Version]
- Tiznado, J.C.; Rodríguez-Roa, F. Seismic lateral movement prediction for gravity retaining walls on granular soils. Soil Dyn. Earthq. Eng. 2011, 31, 391–400. [Google Scholar] [CrossRef]
- Choobbasti, A.J.; Kutanaei, S.S.; Ahangari, H.T.; Kardarkolai, M.M.; Motaghedi, H. Comparison of different local site effect estimation methods in site with high thickness of alluvial layer deposits: A case study of Babol city. Arab. J. Geosci. 2020, 13, 1–9. [Google Scholar] [CrossRef]
- Tavakoli, H.; Kutanaei, S.S.; Hosseini, S.H. Assessment of seismic amplification factor of excavation with support system. Earthq. Eng. Eng. Vib. 2019, 18, 555–566. [Google Scholar] [CrossRef]
- Rawlings, C. Geotechnical finite element analysis-a practical guide. In Proceedings of the Institution of Civil Engineers-Civil Engineering; ICE Publishing: London, UK, 2017; Volume 170, pp. 152–153. [Google Scholar]
- Unterreiner, P.; Benhamida, B.; Schlosser, F. Finite element modelling of the construction of a full-scale experimental soil-nailed wall. French National Research Project CLOUTERRE. In Proceedings of the Institution of Civil Engineers-Ground Improvement; ICE Publishing: London, UK, 1997; Volume 1, pp. 1–8. [Google Scholar]
- Fan, C.C.; Luo, J.H. Numerical study on the optimum layout of soil–nailed slopes. Comput. Geotech. 2008, 35, 585–599. [Google Scholar] [CrossRef]
- Plumelle, C.; Schlosser, F.; Delage, P.; Knochenmus, G. French National Research Project on Soil Nailing: Clouterre; Geotechnical Special Publication No.25; ASCE: New York, NY, USA, 1990; pp. 660–675. [Google Scholar]
- Feng, X.; Xia, X.-H.; Wang, J.-H. The Application of small strain model in excavation, The National Natural Science Foundation of China (No.50679041). J. Shanghai Jiaotong Univ. 2009. [Google Scholar] [CrossRef]
- Plaxis, B. PLAXIS 3D Foundation Material Models Manual; PLAXIS: Rhoon, The Netherlands, 2008. [Google Scholar]
- Benz, T. Small-Strain Stiffness of Soils and Its Numerical Consequences; University of Stuttgart: Stuttgart, Germany, 2007; Volume 5. [Google Scholar]
- Ibrahim, K.M.H.I.; Ibrahim, T.E. Effect of historical earthquakes on pre-stressed anchor tie back diaphragm wall and on near-by building. HBRC J. 2013, 9, 60–67. [Google Scholar] [CrossRef] [Green Version]
- Noorzad, R.; Omidvar, M. Seismic displacement analysis of embankment dams with reinforced cohesive shell. Soil Dyn. Earthq. Eng. 2010, 30, 1149–1157. [Google Scholar] [CrossRef]
- Agency, F.E.M. Quantification of Building Seismic Performance Factors; FEMA P695: Washington, DC, USA, 2001. [Google Scholar]
- Agency, F.E.M. Seismic Performance Assessment of Buildings; FEMA P58: Washington, DC, USA, 2018. [Google Scholar]
- Boore, D.M.; Joyner, W.B.; Fumal, T.E. Estimation of Response Spectra and Peak Accelerations from Western North American Earthquakes: An Interim Report; Open-File Report 93-509; U.S. Geological Survey: Menlo Park, CA, USA, 1993.
- Vamvatsikos, D.; Jalayer, F.; Cornell, C.A. Application of incremental dynamic analysis to an RC-structure. In Proceedings of the FIB Symposium on Concrete Structures in Seismic Regions, Athens, Greece, 6–8 May 2003; pp. 75–86. [Google Scholar]
- Alam, M.S.; Bhuiyan, M.R.; Billah, A.M. Seismic fragility assessment of SMA-bar restrained multi-span continuous highway bridge isolated by different laminated rubber bearings in medium to strong seismic risk zones. Bull. Earthq. Eng. 2012, 10, 1885–1909. [Google Scholar] [CrossRef]
- Zamiran, S.; Osouli, A. Seismic motion response and fragility analyses of cantilever retaining walls with cohesive backfill. Soils Found. 2018, 58, 412–426. [Google Scholar] [CrossRef]
- Cornell, A.C.; Jalayer, F.; Hamburger, R.O. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines. J. Struct. Eng. 2002, 128, 526–532. [Google Scholar] [CrossRef] [Green Version]
- Gardoni, P.; Der Kiureghian, A.; Mosalam, K.M. Probabilistic capacity models an and d fragility estimates for reinforced concrete columns based on experimental observations. J. Eng. Mech. 2002, 128, 1024–1038. [Google Scholar] [CrossRef]
- Kia, M.; Amini, A.; Bayat, M.; Ziehl, P. Probabilistic Seismic Demand Analysis of Structures Using Reliability Approaches. J. Earthq. Tsunami 2020, 2150011. [Google Scholar] [CrossRef]
- Kia, M.; Banazadeh, M.; Bayat, M. Rapid seismic loss assessment using new probabilistic demand and consequence models. Bull. Earthq. Eng. 2019, 17, 3545–3572. [Google Scholar] [CrossRef]
- Box, G.E.; Tiao, G.C. Bayesian Inference in Statistical Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2010; Volume 40. [Google Scholar]



| Backfill | Foundation Soils | |||
|---|---|---|---|---|
| Unit weight | 16.6 | 17 | ||
| Young’s module | ||||
| Poisson’s ration | 0.39 | 0.37 | ||
| Cohesive | 3 | 0 | ||
| The angle of internal friction | 38° | 36° | ||
| Shotcrete facing | ||||
| Unit weight | 24 | |||
| Young’s module | ||||
| Axial stiffness | ||||
| Bending stiffness | ||||
| Shotcrete thickness | 0.08 | |||
| Poisson’s ratio | 0.2 | |||
| Nail (Grouted diameter = 63 mm) | Type A | Type B | Type C–E | |
| Length | 6 | 8 | 6 | |
| Tube thickness | 1 | 2 | 1 | |
| Tube stiffness | 16 | 30 | 40 | |
| Axial stiffness | ||||
| Bending stiffness | 13.39 | 14.05 | 14.3 | |
| Weight | 0.072 | 0.072 | 0.072 | |
| Poisson’s ratio | 0.2 | 0.2 | 0.2 |
| Parameters | Value |
|---|---|
| Vertical wall height H(m) | 8 |
| Wall slope α | 0 |
| The inclination angle of the slope β | 0 |
| Nailing system type | Grouted |
| Nails and shotcrete model | Elastic |
| Rebar yield stress fy (Mpa) | 400 |
| Rebar elasticity modulus En (Kpa) | 2.2 × 108 |
| shotcrete elasticity modulus Eg (Kpa) | 2.19 × 107 |
| Rebar diameter d(mm) | 25, 28 |
| Overall diameter hole drilling Ddh (mm) | 100 |
| Nail length L (m) | 6, 8 |
| Incline angle of soil nail (degree) | 15 |
| Nail spaces Sh × Sv (m × m) | 1/5 × 1 |
| The thickness of the shotcrete(mm) | 120 |
| Parameters | HSS Model | HS Model | MC Model |
|---|---|---|---|
| Cohesion C (KN/m2) | 1 | 1 | 1 |
| Friction angle ϕ | 33 | 33 | 33 |
| Dilatancy angle ψ | 3 | 3 | 3 |
| Unit weight of soil () ( | 18 | 18 | 18 |
| Modulus of elasticity of soil “E” (KN/m2) | - | - | 22,000 |
| Secant stiffness in standard drained triaxial test stres ) | 22,000 | 22,000 | - |
| Tangent stiffness for primary audiometry loading | 22,000 | 22,000 | - |
| Unloading/reloading modulus | 66,000 | 66,000 | - |
| Reference shear modulus | 60,000 | - | - |
| Reference stress for stiffness | 100 | 100 | - |
| Shear strain as shear modulus at which 0.7 G0, | 0.0002 | - | - |
| Poisson ratio V | - | - | 0.35 |
| Unloading and reloading Poisson ratio Vur | 0.2 | 0.2 | - |
| Power for stress level dependency of stiffness m | 0.5 | 0.5 | - |
| Earthquake | Recording Station | ||||||
|---|---|---|---|---|---|---|---|
| ID No | M | R (Km) | PGA (g) | Year | Name | Name | Owner |
| 1 | 7.0 | 14.3 | 0.48 | 1992 | Cape Mendocino | Rio Dell Overpass | USGS |
| 2 | 7.6 | 10 | 0.21 | 1999 | Chi-Chi, Taiwan | CHY101 | CWB |
| 3 | 7.1 | 12 | 0.82 | 1999 | Duzce, Turkey | Bolu | ERD |
| 4 | 6.5 | 15 | 0.45 | 1976 | Friuli, Italy | Tolmezzo | ------------ |
| 5 | 7.1 | 10.4 | 0.35 | 1999 | Hector Mine | Hector | SCSN |
| 6 | 6.5 | 22 | 0.34 | 1979 | Imperial Valley | Delt | UNAMUCSD |
| 7 | 6.5 | 22 | 0.35 | 1979 | Imperial Valley | El Centro Array#1 | USGS |
| 8 | 6.9 | 17 | 0.38 | 1995 | Kobe, Japan | Nishi-Akashi | CUE |
| 9 | 6.9 | 17 | 0.51 | 1995 | Kobe, Japan | Shin-Osaka | CUE |
| 10 | 7.5 | 13.1 | 0.24 | 1999 | Kokaeli, Turkey | Duzce | ERD |
| 11 | 7.3 | 23.6 | 0.36 | 1992 | Landers | Yemo Fire Station | CDMG |
| 12 | 7.3 | 23.6 | 0.24 | 1992 | Landers | Coolwater | SCE |
| 13 | 6.9 | 12.2 | 0.42 | 1989 | Loma Prieta | Capitola | CDMG |
| 14 | 6.9 | 12.2 | 0.53 | 1989 | Loma Prieta | Gilory Arrey#3 | CDMG |
| 15 | 7.4 | 12.6 | 0.56 | 1990 | Manjil | Abbar | BHRC |
| 16 | 6.7 | 12.6 | 0.55 | 1994 | Northridge | Beverly Hills-Mulhol | USC |
| 17 | 6.7 | 12.6 | 0.44 | 1994 | Northridge | Canyon Country-WLC | USC |
| 18 | 6.6 | 22.8 | 0.36 | 1971 | San Ferando | LA-Hollywood Stor | CDMG |
| 19 | 6.5 | 18.2 | 0.51 | 1987 | Superstition Hills | El Centro Imp.Co | CDMG |
| 20 | 6.5 | 18.2 | 0.52 | 1987 | Superstition Hills | Poe Road (temp) | USGS |
| Damage | Slight (DS = 1) | Moderate (DS = 2) | Extensive (DS = 3) |
|---|---|---|---|
| Wall Drift ratio | 0.02 | 0.05 | 0.08 |
| Mean | C.O.V% | Mean | C.O.V% | Mean | C.O.V% | |
| −3.885 | 0.636 | 0.879 | 2.889 | 0.297 | 0.0473 | |
| Mean | C.O.V% | Mean | C.O.V% | Mean | C.O.V% | |
| −4.427 | 0.272 | 0.943 | 1.681 | 0.182 | 0.0351 | |
| a | b | |
| a | 1 | 0.607 |
| b | 0.607 | 1 |
| a | b | |
| a | 1 | −0.031 |
| b | −0.031 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bayat, M.; Kosarieh, A.H.; Javanmard, M. Probabilistic Seismic Demand Analysis of Soil Nail Wall Structures Using Bayesian Linear Regression Approach. Sustainability 2021, 13, 5782. https://doi.org/10.3390/su13115782
Bayat M, Kosarieh AH, Javanmard M. Probabilistic Seismic Demand Analysis of Soil Nail Wall Structures Using Bayesian Linear Regression Approach. Sustainability. 2021; 13(11):5782. https://doi.org/10.3390/su13115782
Chicago/Turabian StyleBayat, Mahdi, Amir Homayoon Kosarieh, and Mehran Javanmard. 2021. "Probabilistic Seismic Demand Analysis of Soil Nail Wall Structures Using Bayesian Linear Regression Approach" Sustainability 13, no. 11: 5782. https://doi.org/10.3390/su13115782
APA StyleBayat, M., Kosarieh, A. H., & Javanmard, M. (2021). Probabilistic Seismic Demand Analysis of Soil Nail Wall Structures Using Bayesian Linear Regression Approach. Sustainability, 13(11), 5782. https://doi.org/10.3390/su13115782





