Optimization of Seismic Base Isolation System Using Adaptive Harmony Search Algorithm
Abstract
:1. Introduction
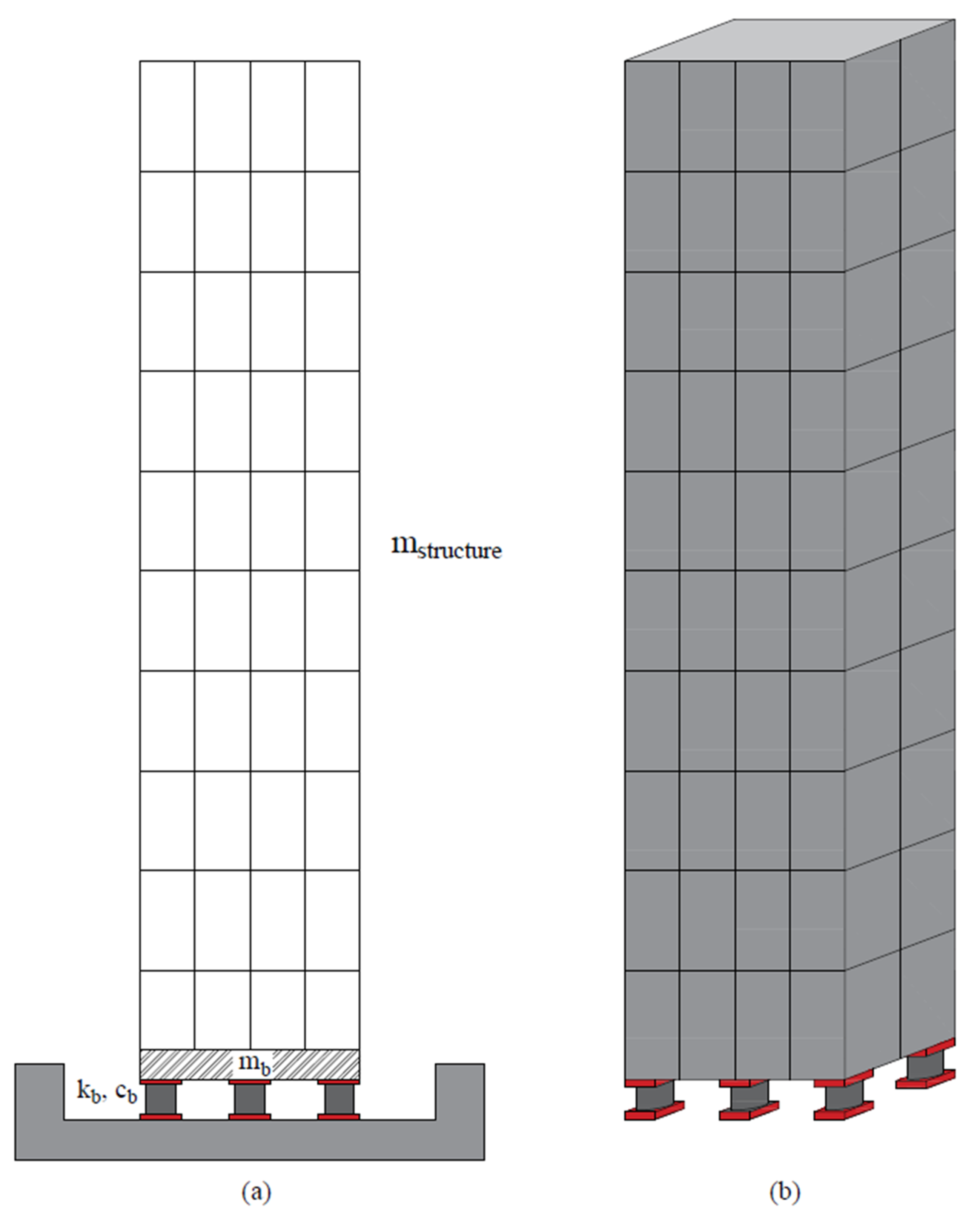
2. Optimization of Seismic Isolator System
3. Numerical Examples
4. Discussion
5. Conclusions
- -
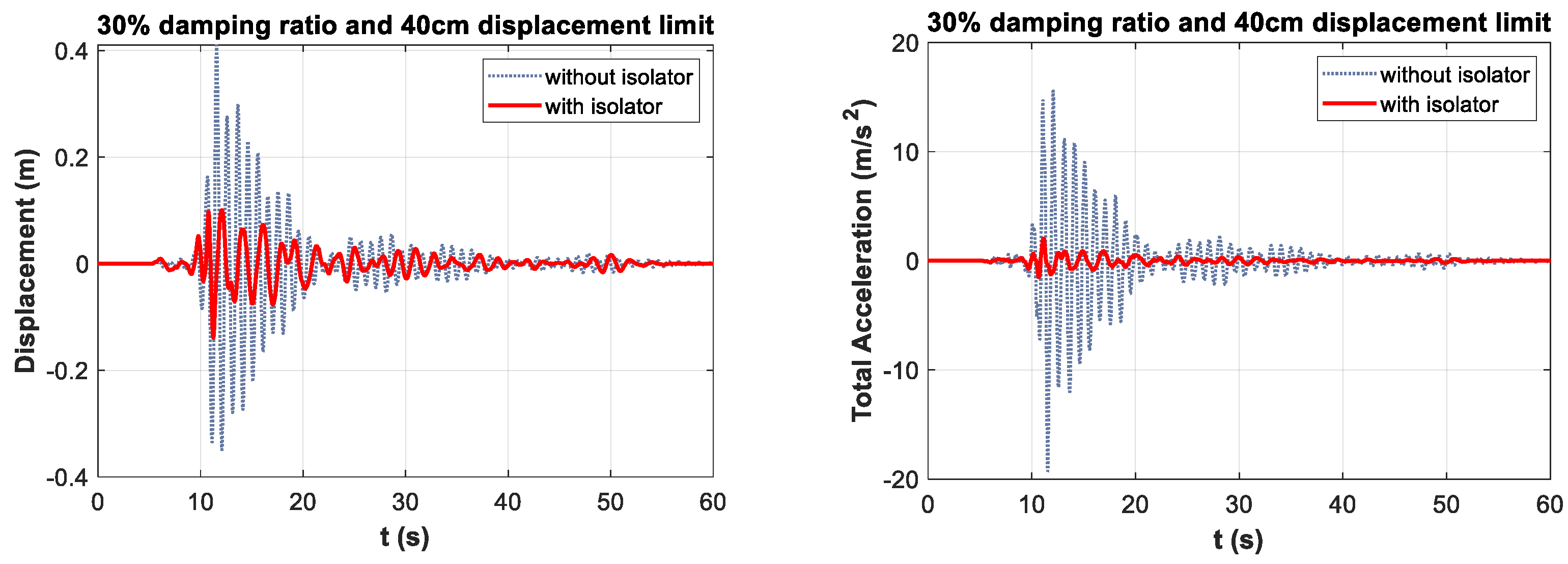
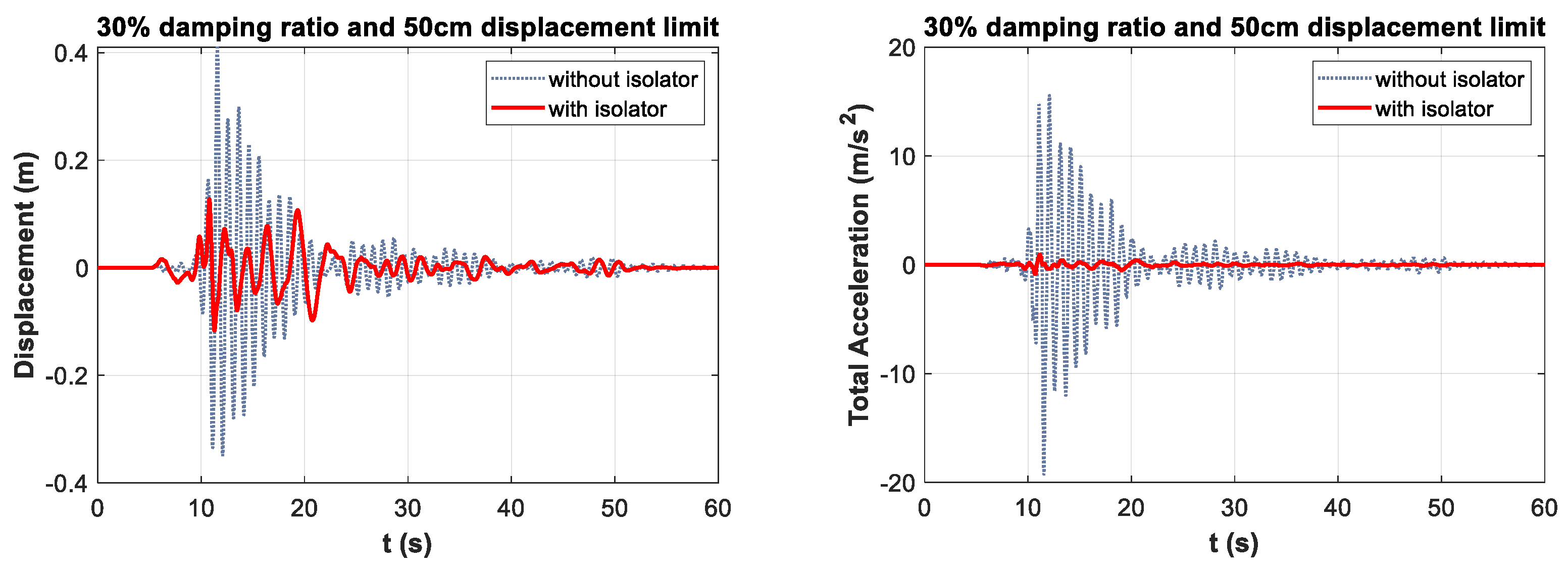
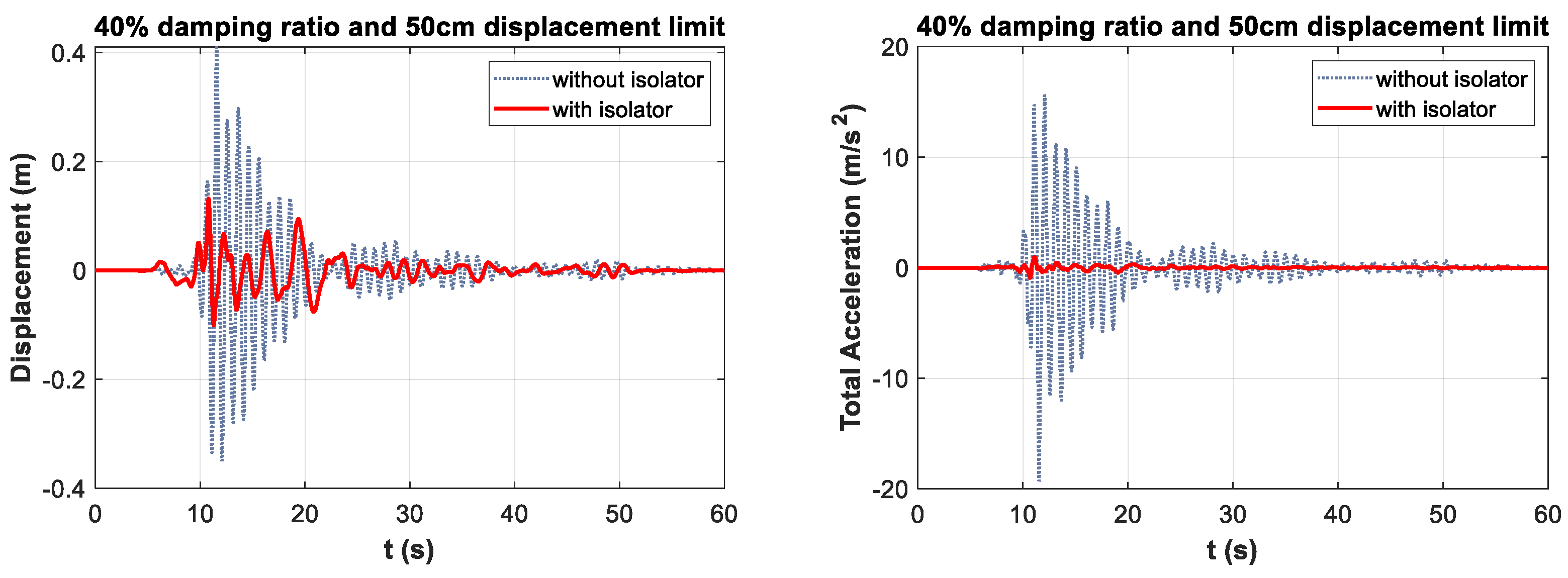
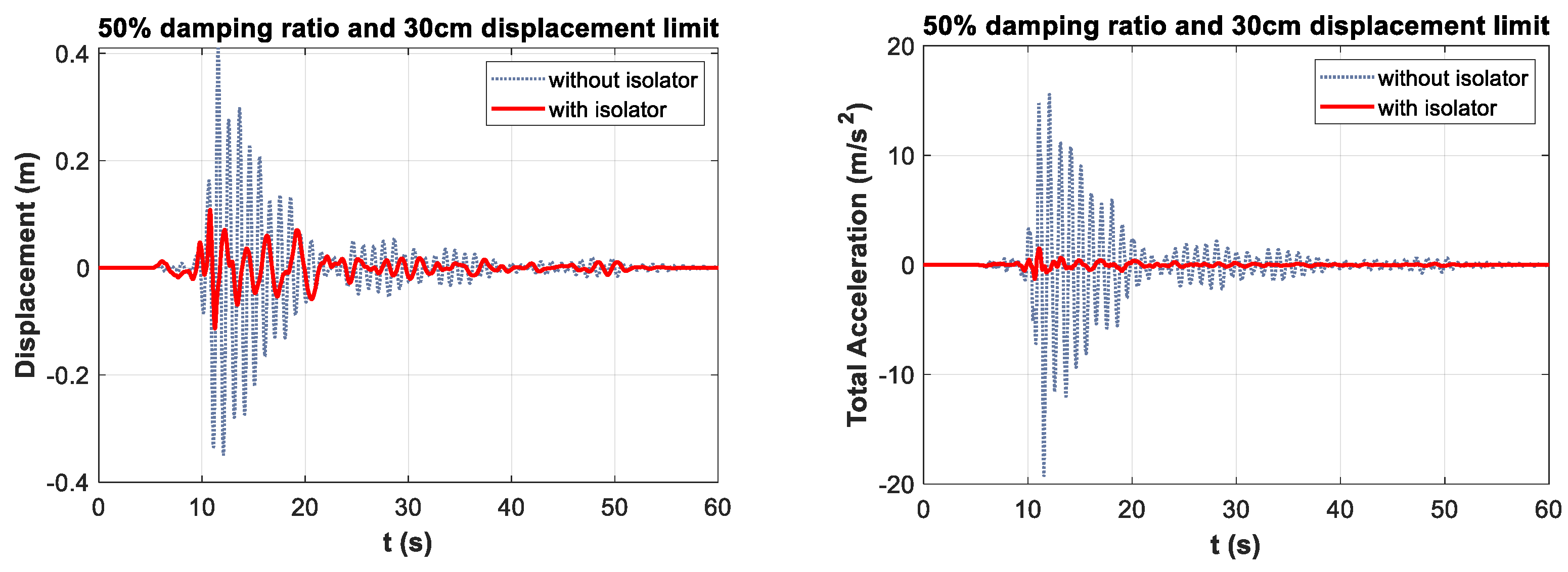
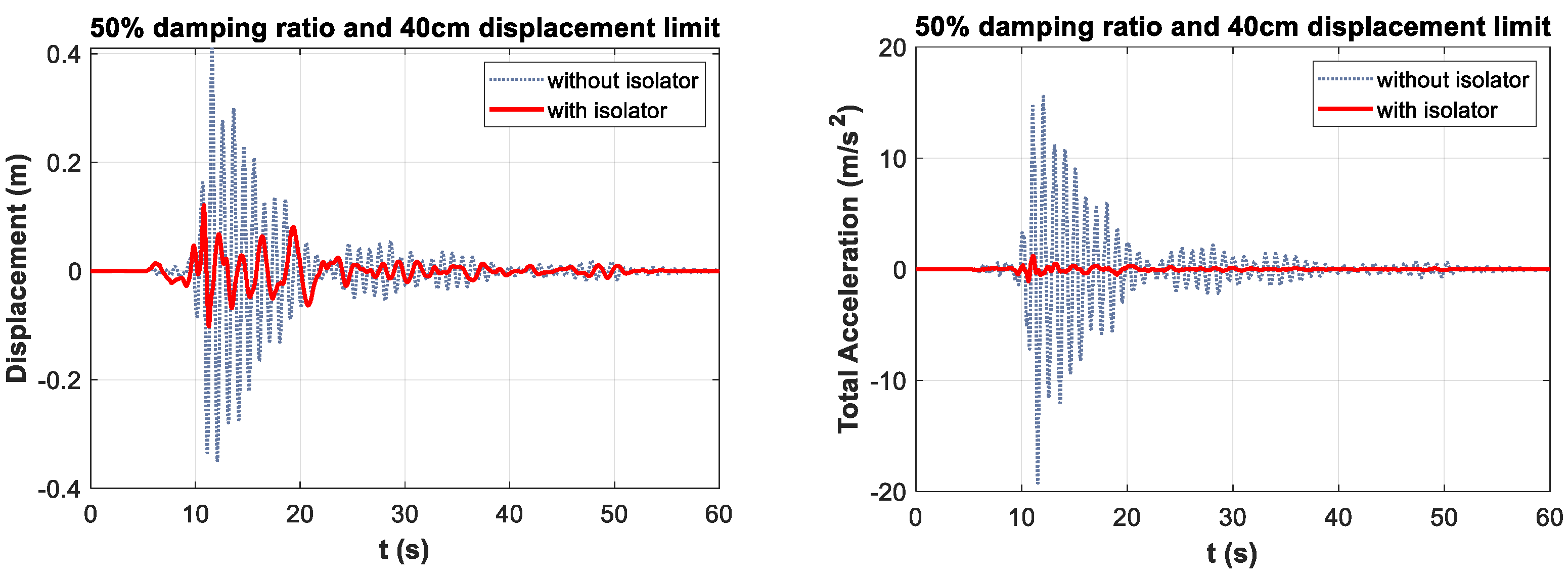
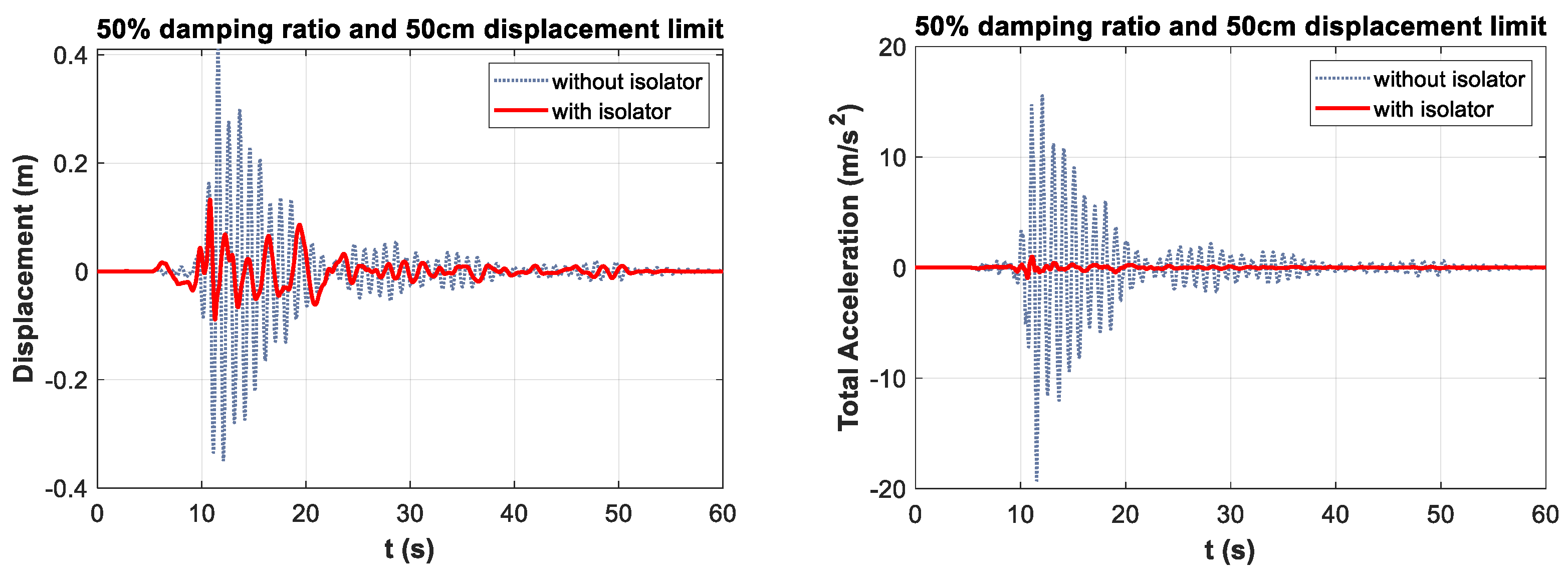
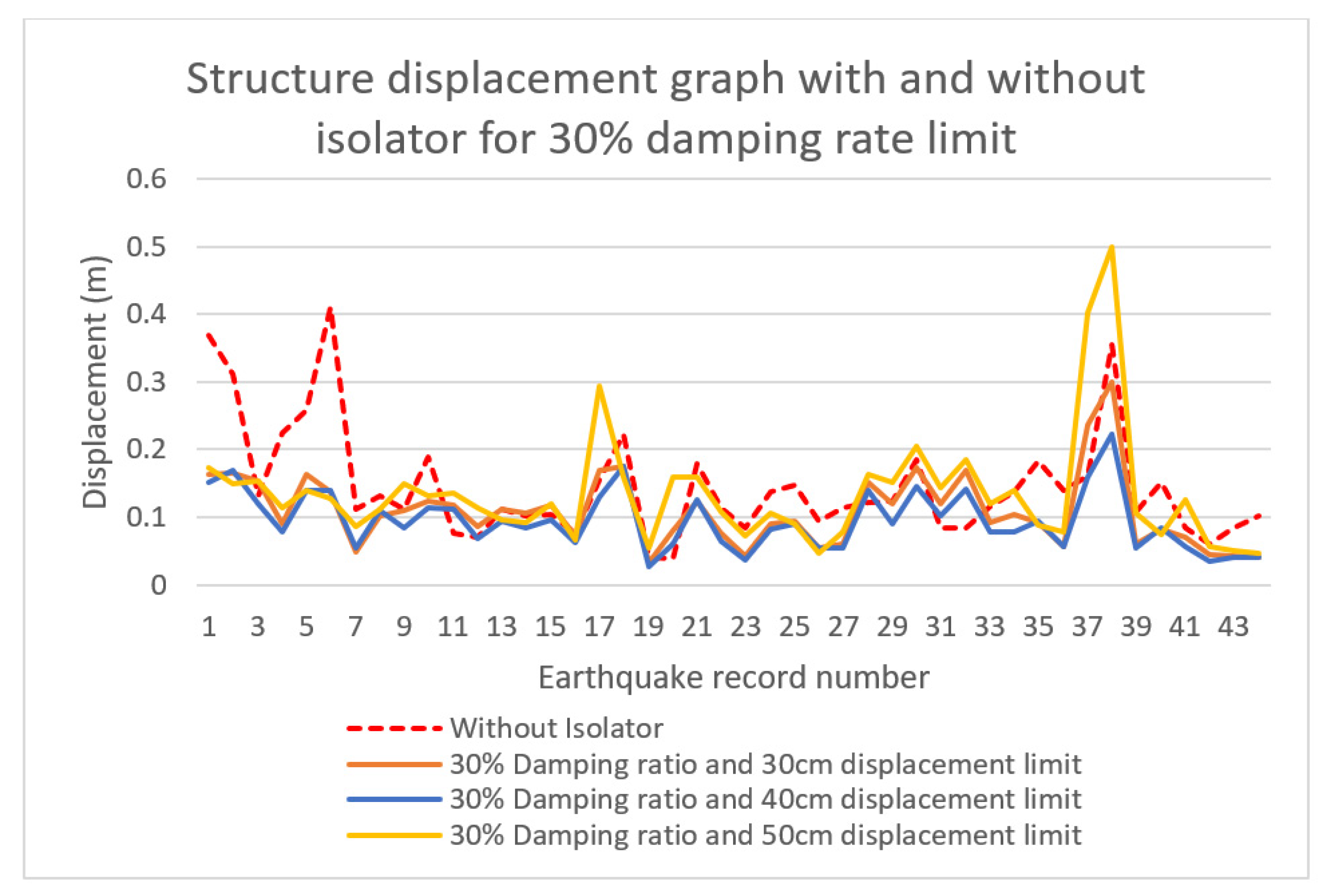
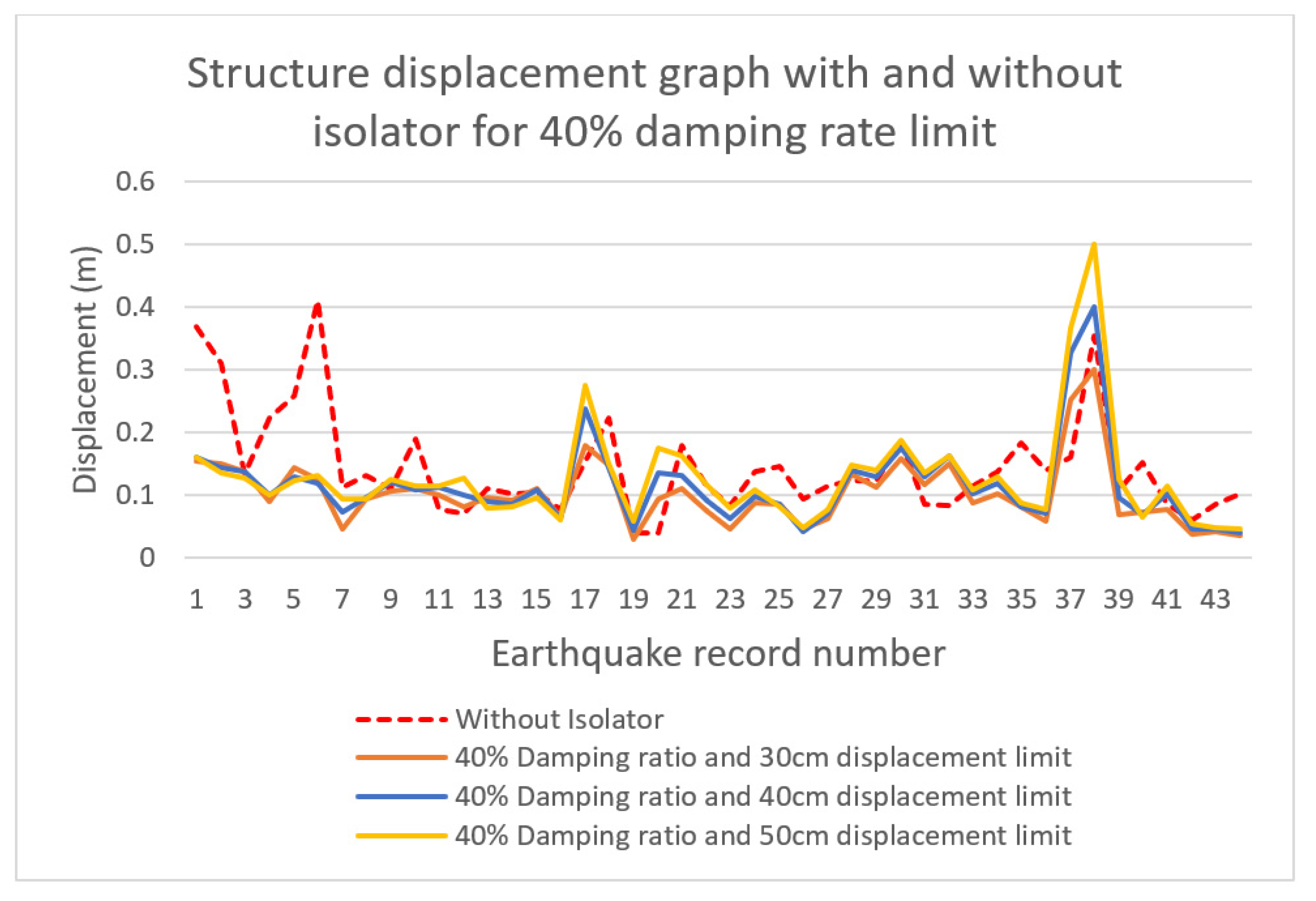
- The maximum displacement reduction rate of approximately 72% was observed at the damping ratio of 50% and the displacement limit of 30 cm. Optimum displacement reductions were observed at 40 cm displacement limit for 40% damping limit and 50 cm displacement limit for 30% damping limit. It was observed that, after the optimum values, the performance decreased with the increase in displacement limit values. Based on these data, it is concluded that to obtain the optimum displacement reduction, it is necessary to reduce the mobility of isolators designed with a high damping ratio.
- -
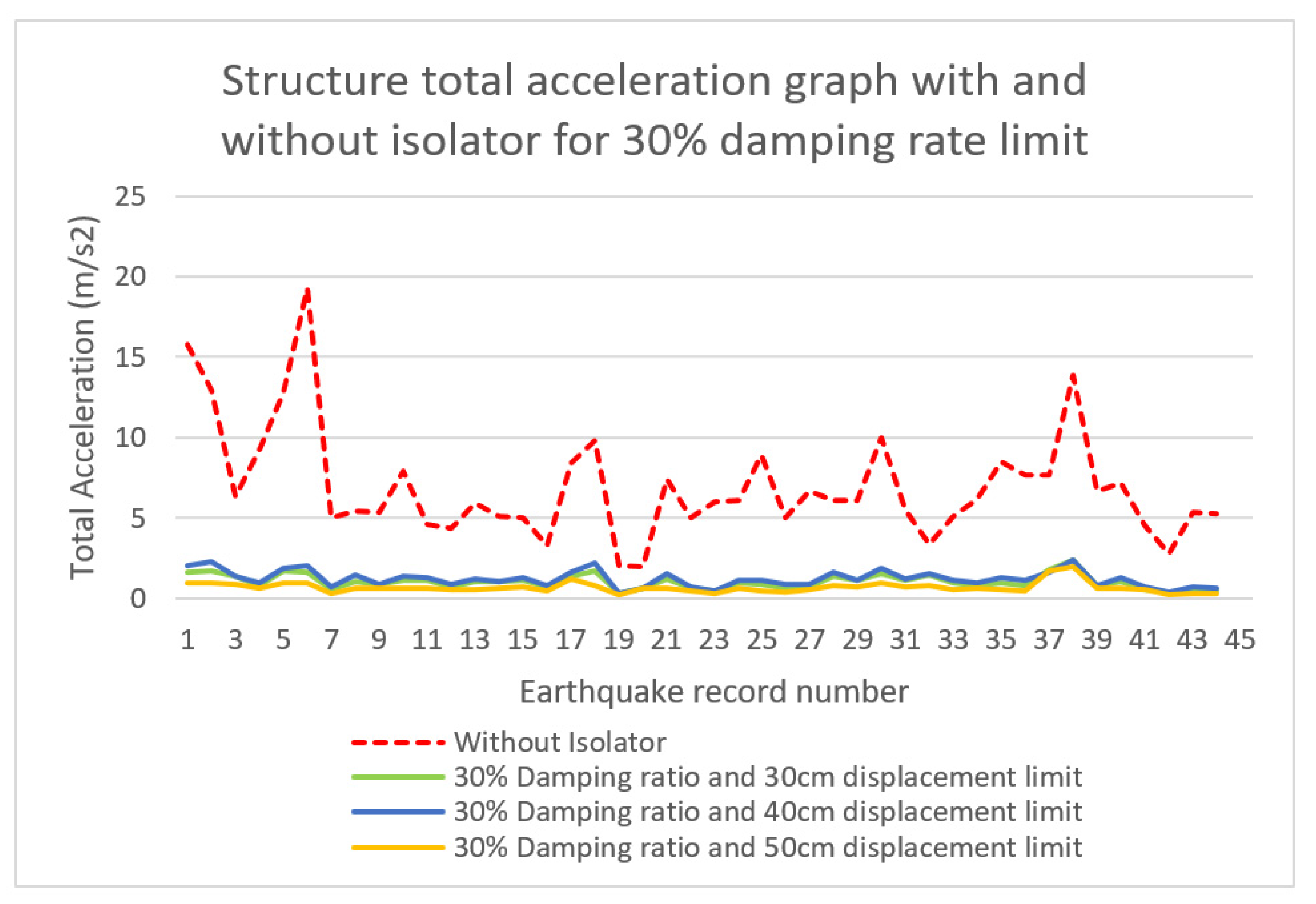
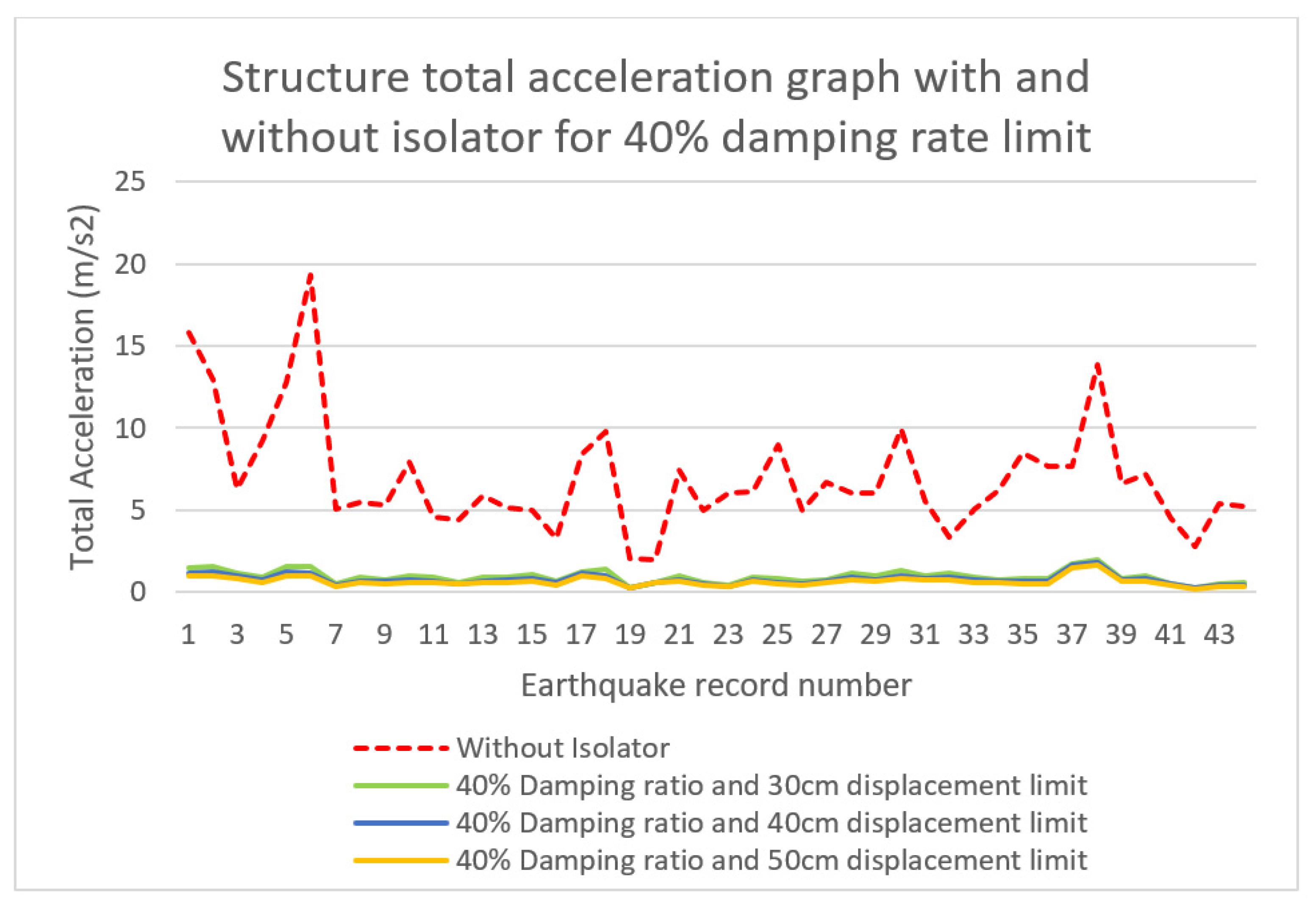
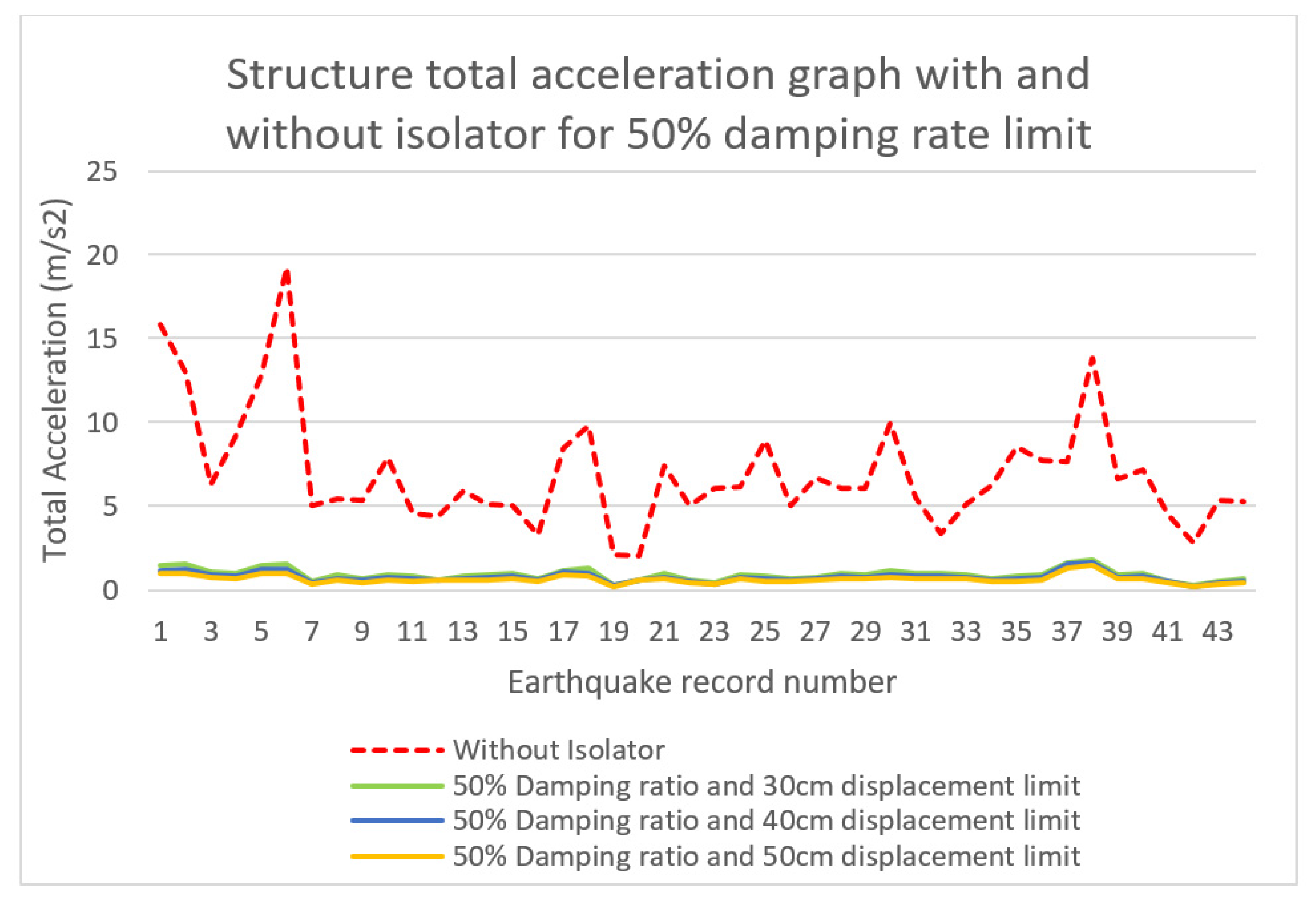
- The maximum total acceleration reduction value was observed at approximately 95% for 30% damping and 50 cm displacement limit. For the 30%, 40%, and 50% damping ratio limits, optimum total acceleration drop rates were obtained at the 50 cm displacement limit. Based on this, it is derived that increasing the displacement limit, and hence the ductility of the isolator, is effective in reducing the total acceleration of the structure.
- -
- While the critical earthquake record of the uncontrolled structure was DUZCE/BOL090 earthquake, when the isolator was added, the critical earthquake record was the CHICHI/CHY101-N earthquake. All movement constraints defined for the structure on all damping ratios reached the limit value in the CHICHI/CHY101-N earthquake and caused the structure with isolators to be strained. Based on this, it is understood that adding an isolator system to the structure can change the earthquake behavior and acceleration values because of the high level of change in the period of the combined structure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bakkaloğlu, E. Seismic İsolator Systems in Hospital Buildings the Effects of the Use Decision on the Building Manufacturing Process. Master’s Thesis, Istanbul Technical Unıversity, Institute of Science, Istanbul, Turkey, 2018. [Google Scholar]
- Sheikh, H.; Van Engelen, N.C.; Ruparathna, R. A review of base isolation systems with adaptive characteristics. In Structures; Elsevier: Amsterdam, The Netherlands, 2022; Volume 38, pp. 1542–1555. [Google Scholar]
- Bao, Y.; Becker, T.C. Inelastic response of base-isolated structures subjected to impact. Eng. Struct. 2018, 171, 86–93. [Google Scholar] [CrossRef]
- Kelly, J.M. The role of damping in seismic isolation. Earthq. Eng. Struct. Dyn. 1999, 28, 3–20. [Google Scholar] [CrossRef]
- Habieb, A.B.; Formisano, A.; Milani, G.; Pianese, G. Seismic performance of Unbonded Fiber-Reinforced Elastomeric Isolators (UFREI) made by recycled rubber. Influence of suboptimal crosslinking. Eng. Struct. 2022, 256, 114038. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, W.; Chen, X.; Yan, L. Fatigue life prediction of vulcanized natural rubber under proportional and non-proportional loading. Fatigue Fract. Eng. Mater. Struct. 2008, 31, 38–48. [Google Scholar] [CrossRef]
- Markou, A.A.; Manolis, G.D. Mechanical models for shear behavior in high damping rubber bearings. Soil Dyn. Earthq. Eng. 2016, 90, 221–226. [Google Scholar] [CrossRef]
- Ozkaya, C.; Akyuz, U.; Caner, A.; Dicleli, M.U.R.A.T.; Pınarbası, S. Development of a new rubber seismic isolator: ‘Ball Rubber Bearing (BRB)’. Earthq. Eng. Struct. Dyn. 2011, 40, 1337–1352. [Google Scholar] [CrossRef]
- Zou, X.K.; Chan, C.M. Optimal drift performance design of base-isolated buildings subject to earthquake loads. In WIT Transactions on The Built Environment; WIT Press: Southampton, UK, 2001; Volume 54. [Google Scholar]
- Iemura, H.; Taghikhany, T.; Jain, S.K. Optimum design of resilient sliding isolation system for seismic protection of equipment. Bull. Earthq. Eng. 2007, 5, 85–103. [Google Scholar] [CrossRef]
- Jangid, R.S. Equivalent linear stochastic seismic response of isolated bridges. J. Sound Vib. 2008, 309, 805–822. [Google Scholar] [CrossRef]
- Bucher, C. Probability-based optimal design of friction-based seismic isolation devices. Struct. Saf. 2009, 31, 500–507. [Google Scholar] [CrossRef]
- Dicleli, M.; Karalar, M. Optimum characteristic properties of isolators with bilinear force-displacement hysteresis for seismic protection of bridges built on various site soils. Soil Dyn. Earthq. Eng. 2011, 31, 982–995. [Google Scholar] [CrossRef]
- Weber, F.; Distl, H.; Braun, C. Isolation performance of optimized triple friction pendulum. Int. Refereed J. Eng. Sci. 2016, 5, 55–69. [Google Scholar]
- Charmpis, D.C.; Komodromos, P.; Phocas, M.C. Optimized earthquake response of multi-story buildings with seismic isolation at various elevations. Earthq. Eng. Struct. Dyn. 2012, 41, 2289–2310. [Google Scholar]
- Xu, Y.; Guo, T.; Yan, P. Design optimization of triple friction pendulums for base-isolated high-rise buildings. Adv. Struct. Eng. 2019, 22, 2727–2740. [Google Scholar] [CrossRef]
- Xu, Y.; Becker, T.C.; Guo, T. Design optimization of triple friction pendulums for high-rise buildings considering both seismic and wind loads. Soil Dyn. Earthq. Eng. 2021, 142, 106568. [Google Scholar] [CrossRef]
- Moeindarbari, H.; Taghikhany, T. Seismic optimum design of triple friction pendulum bearing subjected to near-fault pulse-like ground motions. Struct. Multidiscip. Optim. 2014, 50, 701–716. [Google Scholar] [CrossRef]
- Dang, Y.; Zhao, G.; Tian, H.; Li, G. Two-Stage Optimization Method for the Bearing Layout of Isolated Structure. Adv. Civ. Eng. 2021, 2021, 4895176. [Google Scholar] [CrossRef]
- Aceto, L.; Quaranta, G.; Camata, G.; Briseghella, B.; Spacone, E. Optimum design of a hybrid isolation device for server racks using constrained differential evolution algorithm. In Proceedings of the 8th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering: ECCOMAS Thematic Conference, Athens, Greece, 27–30 June 2021. [Google Scholar]
- Tsipianitis, A.; Tsompanakis, Y. Optimizing the seismic response of base-isolated liquid storage tanks using swarm intelligence algorithms. Comput. Struct. 2021, 243, 106407. [Google Scholar] [CrossRef]
- Çerçevik, A.E.; Avşar, Ö.; Hasançebi, O. Optimum design of seismic isolation systems using metaheuristic search methods. Soil Dyn. Earthq. Eng. 2020, 131, 106012. [Google Scholar] [CrossRef]
- Etedali, S.; Hasankhoie, K.; Sohrabi, M.R. Optimal design of pure-friction isolators with and without restoring device: A multi-objective cuckoo search-based approach for seismic-excited structures. In Structures; Elsevier: Amsterdam, The Netherlands, 2020; Volume 25, pp. 708–719. [Google Scholar]
- Nigdeli, S.M.; Bekdaş, G.; Alhan, C. Optimization of seismic isolation systems via harmony search. Eng. Optim. 2014, 46, 1553–1569. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G. VA new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Keshtegar, B.; Etedali, S. Nonlinear mathematical modeling and optimum design of tuned mass dampers using adaptive dynamic harmony search algorithm. Struct. Control Health Monit. 2018, 25, e2163. [Google Scholar] [CrossRef]
- Alkhadashi, A.; Mohammad, F.; Zubayr, R.O.; Klalib, H.A.; Balik, P. Multi-objective design optimization of steel-framed structures using three different methods. Int. J. Struct. Integr. 2021, 13, 92–111. [Google Scholar] [CrossRef]
- Toklu, Y.C.; Bekdaş, G.; Yücel, M.; Nigdeli, S.M.; Kayabekir, A.E.; Kim, S.; Geem, Z.W. Total Potential Optimization Using Metaheuristic Algorithms for Solving Nonlinear Plane Strain Systems. Appl. Sci. 2021, 11, 3220. [Google Scholar] [CrossRef]
- FEMA P-695. Quantification of Building Seismic Performance Factors; US Department of Homeland Security, FEMA: Washington, DC, USA, 2009. [Google Scholar]
- The MathWorks, Matlab R2018a. Natick, MA. 2018. Available online: https://ww2.mathworks.cn/company/newsroom/mathworks-announces-release-2018a-of-the-matlab-and-simulink-product-families.html (accessed on 3 May 2022).
- Singh, M.P.; Singh, S.; Moreschi, L.M. Tuned mass dampers for response control of torsional buildings. Earthq. Eng. Struct. Dyn. 2002, 31, 749–769. [Google Scholar] [CrossRef]




| Date | Earthquake Name | Earthquake Record Number | Earthquake Record | Earthquake Record Number | Earthquake Record |
|---|---|---|---|---|---|
| 1994 | Northridge | 1 | NORTHR/MUL009 | 2 | NORTHR/MUL279 |
| 1994 | Northridge | 3 | NORTHR/LOS000 | 4 | NORTHR/LA270 |
| 1999 | Duzce, Turkey | 5 | DUZCE/BOL0000 | 6 | DUZCE/BOL090 |
| 1999 | Hector Mine | 7 | HECTOR/HEC000 | 8 | HECTOR/HEC090 |
| 1979 | Imperial Valley | 9 | IMPVALL/H-DLT262 | 10 | IMPVALL/H-DLT352 |
| 1979 | Imperial Valley | 11 | IMPVALL/H-E11140 | 12 | IMPVALL/H-E11230 |
| 1995 | Kobe, Japan | 13 | KOBE/NIS000 | 14 | KOBE/NIS090 |
| 1995 | Kobe, Japan | 15 | KOBE/SHI000 | 16 | KOBE/SHI090 |
| 1999 | Kocaeli, Turkey | 17 | KOCAELI/DZC180 | 18 | KOCAELI/DZC270 |
| 1999 | Kocaeli, Turkey | 19 | KOCAELI/ARC000 | 20 | KOCAELI/ARC090 |
| 1992 | Landers | 21 | LANDERS/PLACE270 | 22 | LANDERS/YER360 |
| 1992 | Landers | 23 | LANDERS/CLW-LN | 24 | LANDERS/CLW-TR |
| 1989 | Loma Prieta | 25 | LOMAP/CAP000 | 26 | LOMAP/CAP090 |
| 1989 | Loma Prieta | 27 | LOMAP/G03000 | 28 | LOMAP/G03090 |
| 1990 | Manjil, Iran | 29 | MANJIL/ABBAR-L | 30 | MANJIL/ABBAR-T |
| 1987 | Superstition Hills | 31 | SUPERST/B-ICC000 | 32 | SUPERST/B-ICC090 |
| 1987 | Superstition Hills | 33 | SUPERST/B-POE270 | 34 | SUPERST/B-POE360 |
| 1992 | Cape Mendocino | 35 | CAPEMEND/RIO270 | 36 | CAPEMEND/RIO360 |
| 1999 | Chi-Chi, Taiwan | 37 | CHICHI/CHY101-E | 38 | CHICHI/CHY101-N |
| 1999 | Chi-Chi, Taiwan | 39 | CHICHI/TCU045-E | 40 | CHICHI/TCU045-N |
| 1971 | San Fernando | 41 | SFERN/PEL090 | 42 | SFERN/PEL180 |
| 1976 | Friuli, Italy | 43 | FRIULI/A-TMZ000 | 44 | FRIULI/A-TMZ270 |
| Symbol | Definition | Value |
|---|---|---|
| Harmony memory considering rate | 0.5–1 | |
| Initial harmony memory considering rate | 0.5 | |
| Fret width | 0–0.05 | |
| Initial fret width | 0.05 | |
| Maximum iteration number | 100 | |
| Iteration number | 1–100 | |
| Population number | 10 | |
| Isolator period | 1–5 s | |
| Isolator damping ratio | 1–50% |
| Variables | Damping Ratio | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| For 30% | For 40% | For 50% | |||||||
| Displacement Limit | Displacement Limit | Displacement Limit | |||||||
| 30 cm | 40 cm | 50 cm | 30 cm | 40 cm | 50 cm | 30 cm | 40 cm | 50 cm | |
| (s) | 2.3714 | 2.0157 | 3.3951 | 2.6866 | 3.3026 | 3.8023 | 3.0414 | 3.6723 | 4.2966 |
| 0.3000 | 0.3000 | 0.3000 | 0.4000 | 0.4000 | 0.4000 | 0.5000 | 0.5000 | 0.5000 | |
| Damping Ratio | Displacement Limit (m) | Displacement (m) | Total Acceleration (m/s2) | |
|---|---|---|---|---|
| With Isolator | 30% | 0.3 | 0.137 | 1.613 |
| 0.4 | 0.139 | 2.047 | ||
| 0.5 | 0.127 | 0.934 | ||
| 40% | 0.3 | 0.125 | 1.548 | |
| 0.4 | 0.119 | 1.177 | ||
| 0.5 | 0.132 | 0.968 | ||
| 50% | 0.3 | 0.113 | 1.511 | |
| 0.4 | 0.121 | 1.201 | ||
| 0.5 | 0.133 | 0.986 | ||
| Without Isolator | 0.410 | 19.283 | ||
| Damping Ratio | Displacement Limit (m) | Displacement (%) | Total Acceleration (%) |
|---|---|---|---|
| 30% | 0.3 | 66.54 | 91.64 |
| 0.4 | 66.19 | 89.39 | |
| 0.5 | 68.95 | 95.16 | |
| 40% | 0.3 | 69.63 | 91.97 |
| 0.4 | 70.97 | 93.90 | |
| 0.5 | 67.91 | 94.98 | |
| 50% | 0.3 | 72.47 | 92.16 |
| 0.4 | 70.40 | 93.77 | |
| 0.5 | 67.69 | 94.89 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ocak, A.; Nigdeli, S.M.; Bekdaş, G.; Kim, S.; Geem, Z.W. Optimization of Seismic Base Isolation System Using Adaptive Harmony Search Algorithm. Sustainability 2022, 14, 7456. https://doi.org/10.3390/su14127456
Ocak A, Nigdeli SM, Bekdaş G, Kim S, Geem ZW. Optimization of Seismic Base Isolation System Using Adaptive Harmony Search Algorithm. Sustainability. 2022; 14(12):7456. https://doi.org/10.3390/su14127456
Chicago/Turabian StyleOcak, Ayla, Sinan Melih Nigdeli, Gebrail Bekdaş, Sanghun Kim, and Zong Woo Geem. 2022. "Optimization of Seismic Base Isolation System Using Adaptive Harmony Search Algorithm" Sustainability 14, no. 12: 7456. https://doi.org/10.3390/su14127456
APA StyleOcak, A., Nigdeli, S. M., Bekdaş, G., Kim, S., & Geem, Z. W. (2022). Optimization of Seismic Base Isolation System Using Adaptive Harmony Search Algorithm. Sustainability, 14(12), 7456. https://doi.org/10.3390/su14127456









