Parametric CFD Thermal Performance Analysis of Full, Medium, Half and Short Length Dimple Solar Air Tube
Abstract
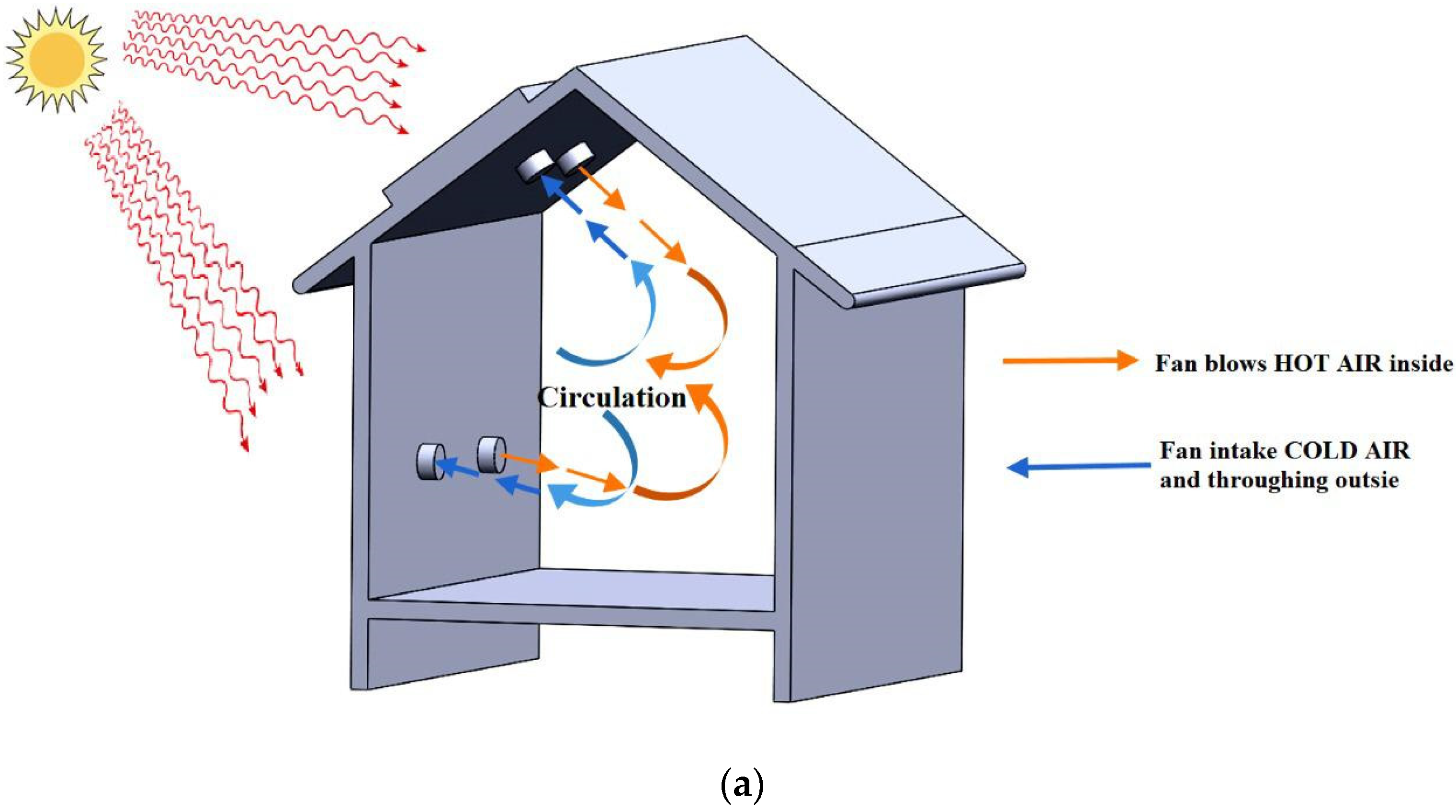
1. Introduction
- To investigate the influence of geometrical parameters on the thermal and flow characteristics inside a dimpled solar air heater tube.
- To investigate the influence of dimple height ratio and pitch ratio on heat transfer (HT), pressure drop (PD), and thermal performance factors (η).
- To find out the best overall thermal performance geometry of dimpled tube and compare with previous published work.
2. Computational Study and Mathematical Model
3. Grid Independent Study and Validation
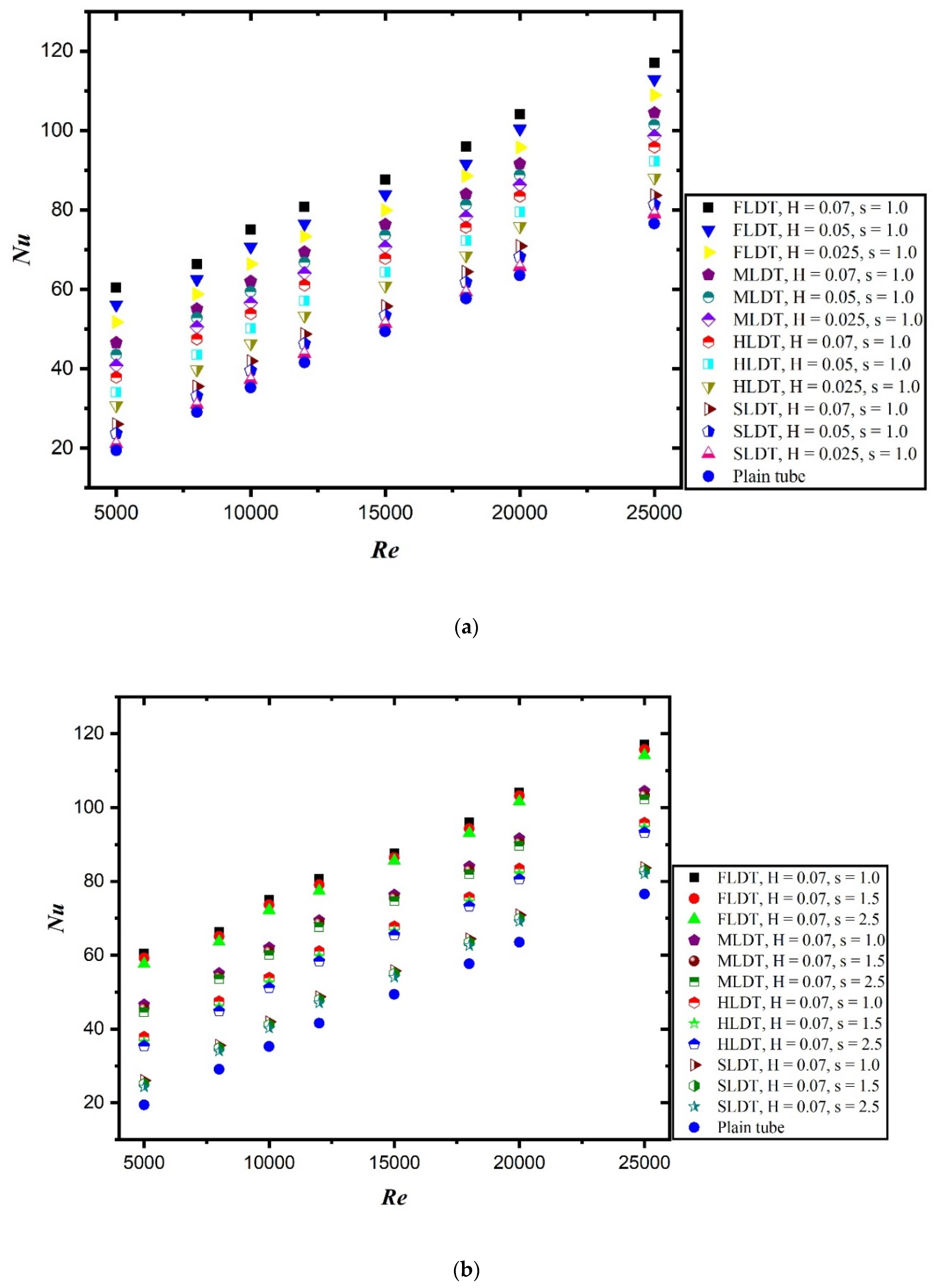
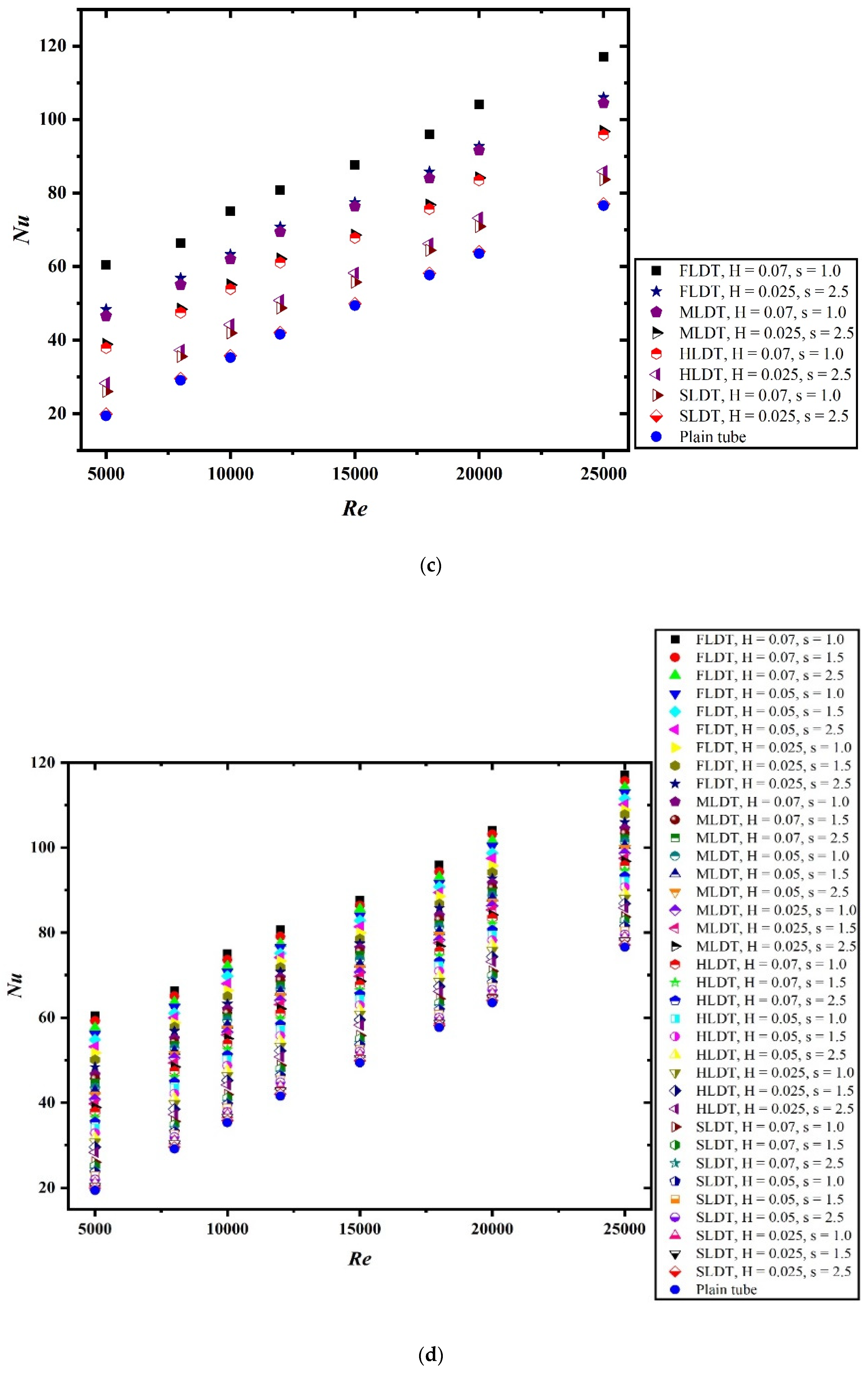
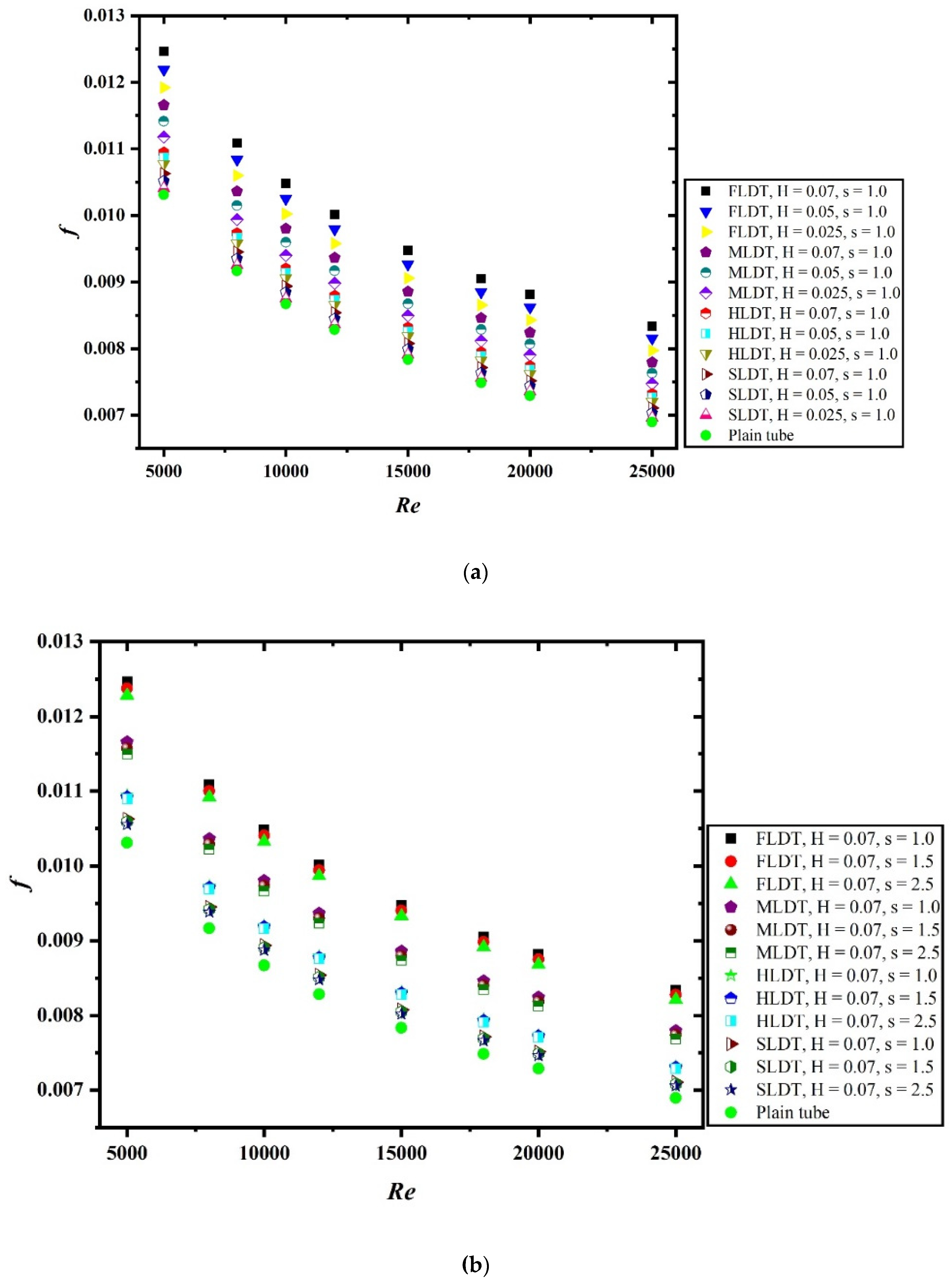
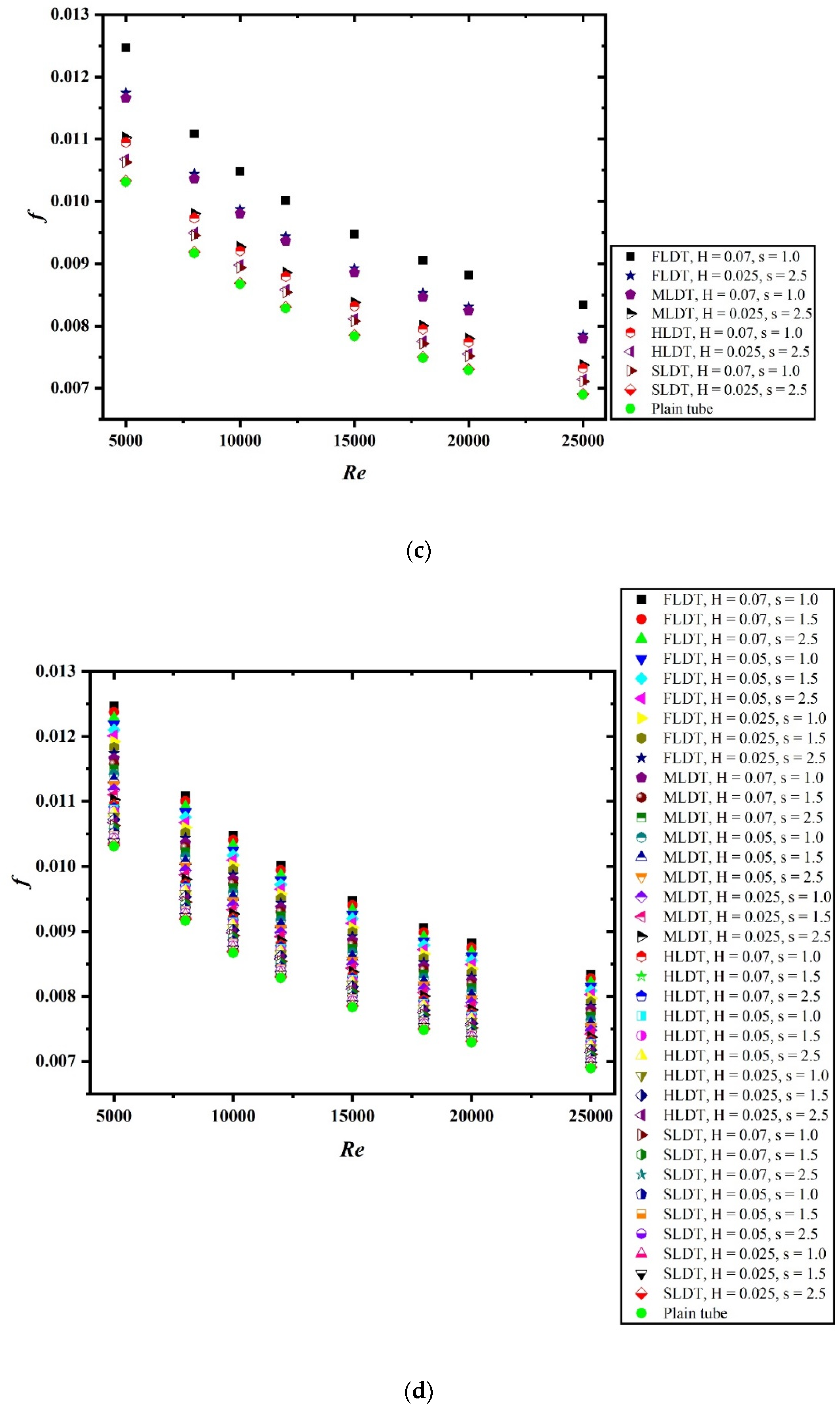
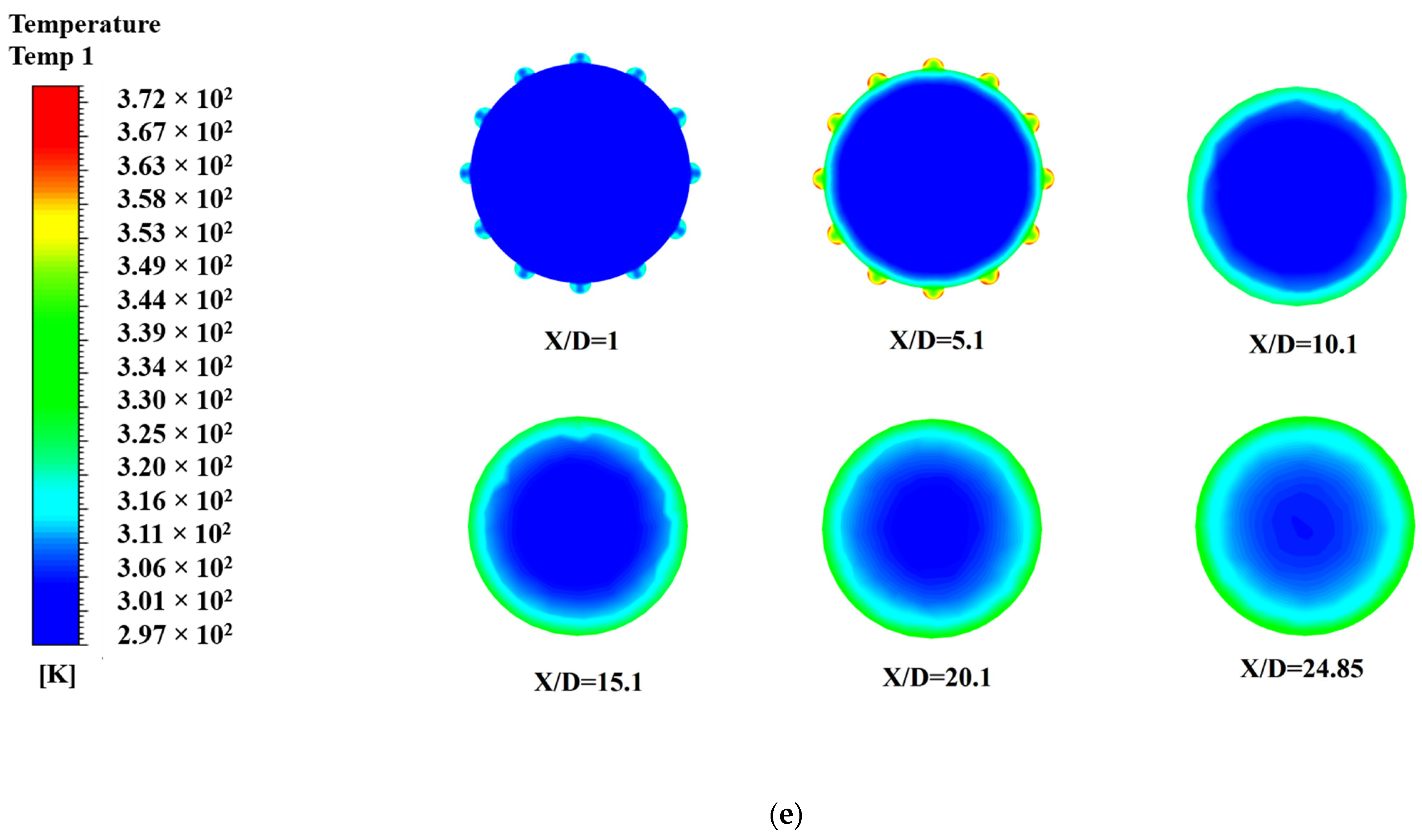
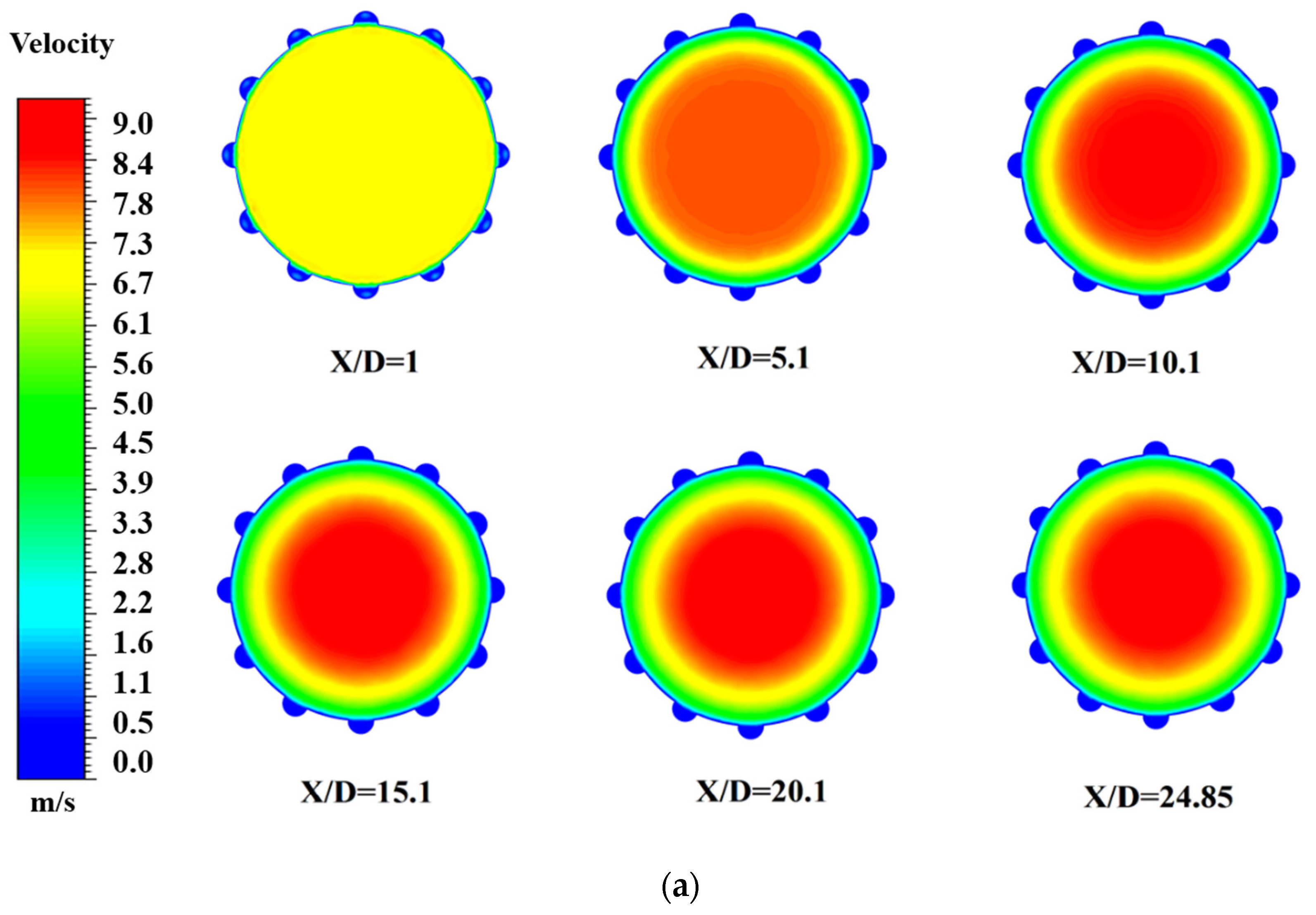
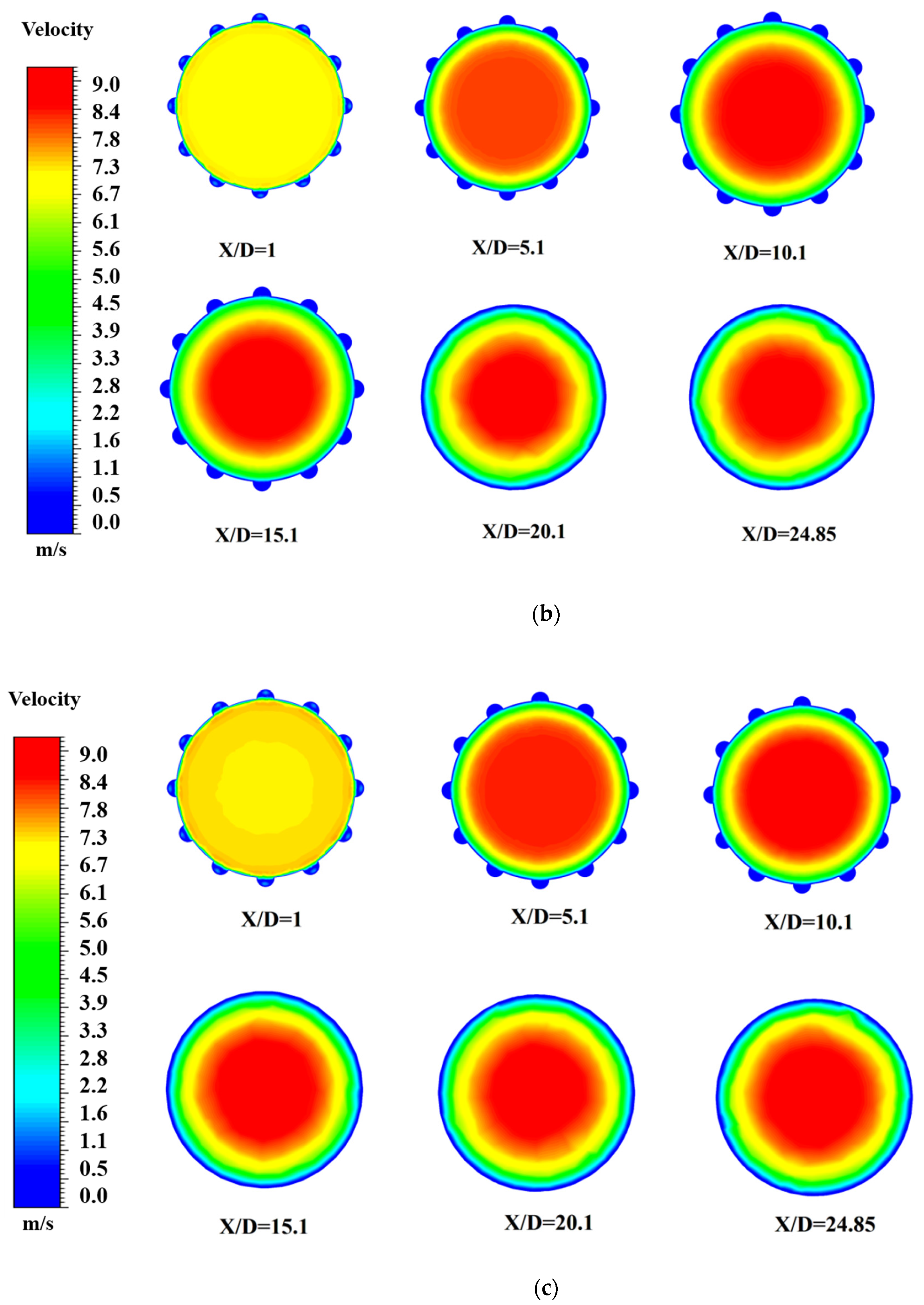
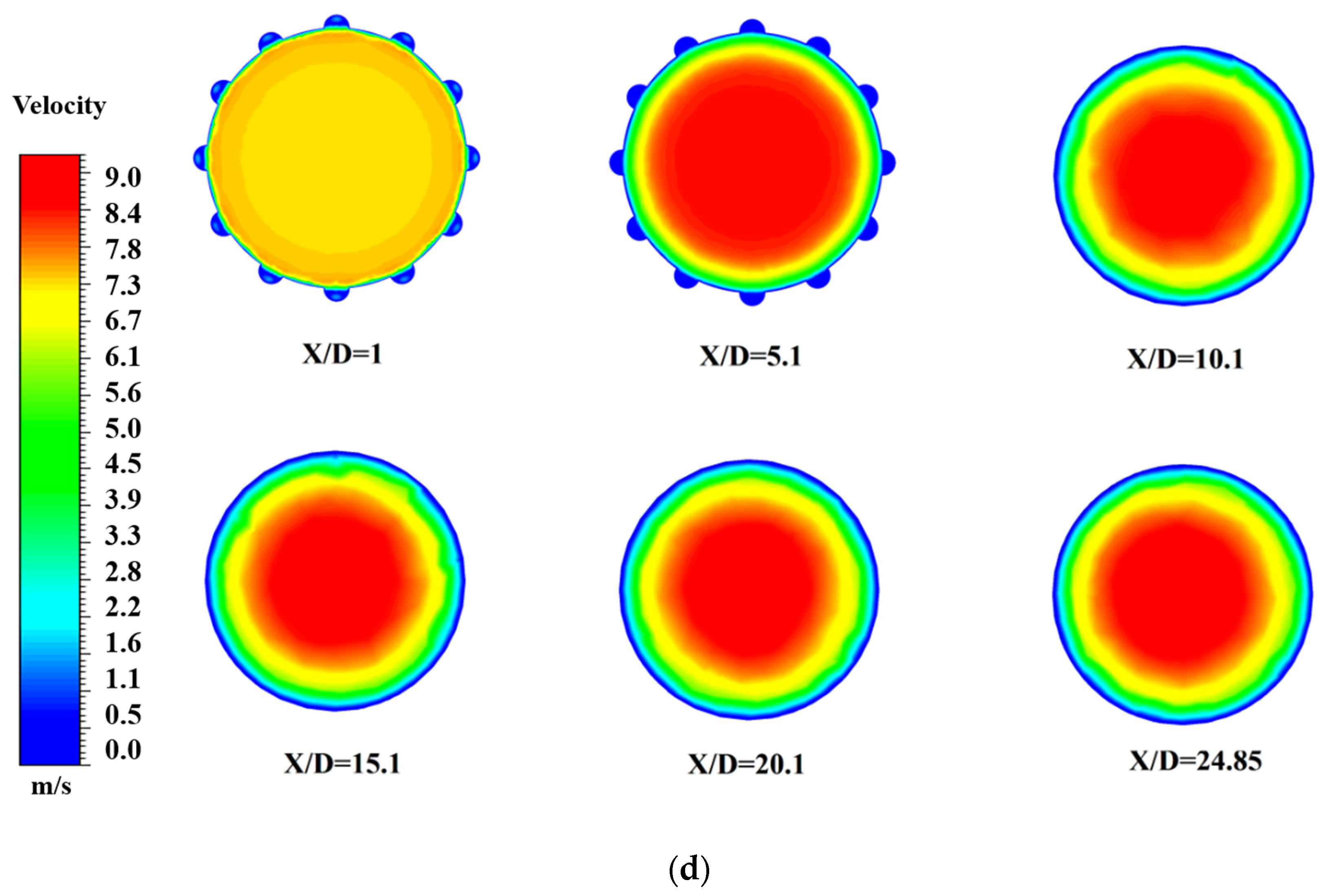
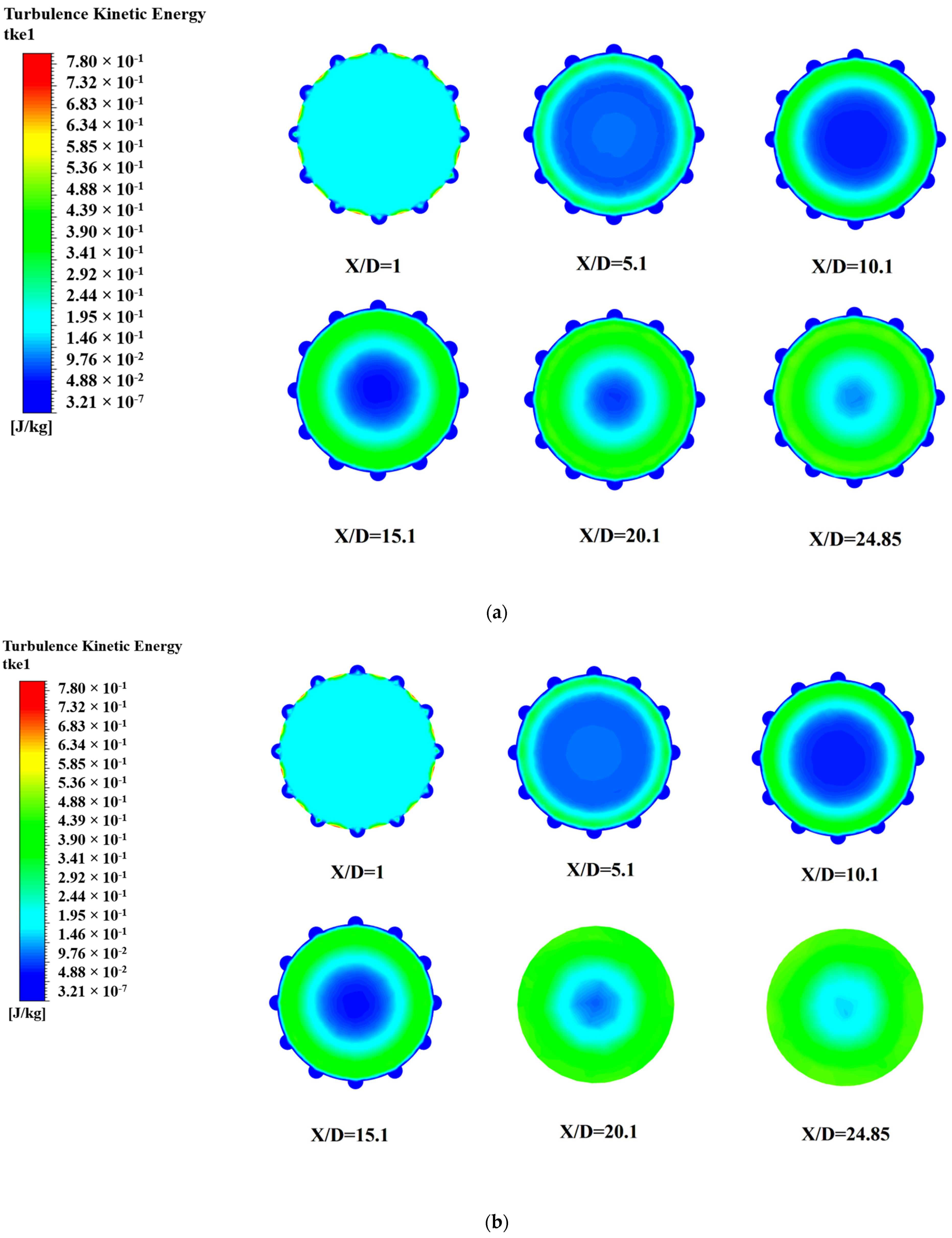
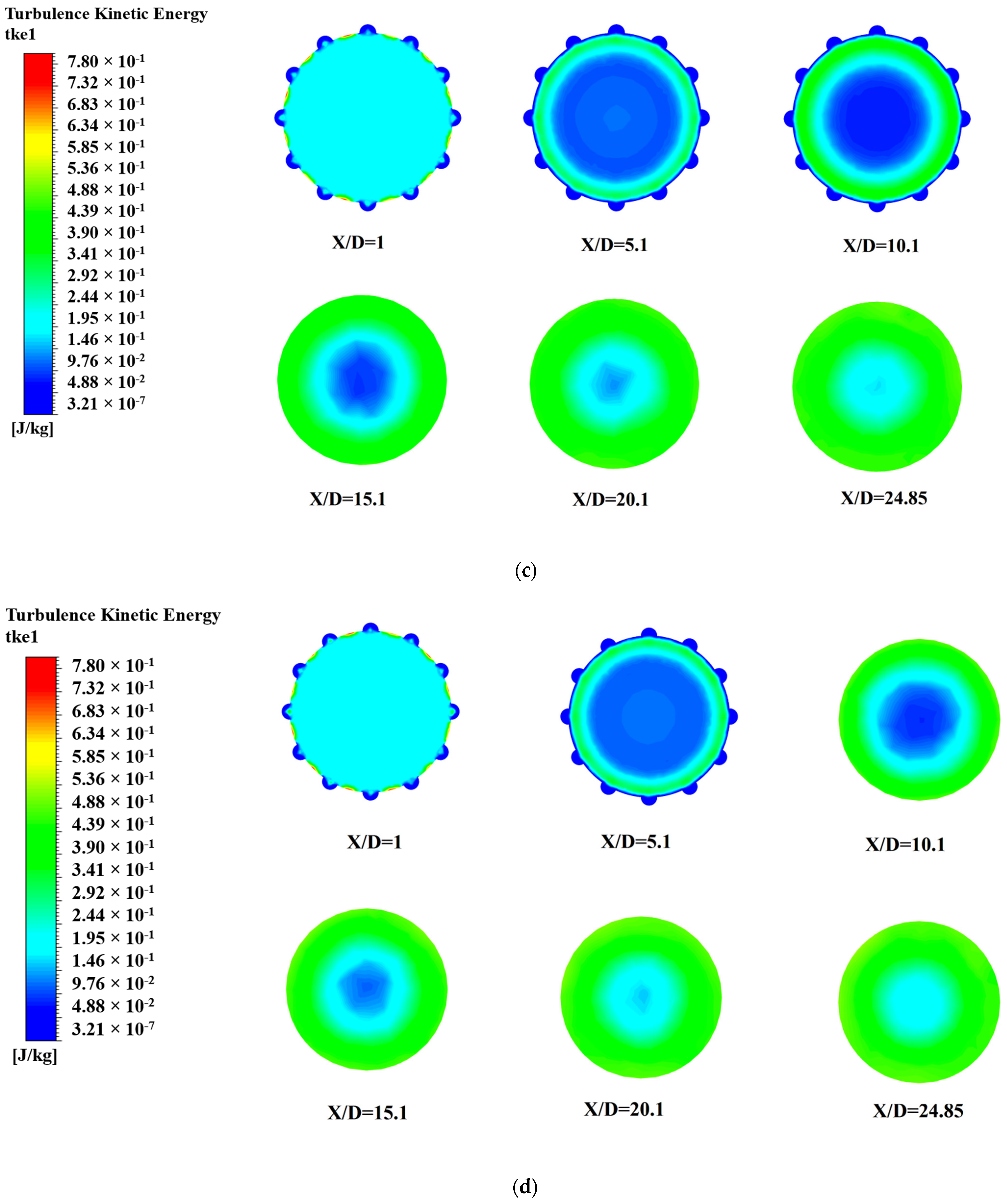
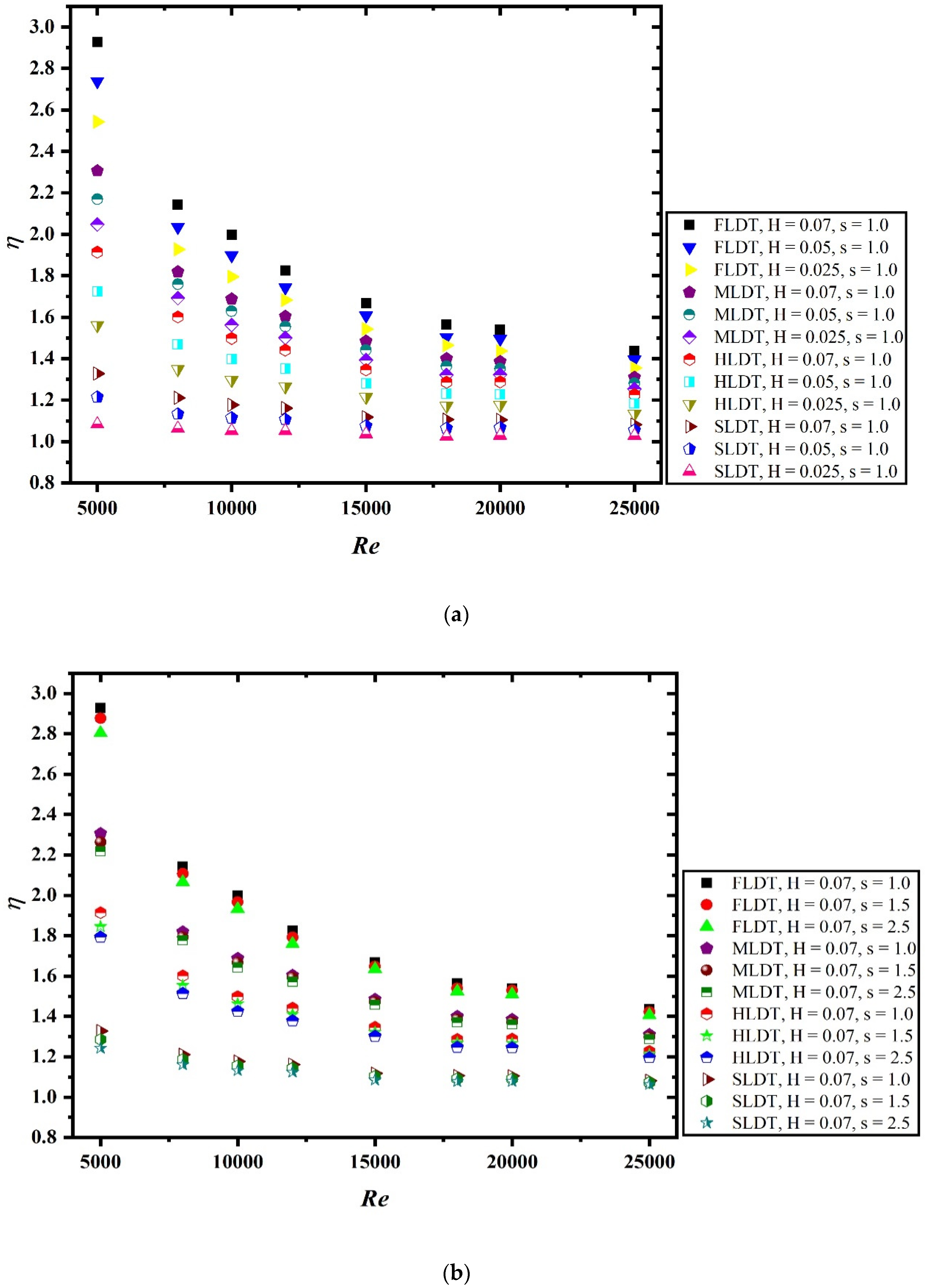
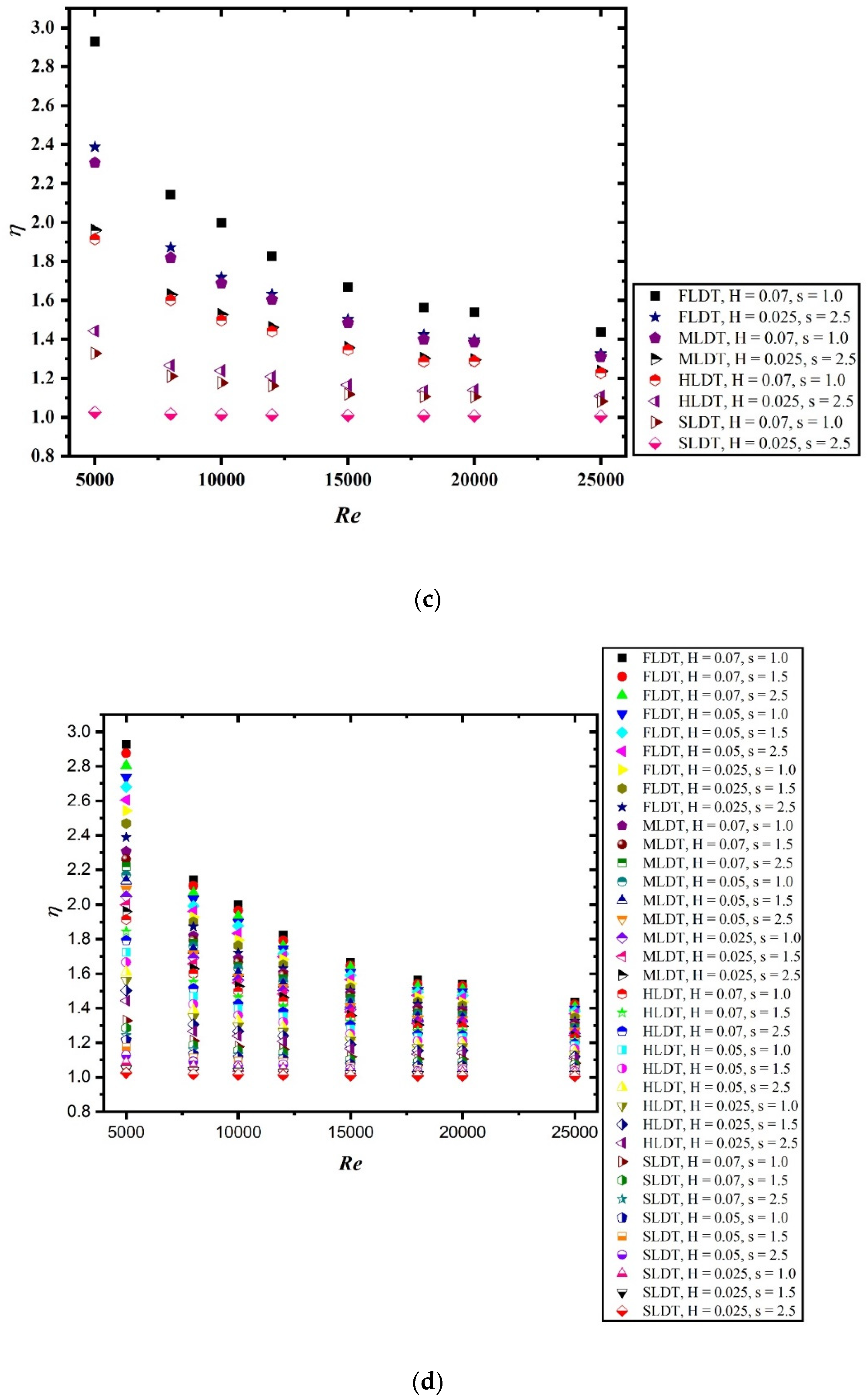
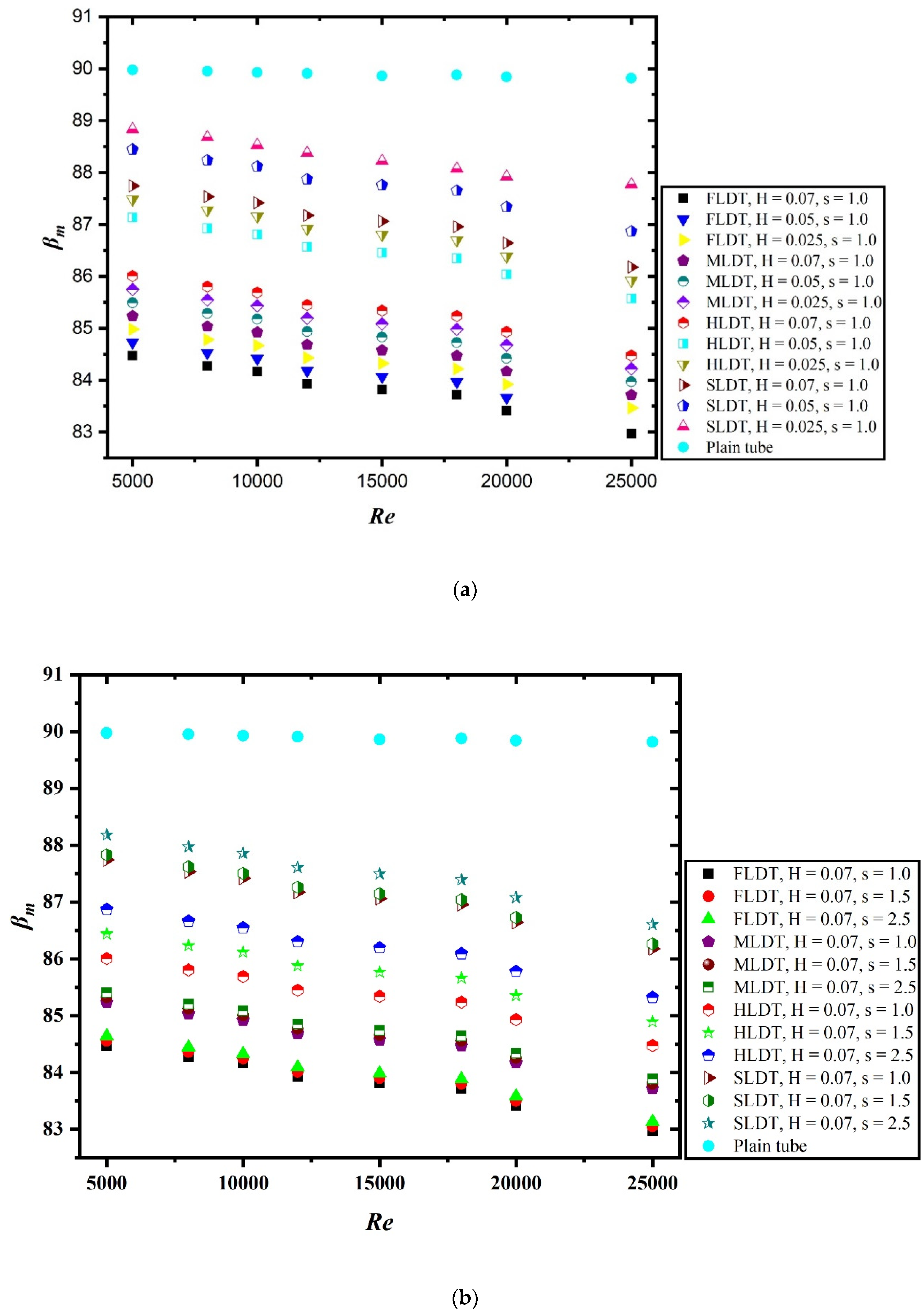
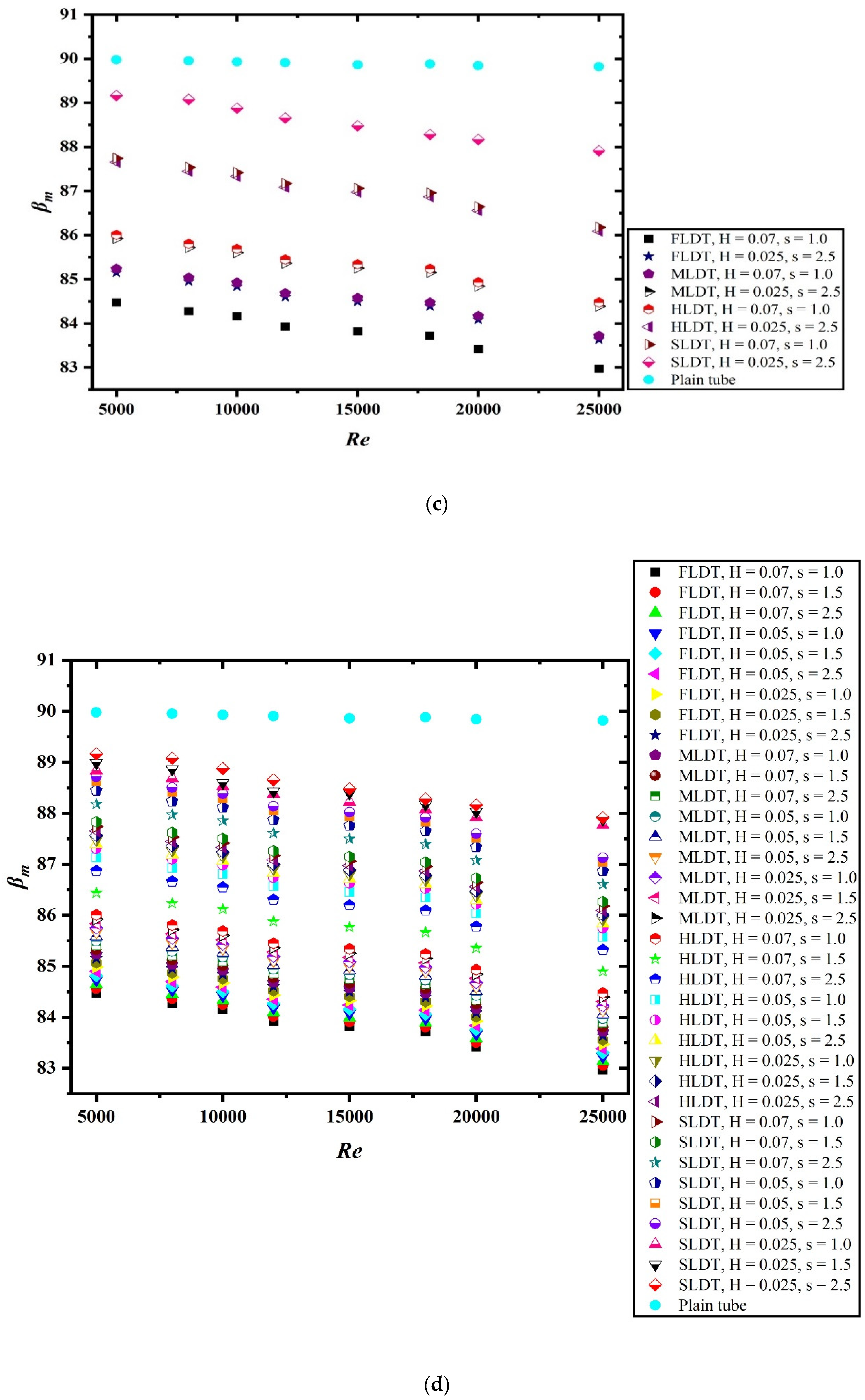
4. Result and Discussion
5. Conclusions
- A numerical investigation with a dimpled tube of different lengths has been carried out. The dimpled tubes of all configurations performed significantly better when compared with the plain tube (without dimple roughness).
- Compared with MLDT, HLDT, and SLDT, the FLDT shows highest enhancement in HT and pressure penalty.
- Nu increases and f decreases with increasing Re for all combinations of H and s. Low s and higher H yields high enhancement of HT and PD.
- The integration of artificial roughness on the tube increases the values of Nu and f by 5.12 times and 77.23 times for H = 0.07, s = 1.0 at Re value of 5000 and 25,000, respectively, in respect to the plain tube.
- The thermal-hydraulic performance is significantly influenced by the geometric parameters considered during the numerical study. The increase in the value of pitch ratio results in lower value of thermal performance. Similarly, the decrease in the value of dimple height ratio also resulted in decreased performance.
- By comparing the thermal performance factor with previous investigations, it has been observed that the present study shows very significant augmentation.
- The outcome from this numerical investigation may be useful for the design of SAHs and HE.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | crosee-sectional area |
| D | hydraulic diameter, m |
| e | depth, m |
| Fi | model blending functions |
| f | friction factor |
| h | heat transfer coefficient, W·m−2·K−1 |
| HT | heat transfer |
| H | dimple height ratio |
| j | Colburn j-factor |
| L | tube length, m |
| M | model constant |
| m | mass flow rate of working fluid, kg/s |
| Nu | Nusselt number |
| Nu0 | Nusselt number without turbulator |
| P | pitch |
| PD | pressure drop |
| Pκ | turbulent kinetic energy production term |
| Pr | molecular Prandtl number |
| Prturb | turbulent Prandtl number |
| q | heat flux, W·m−2 |
| Re | Reynolds number |
| Rw | average thermal resistance of wall, ohm |
| RANS | Reynolds averaged numerical simulation |
| SST | shear stress transport |
| S | pitch ratio |
| U | dimensionless variable of velocity |
| V | bulk velocity, m·s−1 |
| Greek Symbols | |
| α | molecular thermal diffusivity, m2·s−1 |
| βi | model constant |
| β | sygergy angle |
| σi | model constant |
| γ | intermittency |
| ΔP | pressure drop, Pa |
| η | thermo-hydraulic performance factor |
| µ | molecular dynamic viscosity, kg·m−1·s−1 |
| µturb | turbulent dynamic viscosity, kg·m−1·s−1 |
| ν | molecular kinematic viscosity, m2·s−1 |
| νturb | molecular kinematic viscosity, m2·s−1 |
| turbulence kinetic energy, m2·s−2 | |
| specific dissipation rate of , s−1 | |
| Θ | angular cut angle, degree |
| dimensionless variable of temperature | |
References
- Kanojiya, N.C.; Kriplani, V.M.; Walke, P.V. Heat Transfer Enhancement in Heat Exchangers With Inserts: A Review. Int. J. Eng. Res. Technol. 2014, 3, 494–500. [Google Scholar]
- Varun Saini, R.P.; Singal, S.K. A Review on Roughness Geometry Used in Solar Air Heaters. Sol. Energy 2007, 81, 1340–1350. [Google Scholar] [CrossRef]
- Gugulothu, R.; Reddy, K.V.K.; Somanchi, N.S.; Adithya, E.L. A Review on Enhancement of Heat Transfer Techniques. Mater. Today Proc. 2017, 4, 1051–1056. [Google Scholar] [CrossRef]
- Bhattacharyya, S. Fluid Flow and Heat Transfer in a Heat Exchanger Channel with Short-Length Twisted Tape Turbulator Inserts. Iran. J. Sci. Technol. Trans. Mech. Eng. 2020, 44, 217–227. [Google Scholar] [CrossRef]
- Saha, S.K.; Bhattacharyya, S.; Pal, P.K. Thermohydraulics of Laminar Flow of Viscous Oil through a Circular Tube Having Integral Axial Rib Roughness and Fitted with Center-Cleared Twisted-Tape. Exp. Therm. Fluid Sci. 2012, 41, 121–129. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Chattopadhyay, H.; Guin, A.; Benim, A.C. Investigation of Inclined Turbulators for Heat Transfer Enhancement in a Solar Air Heater. Heat Transf. Eng. 2019, 40, 1451–1460. [Google Scholar] [CrossRef]
- Bhattacharyya, S. The Effects of Short Length and Full Length Swirl Generators on Heat Transfer and Flow Fields in a Solar Air Heater Tube. J. Therm. Anal. Calorim. 2020, 140, 1355–1369. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Benim, A.C.; Chattopadhyay, H.; Banerjee, A. Experimental Heat Transfer Experimental Investigation of Heat Transfer Performance of Corrugated Tube with Spring Tape Inserts. Exp. Heat Transf. 2018, 32, 411–425. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Raghavendran, B.H.; Paul, A.R. The Effect of Circular Hole Spring Tape on the Turbulent Heat Transfer and Entropy Analysis in a Heat Exchanger Tube: An Experimental Study. Exp. Heat Transf. Online Publ. 2020, 8, 1–20. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Chattopadhyay, H.; Benim, A.C. Heat Transfer Enhancement of Laminar Flow of Ethylene Glycol through a Square Channel Fitted with Angular Cut Wavy Strip. Procedia Eng. 2016, 157, 19–28. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Sarkar, D.; Mahabaleshwar, U.S.; Soni, M.K.; Mohanraj, M. Experimental Study of Thermohydraulic Characteristics and Irreversibility Analysis of Novel Axial Corrugated Tube with Spring Tape Inserts. Eur. Phys. J. Appl. Phys. 2020, 92, 30901. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Chattopadhyay, H.; Benim, A.C. Computational Investigation of Heat Transfer Enhancement by Alternating Inclined Ribs in Tubular Heat Exchanger. Prog. Comput. Fluid Dyn. 2017, 17, 390–396. [Google Scholar] [CrossRef]
- Souayeh, B.; Bhattacharyya, S.; Hdhiri, N.; Alam, M.W. Heat and Fluid Flow Analysis and ANN-Based Prediction of a Novel Spring Corrugated Tape. Sustainability 2021, 13, 3023. [Google Scholar] [CrossRef]
- Mohamed Ibrahim, N.H.; Udayakumar, M.; Suresh, S.; Bhattacharyya, S.; Sharifpur, M. Coupling LES with soot model for the study of soot volume fraction in a turbulent diffusion jet flames at various Reynolds number configurations. Int. J. Numer. Methods Heat Fluid Flow Online Publ. 2020. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Dey, K.; Paul, A.R.; Biswas, R. A novel CFD analysis to minimize the spread of COVID-19 virus in hospital isolation room. Chaos Solitons Fractals 2020, 139, 110294. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharyya, S.; Benim, A.C.; Bennacer, R.; Dey, K. Influence of Broken Twisted Tape on Heat Transfer Performance in Novel Axial Corrugated Tubes: Experimental and Numerical Study. Heat Transf. Eng. Online Publ. 2021, 1–22. [Google Scholar] [CrossRef]
- Everts, M.; Bhattacharyya, S.; Bashir, A.I.; Meyer, J.P. Heat transfer characteristics of assisting and opposing laminar flow through a vertical circular tube at low Reynolds numbers. Appl. Therm. Eng. 2020, 179, 115696. [Google Scholar] [CrossRef]
- Soni, M.K.; Tamar, N.; Bhattacharyya, S. Numerical simulation and parametric analysis of latent heat thermal energy storage system. J. Therm. Anal. Calorim. 2020, 141, 2511–2526. [Google Scholar] [CrossRef]
- Nakhchi, M.E.; Esfahani, J.A. Numerical Investigation of Heat Transfer Enhancement inside Heat Exchanger Tubes Fitted with Perforated Hollow Cylinders. Int. J. Therm. Sci. 2020, 147, 106153. [Google Scholar] [CrossRef]
- Eiamsa-ard, S.; Wongcharee, K.; Sripattanapipat, S. 3-D Numerical Simulation of Swirling Flow and Convective Heat Transfer in a Circular Tube Induced by Means of Loose-Fit Twisted Tapes. Int. Commun. Heat Mass Transf. 2009, 36, 947–955. [Google Scholar] [CrossRef]
- Sivashanmugam, P.; Nagarajan, P.K.; Suresh, S. Experimental Studies on Heat Transfer and Friction Factor Characteristics of Turbulent Flow through a Circular Tube Fitted with Right and Left Helical Screw-Tape Insert. Chem. Eng. Commun. 2008, 195, 977–987. [Google Scholar] [CrossRef]
- Chang, S.W.; Yang, T.L.; Liou, J.S. Heat Transfer and Pressure Drop in Tube with Broken Twisted Tape Insert. Exp. Therm. Fluid Sci. 2007, 32, 489–501. [Google Scholar] [CrossRef]
- Jayakumar, J.S.; Mahajani, S.M.; Mandal, J.C.; Vijayan, P.K.; Bhoi, R. Experimental and CFD Estimation of Heat Transfer in Helically Coiled Heat Exchangers. Chem. Eng. Res. Des. 2008, 86, 221–232. [Google Scholar] [CrossRef]
- Nagarajan, P.; Sivashanmugam, P. CFD Simulation of Heat Transfer Augmentation in a Circular Tube Fitted with Right-Left Helical Inserts with Spacer. Int. J. Chem. Eng. Res. 2009, 1, 1–11. [Google Scholar]
- Saeidi, R.; Noorollahi, Y.; Esfahanian, V. Numerical Simulation of a Novel Spiral Type Ground Heat Exchanger for Enhancing Heat Transfer Performance of Geothermal Heat Pump. Energy Convers. Manag. 2018, 168, 296–307. [Google Scholar] [CrossRef]
- Mohammadshahi, S.; Nili-Ahmadabadi, M.; Samsam-Khayani, H.; Salimpour, M.R. Numerical Study of a Vortex-Induced Vibration Technique for Passive Heat Transfer Enhancement in Internal Turbulent Flow. Eur. J. Mech. B Fluids 2018, 72, 103–113. [Google Scholar] [CrossRef]
- Bensaci, C.E.; Moummi, A.; Sanchez de la Flor, F.J.; Rodriguez Jara, E.A.; Rincon-Casado, A.; Ruiz-Pardo, A. Numerical and Experimental Study of the Heat Transfer and Hydraulic Performance of Solar Air Heaters with Different Baffle Positions. Renew. Energy 2020, 155, 1231–1244. [Google Scholar] [CrossRef]
- Xie, S.; Liang, Z.; Zhang, J.; Zhang, L.; Wang, Y.; Ding, H. Numerical Investigation on Flow and Heat Transfer in Dimpled Tube with Teardrop Dimples. Int. J. Heat Mass Transf. 2019, 131, 713–723. [Google Scholar] [CrossRef]
- Xie, S.; Liang, Z.; Zhang, L.; Wang, Y.; Ding, H.; Zhang, J. Numerical Investigation on Heat Transfer Performance and Flow Characteristics in Enhanced Tube with Dimples and Protrusions. Int. J. Heat Mass Transf. 2018, 122, 602–613. [Google Scholar] [CrossRef]
- Bhadouriya, R.; Agrawal, A.; Prabhu, S.V. International Journal of Heat and Mass Transfer Experimental and Numerical Study of Fluid Flow and Heat Transfer in a Twisted Square Duct. Heat Mass Transf. 2015, 82, 143–158. [Google Scholar] [CrossRef]
- Muñoz-Esparza, D.; Sanmiguel-Rojas, E. Numerical Simulations of the Laminar Flow in Pipes with Wire Coil Inserts. Comput. Fluids 2011, 44, 169–177. [Google Scholar] [CrossRef]
- Aǧra, Ö.; Demir, H.; Ataylmaz Özgür, S.; Kantaş, F.; Dalklç, A.S. Numerical Investigation of Heat Transfer and Pressure Drop in Enhanced Tubes. Int. Commun. Heat Mass Transf. 2011, 38, 1384–1391. [Google Scholar] [CrossRef]
- Dong, Y.; Huixiong, L.; Tingkuan, C. Pressure Drop, Heat Transfer and Performance of Single-Phase Turbulent Flow in Spirally Corrugated Tubes. Exp. Therm. Fluid Sci. 2001, 24, 131–138. [Google Scholar] [CrossRef]
- Huang, Z.; Yu, G.L.; Li, Z.Y.; Tao, W.Q. Numerical Study on Heat Transfer Enhancement in a Receiver Tube of Parabolic Trough Solar Collector with Dimples, Protrusions and Helical Fins. Energy Procedia 2015, 69, 1306–1316. [Google Scholar] [CrossRef]
- Chen, J.; Müller-Steinhagen, H.; Duffy, G.G. Heat Transfer Enhancement in Dimpled Tubes. Appl. Therm. Eng. 2001, 21, 535–547. [Google Scholar] [CrossRef]
- Vicente, P.G.; García, A.; Viedma, A. Heat Transfer and Pressure Drop for Low Reynolds Turbulent Flow in Helically Dimpled Tubes. Int. J. Heat Mass Transf. 2002, 45, 543–553. [Google Scholar] [CrossRef]
- Cheraghi, M.H.; Ameri, M.; Shahabadi, M. Numerical Study on the Heat Transfer Enhancement and Pressure Drop inside Deep Dimpled Tubes. Int. J. Heat Mass Transf. 2020, 147, 118845. [Google Scholar] [CrossRef]
- Kumar, A.; Maithani, R.; Suri, A.R.S. Numerical and Experimental Investigation of Enhancement of Heat Transfer in Dimpled Rib Heat Exchanger Tube. Heat Mass Transf. Stoffuebertragung 2017, 53, 3501–3516. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Vishwakarma, D.K.; Chakraborty, S.; Roy, R.; Issakhov, A.; Sharifpur, M. Turbulent Flow Heat Transfer through a Circular Tube with Novel Hybrid Grooved Tape Inserts: Thermohydraulic Analysis and Prediction by Applying Machine Learning Model. Sustainability 2021, 13, 3068. [Google Scholar] [CrossRef]
- Choudhary, V.; Kumar, M.; Patil, A.K. Experimental Investigation of Enhanced Performance of Pin Fin Heat Sink with Wings. Appl. Therm. Eng. 2019, 155, 546–562. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, Y.; Li, B.; Li, Y. Numerical Investigation of Tube-Side Fully Developed Turbulent Flow and Heat Transfer in Outward Corrugated Tubes. Int. J. Heat Mass Transf. 2018, 116, 115–126. [Google Scholar] [CrossRef]
- Tang, X.; Dai, X.; Zhu, D. Experimental and Numerical Investigation of Convective Heat Transfer and Fluid Flow in Twisted Spiral Tube. Int. J. Heat Mass Transf. 2015, 90, 523–541. [Google Scholar] [CrossRef]
- Mohammed, H.A.; Abbas, A.K.; Sheriff, J.M. Influence of Geometrical Parameters and Forced Convective Heat Transfer in Transversely Corrugated Circular Tubes. Int. Commun. Heat Mass Transf. 2013, 44, 116–126. [Google Scholar] [CrossRef]
- Mosavati, B.; Mosavati, M.; Kowsary, F. Inverse boundary design solution in a combined radiating-free convecting furnace filled with participating medium containing specularly reflecting walls. Int. Commun. Heat Mass Transf. 2016, 76, 69–76. [Google Scholar] [CrossRef]
- Mosavati, B.; Mosavati, M.; Kowsary, F. Solution of radiative inverse boundary design problem in a combined radiating-free convecting furnace. Int. Commun. Heat Mass Transf. 2013, 45, 130–136. [Google Scholar] [CrossRef]
- Mosavati, M.; Kowsary, F.; Mosavati, B. A Novel, Noniterative Inverse Boundary Design Regularized Solution Technique Using the Backward Monte Carlo Method. J. Heat Transf. 2013, 135, 042701. [Google Scholar] [CrossRef]
- Fang Li, F.; Zhu, W.; He, H. Numerical optimization on microchannel flow and heat transfer performance based on field synergy principle. Int. J. Heat Mass Transf. 2019, 130, 375–385. [Google Scholar]
- Sun, X.Y.; Hua, L.J.; Dai, Y.J.; Ge, T.S.; Wang, R.Z. Field synergy analysis on heat and moisture transfer processes of desiccant coated heat exchanger. Int. J. Therm. Sci. 2021, 164, 106889. [Google Scholar] [CrossRef]
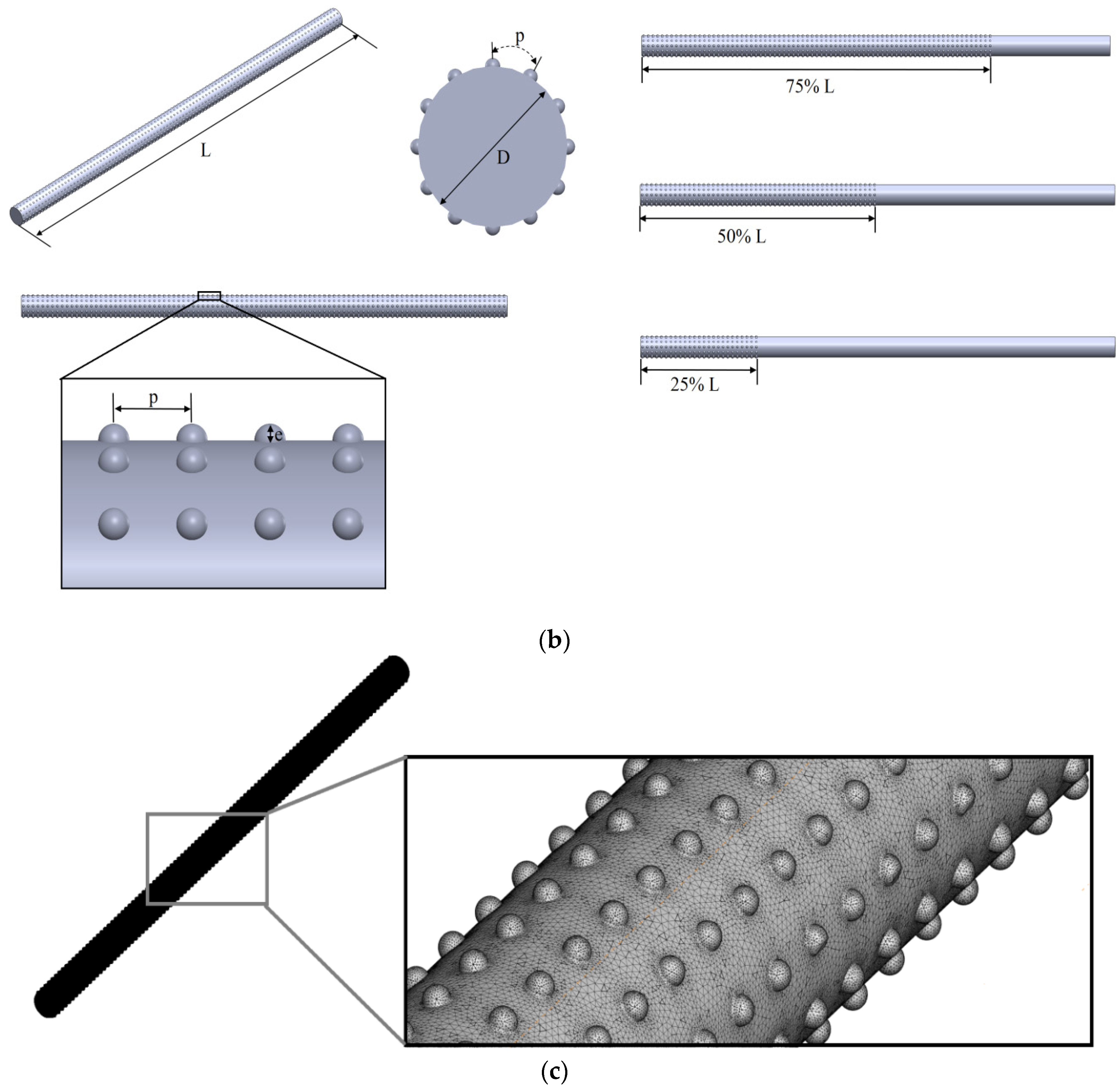
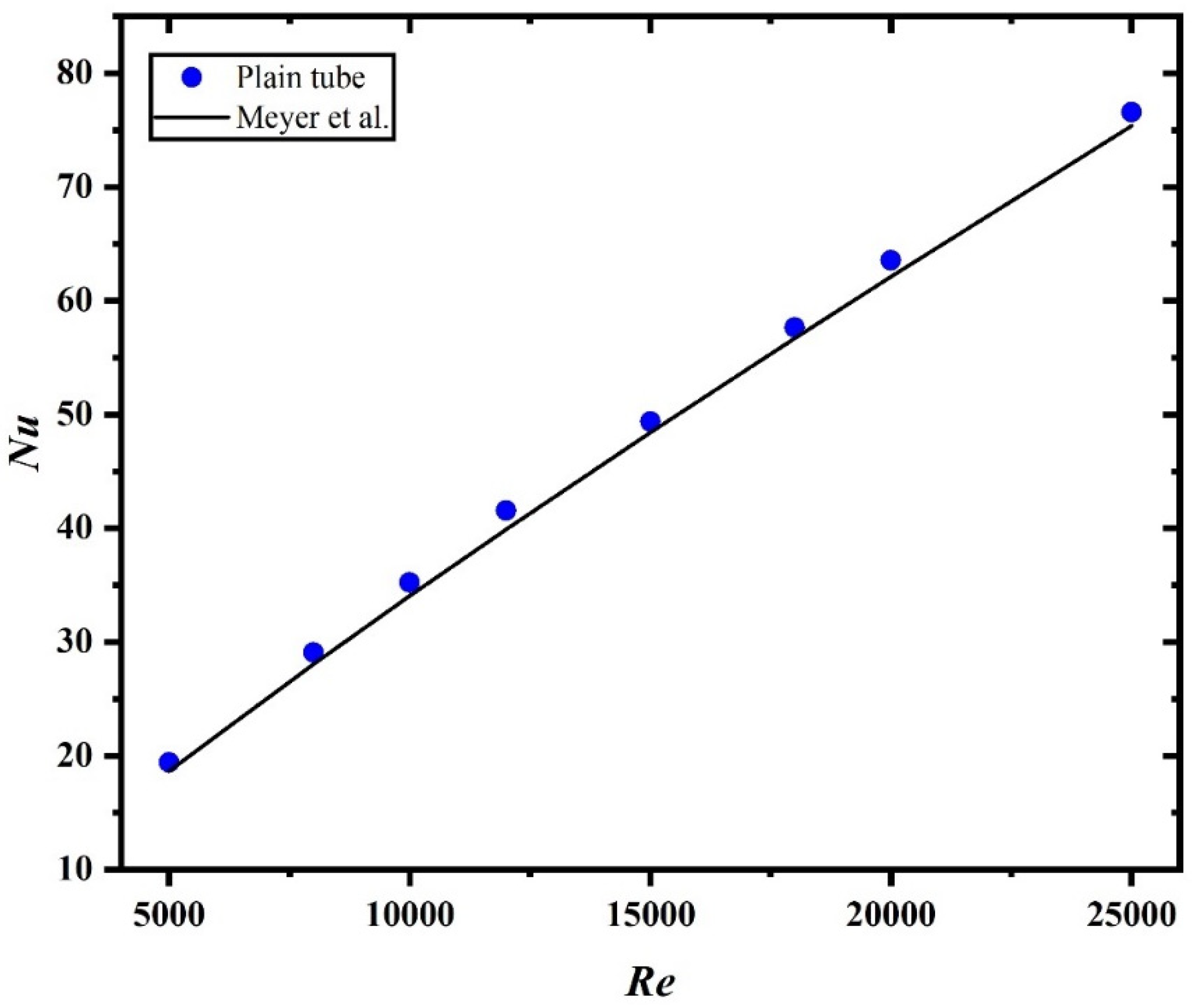
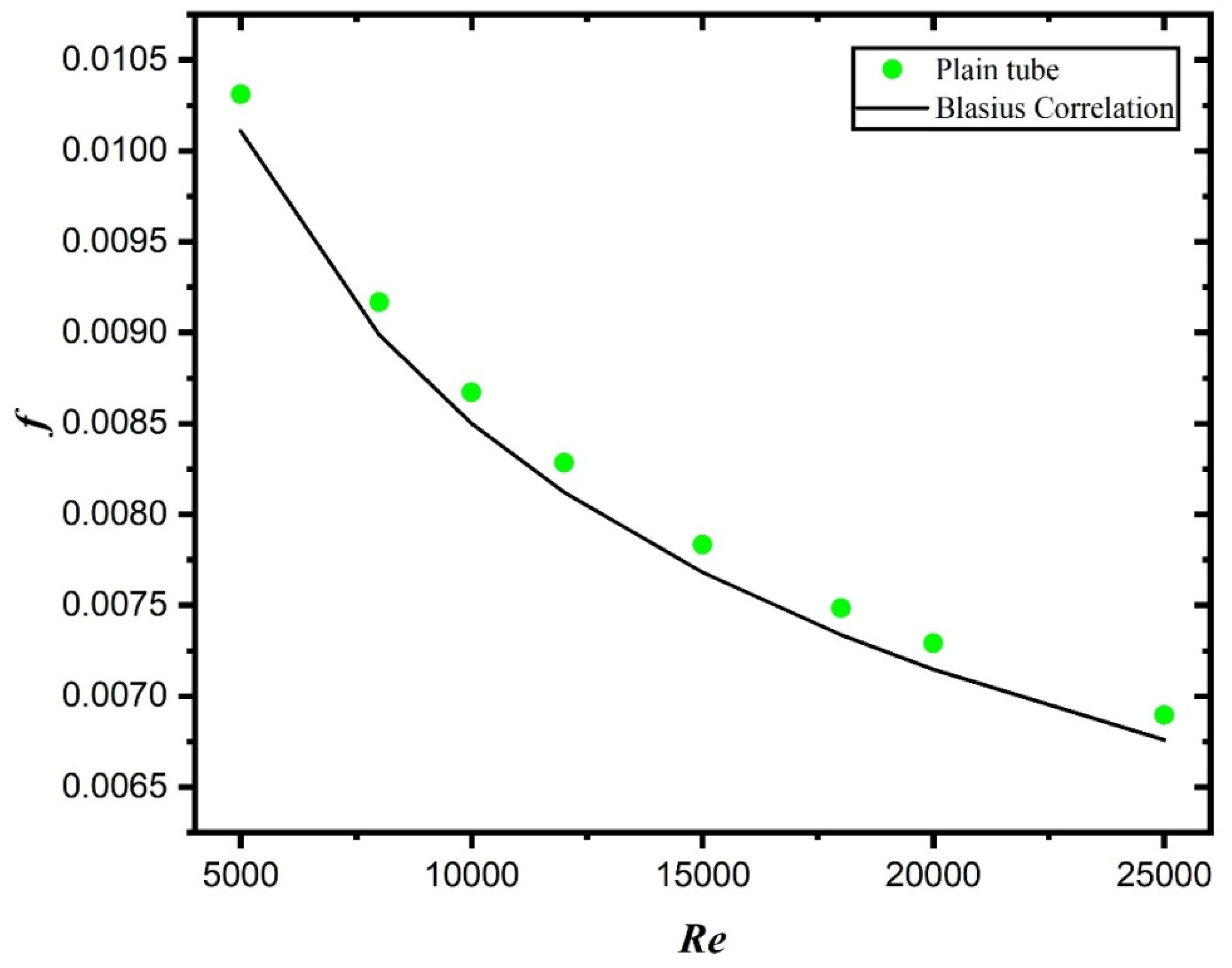
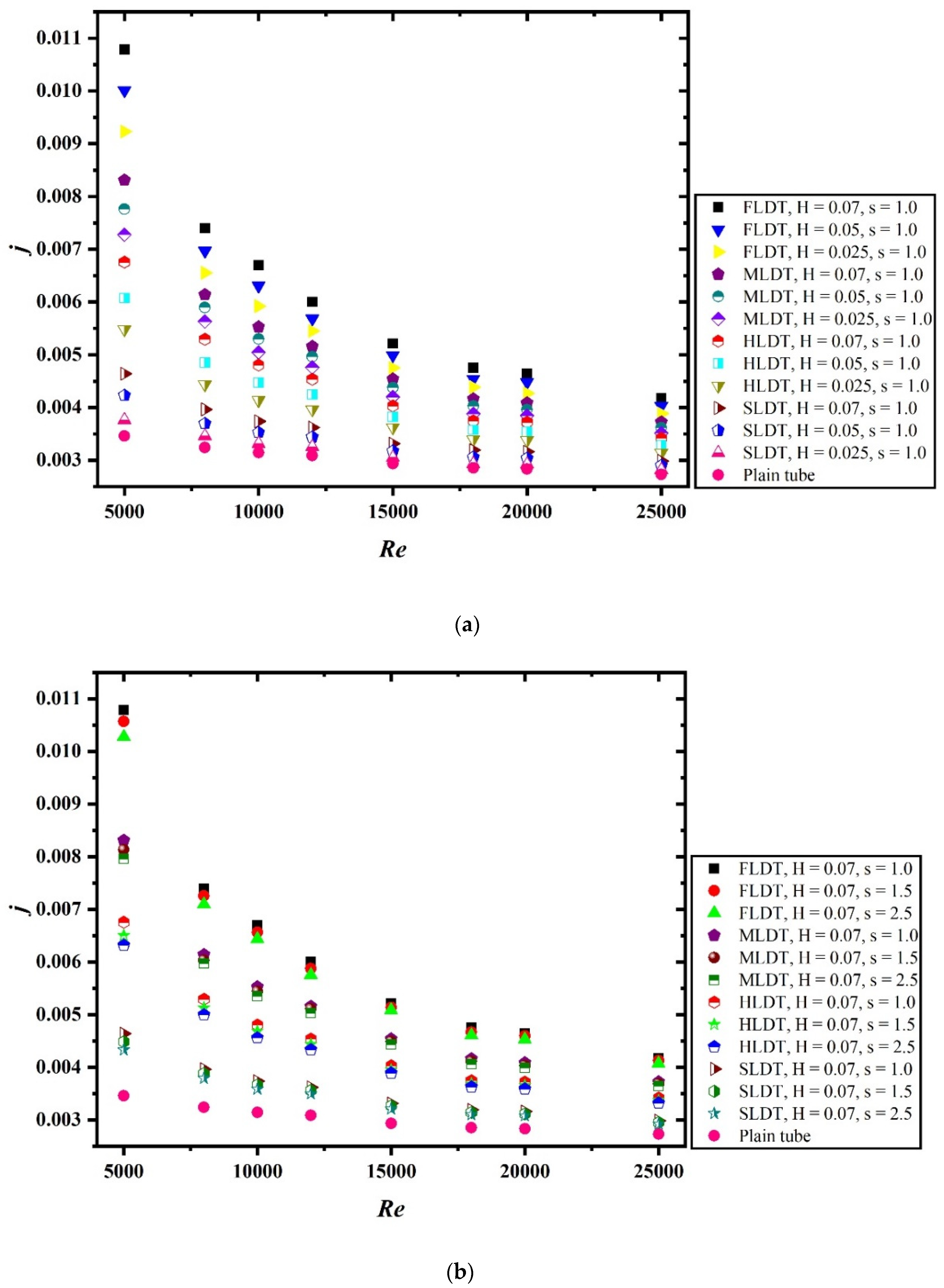
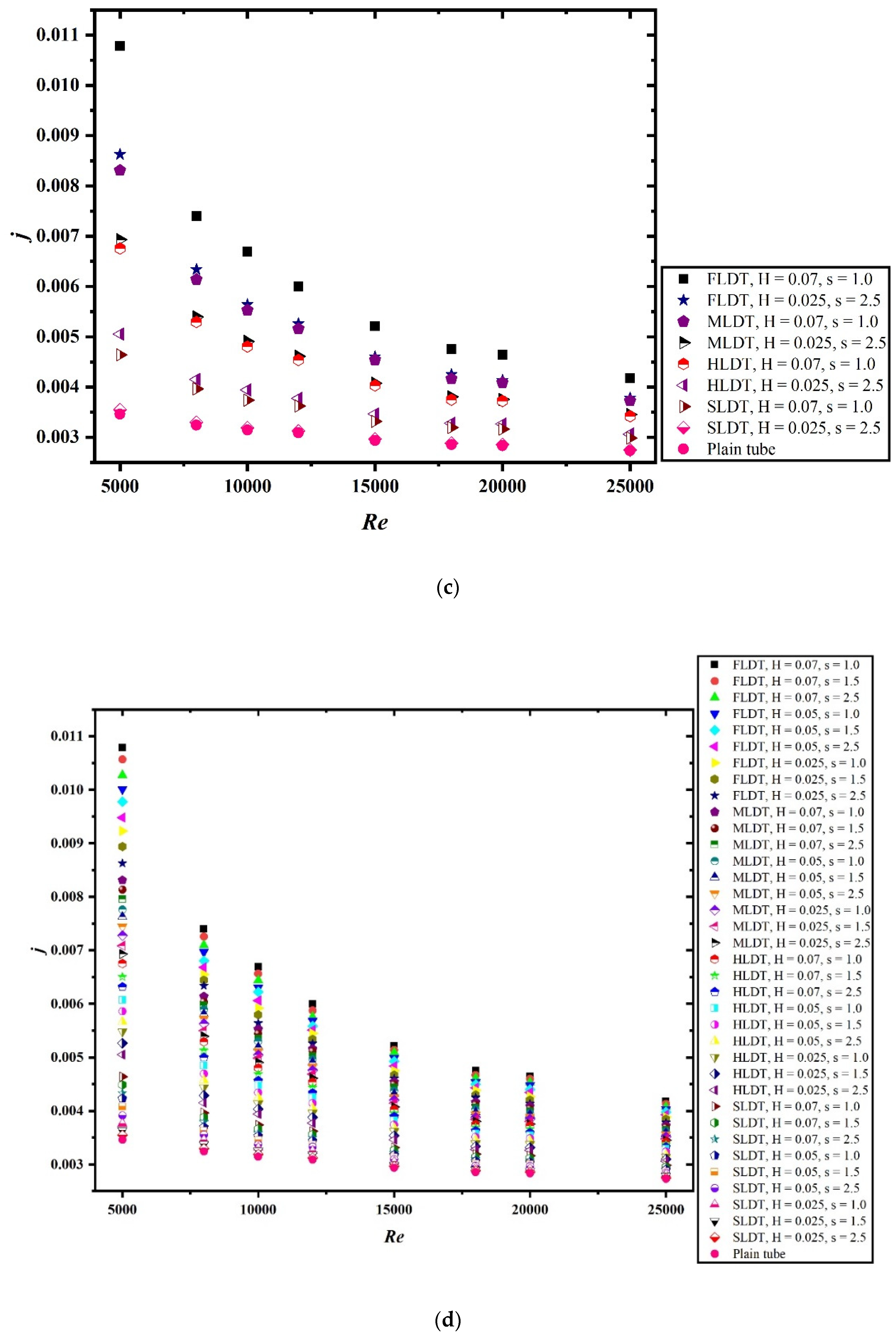
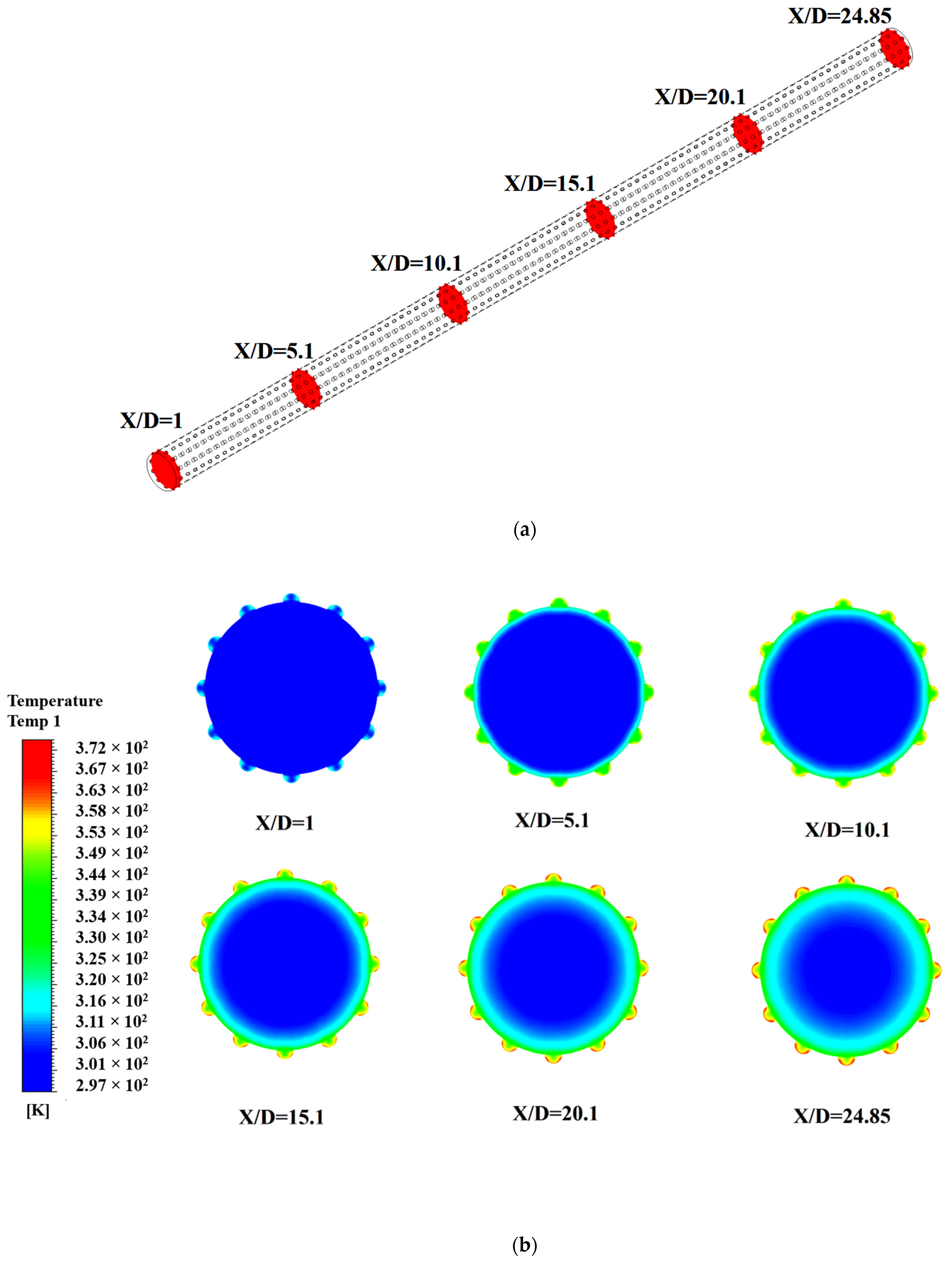
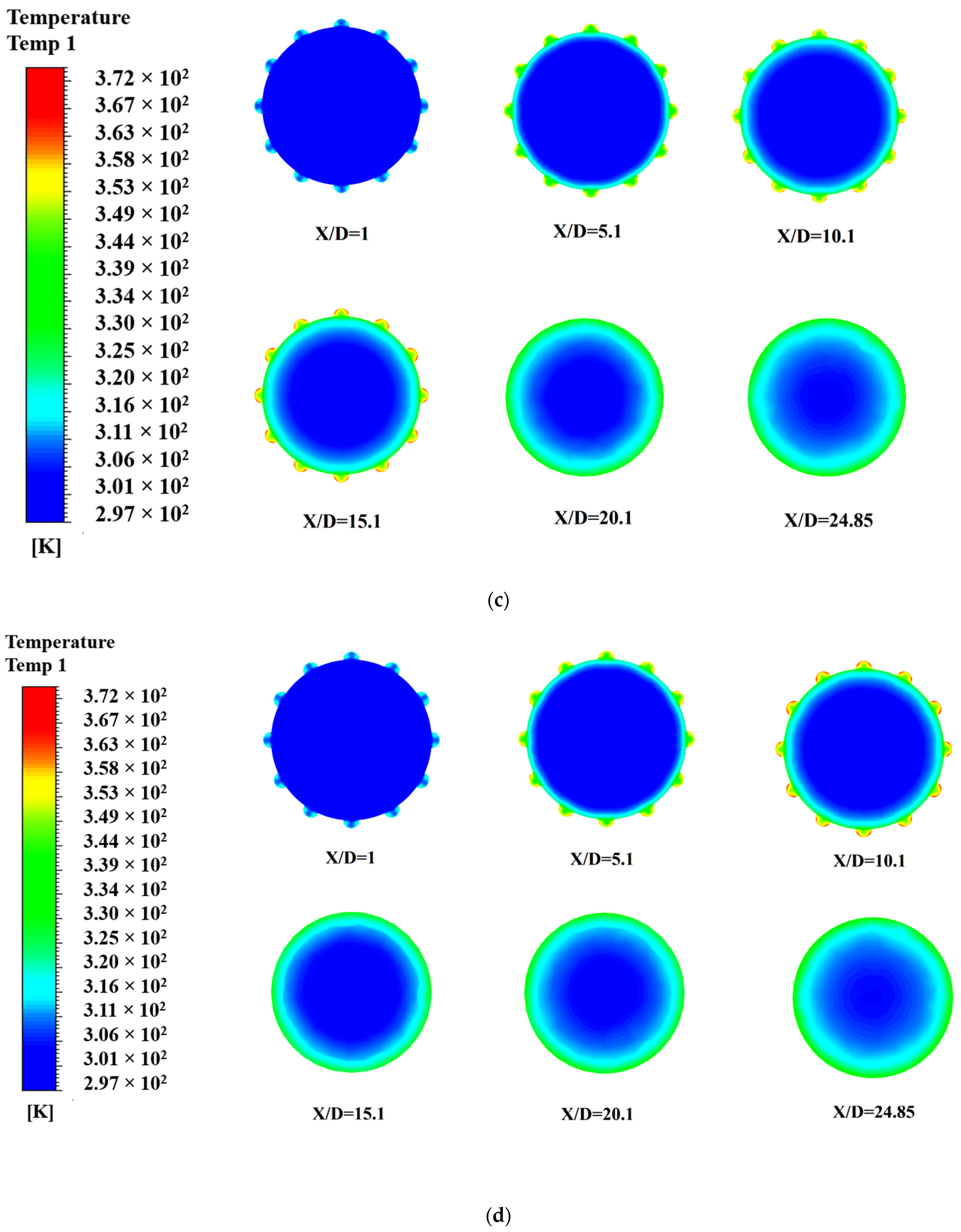

| Parameter | Range |
|---|---|
| Inner diameter of tube, D | 20 mm |
| Dimple height ratio, e/D = H | 0.025, 0.05, 0.07, 0.1 |
| Pitch ratio, P/D = s | 1.0, 1.5, 2.5 |
| Reynolds number (Re) | 5000–25,000 |
| Total Number of Grid Nodes | Nu | f | |
|---|---|---|---|
| Re = 8000, Plain tube | |||
| Grid 1 | 2,696,458 | 29.07 | 0.0091 |
| Grid 2 | 2,902,789 | 29.07 | 0.0091 |
| Grid 3 | 3,422,745 | 30.02 | 0.0092 |
| Re = 12,000, Plain tube. | |||
| Grid 1 | 2,696,458 | 41.53 | 0.0082 |
| Grid 2 | 2,902,789 | 41.54 | 0.0082 |
| Grid 3 | 3,422,745 | 41.56 | 0.0084 |
| Re = 15,000, Plain tube. | |||
| Grid 1 | 2,696,458 | 49.39 | 0.0077 |
| Grid 2 | 2,902,789 | 49.39 | 0.0078 |
| Grid 3 | 3,422,745 | 50.23 | 0.0080 |
| Re = 20,000, Plain tube. | |||
| Grid 1 | 2,696,458 | 63.52 | 0.0072 |
| Grid 2 | 2,902,789 | 63.53 | 0.0072 |
| Grid 3 | 3,422,745 | 64.32 | 0.0074 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alam, M.W.; Souayeh, B. Parametric CFD Thermal Performance Analysis of Full, Medium, Half and Short Length Dimple Solar Air Tube. Sustainability 2021, 13, 6462. https://doi.org/10.3390/su13116462
Alam MW, Souayeh B. Parametric CFD Thermal Performance Analysis of Full, Medium, Half and Short Length Dimple Solar Air Tube. Sustainability. 2021; 13(11):6462. https://doi.org/10.3390/su13116462
Chicago/Turabian StyleAlam, Mir Waqas, and Basma Souayeh. 2021. "Parametric CFD Thermal Performance Analysis of Full, Medium, Half and Short Length Dimple Solar Air Tube" Sustainability 13, no. 11: 6462. https://doi.org/10.3390/su13116462
APA StyleAlam, M. W., & Souayeh, B. (2021). Parametric CFD Thermal Performance Analysis of Full, Medium, Half and Short Length Dimple Solar Air Tube. Sustainability, 13(11), 6462. https://doi.org/10.3390/su13116462







