Application of New Artificial Neural Network to Predict Heat Transfer and Thermal Performance of a Solar Air-Heater Tube

Abstract

In the present study, the heat transfer and thermal performance of a helical corrugation with perforated circular disc solar air-heater tubes are predicted using a machine learning regression technique. This paper describes a statistical analysis of heat transfer by developing an artificial neural network-based machine learning model. The effects of variation in the corrugation angle (θ), perforation ratio (k), corrugation pitch ratio (y), perforated disc pitch ratio (s), and Reynolds number have been analyzed. An artificial neural network model is used for regression analysis to predict the heat transfer in terms of Nusselt number and thermohydraulic efficiency, and the results showed high prediction accuracies. The artificial neural network model is robust and precise, and can be used by thermal system design engineers for predicting output variables. Two different models are trained based on the features of experimental data, which provide an estimation of experimental output based on user-defined input parameters. The models are evaluated to have an accuracy of 97.00% on unknown test data. These models will help the researchers working in heat transfer enhancement-based experiments to understand and predict the output. As a result, the time and cost of the experiments will reduce.

1. Introduction

Conservation of energy is one of the main concerns of today’s world. This is possible using energy-efficient equipment which enables us to utilize less available energy, at the same time without a reduction in its working capacity. Every day, our world is moving one step forward by making new inventions and achievements in the field of energy conservation. However, this growth is surpassed by the need for energy utilization. Growing nations require more energy for the running of businesses, which puts pressure on the power generation units to meet their demands. As of 2019, coal-fired power generation units contribute to 38%, gas-based plants contribute to 23%, hydropower contributes 19%, nuclear power contributes around 10%, while solar and wind energy together contribute 7%. The mentioned figures show that still, we rely mainly on non-renewable energy sources such as coal, gas, and nuclear energy for power generation, however over-exploitation of these resources will vanish soon if we do not find other options. This results in the world economies switching to renewable sources of energy, such as water, wind, tidal, solar, etc. Although hydropower plants have provided energy to us for many decades, the reservoir for the storage of water in very vast quantities damages the ecosystem around the hydropower plant, which creates problems such as habitat loss to the wild animals. Besides, these plants are accident-prone, which has led to flood-like situations. A safe form of energy that is clean and available to us forever is solar energy. The simplest way of harnessing solar energy is by using solar collectors. Solar collectors find applications in space heating, drying industries, process heating, and manufacturing industries, etc.

Solar energy was used for the first time by Greek scientist Archimedes in 212 BC, for burning the Roman fleet with the help of several concave mirrors [1]. In the 19th century, Augustin Mouchot first developed solar-powered steam engines [2], but the cost associated with the construction is not feasible. Many scientists have studied solar power since then but were not able to make any impact and commercialize it. The commercialization of solar-powered devices started in the mid-20th century [3,4]. During this time, researchers investigated the solar devices concerning various aspects. The main disadvantage that researchers come across is the low efficiency of solar-powered equipment. The efficiency of such devices can be increased by employing various passive and active techniques of heat transfer (HT) enhancement, but these techniques need external power such as electric field, magnetic field, etc. [5,6,7,8], which is costly as well as risky. For two mass velocities and various heat fluxes, the effects of an applied DC electric field on flow boiling heat transfer in a vertical mini-channel heat sink are examined experimentally by Feng et al. [5]. Bezaatpour and Goharkhah [6] proposed a new method to improve the heat transfer coefficient in a heat exchanger by involving magnetic nanofluid along with magnetic field. Zhang and Lai [7] carried out a numerical investigation to evaluate heat transfer enhancement in a square channel using corona wind. Cheraghi et al. [8] also incorporate the corona wind for heat transfer enhancement. Passive techniques are simple and safe in operation and utilize surface and geometrical modification for heat transfer enhancement. Some examples of passive techniques involve corrugation on the surface of the duct or channel, use of turbulators such as swirl devices, vortex generators, tapes, and inserts, and artificial roughness such as ribs, dimples, protrusions, etc. [9,10,11,12,13,14,15,16,17,18,19,20]. Various researchers made efforts to increase the thermohydraulic efficiency of devices and decrease the heat losses associated with the operational process. Cheraghi et al. [9] performed a numerical study on the novel geometry of the dimpled tube for thermal and flow performance and reported a 600% enhancement in heat transfer (HT) and a rise in pressure drop (PD). Rainieri et al. [10] experimentally studied the effect of the helically coiled, twisted corrugated tube for mixed convective HT. For the experimental test run, high Prandtl number fluid was used as a working fluid with Re varied from 70 to 1200 and Dean number varied between 12 and 290. Three twist ratios have been used, while the tube corrugation remains the same for all configurations. Enhancement of heat transfer of about 25 times was observed for helically twisted walls in comparison to plain channel, while the pressure drop ranged between 1.5 to 2.5. Ramadhan et al. [11] numerically studied the effect of the square, triangular, trapezoidal, and circular groove carved on the surface of the tube for HT enhancement and flow behavior for Reynolds number (Re) between 10,000 and 20,000. Air is taken as the working fluid. It was revealed that triangular grooves perform best among all other groove geometries for all depths, with a maximum of 64% enhancement in thermal transport. It was also observed that shallow grooves in all cases perform better when compared with smooth channels. Ren et al. [12] experimentally as well as numerically reported the effect of rectangular and triangular surface roughness on the jet impingement cooling augmentation. Air is taken as a working fluid with a Re of 900, 1500, 5000, and 11,000. It was revealed that for low Reynolds numbers (Re) of 900 and 1500, rectangular and triangular roughness results in a drop in Nu and HT coefficients, while increasing the height of rectangular roughness shows an enhancement in Nu and heat transfer rate. At higher Re, the roughness promotes vorticity and turbulent mixing of fluid, which increases heat transfer and Nu. It was also revealed that rectangular roughness performs better in comparison to triangular roughness for all cases. An experimental work on HT enhancement of jet impingement using two geometries (circular protrusion and V-grooves) of surface roughness was conducted by Nagesha et al. [13]. The study was focused on a turbulent region with Re between 10,000 and 27,500 and the application in a heat exchanger (HE). Augmentation in HT was observed in both cases in comparison to the smooth plate, while the plate with circular protrusion showed maximum heat transfer enhancement. Roughness enhances the surface area of the plate as well as helps in the turbulent mixing of fluid, which results in the augmentation of HT. Yadav and Sahu [14] conducted an experimental investigation for analyzing the HT and PD in a double-pipe HE with a smooth inner pipe and corrugated outer pipe, and developed a correlation for predicting Nu and friction factor (f). The study is concluded with 71% augmentation in Nu and 81% enhancement in f as a result.

Jin et al. [15] reported a numerical work on a six-start spirally corrugated duct for investigating the effect of variation in geometric parameters such as pitch, depth of corrugation, Re, and fluid properties on the HT performance. Eiamsa-ard et al. [16] numerically explored a triple-start spirally corrugated tube fitted with twisted tape (TT) inserts with different orientation and width ratio for HT augmentation, and reported enhancement in HT and f with an increase in width ratio, while belly to neck orientation performed better than belly to belly orientation. Andrade et al. [17] performed an investigation for analyzing the thermohydraulic characteristics in the corrugated channel with Re varied between 429 and 6212 for both adiabatic and diabatic conditions, and reported that corrugated tubes are more effective in transitional flow regime (TFR) when compared with the transition in a smoother tube. Wang et al. [18] experimentally studied the novel arrangement of ellipsoidal dimples on tube surface for thermal and flow characteristics and reported enhancement in HT and f. Xie et al. [19] computationally reported the impact of tear-drop dimples on the surface of the tube and compared the results with the ellipsoidal- and spherical-dimpled tube data. A significant drop in recirculation flow, as well as a pressure drop, is reported when results are compared with that of the ellipsoidal- and spherical-dimpled tube. Li et al. [20] performed experiments to explore the influence of dimple-enhanced tubes on the thermal transport and pressure drop for water and water/glycol solution as the working fluids. The results of simulations revealed that dimples disrupt the boundary layers and create secondary flows, which enhance turbulence, resulting in enhanced heat transfer. Bhattacharyya and Chattopadhyay [21] conducted an investigation to study the influence of twisted strips on the thermohydraulic performance of fluid in a turbulent flow regime for different pitch ratios. An increase in Nu and a decrease in f were reported with increasing Re for all configurations. Moghadam et al. [22] performed a computational investigation on a corrugated tube fitted with a wire coil insert for thermal and flow performance, and reported an increase in heat transfer and pressure drop with an increase in Re. Yang et al. [23] conducted a numerical investigation to analyze the influence of TT inserts fitted inside an externally corrugated tube for thermal and flow behavior, and the obtained results are compared with smooth tube results.

A numerical assessment to investigate the influence of nanofluid flow on the HT and PD inside a corrugated tube has been performed by Ahmed et al. [24]. An increment in HT, as well as a slight increase in PD, was reported with an increase in the volume fraction of nanoparticles and Reynolds number. Navaei et al. [25] numerically investigated the influence of different nanofluids flowing inside corrugated tubes of various configurations for thermal and flow characteristics and reported augmentation in Nu for the increase in volume fraction, while a decrease in Nusselt number (Nu) was reported with an increase in the size of the nanoparticles. Wongcharee and Eiamsa-ard [26] experimentally reveal the influence of volume fraction of nanoparticles and twist ratio, an arrangement of twisted tape inserts fitted inside a corrugated tube on thermal and flow behavior, and reported enhancement in HT, f, and thermal performance.

A new efficient technique is gaining momentum, which is more accurate and consumes less time to predict thermal performance, and the technique is known as machine learning (ML) prediction. The utilization of this system helps in reducing the time, cost, and effort associated with experimental and numerical work by predicting the results in a permissible range and learning from previous tasks. Tang et al. [27] employed the ML method for analyzing and optimizing the geometric and operation parameters of a phase-change materials-based hybrid cooling system. Krishnayatra et al. [28] utilized k-nearest neighbor, also known as KNN, for predicting the performance of HE, which resulted in highly accurate predictions. Beig et al. [29] investigated T performance in a tube fitted with three blocks at the bottom, and a triangular bar was used as a vortex generator. The ML method of the genetic algorithm was used for prediction of the Nusselt number, and the Gaussian process was used for predicting the optimal position of the triangular bar in the channel for maximum heat transfer. Methods of ML prediction have been utilized to predict the Nu for nanofluid flowing through the coils [30]. The variables considered for the prediction are Prandtl number (Pr), volumetric concentration (Φ), and the helical number of helically coiled corrugated tubes. The model predicted using the least-squares support vector machine (LSSVM) shows the best performance and approaches the R-square value of 1. Hobold and Silva [31] presented a neural network-based model to predict the heat flux during nucleate boiling and showed that the correlation developed by the model showed a 7% error in the predicted results when compared with the experimentally obtained data. Khairul et al. [32] employed fuzzy logic to investigate the influence of CuO/water nanofluid (NF) flowing inside a corrugated tube to predict the thermal performance of nanofluid. Models have been developed to predict the Nu and f, and the values obtained from such models are fitted well in the acceptable range of 5%. Sotgiu et al. [33] employed ML and tensor representation theory to predict the heat flux in a turbulent flow regime. The validation of Poiseuille flow for different values of Re using the given model shows good agreement between the obtained value and reference values. While an ML model makes decisions according to what it has learned from the data, a neural network is a more sophisticated ML approach that arranges various ML algorithms in a fashion whereby it can make better accurate decisions by itself [34]. An artificial neural network (ANN) works similarly to the human brain’s neural network. It is the foundation of AI and solves problems that would prove impossible or difficult by human or statistical standards [35]. Rabbi et al. [36] predicted the magneto hydro-dynamics flow and entropy production for heat sinks filled with Copper-water nanofluid using the method of artificial neural networking (ANN). The effect of Hartman number (Ha) and Volume fraction (Φ) on the Nu and Bejan number (Be) have been predicted using ANN. Akdag et al. [37] performed experiments to investigate the HT on the flat plate subjected to transverse pulsating jets. Constant heat flux is supplied to the plate. The data obtained from the experimental study were used to process ANN for predicting the solution. The results obtained from the ANN were in very good agreement with the experimental data, with less than 1% error. The ML prediction method is also used to predict the PD during the evaporation of R407C by Khosravi et al. [38]. Three methods of ML, namely MLFFNN, SVR, and GMDH, are employed to predict the pressure drop, and the results obtained from all the methods are compared. Both MLFFNN and GMDH perform better, with errors of less than 1%, compared to the SVR method of ML prediction. Song et al. [39] investigated the application of ultrasound in industrial evaporators. They predicted the thermal performance of an ultrasonic evaporator using seven different algorithms of ML and found that SVM and NNet predicted the results most accurately. Park and Lee [40] employed an ML prediction technique for predicting the wall temperature at critical heat flux (CHF). The ML prediction method utilized here helped in reducing the calculation time by 86%. Kim and Lee [41] utilized convolutional neural networks (CNN) for the prediction of HT in turbulent flow, and the results are associated with the data obtained from direct numerical simulations (DNS). The results obtained from the analysis show great agreement between CNN and DNS, with a correlation coefficient of 0.98. Kahrom et al. [42] employed a pareto genetic algorithm to generate the most suitable edge size and position of a quad insert in a turbulent flow regime to maximize the HT. Kahani et al. [43] predicted the Nu and PD for TiO₂-water NF flowing through a coiled channel using the MLPANN and LSSVM models. The predicted results through MLPANN models show more accuracy when compared with the data obtained by the LSSVM model. Gerdroodbary [44] predicted the heat transfer (HT) rate of MHD NF inside an inclined enclosure with a sinusoidal wall using the ML prediction method of the group method of data handling (GMDH). The data obtained from GMDH are compared with data obtained from the control volume-based method (CVFEM) and results show that GMDH is far more accurate in predicting the heat transfer (HT). ML is also used to predict the thermal conductivity of NFs [45]. Karami et al. [46] employed the ML method of adaptive neuro-fuzzy inference system (ANFIS) to predict the thermal performance of an air-cooler fitted with TT inserts. The result obtained from the prediction showed a maximum error of 2.37% when compared with experimental results. Other authors who also investigated the ML prediction for predicting the heat transfer and pressure drop, thermal performance, and thermal resistance are Nasirzadehroshenin et al. [47], Li and Liu [48], and Zhan et al. [49], respectively.

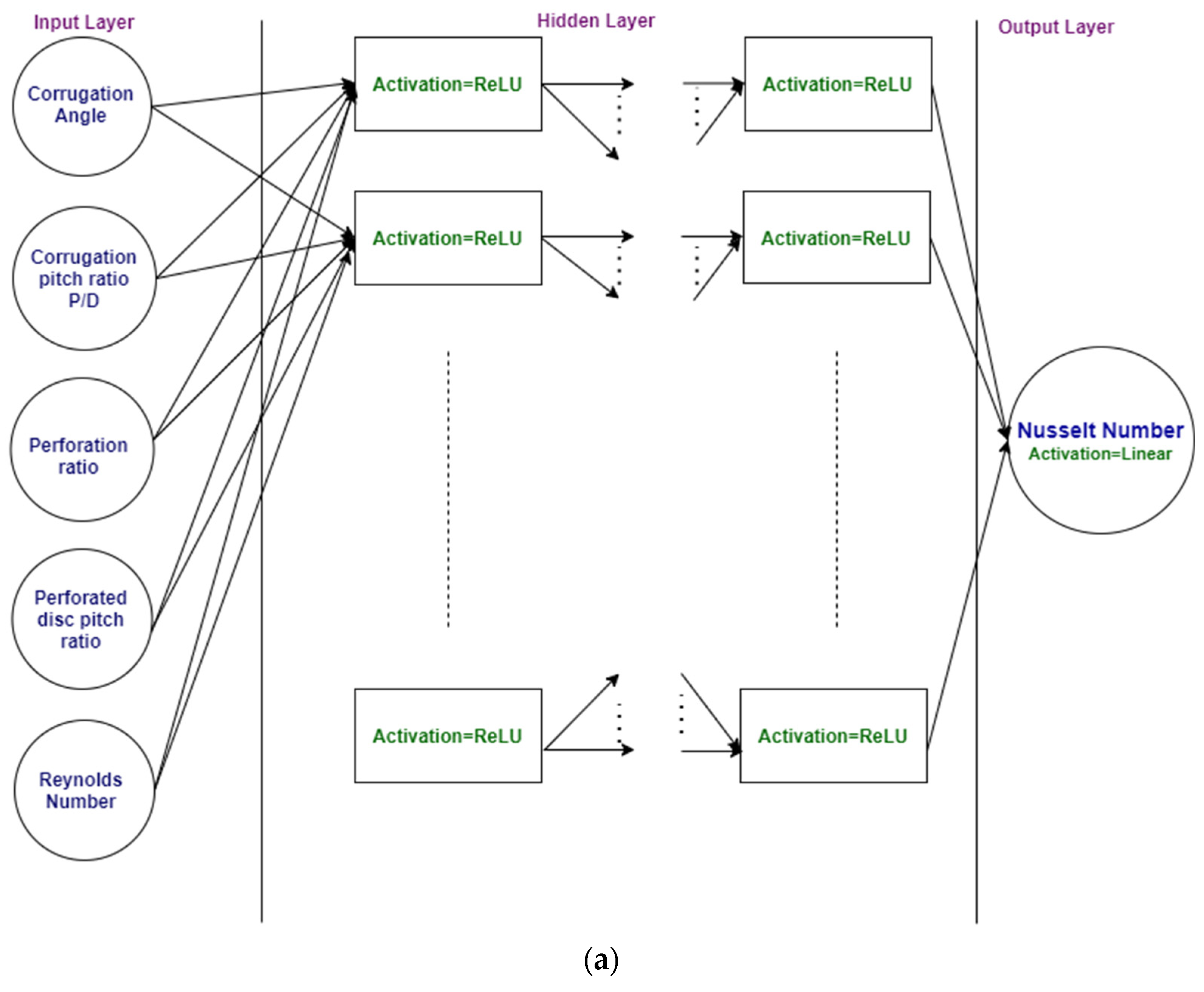
In view of the above literature review, it is clear that a lot of available literature address HT and PD in a helically corrugated tube, but very few studies address helical corrugated tubes with turbulator inserts, and no literature are available on the application of machine learning (ML) prediction of HT and PD in a corrugated tube with inserts. In fact, only a few studies are available to predict thermal performance of unknown parameters by ML techniques. Hence, the main aim and the novelty of this work is to predict the HT and thermal performance in a helically corrugated tube fitted with perforated circular disc turbulator inserts by employing the ML. Additionally, these models will help future investigators working in the field of HT enhancement-based experiments to understand and predict the output.

2. Experimentation and Data Reduction

The basic design of the helical corrugation channel with turbulator disc inserts is shown in Figure 1 [50]. The setup used in this investigative work is quite prominent, and the same test rig (Figure 2) was utilized in previous studies [50].

The tests were conducted in an air-conditioned lab, where the average room temperature varied from 290 to 295 K. A 7 kW air blower was used to draw fresh air from the atmosphere. A rotameter was fitted in the line to quantify the mass flow rate of the air. A manometer was used to display the pressure difference between pressure taps.

Brass was used for the fabrication of the test section. The test section is circular in cross-section, having an internal diameter of 20 mm, while the total length of the test section is fixed at 3500 mm. A total of 28 thermocouples were used at 7 locations to measure the outer wall temperatures. In previous research conducted by the authors [51,52,53,54,55,56,57,58,59,60,61], the basic fabrication method is well-represented. Other specifications of different parameters are outlined in

Table 1. Experimental investigated parameters.

Sl. No.	Parameters	Values
1	Corrugation depth (d)	3 mm
2	Corrugation angle (θ)	30° and 60°
3	Perforation ratio (k)	0.16, 0.25, and 0.33
4	Corrugation pitch ratio (y)	0.7 and 1.0
5	Perforated disc pitch ratio (s)	1.5 and 2.5
6	Reynolds number (Re)	10,000–50,000

, and the ideas of choosing the arrangement of the considered solar air-heater followed Bhattacharyya et al. [50,56].

3. ANN-Based Heat Transfer Prediction

ML is an application of artificial intelligence (AI) where systems automatically learn, develop knowledge, and improve the ability to predict with more accuracy with experience [62,63,64,65,66,67,68]. Shankar et al. [65] developed an ANN approach to predict interface temperature. Farzaneh-Gord et al. [66] employed machine learning for predicting the temperature in the throttle process. Jin et al. [67] also employed the same approach for determining the auto-ignition temperature. Baghban et al. [68] employed the ML for determining the thermal performance of nanofluid under observation.

In this section, the influence of different architectures and their variants and training strategies are exhaustively described. The numerical operation is computed by using user-defined model architecture and is discussed in Section 3.1, the details of the dataset are explained in Section 3.2, and the computational environment is described in Section 3.3.

3.1. Model

The primary step of the ANN-based approach is collecting the experimental data that is used to train the model. The dataset provides a large number of true values for different sets of parameters. Figure 3a,b demonstrate the architecture of the ANN-based approach for the prediction of Nusselt number (Nu) and the thermohydraulic efficiency of the solar air-heater.

3.1.1. Workflow of ANN

At the initial stage, the dataset is divided into three categories: training data, validation data, and test data. A “neuron” in ANN is a single computing cell, and the model is composed of several neurons. Each neuron has activation functions that are mathematical equations of the weighted sum of the outputs of the previous layer with a bias added to it. Different types of activation functions are binary-step functions, linear, and non-linear activation functions, as analyzed by Dabal [62]. A few efficient activation functions were chosen for the particular study and are as follows.

Linear: Linear activation is a straight-line function where the input (that is the weighted sum from the neuron) is proportional to the activation. It can be written as:

A(x) = cx

(1)

Rectified linear units (ReLU): The function’s formula is ambiguously simple: max (0, z). Despite its name and appearance, it is not linear and provides the same benefits as Sigmoid but with much better performance. It can be written as:

A(z) = z if z > 0 or
A(z) = 0 if z ≤ 0

(2)

Exponential linear unit (ELU): It is a function which tends to more quickly converge cost to zero and produce more accurate results. In contrast to other activation functions, an ELU has an extra positive constant, α.

A(z) = α.e^z − 1 if z ≤ 0 or
A(z) = z otherwise z > 0

(3)

3.1.2. ANN Model for Nusselt Number

The five-layered neural network-based machine learning model was used to predict the Nusselt number. Several tests were performed using different models with several numbers of neurons and hidden layers [63,64]. Among them, a model with four hidden layers, with each having 40–50 neurons, was determined to have decent accuracy. The present neural network with four dense hidden layers with 50 neurons in each had the best accuracy, and hence this configuration was selected for comparison of accuracy and calculation speed. The linear error function (Equation (1)) was used in the output layer and the ReLU error function (Equation (2)) was used in all the hidden layers. The training and validation accuracy are shown in

Table 2. Training accuracy for Nusselt number.

Neural Network Model	Training Accuracy	Validation Accuracy
40 × 40 × 40 × 40 neurons	99.90%	99.96%

. The neural network was trained by taking batch size as 32 and epoch size as 200. The change in training and validation loss with an increase in epoch numbers is shown in Figure 4.

3.1.3. ANN Model for Efficiency

The five-layered neural network-based ML model was built to predict thermohydraulic efficiency. The main difference of this model is the error function used in the hidden layers. The ELU error function (Equation (3)) was used here as it provides better results in terms of producing negative outputs. The neural network with four dense hidden layers with 50 neurons in each was predicted to have the best validation set accuracy, and hence this configuration was considered for comparison of accuracy and calculation speed. The neural network was trained by taking batch size as 10 and epoch size as 200. The change in training and validation loss with an increase in epoch numbers is shown in Figure 5. The training and validation accuracy is shown in

Table 3. Training accuracy for efficiency.

Neural Network Model	Training Accuracy	Validation Accuracy
50 × 50 × 50 × 50 neurons	99.91%	99.98%

.

3.2. Dataset

The experimental data consist of five independent input parameters, namely corrugation angle (θ), corrugation pitch ratio (y = P/D), perforated disc pitch ratio (s = H/D), perforation ratio (k = h/D), and Reynolds number. The experimentation was already explained in Section 2, and detailed experimentation can be found in the authors’ previous work [50,51,52,53,54,55,56,57,58,59,60,61]. Depending on the experimental analysis, the two main important dependent output parameters, such as Nusselt number and thermohydraulic efficiency, are taken into consideration. The detailed analysis of the dataset can be visualized in

Table 4. Analysis of experimental data.

	Corrugation Angle	Corrugation Pitch Ratio	Perforation Ratio	Perforated Disc Pitch Ratio	Reynolds Number	Nusselt Number	Efficiency
Count	1347.000	1347.000	1347.000	1347.000	1347.000	1347.000	1347.00
Mean	44.877	0.848	0.235	2.004	30,636.728	144.2535	1.8309
Standard Deviation	15.005	0.150	0.072	0.500	11,836.229	31.294	0.47

. The total count of data points was 1347. The mean and standard deviation of every individual parameter were calculated, showing the statistical analysis of the experimental data which are used to train and test the models.

3.3. Computational Environment

All the experiments were run on Google Colab Notebook with Nvidia GPU version 1.4.0 enabled, and Keras 2.4.0 was used as an API to train and test the neural network models, as a way to clone hardware configuration. This computational environment was used to compare and execute the various possible choices of model for the experimental data studied in this paper. In total, the results for more than 100 experimental trials were summed up.

4. Results and Discussion

The test accuracy is shown in

Table 5. Test accuracy for Nu and thermohydraulic efficiency.

Test accuracy for Nusselt number	98.19%
Test accuracy for thermohydraulic efficiency	97.15%

and the R-squared values (another statistical measure of how close to the data are to the fitted regression line) of test data are shown in

Table 6. R-squared value for Nu and thermohydraulic efficiency.

Test accuracy for Nusselt number	98.22%
Test accuracy for thermohydraulic efficiency	96.83%

for both the trained models. Figure 6 and Figure 7 show the assessment between the predicted and actual experimental value of the test data for Nu and efficiency (η), respectively. From the figures, one can understand that the ANN model fits the dataset acceptably. The performance of both the models reported an accuracy of more than 97.00% on the test dataset.

Some recent work on solar air-heaters with various types of turbulator inserts are reported by many researchers [69,70,71,72,73], but the authors failed to predict unknown parameters. Predicting unknown parameters is very important. So, next, for achieving a better result, a noble work effort is shown, where a set of unknown input parameters were generated to predict the values for Nu and efficiency. The detailed statistical analysis of the generated data is shown in

Table 7. Analysis of generated data.

	Corrugation Angle	Corrugation Pitch Ratio	Perforation Ratio	Perforated Disc Pitch Ratio	Reynolds Number
Count	22,679	22,679	22,679	22,679	22,679
Mean	53.33	0.88	0.255	1.06	37,017.94
Standard Deviation	22.11	0.37	0.14	1.16	28,473.95

, which includes a count of the data, mean, and standard deviation, that elaborates the range or the distribution of the generated data.

The newly generated parameters for prediction are shown in

Table 8. New generated parameters for prediction.

Sl. No.	Parameters	Values
1	Corrugation angle (θ)	20°, 25°, 40°, 45°, 50°, 65°, 70°, 75°, and 90°
2	Perforation ratio (k)	0.08, 0.10, 0.20, 0.30, 0.40, and 0.45
3	Corrugation pitch ratio (y)	0.4, 0.6, 0.8, 1.2, and 1.4
4	Perforated disc pitch ratio (s)	0.14, 0.20, 0.28, 0.35, 1.0, 2.0, and 3.5
5	Reynolds number (Re)	8000–70,000

. The Nusselt number and thermohydraulic efficiency results of the generated data are shown in

Table 9. Predicted result of Nusselt number on generated data.

Sl. No.	Corrugation Angle	Corrugation Pitch Ratio	Perforation Ratio	Perforated Disc Pitch Ratio	Reynolds Number	Nusselt Number
1	20°	0.4	0.08	0.14	9000	119.74
2	20°	0.6	0.45	0.2	70,000	157.08
3	25°	0.8	0.1	0.28	70,000	160.01
4	25°	1.2	0.4	0.35	8000	93.87
5	40°	1.4	0.1	2.0	60,000	138.31
6	40°	0.4	0.2	0.2	65,000	172.10
7	45°	0.6	0.3	0.14	9500	122.91
8	45°	0.8	0.08	1.0	9000	120.67
9	50°	1.2	0.2	3.5	60,000	144.72
10	50°	1.4	0.45	0.28	65,000	150.36
11	65°	0.4	0.3	0.35	8000	138.97
12	65°	0.6	0.4	1.0	9500	134.67
13	70°	0.8	0.1	2.0	9000	133.35
14	70°	1.2	0.08	3.5	70,000	170.15
15	75°	1.4	0.45	0.14	8000	125.46
16	75°	0.4	0.4	0.2	60,000	182.09
17	90°	0.6	0.2	0.35	65,000	193.38
18	90°	0.8	0.08	2.0	9500	149.04

and

Table 10. Predicted result of thermohydraulic efficiency on generated data.

Sl. No.	Corrugation Angle	Corrugation Pitch Ratio	Perforation Ratio	Perforated Disc Pitch Ratio	Reynolds Number	Efficiency
1	20°	0.4	0.08	0.14	9000	2.10
2	20°	0.6	0.45	0.2	70,000	1.48
3	25°	0.8	0.1	0.28	70,000	1.49
4	25°	1.2	0.4	0.35	8000	1.71
5	40°	1.4	0.1	2.0	60,000	1.46
6	40°	0.4	0.2	0.2	65,000	1.60
7	45°	0.6	0.3	0.14	9500	2.19
8	45°	0.8	0.08	1.0	9000	2.16
9	50°	1.2	0.2	3.5	60,000	1.52
10	50°	1.4	0.45	0.28	65,000	2.00
11	65°	0.4	0.3	0.35	8000	1.87
12	65°	0.6	0.4	1.0	9500	1.43
13	70°	0.8	0.1	2.0	9000	1.99
14	70°	1.2	0.08	3.5	70,000	1.47
15	75°	1.4	0.45	0.14	8000	1.73
16	75°	0.4	0.4	0.2	60,000	1.38
17	90°	0.6	0.2	0.35	65,000	1.40
18	90°	0.8	0.08	2.0	9500	2.20

. Here, different combinations of inputs were taken and fed to the model. The inputs are new to the model and hence the accuracy is measured to their outcomes.

Based on the newly generated parameters, Figure 8 is plotted. The 3D plots of HT in terms of Nu and thermohydraulic efficiency are shown in Figure 8a–d, respectively. From Table 5, it may be seen that the accuracy was 98% for Nusselt number and 97% for thermohydraulic efficiency, which indicates that the new ANN model had no complications in learning the Nusselt number and thermohydraulic efficiency. From Figure 8a,b, one can easily observe the Nusselt number (z-axis), Reynolds number (y-axis), and corrugation angle (x-axis) plotted in a 3D graph. In Figure 8a, the Nusselt number is the function of corrugation angle and Reynolds number, and is plotted at a constant corrugation pitch ratio of 0.4, perforation ratio of 0.08, and perforated disc ratio of 0.14, while in Figure 8b, the Nusselt number is the function of corrugation angle and Reynolds number, and is plotted at a constant corrugation pitch ratio of 1.4, perforation ratio of 0.45, and perforated disc ratio of 3.5.

From Figure 8a,b, it can be detected that the Nu is increasing with the increase of Re and corrugation angle, and the proposed ANN model very closely shadowed the experimental pattern [50]. From the figures, one can see that the Nusselt numbers are maximum when the corrugation angle is varied between 70° and 90° at Reynolds numbers between 60,000 and 70,000.

The thermohydraulic efficiency (η) is another very important factor to evaluate the performance of the solar air-heater. In Figure 8c,d, efficiency (z-axis), Re (y-axis), and corrugation angle (x-axis) are plotted in a 3D graph. In Figure 8c, the efficiency is the function of corrugation angle and Reynolds number, and is plotted at a constant corrugation pitch ratio of 0.4, perforation ratio of 0.08, and perforated disc ratio of 0.14, while in Figure 8d, the efficiency is the function of corrugation angle and Re, and is plotted at a constant corrugation pitch ratio of 1.4, perforation ratio of 0.45, and perforated disc ratio of 3.5. From the figures, it can be detected that the efficiency is decreasing with the increase of Re and increasing corrugation angle, and the new ANN model for this particular study is very closely shadowed in the experimental pattern [50]. From the figures, one can see that the thermohydraulic efficiency is maximum (η = 2.36 to 2.54) when the corrugation angle is at 90° and Reynolds numbers are between 8000 and 10,000.

Both the models (for Nusselt number and efficiency) will ease a very huge workload by determining the required outputs. With the given test data, as mentioned in Table 9 and Table 10, researchers working with a similar experimental setup can use these models to help to tune their parameters according to their needs and obtain their required results. It is important to note and consider an error factor of ±3% while considering the results.

5. Conclusions

Based on the experimental investigated results, a new artificial neural network model was offered for the prediction of Nusselt number (Nu) and thermohydraulic efficiency (η) by using machine learning techniques. From the analysis, the following points were made:

• An ANN model was used for regression analysis to predict the heat transfer and thermohydraulic efficiency.
• Two different models were trained based on the features of experimental data, which provide an estimation of experimental output based on user-defined input parameters.
• The models were evaluated to have an accuracy of 97.00% on unknown test data
• The proposed model was able to reasonably forecast the Nu and thermal efficiency.
• Artificial neural networks can be an important method for HT prediction, mainly when large datasets are being used.
• The proposed models will help researchers working in heat transfer enhancement-based experiments to understand and predict the output.