Should There Be Industrial Agglomeration in Sustainable Cities?: A Perspective Based on Haze Pollution
Abstract
:1. Introduction
2. Methodology
2.1. Spatial Econometric Model Derivation and Design
- Production
- Haze pollution
- Let the price of product be exogenously given as .
- Then total revenue , total cost , and profit , assuming that the market is perfectly competitive, i.e., .
2.2. Selection of Spatial Weight Matrix
2.2.1. Contiguity-Based Spatial Weights Matrix
2.2.2. Inverse-Distance-Based Spatial Weights Matrix
2.2.3. Nested Weights Matrix
3. Selection and Explanation of Variables
3.1. Selection of Variables
3.1.1. Explained Variable
3.1.2. Explanatory Variables
3.1.3. Control Variables
3.2. Data Source
4. Empirical Results
4.1. Sample Description Analysis
4.1.1. Spatio-Temporal Distribution of Industrial Agglomeration
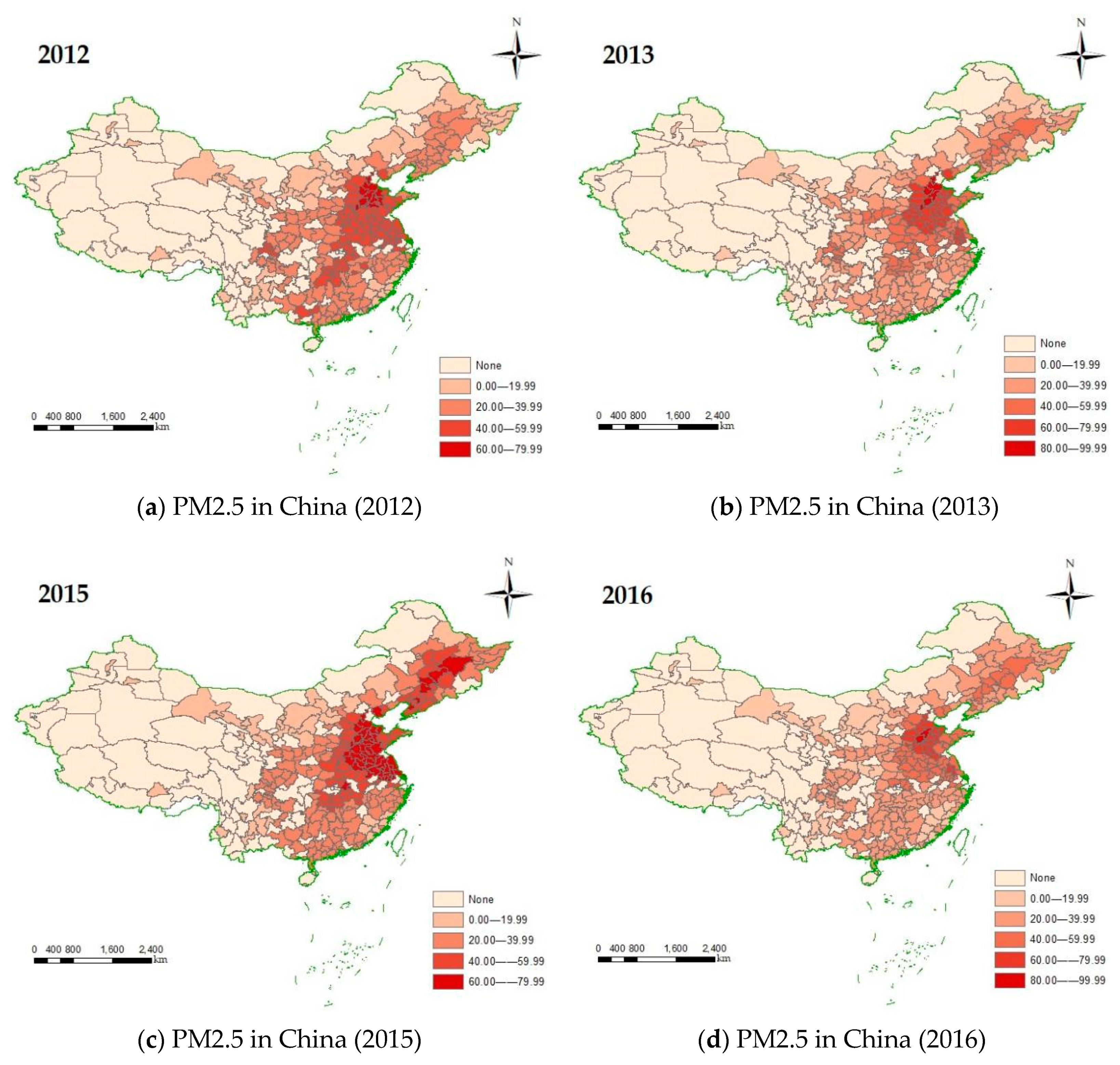
4.1.2. Spatio-Temporal Distribution of PM2.5
4.2. Spatial Auto-Correlation Analysis
4.2.1. Global Spatial Auto-Correlation Analysis
4.2.2. Local Spatial Auto-Correlation Analysis
4.3. Further Improvement of Empirical Model
4.3.1. Panel Model Effects Test
4.3.2. Spatial Model Effects Tests
4.4. Spatial Econometric Analysis
4.4.1. Estimated Results of the Spatial Econometric Model
4.4.2. Conclusion Analysis and Explanation
- Local industrial agglomeration creates economies of scale, brings advanced technology to the local area, promotes the upgrading of local industry [3], improves the energy-saving and emission reduction capabilities of industrial enterprises [6], and develops towards an environment-friendly and clean green economy [12]. The positive externalities brought about by agglomeration, such as reduced transport and information communication costs (labour and technology spillover effects) between enterprises [43], have led to an increase in the overall economic productivity of local enterprises, improved energy efficiency, and reduced pollutant emissions [57], thus improving the efficiency of the green economy in the region [58]. Therefore, the expansion of local industrial agglomeration is beneficial to the control of haze and reduces the concentration of PM2.5 [59].
- Due to the mobility of technology, capital, and talent, when the scale of local industrial agglomeration rises and industrial density becomes too high, the local workforce cannot keep up with the demand for efficient production [2], and thus local enterprises recruit more labour from neighbouring areas and attract more talent, creating a “siphon effect” on neighbouring cities [3]. As a result, technology, capital, and talent will inevitably move to cities with high levels of industrial development, further increasing the technological gap between local and neighbouring areas [60]. At this point, the negative externalities of industrial agglomeration on neighbouring regions are greater than the positive externalities, which is not conducive to neighbouring cities improving their technology and developing a green economy [61]. In addition, due to the existence of promotion tournaments between regional governments in China, when the scale of local industrial agglomeration rises, neighbouring regions are forced to increase their industrial development due to promotion pressure [62], seeking regional economic development and forming inter-regional industrial level competition. However, due to the inadequate technology level of the neighbouring regions, they cannot form economies of scale like the regions with high industrial agglomeration scale [63], making the development of industry in the neighbouring regions instead increase the level of haze pollution.
5. Discussion
5.1. Robustness Test Using Inverse-Distance Matrix and Economic Geography Nested Matrix
5.2. Discussion on Endogeneity Based on GS2SLS
5.3. Limitations and Future Research
- Using spatial econometrics as an analytical tool, this paper extends the study to 253 prefecture-level cities. To a certain extent, it alleviates the endogeneity implications of the lack of freedom in previous studies and the neglect of the causal identification problem, e.g., [3,26]. The possible endogeneity problems due to insufficient causal identification are also discussed. However, due to the difficulty of obtaining data and the limitations of the development of spatial econometrics, the scientific tools for the discussion of the endogeneity problem are still relatively homogeneous. With the introduction of new spatial econometric causal inference methods, further improvements to the study will be made.
- In the baseline regression and robustness tests, three spatial weight matrices are used to discuss the problem, which to some extent ameliorates the problem of unrobustness in previous studies. However, the reasonableness of the choice of spatial weight matrix has been a major problem in such studies. We will also follow up on related studies and improve on them.
- For the reasons of the results, due to the consideration of space and other factors, this paper mainly adopts a qualitative research method based on the combination of previous literature. In subsequent studies, we will try to discuss the mechanism issue in detail empirically.
6. Conclusions and Policy Implications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, X.T.; Ye, C.; Li, S.M. Research progress of sustainable cities and its implications for national territory spatial plan. J. Nat. Resour. 2020, 35, 2120–2133. [Google Scholar]
- Li, Y.; Tang, Y.; Wang, K.; Zhao, Q. Environmental Regulation and China’s Regional Innovation Output—Empirical Research Based on Spatial Durbin Model. Sustainability 2019, 11, 5602. [Google Scholar] [CrossRef]
- Zhao, H.; Cao, X.; Ma, T. A spatial econometric empirical research on the impact of industrial agglomeration on haze pollution in China. Air Qual. Atmos. Health 2020, 13, 1305–1313. [Google Scholar] [CrossRef]
- Wang, K.; Tang, Y.; Chen, Y.; Shang, L.; Ji, X.; Yao, M.; Wang, P. The Coupling and Coordinated Development from Urban Land Using Benefits and Urbanization Level: Case Study from Fujian Province (China). Int. J. Environ. Res. Public Health 2020, 17, 5647. [Google Scholar] [CrossRef] [PubMed]
- Guan, X.; Wei, H.; Lu, S.; Dai, Q.; Su, H. Assessment on the urbanization strategy in China: Achievements, challenges and reflections. Habitat Int. 2018, 71, 97–109. [Google Scholar] [CrossRef]
- Guo, Y.; Tong, L.; Mei, L. The effect of industrial agglomeration on green development efficiency in Northeast China since the revitalization. J. Clean. Prod. 2020, 258, 120584. [Google Scholar] [CrossRef]
- Chen, W.; Lei, Y.; Wu, S.; Li, L. Opportunities for low-carbon socioeconomic transition during the revitalization of Northeast China: Insights from Heilongjiang province. Sci. Total Environ. 2019, 683, 380–388. [Google Scholar] [CrossRef]
- Lin, W.L.; Chen, T.P. China’s widening economic disparities and its ‘Go West Program’. J. Contemp. China 2004, 13, 663–666. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Y.; Jiang, J.; Wu, P. How green is the “Belt and Road Initiative”?—Evidence from Chinese OFDI in the energy sector. Energy Policy 2020, 145, 1117. [Google Scholar] [CrossRef]
- Zeng, D.; Zhao, L. Pollution havens and industrial agglomeration. J. Environ. Econ. Manag. 2009, 58, 141–153. [Google Scholar] [CrossRef] [Green Version]
- Porter, M.E. Towards a dynamic theory of strategy. Strat. Manag. J. 1991, 12, 95–117. [Google Scholar] [CrossRef]
- Kesidou, E.; Wu, L. Stringency of environmental regulation and eco-innovation: Evidence from the eleventh Five-Year Plan and green patents. Econ. Lett. 2020, 190, 109090. [Google Scholar] [CrossRef]
- Wang, X.; Klemeš, J.J.; Dong, X.; Fan, W.; Xu, Z.; Wang, Y.; Varbanov, P.S. Air pollution terrain nexus: A review considering energy generation and consumption. Renew. Sustain. Energy Rev. 2019, 105, 71–85. [Google Scholar] [CrossRef]
- Tang, Y.; Chen, Y.; Wang, K.; Xu, H.; Yi, X. An Analysis on the Spatial Effect of Absorptive Capacity on Regional Innovation Ability Based on Empirical Research in China. Sustainability 2020, 12, 3021. [Google Scholar] [CrossRef] [Green Version]
- Cavaco, S.; Crifo, P. CSR and financial performance: Complementarity between environmental, social and business behaviours. Appl. Econ. 2014, 46, 3323–3333. [Google Scholar] [CrossRef]
- Javorcik, B.S.; Wei, S.J. Pollution Havens and Foreign Direct Investment: Dirty Secret or Popular Myth? Contrib. Econ. Anal. Policy 2005, 3, 12. [Google Scholar] [CrossRef] [Green Version]
- Yao, M.; Zhang, Y. Evaluation and Optimization of Urban Land-Use Efficiency: A Case Study in Sichuan Province of China. Sustainability 2021, 13, 1771. [Google Scholar] [CrossRef]
- Tsai, K.; Yang, S. Firm innovativeness and business performance: The joint moderating effects of market turbulence and competition. Ind. Mark. Manag. 2013, 42, 1279–1294. [Google Scholar] [CrossRef]
- Singh, J.; Gupta, P.; Gupta, D.; Verma, S.; Prakash, D.; Payra, S. Fine particulate pollution and ambient air quality: A case study over an urban site in Delhi, India. J. Earth Syst. Sci. 2020, 129, 1–15. [Google Scholar] [CrossRef]
- Chen, C.; Sun, Y.; Lan, Q.; Jiang, F. Impacts of industrial agglomeration on pollution and ecological efficiency-A spatial econometric analysis based on a big panel dataset of China’s 259 cities. J. Clean. Prod. 2020, 258, 120721. [Google Scholar] [CrossRef]
- Zhu, X.; Zeng, A.; Zhong, M.; Huang, J.; Qu, H. Multiple impacts of environmental regulation on the steel industry in China: A recursive dynamic steel industry chain CGE analysis. J. Clean. Prod. 2019, 210, 490–504. [Google Scholar] [CrossRef]
- Levinson, A.; Taylor, M.S. Unmasking the Pollution Haven Effect. Int. Econ. Rev. 2010, 49, 223–254. [Google Scholar] [CrossRef] [Green Version]
- Bu, M.; Liu, Z.; Wagner, M.; Yu, X. Corporate social responsibility and the pollution haven hypothesis: Evidence from multinationals’ investment decision in China. Asia-Pac. J. Account. Econ. 2013, 20, 85–99. [Google Scholar] [CrossRef]
- Tao, F.; Zhao, J.; Zhou, H. Does Environmental Regulation Improve the Quantity and Quality of Green Innovation: Evidence from the Target Responsibility System of Environmental Protection. China Ind. Econ. 2021, 2, 136–154. [Google Scholar] [CrossRef]
- Lin, Y.; Zou, J.; Wei, Y.; Li, C.Q. A Review of Recent Advances in Research on PM5 in China. Int. J. Environ. Res. Public Health 2018, 15, 438. [Google Scholar] [CrossRef] [Green Version]
- Ethan, C.J.; Mokoena, K.; Yu, Y.; Shale, K.; Fan, Y.; Rong, J.; Liu, F. Association between PM2.5 and mortality of stomach and colorectal cancer in Xi’an: A time-series study. Environ. Sci. Pollut. Res. 2020, 27, 22353–22363. [Google Scholar] [CrossRef]
- Monks, P.; Granier, C.; Fuzzi, S.; Stohl, A.; Williams, M.; Akimoto, H.; Amann, M.; Baklanov, A.; Baltensperger, U.; Bey, I.; et al. Atmospheric composition change—Global and regional air quality. Atmos. Environ. 2009, 43, 5268–5350. [Google Scholar]
- Liu, X.; Zou, B.; Feng, H.; Liu, N.; Zhang, H. Anthropogenic factors of PM5 distributions in China’s major urban agglomerations: A spatial-temporal analysis. J. Clean Prod. 2020, 264, 1217. [Google Scholar] [CrossRef]
- Askariyeh, M.H.; Venugopal, M.; Khreis, H.; Birt, A.; Zietsman, J. Near-Road Traffic-Related Air Pollution: Resuspended PM2.5 from Highways and Arterials. Int. J. Environ. Res. Public Health 2020, 17, 2851. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Lu, J.; Li, B. Does pollution-intensive industrial agglomeration increase residents’ health expenditure? Sustain. Cities Soc. 2020, 56, 10–20. [Google Scholar] [CrossRef]
- Yun, X.; Shen, G.; Shen, H.; Meng, W.; Chen, Y.; Xu, H.; Ren, Y.; Zhong, Q.; Du, W.; Ma, J.; et al. Residential solid fuel emissions contribute significantly to air pollution and associated health impacts in China. Sci. Adv. 2020, 6, eaba7621. [Google Scholar] [CrossRef]
- Reizer, M.; Juda-Rezler, K. Explaining the high PM10 concentrations observed in Polish urban areas. Air Qual. Atmos. Health 2015, 9, 517–531. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Zhu, Y.; Du, K. The impact of industrial agglomeration on industrial pollutant emission: Evidence from China under New Normal. Clean Technol. Environ. Policy 2017, 19, 2327–2334. [Google Scholar] [CrossRef]
- Kyriakopoulou, E.; Xepapadeas, A. Atmospheric pollution in rapidly growing industrial cities: Spatial policies and land use patterns. J. Econ. Geogr. 2016. [Google Scholar] [CrossRef]
- Czechowski, P.O.; Dąbrowiecki, P.; Oniszczuk-Jastrząbek, A.; Bielawska, M.; Czermański, E.; Owczarek, T.; Rogula-Kopiec, P.; Badyda, A. A Preliminary Attempt at the Identification and Financial Estimation of the Negative Health Effects of Urban and Industrial Air Pollution Based on the Agglomeration of Gdańsk. Sustainability 2019, 12, 42. [Google Scholar] [CrossRef] [Green Version]
- Ciccone, A.; Hall, R.E. Productivity and the Density of Economic Activity. Am. Econ. Rev. 1996, 86, 54–70. [Google Scholar]
- Yu, Y. CHINA_SPATDWM: Stata Module to Provide Spatial Distance Matrices for Chinese Provinces and Cities; Statistical Software Components; CORE: Bucks, UK, 2009. [Google Scholar]
- Wang, S.K. The type and selection of weight matrix in spatial econometric model. J. Econ. Math. 2013, 30, 57–63. [Google Scholar]
- Getis, A. Spatial weights matrices. Geogr. Anal. 2009, 41, 404–410. [Google Scholar] [CrossRef]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234. [Google Scholar] [CrossRef]
- Van Donkelaar, A.; Martin, R.V.; Brauer, M.; Boys, B.L. Use of Satellite Observations for Long-Term Exposure Assessment of Global Concentrations of Fine Particulate Matter. Environ. Health Perspect. 2015, 123, 135–143. [Google Scholar] [CrossRef] [Green Version]
- Liu, N.; Zou, B.; Feng, H.; Wang, W.; Tang, Y.; Liang, Y. Evaluation and comparison of multiangle implementation of the atmospheric correction algorithm, Dark Target, and Deep Blue aerosol products over China. Atmos. Chem. Phys. Discuss. 2019, 19, 8243–8268. [Google Scholar] [CrossRef] [Green Version]
- Krugman, P. Increasing Returns and Economic Geography. J. Political Econ. 1991, 99, 483–499. [Google Scholar] [CrossRef]
- Ellison, G.; Glaeser, E.L. Geographic Concentration in U.S. Manufacturing Industries: A Dartboard Approach. J. Political Econ. 1997, 105, 889–927. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Zheng, H.; Zhe, F.; Xie, W.; Song, J. Study on the relationship between urbanization and fine particulate matter (PM2.5) concentration and its implication in China. J. Clean Prod. 2018, 182, 872–882. [Google Scholar] [CrossRef]
- Shen, H.; Tao, S.; Chen, Y.; Ciais, P.; Güneralp, B.; Ru, M.; Zhong, Q.; Yun, X.; Zhu, X.; Huang, T.; et al. Urbanization-induced population migration has reduced ambient PM2.5 concentrations in China. Sci. Adv. 2017, 3, e1700300. [Google Scholar] [CrossRef] [Green Version]
- Ding, Y.; Zhang, M.; Qian, X.; Li, C.; Chen, S.; Wang, W. Using the geographical detector technique to explore the impact of socioeconomic factors on PM2.5 concentrations in China. J. Clean. Prod. 2019, 211, 1480–1490. [Google Scholar] [CrossRef]
- Ji, S.; Cherry, C.R.; Zhou, W.; Sawhney, R.; Wu, Y.; Cai, S.; Wang, S.; Marshall, J.D. Environmental Justice Aspects of Exposure to PM2.5 Emissions from Electric Vehicle Use in China. Environ. Sci. Technol. 2015, 49, 13912–13920. [Google Scholar] [CrossRef]
- Xie, X.; Wang, Y.; Yang, Y.; Xu, J.; Zhang, Y.; Tang, W.; Guo, T.; Wang, Q.; Shen, H.; Zhang, Y. Long-term exposure to fine particulate matter and tachycardia and heart rate: Results from 10 million reproductive-age adults in China. Environ. Pollut. 2018, 242, 1371–1378. [Google Scholar] [CrossRef]
- Jin, Y.; Zhang, S. An Economic Evaluation of the Health Effects of Reducing Fine Particulate Pollution in Chinese Cities. Asian Dev. Rev. 2018, 35, 58–84. [Google Scholar] [CrossRef]
- Li, G.; Fang, C.; Wang, S.; Sun, S. The Effect of Economic Growth, Urbanization, and Industrialization on Fine Particulate Matter (PM2.5) Concentrations in China. Environ. Sci. Technol. 2016, 50, 11452–11459. [Google Scholar] [CrossRef] [PubMed]
- Grossman, G.M.; Krueger, A.B. Economic Growth and the Environment. Q. J. Econ. 2000, 110, 353–377. [Google Scholar] [CrossRef] [Green Version]
- Selden, T.M.; Song, D. Environmental Quality and Development: Is There a Kuznets Curve for Air Pollution Emissions? J. Environ. Econ. Manag. 1994, 27, 147–162. [Google Scholar] [CrossRef]
- Liu, X. Dynamic evolution, spatial spillover effect of technological innovation and haze pollution in China. Energy Environ. 2018, 29, 968–988. [Google Scholar] [CrossRef]
- Anselin, L.; Smirnov, O. Efficient Algorithhms for Constructing Proper Higher. J. Reg. Sci. 1996, 36, 67. [Google Scholar] [CrossRef]
- Elhorst, J.P. Matlab software for spatial panels. Int. Reg. Sci. Rev. 2014, 37, 389–405. [Google Scholar] [CrossRef] [Green Version]
- Cumming, D.J.; Leboeuf, G.; Schwienbacher, A. Crowdfunding cleantech. Energy Econ. 2017, 65, 292–303. [Google Scholar] [CrossRef]
- Bilgaev, A.; Dong, S.; Li, F.; Hao, C.; Sadykova, E.; Mikheeva, A. Assessment of the Current Eco-Socio-Economic Situation of the Baikal Region (Russia) from the Perspective of the Green Economy Development. Sustainability 2020, 12, 3767. [Google Scholar] [CrossRef]
- Li, X.; Xu, Y.; Yao, X. Effects of industrial agglomeration on haze pollution: A Chinese city-level study. Energy Policy 2021, 148, 111928. [Google Scholar] [CrossRef]
- Yin, X.; Guo, L. Industrial efficiency analysis based on the spatial panel model. EURASIP J. Wirel. Commun. Netw. 2021, 2021. [Google Scholar] [CrossRef]
- Antonioli, D.; Borghesi, S.; Mazzanti, M. Are regional systems greening the economy? Local spillovers, green innovations and firms’ economic performances. Econ. Innov. New Technol. 2016, 25, 692–713. [Google Scholar] [CrossRef]
- Wang, F.; Feng, L.; Li, J.; Wang, L. Environmental Regulation, Tenure Length of Officials, and Green Innovation of Enterprises. Int. J. Environ. Res. Public Health 2020, 17, 2284. [Google Scholar] [CrossRef] [Green Version]
- Chen, D.; Chen, S.; Jin, H. Industrial agglomeration and CO2 emissions: Evidence from 187 Chinese prefecture-level cities over 2005–2013. J. Clean. Prod. 2018, 172, 993–1003. [Google Scholar] [CrossRef]


| Variable | Symbol | Explanation |
|---|---|---|
| Demographic factors | POP | Human activity is the primary source of PM2.5 pollution [45]. Scholars have different views on the relationship between population density and haze pollution. Hui et al. believed that areas with concentrated populations consume less energy due to the presence of centralised heating systems [46]. Meanwhile, Ding et al. argued that the higher the population density of an area, the greater the environmental damage it brings. Therefore, this paper adds the population factor to the model [47]. Referring to Ji et al., Xie et al., and Jin and Zhang, the year-end population of each prefecture-level city is used in this paper. [48,49,50] |
| Economic development | GDP | Economic development is a key factor related to environmental issues [51]. According to the “environmental Kuznets curve (EKC)” hypothesis [52], when the level of economic development is low, the level of environmental pollution is low, but as the per capita income increases, the level of environmental pollution tends to increase, and the level of environmental degradation increases with economic growth [3]; when the economic development reaches a certain level of economic development, that is, after a certain critical point or “inflection point” is reached, with a further increase in per capita income, the level of environmental pollution decreases and the quality of the environment gradually improves, i.e., there is an inverted U-shaped relationship between pollutant emissions and GDP per capita [53]. Referring to Liu et al., this paper uses GDP per capita to measure the level of local economic development [54]. |
| Investment in science and technology | TEC | Research and development in science and technology can help reduce the cost of emissions for enterprises, and government investment in science and technology can help develop technologies to reduce pollution emissions [54]. Considering the composition of local government expenditure in China, this paper uses regional government expenditure on science and technology to measure the level of science and technology investment. |
| Transportation | TRA | Transportation is an intensive economic activity that contributes to PM2.5 pollution [29]. Not only are motor vehicle emissions from road transport a primary source of haze pollution, but the pollutants CO2, SO2, and NO2 are also important secondary sources of PM2.5 pollution. Considering the availability of city-level data, we use road passenger traffic to reflect transport intensity. |
| Variable | Unit | N | Mean | Sd | Min | Max |
|---|---|---|---|---|---|---|
| PM | μg/m3 | 1265 | 36.49 | 16.66 | 2.85 | 86.35 |
| IA | % | 1265 | 0.0039 | 0.0200 | 0.0001 | 0.0269 |
| GDP | RMB10,000/person | 1265 | 51,113 | 33,902 | 10,090 | 470,000 |
| TRA | 10 thousand people | 1260 | 8546 | 14,947 | 93 | 290,000 |
| TEC | RMB | 1265 | 68,730 | 170,000 | 753 | 4,000,000 |
| POP | 10 thousand people | 1265 | 436 | 258 | 20 | 1399 |
| Panel A: ln PM | ||
| Year | Moran’s I | p-value |
| 2012 | 0.174 | 0.000 |
| 2013 | 0.162 | 0.000 |
| 2014 | 0.168 | 0.000 |
| 2015 | 0.232 | 0.000 |
| 2016 | 0.194 | 0.000 |
| Panel B: ln IA | ||
| Year | Moran’s I | p-value |
| 2012 | 0.126 | 0.000 |
| 2013 | 0.128 | 0.000 |
| 2014 | 0.113 | 0.000 |
| 2015 | 0.135 | 0.000 |
| 2016 | 0.142 | 0.000 |
| Hypothesis | LR | Durbin–Wu–Hausman |
|---|---|---|
| Hypothesis: Time fixed effect nested in two-way fixed effect | 3448.00 *** | 103.67 *** |
| Hypothesis: Individual fixed effect nested in two-way fixed effect | 43.33 *** |
| Hypothesis | LM | Robust-LM | Hypothesis | LR |
|---|---|---|---|---|
| Null hypothesis: SEM is not better than OLS model | 2406.781 *** | 2396.70 *** | Null hypothesis: SDM can be simplified to SEM | 13.92 ** |
| Alternative hypothesis: SEM is better than OLS model | Alternative hypothesis: SDM cannot be simplified to SEM | |||
| Null hypothesis: SLM is not better than OLS model | 12.667 *** | 2.587 | Null hypothesis: SDM can be simplified to SLM | 26.81 *** |
| Alternative hypothesis: SLM is better than OLS model | Alternative hypothesis: SDM cannot be simplified to SLM |
| Variable | (1) | (2) | (3) | (4) | (5) |
|---|---|---|---|---|---|
| IA | −0.1669 *** (−10.46) | −0.1386 *** (−7.51) | −0.1403 *** (−7.53) | −0. 1198 *** (−6.12) | −0.1124 *** (−5.67) |
| W*IA | 0.3701 *** (3.74) | 0.4452 *** (3.34) | 0.4559 *** (3.37) | 0. 4754 *** (3.49) | 0. 4381 *** (3.17) |
| GDP | −0.0887 *** (−3.02) | −0.0817 *** (−2.72) | −0. 0693 ** (−2.30) | −0.0770 ** (−2.55) | |
| W*GDP | 0.0362 (0.69) | 0.1946 * (1.67) | 0.2921 * (1.91) | 0.3412 ** (2.21) | |
| TRA | −0.0053 (−0.70) | −0.0064 (−0.86) | −0.0065 (−0.86) | ||
| W*TRA | 0.0509 * (1.71) | 0. 0583 * (1.95) | 0. 0521 * (1.72) | ||
| TEC | −0.0308 *** (−3.26) | −0.0294 *** (−3.12) | |||
| W*TEC | −0.0387 (−0.60) | −0. 0149 (−0.22) | |||
| POP | −0.2049 ** (−2.39) | ||||
| W*POP | −1.0508 (−1.31) | ||||
| R2 | 0.1679 | 0.2245 | 0.2451 | 0.2560 | 0.2768 |
| Spat-rho | 0.8125 *** (16.77) | 0.7866 *** (14.18) | 0.7613 *** (12.64) | 0. 7614 *** (12.61) | 0.7475 *** (12.03) |
| Log-L | 1094.5435 | 1099.7333 | 1101.2793 | 1106.7502 | 1110.3296 |
| Direct Effect | Coefficient | Z-Value | p-Value | Indirect Effect | Coefficient | Z-Value | p-Value |
|---|---|---|---|---|---|---|---|
| IA | −0.105 | −5.10 | 0.000 | IA | 1.400 | 3.06 | 0.002 |
| GDP | −0.073 | −2.42 | 0.016 | GDP | 1.165 | 1.49 | 0.137 |
| TRA | −0.004 | −0.66 | 0.507 | TRA | 0.186 | 1.34 | 0.181 |
| TEC | −0.030 | −3.13 | 0.002 | TEC | −0.158 | −0.50 | 0.614 |
| POP | −0.227 | −2.67 | 0.007 | POP | −4.966 | −1.37 | 0.172 |
| Direct Effect | Coefficient | Z-Value | p-Value | Indirect Effect | Coefficient | Z-Value | p-Value |
|---|---|---|---|---|---|---|---|
| IA | −0.099 | −4.50 | 0.000 | IA | 0.213 | 2.42 | 0.015 |
| GDP | −0.063 | −2.06 | 0.040 | GDP | −0.109 | −0.84 | 0.399 |
| TRA | −0.009 | −1.20 | 0.229 | TRA | −0.017 | −0.60 | 0.548 |
| TEC | −0.022 | −2.07 | 0.039 | TEC | 0.059 | 1.21 | 0.227 |
| POP | −0.196 | −2.12 | 0.034 | POP | −0.611 | −1.05 | 0.296 |
| Direct Effect | Coefficient | Z-Value | p-Value | Indirect Effect | Coefficient | Z-Value | p-Value |
|---|---|---|---|---|---|---|---|
| IA | −0.095 | −4.31 | 0.000 | IA | 0.186 | 1.86 | 0.063 |
| GDP | −0.066 | −2.16 | 0.031 | GDP | −0.033 | −0.24 | 0.811 |
| TRA | −0.006 | −0.92 | 0.358 | TRA | −0.014 | −0.50 | 0.616 |
| TEC | −0.023 | −2.21 | 0.027 | TEC | 0.024 | 0.50 | 0.618 |
| POP | −0.188 | −2.04 | 0.041 | POP | −0.204 | −0.30 | 0.763 |
| Variable | 2SLS | GS2SLS | |||
|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | |
| Stage I | Stage II | Results | Direct Effect | Indirect Effect | |
| RDLS | −0.1903 *** (−11.53) | ||||
| IA | −2.0973 *** (−12.23) | −2.1510 *** (−5.01) | −2.0071 *** (−4.42) | 2.7075 *** (3.50) | |
| GDP | 1.2089 *** (34.70) | −2.5677 *** (−11.22) | −2.6906 *** (−4.52) | −2.5340 *** (−4.18) | 2.9479 *** (3.08) |
| TRA | 0.0682 *** (4.44) | −0.1319 *** (−4.09) | 0.0121 (0.14) | 0.0266 (0.33) | 0.2736 (0.68) |
| TEC | 0.0857 *** (4.84) | −0.1580 *** (−4.20) | −0.2570 *** (−3.04) | −0.2242 ** (−2.49) | 0.6174 * (1.96) |
| POP | 0.8425 *** (30.44) | −1.5616 *** (−9.35) | −1.6410 *** (−3.80) | −1.5681 *** (−3.69) | 1.3715 ** (2.32) |
| Constant | −23.88 *** (−64.51) | 52.64 *** (12.08) | 29.85 (1.16) | ||
| R2 | 0.8337 | 0.2110 | |||
| F | 1262.73 | ||||
| Minimum eigenvalue | 132.866 | 10%, 16.38 | |||
| N | 1265 | 1265 | 1265 | 1265 | 1265 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, P.; Lin, Y. Should There Be Industrial Agglomeration in Sustainable Cities?: A Perspective Based on Haze Pollution. Sustainability 2021, 13, 6609. https://doi.org/10.3390/su13126609
Dai P, Lin Y. Should There Be Industrial Agglomeration in Sustainable Cities?: A Perspective Based on Haze Pollution. Sustainability. 2021; 13(12):6609. https://doi.org/10.3390/su13126609
Chicago/Turabian StyleDai, Pingping, and Yuanyuan Lin. 2021. "Should There Be Industrial Agglomeration in Sustainable Cities?: A Perspective Based on Haze Pollution" Sustainability 13, no. 12: 6609. https://doi.org/10.3390/su13126609
APA StyleDai, P., & Lin, Y. (2021). Should There Be Industrial Agglomeration in Sustainable Cities?: A Perspective Based on Haze Pollution. Sustainability, 13(12), 6609. https://doi.org/10.3390/su13126609






