Establishing Surrogate Model to Predict the Optimal Thermodynamic and Economic Performance of a Packed Bed Humidifier via Multi-Objective Optimization

Abstract

In this paper, to optimize the thermodynamic and economic performance of a packed bed humidifier, a multi-objective optimization combined response surface method with a genetic algorithm is employed. The critical parameters, including geometric and thermodynamic parameters, are designated as the impact factors, and the objective functions contain unit humidification capacity of volume and unit humidification capacity of cost in a Box–Behnken design. The results of the analysis of variance demonstrated that the quadratic regression models of objectives are reliable and robust. It is found that the liquid–gas ratio, the interaction of the liquid–gas ratio, and inlet water temperature are simultaneously the strongest influence factors for the thermodynamic and economic indicators among the independent and interactive parameters. In addition, the optimal parameter group is found out through a genetic algorithm, and the actual optimal results are obtained as 0.11 kgs⁻¹m⁻³ for thermodynamic performance and 15.86 kg$⁻¹ for economic performance. Furthermore, it is shown that the thermodynamic performance improves by 56% and the economic performance increases by 6.55%, compared with optimum experimental design points. During the optimization design process, the computational time to find the optimal values reduces from 69,000 s with previous mathematical models to 10 s with established regression models. Additionally, a series of Pareto-optimal points for possible best thermodynamic and economic performance give the reference for the designers of packed bed humidifiers.

1. Introduction

Facing the rapid growth of the global economy and the improvement of the people’s living standards, the demand for water and energy is becoming more and more intense, which promotes the agenda of energy structure optimization tending to be more cost-effective and energy-efficient. In addition to chemical engineering and office buildings, humidifiers are also widely used in people’s daily lives for regulating air humidity. Among them, the packed bed humidifier has tremendous applications thanks to its high energy effectiveness and large contact area [1]. Packings such as wooden slates [2], corrugated aluminum sheets [3], polypropylene [4], and ceramic foam [5] have shown great humidification performance. Designers expect to achieve maximum humidification effectiveness with minimum costs. However, the relationship between humidification capacity and the input cost of the humidifier is proverbially a positive correlation in the physical process. Therefore, it is significant to optimize the overall performance of a packed bed humidifier referred to thermodynamics and economics.

In recent years, many optimization methods were developed and generally can be divided into parameter analysis and mathematical algorithm [6]. The parameters affecting the thermodynamic performance of the packed bed humidifier were highlighted in detail by Xu [5], and many remarkable results were found according to the univariate optimization. It was shown that the independent influences of the liquid–gas ratio, operating pressure, inlet water temperature, and inlet air enthalpy on the thermodynamic performance are important. In addition to the above parameters, the effects of inlet air temperature, inlet relative humidity, inlet wet bulb temperature of the humid air, and the specific surface area of the packing were investigated through theory and experiment at on-design and off-design conditions [7,8]. The main influencing factors, including the liquid–gas ratio, the inlet air temperature, the inlet water temperature, and the specific surface area of the packing, were revealed. It can be summarized that the influencing parameters mainly contain thermodynamic parameters and geometric parameters, while the researches on geometric parameters commonly refer to the packing. It was demonstrated that the size and material of the packing have a significant influence on the thermodynamic and economic performance of the packed bed humidifier [9,10]. For instance, packings such as corrugated aluminum sheets with length × width × height of 650 × 650 × 650 mm³ [3] and corrugated wire mesh with 0.15 m high, 0.39 m diameter [8] showed gratifying thermodynamic and economic performance. The maximum humidification capacity could be reached 15 kg/h utilizing corrugated aluminum sheets, and the maximum values of unit humidification capacity of volume and unit humidification capacity of cost with corrugated wire mesh presented as 3.82 × 10^–2 kgs⁻¹m⁻³ and 12.74 kg$⁻¹, respectively. Moreover, it should be found that the degree of univariate optimization is limited for simultaneously improving the thermodynamic and economic performance of the humidifier, subject to the finite-size and finite-time process.

Furthermore, in order to reduce the residual irreversibilities of the humidification process, which is subject to the second law, the entropy generation minimization method was employed for thermodynamic optimization [11,12]. Thermodynamic optimization means employing some measures to change the flow distribution in the humidification process to make the distributions of the driving forces of the heat and mass transfer process more uniform, such that the energy effectiveness can be improved. For this idea, the water extraction/injection and air extraction/injection between dehumidifier and humidifier in the humidification–dehumidification desalination system were implemented to improve the system performance [13,14]. It was proved that the extraction direction from the dehumidifier to the humidifier was the preferred measure for both the water stream and the air stream. For water extraction/injection, the gained output ratio of single extraction was approximately four times that of zero extraction [13]. For air extraction/injection, the gained output ratio was elevated by 91% and 112% with single and double extraction systems, respectively, compared with that of the base system [14]. Originally, Chen [15,16] successively studied the influences of extraction/injection from both the water side and air side on the thermodynamic performance of the packed bed humidifier. It was found that single water injection and air extraction for the single humidifier are more desirable measures compared with zero and single water extraction and air injection. The energy effectiveness of the packed bed humidifier increased, respectively, by 19.74% with single water injection and 26.32% with air extraction than that of zero measure. Furthermore, it was shown that the liquid–gas ratio and inlet relative humidity of humid air are the main single factors affecting thermodynamic optimization.

For a different parameter analysis (generally for single-objective optimization), mathematical algorithms come in handy when optimization involves multi-objective optimization. Many popular methods, such as the response surface method (RSM) [9], genetic algorithm (GA) [17], particle swarm algorithm [18], etc., can be used to analyze and solve the complex physical problems with multiple objectives that need to be optimized, affected by multiple factors. Among them, RSM is a well-developed experimental design method, and GA is a computational method to search for the optimal solution by following the natural evolution process based on the genetic mechanism of Darwin’s bio evolution theory. Moreover, it is verified that GA is a more complete and sounder model than particle swarm algorithm. A more accurate correlation for the temperature prediction of solar panels was established based on GA, while the independent factors and interaction factors between solar radiation, ambient temperature, wind velocity, and ambient relative humidity were considered [17]. It was found that the prediction accuracy of the solar panel temperature was improved by approximately 2–4 times. For further improvement, combination optimizations between RSM and GA [19] and RSM and the particle swarm algorithm [20] were developed to improve the experimental design. It was demonstrated that most performance parameters after multi-objective optimization were better than those without optimization. The effects of pitch, diameter, pipe length, and inlet velocity on the separation efficiency and pressure drop were investigated based on the RSM and GA [21]. The optimization results showed that the optimization degree of the separation efficiency had a certain limitation at the optimal points, while the pressure drop can be reduced by approximately 50%. Recently, Shahverdian [22] proposed a dynamic multi-objective optimization method in order to improve the power output and simultaneously reduce the cooling water consumption of a photovoltaic module. It was found that the temperature difference between the average and maximum value in a year evaluated by the novel method decreased, respectively, by 79.79% and 54.53%, compared with no-cooling and a constant water flow of 0.1 LPM. These achievements obtained by multi-objective optimization provide a robust foundation for optimizing the overall performance of the packed bed humidifier.

From the literature survey, it was found that the improvement of thermodynamic performance of the packed bed humidifier is generally at the expense of input cost, while the performance optimization is subject to the univariate optimization (single-objective optimization). In addition, the overall optimization of thermodynamic and economic performance for the packed bed humidifier is missing. Moreover, a previous physical model can become too complicated and time-consuming in the optimization process. To simplify the optimization process, save time cost, and improve overall performance simultaneously, in this study, the combination optimization of RSM and GA is employed to assess and optimize the thermodynamic and economic performance of a packed bed humidifier filled with corrugated wire mesh. Surrogate models for quickly searching the optimal thermodynamic and economic performances are established. Furthermore, the influences of independent and interactive factors on designated objective functions are addressed, and an explicit influence degree of the important parameters is given based on the analysis of variance. Finally, a series of Pareto-optimal points for possible optimal thermodynamic and economic performance is given with optimal parameter combination, which can provide significant references for the designer of packed bed humidifiers.

2. Materials and Methods

2.1. Mechanism Description

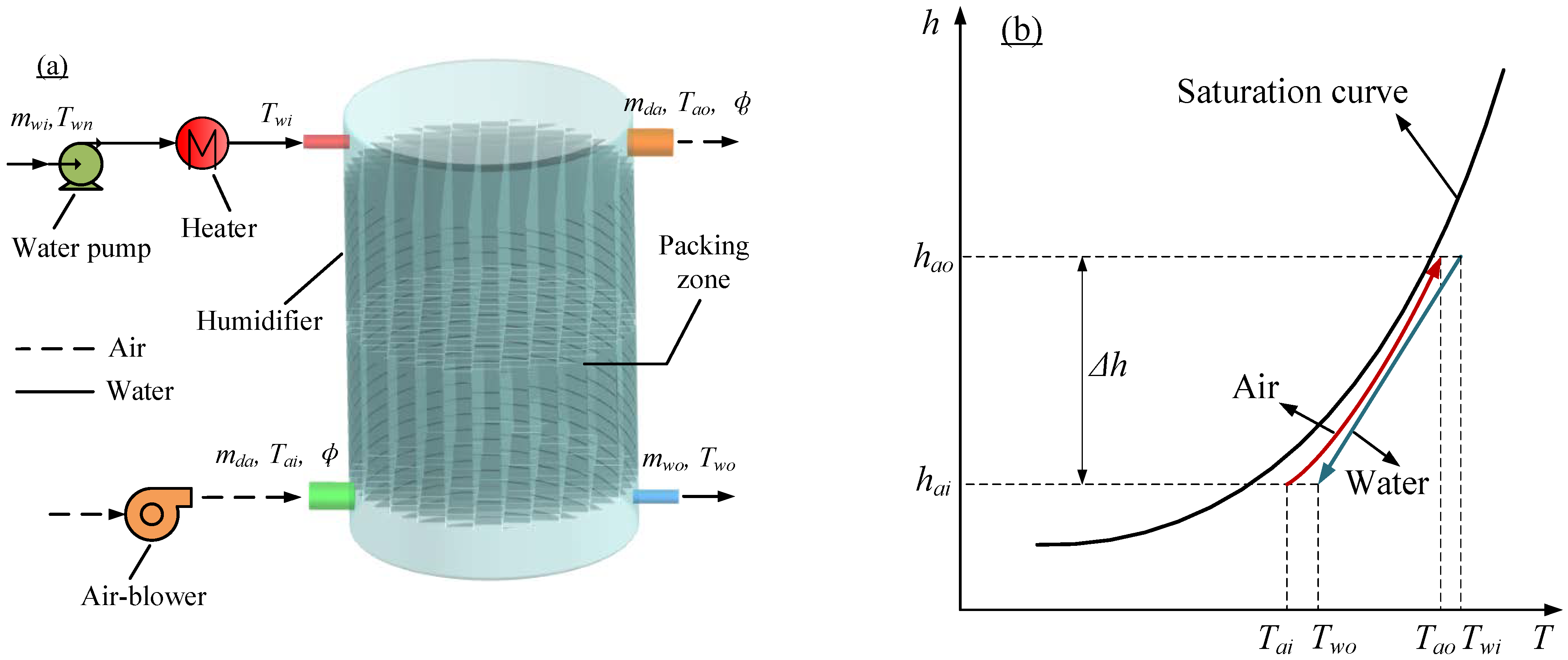
The humidification process is restricted by the thermodynamic state of the humid air. Its humidification ability will be lost once the humid air reaches saturation. In this case, in order for the physical process to continue, the temperature of the humid air should be raised to bring it back to the unsaturated state. The schematic diagram of the humidification process is shown in Figure 1. The packed bed humidifier is mainly composed of cylindrical shell and packing, and the packing can provide a relatively large direct contact area for the heat and mass transfer process. In this study, a counter-flow humidification process with corrugated wire mesh packing, Mellapak 700 Y, is selected as the optimization object. Commonly, hot water is sprayed directly into the packing layer to form a uniform liquid film on the packing surface under the action of gravity, while the relatively cold humid air enters from the bottom of the humidifier. Owing to the direct contact of two-phase fluid, the thermodynamic process of simultaneous heat and mass exchange is intense and intricate in the packing zone. In addition to the temperature difference, the water molecules in the water stream driven by the pressure difference are constantly captured by the humid air, such that the enthalpy of the humid air and water shift along the process curve, as shown in Figure 1b. Finally, the humid air stream with high temperature and humidity is discharged from the top of the humidifier, while the water stream with low temperature is exhausted from the bottom.

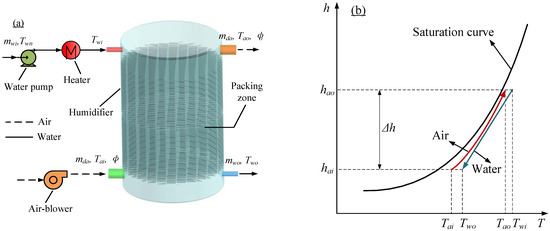
Figure 1. Schematic diagram of packed bed humidification system. (a) physical model; (b) psychrometric chart of humid air.

2.2. Governing Equations

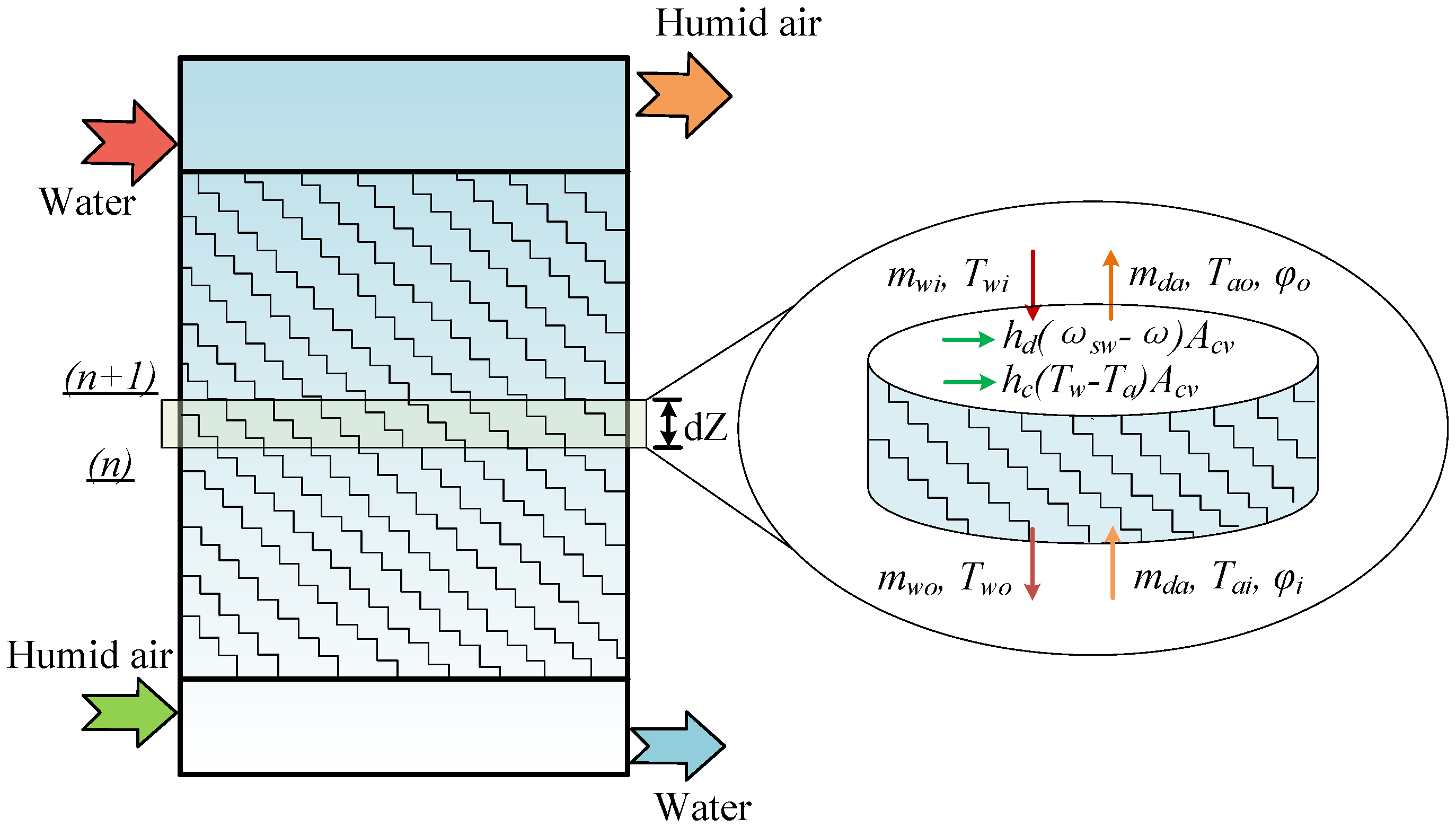
In order to accurately calculate the thermodynamic characteristics of the heat and mass transfer process in the packing zone, the finite difference method [23] is applied from the perspective of the control volume, as shown in Figure 2. By evenly dividing the whole packing zone into abundant control volumes, the differential governing equations can be first established based on the typical control volume, and then the whole heat and mass transfer process is solved by an iterative solver.

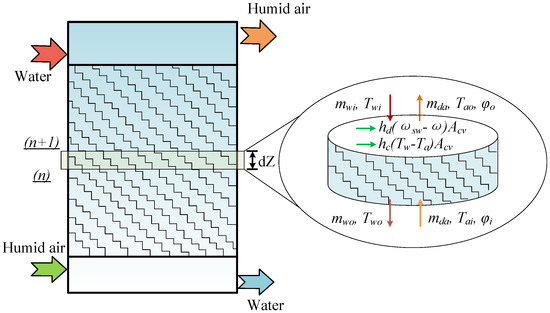
Figure 2. Analysis of humidification process by finite difference method.

Many calculation models were proposed for solving the thermodynamic process of heat and mass transfer, based on the finite difference method, while it was verified that the Poppe model is preferred at counter-flow conditions [24]. In terms of the Poppe assumptions, the following mathematical models can be derived in detail. It is assumed that (1) the humidification process is in a steady-state; (2) the energy loss to the environment, kinetic, and potential energy items are neglected; (3) the distribution of two-phase fluids in the packing zone is even; and (4) flow resistances in pipes, water pump, and air-blower are ignored. For the whole control volume, the mass balance equation for these two streams can be written as:

$$\frac{d{m}_w}{dZ}=m_{da}\frac{d\omega }{dZ}$$

(1)

where Z is the total packing height, ω is the absolute humidity of humid air, and the energy balance equation between water stream and the air stream is obtained as:

$$h_{w}d{m}_w+m_{w}d{h}_w=m_{da}d{h}_a$$

(2)

The enthalpy, h, of humid air consists of the enthalpy of dry air (subscript da), and water vapor (subscript w). Its expression for unsaturated and saturated cases is written as:

$$h_a=c_{pa}{T}_a+\omega \left(h_{fg}+c_{pv}{T}_a\right)$$

(3)

Further, the specific heat capacity, c_pa, of each node of the water is set to a constant value with the above assumptions. Therefore, the following equation can be written at constant pressure:

$$d{h}_w=c_{pw}d{T}_w$$

(4)

Substituting Equation (4) into Equation (2) and divide by control volume height, dZ, on both sides, and Equation (5) can be found upon rearrangement:

$$h_w\frac{d{m}_w}{dZ}+m_w{c}_{pw}\frac{d{T}_w}{dZ}=m_{da}\frac{d{h}_a}{dZ}$$

(5)

At the gas–liquid interface, where the simultaneous heat and mass exchange occurs, the mass balance equation of the air side can be given by:

$$d{m}_w=h_d\left({\omega }_{sw}-\omega \right)dA$$

(6)

Considering the heat loss on the water side due to evaporation in the energy balance equation, the energy balance equation to calculate the sensible heat and latent heat captured by the humid air stream from the water side is expressed as:

$$m_{da}d{h}_a=\left[h_v{h}_d\left({\omega }_{sw}-\omega \right)+h_c\left(T_w-T\right)\right]dA$$

(7)

where subscript s means saturation state, h_d is the mass transfer coefficient. Its empirical correlation for gas absorption system is employed in this work, which can be referred to [25] as follows:

$$h_d={\rho }_{v}f{\mathrm{Re}}_a^{0.7}S{c}_a^{\frac{1}{3}}{\left(a{d}_p\right)}^{-2}a{D}_a$$

(8)

where

$${\mathrm{Re}}_a=\frac{m_{da}\left(1+\omega \right)}{A_{Z}a{\mu }_a}$$

(9)

$$S{c}_a=\frac{{\mu }_a}{{\rho }_a{D}_a}$$

(10)

$$D_a=1.87\times {10}^{-10}\frac{T_a{}^{2.072}}{p/p_0}$$

(11)

where f is the corresponding geometric coefficient, 5.23 for d_p > 0.015 m and 2 for d_p < 0.015 m, and D_a is the diffusion coefficient from the water to the air.

In order to calculate the heat transfer coefficient, h_c, Lewis factor, which represents the indication of the relative rates of heat transfer and mass transfer, is utilized according to the finite difference method. Its definition, Le_f = h_c/c_pah_d, can be referred to Klimanek [26], and the empirical correlation [27] used in this study is shown as:

$$L{e}_f={0.865}^{0.667}\frac{\frac{{\omega }_{sw}+0.622}{\omega +0.622}-1}{\ln \left(\frac{{\omega }_{sw}+0.622}{\omega +0.622}\right)}$$

(12)

where ω_sw is the saturated humidity ratio calculated at the local water temperature, and the contact area of the control volume, dA, can be calculated by:

$$dA=a{A}_{Z}dZ$$

(13)

Then, the following differential equations for unsaturated and saturated cases are found upon rearrangement:

$$\frac{d{h}_a}{dZ}=\frac{h_{d}a{A}_Z}{m_{da}}\left[L{e}_f\left(h_{asw}-h_a\right)+\left(1-L{e}_f\right)h_v\left({\omega }_{sw}-\omega \right)\right]$$

(14)

$$\frac{d\omega }{dZ}=\frac{h_{d}a{A}_Z}{m_{da}}\left({\omega }_{sw}-\omega \right)$$

(15)

$$\frac{d{T}_w}{dZ}=\frac{1}{m_r}\left(\frac{1}{c_{pw}}\frac{d{h}_a}{dZ}-T_w\frac{d\omega }{dZ}\right)$$

(16)

where m_r is the liquid–gas ratio, m_w/m_da kg dry air.

During the humidification process, it is highlighted that excess water vapor will be carried by the humid air, which will be referred to as the supersaturated cases. Considering the all-state thermodynamic of humid air, the governing equations at supersaturated conditions should also be built. In addition to the enthalpy of dry air and basic water vapor, the enthalpy of supersaturated air, h_ss, should include the enthalpy of excess water vapor, expressed by:

$$h_{ss}=c_{pa}{T}_a+{\omega }_{sa}\left(h_{fg}+c_{pv}{T}_a\right)+\left(\omega -{\omega }_{sa}\right)c_{pw}{T}_a$$

(17)

Additionally, the relevant differential equations established for the supersaturated air should also be accordingly replaced by:

$$\frac{d{h}_a}{dZ}=\frac{h_{d}a{A}_Z}{m_{da}}\left\{L{e}_f\left[h_{asw}-h_{ss}+c_{pw}{T}_w\left(\omega -{\omega }_{sa}\right)-h_v\left({\omega }_{sw}-{\omega }_{sa}\right)\right]+h_v\left({\omega }_{sw}-{\omega }_{sa}\right)\right\}$$

(18)

$$\frac{d\omega }{dZ}=\frac{h_{d}a{A}_Z}{m_{da}}\left({\omega }_{sw}-{\omega }_{sa}\right)$$

(19)

$$\frac{d{T}_w}{dZ}=\frac{1}{m_r}\left(\frac{1}{c_{pw}}\frac{d{h}_a}{dZ}-T_w\frac{d\omega }{dZ}\right)$$

(20)

$$L{e}_f={0.865}^{0.667}\frac{\frac{{\omega }_{sw}+0.622}{{\omega }_{sa}+0.622}-1}{\ln \left(\frac{{\omega }_{sw}+0.622}{{\omega }_{sa}+0.622}\right)}$$

(21)

2.3. Objective Functions

2.3.1. Unit Humidification Capacity of Volume

In order to characterize the thermodynamic performance of the packed bed humidifier, considering the effect of packing size, a novel thermodynamic evaluation criterion, unit humidification capacity of volume (UHCV), is established based on humid air in our previous work [8]:

$$UHCV=\frac{m_{da}\left({\omega }_o-{\omega }_i\right)}{V_p}$$

(22)

where V_p is the required packing volume, calculated by:

$$V_p=A_Z{Z}_p$$

(23)

2.3.2. Unit Humidification Capacity of Cost

Here, once referred to the economic performance, the input cost should contain the investment cost and operation cost. The investment cost mainly includes the cost of air-blower, water pump, and packing, while the operation cost means the power consumption of electrical components. For this case, a novel economic criterion, unit humidification capacity of cost (UHCC), is defined [8] as follow:

$$\mathrm{UHCC}=\frac{3600m_{da}\left({\omega }_o-{\omega }_i\right)t}{C_b+C_{wp}+C_p+C_e}$$

(24)

where C_b and C_wp are the cost of air-blower and water pump, depending on the required power, and the packing cost, C_p, is associated with the price of packing 316 L. The cost of each component can be referred to the price shown in Table 1; where C_e is the operation cost, calculated according to the running time of 10 years with 7200 h per year, and the electrovalence of P_e = 0.085$ kW⁻¹h⁻¹:

$$C_e=t\left(N_e+N_b+N_{wp}\right)P_e$$

(25)

Table 1. Price of each component.

Components	Air-Blower	Water Pump		Packing
Specifications	Nb = 0.25 kW	Nwp = 0.18 kW	Nwp = 0.75 kW	a = 250 m2m−3	a = 475 m2m−3	a = 700 m2m−3
Prices	84.64$	23.08$	76.94$	900$ m−3	1200$ m−3	1615.38$ m−3

The detailed calculation formulas of N_e, N_b, and N_wp can be referred to in [5].

2.4. Multi-Objective Optimization Design

In this study, multi-objective optimization is employed to obtain the potential optimal thermodynamic and economic performance of the packed bed humidifier in a combination of a response surface method and genetic algorithm. In this process, the important parameters affecting the given objectives should be specified and combined based on the RSM first. The experimental design method selected currently is the Box–Behnken design (BBD) method, thanks to its efficient and convenient design scheme. As shown in Table 2, thermodynamic parameters (liquid–gas ratio, inlet air temperature, inlet relative humidity, and inlet water temperature) and geometric parameter (specific surface area of the packing) are chosen as the factor items, and the response items contain the unit humidification capacity of volume and the unit humidification capacity of cost.

Table 2. Design of factors and responses.

Items	Parameters (unit)	Codes	Low	High
Factors	Liquid–gas ratio, mr (-)	A	1	5
	Inlet air temperature, Tai (°C)	B	10	30
	Inlet relative humidity, φi (-)	C	0.6	1
	Inlet water temperature, Tai (°C)	D	70	90
	Specific surface area, a (m2m−3)	E	250	700
Responses	Unit humidification capacity of volume, UHCV (kgs−1m−3)
	Unit humidification capacity of cost, UHCC (kg$−1)

Based on the established regression models of responses, multi-objective optimization can be accomplished through the GA program, following the natural evolution process. In the genetic mechanism, genes are derived from the range of the factors in Table 2, and response UCHV, as well as UHCC, are simultaneously expected to be maximum objectives.

3. Results

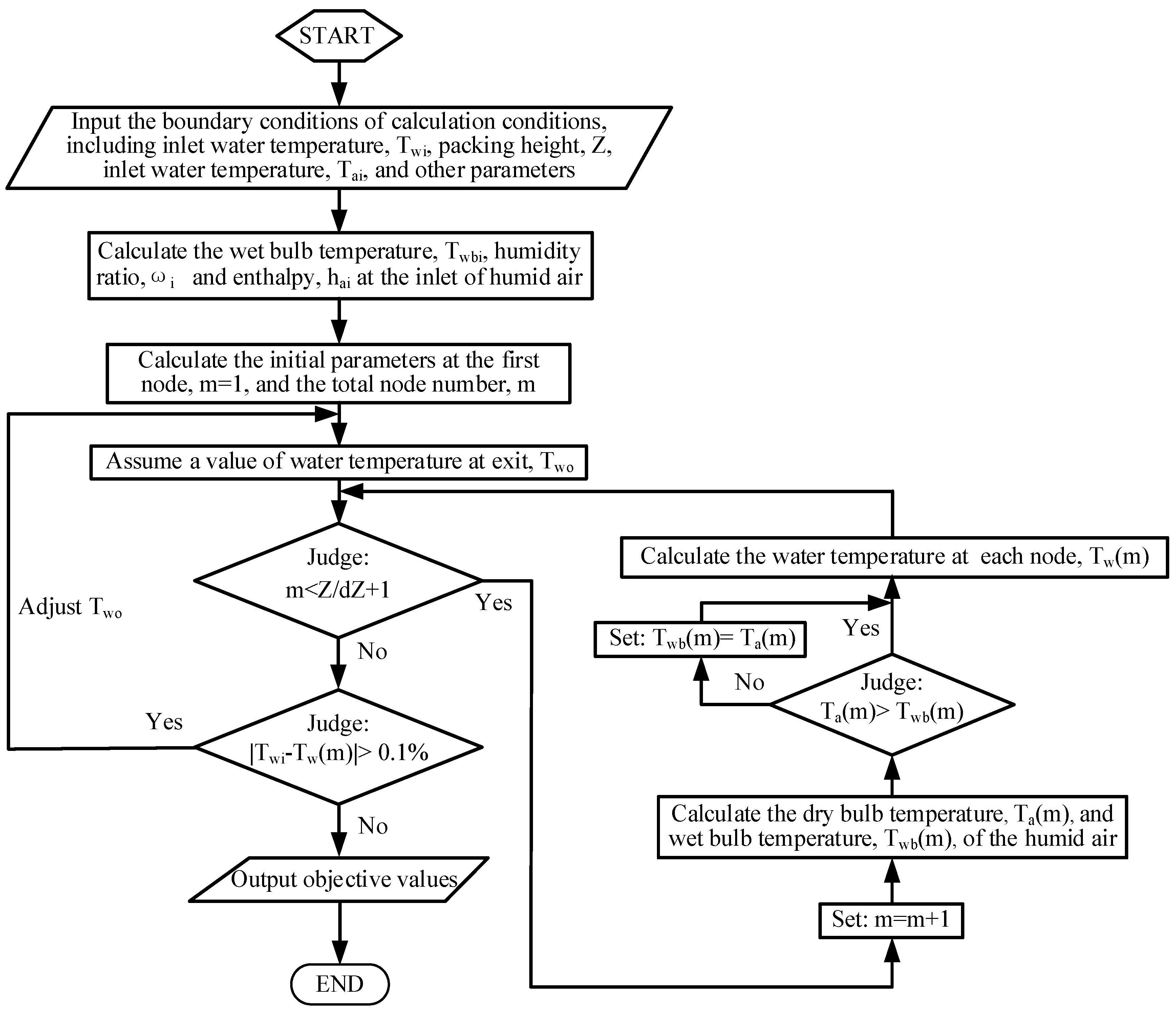
According to the differential governing Equations (12)–(14) and (18)–(20) which were verified to be robust and reliable for the packed bed humidifier based on the experimental results [8], an integrated solver can be coded in the MATLAB software, as shown in Figure 3. The typical conditions of the humidification process are presented in Table 3. For the experimental design, the first step of response surface analysis is to combine design variables reasonably and generate parameter groups. The design results are used to fit the regression equations of the objective functions. After the experimental design, the analysis of variance (ANOVA) is carried out to assess the influence degree of the important factors and their interaction on the responses. Then, the genetic optimization process can be promoted to search for the optimal parameter combination and thermodynamic and economic performance of the packing bed humidifier, according to the fitting regression equations.

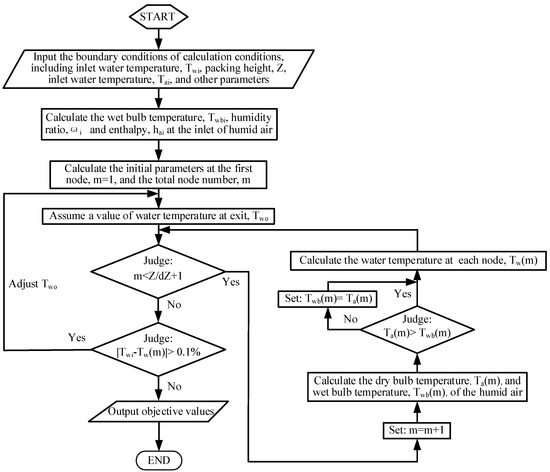
Figure 3. Calculating procedure of humidification process.

Table 3. Typical parameters of packing bed humidifier.

mda(kgs−1)	mr(-)	Twi(°C)	Tai(°C)	φi	P0(kPa)	a(m2m−3)	AZ(m2)	Z(m)
0.016	3	80	20	0.8	101.325	500	0.12	0.45

3.1. Regression Models of Objective Functions

Based on the BBD method, 46 groups of experimental designs are first combined, and then the relevant design results are obtained by the established mathematical models, as exhibited in Table 4. It is found that the maximum UHCV appears as 0.11 kgs⁻¹m⁻³ at group 26, while the value of UHCC is 11.15 kg$⁻¹ in this case. Moreover, the maximum value of UHCC presents as 15.51 kg$⁻¹ at group 22, and the value of UHCV concurrently shows as 0.025 kgs⁻¹m⁻³.

Table 4. Design of factors and responses.

Groups	A(mr)	B(Tai)	C(φi)	D(Twi)	E(a)	UHCV (kgs−1m−3)	UHCC (kg$−1)
1	5	20	0.6	80	475	0.081	10.16
2	1	30	0.8	80	475	0.023	14.18
3	3	10	1	80	475	0.057	11.91
4	3	20	1	90	475	0.073	12.60
5	1	20	0.8	70	475	0.019	14.87
6	5	30	0.8	80	475	0.08	9.93
7	3	20	0.6	90	475	0.073	12.72
8	3	30	0.6	80	475	0.057	11.91
9	3	20	0.8	90	250	0.070	12.19
10	3	20	0.8	90	700	0.076	13.081
11	5	20	0.8	80	250	0.077	9.64
12	3	20	1	80	250	0.055	11.36
13	3	20	1	70	475	0.042	10.91
14	3	10	0.8	90	475	0.073	12.63
15	3	20	0.8	70	700	0.045	11.57
16	3	20	1	80	700	0.059	12.34
17	1	20	1	80	475	0.024	14.84
18	3	30	0.8	80	700	0.058	12.081
19	3	30	0.8	80	250	0.054	11.25
20	1	20	0.8	80	250	0.023	14.55
21	3	30	0.8	70	475	0.041	10.68
22	1	20	0.8	80	700	0.025	15.52
23	3	20	0.8	80	475	0.057	11.92
24	3	20	0.8	80	475	0.057	11.92
25	3	20	0.6	70	475	0.043	11.079
26	5	20	0.8	90	475	0.11	11.15
27	3	20	0.8	80	475	0.057	11.92
28	3	10	0.8	80	700	0.060	12.53
29	3	10	0.8	80	250	0.054	11.27
30	3	20	0.8	80	475	0.057	11.92
31	1	20	0.8	90	475	0.03	15.24
32	5	20	1	80	475	0.081	10.081
33	5	10	0.8	80	475	0.081	10.15
34	3	10	0.6	80	475	0.057	11.90
35	3	20	0.8	70	250	0.04	10.37
36	1	20	0.6	80	475	0.025	15.28
37	5	20	0.8	70	475	0.057	8.80
38	3	10	0.8	70	475	0.043	11.012
39	3	20	0.8	80	475	0.057	11.92
40	3	30	1	80	475	0.055	11.48
41	3	30	0.8	90	475	0.072	12.45
42	5	20	0.8	80	700	0.085	10.56
43	3	20	0.8	80	475	0.057	11.92
44	3	20	0.6	80	700	0.060	12.53
45	3	20	0.6	80	250	0.055	11.44
46	1	10	0.8	80	475	0.024	15.029

According to the numerical results of the experimental design via the BBD method, the quadratic regression models of UHCV and UHCC are fitted as follows:

$$\begin{array}{cc}\hfill \mathrm{UHCV}& =9.16634\ast {10}^{-3}-0.020165\ast \mathrm{A}+4.97222\ast {10}^{-4}\ast \mathrm{B}+4.98958\ast {10}^{-3}\ast \mathrm{C}-4.09375\ast {10}^{-4}\ast \mathrm{D}\hfill \\ & +1.65401\ast {10}^{-5}\ast \mathrm{E}-1.125\ast {10}^{-5}\ast \mathrm{A}\ast \mathrm{B}+1.25\ast {10}^{-4}\ast \mathrm{A}\ast \mathrm{C}+5.025\ast {10}^{-4}\ast \mathrm{A}\ast \mathrm{D}\hfill \\ & +3.11111\ast {10}^{-6}\ast \mathrm{A}\ast \mathrm{E}-2.5\ast {10}^{-4}\ast \mathrm{B}\ast \mathrm{C}+7.5\ast {10}^{-7}\ast \mathrm{B}\ast \mathrm{D}-2.22222{10}^{-7}\ast \mathrm{B}\ast \mathrm{E}\hfill \\ & -4.26841{10}^{-18}\ast \mathrm{C}\ast \mathrm{D}-2.5\ast {10}^{-5}\ast \mathrm{C}\ast \mathrm{E}+6.66667\ast {10}^{-8}\ast \mathrm{D}\ast \mathrm{E}-1.19427\ast {10}^{-3}\ast {\mathrm{A}}^2\hfill \\ & -6.85417\ast {10}^{-6}\ast {\mathrm{B}}^2+6.82292\ast {10}^{-3}\ast {\mathrm{C}}^2+2.39583\ast {10}^{-6}\ast {\mathrm{D}}^2+3.08642\ast {10}^{-9}\ast {\mathrm{E}}^2\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill \mathrm{UHCC}& =9.65762-4.47177\ast \mathrm{A}+0.061542\ast \mathrm{B}-0.97372\ast \mathrm{C}+0.13999\ast \mathrm{D}+0.00666595\ast \mathrm{E}\hfill \\ & +7.87125\ast {10}^{-3}\ast \mathrm{A}\ast \mathrm{B}+0.22519\ast \mathrm{A}\ast \mathrm{C}+0.024683\ast \mathrm{A}\ast \mathrm{D}-2.93889\ast {10}^{-5}\ast \mathrm{A}\ast \mathrm{E}\hfill \\ & -0.054375\ast \mathrm{B}\ast \mathrm{C}+3.8075\ast {10}^{-4}\ast \mathrm{B}\ast \mathrm{D}-4.77889\ast {10}^{-5}\ast \mathrm{B}\ast \mathrm{E}+6.95\ast {10}^{-3}\ast \mathrm{C}\ast \mathrm{D}\hfill \\ & -6.22778\ast {10}^{-4}\ast \mathrm{C}\ast \mathrm{E}-3.44333\ast {10}^{-5}\ast \mathrm{D}\ast \mathrm{E}+0.15898\ast {\mathrm{A}}^2-1.62056\ast {10}^{-3}\ast {\mathrm{B}}^2\hfill \\ & +0.41089\ast {\mathrm{C}}^2-8.18479\ast {10}^{-4}\ast {\mathrm{D}}^2-1.16502\ast {10}^{-7}\ast {\mathrm{E}}^2\hfill \end{array}$$

(27)

3.2. ANOVA Results and Model Diagnosis

Firstly, the accuracy of the established models for the objective functions should be evaluated through the ANOVA, and the relevant assessment indicators are presented in Table 5 in detail. The influences of mentioned independent and interactive parameters on the designative responses are revealed based on the ANOVA results, as presented in Table 6 and Table 7, respectively.

Table 5. ANOVA results of response models.

Responses	F-Value	p-Value (Prob > F)	R-Squared	Adj R-Squared	Pred R-Squared	Adeq Precision
UHCV	2387.81	<0.0001	0.9995	0.9991	0.9979	214.256
UHCC	414.45	<0.0001	0.997	0.9946	0.988	84.571
	significant	significant

Table 6. ANOVA results of UHCV.

Factors	F Value	p-Value (Prob > F)
A-mr	35,473.17	<0.0001	significant
B-Tai	13.87	0.001	significant
C-φi	0.62	0.44
D-Twi	10,238.68	<0.0001	significant
E-a	208.61	<0.0001	significant
AB	0.55	0.46
AC	0.027	0.87
AD	1107.13	<0.0001	significant
AE	21.48	<0.0001	significant
BC	2.74	0.11
BD	0.062	0.81
BE	2.74	0.11
CD	0	1
CE	13.87	0.001	significant
DE	0.25	0.62
A2	545.77	<0.0001	significant
B2	11.24	0.0026	significant
C2	1.78	0.19
D2	1.37	0.25
E2	0.58	0.45

Table 7. ANOVA results of UHCC.

Factors	F Value	p-Value (Prob > F)
A-mr	6785.39	<0.0001	significant
B-Tai	27.067	<0.0001	significant
C-φi	9.99	0.0041	significant
D-Twi	727.94	<0.0001	significant
E-a	294.44	<0.0001	significant
AB	7.065	0.014	significant
AC	2.31	0.14
AD	69.47	<0.0001	significant
AE	0.050	0.83
BC	3.37	0.078
BD	0.41	0.53
BE	3.30	0.081
CD	0.055	0.82
CE	0.22	0.64
DE	1.71	0.20
A2	251.52	<0.0001	significant
B2	16.33	0.00045	significant
C2	0.17	0.69
D2	4.17	0.052
E2	0.022	0.88

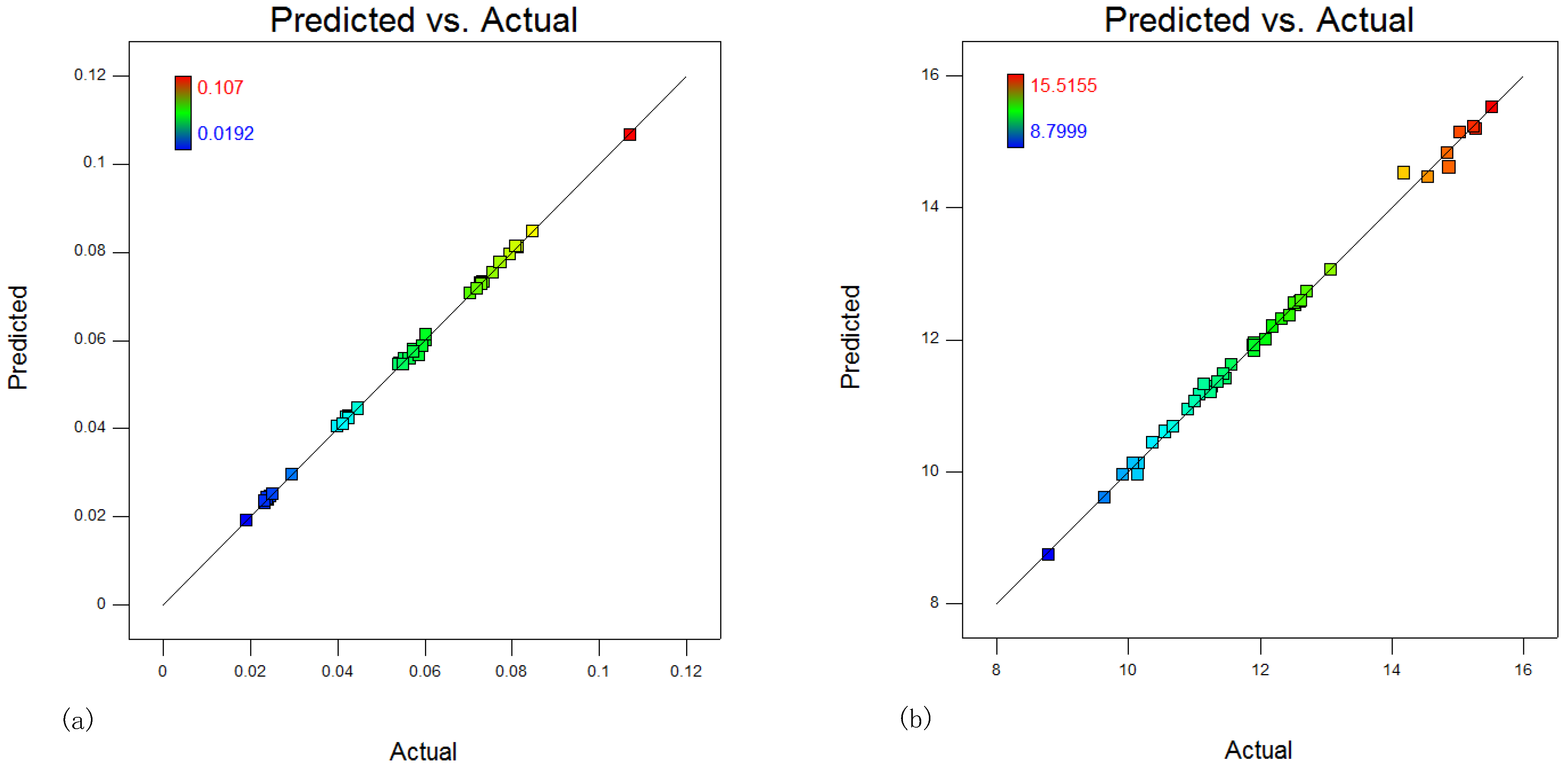
The quadratic regression models obtained by the BBD method can be further diagnosed by the comparisons between predicted values and actual values, as shown in Figure 4.

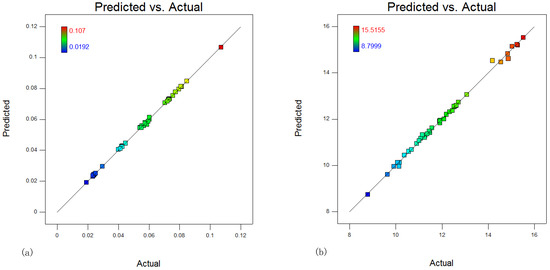
Figure 4. Model diagnoses. (a) for UHCV (b) for UHCC.

3.3. Thermodynamic Performance Results

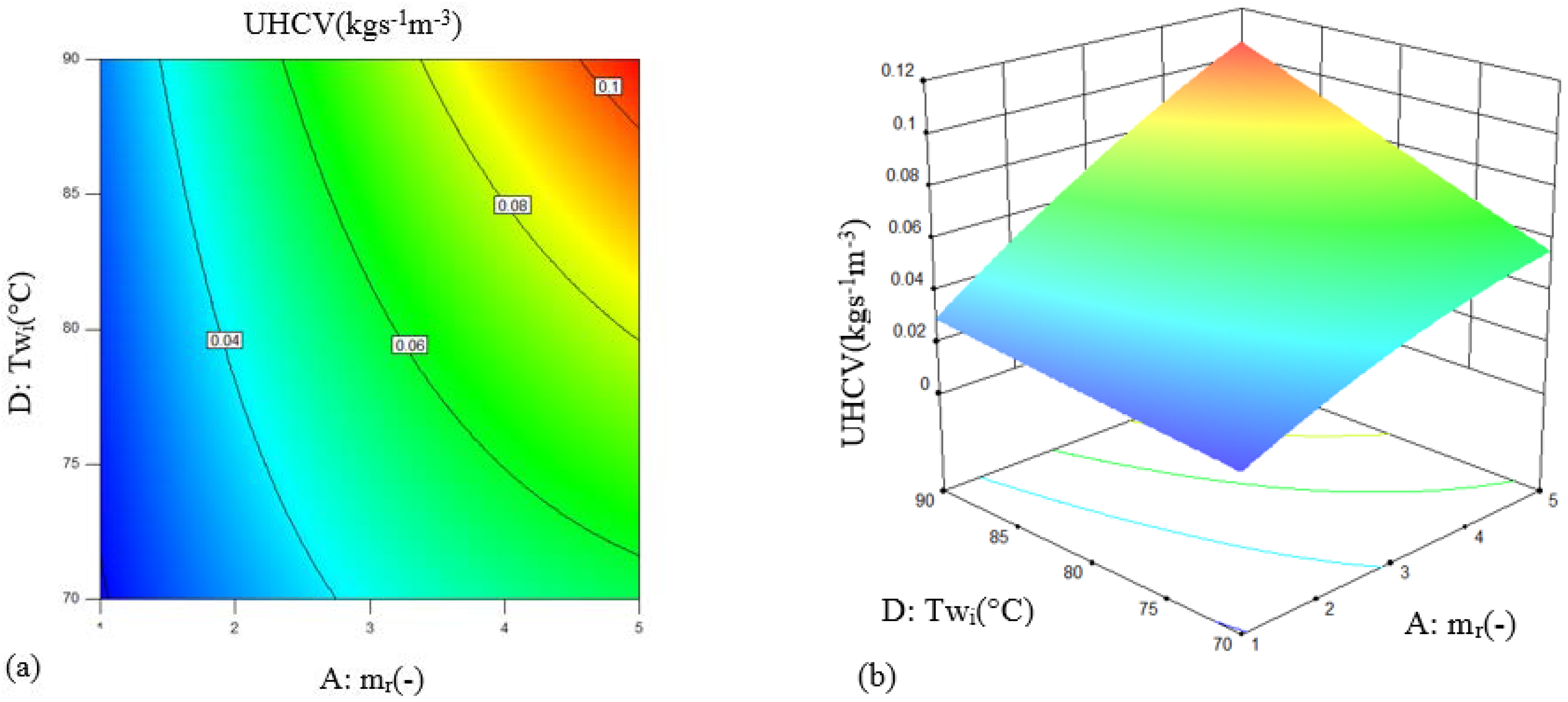
According to the ANOVA, the important parameters affecting the value of the UHCV contain parameters A, B, D, E, AD, AE CE, A², and B². It is found that parameter B (inlet air temperature) is the weakest influence factor among the four important independent parameters, and A (liquid–gas ratio) has the strongest effect on UHCV. Moreover, the interaction parameter AD (liquid–gas ratio and inlet water temperature) has the greatest impact on the UHCV compared with the other interaction parameters AE and CE. Therefore, in order to analyze the interactive influences of parameter AD on the UHCV of the packing bed humidifier, the contour and 3D surface plots of parameter AD are presented in Figure 5 based on the RSM.

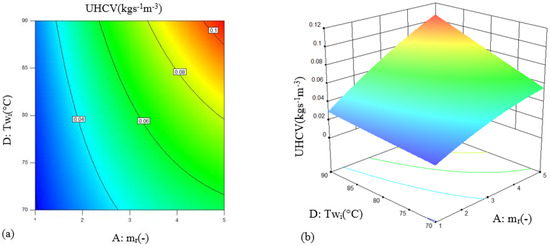
Figure 5. Contour (a) and 3D surface (b) of interaction parameter AD on UHCV.

3.4. Economic Performance Results

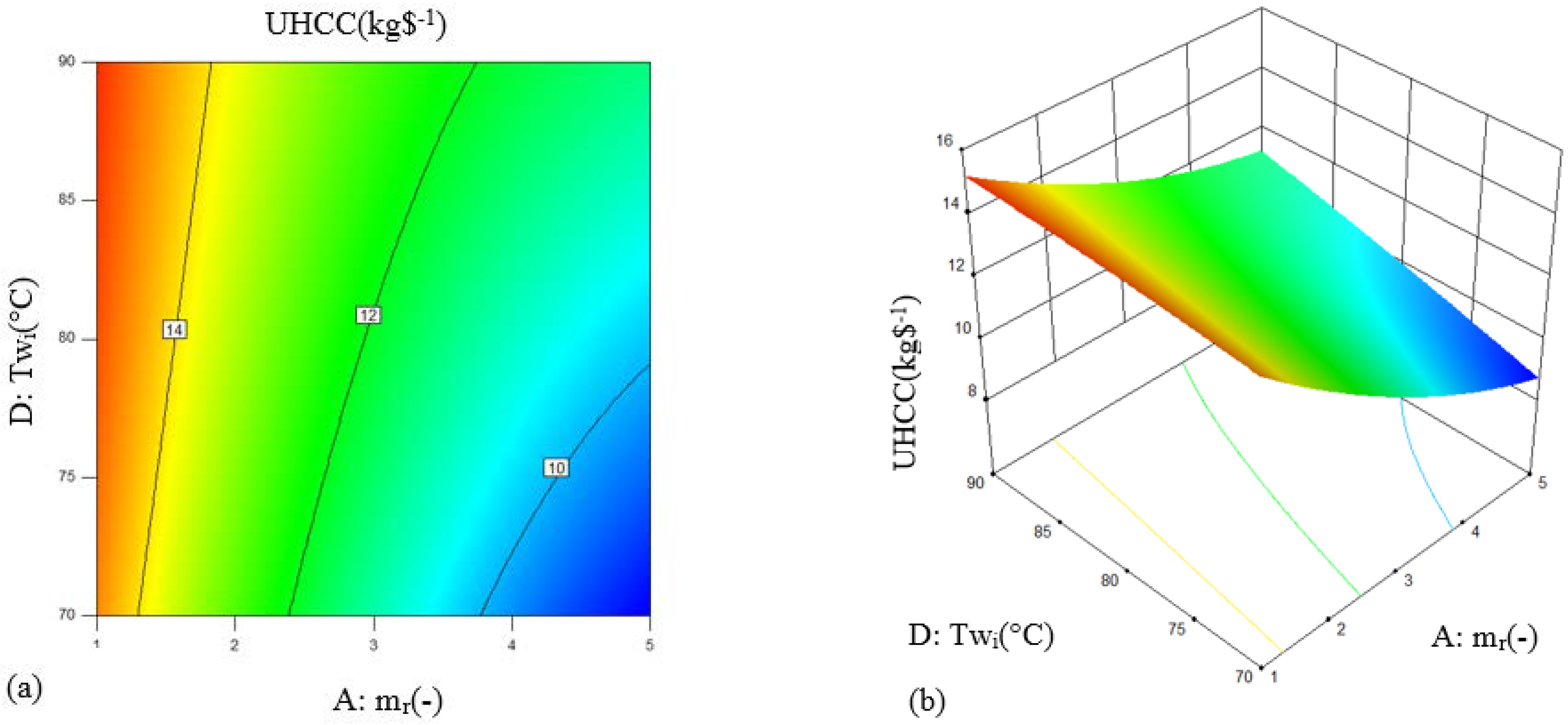
According to the ANOVA, parameters A, B, C, D, E, AB, AD, A², and B² are significant factors influencing the UHCC according to ANOVA results. It is illustrated that parameter A (liquid–gas ratio) has the strongest influence on UHCC than the other important single parameters, and parameter C (inlet relative humidity) is the weakest one. Among the important interaction factors, the influence of AD (liquid–gas ratio and inlet water temperature) is brightly greater than that of AB (liquid–gas ratio and inlet air temperature). Therefore, in order to analyze the interactive influences of parameter AD on the UHCC of the packing bed humidifier, the contour and 3D surface plots of parameter AD are presented in Figure 6.

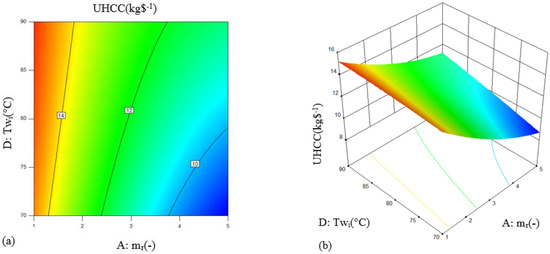
Figure 6. Contour (a) and 3D surface (b) of interaction parameter AD on UHCC.

3.5. Multi-Objective Optimization

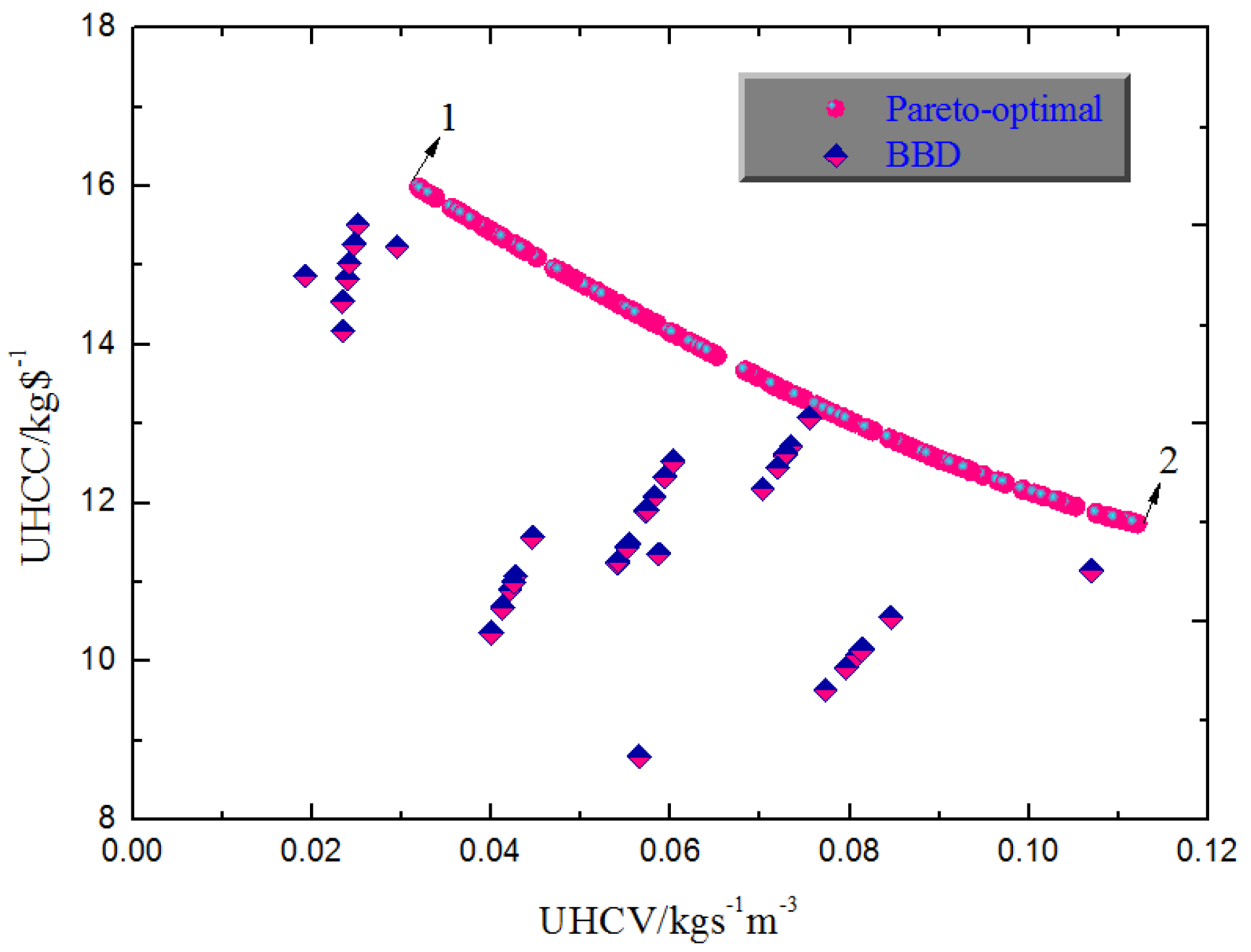
Through the natural evolution process, a series of Pareto-optimal points can be found in Figure 7 compared with the results of the BBD method. In this genetic programming, the size of the population is 100, and the number of generations is set as 600.

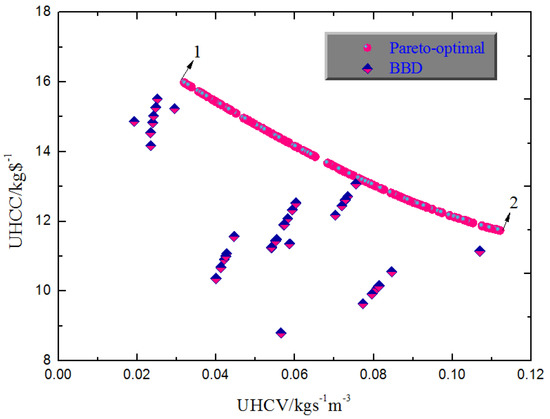
Figure 7. Pareto-optimal points vs. BBD results.

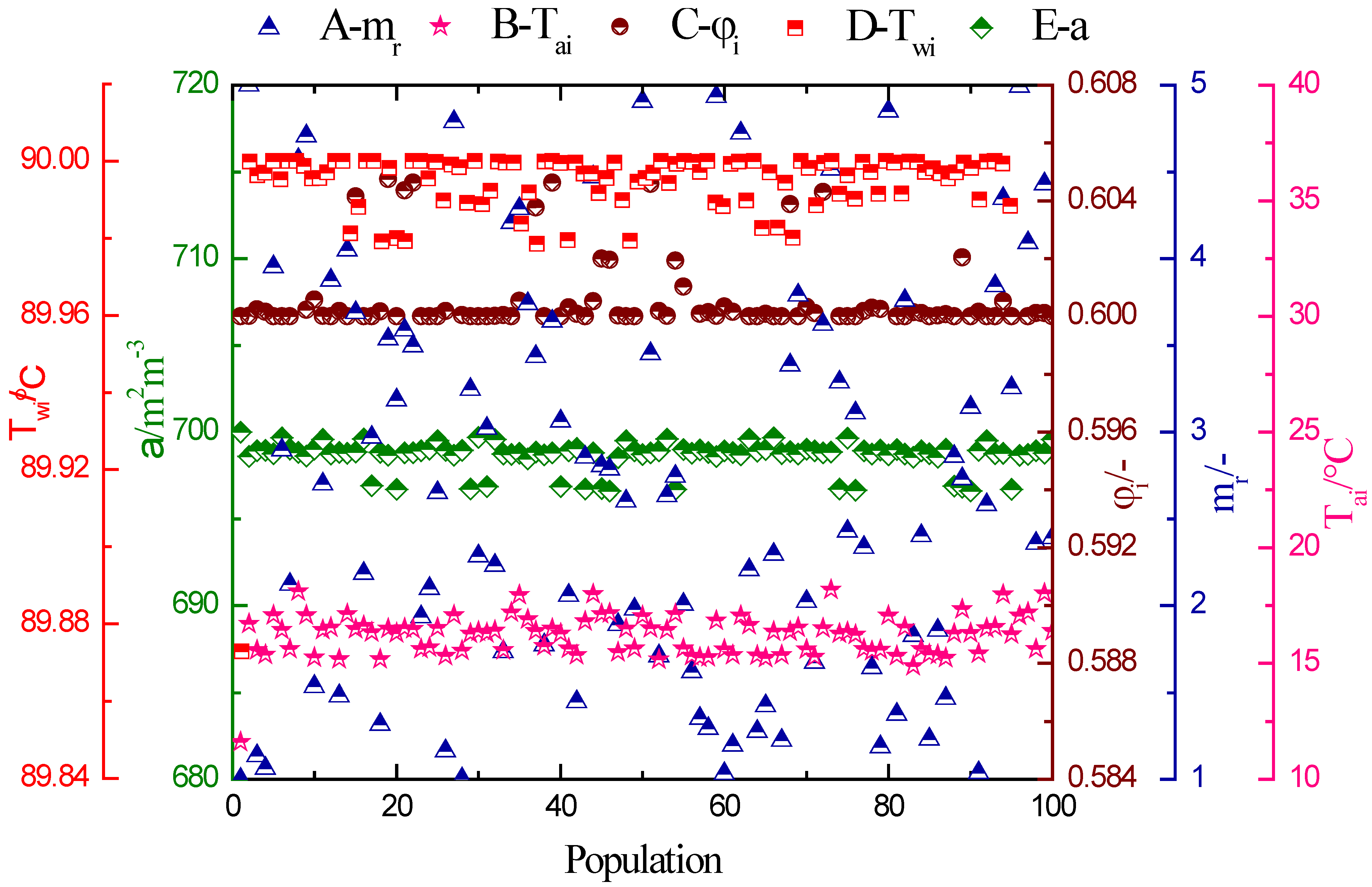
In addition, non-dominant inheritance within the population allows chromosomes to undergo selection, crossover, and mutation so that the optimal solution of the design parameter group can be found out by means of seeking a better fitness in a non-dominated population as presented in Figure 8.

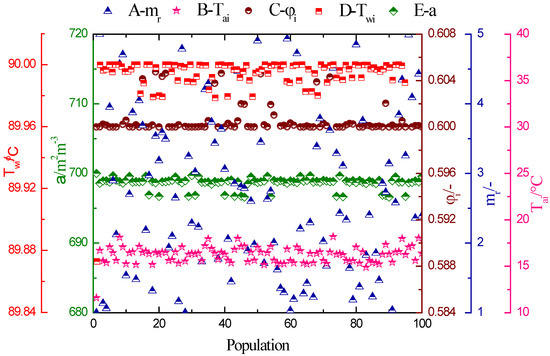
Figure 8. Distribution of optimal solution of design parameters.

4. Discussion

According to the experimental design, it is found from Table 4 that it is extremely difficult for the thermodynamic and economic performance of the packed bed humidifier to be simultaneously optimal as expected at the same condition, based on the simplified orthogonal combination. Furthermore, it is expected that there is still great potential for the UHCV and UHCC to have a higher value through multi-objective optimization.

Based on the ANOVA results, it is found from Table 5 that the F-value of 2387.81 for UHCV and 414.45 for UHCC illustrate that the models are extremely significant. In addition, it is demonstrated that the p-value of both UHCV and UHCC is less than 0.0001, which shows that the regression models are effective, among which the UHCV model has better accuracy. Moreover, according to the values of R-Squared and Adj R-Squared, it is clear each of the models has a great fitting quality. It is also found that the value of Pred R-Squared is in reasonable agreement with the Adj R-Squared value both for UHCV and UHCC, and the differences are both less than 0.2, which confirmed this fact again. Furthermore, the Adeq Precision value of 214.256 for UHCV and 84.571 for UHCC are both greater than 4, which are satisfactory and an adequate signal to navigate the experimental design.

From the results in Table 6 and Table 7, it is said that a p-value less than 0.05 indicates the relevant model term is significant. Therefore, it is summarized that parameters A, B, D, E, AD, AE, CE, A², and B² have significant influences on UHCV, while parameters A, B, C, D, E, AB, AD, A², and B² are significant model terms for UHCC. Here, it is found that in addition to the independent parameters, the interactive parameters such as AB, AD, AE, and CE also have significant impacts on the thermodynamic and economic performance. This is the reason why multi-objective optimization on the overall performance of the packed bed humidifier is developed in this study.

Through model diagnosis, it is shown from Figure 4 that most design points inhabit near the diagonal, and the relationship between predicted values and actual values is linear, which confirms that the proposed models can be employed to predict the thermodynamic and economic performance of the packed bed humidifier.

4.1. Thermodynamic Performance Analysis

Figure 5 exhibits the case that the other independent parameters are constant in the middle value of the variable range. The relationship between liquid–gas ratio and UHCV is a quadratic parabola correlation, while there is a linear relationship between inlet water temperature and UHCV, as shown in Figure 5a. Therefore, a significant interaction influence appears between these two parameters. It is found that higher values of the liquid–gas ratio and the inlet water temperature will lead to a larger UHCV evidently. This is because either increasing the inlet water temperature or increasing the liquid–gas ratio will be beneficial to the heat load of the hot side. Then, the moisture absorption capacity of humid air will rise sharply with the increase in its temperature, which will cause a higher value of the UHCV, as shown in Figure 5b. It is observed that a maximum value of 0.11 kgs⁻¹m⁻³ for the UHCV appears at the conditions of the liquid–gas ratio of 5 and inlet water temperature of 90 °C.

4.2. Economic Performance Analysis

It is highlighted that Figure 6 is plotted when the other parameters are set as the middle value. From Figure 6a, it is found that there is a slight linear relationship between the inlet water temperature and response UHCC, while the influence relationship between the liquid–gas ratio and UHCC is a quadratic parabola. The difference is that the impact trend of these two variables on UHCC is the opposite. It can be seen that the increase in inlet water temperature can enhance the value of the UHCC, while a higher value of the liquid–gas ratio will rapidly reduce the value of the UHCC. It is found that a maximum UHCC of 15.51 kg$⁻¹ emerges at the conditions of the liquid–gas ratio of 1 and inlet water temperature of 90 °C. That is because increasing the inlet water temperature will not only improve the moisture absorption capacity of the humid air but also increase the energy consumption of the electric heater. Therefore, the comprehensive improvement effect is not obvious. However, the decrease in the liquid–gas ratio will greatly reduce the power consumption of the water pump and electric heater. Simultaneously, since the spray water temperature is unchanged, the moisture absorption of the humid air is relatively small compared to the cost increase. As a result, the interaction of parameter AD shows a sloping surface on the UHCC from the front view in Figure 6b.

4.3. Multi-Objective Optimization Analysis

As analyzed in Section 4.1 and Section 4.2, it is summarized that it is laborious to obtain the desirable thermodynamic and economic performance simultaneously for the packed bed humidifier based on BBD. To overcome this problem, a multi-objective optimization is implemented to predict the best performance for the packed bed humidifier employing the Non-dominated Sorting Genetic Algorithm-II. After natural selection, as shown in Figure 7, it can be found that the optimal points obtained are all located in the upper right of the experimental values, which indicates that the overall performance of the packing bed humidifier can be substantially improved.

It is found from Figure 8 that population B (inlet air temperature), C (inlet relative humidity), D (inlet water temperature), and E (specific surface area) have a favorite habitat around 16 °C, 0.6, 90 °C, and 700 m²m⁻³, respectively, while population A (liquid–gas ratio) is randomly distributed in the specific range. Additionally, a higher liquid–gas ratio is beneficial to thermodynamic performance, while a lower value of liquid–gas ratio can improve the economic performance in combination with the optimal parameter group.

4.4. Verification of Optimal Solution

It was shown that the optimal performance obtained through multi-objective optimization is an optimization interval. Here, in order to verify the accuracy of the optimal values, two Pareto-optimal points recorded as point 1 (0.032 kgs⁻¹m⁻³ for UHCV, 15.99 kg$⁻¹ for UHCC) and point 2 (0.11 kgs⁻¹m⁻³ for UHCV, 11.74 kg$⁻¹ for UHCC) are selected as the comparison objects as shown in Figure 7. The corresponding optimal parameter groups are, respectively, 1, 11.62 °C, 0.6, 90 °C, and 700 m²m⁻³, and 5, 16.71 °C, 0.6, 90 °C, and 700 m²m⁻³, successively. Through introducing the optimal groups into the established mathematical model, the actual performances are obtained as 0.031 kgs⁻¹m⁻³ for UHCV, 15.86 kg$⁻¹ for UHCC corresponding to point 1, and 0.11 kgs⁻¹m⁻³ for UHCV, 11.60 kg$⁻¹ for UHCC corresponding to point 2, respectively. It was found that the errors between predicted and actual values are, respectively, +3.22% and +0.82% at point 1 based on the actual value, while +0.63% and +1.21% are at point 2, which demonstrate that the predicted optimal results are desirable and reliable. Furthermore, through multi-objective optimization, the value of UHCV increases by 56% compared with the result of group 22 with the same UHCC, and the value of UHCC raises by 6.55% compared with the value of group 26 with the same UHCV, respectively.

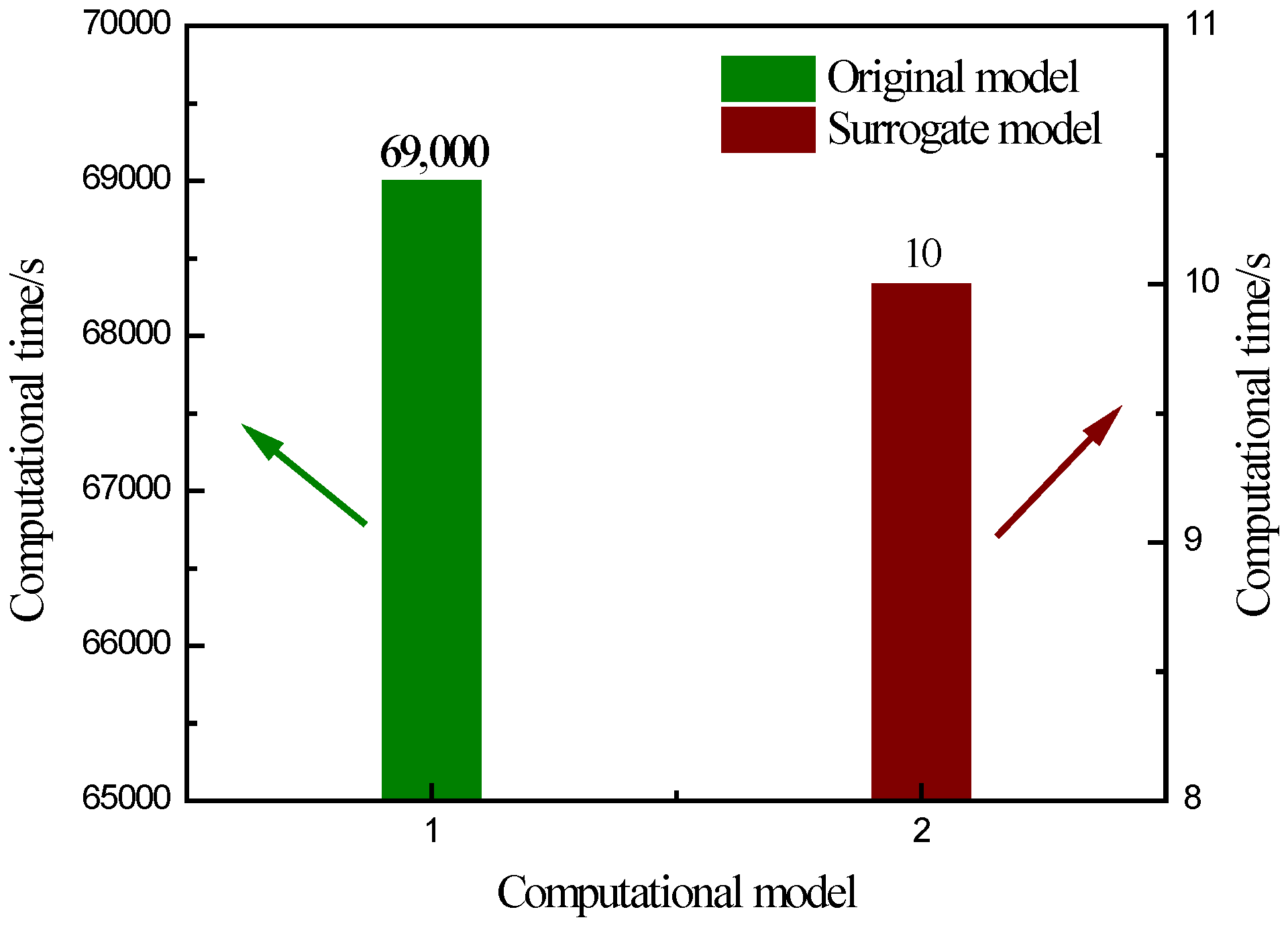
Furthermore, the computational time to find the optimization results using a mathematical model and regression model is extremely different. As shown in Figure 9, the quickest computational time for optimization results employing the original mathematical model is 69,000 s, through the simplified orthogonal method, while the computational time to search the optimization results drops to only 10 s for the novel regression model through genetic algorithm. Therefore, the established regression model can give the optimization results more quickly, which justifies the usefulness and robustness of the surrogate model.

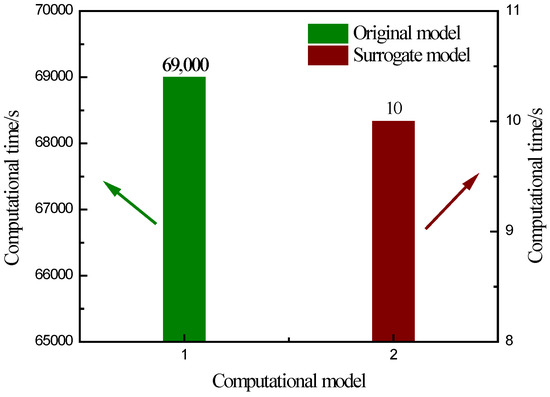
Figure 9. Comparison of computational time of optimization results between original and surrogate models.

Although the proposed method is time-saving, efficient, and accurate, it also has some problems, such as premature convergence and nonstandard coding, especially the specific design conditions given in Table 2. Maybe the coming genetic algorithm-III can improve this limitation.

5. Conclusions

To calculate the thermal characteristics of the combined heat and mass transfer process in the packed bed humidifier, an integrated mathematical model and the relevant objective functions of thermodynamic and economic performance are first established. Then, the quadratic regression models of objective functions are fitted based on the experimental design results through the response surface method. The degrees of the important influences of independent and interactive parameters on the objectives are summarized by means of the analysis of variance. Through multi-objective optimization, some conclusions can be written as follows:

• Feasible regression models of unit humidification capacity of volume and unit humidification capacity of cost are established based on an experimental design scheme consisting of 46 groups, while the thermodynamic model is more accurate than that of economic;
• The liquid–gas ratio has the strongest influence among the independent parameters on thermodynamic and economic performance, simultaneously, and the interaction of the liquid–gas ratio and the inlet water temperature has the greatest impact on thermodynamic and economic performance compared with other interaction factors;
• The optimal parameter groups are found out through genetic programming: the liquid–gas ratio is randomly distributed in the design range, inlet air temperature is around 16 °C, inlet relative humidity is 0.6, inlet water temperature is 90 °C, and specific surface area is 700 m²m⁻³, respectively. Furthermore, the Pareto-optimal points obtained are all superior to the values of experimental design;
• After multi-objective optimization, the thermodynamic performance improves by 56%, and the economic performance elevates by 6.55%, compared with the values of basic experimental design, respectively;
• The computational time to find the optimization results using an established regression model can be reduced by 99.98%, compared with the original mathematical model.