Evaluation of Profiles of Standard Deviation of Vertical Wind in the Urban Area of Rome: Performances of Monin–Obukhov Similarity Theory Using Different Scaling Variables
Abstract
:1. Introduction
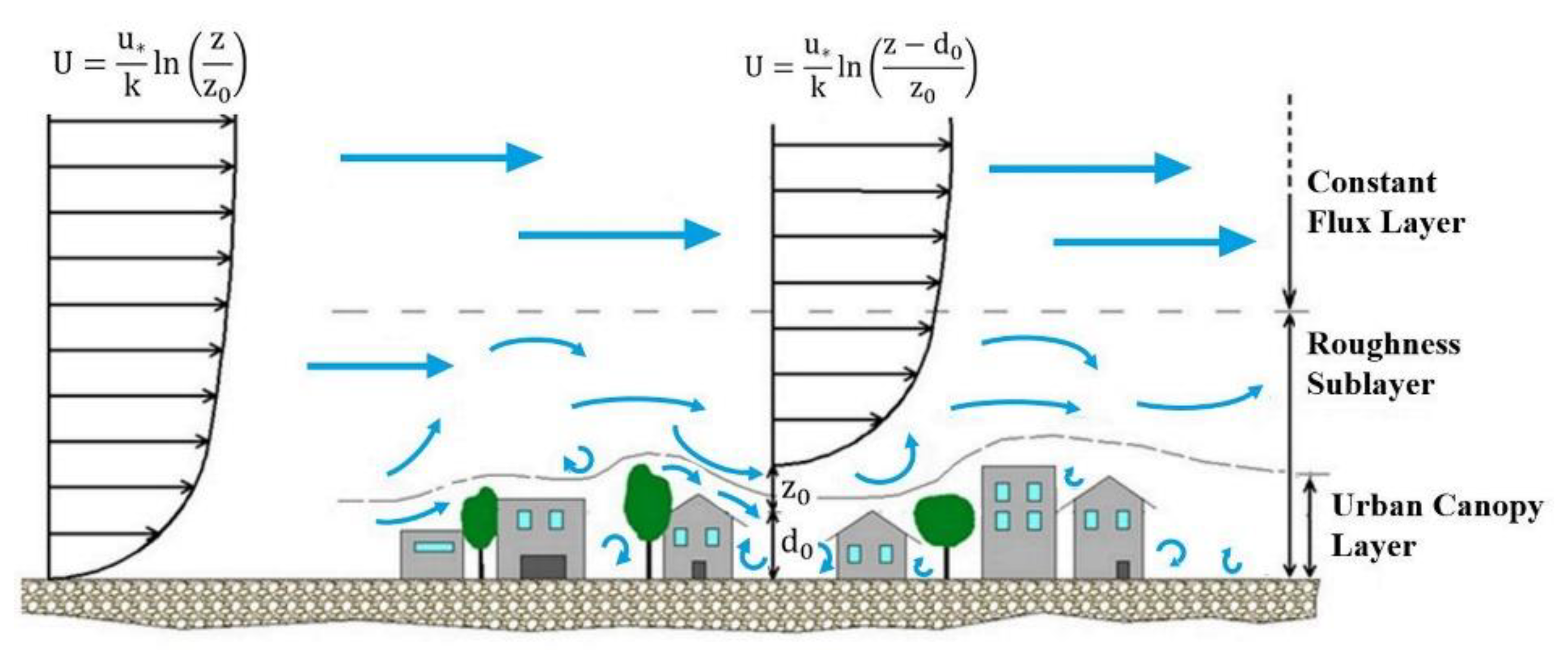
2. Materials and Methods
2.1. Parametrization of the Standard Deviation of Vertical Velocity
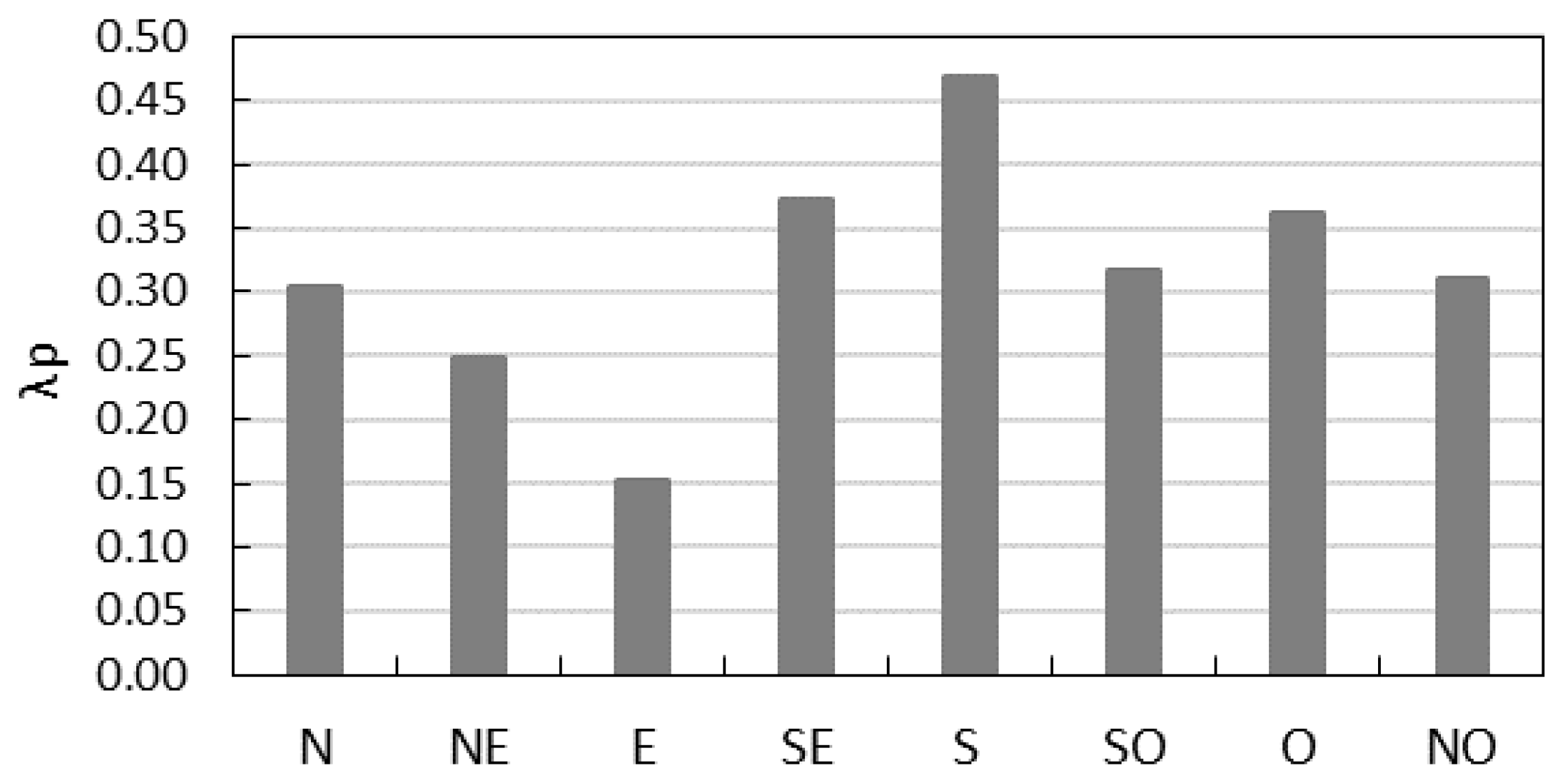
2.2. Site Description and Experimental Setup
2.3. Data Processing
2.3.1. The Normal and Tilted Coordinate Systems
2.3.2. Estimation of Friction Velocity from SODAR Measurements
2.3.3. Data Processing for Comparison with Existing MOST Parameterizations
3. Results and Discussion
3.1. Sonic Anemometer Measurements
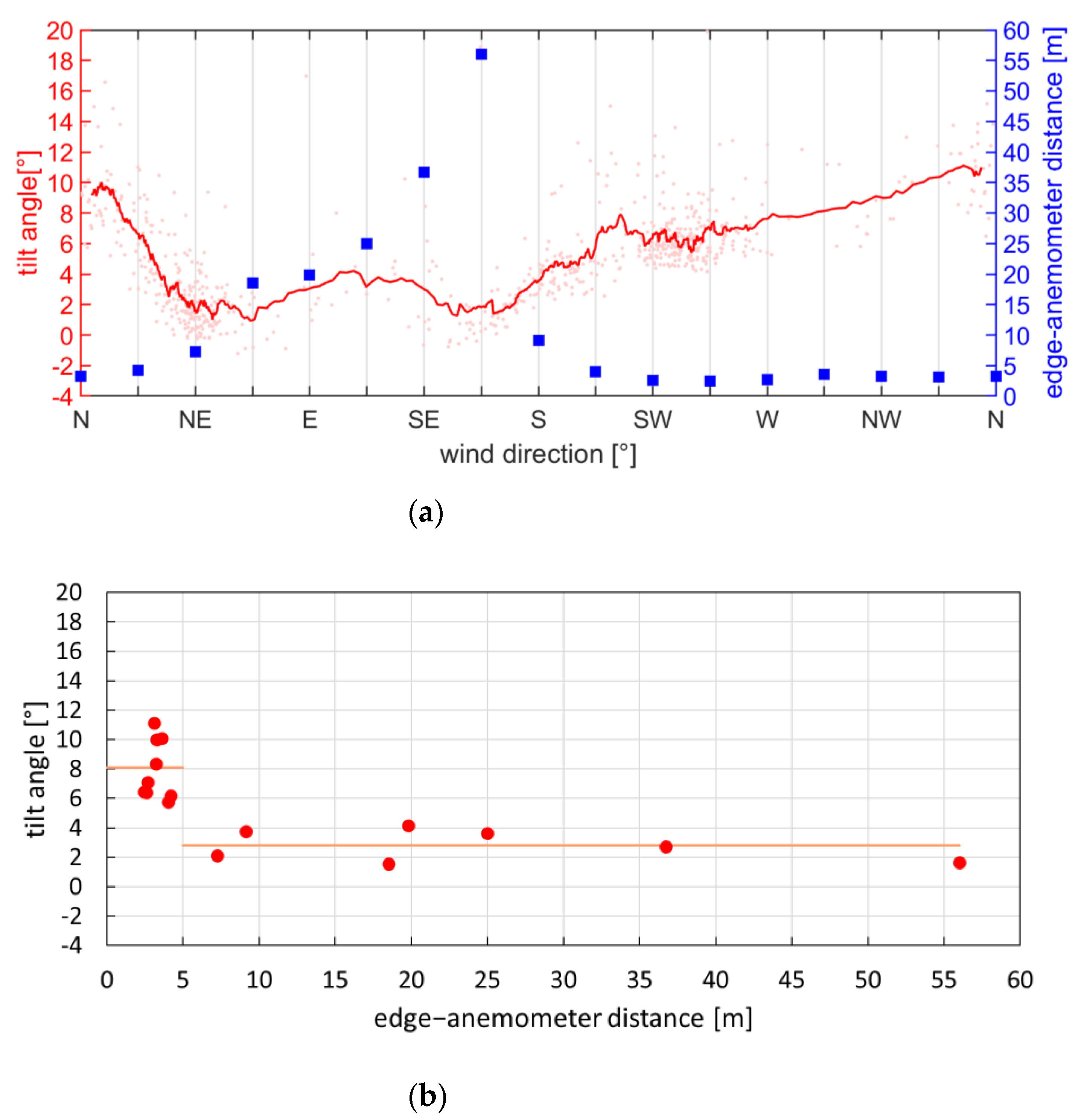
3.1.1. Physical Meaning of the Tilted Coordinate System
3.1.2. Comparison between Turbulent Fluxes in the Normal and Tilted Coordinate Systems
Friction Velocity
Heat Flux
Obukhov Length
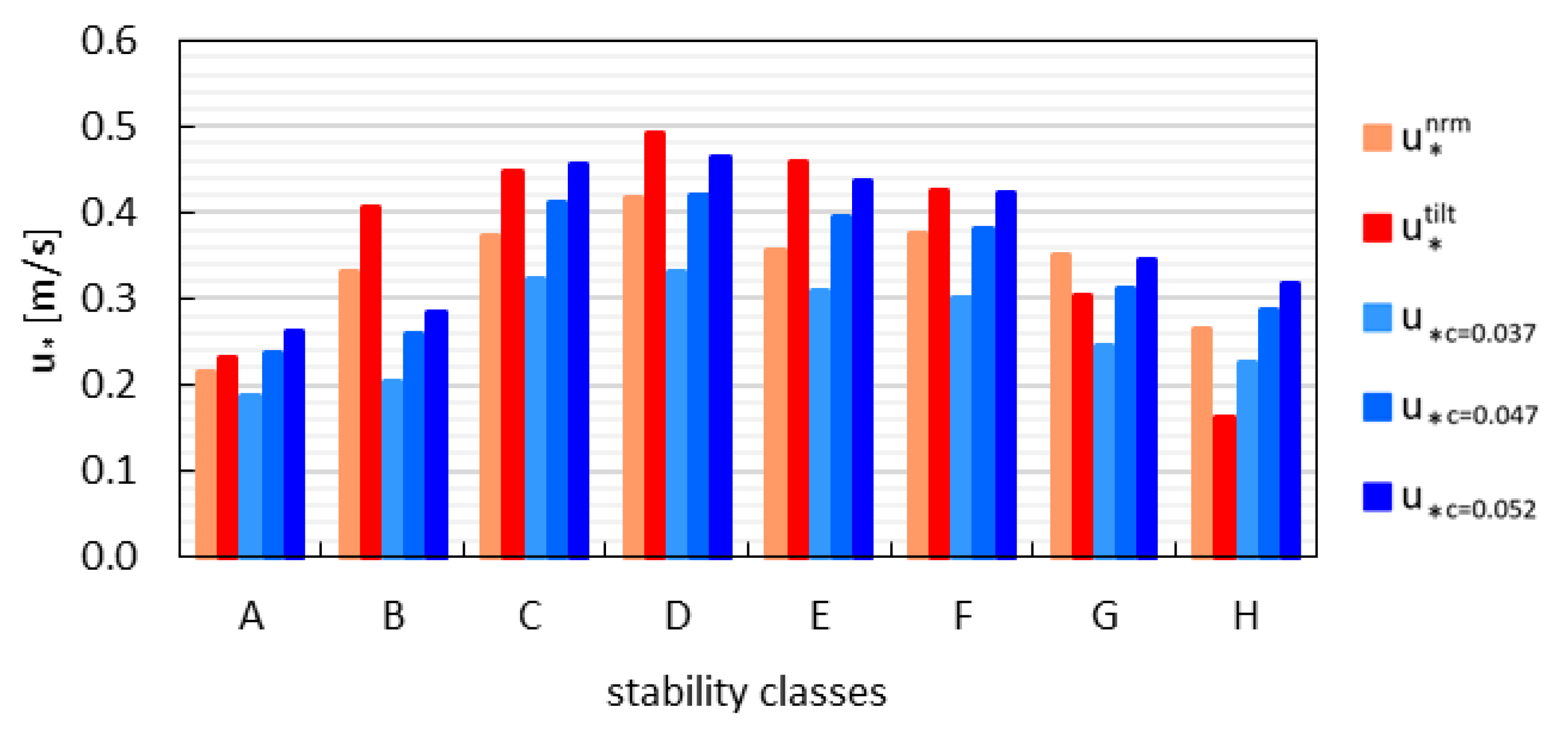
3.2. Estimation of Friction Velocity from SODAR Measurements
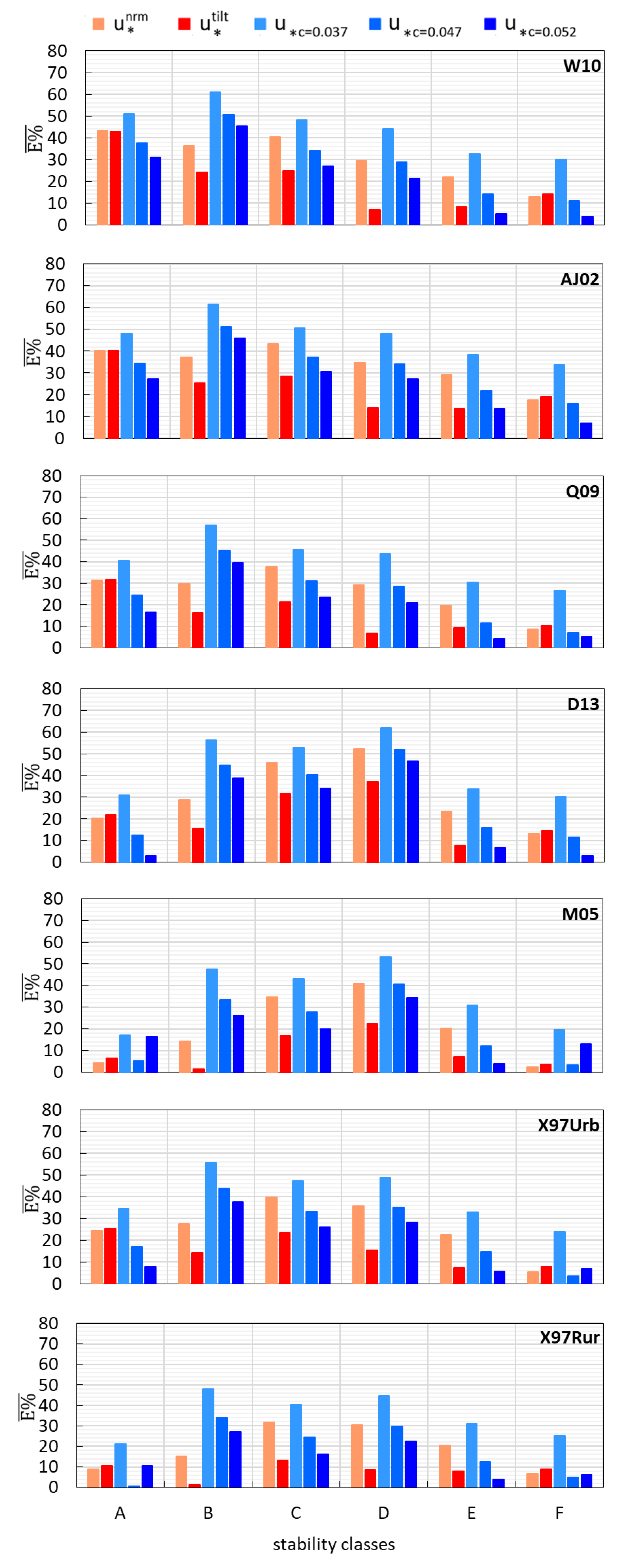
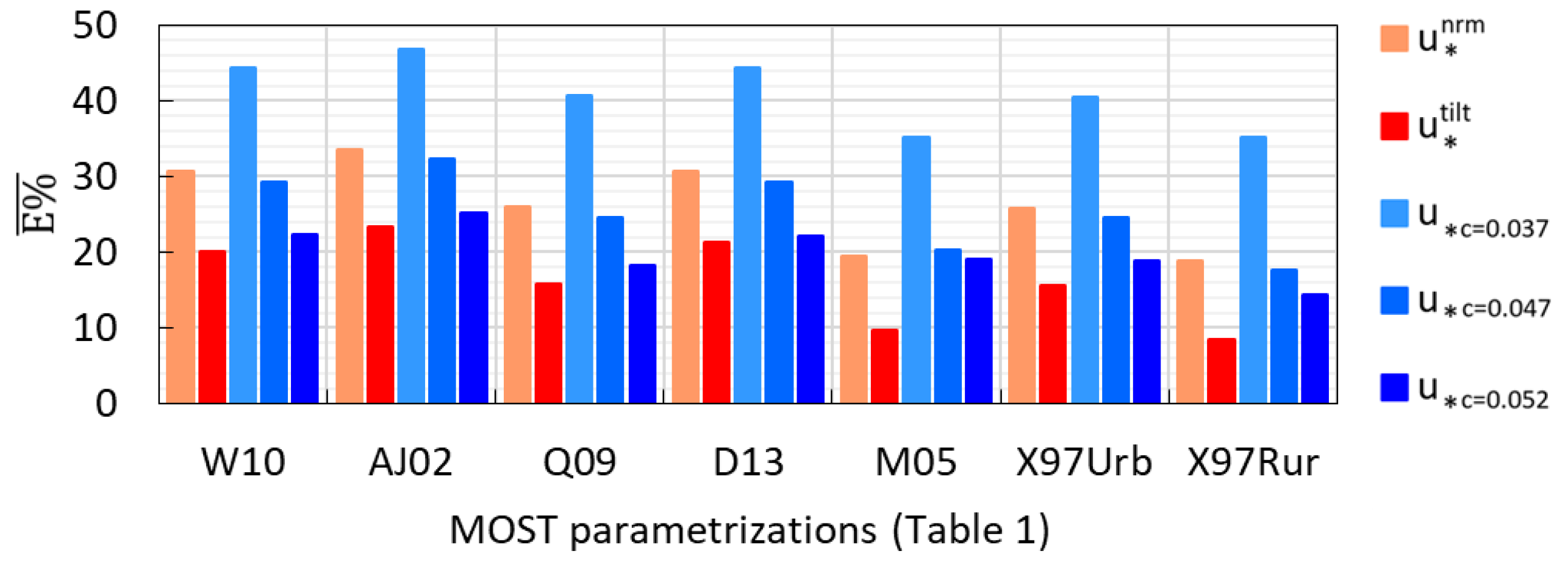
3.3. Applicability of MOST in the Roughness Sublayer above Rome
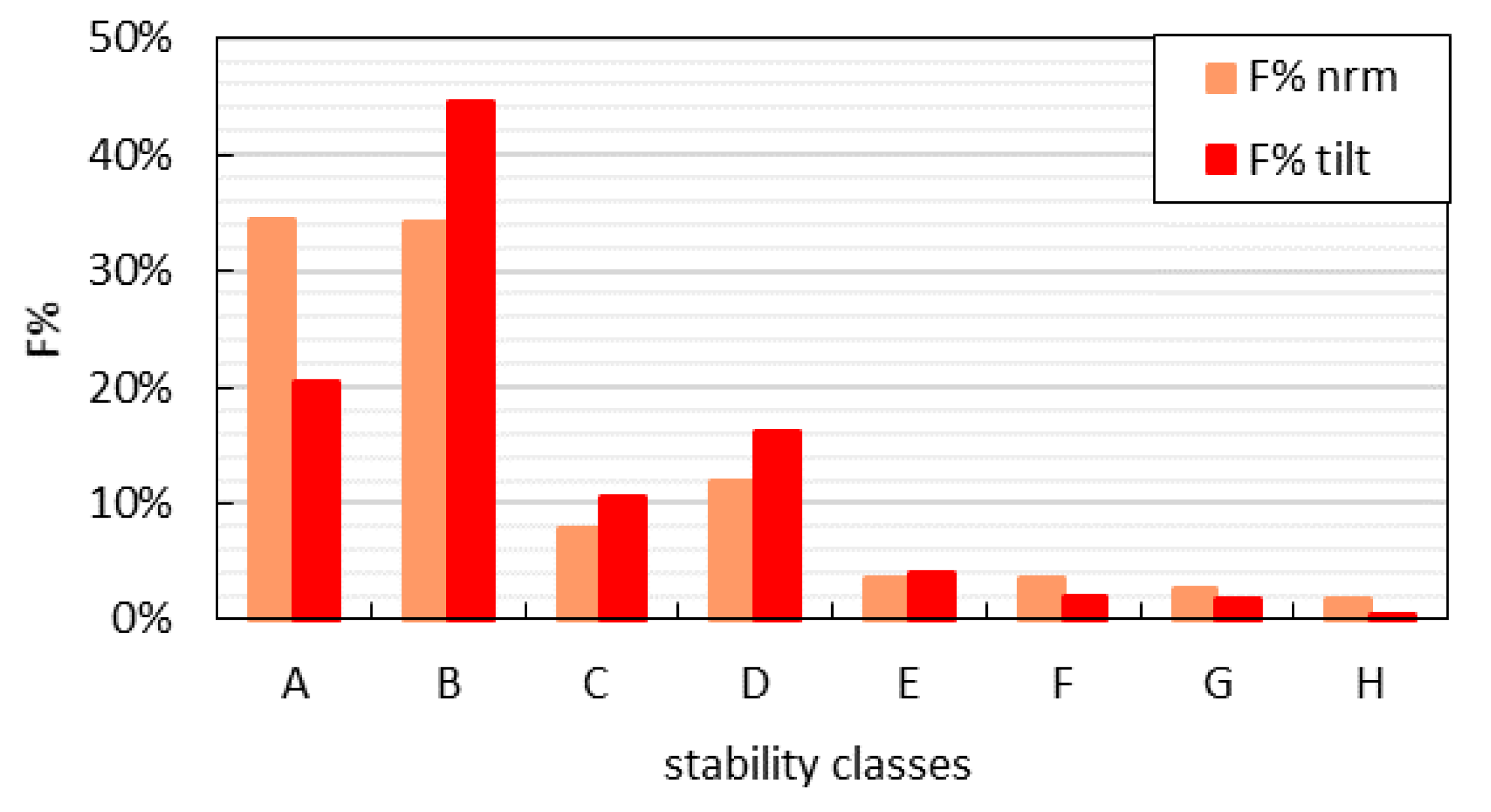
3.3.1. Applicability of MOST Considering Each Stability Class
3.3.2. Overall Applicability of MOST
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pasquill, F. Atmospheric Diffusion, 2nd ed.; Halstead Press: New York, NY, USA, 1974. [Google Scholar]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic Publisher: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Buckingham, E. On physically similar sistems: Illustration of the use of dimensional equations. Phys. Rev. 1914, 4, 345–376. [Google Scholar] [CrossRef]
- Monin, A.S.; Obukhov, A.M. Basic Laws of Turbulent Mixing in the Atmosphere near the Ground. Trudy Geofiz. Inst. 1954, 24, 163–187. [Google Scholar]
- Foken, T. 50 years of the Monin–Obukhov similarity theory. Bound. Layer Meteorol. 2006, 119, 431–447. [Google Scholar] [CrossRef]
- Oke, T.R. The energetic basis of the urban heat island. Q. J. R. Meteorol. Soc. 1982, 108, 1–24. [Google Scholar] [CrossRef]
- Di Bernardino, A.; Iannarelli, A.M.; Casadio, S.; Mevi, G.; Campanelli, M.; Casasanta, G.; Cede, A.; Tiefengraber, M.; Siani, A.M.; Cacciani, M. On the Effect of Sea Breeze Regime on Optical and Physical Aerosol Properties in the Urban Area of Rome, Italy. Urban Clim. 2021, 37, 100842. [Google Scholar] [CrossRef]
- Fernando, H.J.S.; Lee, S.M.; Anderson, J.; Princevac, M.; Pardyjak, E.; Grossman-Clarke, S. Urban Fluid Mechanics: Air circulation and contaminant dispersion in cities. Environ. Fluid Mech. 2001, 1, 107–164. [Google Scholar] [CrossRef]
- Christen, A.; Vogt, R. The energy balance of a central European City. Int. J. Climatol. 2004, 24, 1395–1421. [Google Scholar] [CrossRef]
- Barlow, J.F. Progress in observing and modelling the urban boundary layer. Urban Clim. 2014, 10, 216–240. [Google Scholar] [CrossRef] [Green Version]
- Giovannini, L.; Zardi, D.; De Franceschi, M. Characterization of the thermal structure inside an urban canyon: Field measurements and validation of a simple model. J. Appl. Meteorol. Climatol. 2013, 52, 64–81. [Google Scholar] [CrossRef]
- Conigliaro, E.; Monti, P.; Leuzzi, G.; Cantelli, A. A three-dimensional urban canopy model for mesoscale atmospheric simulations and its comparison with a two-dimensional urban canopy model in an idealized case. Urban Clim. 2021, 37, 100831. [Google Scholar] [CrossRef]
- Rotach, M.W. On the influence of the urban roughness sublayer on turbulence and dispersion. Atmos. Environ. 1999, 33, 4001–4008. [Google Scholar] [CrossRef]
- Dyer, A.J.; Hicks, B.B. Flux-gradient relationships in the constant flux layer. Q. J. R. Meteorol. Soc. 1970, 96, 715–721. [Google Scholar] [CrossRef]
- Arnfield, A.J. Two decades of urban climate research: A review of turbulence, exchanges of energy and water, and the urban heat island. Int. J. Climatol. 2003, 23, 1–26. [Google Scholar] [CrossRef]
- Britter, R.E.; Hanna, S.R. Flow and dispersion in urban areas. Annu. Rev. Fluid Mech. 2003, 35, 469–496. [Google Scholar] [CrossRef]
- Grimmond, C.S.B.; Oke, T.R. Aerodynamic properties of urban areas derived from analysis of urban surface form. J. Appl. Meteorol. 1999, 38, 1261–1292. [Google Scholar] [CrossRef]
- Rotach, M.W. Structure of the Urban Boundary Layer. In COST 715 Final Report: Meteorology Applied to Urban Air Pollution Problems; Fisher, B., Joffre, S., Kukkonen, J., Piringer, M., Rotach, M., Schatzmann, M., Eds.; Demetra Ltd Publishers: Sofia, Bulgaria, 2005. [Google Scholar]
- Dallman, A.; Di Sabatino, S.; Fernando, H.J.S. Flow and turbulence in an industrial/suburban roughness canopy. Environ. Fluid Mech. 2013, 13, 279–307. [Google Scholar] [CrossRef]
- Pelliccioni, A.; Monti, P.; Leuzzi, G. Wind-Speed Profile and Roughness Sublayer Depth Modelling in Urban Boundary Layers. Bound. Layer Meteorol. 2016, 160, 225–248. [Google Scholar] [CrossRef]
- Kastner-Klein, P.; Rotach, M.W. Mean flow and turbulence characteristics in an urban roughness sublayer. Bound. Layer Meteorol. 2004, 111, 55–84. [Google Scholar] [CrossRef]
- Zajic, D.; Fernando, H.J.S.; Brown, M.J.; Pardyjak, E.R. On flows in simulated urban canopies. Environ. Fluid Mech. 2015, 15, 275–303. [Google Scholar] [CrossRef]
- Di Bernardino, A.; Monti, P.; Leuzzi, G.; Querzoli, G. Pollutant fluxes in two-dimensional street canyons. Urban Clim. 2018, 24, 80–93. [Google Scholar] [CrossRef]
- Coceal, O.; Thomas, T.G.; Castro, I.P.; Belcher, S.E. Mean flow and turbulence statistics over groups of urban-like obstacles. Bound. Layer Meteorol. 2006, 121, 491–519. [Google Scholar] [CrossRef]
- Di Bernardino, A.; Monti, P.; Leuzzi, G.; Querzoli, G. Turbulent Schmidt number measurements over three-dimensional cubic arrays. Bound. Layer Meteorol. 2020, 174, 231–250. [Google Scholar] [CrossRef] [Green Version]
- Barlow, J.F.; Dobre, A.; Smalley, R.J.; Arnolds, S.J.; Tomlin, A.S.; Belcher, S.E. Referencing of street-level flows measured during the DAPPLE 2004 campaign. Atmos. Environ. 2009, 43, 5536–5544. [Google Scholar] [CrossRef]
- Pelliccioni, A.; Monti, P.; Cattani, G.; Boccuni, F.; Cacciani, M.; Canepari, S.; Capone, P.; Catrambone, M.; Cusano, M.; D’Ovidio, M.C.; et al. Integrated Evaluation of Indoor Particulate Exposure: The VIEPI Project. Sustainability 2020, 12, 9758. [Google Scholar] [CrossRef]
- Foken, T. Micrometeorology; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Wood, C.R.; Lacser, A.; Barlow, J.F.; Padhra, A.; Belcher, S.E.; Nemitz, E.; Helfter, C.; Famulari, D.; Grimmond, C.S.B. Turbulent Flow at 190 m Height above London during 2006–2008: A Climatology and the Applicability of Similarity Theory. Bound. Layer Meteorol. 2010, 137, 77–96. [Google Scholar] [CrossRef] [Green Version]
- Al-Jiboori, M.H.; Xu, Y.; Qian, Y. Local Similarity Relationships in the Urban Boundary Layer. Bound. Layer Meteorol. 2002, 102, 63–82. [Google Scholar] [CrossRef]
- Quan, L.; Hu, F. Relationship between turbulent flux and variance in the urban canopy. Meteorol. Atmospheric Phys. 2009, 104, 29–36. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, C.; Li, Z. Turbulent structure and local similarity in the tower layer over the nanjing area. Bound. Layer Meteorol. 1997, 82, 1–21. [Google Scholar]
- Moraes, O.L.L.; Acevedo, O.C.; Degrazia, G.A.; Anfossi, D.; da Silva, R.; Anabor, V. Surface layer turbulence parameters over a complex terrain. Atmos. Environ. 2005, 39, 3103–3112. [Google Scholar]
- Hsieh, C.-I.; Katul, G.; Chi, T.-W. An approximate analytical model for footprint estimation of scalar fluxes in thermally stratified atmospheric flows. Adv. Water Resour. 2000, 23, 765–772. [Google Scholar] [CrossRef]
- Kljun, N.; Rotach, M.W.; Calanca, P. A Simple Parameterisation for Flux Footprint Predictions. Bound. Layer Meteorol. 2004, 112, 503–523. [Google Scholar] [CrossRef]
- Pelliccioni, A.; Monti, P.; Leuzzi, G. An alternative wind profile formulation for urban areas in neutral conditions. Environ. Fluid Mech. 2015, 15, 135–146. [Google Scholar] [CrossRef] [Green Version]
- Di Bernardino, A.; Iannarelli, A.M.; Casadio, S.; Perrino, C.; Barnaba, F.; Tofful, L.; Campanelli, M.; Di Liberto, L.; Mevi, G.; Cacciani, M. Impact of synoptic meteorological conditions on air quality in three different case studies in Rome, Italy. Atmos. Pollut. Res. 2021, 12, 76–88. [Google Scholar] [CrossRef]
- Leuzzi, G.; Monti, P. Breeze Analysis by Mast and Sodar Measurements. Il Nuovo Cimento 1997, C20, 343–359. [Google Scholar]
- Monti, P.; Leuzzi, G. A Numerical Study of Mesososcale Airflow and Dispersion over Coastal Complex Terrain. Int. J. Environ. Pollut. 2005, 25, 239–250. [Google Scholar] [CrossRef]
- Mastrantonio, G.; Fiocco, G. Accuracy of wind velocity determinations with Doppler sodars. J. Appl. Meteorol. 1982, 21, 823–830. [Google Scholar] [CrossRef]
- Mastrantonio, G.; Argentini, S.; Viola, A. A new PC-based real system to analyze sodar echoes. In Proceedings of the 5th Workshop Italia Research on Antarctic Atmosphere, Porano, Italy, 19–21 October 1992; pp. 227–235. [Google Scholar]
- Holtslag, A.A.M. Estimates of diabatic wind speed profiles from near-surface weather observations. Bound. Layer Meteorol. 1984, 29, 225–250. [Google Scholar] [CrossRef]
- Wilczak, J.M.; Oncley, S.P.; Stage, S.A. Sonic Anemometer Tilt Correction Algorithms. Bound. Layer Meteorol. 2001, 99, 127–150. [Google Scholar] [CrossRef]
- Bonacquisti, V. Anemometria Sonica per la Determinazione dei Flussi Turbolenti e Caratterizzazione dello Strato Limite Planetario in Ambiente Urbano. Ph.D. Thesis, Sapienza University of Rome, Rome, Italy, 2008. [Google Scholar]
- Nakai, T.; Shimoyama, K. Ultrasonic anemometer angle of attack errors under turbulent conditions. Agric. For. Meteorol. 2012, 162–163, 14–26. [Google Scholar]
- Christen, A. Atmospheric Turbulence and Surface Energy Exchange in Urban Environments: Results from the Basel Urban Boundary Layer Experiment (BUBBLE). Ph.D. Thesis, University of Basel, Basel, Switzerland, 2005. [Google Scholar]
- Businger, J.A.; Wyngaard, J.C.; Izumi, Y.; Bradley, E.F. Flux-profile relationships in the atmospheric surface layer. Int. J. Atmos. Sci. 1971, 28, 181–189. [Google Scholar] [CrossRef]
- Nironi, C.; Salizzoni, P.; Marro, M.; Mejean, P.; Grosjean, N.; Soulhac, L. Dispersion of a Passive Scalar Fluctuating Plume in a Turbulent Boundary Layer. Part I: Velocity and Concentration Measurements. Bound. Layer Meteorol. 2015, 156, 415–446. [Google Scholar] [CrossRef]
- Fackrell, J.E.; Robins, A.G. Concentration fluctuations and fluxes in plumes from point sources in a turbulent boundary layer. J. Fluid Mech. 1982, 117, 1–26. [Google Scholar] [CrossRef]
- Nardecchia, F.; Di Bernardino, A.; Pagliaro, F.; Monti, P.; Leuzzi, G.; Gugliermetti, L. CFD analysis of urban canopy flows employing the V2F model: Impact of different aspect ratios and relative heights. Adv. Meteorol. 2018, 2018. [Google Scholar] [CrossRef]
- Pelliccioni, A.; Monti, P.; Gariazzo, C. Some characteristics of the urban boundary layer above Rome, Italy, and applicability of Monin–Obukhov similarity. Environ. Fluid Mech. 2012, 12, 405–428. [Google Scholar] [CrossRef]
- De Ridder, K. Bulk Transfer Relations for the Roughness Sublayer. Bound. Layer Meteorol. 2010, 134, 257–267. [Google Scholar] [CrossRef]
- Oke, T.R.; Mills, G.; Christen, A.; Voogt, J.A. Urban Climates; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Masson, V. A physically-based scheme for the urban energy budget in atmospheric models. Bound. Layer Meteorol. 2000, 94, 357–397. [Google Scholar] [CrossRef]
- Cantelli, A.; Monti, P.; Leuzzi, G. Numerical study of the urban geometrical representation impact in a surface energy budget model. Environ. Fluid Mech. 2015, 15, 251–273. [Google Scholar] [CrossRef]




| Author | Site | hm [m] | z0 [m] | d0 [m] | z [m] | Layer of Measuring |
|---|---|---|---|---|---|---|
| Wood (2010) W10 | urban area (London) | 8.8 ± 3.0 | 0.87 ± 0.48 | 4.3 ± 1.9 | 190.3 | CFL or above |
| Al-Jiboori (2002) AJ02 | urban area (Beijing) | n.a. | ~3.9 | ~22 | 47, 140, 280 | CFL, RSL, above CFL |
| Quan (2009) Q09 | urban area (Beijing) | n.a. | 1.75 | 40.12 | 47 | UCL |
| Dallman (2013) D13 | suburban area (Phoenix) | 3.54 ÷ 13.13 | 0.04 ÷ 0.18 | 0.52 ÷ 4.33 | ~15 | CFL |
| Moraes (2005) M05 | rural site (rice plantation in a valley) | n.a. | n.a. | n.a. | 10 | CFL |
| Xu (1997) X97Urb | urban area (Nanjing) | 8 | 0.63 | n.a. | 10, 20, 30, 40, 50 | RSL, CFL |
| Xu (1997) X97Rur | rural area (Baguazhou) | n.a. | 0.035 | n.a. | 16, 40, 64, 88, 116, 164 | CFL |
| Authors | Atmospheric Stability | a | b | p |
|---|---|---|---|---|
| W10 | Unstable | 1.31 | −0.65 | 1/3 |
| Stable | 1.40 | 0.46 | 0.19 | |
| AJ02 | Unstable | 1.22 | −1.05 | 1/3 |
| Stable | 1.22 | 1.05 | 1/3 | |
| Q09 | Unstable | 1.33 | −1.27 | 1/3 |
| Stable | 1.42 | 0.54 | 1/3 | |
| D13 | Unstable | 0.98 | −5.64 | 1/3 |
| Stable | 1.35 | 0.55 | 1/3 | |
| M05 | Unstable | 1.2 | −5.3 | 1/3 |
| Stable | 1.2 | 4.3 | 1/3 | |
| X97Urb | Unstable | 1.23 | −2.30 | 1/3 |
| Stable | 1.23 | 2.80 | 1/3 | |
| X97Rur | Unstable | 1.35 | −3.10 | 1/3 |
| Stable | 1.35 | 1.30 | 1/3 |
| Instruments | Variables | Dimensionless Measuring Height |
|---|---|---|
| Sonic anemometer | Meridional wind () | z/H = 1.15 |
| Zonal wind (V) | ||
| Vertical wind (W) | ||
| Virtual temperature () | ||
| Standard deviation of vertical wind () | ||
| Sensible heat turbulent flux in the normal and tilted coordinate system () | ||
| Friction velocity in the normal and tilted coordinate system () | ||
| Obukhov length in the normal and tilted coordinate system () | ||
| Wind direction | ||
| Tilt angle () | ||
| SODAR | Meridional wind () | 1.42 < z/H < 4.25 |
| Zonal wind () | ||
| Vertical wind () | ||
| Standard deviation of vertical wind () |
| Stability Class | Obukhov Length Range |
|---|---|
| A | |
| B | |
| C | |
| D | |
| E | |
| F | |
| G | |
| H |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pelliccioni, A.; Grandoni, L.; Di Bernardino, A. Evaluation of Profiles of Standard Deviation of Vertical Wind in the Urban Area of Rome: Performances of Monin–Obukhov Similarity Theory Using Different Scaling Variables. Sustainability 2021, 13, 8426. https://doi.org/10.3390/su13158426
Pelliccioni A, Grandoni L, Di Bernardino A. Evaluation of Profiles of Standard Deviation of Vertical Wind in the Urban Area of Rome: Performances of Monin–Obukhov Similarity Theory Using Different Scaling Variables. Sustainability. 2021; 13(15):8426. https://doi.org/10.3390/su13158426
Chicago/Turabian StylePelliccioni, Armando, Livia Grandoni, and Annalisa Di Bernardino. 2021. "Evaluation of Profiles of Standard Deviation of Vertical Wind in the Urban Area of Rome: Performances of Monin–Obukhov Similarity Theory Using Different Scaling Variables" Sustainability 13, no. 15: 8426. https://doi.org/10.3390/su13158426
APA StylePelliccioni, A., Grandoni, L., & Di Bernardino, A. (2021). Evaluation of Profiles of Standard Deviation of Vertical Wind in the Urban Area of Rome: Performances of Monin–Obukhov Similarity Theory Using Different Scaling Variables. Sustainability, 13(15), 8426. https://doi.org/10.3390/su13158426







