Predicting Parameters of Heat Transfer in a Shell and Tube Heat Exchanger Using Aluminum Oxide Nanofluid with Artificial Neural Network (ANN) and Self-Organizing Map (SOM)
Abstract
:1. Introduction
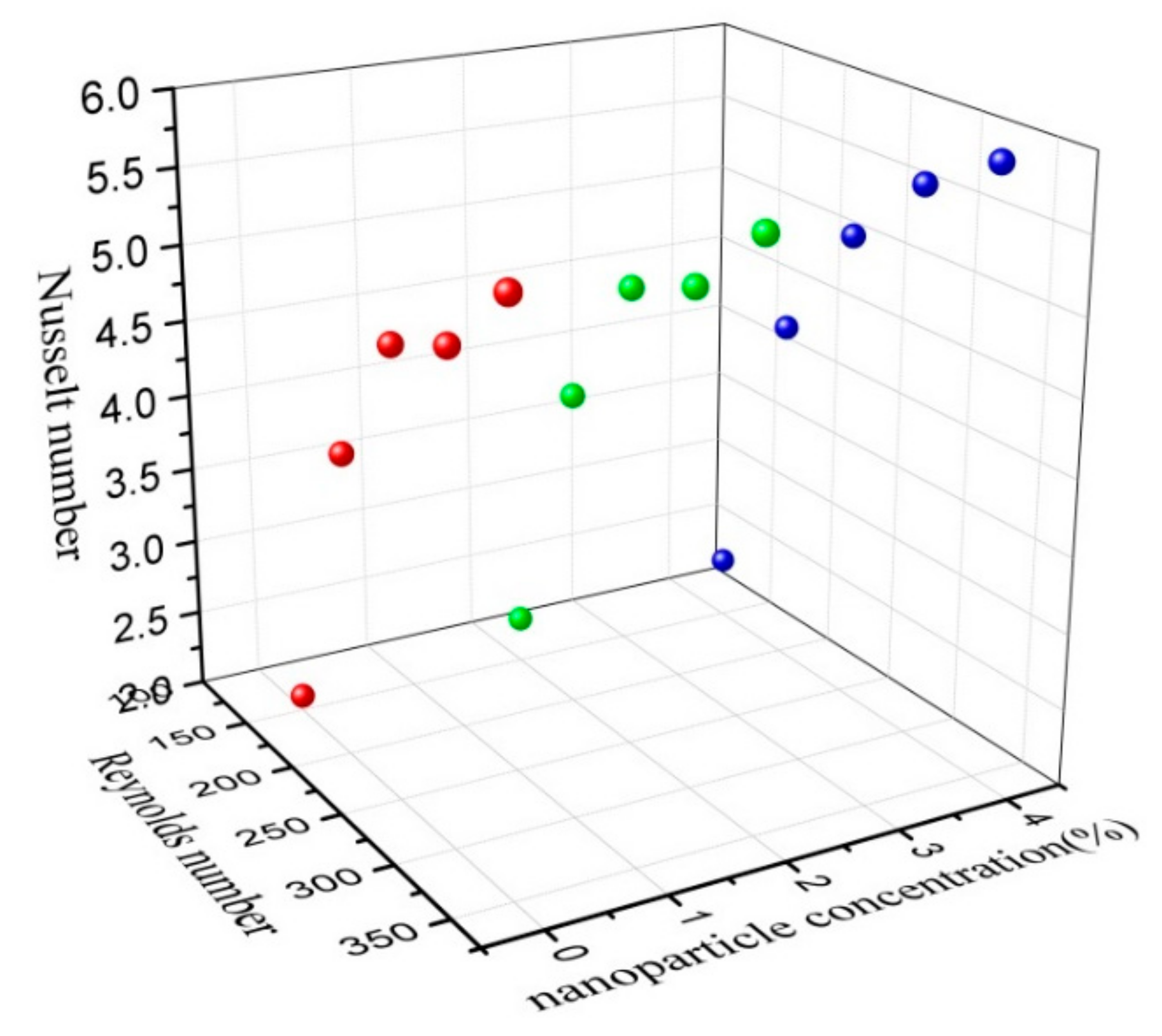
2. Experimental Data
3. Design of Neural Network Structure
3.1. Multilayer Perceptron (MLP) Neural Network
3.2. Radial Base Function Model
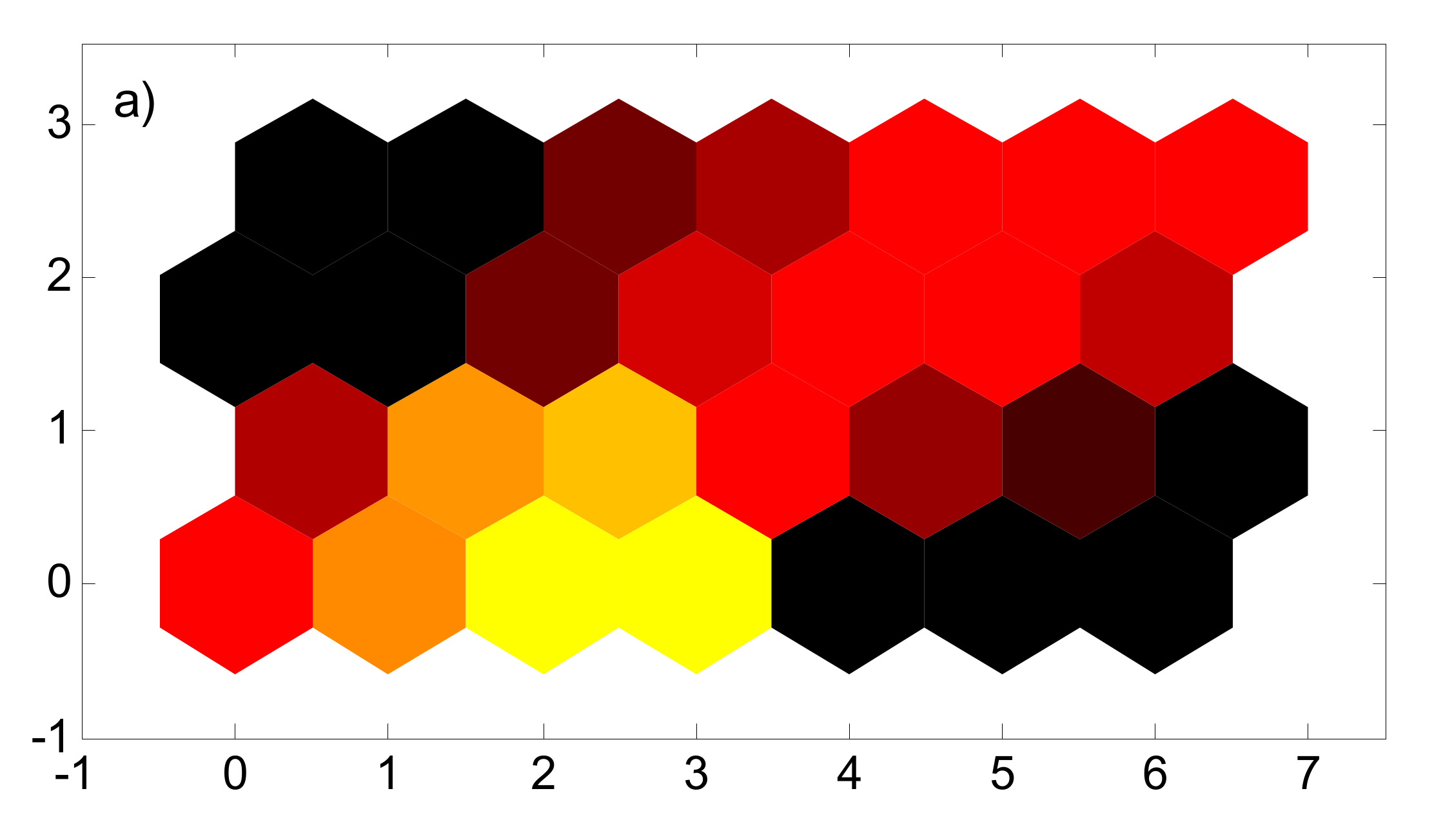
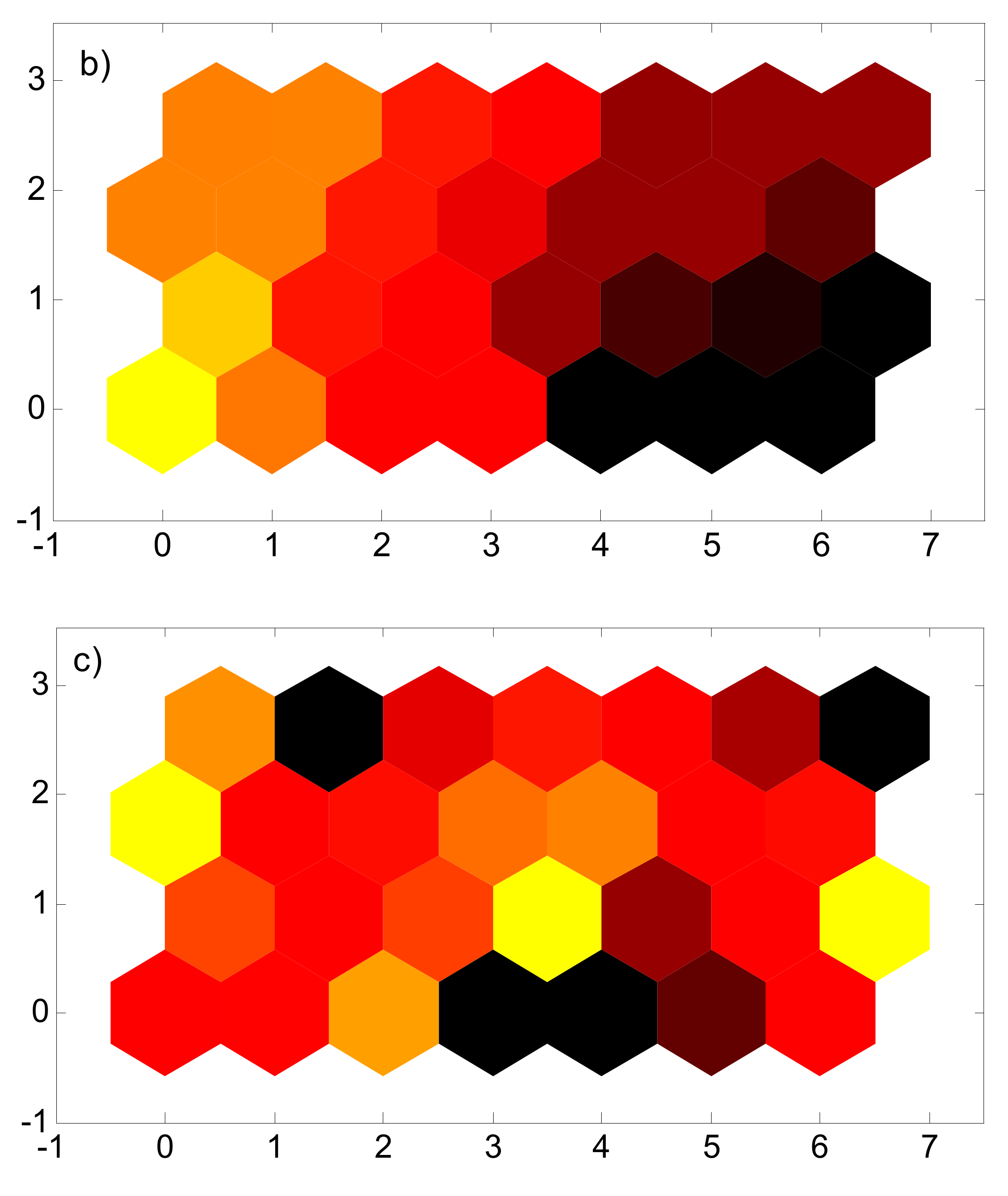
3.3. Self-Organizing Map (SOM) Neural Network
4. Levenberg–Marquardt and Momentum Algorithm
4.1. Back Propagation Learning Algorithm
4.2. Momentum Algorithm
5. Modeling of Artificial Neural Network
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SOM | self-organizing map |
| ANN | artificial neural network |
| MLP | multi-layer perceptron |
| BP | back propagation |
| MSE | mean square error |
| R | correlation coefficients |
| eMAX | maximum error |
| LM | Levenberg-Marquardt |
References
- Elsaid, K.; Abdelkareem, M.A.; Maghrabie, H.M.; Sayed, E.T.; Wilberforce, T.; Baroutaji, A.; Olabi, A.G. Thermophysical properties of graphene-based nanofluids. Int. J. Thermofluids 2021, 10, 100073. [Google Scholar] [CrossRef]
- Ma, M.; Zhai, Y.; Yao, P.; Li, Y.; Wang, H. Effect of surfactant on the rheological behavior and thermophysical properties of hybrid nanofluids. Powder Technol. 2021, 379, 373–383. [Google Scholar] [CrossRef]
- Kumar, A.; Subudhi, S. Experimental investigation on the thermophysical properties of low concentration magnetic colloidal suspensions (nanofluids) with the variations in temperature & magnetic field. J. Magn. Magn. Mater. 2021, 526, 167723. [Google Scholar]
- Hozien, O.; El-Maghlany, W.M.; Sorour, M.M.; Mohamed, Y.S. Experimental study on thermophysical properties of TiO2, ZnO and Ag water base nanofluids. J. Mol. Liq. 2021, 334, 116128. [Google Scholar] [CrossRef]
- Urmi, W.; Rahman, M.M.; Hamzah, W.A.W. An experimental investigation on the thermophysical properties of 40% ethylene glycol based TiO2-Al2O3 hybrid nanofluids. Int. Commun. Heat Mass Transf. 2020, 116, 104663. [Google Scholar] [CrossRef]
- Narankhishig, Z.; Ham, J.; Lee, H.; Cho, H. Convective heat transfer characteristics of nanofluids including the magnetic effect on heat transfer enhancement—A review. Appl. Therm. Eng. 2021, 193, 116987. [Google Scholar] [CrossRef]
- Saleh, B.; Sundar, L.S. Experimental study on heat transfer, friction factor, entropy and exergy efficiency analyses of a corrugated plate heat exchanger using Ni/water nanofluids. Int. J. Therm. Sci. 2021, 165, 106935. [Google Scholar] [CrossRef]
- Singh, K.; Sharma, S.K.; Gupta, S.M. An experimental investigation of hydrodynamic and heat transfer characteristics of surfactant-water solution and CNT nanofluid in a helical coil-based heat exchanger. Mater. Today Proc. 2021, 43, 3896–3903. [Google Scholar]
- Fazeli, I.; Emami MR, S.; Rashidi, A. Investigation and optimization of the behavior of heat transfer and flow of MWCNT-CuO hybrid nanofluid in a brazed plate heat exchanger using response surface methodology. Int. Commun. Heat Mass Transf. 2021, 122, 105175. [Google Scholar] [CrossRef]
- Akbari, O.A.; Toghraie, D.; Karimipour, A.; Safaei, M.R.; Goodarzi, M.; Alipour, H.; Dahari, M. Investigation of rib's height effect on heat transfer and flow parameters of laminar water–Al2O3 nanofluid in a rib-microchannel. Appl. Math. Comput. 2016, 290, 135–153. [Google Scholar]
- Wanatasanapan, V.V.; Abdullah, M.Z.; Gunnasegaran, P. Effect of TiO2-Al2O3 nanoparticle mixing ratio on the thermal conductivity, rheological properties, and dynamic viscosity of water-based hybrid nanofluid. J. Mater. Res. Technol. 2020, 9, 13781–13792. [Google Scholar] [CrossRef]
- Li, L.; Zhai, Y.; Jin, Y.; Wang, J.; Wang, H.; Ma, M. Stability, thermal performance and artificial neural network modeling of viscosity and thermal conductivity of Al2O3-ethylene glycol nanofluids. Powder Technol. 2020, 363, 360–368. [Google Scholar] [CrossRef]
- Sekhar, T.V.R.; Nandan, G.; Prakash, R.; Muthuraman, M. Investigations on viscosity and thermal conductivity of cobalt oxide-water nano fluid. Mater. Today Proc. 2018, 5, 6176–6182. [Google Scholar] [CrossRef]
- Gu, Y.; Xu, S.; Wu, X. Thermal conductivity enhancements and viscosity properties of water based Nanofluid containing carbon nanotubes decorated with ag nanoparticles. Heat Mass Transf. 2018, 54, 1847–1852. [Google Scholar] [CrossRef]
- Bahmani, M.H.; Sheikhzadeh, G.; Zarringhalam, M.; Akbari, O.A.; Alrashed, A.A.; Shabani GA, S.; Goodarzi, M. Investigation of turbulent heat transfer and nanofluid flow in a double pipe heat exchanger. Adv. Powder Technol. 2018, 29, 273–282. [Google Scholar] [CrossRef]
- Maddah, H.; Aghayari, R.; Mirzaee, M.; Ahmadi, M.H.; Sadeghzadeh, M.; Chamkha, A.J. Factorial experimental design for the thermal performance of a double pipe heat exchanger using Al2O3-TiO2 hybrid nanofluid. Int. Commun. Heat Mass Transf. 2018, 97, 92–102. [Google Scholar] [CrossRef]
- Goodarzi, M.; Amiri, A.; Goodarzi, M.S.; Safaei, M.R.; Karimipour, A.; Languri, E.M.; Dahari, M. Investigation of heat transfer and pressure drop of a counter flow corrugated plate heat exchanger using MWCNT based nanofluids. Int. Commun. Heat Mass Transf. 2015, 66, 172–179. [Google Scholar] [CrossRef]
- Fares, M.; Mohammad, A.M.; Mohammed, A.S. Heat transfer analysis of a shell and tube heat exchanger operated with graphene nanofluids. Case Stud. Therm. Eng. 2020, 18, 100584. [Google Scholar] [CrossRef]
- Cox, J.; Kanjirakat, A.; Sadr, R. Application of Nanofluids in a Shell-and-Tube Heat Exchanger. In Proceedings of the International Conference on Nanochannels, Microchannels, and Minichannels, Sapporo, Japan, 10–16 June 2013; American Society of Mechanical Engineers: New York, NY, USA, 2013; V001T02A003. [Google Scholar]
- Shahsavar, A.; Godini, A.; Sardari, P.T.; Toghraie, D.; Salehipour, H. Impact of variable fluid properties on forced convection of Fe3O4/CNT/water hybrid nanofluid in a double-pipe mini-channel heat exchanger. J. Therm. Anal. Calorim. 2019, 137, 1031–1043. [Google Scholar] [CrossRef]
- Maddah, H.; Ghazvini, M.; Ahmadi, M.H.; Bui, D.T.; Bandarr Filho, E.P. Performance evaluation of a U-shaped heat exchanger containing hybrid Cu/CNTs nanofluids: Experimental data and modeling using regression and artificial neural network. J. Therm. Anal. Calorim. 2021, 143, 1503–1521. [Google Scholar] [CrossRef]
- Ghasemi, N.; Aghayari, R.; Maddah, H. Designing an artificial neural network using radial basis function to model exergetic efficiency of nanofluids in mini double pipe heat exchanger. Heat Mass Transf. 2018, 54, 1707–1719. [Google Scholar] [CrossRef]
- Kahani, M.; Ahmadi, M.H.; Tatar, A.; Sadeghzadeh, M. Development of multilayer perceptron artificial neural network (MLP-ANN) and least square support vector machine (LSSVM) models to predict Nusselt number and pressure drop of TiO2/water nanofluid flows through non-straight pathways. Numer. Heat Transf. Part A Appl. 2018, 74, 1190–1206. [Google Scholar] [CrossRef]
- Jafari, S.M.; Jabari, S.S.; Dehnad, D.; Shahidi, S.A. Heat transfer enhancement in thermal processing of tomato juice 333 by application of nanofluids. Food Bioprocess Technol. 2017, 10, 307–316. [Google Scholar] [CrossRef]
- Sadeghzadeh, M.; Maddah, H.; Ahmadi, M.H.; Khadang, A.; Ghazvini, M.; Mosavi, A.; Nabipour, N. Prediction of thermo-physical properties of TiO2-Al2O3/water nanoparticles by using artificial neural network. Nanomaterials 2020, 10, 697. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shah, Z.; Kumam, P.; Selim, M.M.; Alshehri, A. Impact of nanoparticles shape and radiation on the behavior of nanofluid under the Lorentz forces. Case Stud. Therm. Eng. 2021, 26, 101161. [Google Scholar] [CrossRef]
- Esfe, M.H.; Esfandeh, S.; Saedodin, S.; Rostamian, H. Experimental evaluation, sensitivity analyzation and ANN modeling of thermal conductivity of ZnO-MWCNT/EG-water hybrid nanofluid for engineering applications. Appl. Therm. Eng. 2017, 125, 673–685. [Google Scholar] [CrossRef]
- Shah, Z.; Jafaryar, M.; Sheikholeslami, M.; Kumam, P. Heat transfer intensification of nanomaterial with involve of swirl flow device concerning entropy generation. Sci. Rep. 2021, 11, 1–15. [Google Scholar] [CrossRef]
- Shah, Z.; Saeed, A.; Khan, I.; MSelim, M.; Kumam, P. Numerical modeling on hybrid nanofluid (Fe3O4+ MWCNT/H2O) migration considering MHD effect over a porous cylinder. PLoS ONE 2021, 16, e0251744. [Google Scholar] [CrossRef]
- Shah, Z.; Jan, R.; Kumam, P.; Deebani, W.; Shutaywi, M. Fractional Dynamics of HIV with Source Term for the Supply of New CD4+ T-Cells Depending on the Viral Load via Caputo–Fabrizio Derivative. Molecules 2021, 26, 1806. [Google Scholar] [CrossRef]
- Ghasemi, N.; Maddah, H.; Mohebbi, M.; Aghayari, R.; Rohani, S. Proposing a method for combining monitored multilayered perceptron (MLP) and self-organizing map (SOM) neural networks in prediction of heat transfer parameters in a double pipe heat exchanger with nanofluid. Heat Mass Transf. 2019, 55, 2261–2276. [Google Scholar] [CrossRef]
- Maddah, H.; Aghayari, R.; Ahmadi, M.H.; Rahimzadeh, M.; Ghasemi, N. Prediction and modeling of MWCNT/Carbon (60/40)/SAE 10 W 40/SAE 85 W 90 (50/50) nanofluid viscosity using artificial neural network (ANN) and self-organizing map (SOM). J. Therm. Anal. Calorim. 2018, 134, 2275–2286. [Google Scholar] [CrossRef]
- Hojjat, M. Nanofluids as coolant in a shell and tube heat exchanger: ANN modeling and multi-objective optimization. Appl. Math. Comput. 2020, 365, 124710. [Google Scholar] [CrossRef]
- Aghayari, R.; Rohani, S.; Ghasemi, N.; Heiran EN, K.; Mazaheri, H. Numerical investigation of heat transfer in a helically coiled tube using copper/water nano-fluid under constant heat flux and prediction of the results using perceptron and radial basis function networks. Heat Mass Transf. 2020, 56, 1051–1075. [Google Scholar] [CrossRef]
- Esfe, M.H. Designing a neural network for predicting the heat transfer and pressure drop characteristics of Ag/water nanofluids in a heat exchanger. Appl. Therm. Eng. 2017, 126, 559–565. [Google Scholar] [CrossRef]
- Aghayari, R.; Maddah, H.; Pourkiaei, S.M.; Ahmadi, M.H.; Chen, L.; Ghazvini, M. Theoretical and experimental studies of heat transfer in a double-pipe heat exchanger equipped with twisted tape and nanofluid. Eur. Phys. J. Plus 2020, 135, 1–26. [Google Scholar] [CrossRef]
- Ellis, G.W.; Yao, C.; Zhao, R.; Penumadu, D. Stress-strain modeling of sands using artificial neural networks. J. Geotech. Eng. 1995, 121, 429–435. [Google Scholar] [CrossRef]
- Kohonen, T. Self-Organizing Maps; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]












| Authors | Nanoparticles | Heat Exchanger | Response | Method |
|---|---|---|---|---|
| Ghasemi et al. [31] | magnesium oxide | double pipe heat exchanger | Nusselt number, overall heat transfer coefficient and pressure drop | ANN-SOM |
| Maddah et al. [32] | multiwall carbon nanotube/carbon (60/40) | double pipe heat exchanger | relative viscosity | ANN-SOM |
| Hojjat et al. [33] | Aluminum oxide | a shell and tube heat exchanger | Nusselt number, pressure drop | ANN |
| Aghayari et al. [34] | copper oxide | helical coil | Nusselt number, entropy generation | ANN-SOM |
| Hemmat Esfe et al. [35] | Ag | double tube heat exchange | Nusselt number, pressure drop | RBF-ANN |
| Aghayari et al. [36] | iron oxide | double tube heat exchange | Nusselt number | ANN |
| Levenberg-Marquardt Algorithm | Momentum Algorithm | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Nusselt Number | Consumption Energy | Nusselt Number Consumption Energy | |||||||
| Number of Hidden Layers | Number of Neurons in Each Hidden Layer | R | MSE | R | MSE | R | MSE | R | MSE |
| 1 | 2 | 0.97935 | 0.01402 | 0.98868 | 0.00265 | 0.9832 | 0.008365 | 0.9752 | 0.000131 |
| 1 | 4 | 0.99875 | 0.008475 | 0.99925 | 0.001165 | 0.9838 | 0.009472 | 0.9781 | 0.000153 |
| 1 | 6 | 0.99912 | 0.005541 | 0.99945 | 0.000841 | 0.9758 | 0.006047 | 0.9745 | 0.000159 |
| 1 | 8 | 0.99951 | 0.007460 | 0.99869 | 0.000195 | 0.9806 | 0.006814 | 0.9814 | 0.000137 |
| 1 | 10 | 0.98912 | 0.005511 | 0.99865 | 0.006512 | 0.9824 | 0.003764 | 0.9736 | 0.000146 |
| 1 | 12 | 0.99966 | 0.003298 | 0.9954 | 0.005514 | 0.9840 | 0.005381 | 0.9746 | 0.000137 |
| 1 | 14 | 0.9976 | 0.004157 | 0.99875 | 0.000635 | 0.9847 | 0.004375 | 0.9840 | 0.000148 |
| 1 | 16 | 0.99865 | 0.002639 | 0.99868 | 0.000351 | 0.9853 | 0.005592 | 0.9824 | 0.000129 |
| 1 | 18 | 0.9984 | 0.003554 | 0.9925 | 0.0001515 | 0.9858 | 0.005241 | 0.9779 | 0.000136 |
| 1 | 20 | 0.9969 | 0.0060239 | 0.9899 | 0.000412 | 0.9860 | 0.003930 | 0.9804 | 0.000154 |
| 1 | 22 | 0.9994 | 0.0023357 | 0.9993 | 0.00011465 | 0.9869 | 0.003254 | 0.9874 | 0.000123 |
| 1 | 24 | 0.9989 | 0.002714 | 0.9923 | 0.00012365 | 0.9861 | 0.004725 | 0.9796 | 0.000134 |
| 1 | 26 | 0.9991 | 0.003046 | 0.9965 | 0.0006315 | 0.9855 | 0.005695 | 0.9813 | 0.000147 |
| 1 | 28 | 0.9981 | 0.002398 | 0.9994 | 0.0001936 | 0.9859 | 0.003628 | 0.9857 | 0.000149 |
| Levenberg-Marquardt Algorithm | Momentum Algorithm | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Nusselt Number | Consumption Energy | Nusselt Number | Consumption Energy | ||||||
| Number of Hidden Layers | Number of Neurons in Each Hidden Layer | R | MSE | R | MSE | R | MSE | R | MSE |
| 1 | 2 | 0.9836 | 0.0654 | 0.9725 | 0.007461 | 0.9614 | 0.004256 | 0.9756 | 0.007112 |
| 1 | 4 | 0.9940 | 0.0084 | 0.9934 | 0.004629 | 0.9687 | 0.004875 | 0.9732 | 0.006148 |
| 1 | 6 | 0.9894 | 0.00749 | 0.9654 | 0.003324 | 0.9754 | 0.005298 | 0.9785 | 0.008322 |
| 1 | 8 | 0.9774 | 0.00254 | 0.9870 | 0.001782 | 0.9801 | 0.006489 | 0.9821 | 0.008156 |
| 1 | 10 | 0.9568 | 0.00612 | 0.9813 | 0.006514 | 0.9736 | 0.006234 | 0.9713 | 0.008417 |
| 1 | 12 | 0.9740 | 0.00532 | 0.9765 | 0.001487 | 0.9801 | 0.006128 | 0.9724 | 0.006612 |
| 1 | 14 | 0.9900 | 0.003541 | 0.9841 | 0.003621 | 0.9733 | 0.004736 | 0.9776 | 0.006954 |
| 1 | 16 | 0.9811 | 0.00423 | 0.9770 | 0.002140 | 0.9758 | 0.006512 | 0.9637 | 0.007532 |
| 1 | 18 | 0.9638 | 0.006988 | 0.9855 | 0.005541 | 0.9763 | 0.005127 | 0.9635 | 0.007713 |
| 1 | 20 | 0.9891 | 0.05547 | 0.9894 | 0.002342 | 0.9804 | 0.005914 | 0.9646 | 0.003849 |
| 1 | 22 | 0.9898 | 0.003154 | 0.9902 | 0.001411 | 0.9811 | 0.003941 | 0.9878 | 0.003745 |
| 1 | 24 | 0.9768 | 0.003180 | 0.9876 | 0.002514 | 0.9788 | 0.004824 | 0.9744 | 0.004185 |
| 1 | 26 | 0.9735 | 0.00425 | 0.9725 | 0.004156 | 0.9768 | 0.006718 | 0.9785 | 0.004732 |
| 1 | 28 | 0.9888 | 0.00648 | 0.9741 | 0.007416 | 0.9725 | 0.006284 | 0.9796 | 00003924 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zolghadri, A.; Maddah, H.; Ahmadi, M.H.; Sharifpur, M. Predicting Parameters of Heat Transfer in a Shell and Tube Heat Exchanger Using Aluminum Oxide Nanofluid with Artificial Neural Network (ANN) and Self-Organizing Map (SOM). Sustainability 2021, 13, 8824. https://doi.org/10.3390/su13168824
Zolghadri A, Maddah H, Ahmadi MH, Sharifpur M. Predicting Parameters of Heat Transfer in a Shell and Tube Heat Exchanger Using Aluminum Oxide Nanofluid with Artificial Neural Network (ANN) and Self-Organizing Map (SOM). Sustainability. 2021; 13(16):8824. https://doi.org/10.3390/su13168824
Chicago/Turabian StyleZolghadri, Amir, Heydar Maddah, Mohammad Hossein Ahmadi, and Mohsen Sharifpur. 2021. "Predicting Parameters of Heat Transfer in a Shell and Tube Heat Exchanger Using Aluminum Oxide Nanofluid with Artificial Neural Network (ANN) and Self-Organizing Map (SOM)" Sustainability 13, no. 16: 8824. https://doi.org/10.3390/su13168824
APA StyleZolghadri, A., Maddah, H., Ahmadi, M. H., & Sharifpur, M. (2021). Predicting Parameters of Heat Transfer in a Shell and Tube Heat Exchanger Using Aluminum Oxide Nanofluid with Artificial Neural Network (ANN) and Self-Organizing Map (SOM). Sustainability, 13(16), 8824. https://doi.org/10.3390/su13168824







