A Flexible Cap-and-Trade Policy and Limited Demand Information Effects on a Sustainable Supply Chain
Abstract
:1. Introduction
2. Literature Review
2.1. Carbon Emission Policies
2.2. Supply Chain Coordination
2.3. Distribution-Free Newsvendor Model
3. Problem Descriptions, Assumptions, and Notations
4. Model Development
4.1. Analysis of the Newsvendor Model
4.1.1. The Decentralized System
4.1.2. The Centralized System
4.2. Analysis of the Distribution-Free Newsvendor Model
4.2.1. The Decentralized System
4.2.2. The Centralized System
4.3. Analysis of the Coordination under the Distribution-Free Newsvendor Model
4.3.1. Coordination with the RS Contract
4.3.2. Coordination with the TPT Contract
5. Numerical Analyses
5.1. Effectiveness Analysis of the Distribution-Free Newsvendor Model
| Distribution | System | Invest or Not | ||||||
|---|---|---|---|---|---|---|---|---|
| Uniform distribution | C | Yes | 0.84 | 998 | − | − | 28,591 | 139.45 |
| No | 0 | 846 | − | − | 22,655 | 744.85 | ||
| D | Yes | 0.60 | 810 | 7241 | 18,854 | 26,095 | 284.35 | |
| No | 0 | 735 | 5739 | 15,719 | 21,458 | 646.41 | ||
| Normal distribution | C | Yes | 0.86 | 1025 | − | − | 28,226 | 129.46 |
| No | 0 | 822 | − | − | 22,352 | 723.41 | ||
| D | Yes | 0.59 | 782 | 7548 | 18,133 | 25,681 | 285.41 | |
| No | 0 | 708 | 6085 | 15,162 | 21,247 | 623.47 | ||
| Worst-case distribution | C | Yes | 0.95 | 1184 | − | − | 26,250 | 56.06 |
| No | 0 | 820 | − | − | 20,071 | 721.43 | ||
| D | Yes | 0.58 | 767 | 5537 | 17,756 | 23,293 | 285.65 | |
| No | 0 | 695 | 4095 | 14,869 | 18,964 | 611.42 |
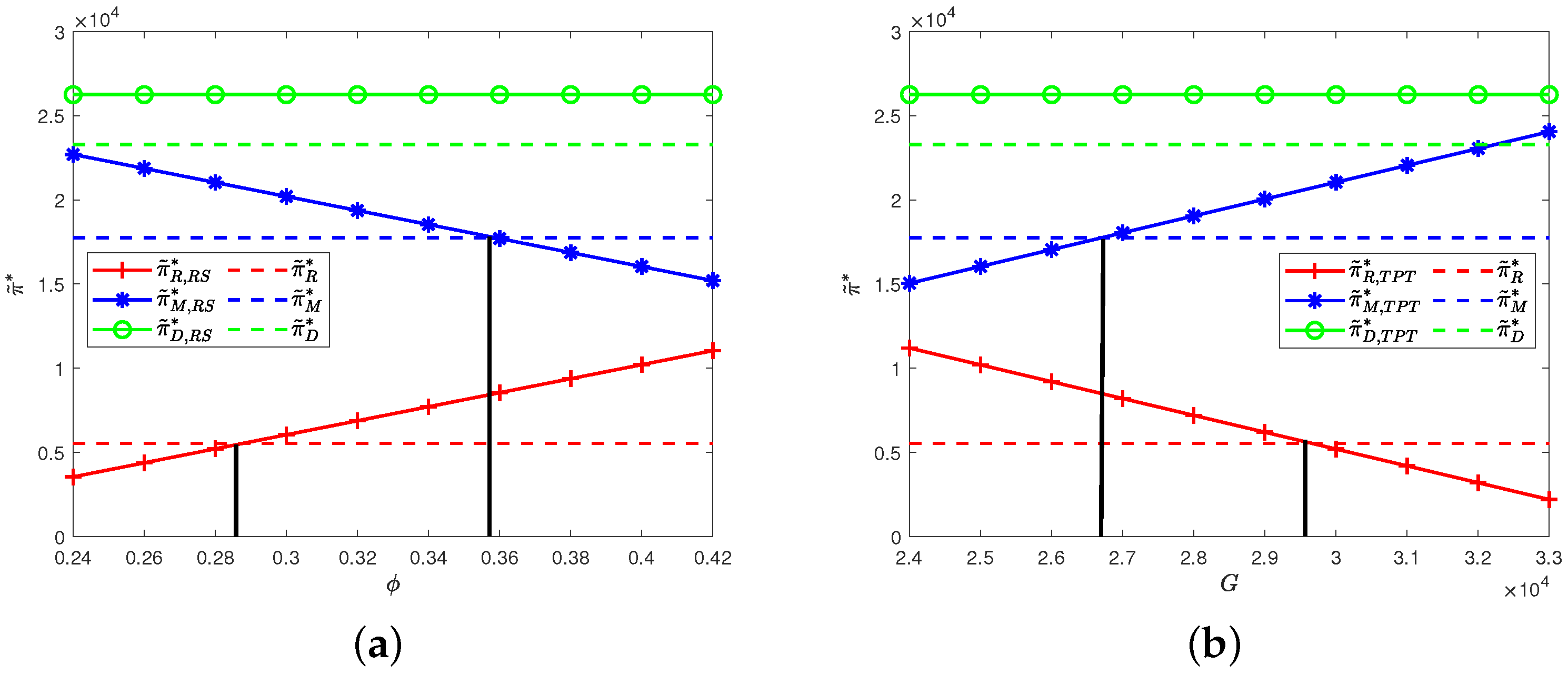
5.2. Performance Analysis of Supply Chain Coordination
5.3. Managerial Insights
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Proof of Theorem 1
Appendix B. The Proof of Theorem 2
Appendix C. The Proof of Theorem 3
Appendix D. The Proof of Corollary 1
Appendix E. The Proof of Theorem 4
Appendix F. The Proof of Theorem 5
Appendix G. The Proof of Theorem 6
References
- Sun, L.X.; Xia, Y.S.; Feng, C. Income gap and global carbon productivity inequality: A meta-frontier data envelopment analysis. Sustain. Prod. Consump. 2021, 26, 548–557. [Google Scholar] [CrossRef]
- Fan, Z.Y.; Friedmann, S.J. Low-carbon production of iron and steel: Technology options, economic assessment, and policy. Joule 2021, 5, 829–862. [Google Scholar] [CrossRef]
- Xu, J.T.; Bai, Q.G.; Xu, L.; Hu, T.T. Effects of and partial demand information on operational decisions of a newsvendor problem. J. Clean. Prod. 2018, 188, 825–839. [Google Scholar] [CrossRef]
- Wang, Z.R.; Wu, Q.H. Carbon emission reduction and product collection decisions in the closed-loop supply chain with cap-and-trade regulation. Int. J. Prod. Res. 2021, 59, 4359–4383. [Google Scholar] [CrossRef]
- Zhang, G.T.; Zhang, X.; Sun, H.; Zhao, X.Y. Three-echelon closed-loop supply chain network equilibrium under cap-and-trade regulation. Sustainaiblity 2021, 13, 6472. [Google Scholar] [CrossRef]
- Fang, Z.M.; Moolchandani, K.; Chao, H.; DeLaurentis, D. A method for emission allowances allocation in air transportation systems from a system-of-systems perspective. J. Clean. Prod. 2019, 226, 419–431. [Google Scholar] [CrossRef]
- Wang, M.; Zhao, L.D.; Herty, M. Modelling carbon trading and refrigerated logistics services within a fresh food supply chain under carbon cap-and-trade regulation. Int. J. Prod. Res. 2018, 56, 4207–4225. [Google Scholar] [CrossRef]
- Wang, S.Y.; Wu, Z.H.; Yang, B.C. Decision and performance analysis of a price-setting manufacturer with options under a flexible-cap emission trading scheme (ETS). Sustainability 2018, 10, 3681. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Ji, J.N.; Wang, M.Z.; Wang, Z.Z. The manufacturer’s joint decisions of channel selections and carbon emission reductions under the cap-and-trade regulation. J. Clean. Prod. 2018, 193, 506–523. [Google Scholar] [CrossRef]
- Wang, S.Y.; Choi, S.H. Pareto-efficient coordination of the contract-based MTO supply chain under flexible cap-and-trade emission constraint. J. Clean. Prod. 2020, 250, 119571. [Google Scholar] [CrossRef]
- Yu, M.; Cao, E.B. Information sharing format and carbon emission abatement in a supply chain with competition. Int. J. Prod. Res. 2020, 58, 6775–6790. [Google Scholar] [CrossRef]
- Dou, G.W.; Choi, T.M. Does implementing trade-in and green technology together benefit the environment? Eur. J. Oper. Res. 2021, 295, 517–533. [Google Scholar] [CrossRef]
- Testa, F.; Nucci, B.; Iraldo, F.; Appolloni, A.; Daddi, T. Removing obstacles to the implementation of LCA among SMEs: A collective strategy for exploiting recycled wool. J. Clean. Prod. 2017, 156, 923–931. [Google Scholar] [CrossRef]
- Ma, X.L.; Xu, J.T.; Peng, W.L.; Wang, S.Y. Optimal freshness and carbon abatement decisions in a two-echelon cold chain. Appl. Math. Model. 2021, 96, 834–859. [Google Scholar] [CrossRef]
- Yang, H.X.; Chen, W.B. Retailer-driven carbon emission abatement with consumer environmental awareness and carbon tax: Revenue-sharing versus cost-sharing. Omega 2018, 78, 179–191. [Google Scholar] [CrossRef]
- Bai, Q.G.; Xu, J.T.; Zhang, Y.Z. The distributionally robust optimization model for a remanufacturing system under cap-and-trade policy: A newsvendor approach. Ann. Oper. Res. 2020. [Google Scholar] [CrossRef]
- Yadav, D.; Kumari, R.; Kumar, N.; Sarkar, B. Reduction of waste and carbon emission through the selection of items with cross-price elasticity of demand to form a sustainable supply chain with preservation technology. J. Clean. Prod. 2021, 297, 126298. [Google Scholar] [CrossRef]
- Ullah, M.; Asghar, I.; Zahid, M.; Omair, M.; AlArjani, A.; Sarkar, B. Rami fi cation of remanufacturing in a sustainable three-echelon closed-loop supply chain management for returnable products. J. Clean. Prod. 2021, 290, 125609. [Google Scholar] [CrossRef]
- Wang, M.; Zhao, L.D.; Herty, M. Joint replenishment and carbon trading in fresh food supply chains. Eur. J. Oper. Res. 2019, 277, 561–573. [Google Scholar] [CrossRef]
- Ji, T.; Xu, X.P.; Yan, X.M.; Yu, Y.G. The production decisions and cap setting with wholesale price and revenue-sharing contracts under cap-and-trade regulation. Int. J. Prod. Res. 2020, 58, 128–147. [Google Scholar] [CrossRef]
- Liu, B.Y.; Hua, Z.S.; Zhang, Q.H.; Yang, H.D.; Migdalas, A. Optimal operational decision making of manufacturers and authorized remanufacturers with patent licensing under carbon cap-and-trade regulations. Complexity 2020, 2020, 1864641. [Google Scholar]
- Bai, Q.G.; Chen, M.Y.; Xu, L. Revenue and promotional cost-sharing contract versus two-part tariff contract in coordinating sustainable supply chain systems with deteriorating items. Int. J. Prod. Econ. 2017, 187, 85–101. [Google Scholar] [CrossRef]
- Qu, S.J.; Jiang, G.Q.; Ji, Y.; Zhang, G.M.; Mohamed, N. Newsvendor’s optimal decisions under stochastic demand and cap-and-trade regulation. Environ. Dev. Sustain. 2021. [Google Scholar] [CrossRef]
- Bai, Q.G.; Meng, F.W. Impact of risk aversion on two-echelon supply chain systems with carbon constraints. J. Ind. Manag. Optim. 2020, 16, 1943–1965. [Google Scholar]
- Zheng, Y.F.; Zhou, W.H.; Chen, X.; Huang, W.X. The effect of emission permit allocation in an early-stage cap-and-trade for a duopoly market. Int. J. Prod. Res. 2020, 59, 909–925. [Google Scholar] [CrossRef]
- Chang, X.Y.; Li, Y.P.; Zhao, Y.B.; Liu, W.J.; Wu, J. Effects of carbon permits allocation methods on remanufacturing production decisions. J. Clean. Prod. 2017, 152, 281–294. [Google Scholar] [CrossRef]
- Ji, J.N.; Zhang, Z.Y.; Yang, L. Comparisons of initial carbon allowance allocation rules in an o2o retail supply chain with the cap-and-trade regulation. Int. J. Prod. Econ. 2017, 187, 68–84. [Google Scholar] [CrossRef]
- Li, L.Q.; Liu, K. Coordination contract design for the newsvendor model. Eur. J. Oper. Res. 2020, 283, 380–389. [Google Scholar] [CrossRef]
- Pasternack, B. Optimal pricing and returns policies for perishable commodities. Mark. Sci. 1985, 4, 131–132. [Google Scholar] [CrossRef]
- Hou, Y.; Wei, F.; Li, S.X.; Huang, Z.; Ashley, A. Coordination and performance analysis for a three-echelon supply chain with a revenue-sharing contract. J. Clean. Prod. 2016, 55, 202–227. [Google Scholar] [CrossRef]
- Wu, C.Q.; Li, K.P.; Shi, T.Q. Supply chain coordination with two-part tariffs under information asymmetry. J. Clean. Prod. 2017, 55, 2575–2589. [Google Scholar] [CrossRef] [Green Version]
- Shen, B.; Xu, X.Y.; Choi, T.M. Simplicity is beauty: Pricing coordination in two-product supply chains with simplest contracts under voluntary compliance. Int. J. Prod. Res. 2019, 57, 2769–2787. [Google Scholar] [CrossRef]
- He, Y.; Huang, H.F.; Li, D. Inventory and pricing decisions for a dual-channel supply chain with deteriorating products. Oper. Res. 2020, 20, 1461–1503. [Google Scholar] [CrossRef]
- Liu, W.; Zhao, H.; Song, S.J.; He, W.X.; Li, X.C. Coping with Loss Aversion and Risk Management in the Supply Chain Coordination. Sustainability 2021, 13, 4364. [Google Scholar] [CrossRef]
- Dubey, V.K.; Chavas, J.P.; Veeramani, D. Analytical framework for sustainable supply chain contract management. Int. J. Prod. Econ. 2018, 200, 240–261. [Google Scholar] [CrossRef]
- Hong, Z.F.; Guo, X.L. Green product supply chain contracts considering environmental responsibilities. Omega 2019, 83, 155–166. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Yu, Z.Q.; Jin, M.Z.; Mao, J.F. Decisions and coordination of retailer-led low-carbon supply chain under altruistic preference. Eur. J. Oper. Res. 2021, 293, 910–925. [Google Scholar] [CrossRef]
- Xu, J.T.; Chen, Y.Y.; Bai, Q.G. A two-echelon sustainable supply chain coordination under cap-and-trade regulation. J. Clean. Prod. 2016, 135, 42–56. [Google Scholar] [CrossRef]
- Dong, C.W.; Shen, B.; Chow, P.S.; Yang, L.; Ng, C.T. Sustainability investment under cap-and-trade regulation. Ann. Oper. Res. 2016, 240, 509–531. [Google Scholar] [CrossRef]
- Bai, Q.G.; Gong, Y.M.; Jin, M.Z.; Xu, X.H. Effects of carbon on supply chain coordination with vendor-managed deteriorating product inventory. Int. J. Prod. Econ. 2019, 208, 83–99. [Google Scholar] [CrossRef]
- Scarf, H.; Arrow, K.J.; Karlin, S. A min-max solution of an inventory problem. Stud. Math. Theory Inventory Prod. 1958, 10, 201–209. [Google Scholar]
- Gallego, G.; Moon, I. The distribution free newsboy problem: Review and extensions. J. Oper. Res. Soc. 1993, 44, 825–834. [Google Scholar] [CrossRef]
- Mostard, J.; Koster, R.D.; Teunter, R. The distribution-free newsboy problem with resalable returns. Int. J. Prod. Econ. 2005, 97, 329–342. [Google Scholar] [CrossRef]
- Alfares, H.K.; Elmorra, H.H. The distribution-free newsboy problem: Extensions to the shortage penalty case. Int. J. Prod. Econ. 2005, 93-94, 465–477. [Google Scholar] [CrossRef]
- Lin, Y.J. Minimax distribution free procedure with backorder price discount. Int. J. Prod. Econ. 2008, 111, 118–128. [Google Scholar] [CrossRef]
- Lee, C.M.; Hsu, S.L. The effect of advertising on the distribution-free newsboy problem. Int. J. Prod. Econ. 2011, 129, 217–224. [Google Scholar] [CrossRef]
- Han, Q.M.; Du, D.L.; Zuluaga, L.F. Technical note-a risk-and ambiguity-averse extension of the max-min newsvendor order formula. Oper. Res. 2014, 62, 535–542. [Google Scholar] [CrossRef]
- Fu, Q.; Sim, C.K.; Teo, C.P. Profit sharing agreements in decentralized supply chains: A distributionally robust approach. Oper. Res. 2018, 66, 500–513. [Google Scholar] [CrossRef] [Green Version]
- Modak, N.M.; Kelle, P. Managing a dual-channel supply chain under price and delivery-time dependent stochastic demand. Eur. J. Oper. Res. 2019, 272, 147–161. [Google Scholar] [CrossRef]
- Raza, S.A.; Govindaluri, S.M. Greening and price differentiation coordination in a supply chain with partial demand information and cannibalization. J. Clean. Prod. 2019, 229, 706–726. [Google Scholar] [CrossRef]
- Fander, A.; Yaghoubi, S. Impact of fuel-efficient technology on automotive and fuel supply chain under government intervention: A case study. Appl. Math. Model. 2021, 97, 771–802. [Google Scholar] [CrossRef]
- Liu, B.Y.; Holmbom, M.; Segerstedt, A.; Chen, W.D. Effects of carbon emission regulations on remanufacturing decisions with limited information of demand distribution. Int. J. Prod. Res. 2015, 53, 532–548. [Google Scholar] [CrossRef]
- Lu, J.; Sun, X.C. Carbon regulations, production capacity, and low-carbon technology level for new products with incomplete demand information. J. Clean. Prod. 2021, 282, 124551. [Google Scholar] [CrossRef]
- Sarkis, J.; Cohen, M.J.; Dewick, P.; Schroder, P. A brave new world: Lessons from the COVID-19 pandemic for transitioning to sustainable supply and production. Resour. Conserv. Recycl. 2020, 159, 104894. [Google Scholar] [CrossRef] [PubMed]
- Leal, W.; Brandli, L.L.; Salvia, A.L.; Rayman-Bacchus, L.; Platje, J. COVID-19 and the UN Sustainable Development Goals: Threat to Solidarity or an Opportunity? Sustainability 2020, 12, 5343. [Google Scholar] [CrossRef]
- Amankwah-Amoah, J. Stepping up and stepping out of COVID-19: New challenges for environmental sustainability policies in the global airline industry. J. Clean. Prod. 2020, 271, 123000. [Google Scholar] [CrossRef]
- Ranjbari, M.; Esfandabadi, Z.S.; Zanetti, M.C.; Scagnelli, S.D.; Siebers, P.O.; Aghbashlo, M.; Peng, W.X.; Quatraro, F.; Tabatabaei, M. Three pillars of sustainability in the wake of COVID-19: A systematic review and future research agenda for sustainable development. J. Clean. Prod. 2021, 297, 126660. [Google Scholar] [CrossRef]
- Ivanov, D.; Dolgui, A. OR-methods for coping with the ripple effect in supply chains during COVID-19 pandemic: Managerial insights and research implications. Int. J. Prod. Econ. 2021. [Google Scholar] [CrossRef] [PubMed]
- Qu, Y.; Yu, Y.; Appolloni, A.; Li, M.R.; Liu, Y. Measuring Green Growth Efficiency for Chinese Manufacturing Industries. Sustainaiblity 2017, 9, 637. [Google Scholar] [CrossRef] [Green Version]
- Raza, S.A. A distribution free approach to newsvendor problem with pricing. 4OR-Q. J. Oper. Res. 2014, 12, 335–358. [Google Scholar] [CrossRef]
- Ahmed, W.; Moazzam, M.; Sarkar, B.; Rehman, S.U. Synergic effect of reworking for imperfect quality items with the integration of multi-period delay-in-payment and partial backordering in global supply chains. Engineering 2020, 7, 260–271. [Google Scholar] [CrossRef]
| Author(s) | Carbon Emission Policies | The C&T Policy | Low-Carbon Preference | Supply Chain Coordination | Distribution-Free Approach |
|---|---|---|---|---|---|
| Wang et al. (2019) [19] | √ | ||||
| Ji et al. (2020) [20] | √ | √ | |||
| Liu et al. (2020) [21] | √ | ||||
| Bai et al. (2017) [22] | √ | √ | |||
| Wang and Wu (2021) [4] | √ | √ | |||
| Bai and Meng (2020) [24] | √ | √ | |||
| Wang and Choi (2020) [10] | √ | √ | √ | √ | |
| Zheng et al. (2020) [25] | √ | √ | |||
| Chang et al. (2017) [26] | √ | √ | |||
| Ji et al. (2017) [27] | √ | √ | √ | ||
| Hou et al. (2016) [30] | √ | ||||
| Wu et al. (2017) [31] | √ | ||||
| Shen et al. (2019) [32] | √ | ||||
| He et al. (2020) [33] | √ | ||||
| Hong and Guo(2019) [36] | √ | √ | |||
| Wang et al. (2021) [37] | √ | √ | |||
| Xu et al. (2016) [38] | √ | √ | √ | ||
| Dong et al. (2016) [39] | √ | √ | √ | ||
| Bai et al. (2019) [40] | √ | √ | √ | ||
| Fu et al. (2018) [48] | √ | √ | |||
| Modak and Kelle (2019) [49] | √ | √ | |||
| Raza and Govindaluri (2019) [50] | √ | √ | |||
| Fander and Yaghoubi (2021) [51] | √ | ||||
| Liu et al. (2015) [52] | √ | √ | |||
| Xu et al. (2018) [3] | √ | √ | |||
| Lu and Sun (2021) [53] | √ | √ | |||
| Bai et al. (2020) [16] | √ | √ | |||
| Our paper | √ | √ | √ | √ | √ |
| Notations | Descriptions |
|---|---|
| Decision Variables | |
| q | Qrder quantity |
| Emission abatement level | |
| Parameters | |
| Market demand, which is positively influenced by the emission abatement level, , where is the basic market demand, is the emission abatement level elasticity parameter, and is the stochastic market demand | |
| The mean of the stochastic market demand | |
| Standard deviation of the stochastic market demand | |
| F | Cumulative distribution function of the stochastic market demand |
| The set of cumulative distribution functions satisfying a mean of and a variance of | |
| p | Unit selling price |
| v | Salvage value of an unsold product |
| s | Shortage cost of an out-of-stock product |
| w | Unit wholesale price |
| c | Unit raw material cost |
| e | Unit carbon emissions without the abatement investment |
| k | Flexible carbon emissions cap given by the government |
| Coefficient of abatement investment | |
| Unit trading price of carbon emission permit | |
| The expected profit | |
| J | Total carbon emissions |
| Revenue-sharing fraction offered by the retailer in the RS contract, where | |
| G | The lump-sum payment of the retailer in the TPT contract |
| Subscripts | |
| R | Retailer |
| M | Manufacturer |
| D | Decentralized system |
| C | Centralized system |
| Supply chain |
| Variables | |||||||
|---|---|---|---|---|---|---|---|
| Centralized system | − | 0.9462 | 1184 | − | − | 26250 | 56.0618 |
| decentralized system | − | 0.5767 | 767 | 5537 | 17,756 | 23,293 | 285.6478 |
| The RS contract | |||||||
| 7.23 | 0.9462 | 1184 | 6048 | 20,202 | 26,250 | 56.0618 | |
| 7.27 | 0.9462 | 1184 | 6881 | 19,369 | 26,250 | 56.0618 | |
| 7.31 | 0.9462 | 1184 | 7714 | 18,536 | 26,250 | 56.0618 | |
| The TPT contract | |||||||
| 8.61 | 0.9462 | 0.9462 | 8203 | 18,047 | 26,250 | 56.0618 | |
| 8.61 | 0.9462 | 0.9462 | 7203 | 19,047 | 26,250 | 56.0618 | |
| 8.61 | 0.9462 | 0.9462 | 6203 | 20,047 | 26,250 | 56.0618 |
| Variables | (±30%) | (±30%) | (±30%) | (±30%) | (±30%) | e(±30%) | k(±30%) |
|---|---|---|---|---|---|---|---|
| Variables with the same percentage under both contracts | |||||||
| 25.93% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | |
| 43.87% | 21.83% | 102.91% | 0.00% | 12.13% | 3.15% | 28.26% | |
| 58.82% | 7.56% | 13.75% | 16.43% | 15.92% | 2.86% | 25.32% | |
| 429.34% | 21.83% | 5.98% | 0.00% | 12.13% | 56.90% | 28.26% | |
| Variables under the RS contract | |||||||
| 22.46% | 0.00% | 0.00% | 0.00% | 27.78% | 5.43% | 45.72% | |
| 85.54% | 18.46% | 12.28% | 0.00% | 56.14% | 7.36% | 74.39% | |
| 49.31% | 3.78% | 14.27% | 21.29% | 7.18% | 1.41% | 11.95% | |
| Variables under the TPT contract | |||||||
| 30.16% | 0.00% | 0.00% | 0.00% | 34.98% | 7.18% | 59.03% | |
| 278.33% | 28.48% | 51.19% | 0.00% | 162.46% | 11.98% | 144.56% | |
| 24.44% | 0.00% | 0.00% | 20.66% | 0.00% | 0.00% | 0.00% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.; Xu, J.; Xu, H. A Flexible Cap-and-Trade Policy and Limited Demand Information Effects on a Sustainable Supply Chain. Sustainability 2021, 13, 10746. https://doi.org/10.3390/su131910746
Gao Y, Xu J, Xu H. A Flexible Cap-and-Trade Policy and Limited Demand Information Effects on a Sustainable Supply Chain. Sustainability. 2021; 13(19):10746. https://doi.org/10.3390/su131910746
Chicago/Turabian StyleGao, Ying, Jianteng Xu, and Huixin Xu. 2021. "A Flexible Cap-and-Trade Policy and Limited Demand Information Effects on a Sustainable Supply Chain" Sustainability 13, no. 19: 10746. https://doi.org/10.3390/su131910746
APA StyleGao, Y., Xu, J., & Xu, H. (2021). A Flexible Cap-and-Trade Policy and Limited Demand Information Effects on a Sustainable Supply Chain. Sustainability, 13(19), 10746. https://doi.org/10.3390/su131910746






