A Simplified Mechanistic-Empirical Flexible Pavement Design Method for Moderate to Hot Climate Regions
Abstract
:1. Introduction
- = Modified Witczak effective temperature for rutting, °F,
- = Modified Witczak effective temperature for fatigue, °F,
- z = Critical depth, in.,
- f = Loading frequency, Hz,
- MAAT = Mean annual air temperature, °F,
- = Standard deviation of the mean monthly air temperature, °F,
- Rain = Annual cumulative rainfall depth, inches,
- Sunshine = Mean annual sunshine percentage, %, and
- Wind = Mean annual wind speed (mph).
- AASHTOWare pavement M-E software is expensive (i.e., 7000 US dollars per year for an individual workstation). It is even more expensive for international licensing to interested parties located outside the US and Canada, and whose organizations are not AASHTO members.
- It is data intensive and sometimes not readily available, such as the axle load spectra and climatic data.
- The latest AASHTOWare Pavement ME kept only the MLEA module to estimate the structural responses at critical locations. The FEM was taken out from the latest version of the software.
- Check the accuracy of the developed simplified M-E design system for flexible pavements, which suits moderate to hot climate regions.
- Calibrate the performance models based on the Long-Term Pavement Performance (LTPP) data.
- Conduct a sensitivity analysis of the performance models based on the main inputs.
- Develop a user-friendly software for the structure design and analysis of flexible pavements in moderate to hot climate regions.
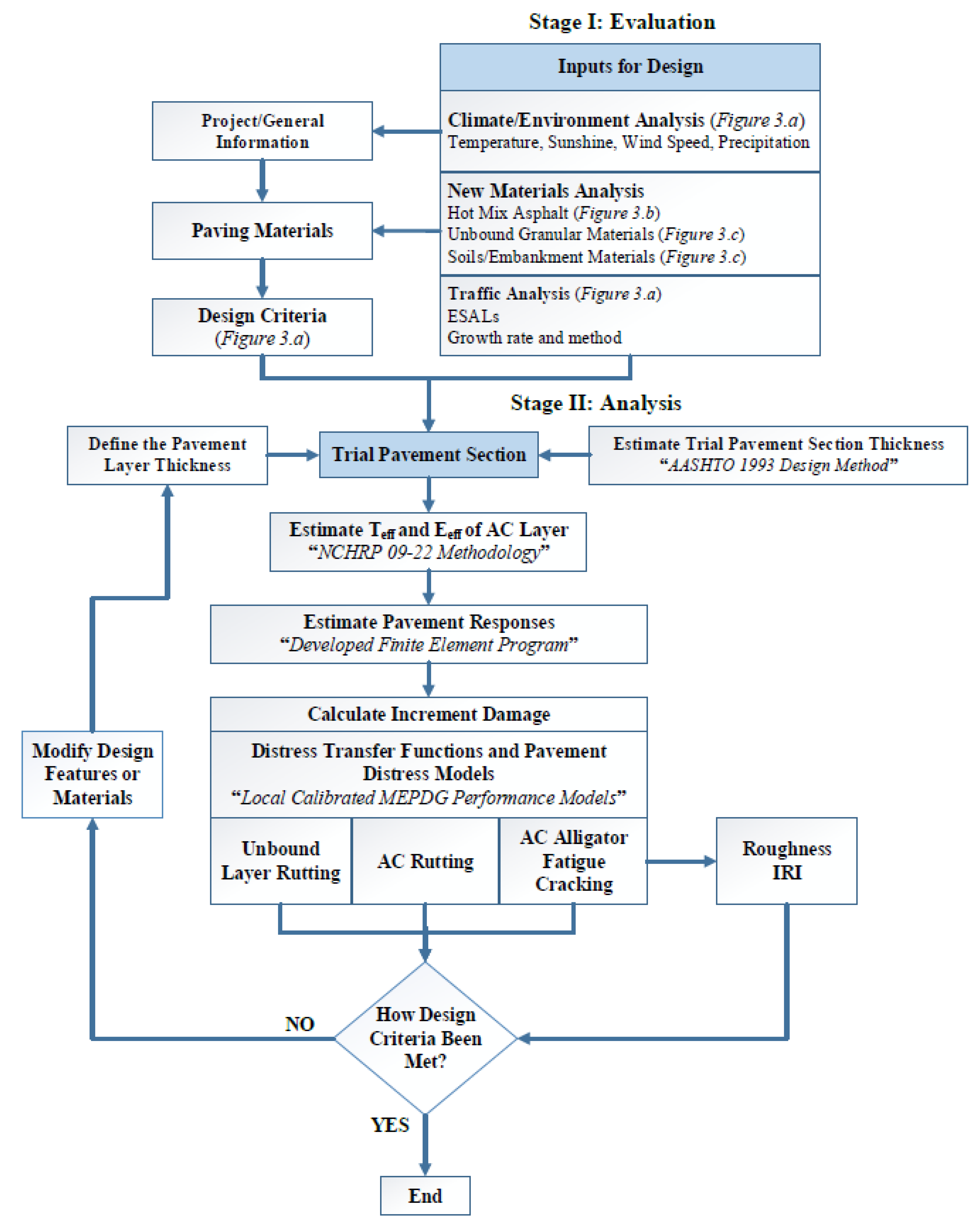
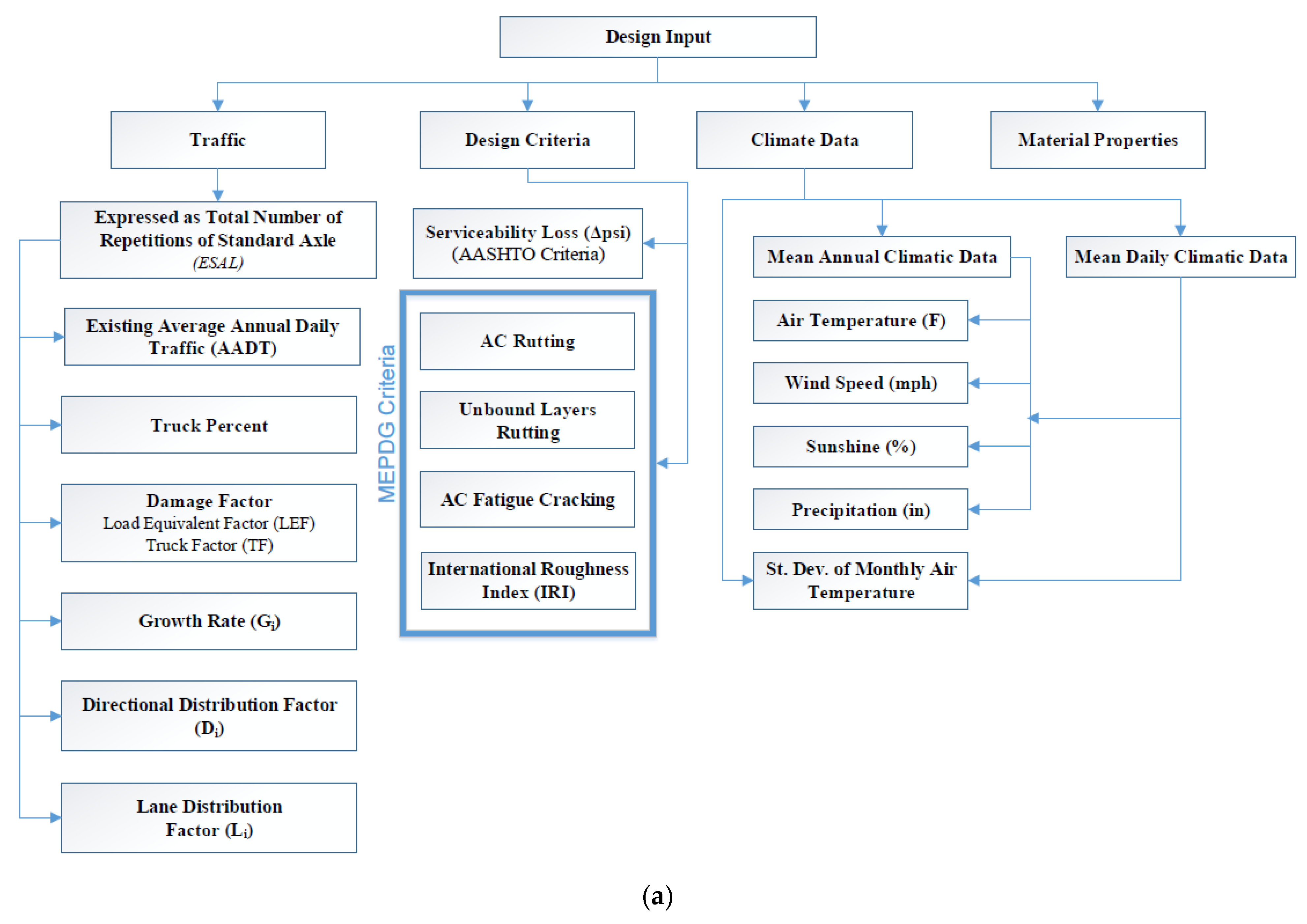
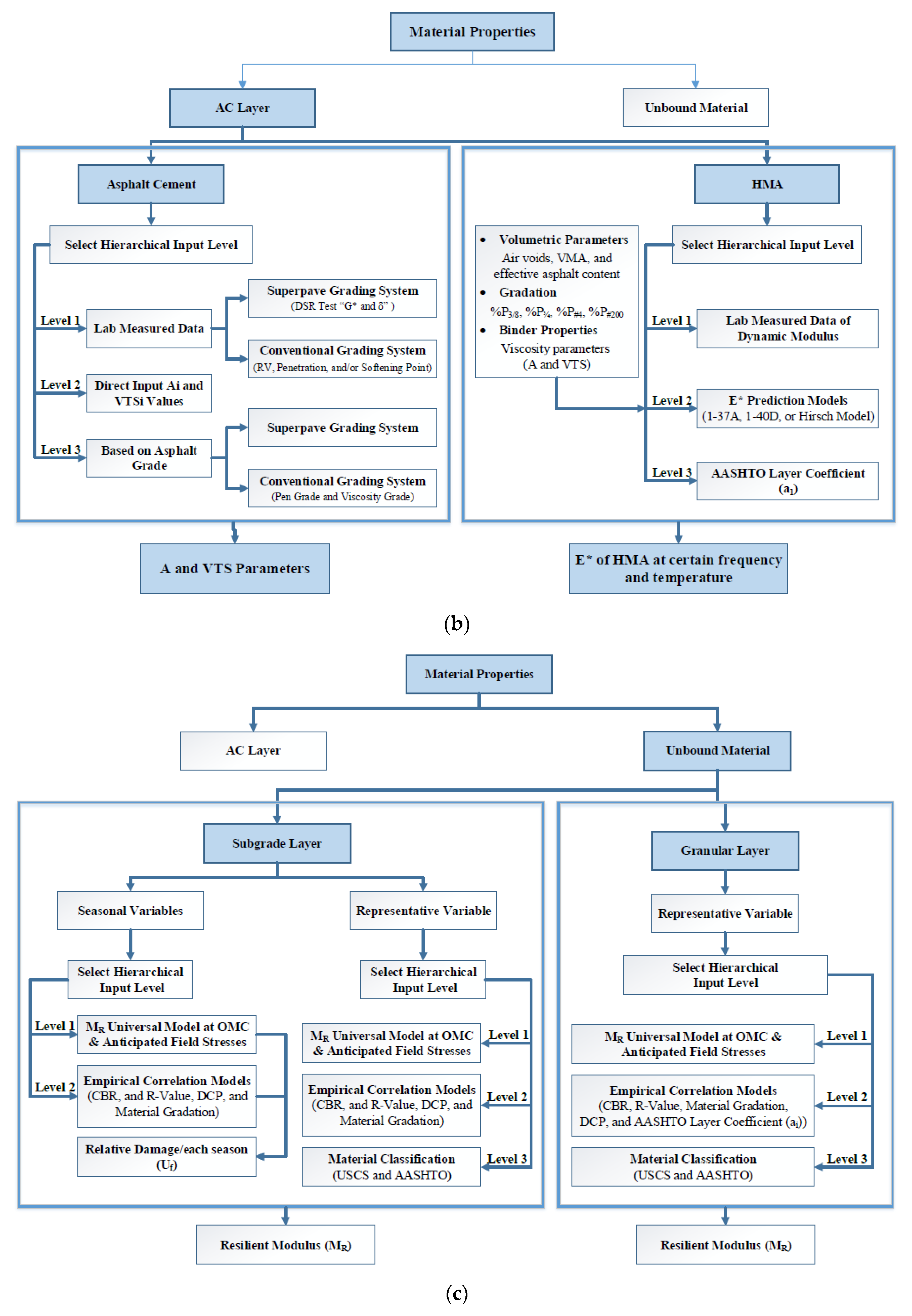
2. Methodology
2.1. Effective Temperature and Modulus
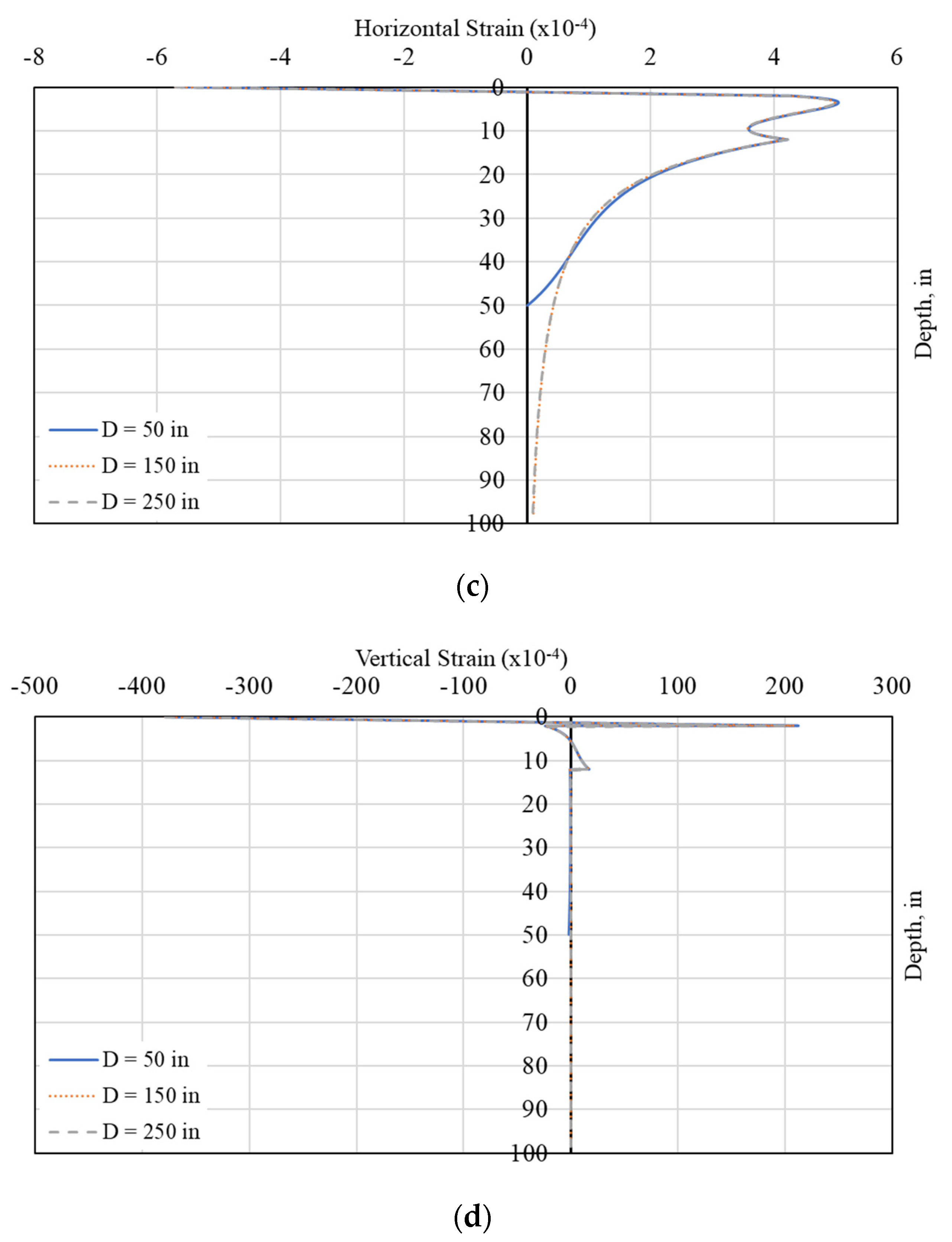
2.2. Finite Element Module
3. Results and Discussion
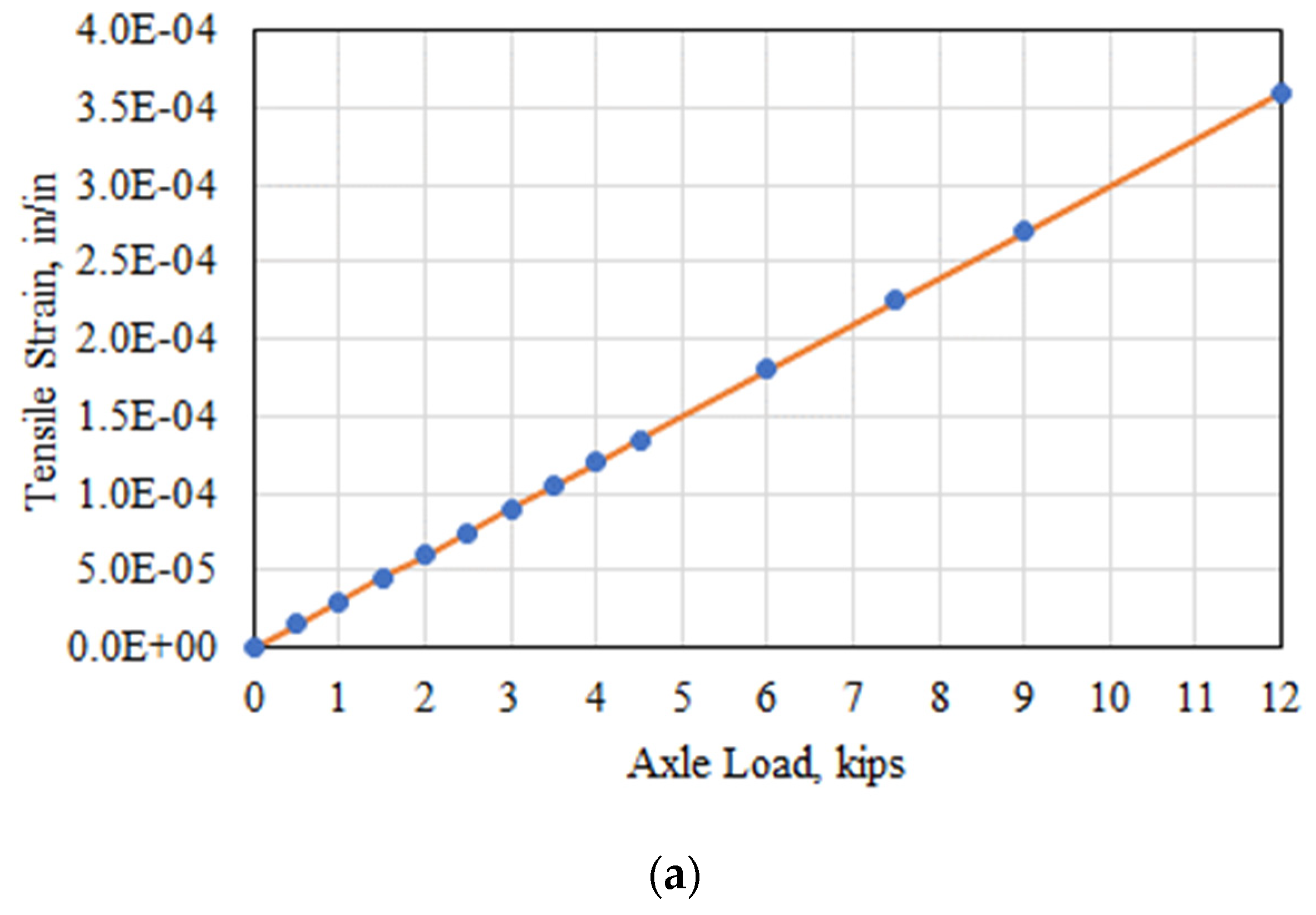
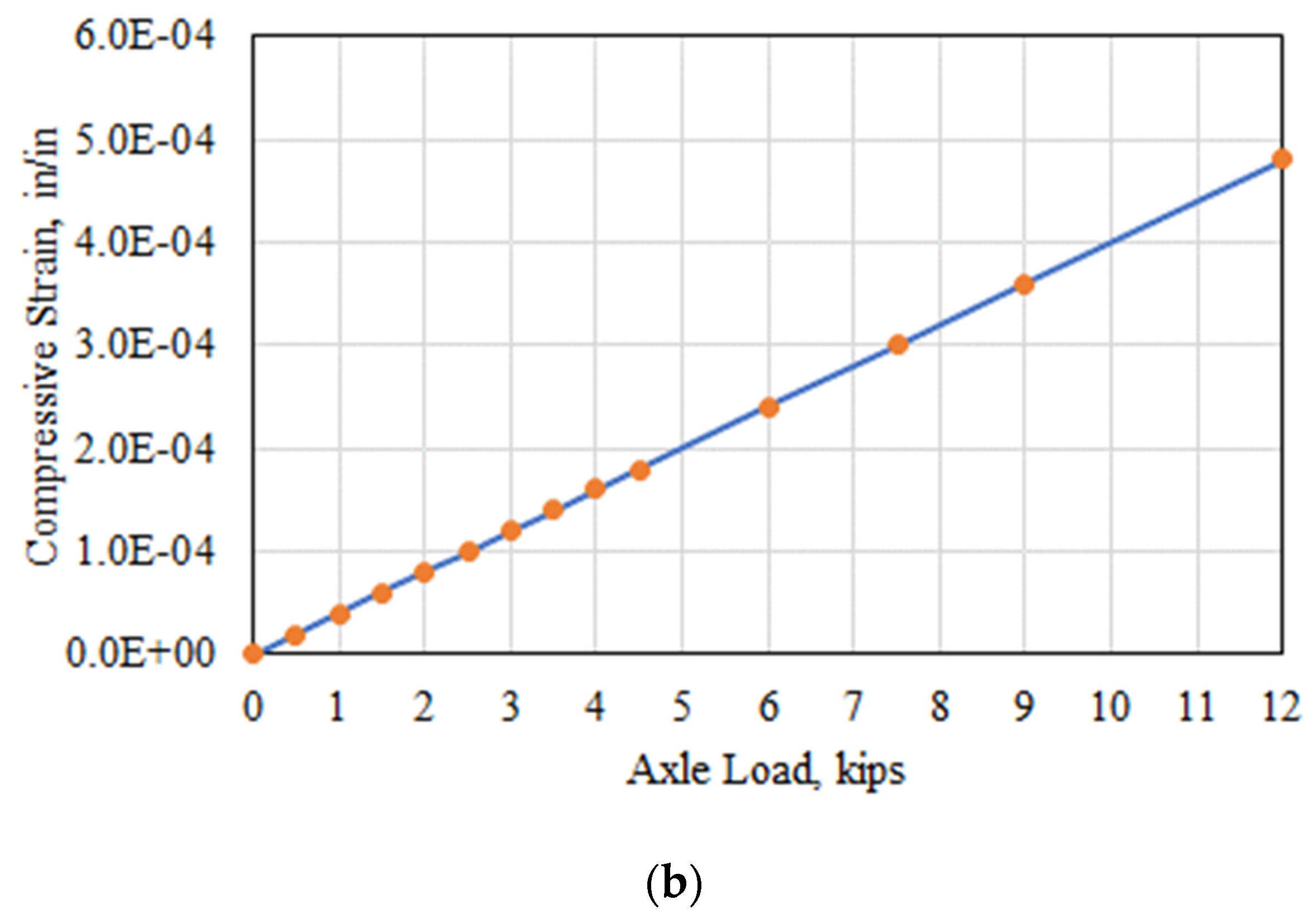
3.1. Verification of the Finite Element Module
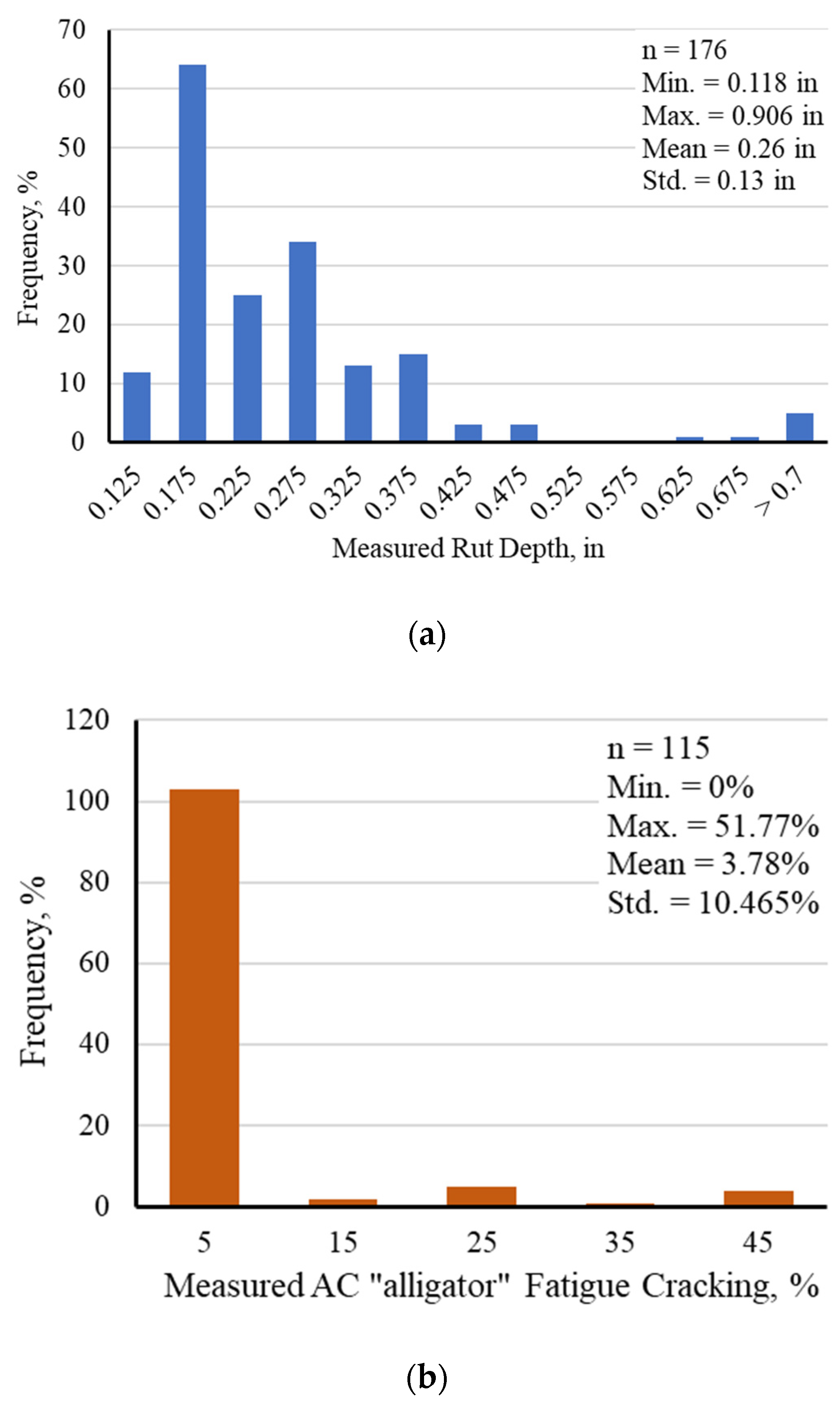
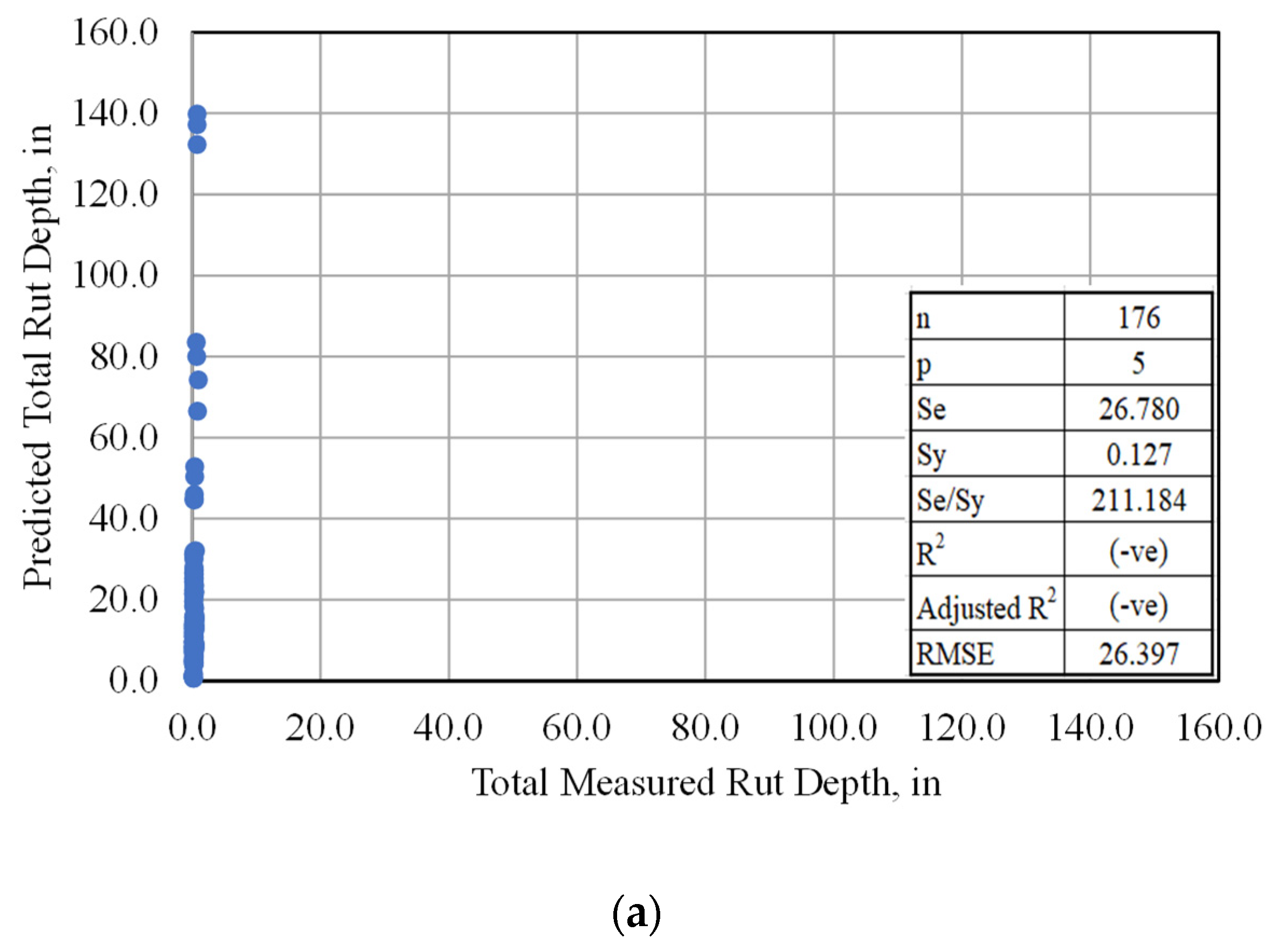
3.2. Calibration of the Distress Models
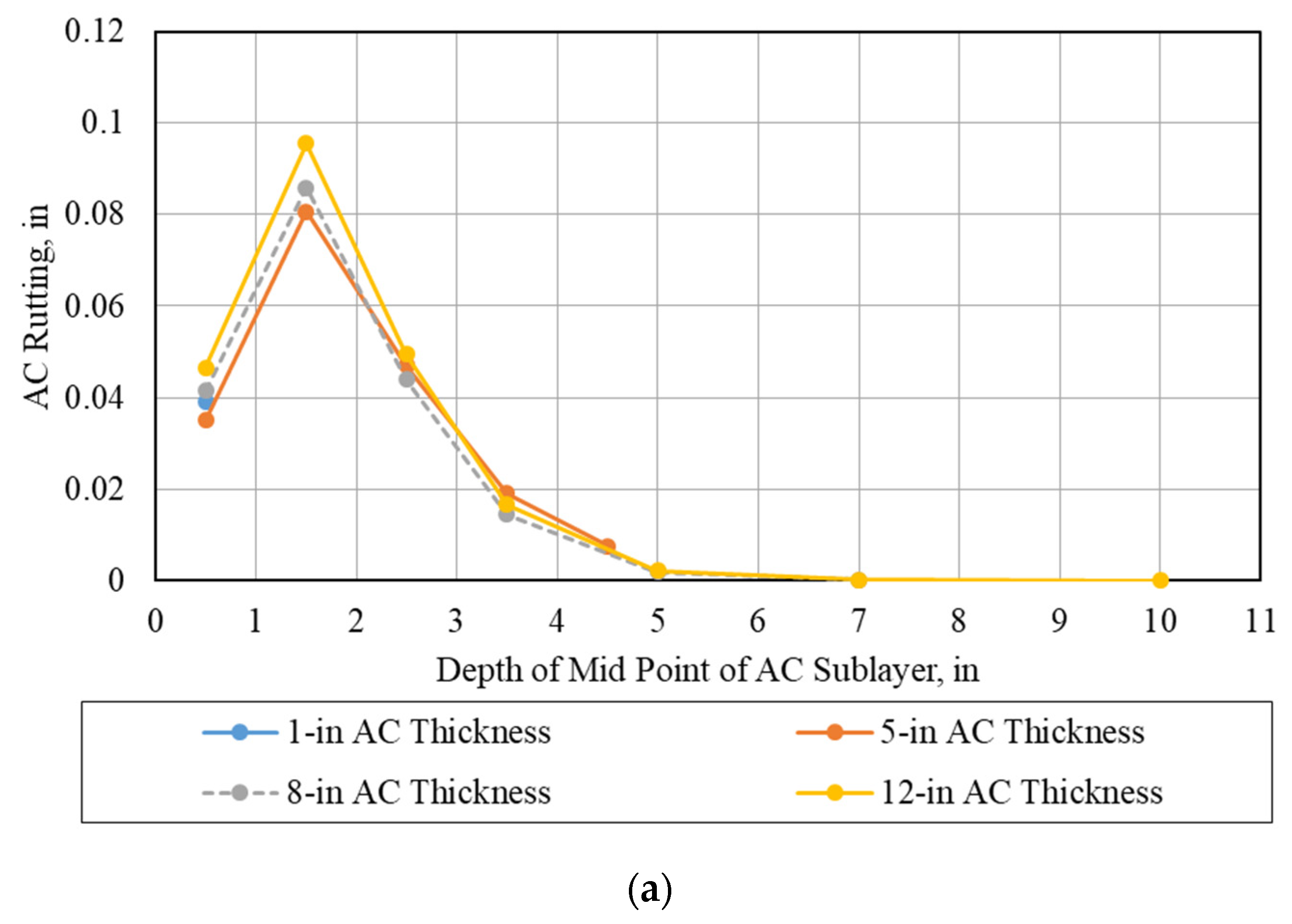
3.2.1. Calibration of the Rutting Models
- ΔAC = Permanent or plastic deformation for the AC layer, in,
- n = Number of sub-layers,
- (εp)i = Vertical plastic strain at mid-depth of layer i,
- Δhi = Thickness of sub-layer i,
- εr = Computed vertical resilient strain at mid-thickness of sub-layer i for a given load,
- Kz = Depth correction factor,
- k1, k2, k3 = Regression coefficients derived from laboratory repeated load permanent deformation test data K1 = −3.35412, K2 = 0.4791, and K3 = 1.5606,
- β1, β2, β3 = Local calibration coefficients,
- T = Temperature, °F, and
- N = Number of repetitions for a given axle load.
- Δp(Soil) = Permanent or plastic deformation for the layer/sub-layer, in,
- ε0 = Intercept determined from laboratory repeated load permanent deformation tests, in/in,
- εr = Resilient strain imposed in laboratory test to obtain material properties ε0, β, and ρ, in/in,
- εv = Average vertical resilient or elastic strain in the layer/sub-layer and calculated by the structural response model, in/in,
- hSoil = Thickness of the unbound layer/sub-layer, in,
- ks1 = Global calibration coefficient for coarse = 1.673 and fine = 1.35, and
- βs1 = Local calibration coefficient for rutting in the unbound layers; for the global calibration βs1 = 1.0.
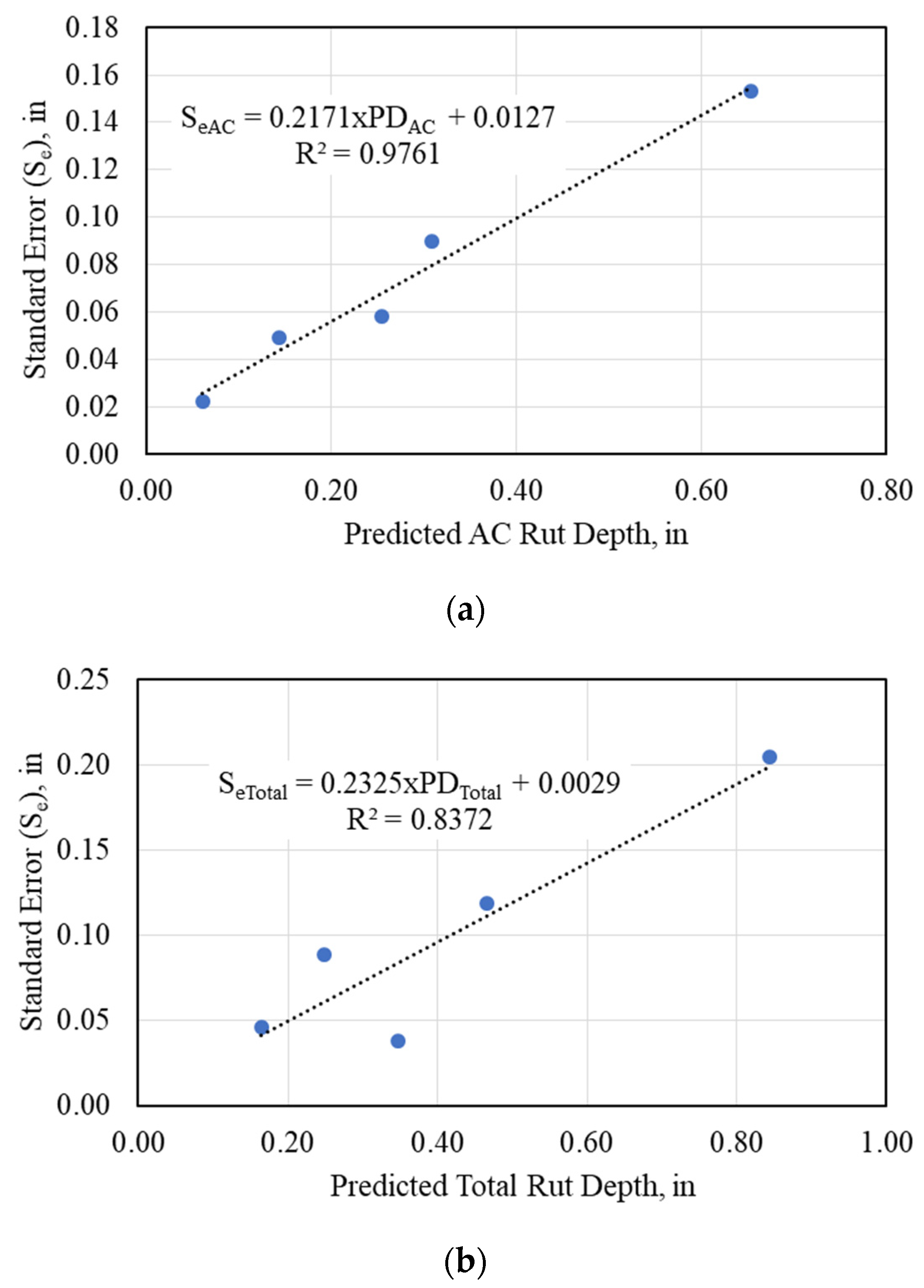
- , and = Expected AC, and total pavement rutting at the design reliability level (R),
- , and = Predicted AC, and total rut depth estimated by the correlation models with average input values for all parameters (at 50% design reliability level),
- SeAC, and SeT = Standard error estimated for the AC, and total rut depth, and
- ZR = Standard normal deviation for the selected reliability level (R).
3.2.2. Calibration of the Fatigue Cracking Model
- kt = Thickness correction factor,
- β1, β2, β3 = Field calibration coefficients,
- k1, k2, k3 = Material properties determined from regression analysis of laboratory test data: K1 = 0.007566, K2 = 3.9492, and K3 = 1.281,
- C = Field calibration factor,
- εt = The critical tensile strain in AC layer, and
- E = Stiffness of asphalt concrete at specific temperature.
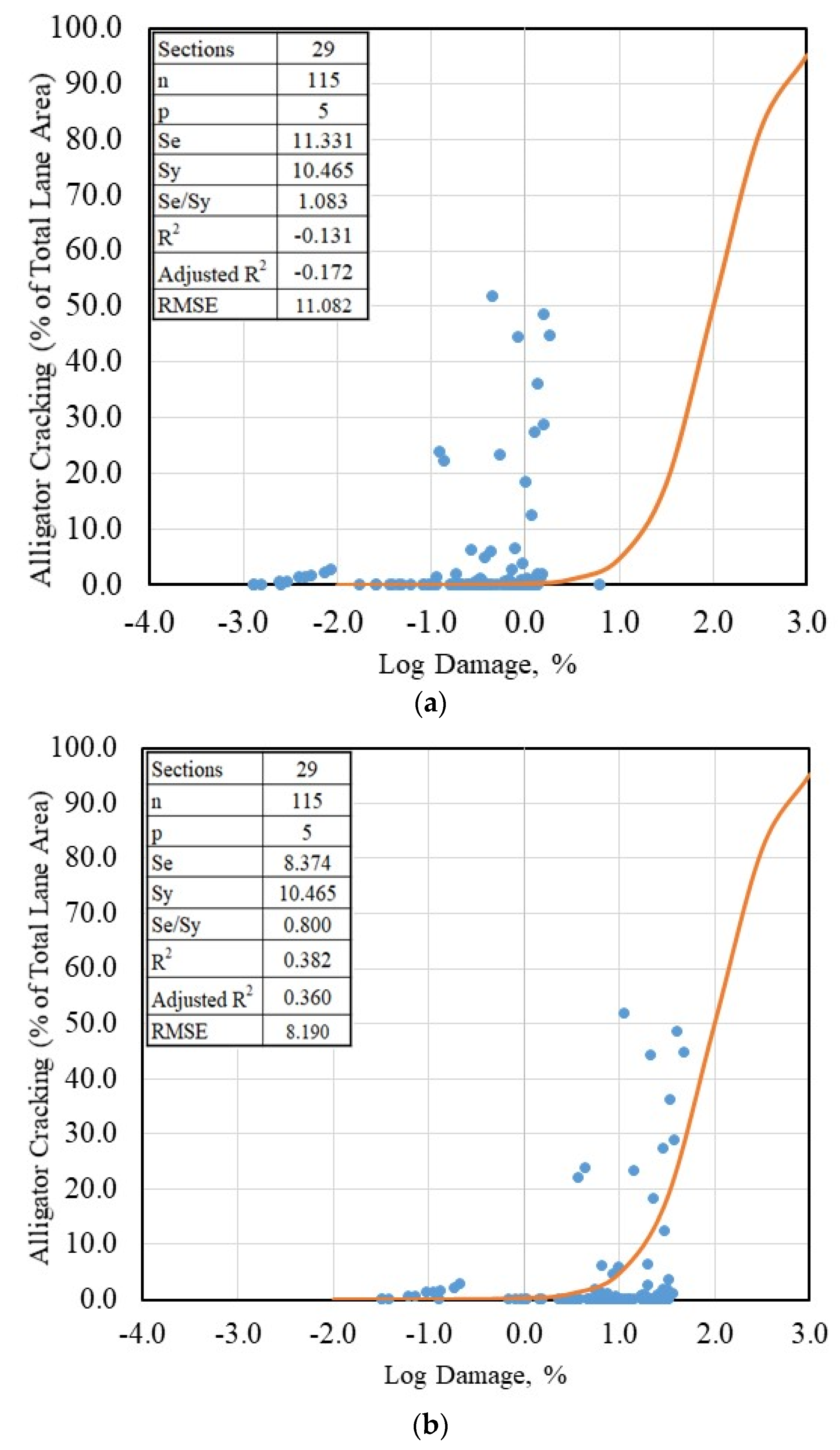
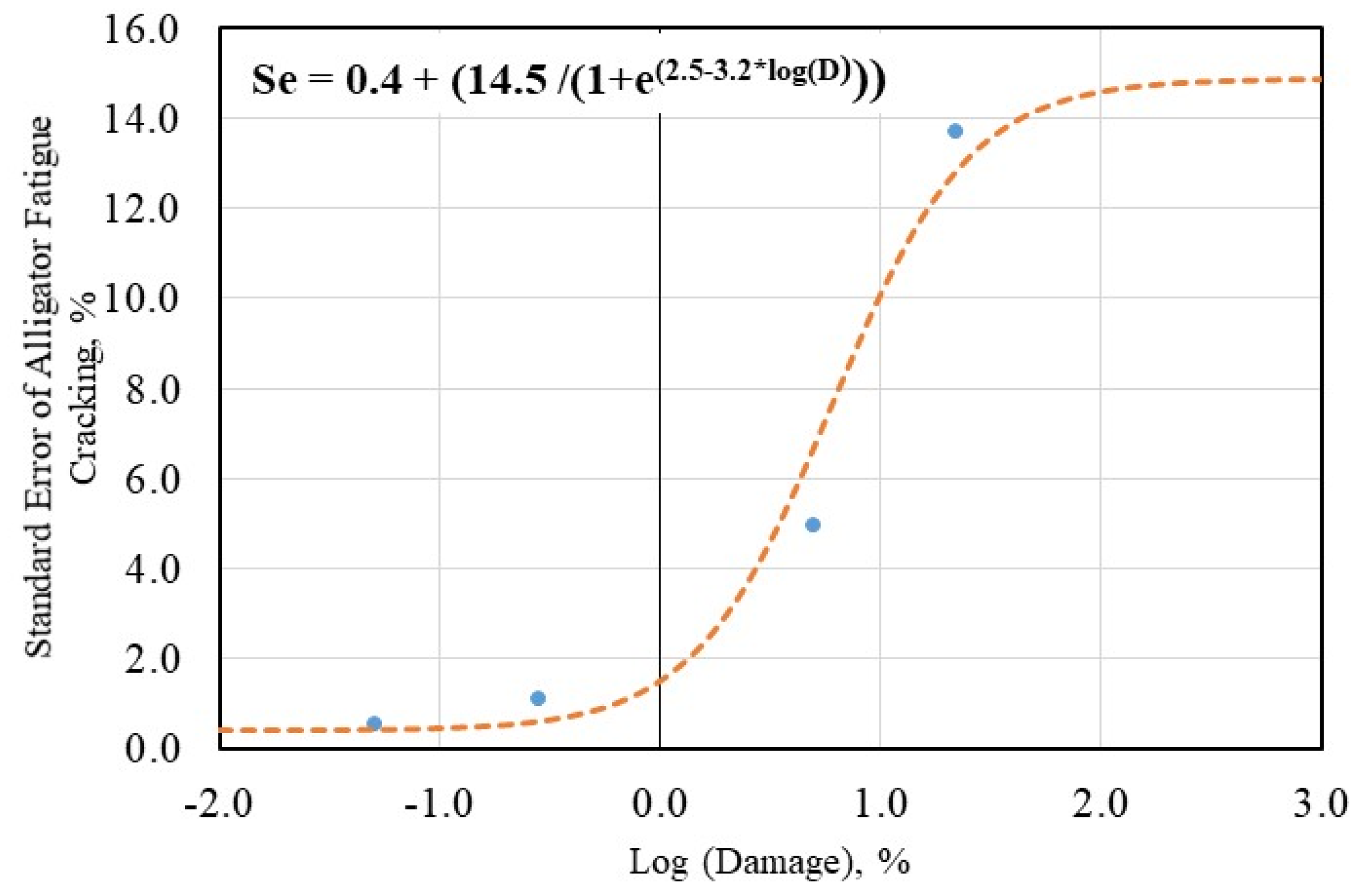
- FCR = Expected AC “alligator” fatigue cracking at the design reliability level, R,
- = Predicted AC “alligator” fatigue cracking estimated at 50% design reliability level, and
- SeFC = Standard error estimated for AC “alligator” fatigue cracking.
3.2.3. IRI Prediction Model
- IRI = International Roughness Index at any age, m/km,
- IRI0 = IRI just after construction, m/km,
- Age = Pavement age starting from construction or overlay, years,
- (F.C)all = Fatigue cracking (all severity levels), % of wheel path area,
- (T.C)all = Transverse cracks length (all severity levels), m/km, and
- SDRUT = Standard deviation of rutting, mm.
4. Sensitivity Analysis
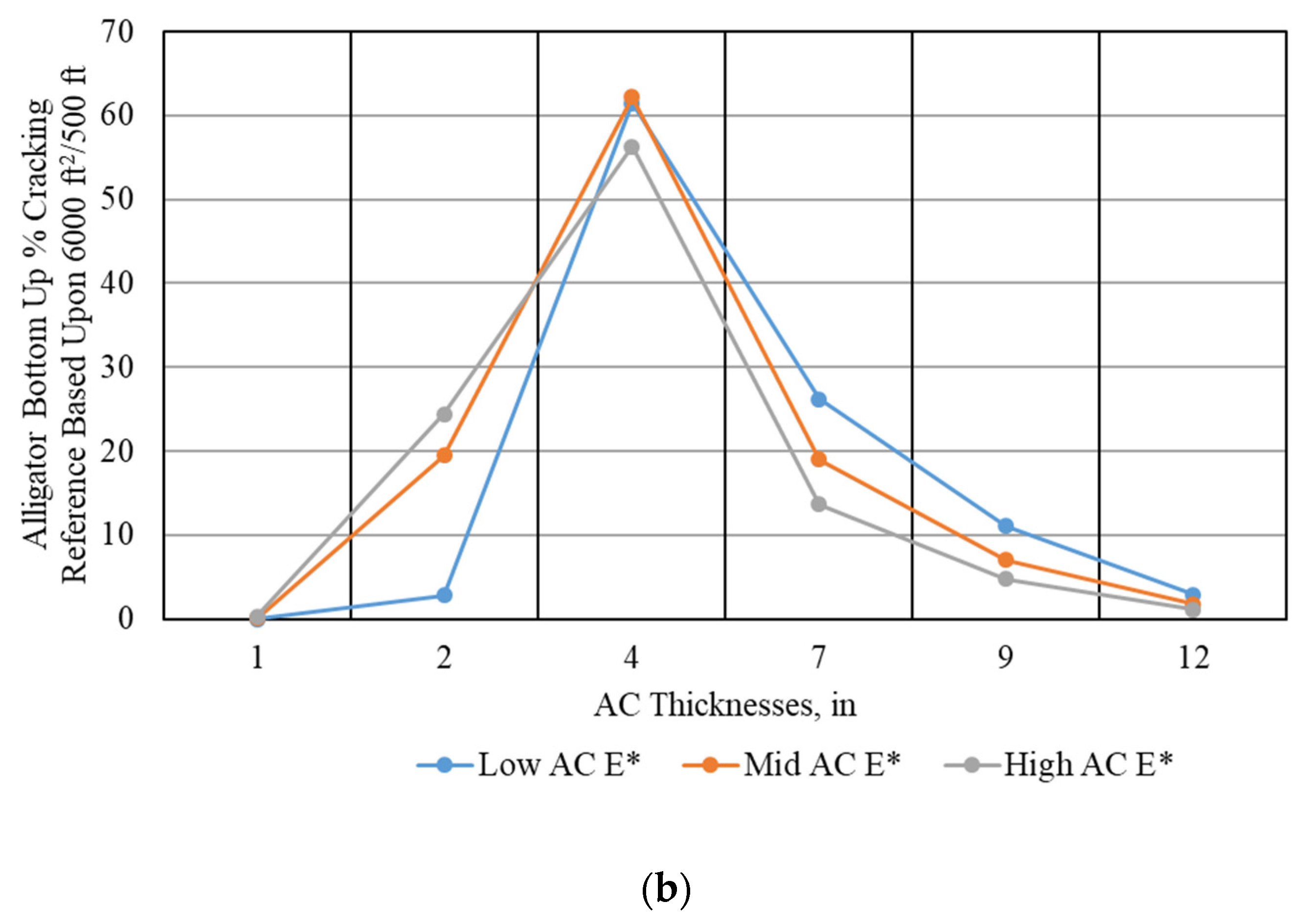
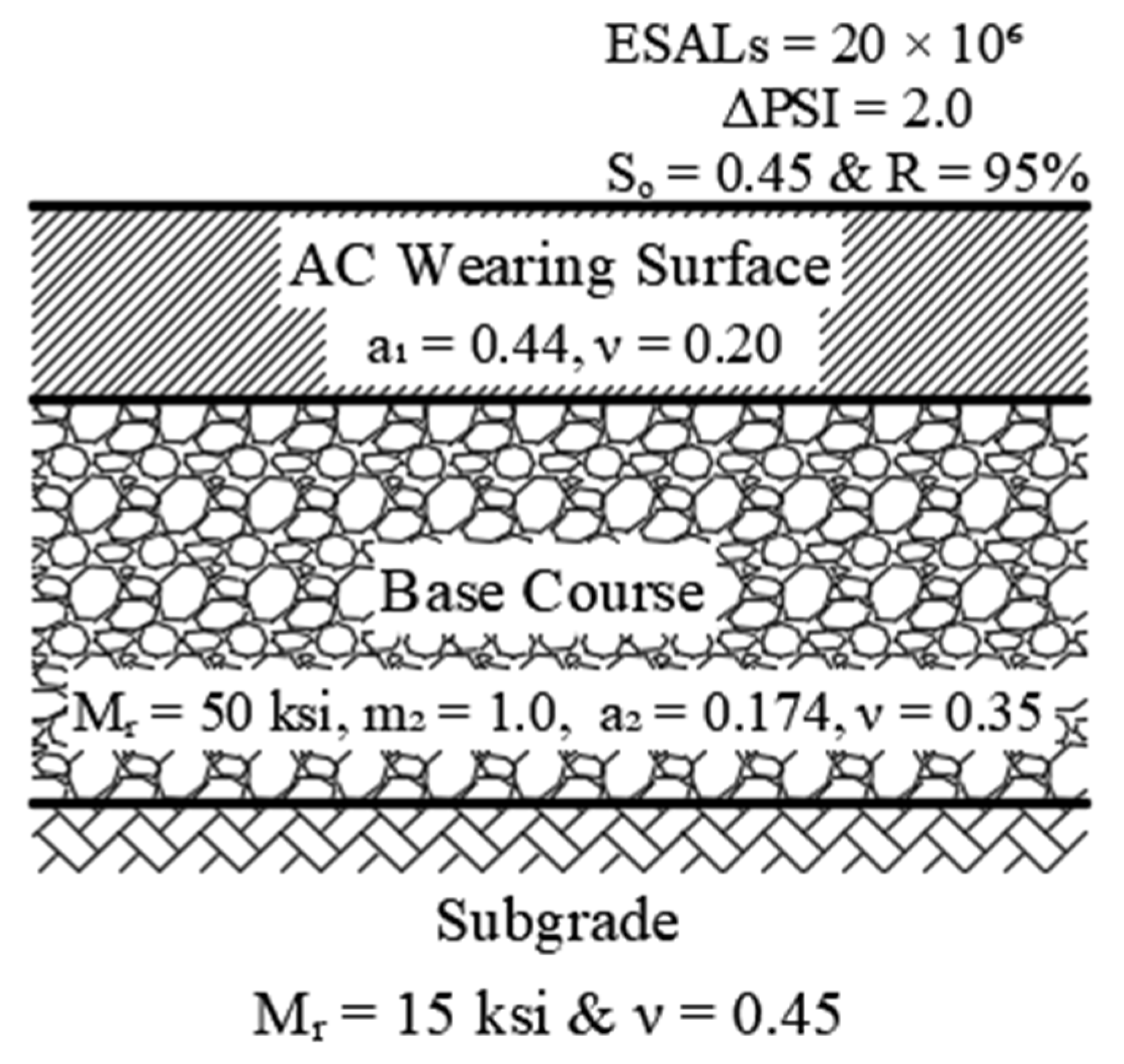
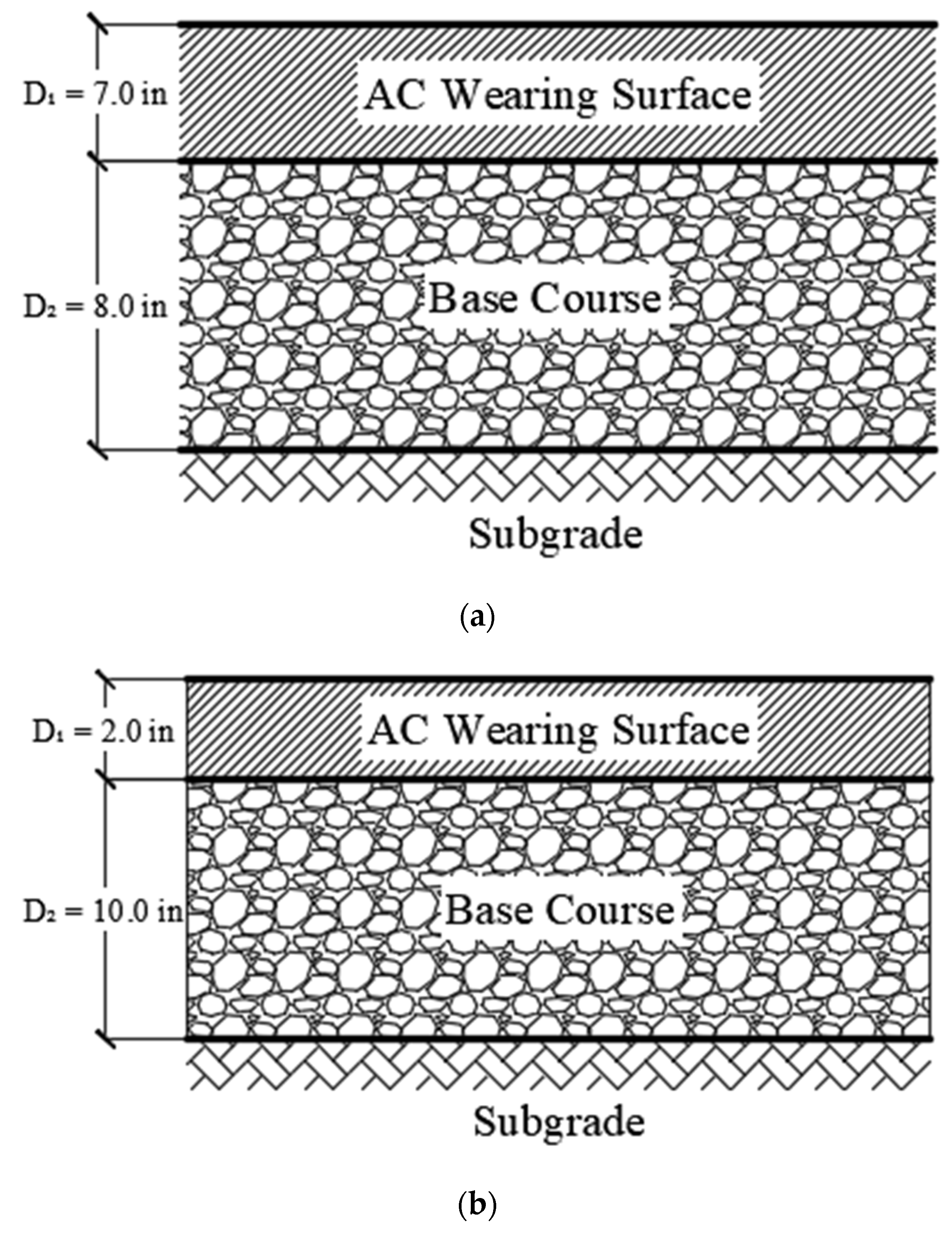
5. Case Study
- Change the modulus and/or the stiffness of AC layer.
- Increase the modulus and the thickness of unbound granular layer (base layer).
- Convert the pavement structure from thick to thin structure (AC thickness less than 4-in (10.2-cm)), as illustrated in Figure 16b.
6. Summary and Conclusions
- The structural responses are computed at critical predefined locations in the pavement system by using Axisymmetric FEM. The incorporated FEM in the ME-PAVE provides a chance to consider the nonlinearity and visco-nonlinear analyses in the future.
- The pavement distress prediction models were calibrated based on LTPP data for wet and dry non-freeze climatic regions.
- The proposed methodology is implemented into a user-friendly computer code (ME-PAVE) that takes only 40 s to simulate a 20-year analysis period.
- A sensitivity analysis was conducted to measure the rationality of the predicted distresses, and it was observed that the results are logical and agree with the results of the MEPDG.
- ○
- For the rutting model, the simplification of the proposed methodology demonstrated a slight reduction, with acceptable limits in the accuracy of the predicted rut depth values compared to the reported results of current practices (i.e., NCHRP 1-37A and NCHRP 1-40D).
- ○
- For the AC “alligator” fatigue cracking model, the calibrated model yielded slightly better prediction compared to the reported results of current practices (i.e., NCHRP 1-40D).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Acronyms | Descriptions |
| AASHTO | American Association of State Highway Transportation Officials |
| NCHRP | National Cooperative Highway Research Program |
| M-E/ME | Mechanistic-Empirical |
| AC | Asphalt Concrete |
| FEM | Finite Element Module |
| LTPP | Long-Term Pavement Performance |
| US | United States of America |
| MEPDG | Mechanistic Empirical Pavement Design Guide |
| NSF | National Science Foundation |
| DOT | departments of transportation |
| HMA | Hot Mix Asphalt |
| MLET | Multi-Layer Elastic Theory |
| QRSS | Quality-Related Specifications Software |
| Teff | effective temperature |
| E*eff | effective dynamic modulus |
| ESAL | Equivalent Single Axle Load |
| GPS | General Pavement Studies |
| PD | Permanent Deformation |
| Se | Standard Error |
| IRI | International Roughness Index |
| MAAT | Mean Annual Air Temperature |
| σMMAT | Standard deviation of the mean monthly air temperature |
References
- U.S. Army Corps of Engineers. The California Bearing Ratio Test as Applied to the Design of Flexible Pavements for Airports. Technical Memory; Number 213-1; Waterways Experiment Station: Vicksburg, MS, USA, 1945. [Google Scholar]
- Highway Research Board (HRB). Final Report on Road Test One Maryland; Special Report 4; HRB: Washington, DC, USA, 1952. [Google Scholar]
- Highway Research Board (HRB). The WASHO Road Test, Part 1: Design, Construction and Testing Procedure; Special Report 18; HRB: Washington, DC, USA, 1952. [Google Scholar]
- Highway Research Board (HRB). The WASHO Road Test, Part 2: Test Data, Analyses Finding; Special Report 22; HRB: Washington, DC, USA, 1955. [Google Scholar]
- American Association of State Highway and Transportation Officials (AASHTO). AASHTO Guide for Design of Pavement Structures; AASHTO: Washington, DC, USA, 1961. [Google Scholar]
- AASHTO. AASHTO Guide for Design of Pavement Structures; AASHTO: Washington, DC, USA, 1972. [Google Scholar]
- AASHTO. AASHTO Guide for Design of Pavement Structures; AASHTO: Washington, DC, USA, 1986. [Google Scholar]
- Highway Research Board (HRB). The AASHO Road Test, Report 7; Special Report 61-G; HRB: Washington, DC, USA, 1962. [Google Scholar]
- Shell International Petroleum Company Ltd. Shell Pavement Design Manual: Asphalt Pavements and Overlays for Road Traffic; Shell International Petroleum Company Ltd.: London, UK, 1978. [Google Scholar]
- LCPC. French Design Manual for Pavement Structures Guide Technique; Laboratoire Central des Ponts et Chaussées: Paris, France, 1994. [Google Scholar]
- Powell, W.D.; Potter, J.F.; Mayhew, H.C. The Structural Design of Bituminous Roads; LR 1132; Transport and Road Research Laboratory: Crowthorne, UK, 1984. [Google Scholar]
- ARA. Guide for Mechanistic Empirical Design of New and Rehabilitated Pavement Structures; National Cooperative Highway Research Program: Springfield, IL, USA, 2004. [Google Scholar]
- ARA. A Manual of Practice; American Association of State Highway and Transportation Officials; ARA: Antioch, IL, USA, 2008. [Google Scholar]
- Pereira, P.; Pais, J. Main flexible pavement and mix design methods in Europe and challenges for the development of an European method. J. Traffic Trans. Eng. 2017, 4, 316–346. [Google Scholar] [CrossRef] [Green Version]
- Timm, D.H.; Robbins, N.; Tran, C. Flexible Pavement Design-State of the Practice. National Center for Asphalt Technology; Auburn University: Auburn, AL, USA; National Asphalt Pavement Association: Lanham, MD, USA, 2014; Available online: http://www.ncat.us/files/reports/2014/rep14-04.pdf (accessed on 23 September 2021).
- PVD. AASHTOWare Pavement ME Design v2.5.5; ARC, Inc.: Boise, ID, USA, 2010; Available online: https://me-design.com/MEDesign/Home.aspx (accessed on 2 June 2020).
- Hamdar, Y.S. Effective Incorporation of Asphalt Mixture Properties in the Structural Design of Asphalt Pavements as a Precursor for Implementing Performance-Based Design. Master’s Dissertation, American University of Beirut, Beirut, Lebanon, 2016. Available online: https://scholarworks.aub.edu.lb/bitstream/handle/10938/10968/et-6398.pdf?sequence=1 (accessed on 23 September 2021).
- Hamdar, Y.S.; Chehab, G.R. Integrating the Dynamic Modulus of Asphalt Mixes in the 1993 AASHTO Design Method. Transp. Res. Rec. J. Transp. Res. Board 2017, 2640, 29–40. [Google Scholar] [CrossRef]
- Pierce, L.M.; McGovern, G. Implementation of the AASHTO Mechanistic-Empirical Pavement Design Guide and Software (No. Project 20-05, Topic 44-06); Transportation Research Record: Washington, DC, USA, 2014; Available online: http://www.trb.org/Publications/Blurbs/170576.aspx (accessed on 23 September 2021).
- El-Basyouny, M.M.; Witczak, M.W. Verification of the Calibrated Fatigue Cracking Models for the 2002 Design Guide. J. Assoc. Asph. Paving Technol. 2005, 74, 653–696. [Google Scholar]
- Von Quintus, H.L.; Moulthrop, J.S. Mechanistic-Empirical Pavement Design Guide Flexible Pavement Performance Prediction Models: Volume I Executive Research Summary (No. FHWA/MT-07-008/8158-1); Montana Department of Transportation, Research Programs: 2007. Available online: https://rosap.ntl.bts.gov/view/dot/24868 (accessed on 23 September 2021).
- Hall, K.D.; Xiao, D.X.; Wang, K.C. Calibration of the mechanistic–empirical pavement design guide for flexible pavement design in Arkansas. Transp. Res. Rec. 2011, 2226, 135–141. [Google Scholar] [CrossRef]
- Bayomy, F.; El-Badawy, S.; Awed, A. Implementation of the MEPDG for Flexible Pavements in Idaho (No. FHWA-ID-12-193); Idaho Transportation Department: Boise, ID, USA, 2012. Available online: http://itd.idaho.gov/highways/research (accessed on 23 September 2021).
- Caliendo, C. Local Calibration and Implementation of the Mechanistic-Empirical Pavement Design Guide for Flexible Pavement Design. J. Transp. Eng. 2012, 138, 348–360. [Google Scholar] [CrossRef]
- Lu, P.; Bratlien, A.; Tolliver, D. North Dakota Implementation of Mechanistic-Empirical Pavement Design Guide (MEPDG) (No. MPC 14-274); Mt. Plains Consort: 2014. Available online: https://rosap.ntl.bts.gov/view/dot/28527 (accessed on 23 September 2021).
- Rahman, M.M.; Gassman, S.L. Data collection experience for preliminary calibration of the AASHTO pavement design guide for flexible pavements in South Carolina. Int. J. Pavement Res. Technol. 2018, 11, 445–457. [Google Scholar] [CrossRef]
- Li, Q.J.; Wang, K.C.P.; Yang, G.; Zhan, J.Y.; Qiu, Y. Data needs and implementation of the Pavement ME Design. Transp. A Transp. Sci. 2019, 15, 135–164. [Google Scholar] [CrossRef]
- Azadi, M.; Nasimifar, S.M.; Pouranian, M.R. Determination of Local Fatigue Model Calibration Used in MEPDG for Iran’s Dry-No Freeze Region. Arab. J. Sci. Eng. 2012, 38, 1031–1039. [Google Scholar] [CrossRef]
- Tarefder, R.; Rodriguez-Ruiz, J.I. Local Calibration of MEPDG for Flexible Pavements in New Mexico. J. Transp. Eng. 2013, 139, 981–991. [Google Scholar] [CrossRef]
- Elshaeb, M.; El-Badawy, S.M.; Shawaly, A.E.-S. Development and Impact of the Egyptian Climatic Conditions on Flexible Pavement Performance. Am. J. Civ. Eng. Archit. 2014, 2, 115–121. [Google Scholar] [CrossRef] [Green Version]
- Sadek, H.A.; Masad, E.A.; Sirin, O.; Al-Khalid, H.; Sadeq, M.A.; Little, D. Implementation of mechanistic-empirical pavement analysis in the State of Qatar. Int. J. Pavement Eng. 2013, 15, 495–511. [Google Scholar] [CrossRef]
- Ma, H.; Wang, D.; Zhou, C.; Feng, D. Calibration on MEPDG Low Temperature Cracking Model and Recommendation on Asphalt Pavement Structures in Seasonal Frozen Region of China. Adv. Mater. Sci. Eng. 2015, 2015, 830426. [Google Scholar] [CrossRef] [Green Version]
- Alqaili, A.H.; Alsoliman, H.A. Preparing Data for Calibration of Mechanistic-Empirical Pavement Design Guide in Central Saudi Arabia. Technol. Int. J. Urban Civ. Eng. 2017, 11, 248–255. [Google Scholar]
- Chehab, G.R.; Chehade, R.H.; Houssami, L.; Mrad, R. Implementation Initiatives of the Mechanistic-Empirical Pavement Design Guide in Countries with Insufficient Design Input Data—The Case of Lebanon. In Advancement in the Design and Performance of Sustainable Asphalt Pavements; Springer Science and Business Media LLC: Berlin, Germany, 2018; pp. 147–167. [Google Scholar]
- Eyada, S.O.; Celik, O.N. A Plan for the implementation of Mechanistic-Empirical Pavement Design Guide in Turkey. Pertanika J. Sci. Technol. 2018, 26, 4. [Google Scholar]
- Chhade, R.H.; Mrad, R.; Houssami, L.; Chehab, G. Formulation of Traffic Inputs Required for the Implementation of the M-E PDG in Data-Scarce Regions: Lebanon Case Study. J. Mater. Civ. Eng. 2018, 30, 04018198. [Google Scholar] [CrossRef]
- El-Ashwah, A.S.; Mousa, E.; El-Badawy, S.M.; Abo-Hashema, M. Advanced characterization of unbound granular materials for pavement structural design in Egypt. Int. J. Pavement Eng. 2020, 1–13. [Google Scholar] [CrossRef]
- Trautvain, A. Analysis of the Influence of the Qualitative Composition of the Asphalt-Concrete Mixture on the Main Performance Characteristics of Asphaltic Concrete Pavement. Constr. Mater. Prod. 2020, 2, 17–23. [Google Scholar] [CrossRef]
- El-Ashwah, A.S.; Awed, A.M.; El-Badawy, S.M.; Gabr, A.R. A new approach for developing resilient modulus master surface to characterize granular pavement materials and subgrade soils. Constr. Build. Mater. 2019, 194, 372–385. [Google Scholar] [CrossRef]
- Awed, A.M.; Aboelela, A.E.; El-Ashwah, A.S.; Allam, M.; El-Badawy, S.M. Improvement of unbound granular pavement layers and subgrade with cement dust in Egypt. Int. J. Pavement Res. Technol. 2020, 13, 621–629. [Google Scholar] [CrossRef]
- Moulthrop, J.; Witczak, M. NCHRP Report 704: A Performance-Related Specification for Hot-Mixed Asphalt; Transportation Research Board: Washington, DC, USA, 2011. [Google Scholar]
- Arisha, A.M.; Gabr, A.R.; El-Badawy, S.M.; Shwally, S.A. Performance Evaluation of Construction and Demolition Waste Materials for Pavement Construction in Egypt. J. Mater. Civ. Eng. 2018, 30, 04017270. [Google Scholar] [CrossRef]
- Ezzat, H.; El-Badawy, S.; Gabr, A.; Zaki, S.; Breakah, T. Predicted performance of hot mix asphalt modified with nano-montmorillonite and nano-silicon dioxide based on Egyptian conditions. Int. J. Pavement Eng. 2020, 21, 642–652. [Google Scholar] [CrossRef]
- Mousa, E.; Azam, A.; El-Shabrawy, M.; El-Badawy, S. Laboratory characterization of reclaimed asphalt pavement for road construction in Egypt. Can. J. Civ. Eng. 2017, 44, 417–425. [Google Scholar] [CrossRef] [Green Version]
- Mousa, E.; El-Badawy, S.; Azam, A. Effect of reclaimed asphalt pavement in granular base layers on predicted pavement performance in Egypt. Innov. Infrastruct. Solut. 2020, 5, 1–18. [Google Scholar] [CrossRef]
- Shiha, M.; El-Badawy, S.; Gabr, A. Modeling and performance evaluation of asphalt mixtures and aggregate bases containing steel slag. Constr. Build. Mater. 2020, 248, 118710. [Google Scholar] [CrossRef]
- El-Badawy, S.M.; Jeong, M.G.; El-Basyouny, M. Methodology to Predict Alligator Fatigue Cracking Distress Based on Asphalt Concrete Dynamic Modulus. Transp. Res. Rec. J. Transp. Res. Board 2009, 2095, 115–124. [Google Scholar] [CrossRef]
- El-Basyouny, M.; Jeong, M.G. Effective Temperature for Analysis of Permanent Deformation and Fatigue Distress on Asphalt Mixtures. Transp. Res. Rec. J. Transp. Res. Board 2009, 2127, 155–163. [Google Scholar] [CrossRef]
- El-Basyouny, M.; Jeong, M.G. Probabilistic Performance-Related Specifications Methodology Based on Mechanistic–Empirical Pavement Design Guide. Transp. Res. Rec. J. Transp. Res. Board 2010, 2151, 93–102. [Google Scholar] [CrossRef]
- El-Badawy, S.; Bayomy, F.; Fugit, S. Traffic Characteristics and Their Impact on Pavement Performance for the Implementation of the Mechanistic-Empirical Pavement Design Guide in Idaho. Int. J. Pavement Res. Technol. 2012, 5, 386–394. [Google Scholar]
- National Cooperative Highway Research Program Project 9-22. Beta Testing and Validation of HMA PRS; Washington, DC, USA, 2011. Available online: https://apps.trb.org/cmsfeed/TRBNetProjectDisplay.asp?ProjectID=958 (accessed on 23 September 2021).
- Chen, D.H.; Zaman, M.; Laguros, J.; Soltani, A. Assessment of Computer Programs for Analysis of Flexible Pavement Structure. Transp. Res. Rec. 1995, 1482, 123–133. [Google Scholar]
- Duncan, J.M.; Monismith, C.L.; Wilson, E.L. Finite Element Analysis of Pavements. Highw. Res. Rec. 1968, 228, 18–33. [Google Scholar]
- AASHTO. Guide for the Local Calibration of the Mechanistic-Empirical Pavement Design Guide; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2010. [Google Scholar]
- Abdelaziz, N.; El-Hakim, R.T.A.; El-Badawy, S.M.; Afify, H.A. International Roughness Index prediction model for flexible pavements. Int. J. Pavement Eng. 2018, 21, 88–99. [Google Scholar] [CrossRef]
- Amin, I.; El-Badawy, S.M.; Breakah, T.; Ibrahim, M.H.Z. Laboratory evaluation of asphalt binder modified with carbon nanotubes for Egyptian climate. Constr. Build. Mater. 2016, 121, 361–372. [Google Scholar] [CrossRef]

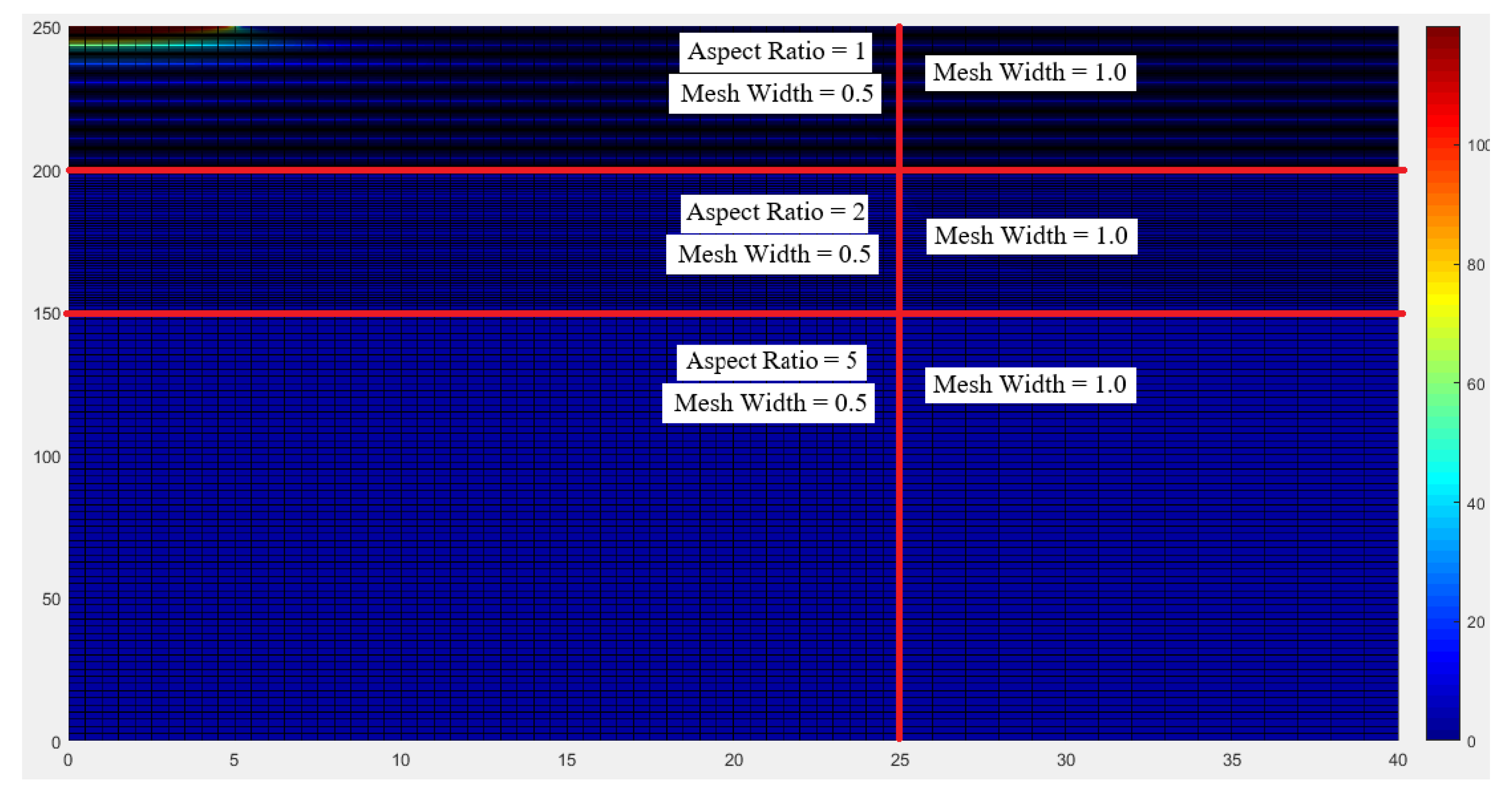
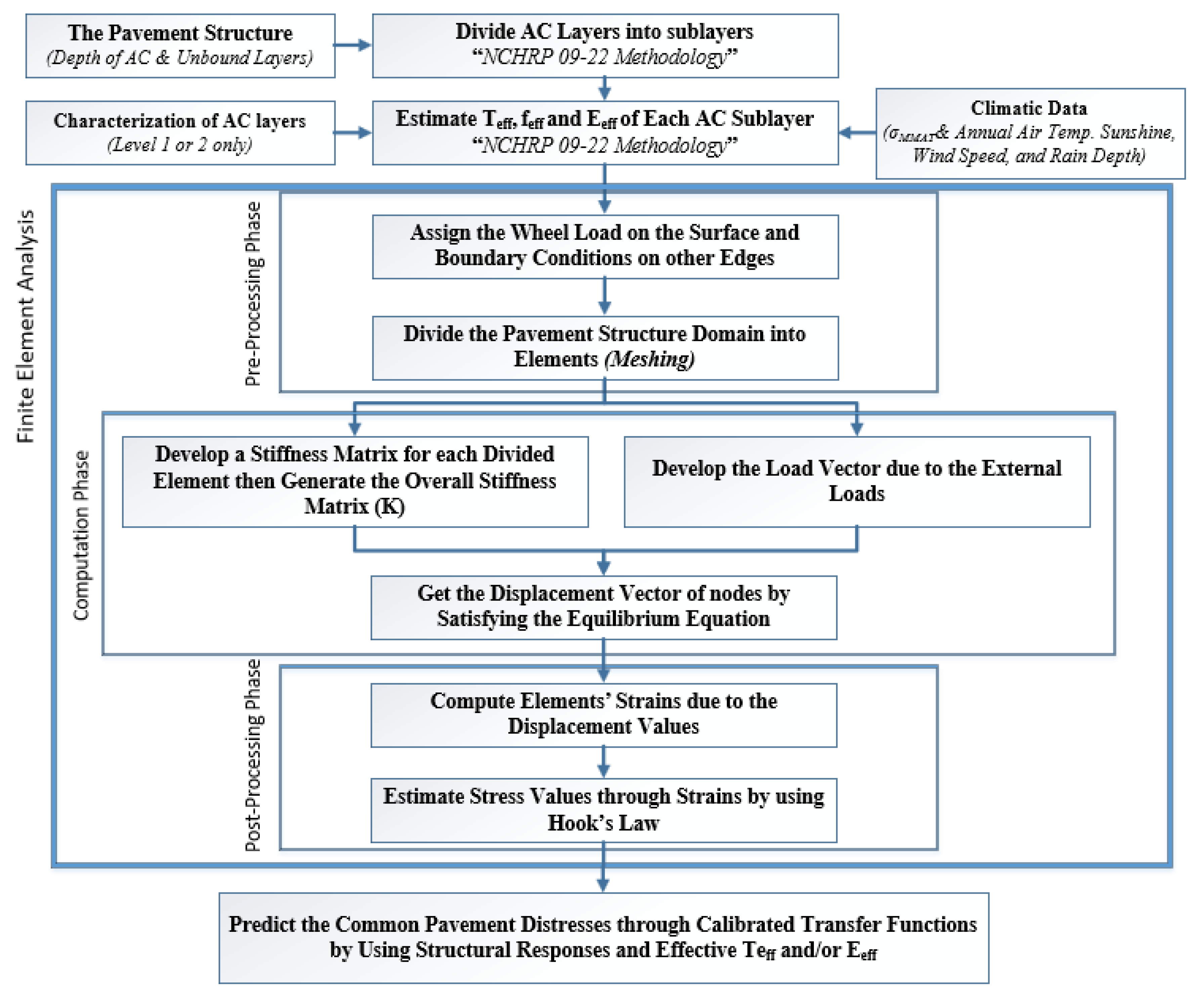
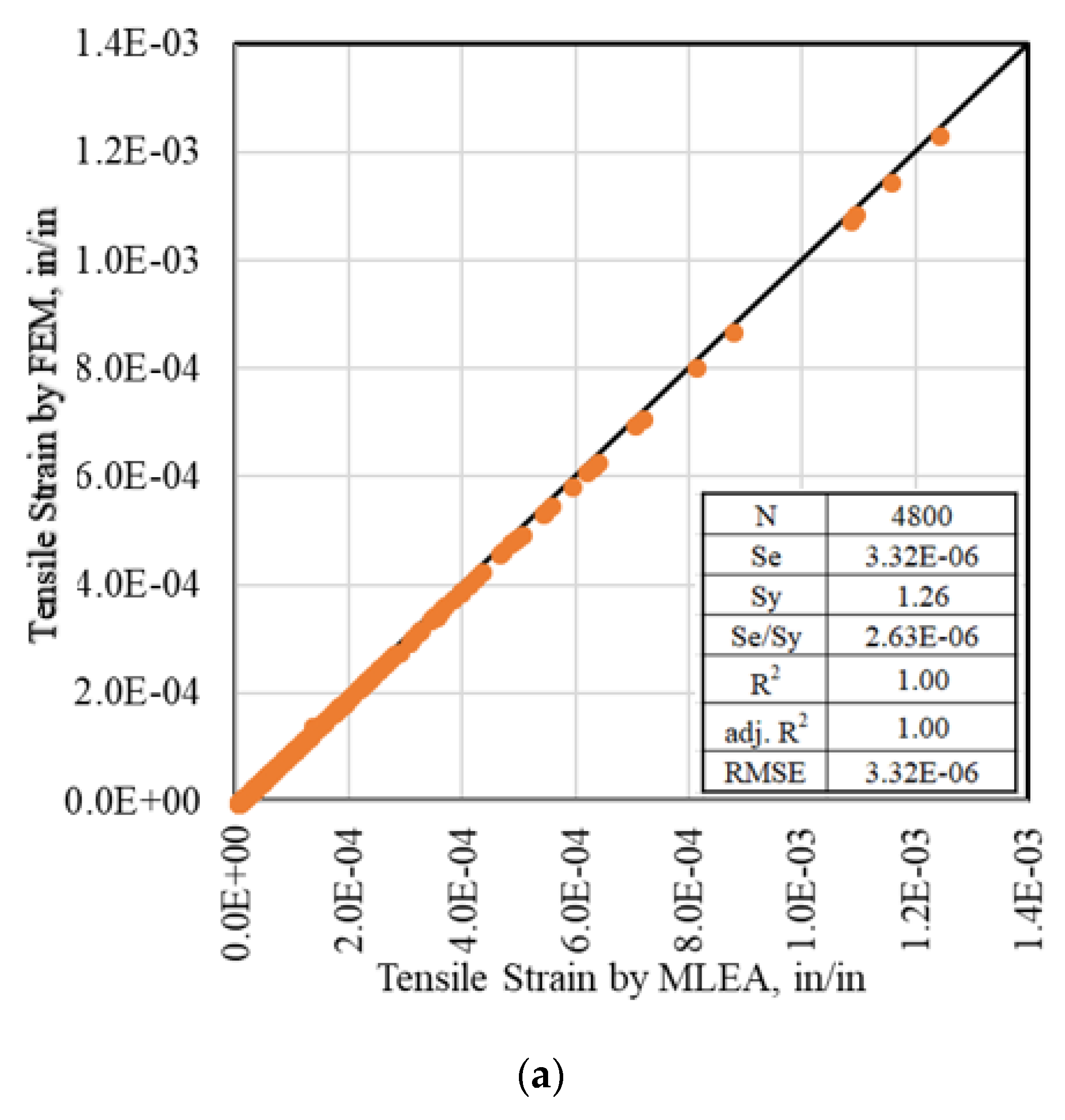
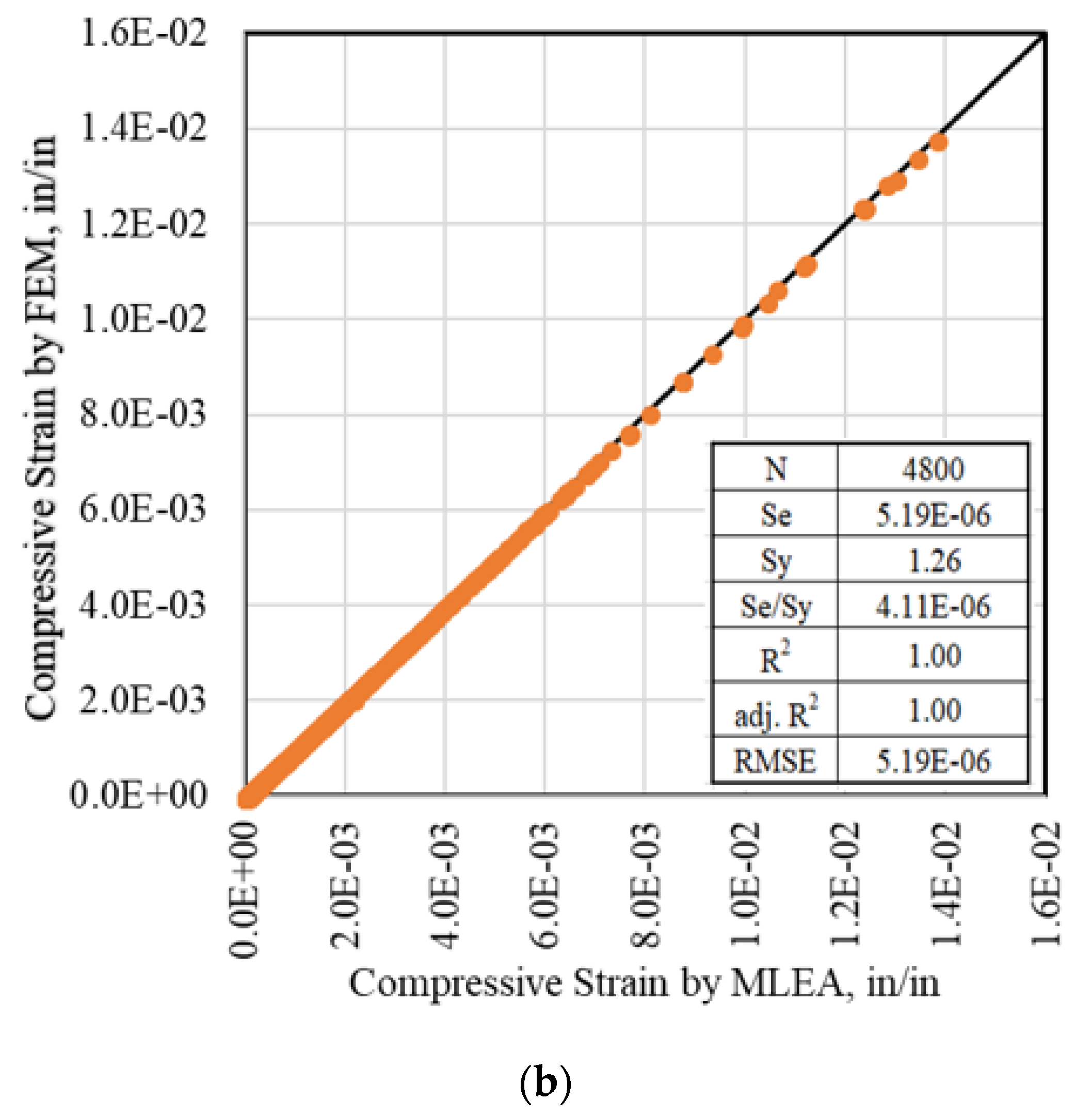

| Layer | Modulus, ksi (MPa) | Depth, in (cm) |
|---|---|---|
| AC layer | 50, 250, 450, and 1000 (344.7, 1723.7, 3102.64, and 6894.75) | 2, 6, 12, and 18 (5.08, 15.24, 30.48, and 45.72) |
| Subgrade | 4, 10, and 20 (27.6, 69, and 137.9) | - |
| Parameter | Calibration Coefficient | ME-PAVE | MEPDG | |
|---|---|---|---|---|
| 1-37A | 1-40D | |||
| Calibration Coefficients | βr1 | 0.80 | 1.0 | 1.0 |
| βr2 | 0.715 | 1.0 | 1.0 | |
| βr3 | 0.715 | 1.0 | 1.0 | |
| βrGB | 0.11 | 1.0 | 1.0 | |
| βrSG | 1.05 | 1.0 | 1.0 | |
| Statistical Goodness of fit parameters | Se/Sy | 0.834 | 0.822 | 0.818 |
| R2 | 0.317 | 0.399 | 0.577 | |
| Parameters | Calibration Coefficients | ME-PAVE | MEPDG | |
|---|---|---|---|---|
| 1-37A | 1-40D | |||
| Calibration Coefficients | β1 | 1.0 | 1.0 | 1.0 |
| β2 | 0.86 | 1.0 | 1.0 | |
| β3 | 0.93 | 1.0 | 1.0 | |
| Statistical goodness of fit parameters | Se/Sy | 0.800 | 0.947 | 0.815 |
| R2 | 0.382 | - | 0.275 | |
| Parameter | AASHTOWare | ME-PAVE |
|---|---|---|
| User Friendly Software | Yes | Yes |
| Pavement Type | ||
| New Pavement Design (Flexible or Rigid) | Yes | Flexible Only |
| Rehabilitation: AC over Fractures Portland Cement Concrete (PCC) Slab (Crack and Seat, Break and Seat, Rubblized) | Yes | No |
| Inputs | ||
| Input Level Hierarchy | Yes | Yes |
| Traffic | ||
| Axle Load Spectra | Yes | No |
| 18-Kips ESALs | Yes | Yes |
| Traffic Distribution (Hourly, Daily, Monthly) | Yes | No |
| Traffic Wander | Yes | No |
| Traffic Speed (Rate of Loading) | Yes | Yes |
| Special Vehicle Damage Analysis | Yes | Yes |
| Climate | ||
| Hourly Climatic Data (Temperature, Precipitation, Wind Speed, Percentage Sunshine, and Relative Humidity) | Yes | No, Average Yearly Climatic Data and σMMAT |
| Groundwater Table Depth | Yes | No |
| Surface Shortwave Absorptivity, | Yes | No |
| Infiltration | Yes | No |
| Drainage Path Length, | Yes | No |
| Cross Slope. | Yes | No |
| Distress | ||
| AC and Unbound Materials Rutting | Yes | Yes |
| Alligator Fatigue Cracking | Yes | Yes |
| Longitudinal Fatigue Cracking | Yes | No |
| Transverse Cracking | Yes | No |
| International Roughness Index, IRI | Yes | Yes |
| Design Reliability for Each Distress | Yes | Yes |
| Models Calibration | ||
| Nationally Calibrated/Validated Models | Yes, based on LTPP database for freeze to high climate | Yes, based on LTPP database for Moderate to high climate |
| Analysis Time for 20 years analysis period | About 10 min | Only 40 s |
| Very Low | Low (L) | Medium (M) | Medium High | High (H) | Very High | |||
|---|---|---|---|---|---|---|---|---|
| Traffic Levels (×105 ESALs) | 2 | 20 | 150 | 500 | 1000 | 1600 | ||
| Operating Speed, mph (km/h) | 2 (3.2) | 25 (40.2) | 45 (72.4) | - | 60 (96.6) | |||
| AC Thickness, in (cm) | 1 (2.5) | 2 (5.1) | 4 (10.2) | 12 (30.5) | ||||
| AC Gradation [56] | Low Mix | Med. Mix | High Mix | |||||
| % P¾″ | 95 | |||||||
| % P3/8″ | 76.5 | |||||||
| % P#4 | 49.1 | |||||||
| % P#200 | 4.8 | |||||||
| AC Grade | Ai | 9.224 [56] | 10.6508 [13] | 10.808 [43] | ||||
| VTSi | −3.065 [56] | −3.5537 [13] | −3.598 [43] | |||||
| AC Air Voids, % | 4 | 7 | 10 | |||||
| Vbe, % | 8 | 11 | 15 | |||||
| Base Layer | Thickness, in (cm) | 4 (10.16) | 10 (25.4) | 25 (63.5) | ||||
| Modulus, ksi (MPa) | 20 (137.9) | 30 (206.8) | 38.5 (265.5) | 50 (344.7) | 60 (413.7) | |||
| Subgrade Modulus, ksi (MPa) | 3 (20.7) | 8 (55.2) | 15 (103.4) | 30 (206.8) | ||||
| Climate Conditions [30] | Cities | Alex. | Cairo | Aswan | ||||
| Parameters | ||||||||
| MAAT, °F (C) | 71.34 (21.86) | 74.42 (23.57) | 76.06 (24.48) | |||||
| σMMAT, °F | 8.33 | 11.60 | 12.39 | |||||
| Wind Speed, mph (km/h) | 10.68 (17.19) | 6.39 (10.28) | 5.36 (8.63) | |||||
| Sunshine (%) | 88.89 | 90.09 | 96.08 | |||||
| Rain, inch (cm) | 9.15 (23.24) | 2.75 (7.0) | 0.38 (0.97) | |||||
| Design Parameters | Rutting Depth | Fatigue Cracking | ||||
|---|---|---|---|---|---|---|
| AC | Base | Subgrade | Thin AC (dAC ≤ 4” (10.2-cm)) | Thick AC (dAC > 4” (10.2-cm)) | ||
| Traffic Level (ESALs) | + | = | = | + | + | |
| AC Thickness | + | - | - | + 1 | - 1 | |
| HMA Properties | Asphalt Grade | - | =+ | =+ | + | - |
| %Va | + | = | = | + | + | |
| %Vbe | + | = | = | - | - | |
| Climatic Conditions (MAAT) | + | = | = | - | + | |
| Base Thickness | = | + | - | - | =- | |
| Base Modulus | =+ | - | - | - | - | |
| Subgrade Modulus | =+ | = | - | - | - | |
| Operating Speed | - | = | = | + | - | |
| Wheel Load | = | + | + | + | - | |
| Tire Pressure | + | =+ | = | + | + | |
| Design Reliability | + | + | + | + | + | |
| Traffic Data | |||
|---|---|---|---|
| Traffic Levels (106 ESALs) | 20 | ||
| Tire Pressure, psi (kPa) | 120 (827.4) | ||
| Wheel Load, kips (kN) | 9 (40) | ||
| Operating Speed, mph (km/h) | 60 (96.6) | ||
| Pavement Layers Properties (Level 2) | |||
| AC layer Gradation [56] | % P¾” | 95 | |
| % P3/8” | 76.5 | ||
| % P#4 | 49.1 | ||
| % P#200 | 4.8 | ||
| AC Grade [13] | Ai | 10.980 | |
| VTSi | −3.680 | ||
| AC in place Air Voids, % | 7 | ||
| Vbe, % | 11 | ||
| Base layer modulus, ksi (MPa) | 50 (344.7) | ||
| Subgrade layer modulus, ksi (MPa) | 15 (103.4) | ||
| Climate Conditions [30] | Cities | Cairo | |
| Parameters | |||
| MAAT, °F (C) | 74.42 (23.6) | ||
| σMMAT (°F) | 11.60 | ||
| Wind Speed, mph (km/h) | 6.39 (10.3) | ||
| Sunshine (%) | 90.09 | ||
| Rain, in (cm) | 2.75 (7.0) | ||
| Parameters | 1993 Designed Section | Alternative Section | Design Criteria | |
|---|---|---|---|---|
| AC Rutting, in (cm) | Mean | 0.110 (0.279) | 0.084 (0.21) | |
| at 90% R | 0.157 (0.4) | 0.124 (0.315) | 0.20-in (0.51) | |
| Total Rutting, in (cm) | Mean | 0.189 (0.48) | 0.261 (0.663) | |
| at 90% R | 0.251 (0.638) | 0.343 (0.871) | 0.5-in (1.27) | |
| AC Fatigue Cracking, % | Mean | 20.785 | 7.335 | |
| at 90% R | 48.026 | 24.093 | 25% | |
| IRI Distress, in/mile (m/km) | Mean | 90.943 (1.44) | 88.133 (1.39) | |
| at 90% R | 96.930 (1.53) | 94.31 (1.49) | 120 (1.89) | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El-Ashwah, A.S.; El-Badawy, S.M.; Gabr, A.R. A Simplified Mechanistic-Empirical Flexible Pavement Design Method for Moderate to Hot Climate Regions. Sustainability 2021, 13, 10760. https://doi.org/10.3390/su131910760
El-Ashwah AS, El-Badawy SM, Gabr AR. A Simplified Mechanistic-Empirical Flexible Pavement Design Method for Moderate to Hot Climate Regions. Sustainability. 2021; 13(19):10760. https://doi.org/10.3390/su131910760
Chicago/Turabian StyleEl-Ashwah, Ahmed S., Sherif M. El-Badawy, and Alaa R. Gabr. 2021. "A Simplified Mechanistic-Empirical Flexible Pavement Design Method for Moderate to Hot Climate Regions" Sustainability 13, no. 19: 10760. https://doi.org/10.3390/su131910760
APA StyleEl-Ashwah, A. S., El-Badawy, S. M., & Gabr, A. R. (2021). A Simplified Mechanistic-Empirical Flexible Pavement Design Method for Moderate to Hot Climate Regions. Sustainability, 13(19), 10760. https://doi.org/10.3390/su131910760








