A Group-Decision-Making Framework for Evaluating Urban Flood Resilience: A Case Study in Yangtze River
Abstract
:1. Introduction
- The proposed evaluation method considers all possible preferences among the results provided by various MCDM methods. The final result can be viewed as a group consensus of different experts. Thus, the decision bias can be largely reduced, making the results more acceptable and robust.
- The holistic acceptability index, which takes into account all the possible ranks of each city, is used to measure the performance. This scheme is completely new in the literature related to the flood resilience evaluation problem.
- We consider 41 cities located near to the Yangtze River Basin as research objects and carry out a numerical experiment. This is the first time that urban resilience to Yangtze River flooding has been explicitly quantified.
2. Materials and Methods
2.1. Study Area
2.2. Group-Decision-Making Framework
2.2.1. Data Normalization
2.2.2. Weights Determination
Variation Coefficient Method
Entropy Weighting Method
CRITIC Method
Ideal Point Method
2.2.3. Results Aggregation
3. Results and Discussions
3.1. Criteria Selection
3.2. Urban Flooding Resilience Derived from Standard MCDM Methods
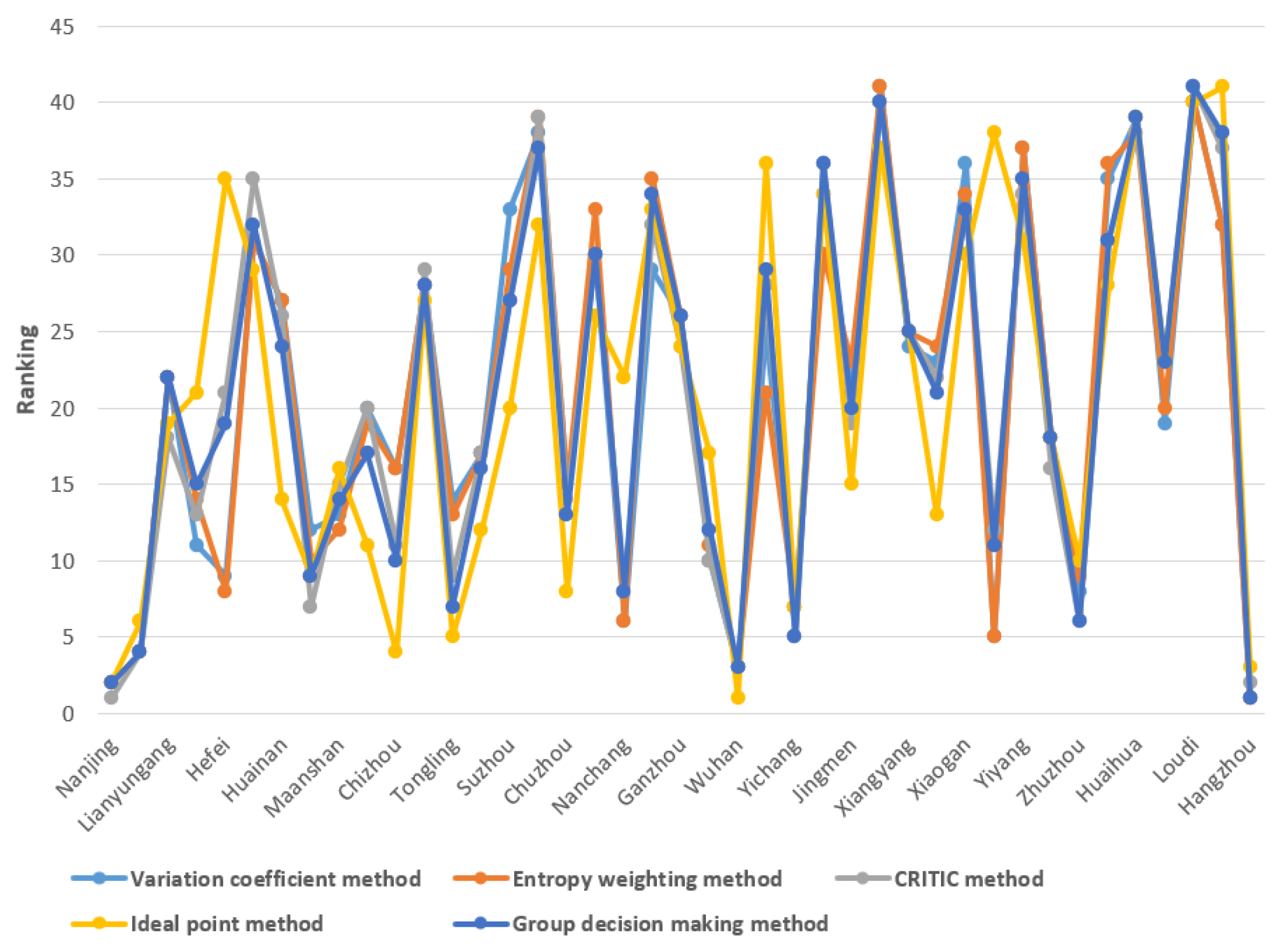
- Obviously, no city has the same ranking position among the four results.
- The four methods have a general consensus on the rankings of the cities which are evaluated relative high or low. For example, Nanjing, Hangzhou and Wuhan are always ranked in top three no matter what method is used.
- The rankings of cities which are evaluated in the middle are diverse. The largest difference occurs in Hefei, where the best ranking is 9 obtained by variation coefficient method and the worst ranking is 35 obtained by ideal point method.
3.3. Urban Flooding Resilience Derived from Proposed Method
Comparison between the Proposed Method and the Standard MCDM Methods
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khosravi, K.; Melesse, A.M.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Hong, H. Flood susceptibility mapping at Ningdu catchment, China using bivariate and data mining techniques. In Extreme Hydrology and Climate Variability; Melesse, A.M., Abtew, W., Senay, G., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 419–434. [Google Scholar]
- Kastridis, A.; Kirkenidis, C.; Sapountzis, M. An integrated approach of flash flood analysis in ungauged Mediterranean watersheds using post-flood surveys and unmanned aerial vehicles. Hydrol. Process. 2020, 34, 4920–4939. [Google Scholar] [CrossRef]
- Hall, J.; Arheimer, B.; Borga, M.; Brázdil, R.; Claps, P.; Kiss, A.; Kjeldsen, T.R.; Kriauciuniene, J.; Kundzewicz, Z.W.; Lang, M.; et al. Understanding flood regime changes in Europe: A state-of-the art assessment. Hydrol. Earth Syst. Sci. 2014, 18, 2735–2772. [Google Scholar] [CrossRef] [Green Version]
- UNISDR; CRED. The Human Cost of Weather-Related Disasters 1995–2015; UNISDR Publications: Geneva, Switzerland, 2015. [Google Scholar]
- Gaume, E.; Bain, V.; Bernardara, P.; Newinger, O.; Barbuc, M.; Bateman, A.; Viglione, A. A compilation of data on European flash floods. J. Hydrol. 2009, 367, 70–78. [Google Scholar] [CrossRef] [Green Version]
- Tzioutzios, C.; Kastridis, A. Multi-Criteria Evaluation (MCE) Method for the Management of Woodland Plantations in Floodplain Areas. ISPRS Int. J. Geo Inf. 2020, 9, 725. [Google Scholar] [CrossRef]
- Suriya, S.; Mudgal, B.V. Impact of urbanization on flooding; The Thirusoolam sub-watershed—A case study. J. Hydrol. 2012, 412–413, 210–219. [Google Scholar] [CrossRef]
- Du, J.; Li, Q.; Rui, H.; Zuo, T.; Zheng, D.; Xu, Y.; Xu, C. Assessing the effects of urbanization on annual runoff and flood events using an integrated hydrological modeling system for Qinhuai River basin, China. J. Hydrol. 2012, 464–465, 127–139. [Google Scholar] [CrossRef]
- Sun, H.; Cheng, X.; Dai, M. Regional flood disaster resilience evaluation based on analytic network process: A case study of the Chaohu Lake Basin, Anhui Province, China. Nat. Hazards 2016, 82, 39–58. [Google Scholar] [CrossRef]
- Gaume, E.; Borga, M.; Llasat, M.C.; Maouche, S.; Lang, M.; Diakakis, M. Mediterranean extreme floods and flash floods. Into Hydrometeorological extremes. In The Mediterranean Region under Climate Change. A Scientific Update; Institut de Recherche Pour le Développement: Marseille, France, 2016; pp. 133–144. [Google Scholar]
- Kastridis, A.; Stathis, D. The Effect of Rainfall Intensity on the Flood Generation of Mountainous Watersheds (Chalkidiki Prefecture, North Greece). In Perspectives on Atmospheric Sciences; Karacostas, T., Bais, A., Nastos, P., Eds.; Springer: Cham, Switzerland, 2017; pp. 341–347. [Google Scholar]
- Morrison, A.; Westbrook, C.; Noble, B. A review of the flood risk management governance and resilience literature. J. Flood Risk Manag. 2018, 11, 291–304. [Google Scholar] [CrossRef]
- Holling, C.; Meffe, G.K. Command and Control and the Pathology of Natural Resource Management. Conserv. Biol. 1996, 10, 328–337. [Google Scholar] [CrossRef] [Green Version]
- Vis, M.; Klijn, F.; Bruijn, K.M.D.; Buuren, M.V. Resilience strategies for flood risk management in the netherlands. Int. J. River Basin Manag. 2003, 1, 33–40. [Google Scholar] [CrossRef]
- Jones, H.P.; Hole, D.G.; Zavaleta, E.S. Harnessing nature to help people adapt to climate change. Nat. Clim. Chang. 2012, 2, 504–509. [Google Scholar] [CrossRef]
- Asian Development Bank. Managing Asian Cities: Sustainable and Inclusive Urban Solutions; Asian Development Bank: Tokyo, Japan, 2008; pp. 89–92. [Google Scholar]
- Kotzee, I.; Reyers, B. Piloting a social-ecological index for measuring flood resilience: A composite index approach. Ecol. Indic. 2016, 60, 45–53. [Google Scholar] [CrossRef]
- Chen, K.F.; Leandro, J. A conceptual time-varying flood resilience index for urban areas: Munich city. Water 2019, 11, 830. [Google Scholar] [CrossRef] [Green Version]
- Holling, C.S. Resilience and Stability of Ecological Systems. Annu. Rev. Ecol. Syst. 1973, 4, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Andoh, R.Y.G.; Iwugo, K.O. Sustainable Urban Drainage Systems: A UK Perspective. Urban Drain 2002, 4, 1–16. [Google Scholar]
- Levy, J.K.; Hartmann, J.; Li, K.W.; An, Y.; Asgary, A. Multi-Criteria Decision Support Systems for Flood Hazard Mitigation and Emergency Response in Urban Watersheds. J. Am. Water Resour. Assoc. 2007, 43, 346–358. [Google Scholar] [CrossRef]
- Carter, J.G.; White, I.; Richards, J. Sustainability appraisal and flood risk management. Environ. Impact Assess. Rev. 2009, 29, 7–14. [Google Scholar] [CrossRef]
- Liao, K.H. A Theory on Urban Resilience to Floods—A Basis for Alternative Planning Practices. Ecol. Soc. 2012, 17, 48. [Google Scholar] [CrossRef]
- Rosner, A.; Vogel, R.M.; Kirshen, P.H. A risk-based approach to flood management decisions in a nonstationary world. Water Resour. Res. 2014, 50, 1928–1942. [Google Scholar] [CrossRef]
- de Bruijn, K.M. Resilience and flood risk management. Water Policy 2004, 6, 53–66. [Google Scholar] [CrossRef]
- Keating, A.; Campbell, K.; Szoenyi, M.; McQuistan, C.; Nash, D.; Burer, M. Development and testing of a community flood resilience measurement tool. Nat. Hazards Earth Syst. Sci. 2017, 17, 77–101. [Google Scholar] [CrossRef] [Green Version]
- Bertilsson, L.; Wiklund, K.; Tebaldi, I.M.; Rezende, O.M.; Veról, A.P.; Miguez, M.G. Urban flood resilience—A multi-criteria index to integrate flood resilience into urban planning. J. Hydrol. 2019, 573, 970–982. [Google Scholar] [CrossRef]
- McClymont, K.; Morrison, D.; Beevers, L.; Carmen, E. Flood resilience: A systematic review. J. Environ. Plan. Manag. 2020, 63, 1151–1176. [Google Scholar] [CrossRef] [Green Version]
- Odemerho, F.O. Building climate change resilience through bottom-up adaptation to flood risk in Warri, Nigeria. Environ. Urban. 2015, 27, 139–160. [Google Scholar] [CrossRef]
- Mavhura, E. Applying a systems-thinking approach to community resilience analysis using rural livelihoods: The case of Muzarabani district, Zimbabwe. Int. J. Disaster Risk Reduct. 2017, 25, 248–258. [Google Scholar] [CrossRef]
- Hegger, D.L.T.; Driessen, P.P.J.; Wiering, M.; Van Rijswick, H.F.M.W.; Kundzewicz, Z.W.; Matczak, P.; Crabbé, A.; Raadgever, G.T.; Bakker, M.H.N.; Priest, S.J.; et al. Toward more flood resilience: Is a diversification of flood risk management strategies the way forward? Ecol. Soc. 2016, 21, 52. [Google Scholar] [CrossRef]
- Gamper, C.D.; Thöni, M.; Weck-Hannemann, H. A Conceptual Approach to the Use of Cost Benefit and Multi Criteria Analysis in Natural Hazard Management. Nat. Hazards Earth Syst. Sci. 2006, 6, 293–302. [Google Scholar] [CrossRef] [Green Version]
- Serre, D.; Barroca, B.; Balsells, M.; Becue, V. Contributing to urban resilience to floods with neighbourhood design: The case of am sandtorkai/dalmannkai in hamburg. J. Flood Risk Manag. 2018, 11, S69–S83. [Google Scholar] [CrossRef]
- Golz, S.; Schinke, R.; Naumann, T. Assessing the effects of flood resilience technologies on building scale. Urban Water J. 2015, 12, 30–43. [Google Scholar] [CrossRef]
- Song, J.; Huang, B.; Li, R. Measuring Recovery to Build up Metrics of Flood Resilience Based on Pollutant Discharge Data: A Case Study in East China. Water 2017, 9, 619. [Google Scholar] [CrossRef]
- Miguez, M.G.; Veról, A.P. A catchment scale integrated flood resilience index to support decision making in urban flood control design. Environ. Plan. B 2017, 44, 925–946. [Google Scholar] [CrossRef]
- Moghadas, M.; Asadzadeh, A.; Vafeidis, A.; Fekete, A.; Kötter, T. A multi-criteria approach for assessing urban flood resilience in Tehran, Iran. Int. J. Disaster Risk Reduct. 2019, 35, 101069. [Google Scholar] [CrossRef]
- Lu, C.; You, J.-X.; Liu, H.-C.; Li, P. Health-Care Waste Treatment Technology Selection Using the Interval 2-Tuple Induced TOPSIS Method. Int. J. Environ. Res. Public Health 2016, 13, 562. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paliaga, G.; Faccini, F.; Luino, F.; Turconi, L. A Spatial Multicriteria Prioritizing Approach for Geohydrological Risk Mitigation Planning in Small and Densely Urbanized Mediterranean Basins. Nat. Hazards Earth Syst. Sci. 2019, 19, 53–69. [Google Scholar] [CrossRef] [Green Version]
- Song, L.; Liu, F. An improvement in DEA cross-efficiency aggregation based on the Shannon entropy. Int. Trans. Oper. Res. 2016, 25, 705–714. [Google Scholar] [CrossRef]
- Kumar, R.; Garg, R.K. Optimal selection of robots by using distance based approach method. Robot. Comput. Integr. Manuf. 2010, 26, 500–506. [Google Scholar] [CrossRef]
- Liu, F.; Ma, N. Multicriteria ABC Inventory Classification Using the Social Choice Theory. Sustainability 2020, 12, 182. [Google Scholar] [CrossRef] [Green Version]
- Melkonyan, T.; Safra, Z. Intrinsic Variability in Group and Individual Decision Making. Manag. Sci. 2016, 62, 2651–2667. [Google Scholar] [CrossRef] [Green Version]
- Yu, L.; Lai, K.K. A distance-based group decision-making methodology for multi-person multi-criteria emergency decision support. Decis. Support Syst. 2011, 51, 307–315. [Google Scholar] [CrossRef]
- Fu, Y.; Li, M.; Luo, H.; Huang, G.Q. Industrial robot selection using stochastic multicriteria acceptability analysis for group decision making. Robot. Auton. Syst. 2019, 122, 103304. [Google Scholar] [CrossRef]
- Faber, D.S.; Korn, H. Applicability of the coefficient of variation method for analyzing synaptic plasticity. Biophys. J. 1991, 60, 1288–1294. [Google Scholar] [CrossRef] [Green Version]
- Adali, E.A.; Isik, A.T. Critic and Maut Methods for the Contract Manufacturer Selection Problem. Eur. J. Multidiscip. Stud. 2017, 2, 93–101. [Google Scholar] [CrossRef] [Green Version]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The critic method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Peng, C.; Wu, X.; Fu, Y.; Lai, K.K. Alternative approaches to constructing composite indicators: An application to construct a Sustainable Energy Index for APEC economies. Oper. Res. 2017, 17, 747–759. [Google Scholar] [CrossRef]
- Lahdelma, R.; Makkonen, S.; Salminen, P. Multivariate Gaussian criteria in SMAA. Eur. J. Oper. Res. 2006, 170, 957–970. [Google Scholar] [CrossRef]
- Lahdelma, R.; Salminen, P. SMAA-2: Stochastic Multicriteria Acceptability Analysis for Group Decision Making. Oper. Res. 2001, 49, 444–454. [Google Scholar] [CrossRef]
- Harrell, F.E.; Califf, R.M.; Pryor, D.B.; Lee, K.L.; Rosati, R.A. Evaluating the Yield of Medical Tests. JAMA 1982, 247, 2543–2546. [Google Scholar] [CrossRef]
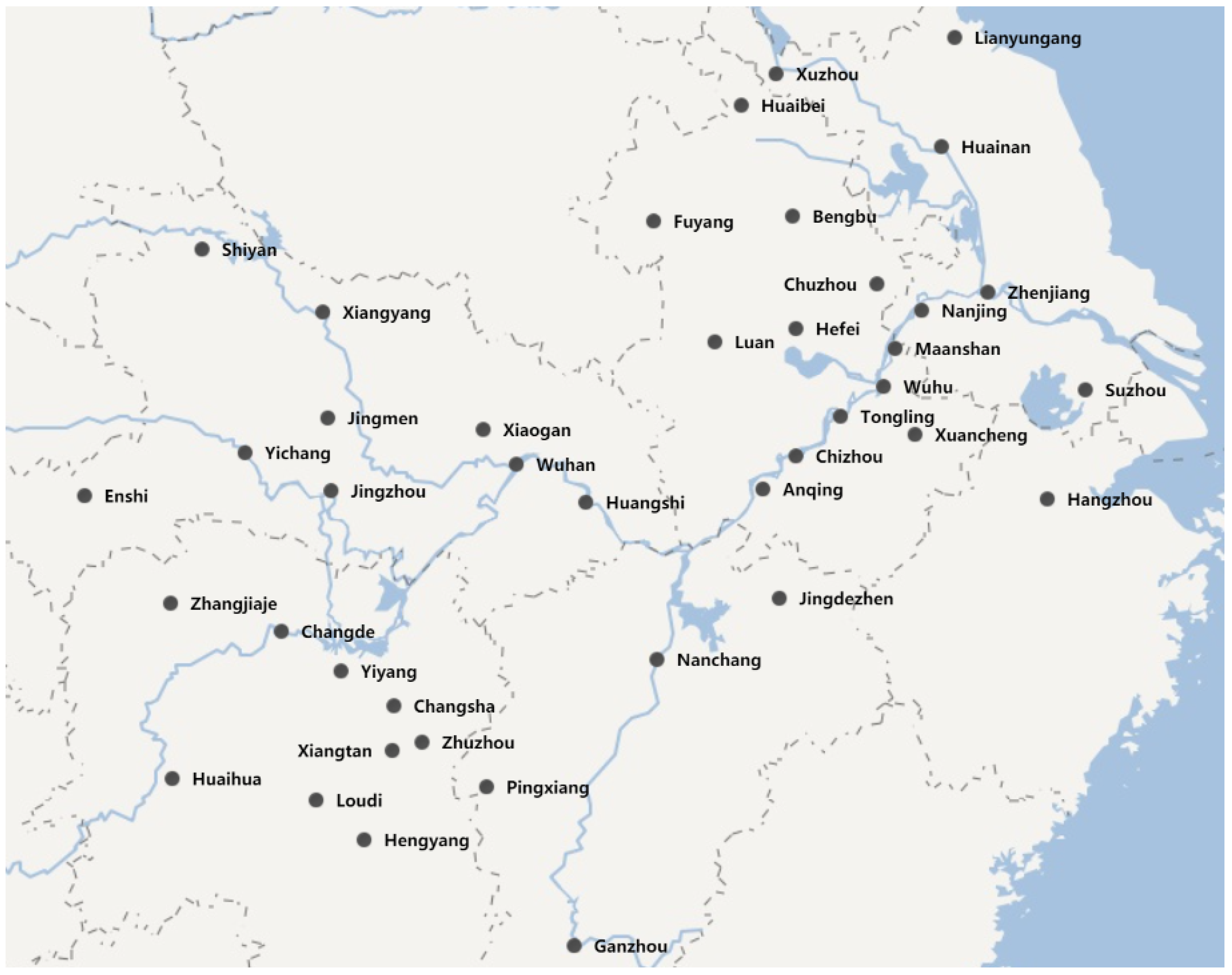

| Criteria | Description | Type |
|---|---|---|
| Age Dependency Ratio (ADR) | % Population aged under 15 and above 65 | Cost |
| CPI (CPI) | Consumer Price Index | Cost |
| Figure-Ground Diagram (FGD) | Ratio of built & unbuilt space | Cost |
| Population Density (PD) | Number of people/km2 | Cost |
| Unemploymet rate (UER) | % of unemployment | Cost |
| Access/evacuation potential (AEP) | Per capita square meters of arterial area | Benefit |
| Average Income (AI) | Per capita disposable income of Residents | Benefit |
| Average Savings (AS) | Per capita savings of residents | Benefit |
| Communication Capacity (CC) | % Population owning a cell phone | Benefit |
| Civic Involvement (CI) | Number of civic organisations per 1000 population | Benefit |
| Drainage capacity (DC) | Length of drain-pipe per square kilometer | Benefit |
| Ecological Buffer (EB) | % Natural vegetaton | Benefit |
| Econmoic risk-resisting ability (ERA) | Per capita property insurance | Benefit |
| Green Area (GA) | Per capita square meters of green area | Benefit |
| Medical care capacity (MCC) | Number of hospital beds per 1000 people | Benefit |
| Redundancy of emergency services (RES) | Number of stations, police stations & emergency operation centers per 1000 people | Benefit |
| Soil retention (SR) | % deep permeable soil | Benefit |
| City | PD | ADR | UER | MCC | RES | CI | CC | AI | AS | ERA | CPI | EB | GA | FGD | AEP | SR | DC |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nanjing | 0.9322 | 0.9600 | 0.7857 | 0.4397 | 0.8235 | 0.7236 | 0.6452 | 0.9298 | 0.8289 | 0.8014 | 0.4839 | 0.5056 | 0.6657 | 0.6828 | 0.4275 | 0.5000 | 0.5035 |
| Zhenjiang | 0.9188 | 0.8300 | 0.7569 | 0.1935 | 0.2353 | 0.4878 | 0.4000 | 0.6665 | 0.6195 | 0.3633 | 0.6452 | 0.4956 | 1.0000 | 0.6497 | 0.5006 | 0.4844 | 0.6652 |
| Lianyungang | 0.9344 | 0.2980 | 0.5311 | 0.2716 | 0.3529 | 0.2520 | 0.3806 | 0.0064 | 0.1342 | 0.2025 | 0.6774 | 0.3359 | 0.6031 | 0.7859 | 0.4406 | 0.7500 | 0.4487 |
| Xuzhou | 0.7587 | 0.3140 | 0.5611 | 0.4346 | 0.4706 | 0.5285 | 0.3806 | 0.2372 | 0.3156 | 0.2327 | 0.6129 | 0.5370 | 0.7026 | 0.7750 | 0.4565 | 0.4375 | 0.3669 |
| Hefei | 0.6991 | 0.7067 | 0.4816 | 0.3939 | 0.4706 | 0.2927 | 0.4645 | 0.4437 | 0.3717 | 0.4900 | 0.5161 | 0.3856 | 0.4963 | 0.0000 | 0.2514 | 0.8750 | 0.6381 |
| Bengbu | 0.8045 | 0.2667 | 0.2949 | 0.2343 | 0.3529 | 0.2114 | 0.2194 | 0.1714 | 0.0855 | 0.1757 | 0.8387 | 0.1810 | 0.4530 | 0.5829 | 0.3372 | 0.7031 | 0.3683 |
| Huainan | 0.8462 | 0.5480 | 0.3214 | 0.0849 | 0.3529 | 0.4797 | 0.1871 | 0.2269 | 0.1711 | 0.1103 | 0.9677 | 0.3678 | 0.4134 | 0.8409 | 0.2065 | 0.6406 | 0.2821 |
| Wuhu | 1.0000 | 0.6520 | 0.4136 | 0.2530 | 0.3529 | 0.3902 | 0.2968 | 0.3622 | 0.3053 | 0.2141 | 0.7097 | 0.2383 | 0.4890 | 0.6655 | 0.5106 | 0.8438 | 0.7899 |
| Maanshan | 0.6257 | 0.6467 | 0.4862 | 0.0543 | 0.2941 | 0.3089 | 0.3161 | 0.5493 | 0.3732 | 0.2205 | 0.7419 | 0.5636 | 0.6326 | 0.6306 | 0.3099 | 0.7344 | 0.7421 |
| Xuancheng | 0.7941 | 0.4760 | 0.0000 | 0.1851 | 0.2941 | 0.2846 | 0.2839 | 0.3161 | 0.2109 | 0.1589 | 0.8710 | 0.2839 | 0.5516 | 0.9651 | 0.6380 | 0.6250 | 0.6578 |
| Chizhou | 0.9637 | 0.4507 | 0.1071 | 0.1426 | 0.1765 | 0.3496 | 0.2516 | 0.1679 | 0.3053 | 0.1684 | 0.8065 | 0.1502 | 0.8260 | 0.9821 | 0.4914 | 0.9531 | 0.9507 |
| Anqing | 0.8429 | 0.4160 | 0.0760 | 0.0000 | 0.3529 | 0.1951 | 0.2194 | 0.1756 | 0.1932 | 0.0000 | 0.7742 | 0.6109 | 0.5387 | 0.7062 | 0.2974 | 0.6250 | 0.5769 |
| Tongling | 0.8163 | 0.6180 | 0.2972 | 0.3396 | 0.0000 | 0.2520 | 0.2194 | 0.3082 | 0.3673 | 0.1557 | 1.0000 | 0.6032 | 0.8803 | 0.8284 | 0.1134 | 0.7500 | 0.8294 |
| Huaibei | 0.6995 | 0.4667 | 0.3364 | 0.3548 | 0.1176 | 0.5203 | 0.2516 | 0.1996 | 0.1858 | 0.1793 | 0.9355 | 0.7002 | 0.7928 | 0.6957 | 0.2478 | 0.8438 | 0.3240 |
| Suzhou | 0.7069 | 0.1867 | 0.0945 | 0.0424 | 0.1765 | 0.0000 | 0.2581 | 0.1445 | 0.0487 | 0.0994 | 0.9032 | 0.3903 | 0.4880 | 0.9461 | 0.5541 | 1.0000 | 0.5039 |
| Fuyang | 0.8343 | 0.0000 | 0.0242 | 0.1715 | 0.3529 | 0.0407 | 0.1806 | 0.1429 | 0.0988 | 0.1542 | 0.8710 | 0.1011 | 0.5378 | 0.8383 | 0.5072 | 0.3906 | 0.3674 |
| Chuzhou | 0.9206 | 0.3440 | 0.0449 | 0.1426 | 0.2941 | 0.2602 | 0.2903 | 0.1687 | 0.1490 | 0.1788 | 0.8065 | 0.3702 | 0.5866 | 0.8486 | 1.0000 | 0.7500 | 1.0000 |
| Luan | 0.6905 | 0.2987 | 0.1290 | 0.0696 | 0.3529 | 0.0081 | 0.1871 | 0.1187 | 0.1106 | 0.1609 | 0.6774 | 0.3365 | 0.6197 | 0.9684 | 0.4521 | 0.7813 | 0.3994 |
| Nanchang | 0.2389 | 0.4620 | 0.7903 | 0.4160 | 0.4706 | 1.0000 | 0.5419 | 0.4362 | 0.5723 | 0.4105 | 0.6774 | 0.4009 | 0.3407 | 0.7264 | 0.1129 | 0.6406 | 0.3895 |
| Pingxiang | 0.4902 | 0.3287 | 0.9159 | 0.3328 | 0.1765 | 0.3740 | 0.2774 | 0.3081 | 0.1431 | 0.1259 | 0.6774 | 0.4630 | 0.2311 | 0.8866 | 0.2171 | 0.2188 | 0.0000 |
| Ganzhou | 0.5792 | 0.0440 | 0.6636 | 0.1817 | 1.0000 | 0.3008 | 0.2452 | 0.1944 | 0.1504 | 0.0298 | 0.7097 | 0.2295 | 0.3076 | 0.9359 | 0.1909 | 0.6563 | 0.4901 |
| Jingdezhen | 0.8413 | 0.4087 | 0.6417 | 0.3209 | 0.1765 | 0.7967 | 0.0000 | 0.3334 | 0.2581 | 0.1019 | 0.7742 | 1.0000 | 0.8352 | 0.5923 | 0.5624 | 0.3125 | 0.3693 |
| Wuhan | 0.5518 | 1.0000 | 0.8260 | 0.7946 | 0.9412 | 0.7967 | 0.6645 | 0.6004 | 0.6327 | 0.5019 | 0.9677 | 0.1336 | 0.2099 | 0.8266 | 0.1775 | 0.4531 | 0.7362 |
| Huangshi | 0.6793 | 0.5280 | 0.5841 | 0.4771 | 0.0000 | 0.3821 | 0.3161 | 0.2849 | 0.2330 | 0.1304 | 0.6774 | 0.2076 | 0.3444 | 0.0357 | 0.3333 | 0.8594 | 0.7737 |
| Yichang | 0.9091 | 0.7687 | 0.7419 | 0.5501 | 0.4118 | 0.4472 | 0.3935 | 0.2794 | 0.3850 | 0.2665 | 0.6129 | 0.3010 | 0.5967 | 0.9110 | 0.3974 | 0.5625 | 0.2929 |
| Jingzhou | 0.0000 | 0.6673 | 0.5818 | 0.2869 | 0.4118 | 0.3089 | 0.4000 | 0.2130 | 0.2035 | 0.1142 | 0.7742 | 0.0272 | 0.2155 | 0.8664 | 0.1159 | 0.6094 | 0.2894 |
| Jingmen | 0.8601 | 0.8353 | 0.7074 | 0.4109 | 0.1176 | 0.3984 | 0.2645 | 0.2532 | 0.3053 | 0.1406 | 0.7097 | 0.0000 | 0.3425 | 0.9441 | 0.3498 | 0.2031 | 0.6203 |
| Enshi | 0.5368 | 0.2320 | 0.4493 | 0.3650 | 0.3529 | 0.0732 | 0.2774 | 0.1775 | 0.0000 | 0.0754 | 0.6452 | 0.0739 | 0.1648 | 1.0000 | 0.0276 | 0.4531 | 0.2436 |
| Xiangyang | 0.7300 | 0.6413 | 0.6532 | 0.4465 | 0.2941 | 0.4309 | 0.3097 | 0.3128 | 0.2625 | 0.1499 | 0.6452 | 0.1023 | 0.3978 | 0.8907 | 0.2673 | 0.2813 | 0.3013 |
| Shiyan | 0.9439 | 0.6333 | 0.2719 | 0.8217 | 0.4118 | 0.1789 | 0.3290 | 0.1693 | 0.3820 | 0.1117 | 0.7419 | 0.0970 | 0.2735 | 0.9646 | 0.0928 | 0.4688 | 0.5340 |
| Xiaogan | 0.5413 | 0.6413 | 0.5000 | 0.1392 | 0.2941 | 0.2195 | 0.2000 | 0.2218 | 0.1652 | 0.0295 | 0.6452 | 0.0993 | 0.1372 | 0.8729 | 0.4231 | 0.4375 | 0.6351 |
| Changsha | 0.9946 | 0.7007 | 1.0000 | 1.0000 | 0.5294 | 0.5691 | 0.6645 | 0.7146 | 0.6873 | 0.6496 | 0.0000 | 0.1603 | 0.2431 | 0.2387 | 0.2046 | 0.0000 | 0.2983 |
| Yiyang | 0.4175 | 0.4633 | 0.8226 | 0.3633 | 0.2353 | 0.2195 | 0.2194 | 0.1192 | 0.1165 | 0.0909 | 0.7419 | 0.4122 | 0.0866 | 0.9063 | 0.1265 | 0.2344 | 0.5163 |
| Changde | 0.5216 | 0.5627 | 0.7212 | 0.4092 | 0.7059 | 0.6098 | 0.2710 | 0.1766 | 0.1593 | 0.1257 | 0.6774 | 0.4287 | 0.5083 | 0.9189 | 0.0571 | 0.6875 | 0.1519 |
| Zhuzhou | 0.9565 | 0.5700 | 0.8882 | 0.4703 | 0.4118 | 0.3659 | 0.2258 | 0.5071 | 0.3097 | 0.1549 | 0.7742 | 0.4654 | 0.4199 | 0.5551 | 0.3208 | 0.8125 | 0.4038 |
| Zhangjiajie | 0.6563 | 0.2800 | 0.5438 | 0.3548 | 0.1176 | 0.5447 | 0.2516 | 0.0000 | 0.1298 | 0.1304 | 0.7419 | 0.1833 | 0.1022 | 0.9892 | 0.3620 | 0.5469 | 0.3185 |
| Huaihua | 0.0073 | 0.3693 | 0.5910 | 0.4754 | 0.6471 | 0.2520 | 0.2387 | 0.0489 | 0.0973 | 0.0658 | 0.6774 | 0.1153 | 0.0000 | 0.7674 | 0.0000 | 0.8750 | 0.2712 |
| Xiangtan | 0.5546 | 0.5113 | 0.9574 | 0.4788 | 0.1765 | 0.1382 | 0.3355 | 0.3395 | 0.3614 | 0.2073 | 0.8065 | 0.3596 | 0.1133 | 0.6705 | 0.2873 | 0.5156 | 0.6085 |
| Loudi | 0.1935 | 0.2640 | 0.8214 | 0.4211 | 0.1765 | 0.1626 | 0.2452 | 0.0847 | 0.1431 | 0.0719 | 0.7097 | 0.1869 | 0.1326 | 0.6857 | 0.0608 | 0.2031 | 0.4458 |
| Hengyang | 0.1216 | 0.2500 | 0.7638 | 0.4228 | 0.5882 | 0.4309 | 0.2065 | 0.2509 | 0.1799 | 0.0724 | 0.5484 | 0.3063 | 0.1897 | 0.4391 | 0.1341 | 0.5156 | 0.3496 |
| Hangzhou | 0.6723 | 0.8467 | 0.6601 | 0.6995 | 0.7059 | 0.7073 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.5161 | 0.3099 | 0.5810 | 0.7015 | 0.1196 | 0.7656 | 0.4931 |
| 1.0000 | ||||
| 0.5229 | 1.0000 | |||
| −0.5377 | −0.6233 | 1.0000 | ||
| −0.8269 | −0.8532 | 0.5296 | 1.0000 |
| City | Ranking and Score | |||
|---|---|---|---|---|
| Variation Coefficient Method | Entropy Weighting Method | CRITIC Method | Ideal Point Method | |
| Nanjing | 2(0.6982) | 2(0.6777) | 1(0.6821) | 2(0.6710) |
| Zhenjiang | 4(0.5580) | 4(0.5633) | 4(0.5925) | 6(0.6308) |
| Lianyungang | 22(0.3774) | 22(0.3955) | 18(0.4679) | 19(0.5543) |
| Xuzhou | 11(0.4457) | 14(0.4539) | 13(0.5001) | 21(0.5463) |
| Hefei | 9(0.4589) | 8(0.4742) | 21(0.4644) | 35(0.4629) |
| Bengbu | 31(0.3147) | 31(0.3319) | 35(0.3925) | 29(0.4922) |
| Huainan | 27(0.3483) | 27(0.3669) | 26(0.4404) | 14(0.5691) |
| Wuhu | 12(0.4450) | 10(0.4684) | 7(0.5191) | 9(0.5997) |
| Maanshan | 13(0.4428) | 12(0.4632) | 15(0.4969) | 16(0.5626) |
| Xuancheng | 20(0.3861) | 19(0.4091) | 20(0.4645) | 11(0.5843) |
| Chizhou | 16(0.4102) | 16(0.4412) | 11(0.5103) | 4(0.6365) |
| Anqing | 28(0.3266) | 28(0.3548) | 29(0.4077) | 27(0.5123) |
| Tongling | 14(0.4243) | 13(0.4546) | 9(0.5116) | 5(0.6350) |
| Huaibei | 17(0.4060) | 17(0.4301) | 17(0.4815) | 12(0.5785) |
| Suzhou | 33(0.3109) | 29(0.3370) | 27(0.4148) | 20(0.5514) |
| Fuyang | 38(0.2743) | 39(0.2831) | 39(0.3542) | 32(0.4787) |
| Chuzhou | 15(0.4174) | 15(0.4484) | 14(0.4993) | 8(0.6014) |
| Luan | 30(0.3149) | 33(0.3301) | 30(0.4048) | 26(0.5125) |
| Nanchang | 6(0.4920) | 6(0.4976) | 8(0.5172) | 22(0.5454) |
| Pingxiang | 29(0.3242) | 35(0.3222) | 32(0.3957) | 33(0.4680) |
| Ganzhou | 26(0.3502) | 26(0.3674) | 24(0.4513) | 24(0.5296) |
| Jingdezhen | 10(0.4561) | 11(0.4660) | 10(0.5115) | 17(0.5585) |
| Wuhan | 3(0.6077) | 3(0.6223) | 3(0.6447) | 1(0.6989) |
| Huangshi | 25(0.3621) | 21(0.3964) | 28(0.4093) | 36(0.4480) |
| Yichang | 7(0.4761) | 7(0.4836) | 5(0.5475) | 7(0.6116) |
| Jingzhou | 34(0.3079) | 30(0.3326) | 36(0.3812) | 34(0.4656) |
| Jingmen | 21(0.3806) | 23(0.3953) | 19(0.4662) | 15(0.5664) |
| Enshi | 41(0.2440) | 41(0.2549) | 40(0.3393) | 37(0.4469) |
| Xiangyang | 24(0.3728) | 25(0.3809) | 25(0.4450) | 25(0.5247) |
| Shiyan | 23(0.3754) | 24(0.3948) | 22(0.4620) | 13(0.5723) |
| Xiaogan | 36(0.3065) | 34(0.3290) | 33(0.3929) | 30(0.4855) |
| Changsha | 5(0.5434) | 5(0.5148) | 12(0.5047) | 38(0.4346) |
| Yiyang | 37(0.3038) | 37(0.3194) | 34(0.3926) | 31(0.4820) |
| Changde | 18(0.4026) | 18(0.4191) | 16(0.4899) | 18(0.5563) |
| Zhuzhou | 8(0.4607) | 9(0.4735) | 6(0.5361) | 10(0.5966) |
| Zhangjiajie | 35(0.3072) | 36(0.3201) | 31(0.4015) | 28(0.5115) |
| Huaihua | 39(0.2726) | 38(0.2982) | 38(0.3580) | 39(0.4271) |
| Xiangtan | 19(0.3922) | 20(0.4053) | 23(0.4617) | 23(0.5333) |
| Loudi | 40(0.2500) | 40(0.2656) | 41(0.3230) | 40(0.3947) |
| Hengyang | 32(0.3142) | 32(0.3308) | 37(0.3633) | 41(0.3806) |
| Hangzhou | 1(0.7151) | 1(0.6938) | 2(0.6768) | 3(0.6677) |
| City | Rank Acceptability Index | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Nanjing | 0.1176 | 0.8646 | 0.0178 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Zhenjiang | 0.0000 | 0.0000 | 0.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Lianyungang | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Xuzhou | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Hefei | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Bengbu | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Huainan | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Wuhu | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Maanshan | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Xuancheng | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Chizhou | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0084 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Anqing | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Tongling | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0785 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Huaibei | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Suzhou | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Fuyang | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.5040 | 0.2601 | 0.2030 | 0.0000 | 0.0000 |
| Chuzhou | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Luan | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Nanchang | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0011 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Pingxiang | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Ganzhou | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Jingdezhen | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Wuhan | 0.0542 | 0.0072 | 0.9386 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Huangshi | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0297 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Yichang | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.7305 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Jingzhou | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0018 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Jingmen | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Enshi | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.1023 | 0.1379 | 0.6810 | 0.0788 |
| Xiangyang | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Shiyan | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Xiaogan | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Changsha | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.1815 | 0.0014 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Yiyang | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0464 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Changde | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Zhuzhou | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Zhangjiajie | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Huaihua | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.4733 | 0.5267 | 0.0000 | 0.0000 |
| Xiangtan | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Loudi | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0916 | 0.9084 |
| Hengyang | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.4167 | 0.1643 | 0.1324 | 0.2274 | 0.0128 |
| Hangzhou | 0.8282 | 0.1282 | 0.0436 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Data 1 | Data 2 | Data 3 | Data 4 | Data 5 |
|---|---|---|---|---|
| Suzhou | Anqing | Hefei | Maanshan | Wuhu |
| Hengyang | Xuzhou | Hengyang | Yichang | Xiaogan |
| Hangzhou | Loudi | Huaihua | Zhangjiajie | Zhenjiang |
| Chuzhou | Hangzhou | Xuancheng | Zhuzhou | Maanshan |
| Huaibei | Chuzhou | Xiangyang | Nanchang | Xuzhou |
| Shiyan | Tongling | Suzhou | Huainan | Anqing |
| Huangshi | Bengbu | Tongling | Luan | Lianyungang |
| Shiyan | Yiyang | Nanjing | Tongling | Huainan |
| Enshi | Enshi | Xuzhou | Huaibei | Wuhan |
| Jingmen | Changde | Shiyan | Xiangtan | Zhangjiajie |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.; Liu, F. A Group-Decision-Making Framework for Evaluating Urban Flood Resilience: A Case Study in Yangtze River. Sustainability 2021, 13, 665. https://doi.org/10.3390/su13020665
Zhu H, Liu F. A Group-Decision-Making Framework for Evaluating Urban Flood Resilience: A Case Study in Yangtze River. Sustainability. 2021; 13(2):665. https://doi.org/10.3390/su13020665
Chicago/Turabian StyleZhu, Huagui, and Fan Liu. 2021. "A Group-Decision-Making Framework for Evaluating Urban Flood Resilience: A Case Study in Yangtze River" Sustainability 13, no. 2: 665. https://doi.org/10.3390/su13020665
APA StyleZhu, H., & Liu, F. (2021). A Group-Decision-Making Framework for Evaluating Urban Flood Resilience: A Case Study in Yangtze River. Sustainability, 13(2), 665. https://doi.org/10.3390/su13020665




