Data-Driven Forecasting and Modeling of Runoff Flow to Reduce Flood Risk Using a Novel Hybrid Wavelet-Neural Network Based on Feature Extraction

Abstract

The reliable forecasting of river flow plays a key role in reducing the risk of floods. Regarding nonlinear and variable characteristics of hydraulic processes, the use of data-driven and hybrid methods has become more noticeable. Thus, this paper proposes a novel hybrid wavelet-neural network (WNN) method with feature extraction to forecast river flow. To do this, initially, the collected data are analyzed by the wavelet method. Then, the number of inputs to the ANN is determined using feature extraction, which is based on energy, standard deviation, and maximum values of the analyzed data. The proposed method has been analyzed by different input and various structures for daily, weekly, and monthly flow forecasting at Ellen Brook river station, western Australia. Furthermore, the mean squares error (MSE), root mean square error (RMSE), and the Nash-Sutcliffe efficiency (NSE) is used to evaluate the performance of the suggested method. Furthermore, the obtained findings were compared to those of other models and methods in order to examine the performance and efficiency of the feature extraction process. It was discovered that the proposed feature extraction model outperformed their counterparts, especially when it came to long-term forecasting.

1. Introduction

Water demand is increasing daily due to population growth, irrigation, and industrial developments. Excessive groundwater exploitation has reduced access to surface water. On the other hand, severe weather conditions have led to floods and irreparable damage [1]. Modeling and forecasting surface water resources is a major issue in water resources management and disaster reduction [2]. Water flow forecasting plays a key role in flood reduction, reservoir optimization, and reservoir management [3]. forecasting hydrological reactions invariably involves uncertainty [4]. Numerous studies have been performed to improve the reliability and accuracy of hydrological forecasts, resulting in reduced risk error [5]. Different types of forecasting methods have been proposed over the decades. A physics-based method, which has the potential advantage of providing physical insight into the hydrological system, is one of these methods [6]. The main disadvantage of these methods is that they require a large amount of data and numerous parameters.

The next model is concept-based, data-driven, and uses linear methods that are relatively simpler. One of the advantages of this model is the need for only minimal data and the ability to simulate the nonlinear features of hydrological processes with minimal observation data [7]. Various data-driven methods have been studied in hydrology, but they are not yet to prove highly forecasting accuracy [8]. Among these methods, computational intelligence (CI) techniques are capable of simulating the nonlinear equations of hydrological processes [9]. Adaptive Neural/Fuzzy Inference System (ANFIS) is one of the CI techniques based on fuzzy logic, which is suggested by Zadeh [10]. The application of ANFIS has been investigated in several hydrological studies, including river flow forecasts [11,12,13].

The results of these studies show that ANFIS is a promising approach to achieve accurate and fast forecasts. However, due to the limited structure of fuzzy inference systems (FISs), ANFIS has several limitations. For example, this approach is not suitable for training very large input/output systems and may also be unreliable for forecasting extremely acute conditions [14]. River flow time series are very complex and cover a wide range of frequency components. One recent development to improve forecasting accuracy is the use of multivariate wavelet analysis in fluid flow time series. Over the past decade, some researchers have developed hybrid models by combining the “wavelet and forecasting model”. The most common hybrid wavelet model for flow forecasting is the wavelet-neural network (WNN) method [15,16,17]. The application of a combination of wavelet analysis and neural/fuzzy techniques for hydrological forecasting has been investigated in only a very few studies.

Adamowski and Chan [18] utilized the WNN to forecast the groundwater level of the Chatuga Basin in Canada in 2002–2009 and showed that the WNN has a high potential in forecasting groundwater levels and can be useful in groundwater management. Mousavi et al. [19] investigated the efficiency of four models of WNN, artificial neural network (ANN), FIS, and fuzzy system combined with wavelet network to forecast groundwater level in Khorasan Razavi plain using precipitation, evaporation, and temperature parameters during 1992–2007 and showed that the ANN outperforms other models. On the other hand, Chitsazan et al. [20] examined the efficiency of ANNs to forecast the groundwater level of the Aqeel Plain using parameters of rain, evaporation, relative humidity, and temperature during the statistical period 2009–2010 and stated that the ANN has significant accuracy for forecasting groundwater levels. Husna et al. [21] employed an ANN to forecast the groundwater level of the Chandpur Plain of Bangladesh during 1982–2007 and showed that the ANN has a small error in forecasting the groundwater level.

In [22] four distinct forms of data-driven approaches have been attempted, namely, standard ANN, ANFIS, WNN and multi-resolution hybrid ANFIS utilizing wavelet processing (WNF). The models applied at the Casino station on Richmond River, Australia, is highly vulnerable to flooding and is real-time flood forecasting. This research [23] indicated the possible usage of the WNN by designing a rainfall-runoff model for the Malaprabha basin in India for river flow modeling. For modeling, daily runoff, discharge and evaporation data were used for 21 years (from 1980 to 2000). In [24], the usage was a total of 367 monthly GWLs (m) datasets (September 1985–March 2016) separated into two sub-sets; the first 312 datasets (85% of the total) were used for model production (training) and the remaining 55 datasets (15% of the total) were used for model evaluation (testing). Stepwise filtering was used to pick, as the inputs of the proposed models, the necessary lag times. To determine the efficiency of the models, output metrics such as coefficient of determination (R2), root mean square error (RMSE) and Nash-Sutcliffe efficiency (NSE) coefficient were used.

Their proposed hybrid wavelet fuzzy model involves some uncertainty. Nourani et al. [25] developed ANFIS precipitation/runoff models with discrete wavelet transform (WT). They incorporated this model for both daily and monthly time scales and concluded that combining WT with the ANFIS model in runoff forecasting yields promising results, especially for monthly forecasting. Ren et al. [26] established an ANFIS model based on wavelet analysis to forecast monthly runoff. By comparing the observed and forecasted values, they concluded that the results need further improvement.

Moreover, Several researchers proposed novel methods to resolve different problems in a wide area of applications, such as a deep convolutional neural network for Classification underwater cable images [27], a hybrid approach of stacked autoencoders and long short term memory, for feature extraction and fault detection [28], the coevolutionary multi-objective particle swarm optimization approach for maintenance optimization [29].

In [30] looked at how a wavelet-artificial neural network (WANN) hybrid system used wavelet transforms to forecast daily stream flows into the Sobradinho Reservoir seven days ahead. This research also identified the best mother-wavelet for this kind of ANN forecasting, conducted 1836 simulations with the WANN hybrid systems, and compared the results to forecasts produced without using a wavelet transform.

Ahmed, et al. [31] shows how to achieve substantially accurate stream water level predictions, researchers used the large antecedent lag memory of climatic mode indices, rainfall, and the monthly factor based on periodicity as predictor factors. Through the aggregation of large lagged datasets preserving historical characteristics, this new approach finds an enhanced connection between stream water level and climate mode indices to forecast future streamflow water levels.

Ref. [32] created two hybrid models for monthly streamflow and rainfall forecasting based on long short-term memory networks (LSTM). The wavelet-LSTM model used a trous method of wavelet transform to decompose series, whereas the convolutional LSTM model used a linked convolutional neural network to extract temporal characteristics. The suggested models are evaluated using two streamflow datasets and two rainfall datasets.

In [33] using the US Army Corps of Engineers Hydrologic Engineering Centre River Analysis System model, a geographic information system, and Landsat-8 satellite photos, this study describes the 2014 flood of the Indus River in Pakistan. The model is used to quantify the flood’s geographical extent and evaluate the damage it produced by analysing changes in the river basin’s various land-use/land-cover categories.

A review of the literature highlights that there is a large research gap in selecting the appropriate hybrid wavelet neuro-fuzzy model. Moreover, the nonlinear behavior of water flow, which causes computational complexity, reduces the accuracy of the forecast and sometimes leads to errors in forecasting. For this reason, in most articles, a new method of processing and classification has been discussed. To the best knowledge of the researchers, no effective research has been conducted to increase the accuracy of the data reduction method. Therefore, to overcome computational problems and complexities and increase the accuracy of forecasting, a new method based on a feature extraction method is presented in this paper. However, based on previous methods, all inputs are similar and are in the same element. Hence, the neural network cannot train the weighted coefficients correctly, or the ANFIS is unable to train the membership functions properly. Furthermore, if all data are given to the fuzzy, it cannot train for obtaining many membership functions and cannot support the whole data. Consequently, it needs a longer time for calculations, leading to less accuracy. That is the reason previous papers applied less volume of data. Because model parameters were adjusted based on the specific features of the chosen watershed, the developed model is not applicable to any other catchments.

In this paper, a new combined method for forecasting river flow is presented based on neural networks and wavelet transform. While this type of hybrid method has been used in previous research, but in this paper, an intermediate step is considered to reduce the complexity and increase the accuracy. This is the middle step of extracting some special features from the signals and data processed in the wavelet section. Also, by using this method, feature extraction that reduces the volume of neural network input data increase the accuracy of forecasting and even reduce the processing and training time. Additionally, it makes it possible to use the properties of all data in a certain range, unlike references that consider only several previous days. This proposed method focuses on improving accuracy and reducing the risk of river flow forecasting (Ellen Brook River, western Australia) by presenting the new WNN model and applying it to three daily, weekly, and monthly time scales. In this method, the data are applied daily, weekly, and monthly, and by taking into account these considerations, an attempt has been made to improve the forecasting of short, medium, and long-term river flows. Given the seasonality of the Ellen Brook River, this paper can provide more accurate tools to assist decision-makers in planning sustainable water resources and flood prevention by improving the proposed method.

A summary of the contributions of this study is as follows:

• − Presenting a hybrid WNN method
• − Using wavelet to increase forecasting accuracy
• − Using feature extraction (energy, standard deviation, and maximum values, etc.)
• − Reducing the computation time using feature extraction
• − Reducing computational complexity by using feature extraction
• − Using all daily, weekly, and monthly data
• − Comparison with other previous methods.

The organization of the paper will be as follows: In Section 2, neural network, and wavelet modeling, as well as feature extraction, is described, while in Section 3, a case study is explained along with the data and how to determine the input data. In Section 4, the simulation results for different models are reviewed and compared with other methods. Finally, in Section 5, the conclusion of the proposed method is presented.

2. Materials and Methods

2.1. Wavelet Neural Network (WNN)

Wavelet-based neural networks are a combination of the two theories of wavelet and neural networks [34]. These networks have both the advantages and features of neural networks and the attractiveness, flexibility, and solid mathematical foundations of wavelet and multiscale analysis. Wavelets use two sets of wavelet functions and scaling functions. A family of scale functions $\varphi \left(x\right)$ is introduced as follows:

$${\varphi }_{m,k}\left(x\right)=2^{-m/2}\varphi \left(2^{-m}x-k\right) m,k \in z$$

(1)

If $\varphi \left(x\right)$ is considered as a mother scale function, the values of 2^−m and k are related to the expansion and transfer of the mother scale function, respectively. The resolution scale functions of m, ${\varphi }_{m,k}\left(x\right)$ are essentially the orthogonal bases of the vector space in resolution m. In other words, the v_m vector space contains all the approximations of the function f(x) with resolution m and by the slave ${\varphi }_{m,k}\left(x\right)$ functions. Therefore, the vector spaces $\left\{{\nu }_m\right\}$ contain different approximations of the function f(x) in different resolutions. Now, if wm is assumed as a vector space orthogonal to v_m at a resolution of m, then we can also express other sets of orthogonal bases of the wm space called wavelets $\mathsf{\Psi }\left(x\right)$ as follows [35]:

$${\mathsf{\Psi }}_{m,k}\left(x\right)=2^{-m/2}\mathsf{\Psi }\left(2^{-m}x-k\right) m,k \in z$$

(2)

In general, all physical functions can be expressed with the help of wavelets and scale functions as following [35]:

$$f_o\left(x\right)={\displaystyle \sum }_O{a}_{a,k }{\varphi }_{a,k}\left(x\right)$$

(3)

$$f\left(x\right)=f_o\left(x\right)+{\displaystyle \sum }{\displaystyle \sum }{d}_{a,k}{\mathsf{\Psi }}_{a,k}\left(x\right)$$

(4)

The above equations state that each physical function can be approximated, first, by several scale functions at low resolution and, then, with the help of wavelet functions at different resolutions to continue the approximation to the desired accuracy. Wavelet neural network is established based on Equations (3) and (4) and has its training algorithms that have been fully studied by Shin et al. [36]. It should be noted that, in general, the family of continuous wavelets is also expressed as follows:

$${\mathsf{\Psi }}_{a,b}\left(t\right)=\frac{1}{\sqrt{a}}\mathsf{\Psi }\left(\frac{t-b}{a}\right)$$

(5)

and the wavelet transform for continuous functions is calculated by the following equation

$$W_{a,b}\left(f\right)=f_{\left(a,b\right)=\left({\mathsf{\Psi }}_{a,b}\left(t\right),f\left(t\right)\right)=\frac{1}{\sqrt{a} }{{\displaystyle \int }}_{-\infty }^{+\infty }f\left(t\right){\mathsf{\Psi }}^t\left(\frac{t-b}{a}\right)dt}$$

(6)

Here, parameter a is the extension parameter, which is proportional to the frequency (in other words, the small delay parameter corresponds to the high frequency and vice versa), and parameter b is the transmission parameter, which is proportional to time.

2.2. Wavelet Algorithm

Combining wavelet theory can be a good alternative in Radial Basis Function (RBF) neural networks for estimating and approximating optional nonlinear functions. The RBF have an activation function in the hidden layer, while in wavelet neural networks, wavelet functions are considered as a hidden layer activation function of the RBF network. In these networks, both transmission parameters and scaling of the waves along with their weights are optimized. The important steps in training and validating the WNN are as follows: (a) input data are used in two groups for network train and testing; (b) by fulfilling the mentioned conditions after applying the appropriate transfer coefficients and using a proper scale, the mother wavelet is transformed into an offspring wavelet; (c) activation functions in the hidden layer neurons of the neural network are replaced with different types of offspring wavelets; (d) the established WNN is trained using a set of data belonging to network training; (e) the overall performance of the wavelet network is examined by analyzing how the validation data are estimated, and the training phase ends with the satisfaction of the network performance. Otherwise, the previous steps will be evaluated until the best condition is achieved. An example of a three-layer network structure consisting of an input layer, a hidden layer, and an output layer is shown in Figure 1 [24].

Figure 2 shows the model structure of the proposed method. This model includes three main sub-models called wavelet, feature extraction, and artificial neural network and the output of the wavelet sub-model is not decomposed and is applied as input to the neural network model.

Figure 3 shows the flowchart of the hybrid WNN model. After decomposition, the input signals are converted to the desired wavelet coefficients, and then these subsets, which have different roles in time series, are fed to the next ANN model, and all of them must be maintained as input to neural networks.

As a result of this method, the number of inputs is reduced and the processing speed is increased. Initially, the available data are obtained as a 12,410 × 12,410 matrix and the output is given to a wavelet that can analyze it in eight different levels. From the obtained signal seven features as input are extracted, and finally, the output is in the form of a matrix and is given to the ANN to be tuned. Therefore, according to the proposed model, a series of signals are provided to the wavelet to be analyzed at different levels and to extract a series of unique features from the desired output in the wavelet. As a result of this method, the number of inputs is reduced and the processing speed is increased.

3. Case Study and the Dataset

In this study, the Ellen Brook River dataset are used to illustrate the proposed new model approach. Figure 4 shows this river, which covers an area of 750 km² and is located 20 km northeast of Perth in western Australia. The climate of the catchment is warm and temperate Mediterranean style and also the forecasts of climate change include a decrease in rainfall and runoff and an increase in temperature and evaporation, all of which will have a significant impact on water resources in this region.

In the first stage, the effect of multivariate input selection on daily, weekly, and monthly data river flow forecasting is investigated, at which time the amount of river flow is used as input. All data and information from 1977 to 2010 are collected from the meteorological website. Of the total data, 70% collected by 2000 is utilized for training purposes and the rest, 30% by 2010, is used for testing.

The average daily fluid flow of the station is 0.88 m³/s and its maximum flow is 41.28 m³/s. Daily, weekly, and monthly river time series are also prepared for short-term and long-term forecasts. The daily, weekly, and monthly data are tabulated in

Table 1. Daily, weekly, and monthly statistical parameters of the Ellen Brook River.

	Dataset	Mean	Max	Min	STD
Daily river flow m3/s	Total	0.88	41.29	0	2.45
Weekly river flow m3/s	Total	0.84	20.44	0	1.99
Monthly river flow m3/s	Total	0.87	8.96	0	1.58

 Section 4.1, including the mean, minimum, maximum, and standard deviation criteria.

For practical modeling, since higher flow rates are included in the training dataset, zero values in time series are substituted with a small value of 0.001.

The square value of the Pearson correlation is the coefficient of decision. Consequently, the spectrum of the decision coefficient lies between 0 and 1. To obtain the values of the mean squares error, root means square error and the nash-sutcliffe efficiency Equations (7)–(9) are used as shown below:

$$MSE=\frac{1}{N}{\displaystyle \sum }_{i=1}^N(Q_{sim}\left(i\right)-Q_{obs}{\left(i\right)}^2$$

(7)

$$RMSE=\sqrt{\frac{1}{N}{\displaystyle \sum }_{i=1}^N(Q_{sim}\left(i\right)-Q_{obs}{\left(i\right)}^2}=\sqrt{\left(MSE\right)}$$

(8)

$$NSE=1-\frac{{{\displaystyle \sum }}_{i=1}^N{\left(Q_{sim}\left(i\right)-Q_{obs}\left(i\right)\right)}^2}{{{\displaystyle \sum }}_{i=1}^N{\left(Q_{obs}\left(i\right)-{\overline{Q}}_{obs}\right)}^2}=1-\frac{MSE}{STD{V}_{obs}}$$

(9)

In this equation, Q_obs and Q_sim denote the average observed and forecasted time series of the river flow, respectively. This coefficient is identical to the NSE coefficient in the case of linear regression [37].

It is based on the application to select the optimal success criterion. Among all these success criteria, the efficiency coefficient and commitment coefficient of Nash-Sutcliffe are very responsive to peak flows.

4. Results and Discussion

This section analyzes the application of the previous model and the proposed new model for river flow forecasting. The forecasting of the Ellen Brook river flow is carried out once the framework of the model and its inputs are specified.

4.1. Scenario 1

To compare the hybrid wavelet neuro-fuzzy model [38] with the proposed new model, the old model is first analyzed in this section as it has the same input so that the results can be compared with those of the proposed new model. In this scenario, the number of input data is equal to the input data of [38] and the results are tabulated in

Table 2. Simulation results for proposed and hybrid wavelet neuro-fuzzy model.

	Data		MSE			RMSE						NSE
						(Mm3)			(m3/s)
			All	Train	Test	All	Train	Test	All	Train	Test	All	Train	Test
Daily	Proposed	Senario 1	0.0051	0.0055	0.0041	0.0062	0.0065	0.0055	0.0718	0.0747	0.0642	0.982	0.98736	0.98648
		Senario 2	0.0059	0.0064	0.0048	0.0067	0.0070	0.0060	0.0774	0.0805	0.0697	0.999	0.99932	0.99888
	Ref [38]		-	-	-	-	0.017	0.020	-	0.19	0.23	-	0.89	0.83
Weekly	Proposed	Senario 1	0.0079	0.0100	0.0032	0.0540	0.0605	0.0345	0.0893	0.1000	0.0571	0.99797	0.99766	0.99812
		Senario 2	0.0050	0.0061	0.0023	0.0428	0.0475	0.0292	0.0708	0.0785	0.0482	0.99872	0.99844	0.99886
	Ref [38]		-	-	-	-	0.40	0.46	-	0.66	0.76	-	0.87	0.68
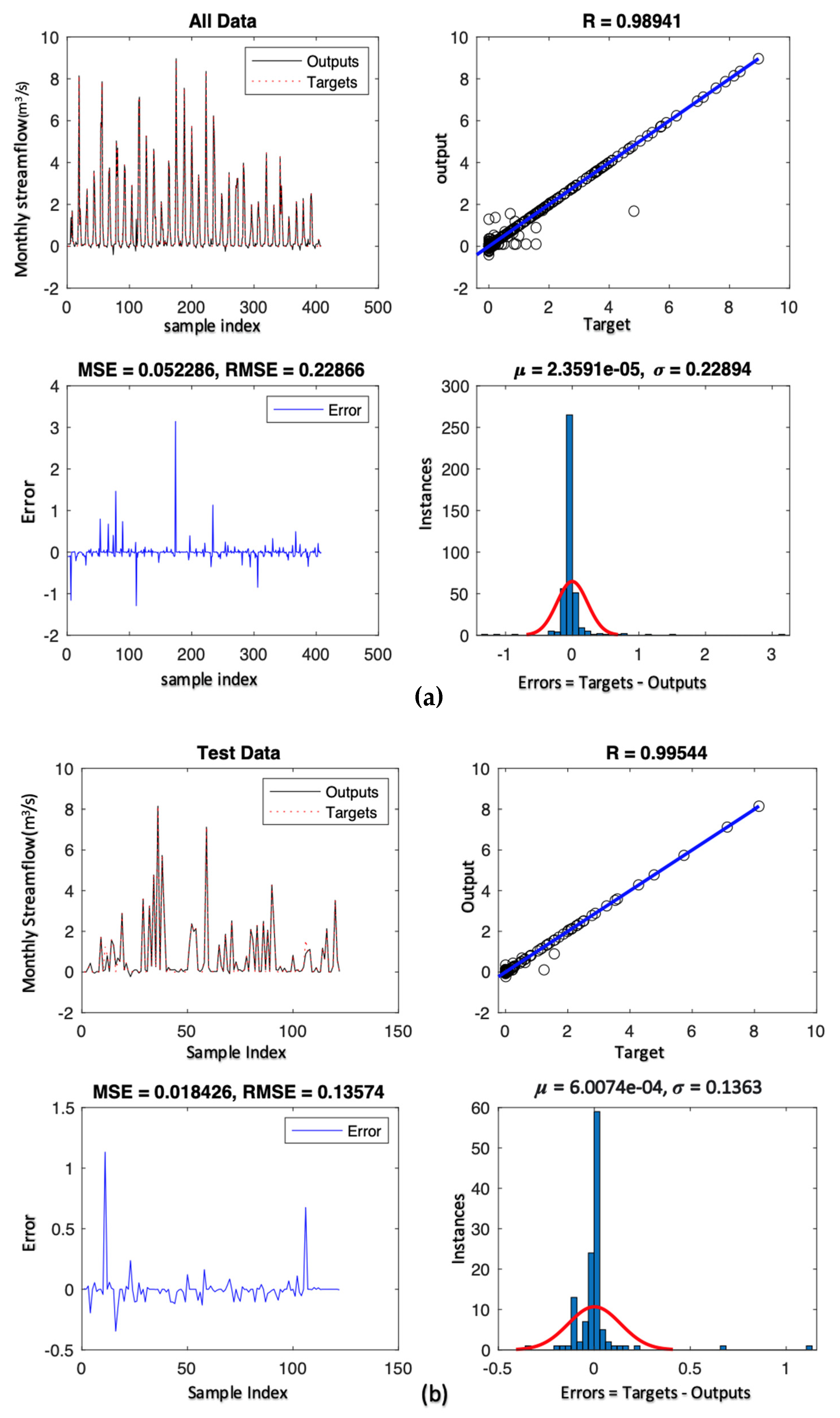
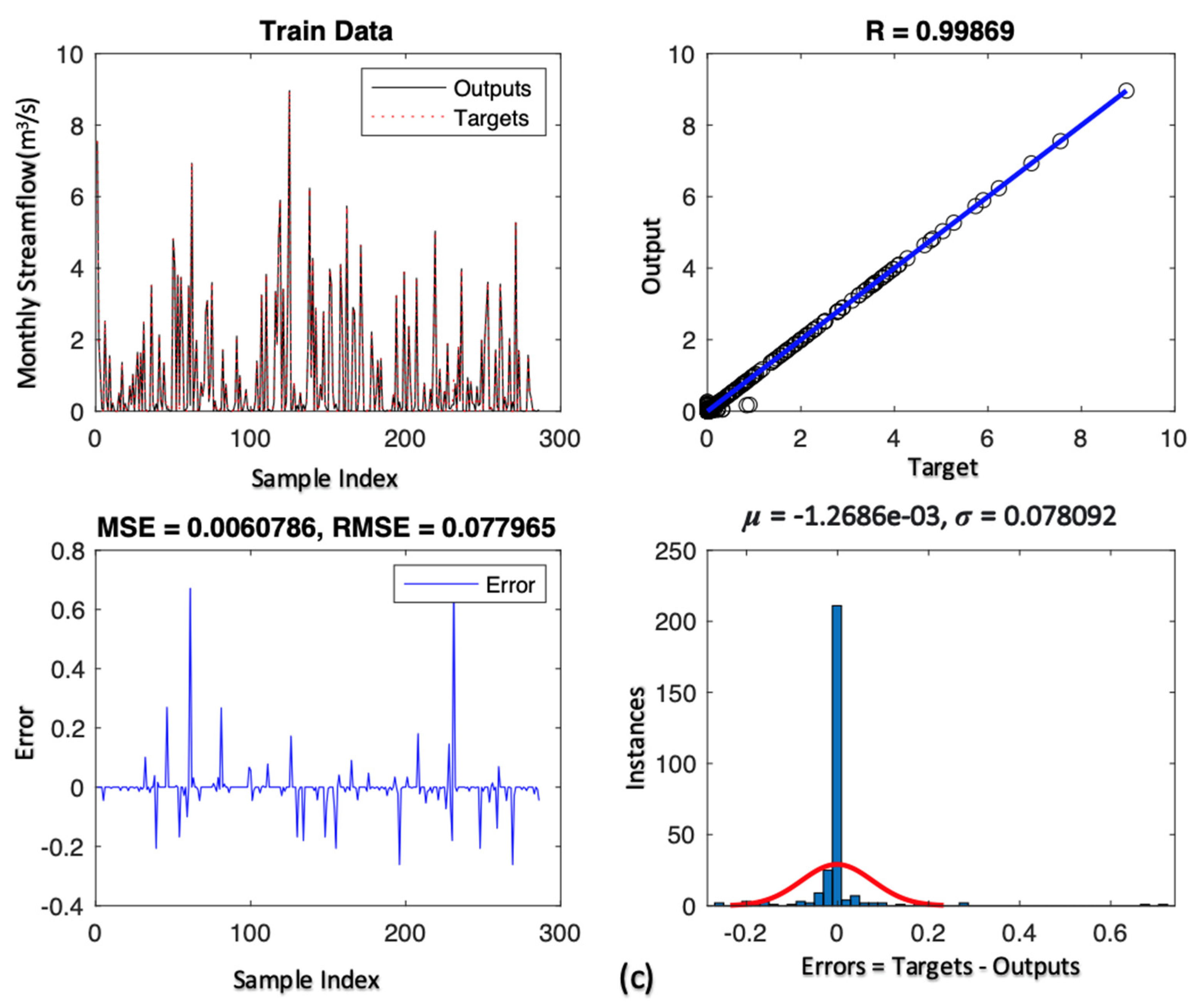
Monthly	Proposed	Senario 1	0.0522	0.0667	0.0184	0.5925	0.6695	0.3517	0.2286	0.2583	0.1357	0.97872	0.94999	0.99581
		Senario 2	0.0129	0.0060	0.0292	0.2952	0.2019	0.4427	0.1139	0.0779	0.1708	0.99477	0.98552	0.99742
	Ref [38]		-	-	-	-	1.55	1.74	-	0.60	0.67	-	0.84	0.59

 Section 4.2. From the comparison between the results, it is initially clear that the proposed method performs well and also has a higher speed and accuracy than the previous method. Table 1 reports the considered parameters and inputs used for both models. All data, coefficient of correlation, scatter plots, and RMSE for the hybrid wavelet neuro-fuzzy model monthly are shown in Figure 5.

4.2. Scenario 2

In the second scenario, the number of input data is increased compared to the previous method, which shows that more data can be applied to the proposed method. For this reason, it has higher speed and accuracy than the previous method. Table 2 compares the results of this scenario with the previous method. The mean squares error (MSE), root mean square error (RMSE), and the Nash-Sutcliffe coefficient of efficiency (NSE) were used to evaluate the performance of the suggested method. Table 2 reveals that the performance of the proposed model is much better than that of the previous model in terms of training. The Nash sutcliffe coefficient of efficiency was improved and root mean square error was changed. The authors in [38] did not mention the MSE value, all data in NSE. This is a benefit of the proposed method.

Figure 6 illustrates the obtained results from the proposed new model. According to the values given in this figure, the increased accuracy compared to the hybrid wavelet neuro-fuzzy is clearly seen.

The output value is specified and the same target value is obtained according to the output. This amount of the target indicates that it has reached a certain value. In part (a2), the value of correlation (R) is shown. This value has reached a significant amount of 0.099738. Part (a3) shows the amount of error, which, as can be seen, has very little error, and in part (a4), there are normal parameters. According to the curve drawn in this figure, no scattering was observed. The same is true for Figure 6b,c, but the only difference is the number of data entered.

In [38] for weekly and monthly forecasting, the NSE of the ANFIS model rose from 0.69 to 0.82 and from 0.61 to 0.81, respectively. In our study, the output value is given, and the output value is used to determine the goal value. This goal amount signifies that it has achieved a specific value. The value of correlation (R) is given in Section (a2). This number has risen to 0.099738, which is a considerable amount.

5. Conclusions

This study proposed a new hybrid WNN method to improve fluid flow simulation and forecasting. The application of multi-resolution analysis of input data on the performance of the proposed models to forecast daily, weekly, and monthly flow was investigated. To reduce the complexity and increase the forecasting accuracy, the analyzed data in this method, unlike its counterparts, is not applied directly to the neural network after the wavelet section. To address these issues, to make them dissimilar, and to differentiate them more in an element, standard deviation, energy, and maximum value of each signal per day are obtained based on the literature and tests carried out. Besides, the feature extraction is calculated to put them together. In the next step, the specificity of the features is shown and finally, the feature extraction reduces the volume of the data so that the data are specific and different. In the middle part of wavelet and neural, the feature extraction selection method is employed. The overall results show that the preprocessing of raw data with wavelets improves the forecasting accuracy significantly, especially for peak values. The result of this study will be useful for hydrological system designers and decision-makers in the field of fluid flow forecasting and sustainable water distribution program development. As a result, increasing forecasting accuracy is a never-ending research project, since each hydrological forecasting method has its unique set of features and limits.