Influence of Pavement Heterogeneity and Observation Angle on Lighting Design: Study with New Metrics
Abstract
:1. Introduction
2. Materials and Methods
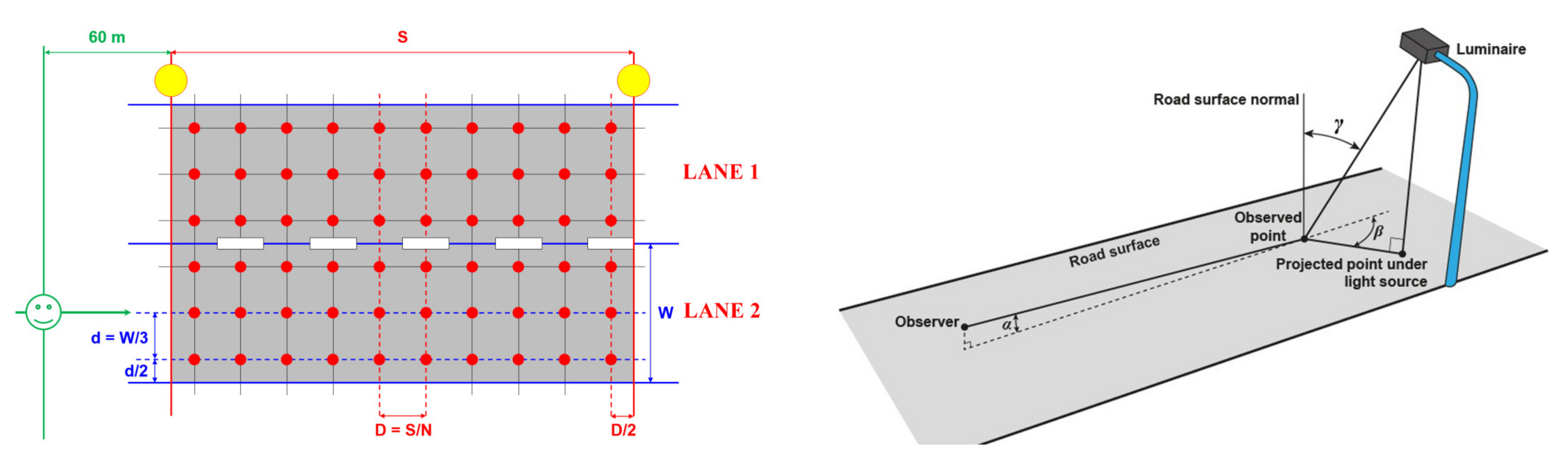
2.1. Road Lighting Basics
- D = S/N in the longitudinal direction where D is the spacing between points in the longitudinal direction in meters and S is the spacing between luminaires in the same row in meters. N is the number of points in the longitudinal direction with N = 10 for S ≤ 30 m and N is the smallest integer giving D ≤ 3 m if S > 30 m.
- d = W/3 in the transverse direction where d is the spacing between points in the transverse direction in meters and W is the width of the lane in meters.
- The average luminance is the arithmetic mean of the luminance at the grid points in the field of measurement;
- The overall uniformity is the ratio of the lowest luminance, occurring at any grid point in the field of measurement, to the average luminance;
- The longitudinal uniformity is the ratio of the lowest to the highest luminance on points in the longitudinal direction along the center line of the lane.
2.2. Ecl_R
- Classic lighting design: calculation of the photometric quantities representative of the performances of a lighting installation, using the standard CIE r-tables with or without Q0-scaling;
- Advanced lighting design: calculations with measured r-tables;
- Implementation of the concept of the moving observer: lighting calculations with a moving observer;
- Consideration of the road photometric heterogeneity: lighting calculations with r-tables measured at different points of the grid;
- Consideration of the new needs of road lighting: lighting calculations with r-tables measured at different observation angles.
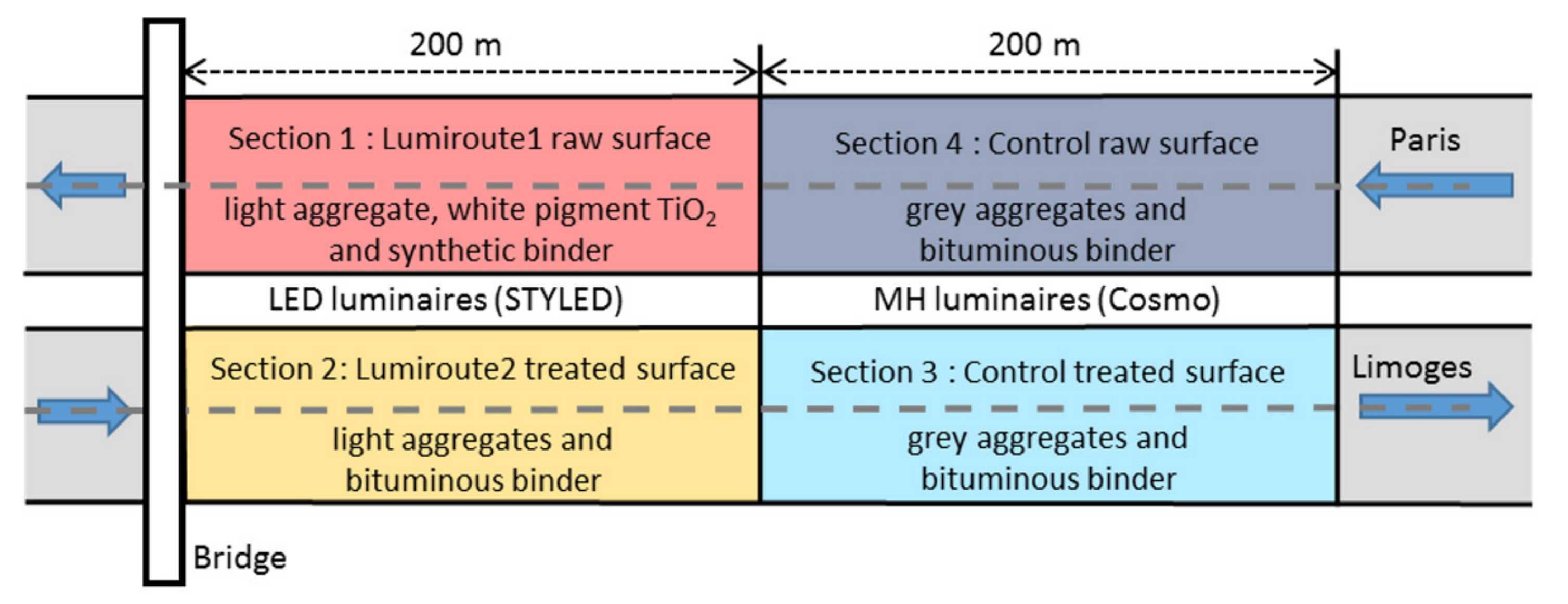
2.3. Experimental Site
- Section 1 is composed of the LUMIROUTE® 1 pavement (raw surface with light-colored aggregates, a synthetic binder and white pigment TiO2) combined with an LED illumination of 77 W (STYLED lamp, color temperature 4000 K);
- Section 2 consists of the LUMIROUTE® 2 pavement (water jet scrubbed pavement with light aggregates and a bituminous binder) combined with an LED illumination of 103 W (STYLED lamp, color temperature 4000 K);
- Section 3 is composed of a “Control treated” road surface (water jet scrubbed pavement with grey aggregate and a bituminous binder) combined with traditional lighting consisting of a 140 W MH discharge source (COSMO lamp, color temperature of 2811 K);
- Section 4 is composed of a “Control raw” road surface (current pavement with grey aggregate and a bituminous binder) combined with the same 140 W MH discharge source.
2.4. Experimental Measurements and Devices
2.4.1. On-Site Measurement of Road Photometry
2.4.2. Description of the Laboratory Gonioreflectometer
2.4.3. On-Site Luminance Measurement
2.5. Methodology
2.5.1. New Metrics for Assessing the Link between Pavement Reflection Properties Deviations and Lighting Performance Criteria Deviations
2.5.2. Experimental Measurements
2.5.3. Lighting Calculations with Ecl_R
- A calculation using the standard r-table corresponding to the class of the pavement established from the thirty measurements;
- A calculation using the standard r-table scaled with the average of thirty Q0;
- Ten calculations using the ten r-tables measured on the central tracks;
- Twenty calculations using the twenty r-tables measured on the central tracks;
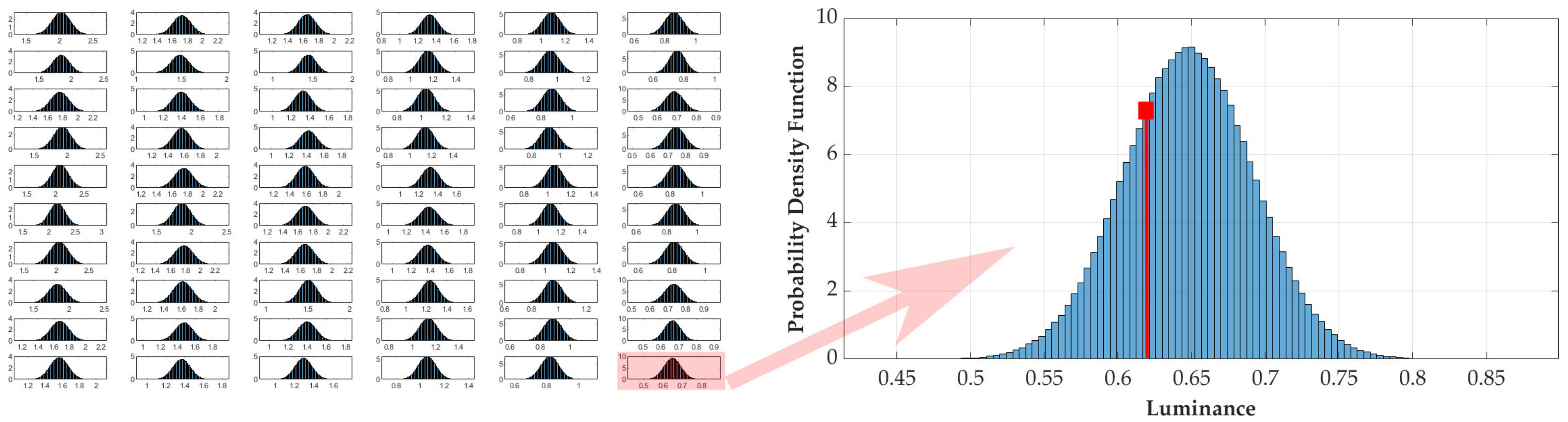
- A complete calculation using a dedicated r-table for each grid point. For the grid points where we did not directly have a measured r-table, we used the nearest neighbor according to the principle illustrated in Figure 6 (on the right).
3. Results and Discussions
3.1. Spatial Heterogeneity Study
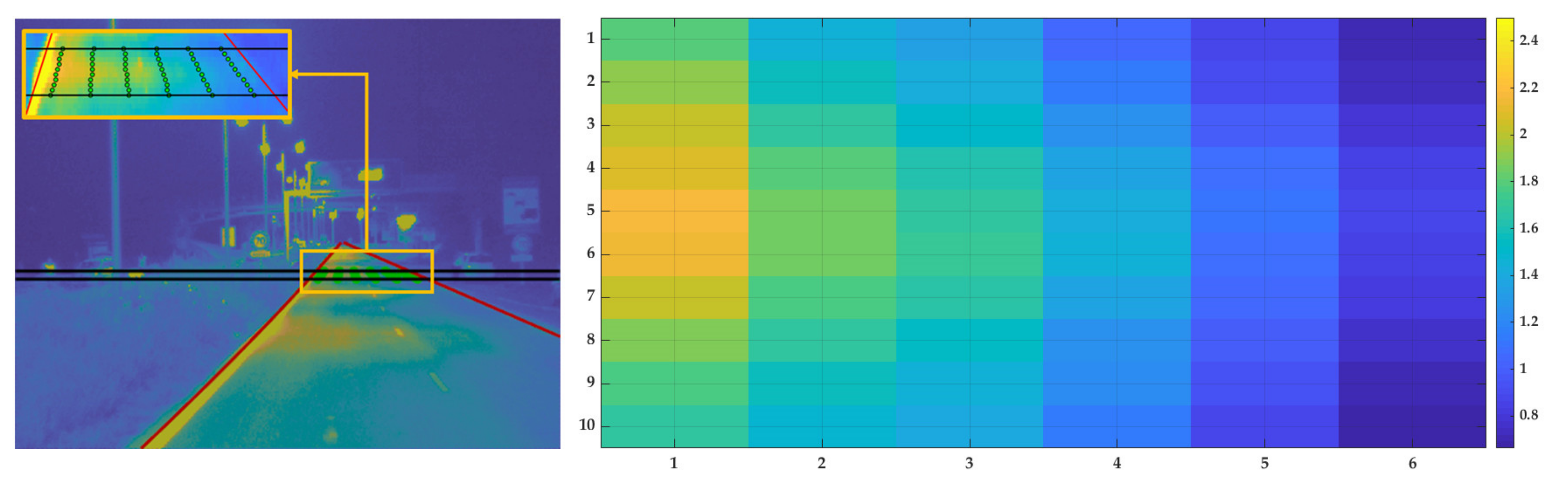
3.1.1. Analysis of Experimental Measurements
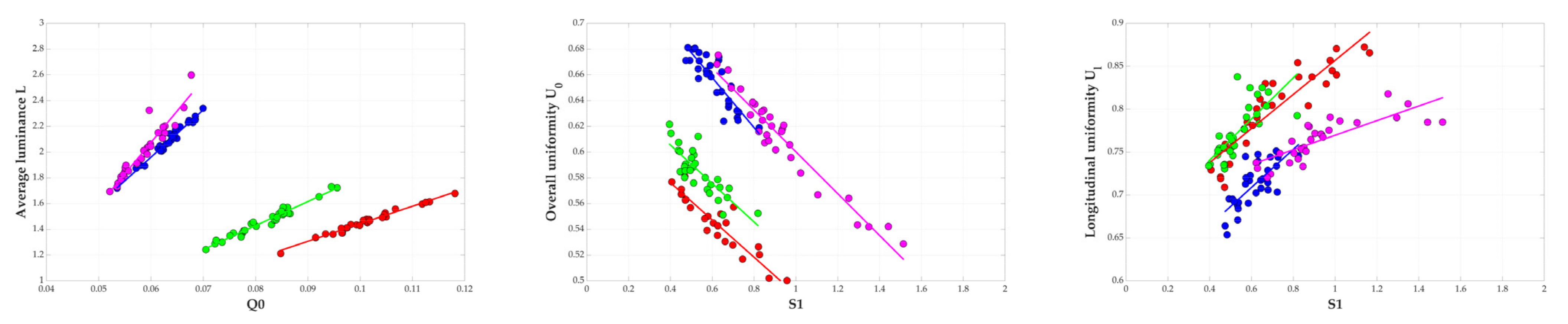
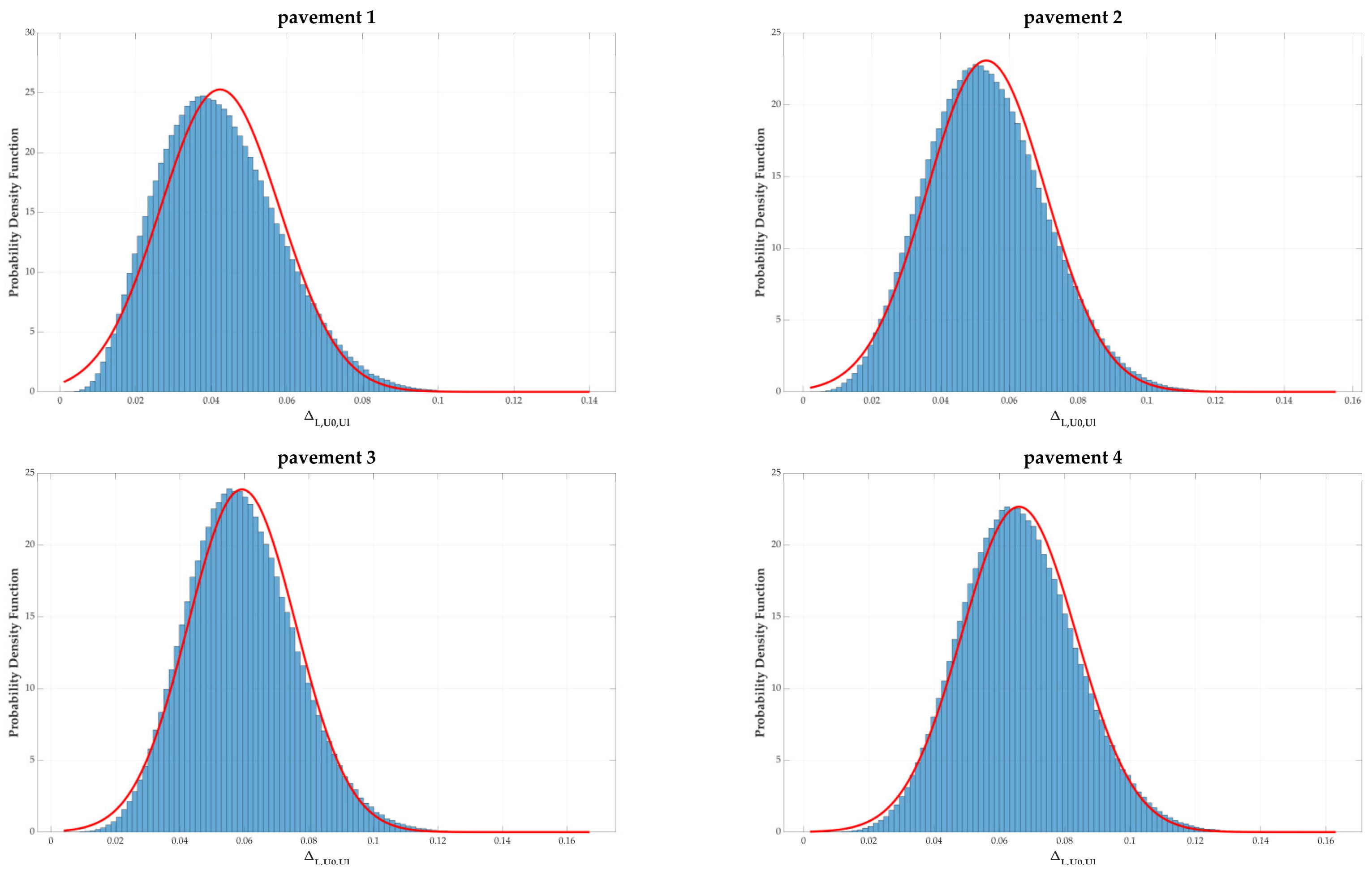
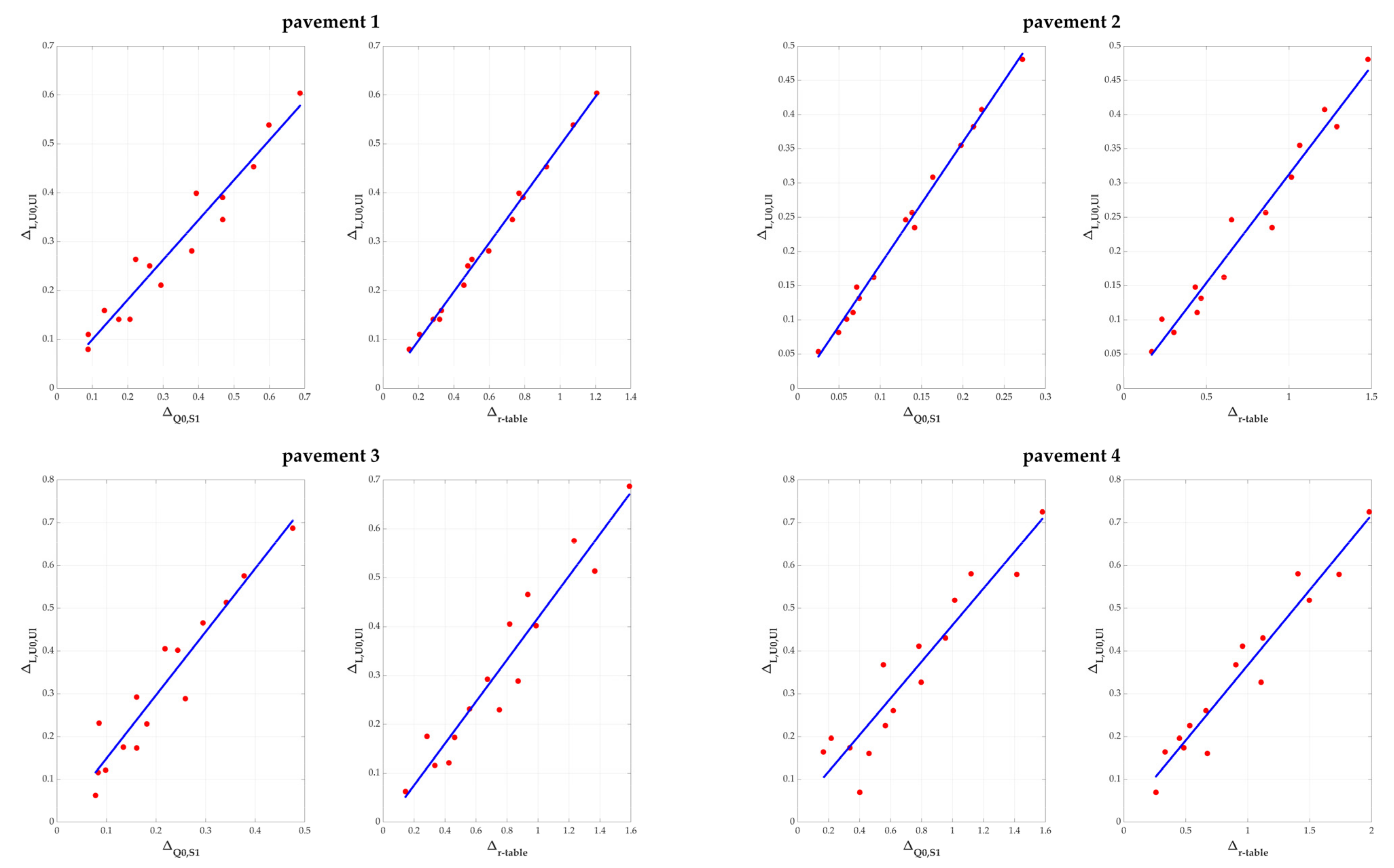
3.1.2. Implementation of the Proposed Metrics
3.1.3. Calculation of a Threshold on
3.1.4. Analysis of the Calculations
- Calculation with the standard r-table;
- Calculation with the standard r-table Q0-scaled using the values from Table 3;
- Calculations with the r-tables measured in central tracks which give the minimum and the maximum values among the ten calculations performed;
- Calculations with the r-tables measured in wheel tracks which give the minimum and the maximum values among the twenty calculations performed;
- Complete calculation using a dedicated r-table for each point of the grid.
3.1.5. Implications for On-Site Measurements Methodology
- The first scenario consists of making a naive measurement, i.e., completely at random. It was therefore examined, for each pavement, how many of the thirty calculations made from the thirty available r-tables met the requirement.
- The second scenario is to make a single central track measurement. For each pavement, the number of calculations that met the requirement was examined from among the ten calculations made from the ten available r-tables in the central tracks.
- The third scenario is to make a single wheel track measurement. For each pavement, the number of calculations that met the requirement was examined from the twenty calculations made from the twenty available r-tables in the wheel tracks.
- The fourth scenario is to make one measurement in the central tracks and one in the wheel tracks. Additional calculations were made with Ecl_R to test the 200 () possible combinations. The r-table used in each calculation is the average of the selected central track r-table and the selected wheel track r-table. It was then examined for each pavement how many of these calculations met the requirement out of the 200 performed.
- The fifth scenario is to make two measurements in the central tracks and two in the wheel tracks. New calculations were performed to test 8550 () possible combinations. The r-table used in each calculation is the average of the four selected r-tables. It was then examined for each pavement how many of these calculations met the requirement out of the 8550 performed.
- The sixth scenario is to make three measurements in the central tracks and three in the wheel tracks. New calculations were performed to test 136,800 () possible combinations. The r-table used in each calculation is the average of the six selected r-tables. It was then examined, for each pavement, how many of the 136,800 calculations met the requirement.
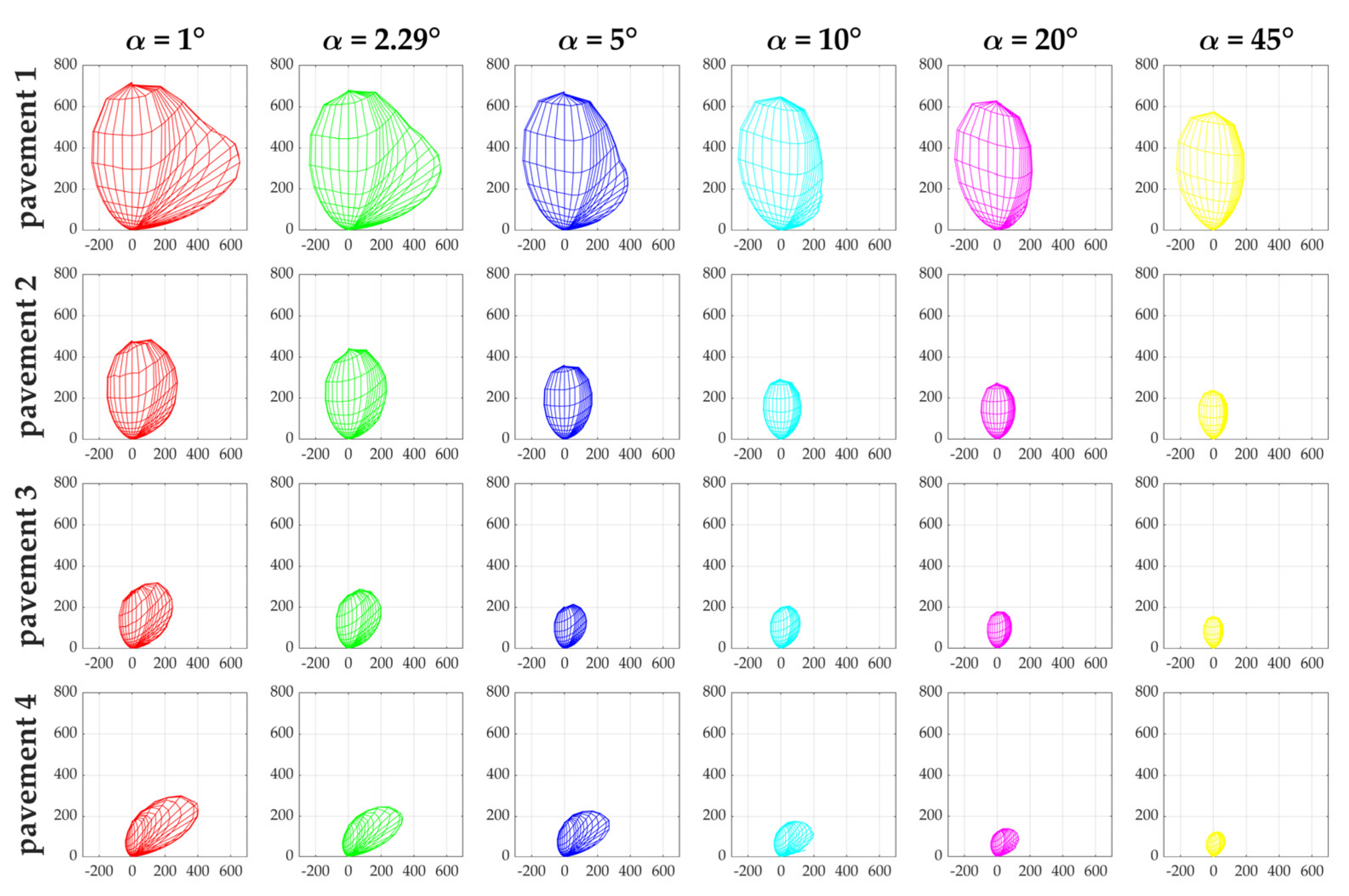
3.2. Influence of Observation Angle on Pavement Reflection Properties
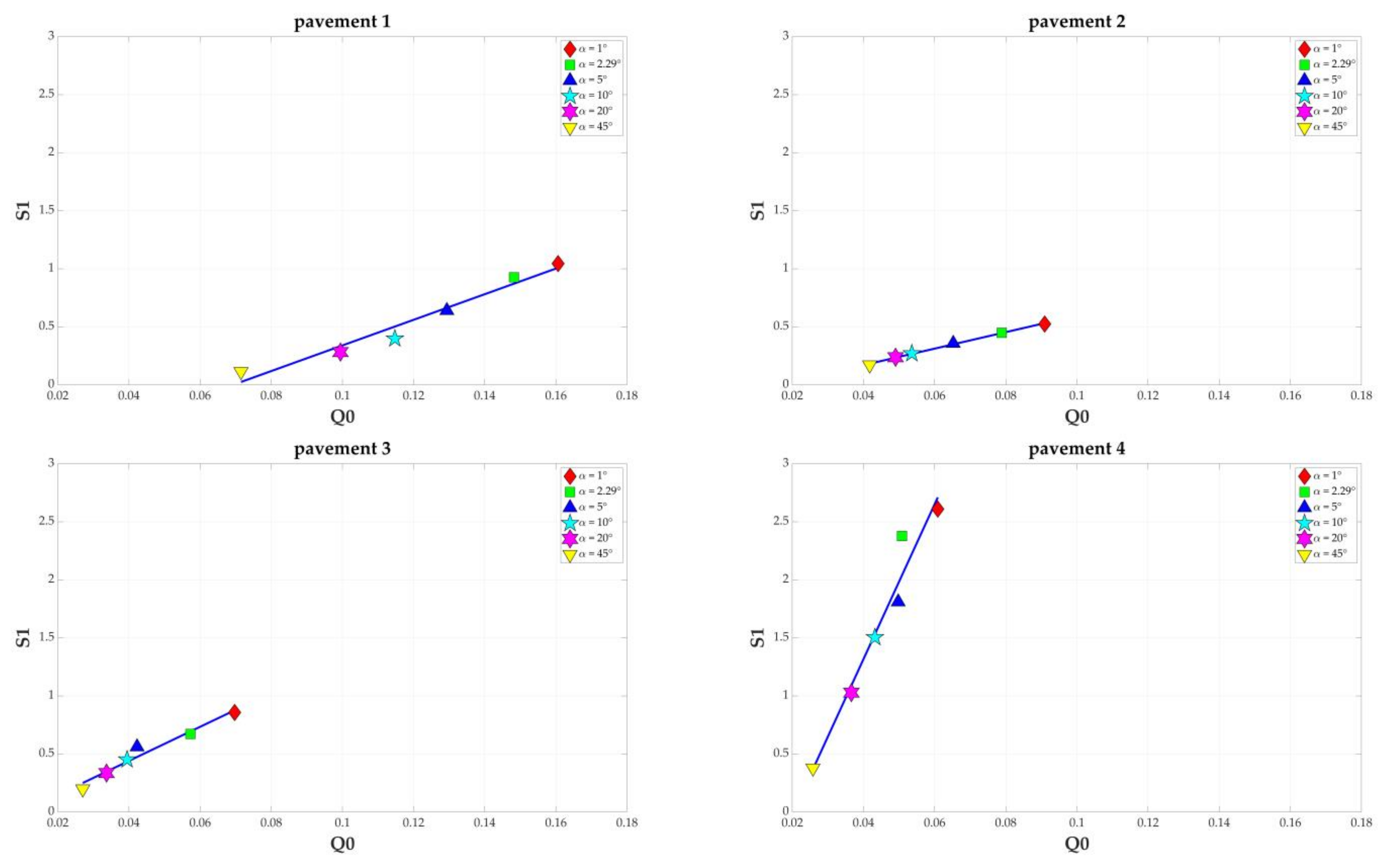
3.2.1. Analysis of Experimental Measurements
3.2.2. Analysis of the Calculations
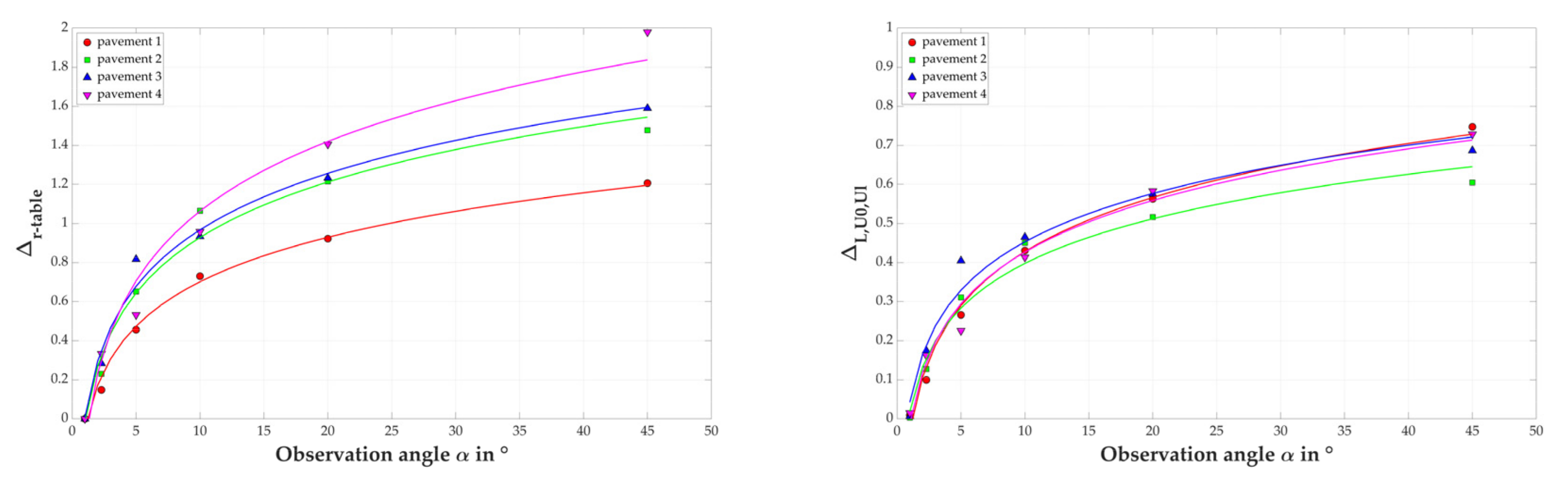
3.2.3. Implementation of the Proposed Metrics
4. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Road Lighting Situation | CIE 140:2019 | DIALux® | Ecl_R | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fixed Observer | Moving Observer | ||||||||||||
| Lane 1 | Lane 2 | Lane 3 | Lane 1 | Lane 2 | Lane 3 | Lane 1 | Lane 2 | Lane 3 | Lane 1 | Lane 2 | Lane 3 | ||
| Situation 5 | Lave | 0.44 | 0.42 | 0.41 | 0.43 | 0.41 | 0.40 | 0.44 | 0.42 | 0.41 | 0.44 | 0.42 | 0.40 |
| U0 | 0.45 | 0.57 | 0.67 | 0.43 | 0.56 | 0.72 | 0.45 | 0.57 | 0.67 | 0.48 | 0.59 | 0.68 | |
| Ul | 0.79 | 0.71 | 0.75 | 0.79 | 0.72 | 0.73 | 0.79 | 0.73 | 0.75 | 0.79 | 0.73 | 0.75 | |
| Lv | 0.105 | 0.095 | 0.063 | - | - | - | 0.105 | 0.095 | 0.063 | 0.105 | 0.095 | 0.063 | |
| TI | 11.0 | 10.4 | 7.10 | 11 | 10 | 7 | 11.0 | 10.4 | 7.10 | 11.0 | 10.4 | 7.10 | |
| Eh | 7.00 | 7.04 | 7.04 | ||||||||||
| Uh | 0.28 | 0.27 | 0.28 | ||||||||||
| REI | 0.76 | - | 0.76 | ||||||||||
| Road Lighting Situations | CIE 140:2019 | DIALux® | Ecl_R | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Fixed Observer | Mobile Observer | ||||||||
| Lane 1 | Lane 2 | Lane 1 | Lane 2 | Lane 1 | Lane 2 | Lane 1 | Lane 2 | ||
| Situation 1 | Lave | 0.26 | 0.26 | 0.25 | 0.26 | 0.26 | 0.26 | 0.26 | 0.27 |
| U0 | 0.14 | 0.15 | 0.14 | 0.15 | 0.14 | 0.15 | 0.14 | 0.15 | |
| Ul | 0.56 | 0.64 | 0.55 | 0.68 | 0.56 | 0.64 | 0.56 | 0.64 | |
| Lv | 0.877 | 0.314 | - | - | 0.897 | 0.329 | 0.897 | 0.329 | |
| TI | 141 | 49.7 | 126 | 50 | 145 | 52.0 | 143 | 51.6 | |
| Eh | 2.50 | 2.54 | 2.52 | ||||||
| Uh | 0.28 | 0.28 | 0.28 | ||||||
| REI | 0.32 | - | 0.31 | ||||||
| Situation 2 | Lave | 0.26 | 0.26 | 0.26 | 0.26 | 0.26 | 0.26 | 0.26 | 0.26 |
| U0 | 0.35 | 0.32 | 0.31 | 0.32 | 0.35 | 0.32 | 0.37 | 0.37 | |
| Ul | 0.33 | 0.33 | 0.33 | 0.33 | 0.33 | 0.33 | 0.33 | 0.33 | |
| Lv | 0.636 | 0.626 | - | - | 0.653 | 0.644 | 0.653 | 0.644 | |
| TI | 101 | 99 | 95 | 95 | 104 | 102 | 103 | 102 | |
| Eh | 2.50 | 2.54 | 2.52 | ||||||
| Uh | 0.32 | 0.32 | 0.31 | ||||||
| REI | 0.47 | - | 0.46 | ||||||
| Situation 3 | Lave | 0.55 | 0.60 | 0.54 | 0.60 | 0.55 | 0.60 | 0.55 | 0.60 |
| U0 | 0.52 | 0.54 | 0.51 | 0.52 | 0.52 | 0.54 | 0.54 | 0.54 | |
| Ul | 0.68 | 0.70 | 0.67 | 0.68 | 0.68 | 0.70 | 0.68 | 0.70 | |
| Lv | 0.130 | 0.138 | - | - | 0.131 | 0.139 | 0.131 | 0.139 | |
| TI | 11.5 | 11.3 | 10 | 11 | 11.6 | 11.3 | 11.5 | 11.3 | |
| Eh | 7.80 | 7.85 | 7.77 | ||||||
| Uh | 0.34 | 0.33 | 0.34 | ||||||
| REI | 0.64 | - | 0.64 | ||||||
| Situation 4 | Lave | 0.88 | 0.87 | 0.87 | 0.86 | 0.88 | 0.87 | 0.87 | 0.87 |
| U0 | 0.54 | 0.51 | 0.52 | 0.50 | 0.54 | 0.51 | 0.53 | 0.53 | |
| Ul | 0.53 | 0.53 | 0.51 | 0.51 | 0.53 | 0.53 | 0.53 | 0.53 | |
| Lv | 0.228 | 0.227 | - | - | 0.228 | 0.228 | 0.228 | 0.228 | |
| TI | 13.8 | 13.8 | 13 | 13 | 13.8 | 13.9 | 13.9 | 13.8 | |
| Eh | 12.0 | 12.0 | 12.0 | ||||||
| Uh | 0.49 | 0.49 | 0.49 | ||||||
| REI | 0.61 | - | 0.61 | ||||||
| Situation 6 | Lave | 1.17 | 1.30 | 1.16 | 1.30 | 1.17 | 1.31 | 1.17 | 1.31 |
| U0 | 0.49 | 0.49 | 0.47 | 0.48 | 0.49 | 0.49 | 0.50 | 0.50 | |
| Ul | 0.62 | 0.72 | 0.61 | 0.69 | 0.62 | 0.72 | 0.62 | 0.72 | |
| Lv | 0.239 | 0.181 | - | - | 0.243 | 0.184 | 0.243 | 0.184 | |
| TI | 11.5 | 8.00 | 11 | 7 | 11.6 | 8.11 | 11.7 | 8.10 | |
| Eh | 16.2 | 16.0 | 16.2 | ||||||
| Uh | 0.50 | 0.50 | 0.50 | ||||||
| REI | 0.67 | - | 0.67 | ||||||
| Situation 7 | Lave | 0.53 | 0.58 | 0.53 | 0.58 | 0.53 | 0.58 | 0.53 | 0.59 |
| U0 | 0.45 | 0.46 | 0.44 | 0.46 | 0.45 | 0.46 | 0.46 | 0.47 | |
| Ul | 0.84 | 0.91 | 0.86 | 0.89 | 0.84 | 0.91 | 0.84 | 0.91 | |
| Lv | 0.173 | 0.127 | - | - | 0.173 | 0.127 | 0.173 | 0.127 | |
| TI | 15.6 | 10.6 | 15 | 10 | 15.6 | 10.6 | 15.6 | 10.6 | |
| Eh | 7.00 | 7.04 | 7.01 | ||||||
| Uh | 0.50 | 0.50 | 0.50 | ||||||
| REI | 0.62 | - | 0.62 | ||||||
References
- Outdoor LED Lighting Market|Size, Growth, Trend and Forecast to 2023|Markets and Markets. Available online: https://www.marketsandmarkets.com/Market-Reports/outdoor-led-lighting-market-%20211822268.html (accessed on 11 July 2021).
- Kyba, C.; Kuester, T.; Sanchez de Miguel, A.; Baugh, K.; Jechow, A.; Hölker, F.; Bennie, J.; Elvidge, C.; Gaston, K.; Guanter, L. Artificially Lit Surface of Earth at Night Increasing in Radiance and Extent. Sci. Adv. 2017, 3, e1701528. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tardieux, P.; Greffier, F.; Taron, A. Projet Lumiroute®: Évaluation Du Système EQflux®. RGRA 2017, 950, 18–21. [Google Scholar]
- Soardo, P.; Iacomussi, P.; Rossi, G. The Luminance Coefficient in Road Lighting. A Parameter to Save Energy and Reducing Atmospheric Pollution. In Proceedings of the 11th Lux Europa International Congress, Istanbul, Turkey, 9–11 September 2009. [Google Scholar]
- Sordello, R. Pollution lumineuse et trame verte et bleue: Vers une trame noire en France? Territ. Mouv. Rev. Géographie Aménagement Territ. Mov. J. Geogr. Plan. 2017. [Google Scholar] [CrossRef]
- Aménagement, Urbanisme, Biodiversité, Éclairage: Une Série de Fiches Pratiques Pour les Différents Acteurs. Available online: http://www.cerema.fr/fr/actualites/amenagement-urbanisme-biodiversite-eclairage-serie-fiches (accessed on 11 July 2021).
- Fotios, S.; Gibbons, R. Road Lighting Research for Drivers and Pedestrians: The Basis of Luminance and Illuminance Recommendations. Lighting Res. Technol. 2018, 50, 154–186. [Google Scholar] [CrossRef]
- CIE 115: 2010 Lighting of Roads for Motor and Pedestrian Traffic; International Commission on Illumination (CIE): Vienna, Austria, 2010.
- CIE 140:2019 Road Lighting Calculations, 2nd ed.; International Commission on Illumination (CIE): Vienna, Austria, 2019.
- EN 13201-2:2015. Road Lighting—Part 2: Performance Requirements; CEN: Brussels, Belgium, 2015. [Google Scholar]
- Brémond, R. Visual Performance Models in Road Lighting: A Historical Perspective. LEUKOS 2020, 17, 1–30. [Google Scholar] [CrossRef]
- Fotios, S.; Boyce, P.; Ellis, C. The Effect of Pavement Material on Road Lighting Performance; Sheffield Hallam University: Sheffield, UK, 2005. [Google Scholar]
- CIE 144:2001 Road Surface and Road Marking Reflection Characteristics; International Commission on Illumination (CIE): Vienna, Austria, 2001.
- van Bommel, W. Road Lighting: Fundamentals, Technology and Application; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; ISBN 978-3-319-37835-0. [Google Scholar]
- Dumont, E. Photométrie Des Chaussées et Éclairage Public; Etudes et Recherches des Laboratoires des Ponts et Chaussees—Serie Routes et Securite Routiere; Laboratoire Central des Ponts et Chaussées (LCPC): Paris, France, 2007; ISBN 2-7208-2480-1. [Google Scholar]
- Dumont, E.; Paumier, J.-L.; Ledoux, V. Are Standard R-Tables Still Representative of Road Surface Photometric Characteristics in France? In Proceedings of the 2nd CIE Expert Symposium on “Advances in Photometry and Colorimetry”, CIE, Turin, Italy, 7–8 July 2008; Volume CIE x033.
- Muzet, V.; Greffier, F.; Nicolaï, A.; Taron, A.; Verny, P. Evaluation of the Performance of an Optimized Road Surface/Lighting Combination. Lighting Res. Technol. 2019, 51, 576–591. [Google Scholar] [CrossRef]
- Buschmann, S.; Steblau, J.; Voelker, S. New Image Based Measurement Method. In Proceedings of the CIE 2017 Midterm Meetings and Conference on Smarter Lighting for Better Life, International Commission on Illumination, CIE, Jeju Island, Korea, 23–25 October 2017. [Google Scholar]
- Ogando-Martínez, A.; Troncoso-Pastoriza, F.; Eguía-Oller, P.; Granada-Álvarez, E.; Erkoreka, A. Model Calibration Methodology to Assess the Actual Lighting Conditions of a Road Infrastructure. Infrastructures 2020, 5, 2. [Google Scholar] [CrossRef] [Green Version]
- Ogando-Martínez, A.; Troncoso-Pastoriza, F.; Granada-Álvarez, E.; Eguía-Oller, P. Ellipsoid-Based Approximation Method for the Estimation of the Actual Reduced Luminance Coefficients of Road Surfaces for Accurate Lighting Simulations. Sustain. Cities Soc. 2020, 63. [Google Scholar] [CrossRef]
- Li, W.; Zhang, Z.; Yang, Y.; Liu, M.; Shen, H. Modeling Reflection Properties of Road Surfaces by Database Method. In Proceedings of the 29th Quadrennial Session of the CIE, Washington, DC, USA, 14–22 June 2019; pp. 1796–1801. [Google Scholar]
- Boucher, V.; Greffier, F. Space of Basis Functions to Retrieve Road Surface Reflection Tables from Luminance Maps. Lighting Res. Technol. to be submitted.
- Galatanu, C.D.; Canale, L. Measurement of Reflectance Properties of Asphalt Using Photographical Methods. In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I CPS Europe), Madrid, Spain, 9–12 June 2020; pp. 1–6. [Google Scholar]
- Muzet, V.; Colomb, M.; Toinette, M.; Gandon-Leger, P.; Christory, J.-P. Towards an Optimization of Urban Lighting through a Combined Approach of Lighting and Road Building Activities. In Proceedings of the 29th Quadrennial Session of the CIE, International Commission on Illumination, CIE, Washington DC, USA, 14–22 June 2019; pp. 789–800. [Google Scholar]
- Arrêté N°2021P110904 Limitant La Vitesse à 30 Km/h Sur l’ensemble Des Voies de La Ville de Paris. 2021. Available online: https://cdn.paris.fr/paris/2021/07/09/0537b3f7665d1956261b6524e37dab35.pdf (accessed on 20 October 2021).
- Chain, C.; Marchaut, V. R-Tables for Other Observation Angles: Specific Needs for Two Applications in the Field of Public Lighting. In Proceedings of the 2nd CIE Expert Symposium on “Advances in Photometry and Colorimetry”, International Commission on Illumination, CIE, Turin, Italy, 7–8 July 2008. [Google Scholar]
- Muzet, V.; Bernasconi, J.; Iacomussi, P.; Liandrat, S.; Greffier, F.; Blattner, P.; Reber, J.; Lindgren, M. Review of Road Surface Photometry Methods and Devices—Proposal for New Measurement Geometries. Lighting Res. Technol. 2021, 53, 1–16. [Google Scholar] [CrossRef]
- Greffier, F.; Muzet, V.; Boucher, V.; Fournela, F.; Dronneau, R. Use of an Imaging Luminance Measuring Device to Evaluate Road Lighting Performance at Different Angles of Observation. In Proceedings of the 29th Quadrennial Session of the CIE, International Commission on Illumination, CIE, Washington DC, USA, 14–22 June 2019; pp. 553–562. [Google Scholar]
- EN 13201-3:2015. Road Lighting—Part 3: Calculation of Performance; CEN: Brussels, Belgium, 2015. [Google Scholar]
- De Boer, J.B.; Oñate, V.; Oostrijck, A. Practical Methods for Measuring and Calculating the Luminance of Road Surfaces. Philips Res. Rep. 1952, 7, 54–76. [Google Scholar]
- Stockmar, A. Extension of the Luminance Concept in Road and Tunnel Lighting. In Proceedings of the 28th Quadrennial Session of the CIE, International Commission on Illumination, CIE, Manchester, United Kingdom, 28 July 2015; Volume CIE 216, pp. 751–753. [Google Scholar]
- EN 13201-4:2015. Road Lighting—Part 4: Methods of Measuring Lighting Performance; CEN: Brussels, Belgium, 2015. [Google Scholar]
- CIE 146/147:2002—CIE Collection on Glare; International Commission on Illumination (CIE): Brussels, Belgium, 2002.
- Saint-Jacques, E.; Prevost, C.; Villa, C. Evaluation of the Performance of a Road Surface Gonioreflectometer. In Proceedings of the 29th Quadrennial Session of the CIE, International Commission on Illumination, CIE, Washington DC, USA, 14–22 June 2019; pp. 536–545. [Google Scholar]
- Saint-Jacques, E.; Dumont, E.; Villa, C. Characterisation of the Reflection Properties of Road Surfaces Using an In-Lab Gonioreflectometer. In Proceedings of the CIE 2017 Midterm Meetings and Conference on Smarter Lighting for Better Life, International Commission on Illumination, CIE, Jeju Island, Korea, 23–25 October 2017; Volume CIE x044. [Google Scholar]
- Muzet, V.; Paumier, J.-L.; Guillard, Y. COLUROUTE: A Mobile Gonio-Reflectometer to Characterize the Road Surface Photometry. In Proceedings of the 2nd CIE Expert Symposium on “Advances in Photometry and Colorimetry”, CIE, Turin, Italy, 7–8 July 2008; Volume CIE x033. [Google Scholar]
- Jackett, M.; Frith, W. Measurement of the Reflection Properties of Road Surfaces to Improve the Safety and Sustainability of Road Lighting. NZ Transp. Agency Res. Rep. 2009, 383. Available online: https://www.researchgate.net/publication/237694738_Measurement_of_the_reflection_properties_of_road_surfaces_to_improve_the_safety_and_sustainability_of_road_lighting (accessed on 20 October 2021).
- Sørensen, K.; Ekrias, A.; Hafdell, P.; Corell, D. Reflection Properties of Road Surfaces in Denmark. 2017. Available online: https://nmfv.dk/wp-content/uploads/2012/03/Reflection-properties-of-road-surfaces-in-Denmark-version-17-May-2017-1.pdf (accessed on 20 October 2021).
- Corell, D.; Sørensen, K. An Instrument for the Measurement of Road Surface Reflection Properties. In Proceedings of the CIE 2017 Midterm Meetings and Conference on Smarter Lighting for Better Life, International Commission on Illumination, CIE, Jeju Island, Korea, 23–25 October 2017; pp. 443–452. [Google Scholar]
- Jackett, M.; Frith, W. Reflection Properties of New Zealand Road Surfaces for Road Lighting Design. In Proceedings of the IPENZ Transportation Group Conference, Christchurch, NZ, USA, 14–17 March 2010; p. 15. [Google Scholar]
- Li, W.; Zheng, S.; Demirdes, H. New Achievements in Practical Determination of Road Surface Reflection Table from in Situ Measurements. In Proceedings of the 28th Quadrennial Session of the CIE, International Commission on Illumination, CIE, Manchester, UK, 28 July 2015; Volume CIE 216, pp. 1676–1681. [Google Scholar]
- CIE 194:2011 On Site Measurement of the Photometric Properties of Road and Tunnel Lighting; International Commission on Illumination (CIE): Brussels, Belgium, 2011.
- Adrian, W. Visibility of Targets: Model for Calculation. Lighting Res. Technol. 1989, 21, 181–188. [Google Scholar] [CrossRef]
- Gibbons, R.B. Influence of Pavement Reflection on Target Visibility, University of Waterloo. 1998. Available online: https://uwspace.uwaterloo.ca/handle/10012/244 (accessed on 20 October 2021).
- SURFACE Project: Pavement Surface Characterisation for Smart and Efficient Road Lighting. Available online: https://surface-nrm02.eu/ (accessed on 11 July 2021).
- Greffier, F.; Charbonnier, P.; Tarel, J.-P.; Boucher, V.; Fournela, F. An Automatic System for Measuring Road and Tunnel Lighting Performance. In Proceedings of the 28th Quadrennial Session of the CIE, International Commission on Illumination, CIE, Manchester, UK, 28 July 2015; Volume CIE 216, pp. 1647–1656. [Google Scholar]
- Boucher, V.; Dumont, E.; Dronneau, R.; Fournela, F.; Greffier, F. High Dynamic Range Imaging Luminance Measuring Device (HDR-ILMD) and Applications in Motion. In Proceedings of the CIE 2017 Midterm Meetings and Conference on Smarter Lighting for Better Life, International Commission on Illumination, CIE, Jeju Island, Korea, 23–25 October 2017; pp. 923–932. [Google Scholar]
- Greffier, F.; Muzet, V.; Boucher, V. How to Take into Account the Heterogeneity of Optical Properties of a Pavement in Lighting Design? In Proceedings of the CIE 2021 Midterm Meeting and Conference, International Commission on Illumination, CIE, Kuala Lumpur, Malaysia, 27–29 September 2021. [Google Scholar]
- Li, W.; Zheng, X.; Zhu, X.; Whang, G.; Shen, H. Measurement System and Method for Reflection Properties of Wet Road Surfaces. In Proceedings of the CIE 2017 Midterm Meetings and Conference on Smarter Lighting for Better Life, CIE, Jeju Island, Korea, 23–25 October 2017; pp. 294–302. [Google Scholar]
- Frederiksen, E.; Sørensen, K. Reflection Classification of Dry and Wet Road Surfaces. Lighting Res. Technol. 1976, 8, 175–186. [Google Scholar] [CrossRef]
- Sørensen, K.; Nielsen, B. Road Surfaces in Traffic Lighting; Danish Illuminating Engineering Laboratory Report 9. 1974. Available online: https://trid.trb.org/view/37817 (accessed on 20 October 2021).
- Erbay, A. Of the Reflection Properties of Road Surfaces; Technische University of Berlin: Berlin, Germany, 1974. [Google Scholar]
- ISO/IEC Guide 98-3:2008/Suppl 1:2008; ISO/IEC: Geneva, Switzerland, 2008.
- Kolmogorov–Smirnov Test. In The Concise Encyclopedia of Statistics; Springer: New York, NY, USA, 2008; pp. 283–287. ISBN 978-0-387-32833-1.
- Rusu, A.V.; Galatanu, C.D.; Livint, G.; Lucache, D.D. Average Luminance Calculation in Street Lighting Design, Comparison between BS-EN 13201 and RP-08 Standards. Sustainability 2021, 13, 10143. [Google Scholar] [CrossRef]
- CIE TC 4-50: Road Surface Characterization for Lighting Applications. Available online: https://cie.co.at/technicalcommittees/road-surface-characterization-lighting-applications (accessed on 20 October 2021).
- Luo, W.; Puolakka, M.; Zhang, Q.; Yang, C.; Halonen, L. Pedestrian Way Lighting: User Preferences and Eye Fixation Measurements. Ing. Illum. 2013, 15, 19–34. [Google Scholar]
- Cengiz, C.; Kotkanen, H.; Puolakka, M.; Lappi, O.; Lehtonen, E.; Halonen, L.; Summala, H. Combined Eye-Tracking and Luminance Measurements While Driving on a Rural Road: Towards Determining Mesopic Adaptation Luminance. Lighting Res. Technol. 2014, 46, 676–694. [Google Scholar] [CrossRef]
- Winter, J.; Fotios, S.; Völker, S. Gaze Direction When Driving after Dark on Main and Residential Roads: Where Is the Dominant Location? Lighting Res. Technol. 2017, 49, 574–585. [Google Scholar] [CrossRef]
- CIE 115:1995 Recommendations for the Lighting of Roads for Motor and Pedestrian Traffic; International Commission on Illumination (CIE): Vienna, Austria, 1995.





| Class | S1 Range | r-Table Name | Typical Q0 | Typical S1 |
|---|---|---|---|---|
| RI | 0.42 ≤ S1 < 0.42 | R1 | 0.100 | 0.25 |
| RII | 0.42 ≤ S1 < 0.85 | R2 | 0.070 | 0.58 |
| RIII | 0.85 ≤ S1 < 1.35 | R3 | 0.070 | 1.11 |
| RIV | 1.35 ≤ S1 < 0.85 | R4 | 0.080 | 1.55 |
| Pavement 1 | Pavement 2 | Pavement 3 | Pavement 4 | |
|---|---|---|---|---|
| Road width | 6.5 m | |||
| Number of lanes | 2 | |||
| Central reservation | 4.25 m | |||
| Luminaire | STYLED | COSMO | ||
| Initial power | 77 W | 103 W | 140 W | |
| Flux (T18) | 4600 lm | 6000 lm | 16,500 lm | |
| Spacing | 29 m | |||
| Mounting height | 9 m | |||
| Cross | 1.5 m | |||
| Overhang | −0.62 m | |||
| Tilt | 0° | 5° | ||
| Maintenance factor | 1 | |||
| Pavement 1 | Pavement 2 | Pavement 3 | Pavement 4 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Q0 | S1 | Q0 | S1 | Q0 | S1 | Q0 | S1 | ||
| Thirty measurements | average | 0.101 | 0.72 | 0.082 | 0.54 | 0.064 | 0.61 | 0.059 | 0.94 |
| std | 0.007 | 0.22 | 0.006 | 0.10 | 0.004 | 0.09 | 0.004 | 0.23 | |
| Central tracks measurements | average | 0.095 | 0.57 | 0.075 | 0.54 | 0.060 | 0.57 | 0.057 | 0.86 |
| std | 0.006 | 0.08 | 0.003 | 0.12 | 0.003 | 0.07 | 0.002 | 0.07 | |
| Wheel tracks measurements | average | 0.104 | 0.79 | 0.085 | 0.54 | 0.065 | 0.64 | 0.059 | 0.97 |
| std | 0.006 | 0.23 | 0.004 | 0.08 | 0.002 | 0.09 | 0.004 | 0.27 | |
| Pavement 1 | Pavement 2 | Pavement 3 | Pavement 4 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CT | WT | CT + WT | CT | WT | CT + WT | CT | WT | CT + WT | CT | WT | CT + WT | ||
| Luminance in cd/m2 | min | 1.21 | 1.37 | 1.21 | 1.24 | 1.39 | 1.24 | 1.72 | 2.01 | 1.72 | 1.81 | 1.69 | 1.69 |
| max | 1.53 | 1.68 | 1.68 | 1.46 | 1.73 | 1.73 | 2.20 | 2.34 | 2.34 | 2.03 | 2.60 | 2.60 | |
| Δ | 26% | 22% | 38% | 17% | 24% | 39% | 28% | 16% | 36% | 13% | 53% | 53% | |
| Overall uniformity | min | 0.53 | 0.46 | 0.46 | 0.55 | 0.55 | 0.55 | 0.65 | 0.62 | 0.62 | 0.61 | 0.53 | 0.53 |
| max | 0.57 | 0.58 | 0.58 | 0.62 | 0.61 | 0.62 | 0.68 | 0.68 | 0.68 | 0.65 | 0.68 | 0.68 | |
| Δ | 8% | 26% | 26% | 13% | 11% | 13% | 5% | 10% | 10% | 7% | 28% | 28% | |
| Longitudinal uniformity | min | 0.72 | 0.71 | 0.71 | 0.73 | 0.73 | 0.73 | 0.65 | 0.67 | 0.65 | 0.75 | 0.72 | 0.72 |
| max | 0.83 | 0.87 | 0.87 | 0.79 | 0.84 | 0.84 | 0.75 | 0.75 | 0.75 | 0.78 | 0.82 | 0.82 | |
| Δ | 15% | 23% | 23% | 8% | 15% | 15% | 15% | 12% | 15% | 4% | 14% | 14% | |
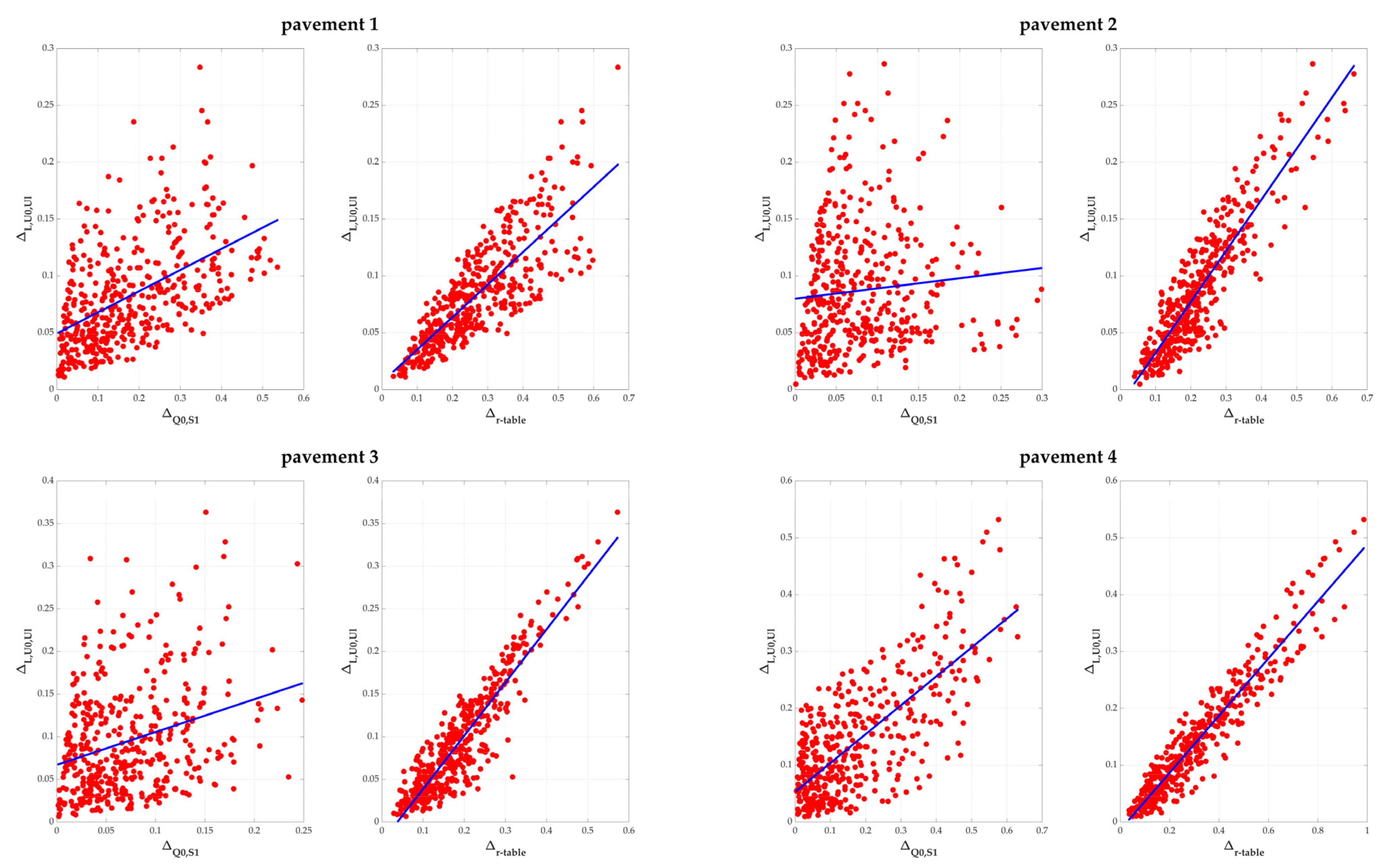
| R2 for Lave = f(Q0) | R2 for U0 = f(S1) | R2 for Ul = f(S1) | |
|---|---|---|---|
| Pavement 1 | 0.990 | −0.966 | 0.906 |
| Pavement 2 | 0.982 | −0.822 | 0.737 |
| Pavement 3 | 0.987 | −0.864 | 0.739 |
| Pavement 4 | 0.948 | −0.968 | 0.803 |
| Pavement 1 | 0.518 | 0.815 |
| Pavement 2 | 0.095 | 0.896 |
| Pavement 3 | 0.293 | 0.912 |
| Pavement 4 | 0.734 | 0.954 |
| Pavement 1 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lane 1 | Lane 2 | ||||||||||||
| 10 | 2.03 | 1.73 | 1.65 | 1.33 | 1.09 | 0.86 | 10 | 2.07 | 1.61 | 1.55 | 1.19 | 0.97 | 0.69 |
| 9 | 1.85 | 1.48 | 1.45 | 1.15 | 0.95 | 0.76 | 9 | 2.17 | 1.77 | 1.66 | 1.28 | 1.03 | 0.73 |
| 8 | 1.76 | 1.39 | 1.33 | 1.04 | 0.87 | 0.69 | 8 | 2.24 | 1.91 | 1.77 | 1.44 | 1.13 | 0.80 |
| 7 | 1.93 | 1.57 | 1.42 | 1.14 | 0.93 | 0.74 | 7 | 2.21 | 1.95 | 1.83 | 1.53 | 1.19 | 0.84 |
| 6 | 2.08 | 1.75 | 1.59 | 1.32 | 1.06 | 0.84 | 6 | 2.12 | 1.90 | 1.83 | 1.52 | 1.19 | 0.83 |
| 5 | 2.16 | 1.86 | 1.70 | 1.44 | 1.11 | 0.86 | 5 | 2.00 | 1.77 | 1.72 | 1.45 | 1.14 | 0.81 |
| 4 | 2.04 | 1.78 | 1.65 | 1.37 | 1.06 | 0.81 | 4 | 1.89 | 1.63 | 1.59 | 1.32 | 1.05 | 0.76 |
| 3 | 1.84 | 1.62 | 1.51 | 1.24 | 0.96 | 0.73 | 3 | 1.80 | 1.52 | 1.50 | 1.23 | 0.97 | 0.71 |
| 2 | 1.68 | 1.47 | 1.40 | 1.14 | 0.88 | 0.67 | 2 | 1.74 | 1.45 | 1.44 | 1.18 | 0.91 | 0.68 |
| 1 | 1.57 | 1.37 | 1.29 | 1.06 | 0.82 | 0.65 | 1 | 1.67 | 1.38 | 1.41 | 1.14 | 0.88 | 0.63 |
| 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 | 5 | 6 | ||
| Average Luminance | Overall Uniformity | Longitudinal Uniformity | ||||
|---|---|---|---|---|---|---|
| Lane 1 | Lane 2 | Lane 1 | Lane 2 | Lane 1 | Lane 2 | |
| Pavement 1 | 1.33 | 1.41 | 0.49 | 0.45 | 0.73 | 0.74 |
| Pavement 2 | 1.43 | 1.48 | 0.56 | 0.56 | 0.79 | 0.81 |
| Pavement 3 | 2.11 | 2.23 | 0.72 | 0.72 | 0.76 | 0.82 |
| Pavement 4 | 1.85 | 1.97 | 0.70 | 0.68 | 0.91 | 0.82 |
| Pavement 1 | 0.042 | 0.016 | 0.090 |
| Pavement 2 | 0.053 | 0.017 | 0.105 |
| Pavement 3 | 0.059 | 0.017 | 0.109 |
| Pavement 4 | 0.066 | 0.018 | 0.119 |
| Average Luminance | Overall Uniformity | Longitudinal Uniformity | ||||||
|---|---|---|---|---|---|---|---|---|
| Lane 1 | Lane 2 | Lane 1 | Lane 2 | Lane 1 | Lane 2 | |||
| Pavement 1 | R2 | 0.82 | 0.87 | 0.61 | 0.61 | 0.81 | 0.86 | 0.317 |
| R2 scaled | 1.29 | 1.36 | 0.61 | 0.61 | 0.81 | 0.86 | 0.102 | |
| Central track best | 1.42 | 1.50 | 0.54 | 0.54 | 0.78 | 0.75 | 0.056 | |
| Central track worst | 1.19 | 1.24 | 0.56 | 0.56 | 0.75 | 0.72 | 0.110 | |
| Wheel track best | 1.43 | 1.55 | 0.50 | 0.50 | 0.84 | 0.77 | 0.056 | |
| Wheel track worst | 1.60 | 1.75 | 0.48 | 0.48 | 0.91 | 0.80 | 0.198 | |
| Complete | 1.38 | 1.46 | 0.50 | 0.52 | 0.65 | 0.74 | 0.054 | |
| Measurement | 1.33 | 1.41 | 0.49 | 0.45 | 0.73 | 0.74 | ||
| Pavement 2 | R2 | 1.01 | 1.07 | 0.62 | 0.62 | 0.80 | 0.87 | 0.244 |
| R2 scaled | 1.29 | 1.36 | 0.62 | 0.62 | 0.80 | 0.87 | 0.089 | |
| Central track best | 1.41 | 1.50 | 0.56 | 0.55 | 0.82 | 0.76 | 0.026 | |
| Central track worst | 1.22 | 1.27 | 0.59 | 0.60 | 0.76 | 0.76 | 0.128 | |
| Wheel track best | 1.41 | 1.48 | 0.56 | 0.57 | 0.83 | 0.80 | 0.021 | |
| Wheel track worst | 1.69 | 1.76 | 0.58 | 0.58 | 0.73 | 0.74 | 0.161 | |
| Complete | 1.42 | 1.48 | 0.65 | 0.64 | 0.75 | 0.76 | 0.057 | |
| Measurement | 1.43 | 1.48 | 0.56 | 0.56 | 0.79 | 0.81 | ||
| Pavement 3 | R2 | 1.86 | 1.99 | 0.71 | 0.71 | 0.76 | 0.77 | 0.144 |
| R2 scaled | 1.83 | 1.96 | 0.71 | 0.71 | 0.76 | 0.77 | 0.159 | |
| Central track best | 1.98 | 2.09 | 0.67 | 0.68 | 0.76 | 0.72 | 0.066 | |
| Central track worst | 1.68 | 1.76 | 0.68 | 0.68 | 0.65 | 0.66 | 0.274 | |
| Wheel track best | 2.07 | 2.18 | 0.67 | 0.68 | 0.76 | 0.73 | 0.051 | |
| Wheel track worst | 2.05 | 2.20 | 0.62 | 0.63 | 0.73 | 0.68 | 0.116 | |
| Complete | 2.01 | 2.12 | 0.64 | 0.65 | 0.71 | 0.64 | 0.108 | |
| Measurement | 2.11 | 2.23 | 0.72 | 0.72 | 0.76 | 0.82 | ||
| Pavement 4 | R3 | 1.73 | 1.92 | 0.66 | 0.64 | 0.86 | 0.82 | 0.062 |
| R3 scaled | 1.59 | 1.77 | 0.66 | 0.64 | 0.86 | 0.82 | 0.138 | |
| Central track best | 1.94 | 2.09 | 0.62 | 0.63 | 0.82 | 0.74 | 0.070 | |
| Central track worst | 1.97 | 2.12 | 0.62 | 0.63 | 0.80 | 0.71 | 0.110 | |
| Wheel track best | 1.80 | 1.95 | 0.61 | 0.63 | 0.81 | 0.72 | 0.075 | |
| Wheel track worst | 2.46 | 2.73 | 0.54 | 0.54 | 0.85 | 0.72 | 0.413 | |
| Complete | 1.86 | 2.03 | 0.64 | 0.67 | 0.83 | 0.71 | 0.067 | |
| Measurement | 1.85 | 1.97 | 0.70 | 0.68 | 0.91 | 0.82 | ||
| Scenario 1 Random | Scenario 2 CT | Scenario 3 WT | Scenario 4 CT + WT | Scenario 5 2CT + 2WT | Scenario 6 3CT + 3WT | |
|---|---|---|---|---|---|---|
| Pavement 1 | 57% | 80% | 45% | 78% | 87% | 93% |
| Pavement 2 | 87% | 90% | 85% | 100% | 100% | 100% |
| Pavement 3 | 73% | 40% | 90% | 72% | 79% | 85% |
| Pavement 4 | 53% | 100% | 30% | 73% | 83% | 88% |
| Pavement 1 | Pavement 2 | Pavement 3 | Pavement 4 | |||||
|---|---|---|---|---|---|---|---|---|
| Q0 | S1 | Q0 | S1 | Q0 | S1 | Q0 | S1 | |
| 1° | 0.161 | 1.04 | 0.091 | 0.52 | 0.070 | 0.86 | 0.061 | 2.61 |
| 2.29° | 0.148 | 0.93 | 0.079 | 0.45 | 0.057 | 0.67 | 0.051 | 2.38 |
| 5° | 0.129 | 0.64 | 0.065 | 0.36 | 0.042 | 0.56 | 0.050 | 1.81 |
| 10° | 0.115 | 0.40 | 0.054 | 0.27 | 0.040 | 0.45 | 0.043 | 1.50 |
| 20° | 0.100 | 0.28 | 0.049 | 0.24 | 0.034 | 0.34 | 0.037 | 1.03 |
| 45° | 0.072 | 0.11 | 0.042 | 0.17 | 0.027 | 0.20 | 0.026 | 0.38 |
| R2 for S1 = f(Q0) | 0.980 | 0.998 | 0.979 | 0.978 | ||||
| Average Luminance | Overall Uniformity | Longitudinal Uniformity | |||||
|---|---|---|---|---|---|---|---|
| Lane 1 | Lane 2 | Lane 1 | Lane 2 | Lane 1 | Lane 2 | ||
| Pavement 1 | 1° (fixed observer) | 1.72 | 1.90 | 0.46 | 0.46 | 0.89 | 0.80 |
| 1° | 1.73 | 1.89 | 0.47 | 0.46 | 0.89 | 0.80 | |
| 2.29° | 1.56 | 1.80 | 0.46 | 0.45 | 0.90 | 0.78 | |
| 5° | 1.37 | 1.53 | 0.50 | 0.49 | 0.81 | 0.76 | |
| 10° | 1.22 | 1.26 | 0.55 | 0.58 | 0.70 | 0.71 | |
| 20° | 1.10 | 1.05 | 0.57 | 0.63 | 0.60 | 0.67 | |
| 45° | 0.86 | 0.81 | 0.54 | 0.59 | 0.47 | 0.55 | |
| Pavement 2 | 1° (fixed observer) | 1.25 | 1.30 | 0.62 | 0.64 | 0.84 | 0.86 |
| 1° | 1.25 | 1.30 | 0.63 | 0.64 | 0.84 | 0.86 | |
| 2.29° | 1.07 | 1.14 | 0.61 | 0.63 | 0.82 | 0.81 | |
| 5° | 0.84 | 0.89 | 0.62 | 0.64 | 0.71 | 0.77 | |
| 10° | 0.66 | 0.68 | 0.64 | 0.67 | 0.68 | 0.76 | |
| 20° | 0.58 | 0.59 | 0.61 | 0.67 | 0.65 | 0.74 | |
| 45° | 0.48 | 0.48 | 0.61 | 0.64 | 0.55 | 0.67 | |
| Pavement 3 | 1° (fixed observer) | 1.69 | 1.82 | 0.66 | 0.67 | 0.81 | 0.75 |
| 1° | 1.69 | 1.81 | 0.67 | 0.68 | 0.81 | 0.75 | |
| 2.29° | 1.37 | 1.53 | 0.65 | 0.66 | 0.76 | 0.74 | |
| 5° | 0.99 | 1.11 | 0.66 | 0.69 | 0.75 | 0.74 | |
| 10° | 0.90 | 0.99 | 0.68 | 0.72 | 0.72 | 0.74 | |
| 20° | 0.74 | 0.78 | 0.68 | 0.63 | 0.69 | 0.73 | |
| 45° | 0.57 | 0.58 | 0.65 | 0.64 | 0.56 | 0.67 | |
| Pavement 4 | 1° (fixed observer) | 1.61 | 1.88 | 0.47 | 0.50 | 0.86 | 0.86 |
| 1° | 1.63 | 1.86 | 0.49 | 0.52 | 0.86 | 0.86 | |
| 2.29° | 1.30 | 1.65 | 0.45 | 0.45 | 0.90 | 0.84 | |
| 5° | 1.18 | 1.54 | 0.47 | 0.50 | 0.94 | 0.85 | |
| 10° | 0.92 | 1.15 | 0.48 | 0.54 | 0.91 | 0.86 | |
| 20° | 0.68 | 0.80 | 0.51 | 0.51 | 0.88 | 0.82 | |
| 45° | 0.47 | 0.52 | 0.60 | 0.56 | 0.73 | 0.77 | |
| R2 for Lave = f(Q0) | R2 for U0 = f(S1) | R2 for Ul = f(S1) | |
|---|---|---|---|
| Pavement 1 | 0.997 | −0.919 | 0.953 |
| Pavement 2 | 0.999 | −0.257 | 0.972 |
| Pavement 3 | 0.999 | 0.355 | 0.886 |
| Pavement 4 | 0.987 | −0.782 | 0.714 |
| Pavement 1 | 0.970 | 0.997 |
| Pavement 2 | 0.997 | 0.982 |
| Pavement 3 | 0.954 | 0.960 |
| Pavement 4 | 0.939 | 0.969 |
| 1° | 2.29° | 5° | 10° | 20° | 45° | ||
|---|---|---|---|---|---|---|---|
| Pavement 1 | - | 0.148 | 0.456 | 0.730 | 0.922 | 1.207 | |
| Pavement 2 | - | 0.230 | 0.652 | 1.065 | 1.215 | 1.478 | |
| Pavement 3 | - | 0.283 | 0.817 | 0.934 | 1.233 | 1.590 | |
| Pavement 4 | - | 0.333 | 0.532 | 0.958 | 1.405 | 1.980 | |
| Pavement 1 | 0.007 | 0.080 | 0.213 | 0.348 | 0.456 | 0.606 | |
| Pavement 2 | 0.003 | 0.100 | 0.246 | 0.355 | 0.407 | 0.480 | |
| Pavement 3 | 0.006 | 0.174 | 0.405 | 0.465 | 0.575 | 0.687 | |
| Pavement 4 | 0.015 | 0.162 | 0.225 | 0.413 | 0.583 | 0.728 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Greffier, F.; Muzet, V.; Boucher, V.; Fournela, F.; Lebouc, L.; Liandrat, S. Influence of Pavement Heterogeneity and Observation Angle on Lighting Design: Study with New Metrics. Sustainability 2021, 13, 11789. https://doi.org/10.3390/su132111789
Greffier F, Muzet V, Boucher V, Fournela F, Lebouc L, Liandrat S. Influence of Pavement Heterogeneity and Observation Angle on Lighting Design: Study with New Metrics. Sustainability. 2021; 13(21):11789. https://doi.org/10.3390/su132111789
Chicago/Turabian StyleGreffier, Florian, Valérie Muzet, Vincent Boucher, Fabrice Fournela, Laure Lebouc, and Sébastien Liandrat. 2021. "Influence of Pavement Heterogeneity and Observation Angle on Lighting Design: Study with New Metrics" Sustainability 13, no. 21: 11789. https://doi.org/10.3390/su132111789
APA StyleGreffier, F., Muzet, V., Boucher, V., Fournela, F., Lebouc, L., & Liandrat, S. (2021). Influence of Pavement Heterogeneity and Observation Angle on Lighting Design: Study with New Metrics. Sustainability, 13(21), 11789. https://doi.org/10.3390/su132111789






