Optimal Sizing and Assessment of a Renewable Rich Standalone Hybrid Microgrid Considering Conventional Dispatch Methodologies
Abstract
:1. Introduction
1.1. Core Contribution of This Research Work
- HOMER optimization is utilized for the evaluation and design of the proposed Integrated Hybrid Microgrid System (IHMS), which will guarantee the least CO2 production, Cost of Energy (COE), and Net Present Cost (NPC) for the planned areas for different dispatch methodologies;
- Microgrids’ response (voltage and frequency) is evaluated in Simulink to guarantee achievable, effective, and reliable performance;
- Five alternative dispatch techniques have been considered in this study and on the basis of their performances in terms of minimum cost, GHG release and power system responses, the worst and best dispatch approaches for the proposed microgrids have been declared.
1.2. Paper Organization
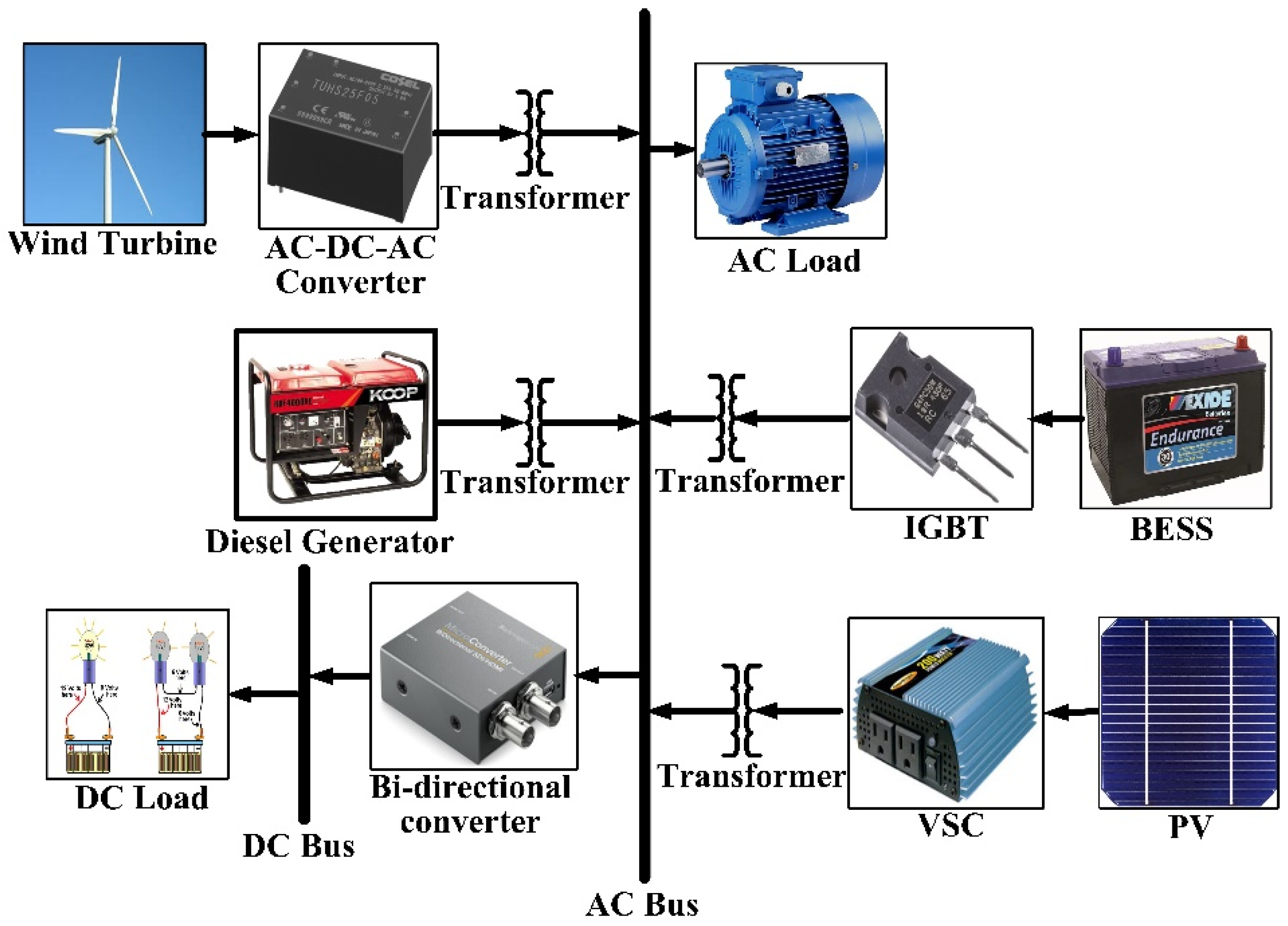
2. Proposed IHMS Modeling
2.1. Site and Load Profile
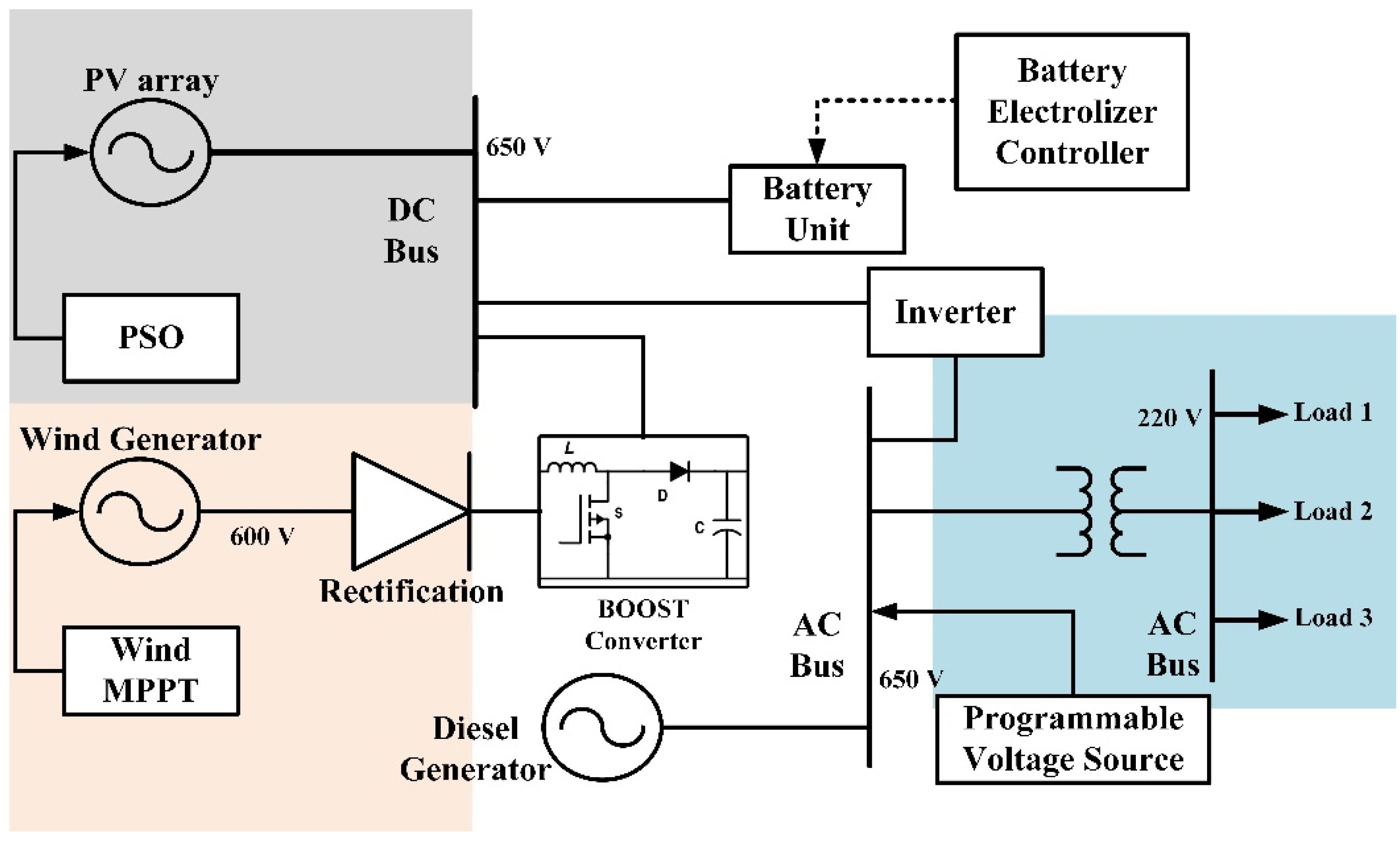
2.2. Proposed IHMS Model
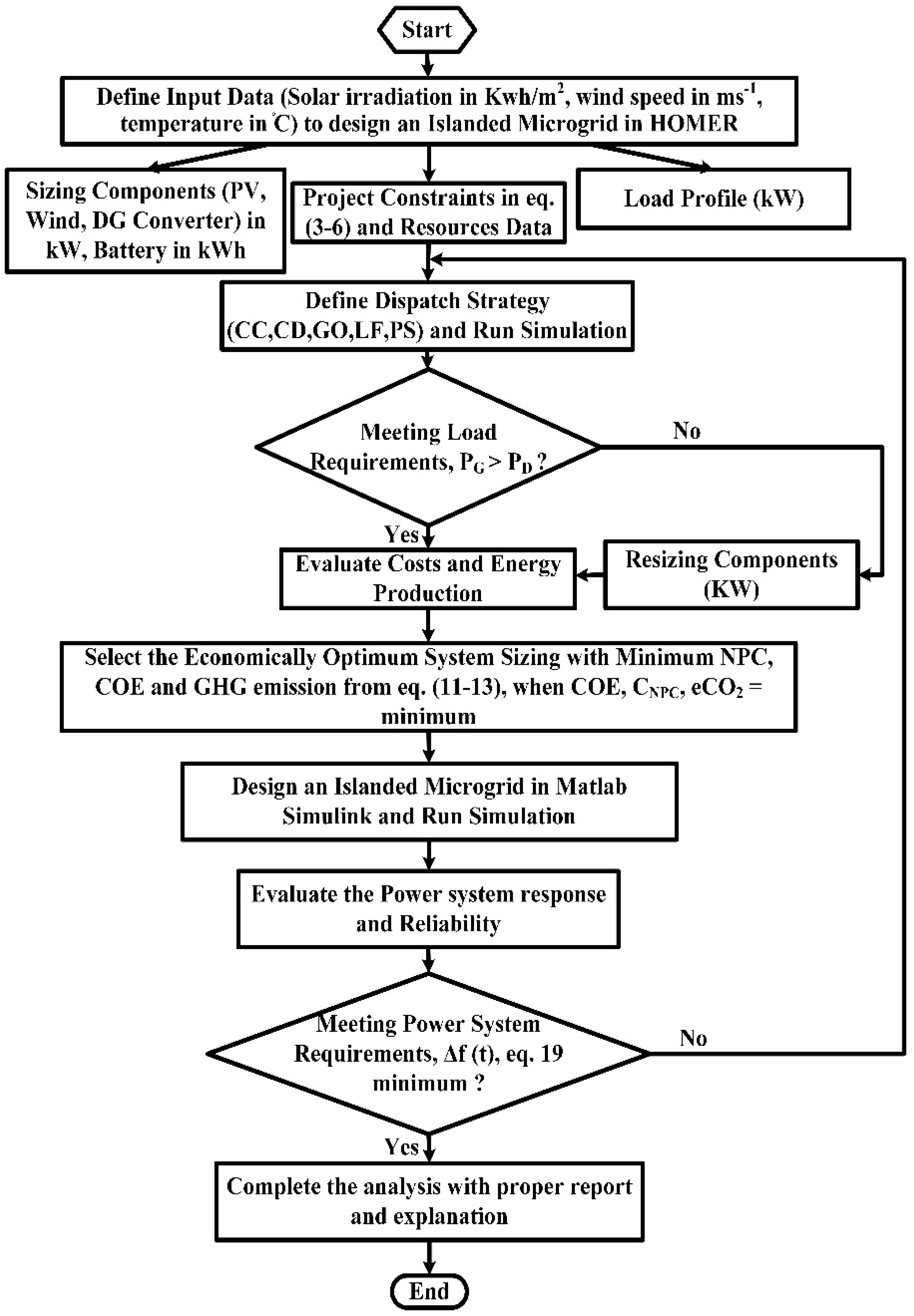
3. Methodology
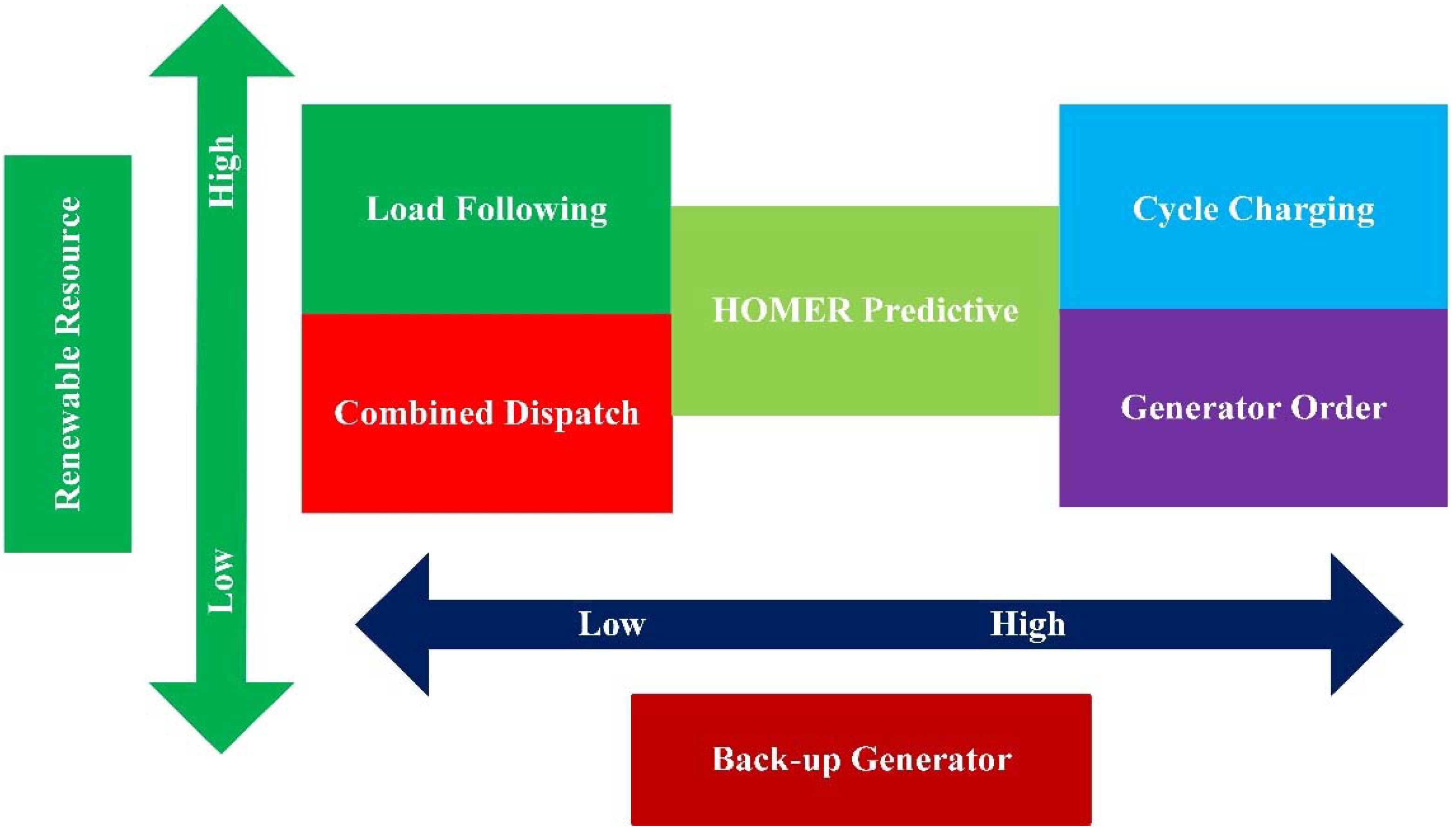
3.1. Dispatch Algorithms
3.2. Formulation of Problem
3.2.1. Objective Function
3.2.2. Equality Inequality Constraints
Active Power Balance Constraint
Constraints for Generation Capacity
3.2.3. Cost Function Minimization and Optimal Sizing
3.2.4. COE Calculation
3.2.5. NPC Calculation
3.2.6. Evaluation of CO2 Release
3.2.7. Evaluation of ED
3.2.8. Stabilization of Frequency
3.2.9. Voltage Stabilization
4. Results and Discussion
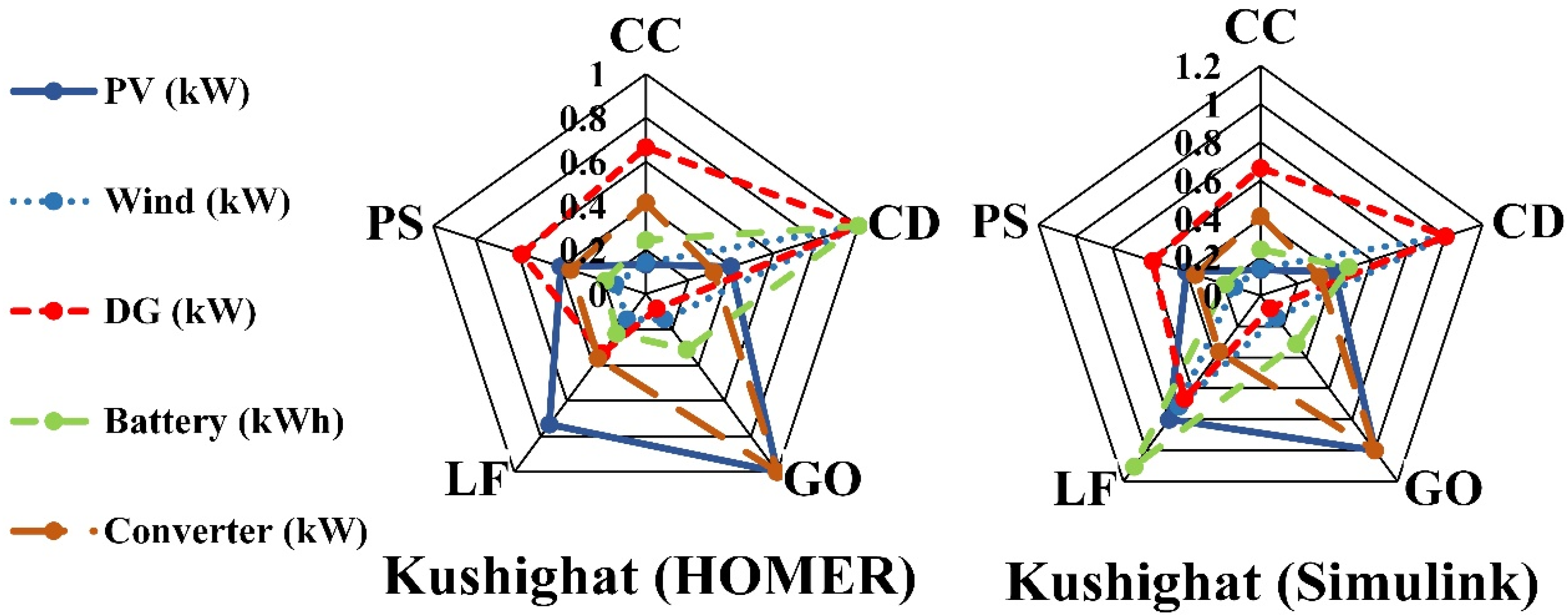
4.1. The IHMS’s Techno-Economic Study and Optimum Sizing
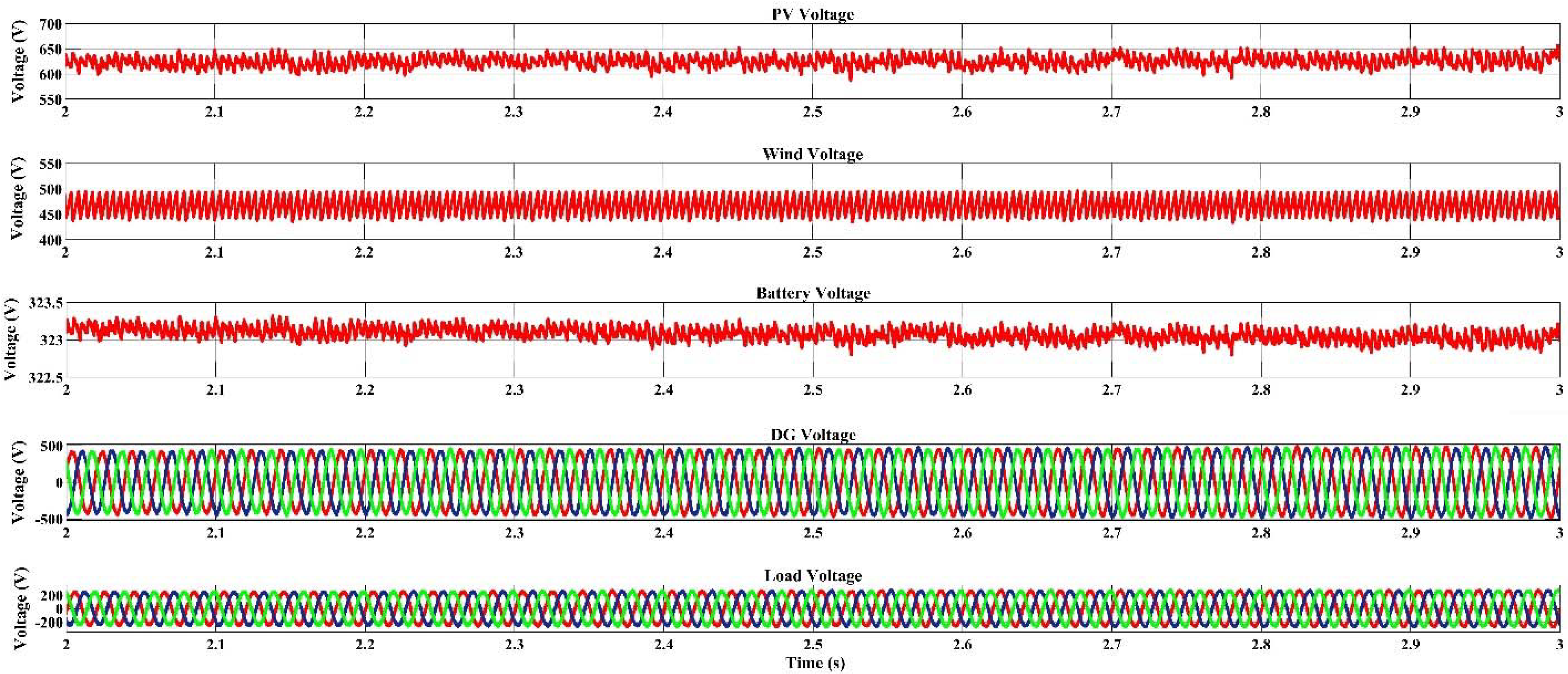
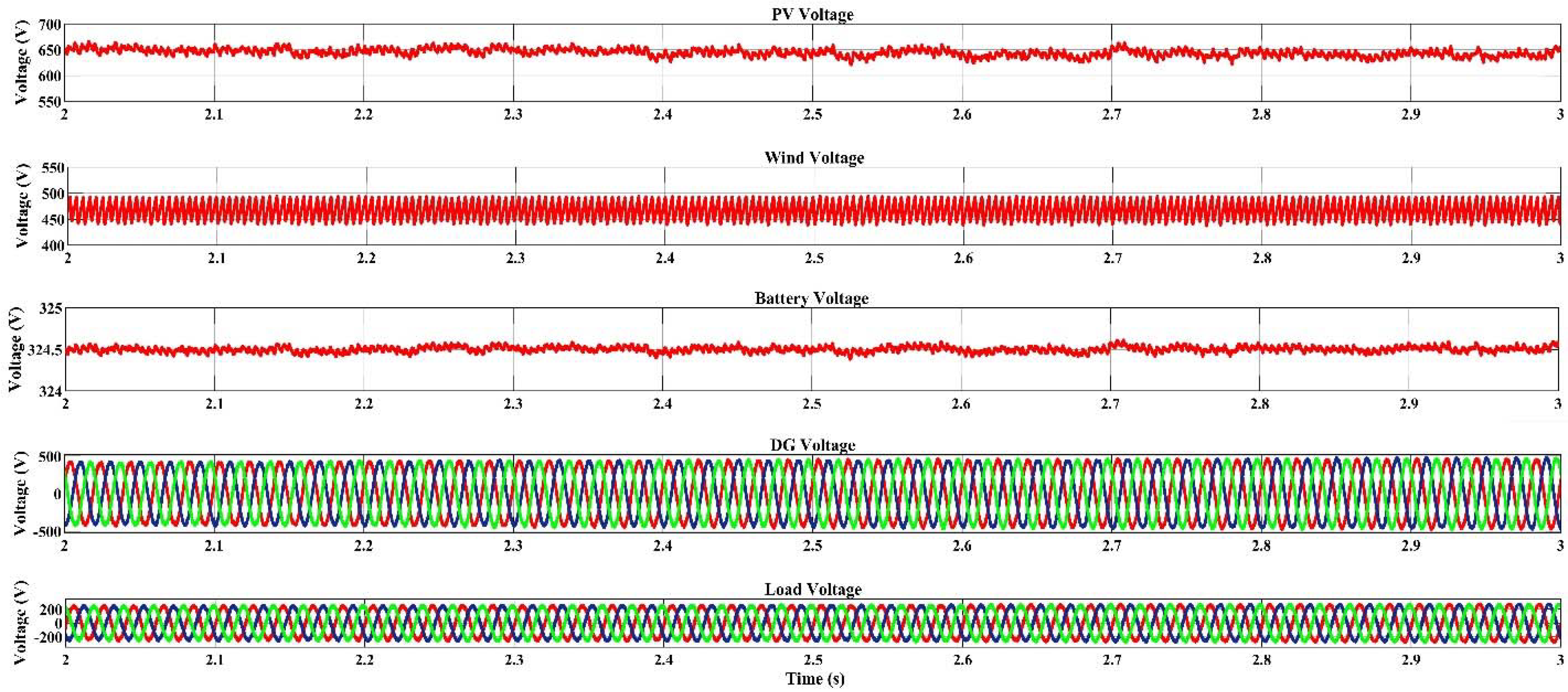
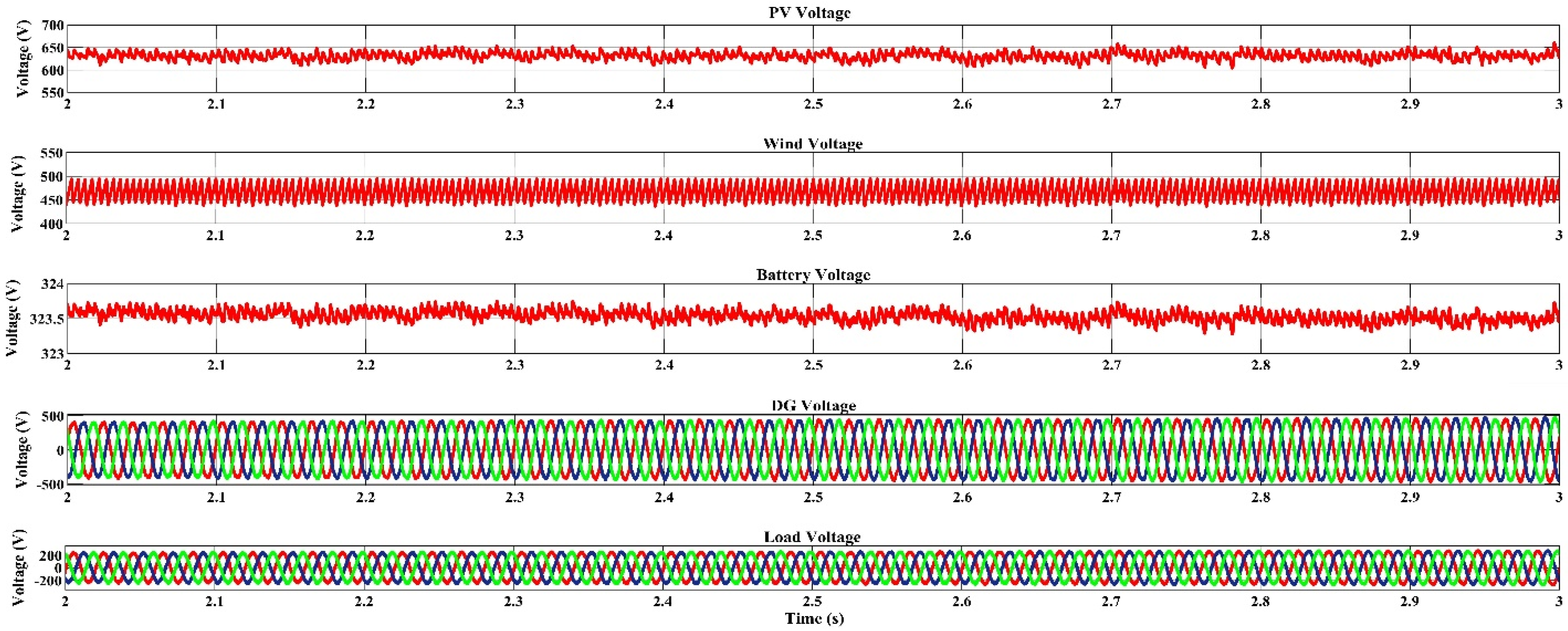
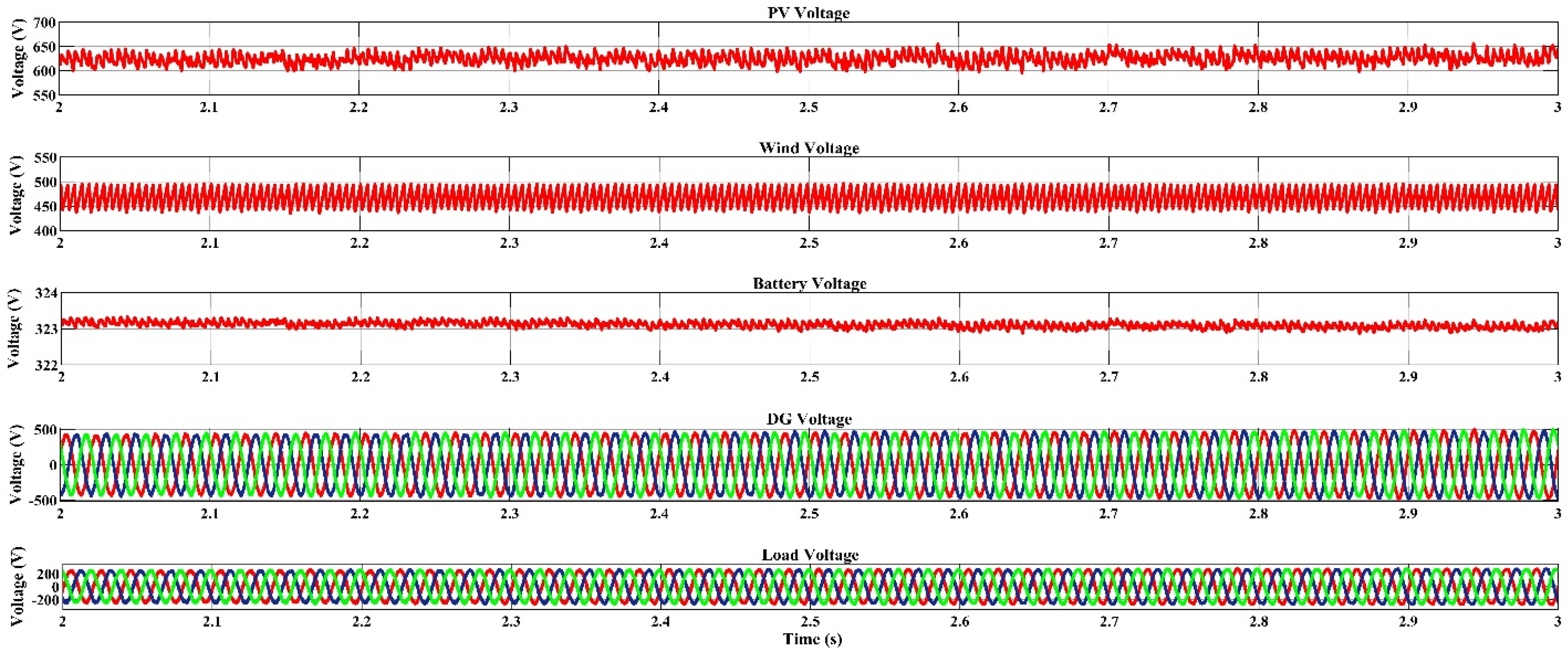
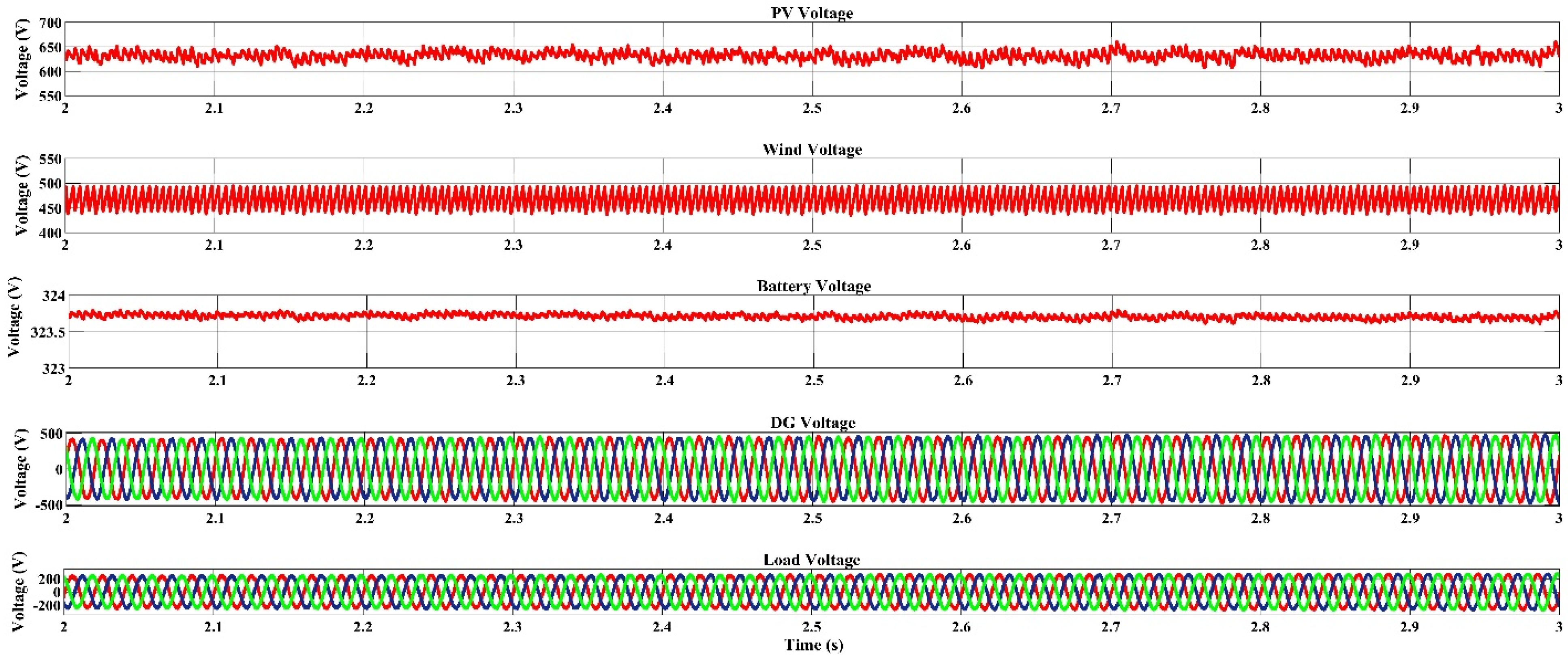
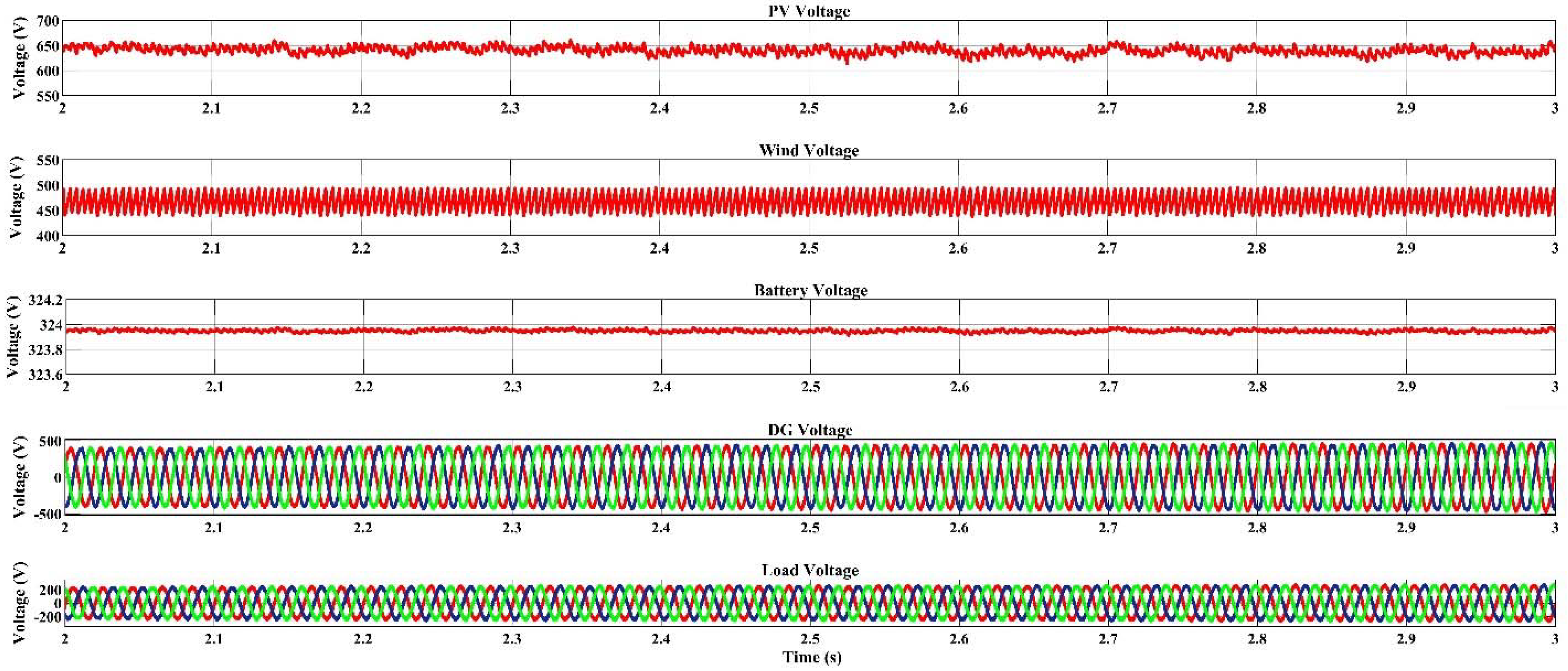
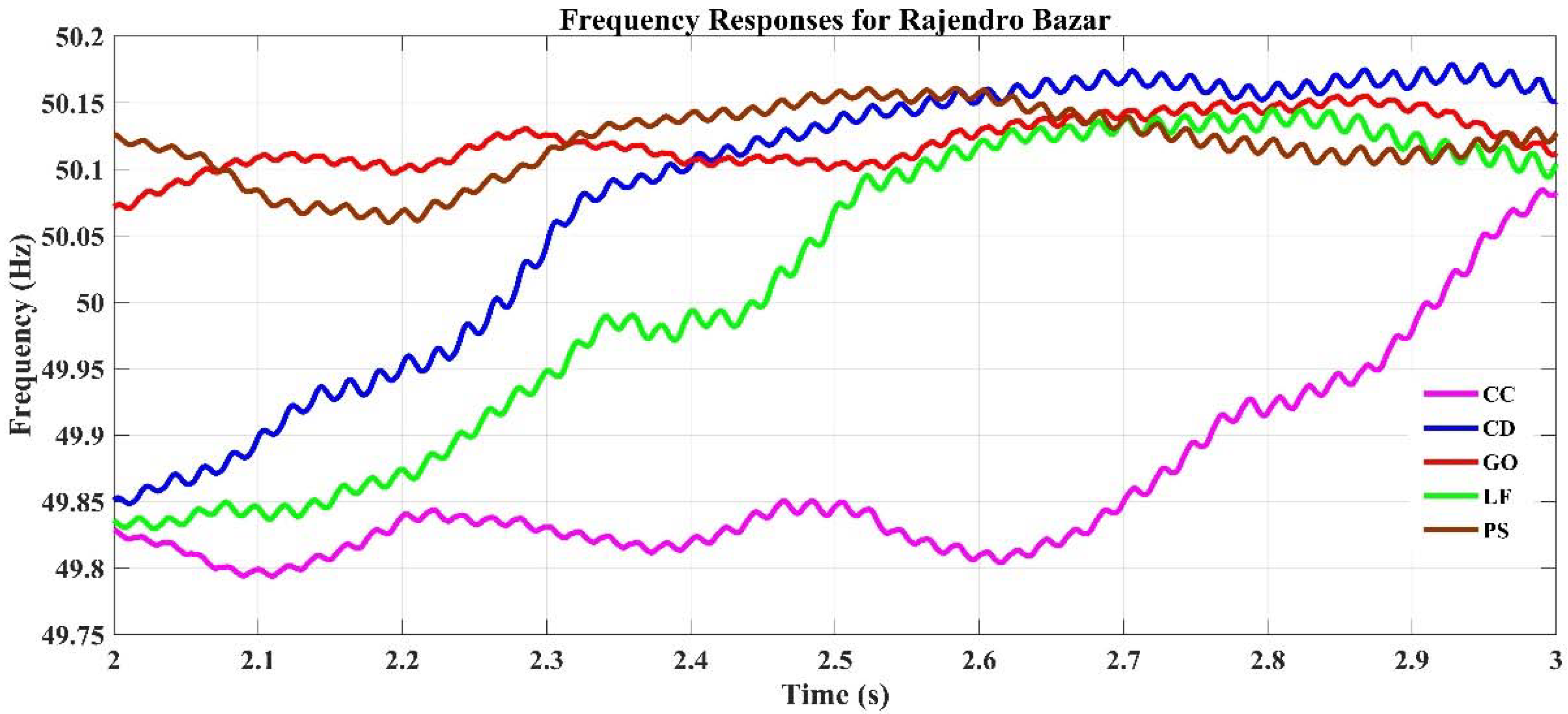
4.2. Dispatch Strategy Based Voltage–Frequency Response of the Microgrids
4.2.1. Voltage Outputs
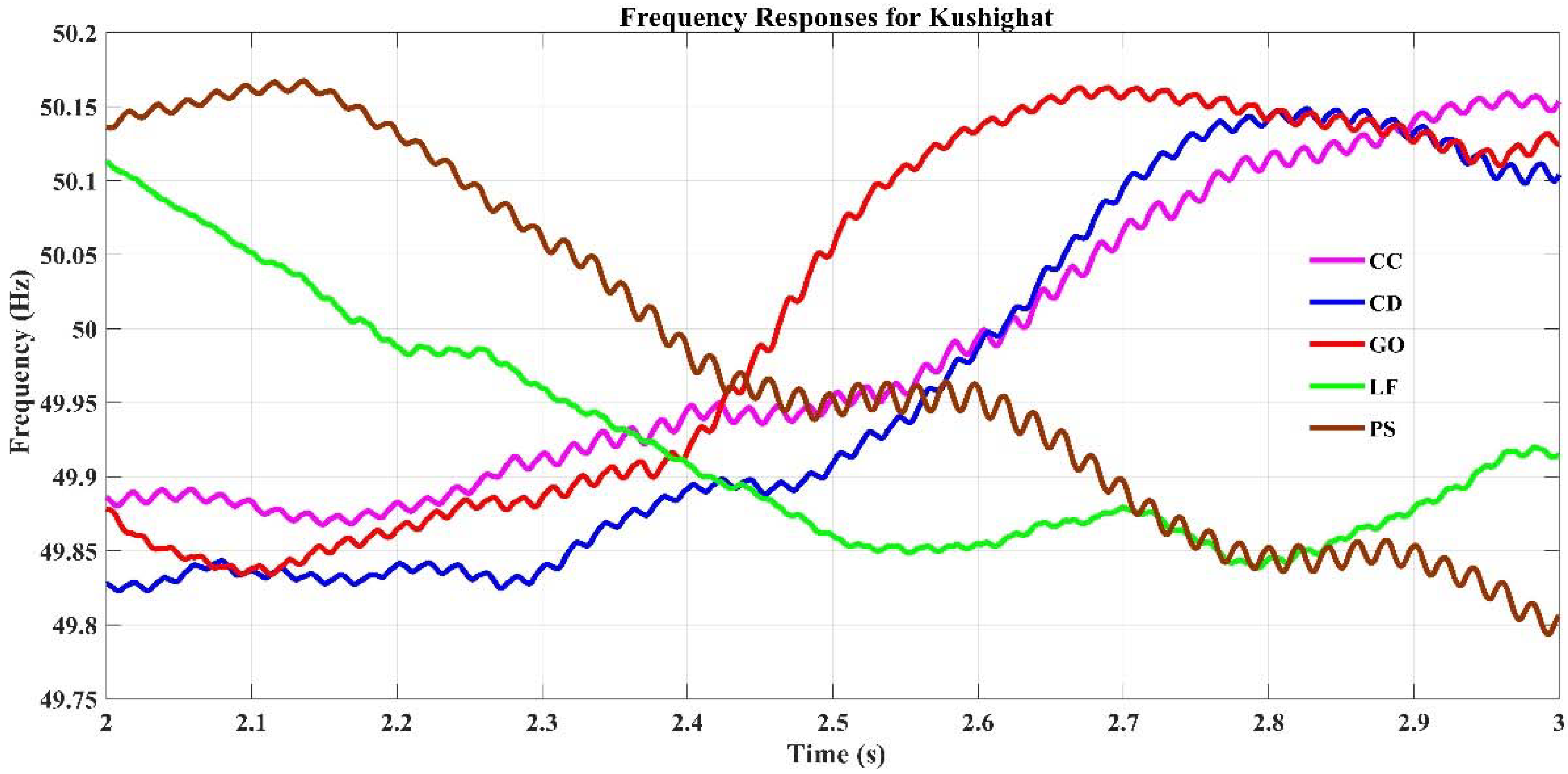
4.2.2. Frequency Output and Feasibility Study
4.3. Comparison
4.4. Determining the Best and Worst Dispatch Approaches
4.5. Discussion on Results
4.6. Advantages of the Proposed System
5. Conclusions
6. Limitations and Future Research Recommendations
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Elaborative form |
| HOMER | Hybrid Optimization of Multiple Electric Renewables |
| NPC | Net Present Cost |
| COE | Cost of Energy |
| GHG | Green House Gas |
| BESS | Battery Energy Storage System |
| AC | Alternating Current |
| DC | Direct Current |
| ED | Economic Dispatch |
| RTED | Real Time Economic Dispatch |
| IHMS | Integrated Hybrid Microgrid System |
| WT | Wind Turbines |
| DG | Diesel Generator |
| PV | Photo Voltaic |
| CC | Cycle Charging |
| LF | Load Following |
| CD | Combined Dispatch |
| PS | HOMER Predictive dispatch |
| GO | Generator Order |
| RoCoF | Rate of Change of Frequency |
| HRES | Hybrid Renewable Energy Systems |
| Nomenclature | |
| Ngen | number of generator units |
| aj, bj, cj | fuel cost coefficients of the jth generator |
| Fj(Pj) | cost function of fuel of the jth generator in USD/hour |
| Pj | power output of the jth generator in MW |
| Ploss | net system loss |
| Pdemand | net consumer demand |
| Bij, B0i, B00 | coefficients of loss |
| electricity generated from the ith generator | |
| lowest generation range, | |
| highest source capacity | |
| storage power | |
| a, b, c, d | corresponding capacities of various microgrid components |
| f1, f2, f3 | weights to mean the corresponding component’s significance |
| Cannual | yearly net cost |
| Lprimary | net primary demand |
| Egs | net energy brought by the traditional grid each year |
| Ld | net deferrable demand |
| i | rate of interest (annualized) |
| Cannual | annual net cost |
| Tproject | longevity of the project |
| CRF (.) | capital recovery factor |
| eCO2 | amount of CO2 gas |
| mfuel | amount of fuel in Liter |
| FHV | Fuel heating value in MJ/L |
| CEFfuel | carbon emission factor in ton carbon/TJ |
| Xc | oxidized carbon fraction |
| fnadir | frequency nadir |
| RoCoF | Rate of Change of Frequency |
| H | microgrid’s inertia |
| D | load damping factor |
| Δf (t) | frequency deviation |
| PM | microgrids power imbalance |
| ΔPSj (t) | power differences of generation unit i |
| ΔPGi (t) | power differences of battery j |
References
- Ma, Y.; Chen, Y.; Chen, X.; Deng, F.; Song, X. Optimal Dispatch of Hybrid Energy Islanded Microgrid Considering V2G Under TOU Tariffs. E3S Web Conf. 2019, 107, 02007. [Google Scholar] [CrossRef]
- Nwani, C.; Omoke, P.C. Does bank credit to the private sector promote low-carbon development in Brazil? An extended STIRPAT analysis using dynamic ARDL simulations. Env. Sci. Pollut. Res. Int. 2020, 27, 31408–31426. [Google Scholar] [CrossRef]
- Chang, X.; Xu, Y.; Gu, W.; Sun, H.; Chow, M.-Y.; Yi, Z. Accelerated distributed hybrid stochastic/robust energy management of smart grids. IEEE Trans. Ind. Inform. 2020, 17, 5335–5347. [Google Scholar] [CrossRef]
- Mohamed, S.; Shaaban, M.F.; Ismail, M.; Serpedin, E.; Qaraqe, K.A. An efficient planning algorithm for hybrid remote microgrids. IEEE Trans. Sustain. Energy 2018, 10, 257–267. [Google Scholar] [CrossRef]
- Papari, B.; Edrington, C.S.; Bhattacharya, I.; Radman, G. Effective energy management of hybrid AC–DC microgrids with storage devices. IEEE Trans. Smart Grid 2017, 10, 193–203. [Google Scholar] [CrossRef]
- Duan, J.; Yi, Z.; Shi, D.; Lin, C.; Lu, X.; Wang, Z. Reinforcement-learning-based optimal control of hybrid energy storage systems in hybrid AC–DC microgrids. IEEE Trans. Ind. Inform. 2019, 15, 5355–5364. [Google Scholar] [CrossRef]
- Dabbaghjamanesh, M.; Kavousifard, A.; Mehraeen, S.; Zhang, J.; Dong, Z.Y. Sensitivity Analysis of Renewable Energy Integration on Stochastic Energy Management of Automated Reconfigurable Hybrid AC-DC Microgrid Considering DLR Security Constraint. IEEE Trans. Ind. Inform. 2019, 16, 120–131. [Google Scholar] [CrossRef]
- Shezan, S.A.; Ishraque, M.F. Assessment of a Micro-grid Hybrid Wind-Diesel-Battery Alternative Energy System Applicable for Offshore Islands. In Proceedings of the 2019 5th International Conference on Advances in Electrical Engineering (ICAEE), Dhaka, Bangladesh, 26–28 September 2019; pp. 457–462. [Google Scholar]
- Barbaro, M.; Castro, R. Design optimisation for a hybrid renewable microgrid: Application to the case of Faial island, Azores archipelago. Renew. Energy 2020, 151, 434–445. [Google Scholar] [CrossRef]
- Ishraque, M.F.; Shezan, S.A.; Nur, J.N.; Islam, M.S. Optimal Sizing and Assessment of an Islanded Photovoltaic-Battery-Diesel Generator Microgrid Applicable to a Remote School of Bangladesh. Eng. Rep. 2021, 3, e12281. [Google Scholar] [CrossRef]
- Ishraque, M.F.; Ali, M.M. Optimized Design of a Hybrid Microgrid using Renewable Resources Considering Different Dispatch Strategies. In Proceedings of the 2021 International Conference on Automation, Control and Mechatronics for Industry 4.0 (ACMI), Rajshahi, Bangladesh, 8–9 July 2021; pp. 1–6. [Google Scholar]
- Liu, B.; Liu, S.; Guo, S.; Zhang, S. Economic study of a large-scale renewable hydrogen application utilizing surplus renewable energy and natural gas pipeline transportation in China. Int. J. Hydrog. Energy 2020, 45, 1385–1398. [Google Scholar] [CrossRef]
- Shezan, S.A.; Saidur, R.; Ullah, K.; Hossain, A.; Chong, W.T.; Julai, S. Feasibility analysis of a hybrid off-grid wind–DG-battery energy system for the eco-tourism remote areas. Clean Technol. Environ. Policy 2015, 17, 2417–2430. [Google Scholar] [CrossRef]
- Li, P.; Liu, Y.; Xin, H.; Jiang, X. A Robust Distributed Economic Dispatch Strategy of Virtual Power Plant Under Cyber-Attacks. IEEE Trans. Ind. Inform. 2018, 14, 4343–4352. [Google Scholar] [CrossRef]
- Barley, C.D.; Winn, C.B. Optimal dispatch strategy in remote hybrid power systems. Sol. Energy 1996, 58, 165–179. [Google Scholar] [CrossRef]
- Jiang, K.; Wu, F.; Zong, X.; Shi, L.; Lin, K. Distributed Dynamic Economic Dispatch of an Isolated AC/DC Hybrid Microgrid Based on a Finite-Step Consensus Algorithm. Energies 2019, 12, 4637. [Google Scholar] [CrossRef] [Green Version]
- Coelho, L.S.; Mariani, V.C. Combining of chaotic differential evolution and quadratic programming for economic dispatch optimization with valve-point effect. IEEE Trans. Power Syst. 2006, 21, 989–996. [Google Scholar]
- Xiong, G.; Shi, D.; Duan, X. Multi-strategy ensemble biogeography-based optimization for economic dispatch problems. Appl. Energy 2013, 111, 801–811. [Google Scholar] [CrossRef]
- Augustine, N.; Suresh, S.; Moghe, P.; Sheikh, K. In Economic dispatch for a microgrid considering renewable energy cost functions. In Proceedings of the 2012 IEEE PES Innovative Smart Grid Technologies (ISGT), Washington, DC, USA, 16–20 January 2012; pp. 1–7. [Google Scholar]
- Zhu, J.; Zhu, T.; Mo, X.; Liu, M. A spatiotemporal decomposition algorithm for fully decentralized dynamic economic dispatch in a microgrid. Electr. Power Syst. Res. 2020, 185, 106361. [Google Scholar] [CrossRef]
- Gil-González, W.; Montoya, O.D.; Grisales-Noreña, L.F.; Cruz-Peragón, F.; Alcalá, G. Economic Dispatch of Renewable Generators and BESS in DC Microgrids Using Second-Order Cone Optimization. Energies 2020, 13, 1703. [Google Scholar] [CrossRef] [Green Version]
- Ross, D.W.; Kim, S. Dynamic economic dispatch of generation. IEEE Trans. Power Appar. Syst. 1980, 6, 2060–2068. [Google Scholar] [CrossRef]
- Tang, C.; Zhang, F.; Zhao, Z. Real-Time Economic Dispatch and Subinterval Coordination Strategy to Benefit System Operations. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 2881–2886. [Google Scholar]
- Liu, W.; Zhuang, P.; Liang, H.; Peng, J.; Huang, Z. Distributed economic dispatch in microgrids based on cooperative reinforcement learning. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 2192–2203. [Google Scholar] [CrossRef]
- Mohy-ud-din, G.; Muttaqi, K.M.; Sutanto, D. An Effective Power Dispatch Strategy to Improve Generation Schedulability by Mitigating Wind power Uncertainty with a Data Driven flexible Dispatch Margin for a Wind Farm using a Multi-Unit Battery Energy Storage System. In Proceedings of the 2018 IEEE Industry Applications Society Annual Meeting (IAS), Portland, OR, USA, 23–27 September 2018; pp. 1–8. [Google Scholar]
- Wang, R.; Li, Q.; Li, G.; Liu, H. A Gossip-Based Distributed Algorithm for Economic Dispatch in Smart Grids With Random Communication Link Failures. IEEE Trans. Ind. Electron. 2019, 67, 4635–4645. [Google Scholar] [CrossRef]
- Das, B.K.; Zaman, F. Performance analysis of a PV/Diesel hybrid system for a remote area in Bangladesh: Effects of dispatch strategies, batteries, and generator selection. Energy 2019, 169, 263–276. [Google Scholar] [CrossRef]
- Xu, Y.; Sun, H.; Gu, W.; Xu, Y.; Li, Z. Optimal distributed control for secondary frequency and voltage regulation in an islanded microgrid. IEEE Trans. Ind. Inform. 2018, 15, 225–235. [Google Scholar] [CrossRef]
- Fatin Ishraque, M.; Shezan, S.A.; Ali, M.M.; Rashid, M.M. Optimization of load dispatch strategies for an islanded microgrid connected with renewable energy sources. Appl. Energy 2021, 292, 116879. [Google Scholar] [CrossRef]
- Ishraque, M.F.; Shezan, S.A.; Rashid, M.M.; Bhadra, A.B.; Hossain, M.A.; Chakrabortty, R.K.; Ryan, M.J.; Fahim, S.R.; Sarker, S.K.; Das, S.K. Techno-Economic and Power System Optimization of a Renewable Rich Islanded Microgrid Considering Different Dispatch Strategies. IEEE Access 2021, 9, 77325–77340. [Google Scholar] [CrossRef]
- NASA. Available online: https://power.larc.nasa.gov/ (accessed on 20 February 2021).
- He, Y.; Wang, W.; Wu, X. Multi-Agent Based Fully Distributed Economic Dispatch in Microgrid Using Exact Diffusion Strategy. IEEE Access 2020, 8, 7020–7031. [Google Scholar] [CrossRef]
- Ashari, M.; Nayar, C.V. An optimum dispatch strategy using set points for a photovoltaic (PV)–diesel–battery hybrid power system. Sol. Energy 1999, 66, 1–9. [Google Scholar] [CrossRef]
- Xu, H.; Meng, Z.; Zhao, R.; Wang, Y.; Yan, Q. Optimal Dispatching Strategy of an Electric-Thermal-Gas Coupling Microgrid Considering Consumer Satisfaction. IEEE Access 2020, 8, 173169–173176. [Google Scholar] [CrossRef]
- Wu, N.; Wang, H.; Yin, L.; Yuan, X.; Leng, X. Application Conditions of Bounded Rationality and a Microgrid Energy Management Control Strategy Combining Real-Time Power Price and Demand-Side Response. IEEE Access 2020, 8, 227327–227339. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Z.; Wang, H.; Zhang, H.; Yang, W.; Cao, R. Research on Bi-Level Optimized Operation Strategy of Microgrid Cluster Based on IABC Algorithm. IEEE Access 2021, 9, 15520–15529. [Google Scholar] [CrossRef]
- Dong, X.; Li, X.; Cheng, S. Energy Management Optimization of Microgrid Cluster Based on Multi-Agent-System and Hierarchical Stackelberg Game Theory. IEEE Access 2020, 8, 206183–206197. [Google Scholar] [CrossRef]
- Xi, L.; Zhang, L.; Liu, J.; Li, Y.; Chen, X.; Yang, L.; Wang, S. A Virtual Generation Ecosystem Control Strategy for Automatic Generation Control of Interconnected Microgrids. IEEE Access 2020, 8, 94165–94175. [Google Scholar] [CrossRef]
- Malik, M.M.; Kazmi, S.A.A.; Asim, H.W.; Ahmed, A.B.; Shin, D.R. An Intelligent Multi-Stage Optimization Approach for Community Based Micro-Grid Within Multi-Microgrid Paradigm. IEEE Access 2020, 8, 177228–177244. [Google Scholar] [CrossRef]
- Pro, H. Available online: https://www.homerenergy.com/products/pro/docs/latest/predictive_dispatch.html#:~:text=Under%20the%20HOMER%20Predictive%20dispatch,dispatch%20strategies%20in%20HOMER%20Pro (accessed on 20 October 2020).
- Moretti, L.; Polimeni, S.; Meraldi, L.; Raboni, P.; Leva, S.; Manzolini, G. Assessing the impact of a two-layer predictive dispatch algorithm on design and operation of off-grid hybrid microgrids. Renew. Energy 2019, 143, 1439–1453. [Google Scholar] [CrossRef]
- Xu, Q.; Xiao, J.; Wang, P.; Wen, C. A decentralized control strategy for economic operation of autonomous AC, DC, and hybrid AC/DC microgrids. IEEE Trans. Energy Convers. 2017, 32, 1345–1355. [Google Scholar] [CrossRef]
- Ahmad, J.; Tahir, M.; Mazumder, S.K. Dynamic economic dispatch and transient control of distributed generators in a microgrid. IEEE Syst. J. 2018, 13, 802–812. [Google Scholar] [CrossRef]
- Zhou, Q.; Shahidehpour, M.; Li, Z.; Che, L.; Alabdulwahab, A.; Abusorrah, A. Compartmentalization Strategy for the Optimal Economic Operation of a Hybrid AC/DC Microgrid. IEEE Trans. Power Syst. 2019, 35, 1294–1304. [Google Scholar] [CrossRef]
- Arefin, S.S. Optimization Techniques of Islanded Hybrid Microgrid System. In Renewable Energy-Resources, Challenges and Applications; IntechOpen: Hague, The Netherlands, 2020. [Google Scholar]
- Shezan, S.A.; Julai, S.; Kibria, M.A.; Ullah, K.R.; Saidur, R.; Chong, W.T.; Akikur, R.K. Performance analysis of an off-grid wind-PV (photovoltaic)-diesel-battery hybrid energy system feasible for remote areas. J. Clean. Prod. 2016, 125, 121–132. [Google Scholar] [CrossRef]
- Chatzivasileiadis, S. Optimization in modern power systems. Lecture Notes Tech. Univ. Den. 2018. Available online: https://arxiv.org/pdf/1811.00943.pdf (accessed on 20 June 2021).
- Wen, Y.; Chung, C.; Liu, X.; Che, L. Microgrid dispatch with frequency-aware islanding constraints. IEEE Trans. Power Syst. 2019, 34, 2465–2468. [Google Scholar] [CrossRef]







| Rajendro Bazar | ||||
| Dispatch Methodology | NPC (USD) | Operating Cost (USD/year) | COE (USD/kWh) | CO2 Emission (kg/year) |
| LF | 152,023 | 3738 | 0.208 | 3375 |
| CD | 343,996 | 14,654 | 0.440 | 20,961 |
| CC | 302,953 | 18,850 | 0.388 | 38,272 |
| GO | 171,678 | 2760 | 0.236 | 0 |
| PS | 191,593 | 9405 | 0.245 | 16,797 |
| Kushighat | ||||
| Dispatch Methodology | NPC (USD) | Operating Cost (USD/year) | COE (USD/kWh) | CO2 Emission (kg/year) |
| LF | 157,561 | 4456 | 0.215 | 5035 |
| CD | 415,030 | 15,394 | 0.532 | 17,266 |
| CC | 311,015 | 19,349 | 0.398 | 39,159 |
| GO | 181,449 | 3039 | 0.250 | 0 |
| PS | 202,677 | 10,263 | 0.259 | 18,891 |
| Rajendro Bazar | |||||
| Dispatch Methodology | PV (kW) | Wind (kW) | DG (kW) | Battery (kWh) | Converter (kW) |
| LF | 55 | 3 | 3 | 138 | 13.9 |
| CD | 25 | 4 | 12 | 388 | 21.9 |
| CC | 10 | 2 | 8 | 132 | 15.6 |
| GO | 75 | 1 | 1 | 158 | 41.8 |
| PS | 30 | 1 | 7 | 110 | 13.9 |
| Kushighat | |||||
| Dispatch Methodology | PV (kW) | Wind (kW) | DG (kW) | Battery (kWh) | Converter (kW) |
| LF | 55 | 1 | 4 | 129 | 14.3 |
| CD | 30 | 7 | 12 | 578 | 12.6 |
| CC | 10 | 1 | 8 | 141 | 16.3 |
| GO | 75 | 1 | 1 | 181 | 39.4 |
| PS | 30 | 1 | 7 | 110 | 13.9 |
| Rajendro Bazar | |||||
| Dispatch Methodology | PV (kW) | Wind (kW) | DG (kW) | Battery (kWh) | Converter (kW) |
| LF | 60 | 5 | 8 | 638.7 | 13.9 |
| CD | 25 | 4 | 12 | 386.8 | 21.9 |
| CC | 10 | 2 | 8 | 132 | 15.6 |
| GO | 75 | 1 | 1 | 180 | 41.8 |
| PS | 30 | 1 | 7 | 110.8 | 13.9 |
| Kushighat | |||||
| Dispatch Methodology | PV (kW) | Wind (kW) | DG (kW) | Battery (kWh) | Converter (kW) |
| LF | 60 | 5 | 8 | 638.7 | 14.3 |
| CD | 30 | 7 | 12 | 275.4 | 12.6 |
| CC | 10 | 1 | 8 | 139 | 16.3 |
| GO | 75 | 1 | 1 | 181 | 39.4 |
| PS | 30 | 1 | 7 | 110.8 | 13.9 |
| Parameters | Designed IHMS | Other HRES [46] |
|---|---|---|
| CO2 release/Year (Kt) | 0.003375 | 198,347.984 |
| Operating Cost (USD) | 3738 | 19,516 |
| NPC/Year (USD) | 152,023 | 288,194 |
| COE (USD/kWh) | 0.208 | 1.877 |
| Parameters | Designed IHMS | Traditional Power Station [46] |
|---|---|---|
| COE (USD/kWh) | 0.208 | 0.380 |
| NPC/Year (USD) | 152,023 | 297,000.00 |
| CO2 release/Year (Kt) | 0.003375 | 198,348.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ishraque, M.F.; Shezan, S.A.; Rana, M.S.; Muyeen, S.M.; Rahman, A.; Paul, L.C.; Islam, M.S. Optimal Sizing and Assessment of a Renewable Rich Standalone Hybrid Microgrid Considering Conventional Dispatch Methodologies. Sustainability 2021, 13, 12734. https://doi.org/10.3390/su132212734
Ishraque MF, Shezan SA, Rana MS, Muyeen SM, Rahman A, Paul LC, Islam MS. Optimal Sizing and Assessment of a Renewable Rich Standalone Hybrid Microgrid Considering Conventional Dispatch Methodologies. Sustainability. 2021; 13(22):12734. https://doi.org/10.3390/su132212734
Chicago/Turabian StyleIshraque, Md. Fatin, Sk. A. Shezan, Md. Sohel Rana, S. M. Muyeen, Akhlaqur Rahman, Liton Chandra Paul, and Md. Shafiul Islam. 2021. "Optimal Sizing and Assessment of a Renewable Rich Standalone Hybrid Microgrid Considering Conventional Dispatch Methodologies" Sustainability 13, no. 22: 12734. https://doi.org/10.3390/su132212734
APA StyleIshraque, M. F., Shezan, S. A., Rana, M. S., Muyeen, S. M., Rahman, A., Paul, L. C., & Islam, M. S. (2021). Optimal Sizing and Assessment of a Renewable Rich Standalone Hybrid Microgrid Considering Conventional Dispatch Methodologies. Sustainability, 13(22), 12734. https://doi.org/10.3390/su132212734










