Investigations of a Weathered and Closely Jointed Rock Slope Failure Using Back Analyses
Abstract
:1. Introduction
2. Principles of Analysis
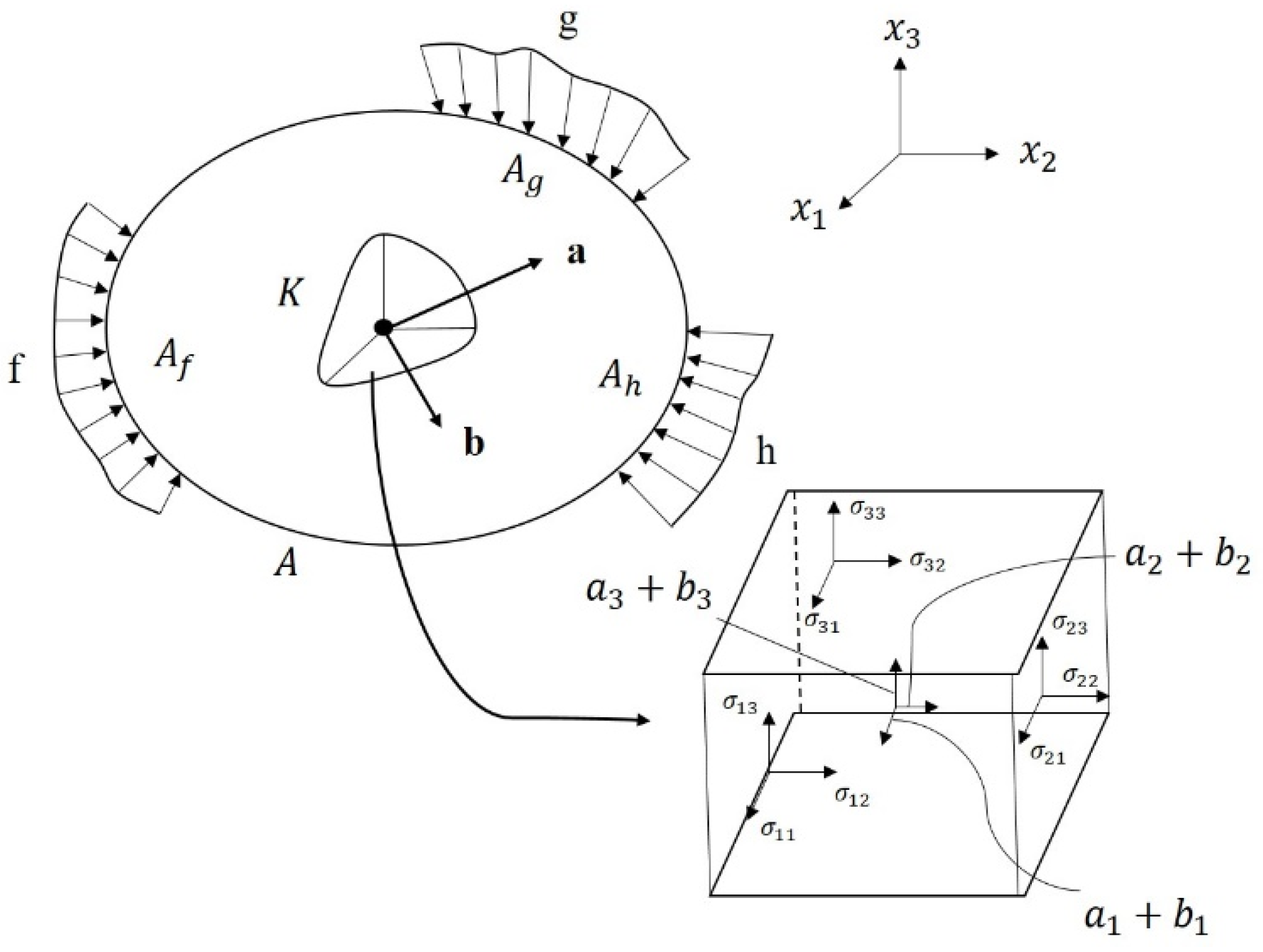
2.1. Finite Element Limit Analysis (FELA)
2.2. Hoek–Brown Failure Criterion
3. Description and Numerical Analysis Model of the Case Landslide
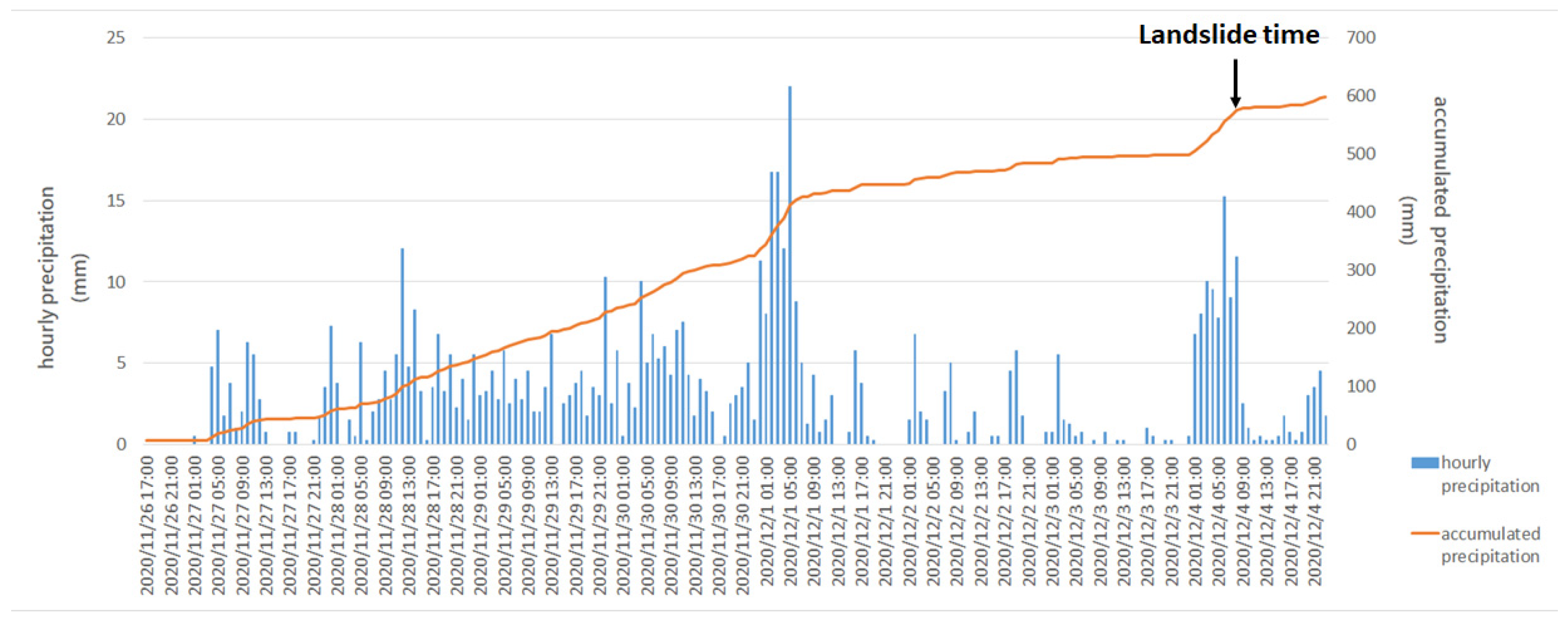
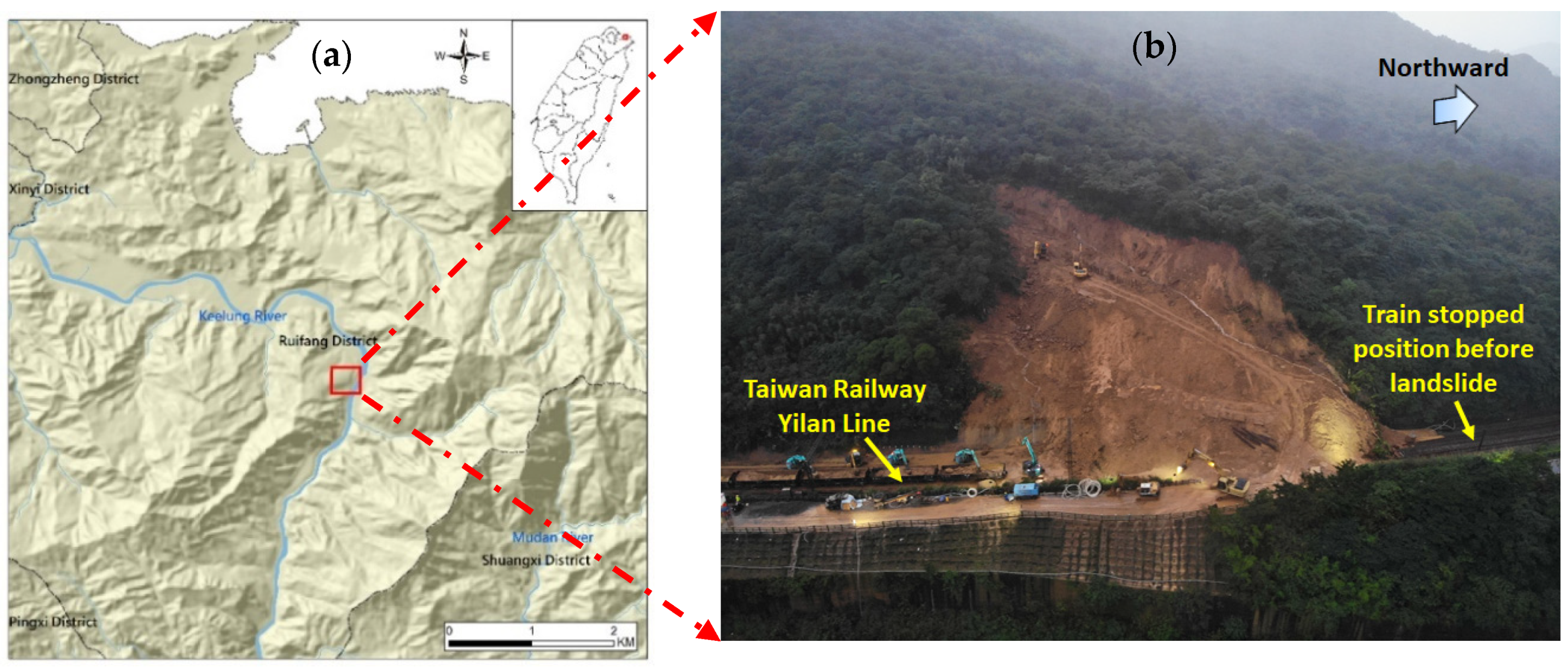
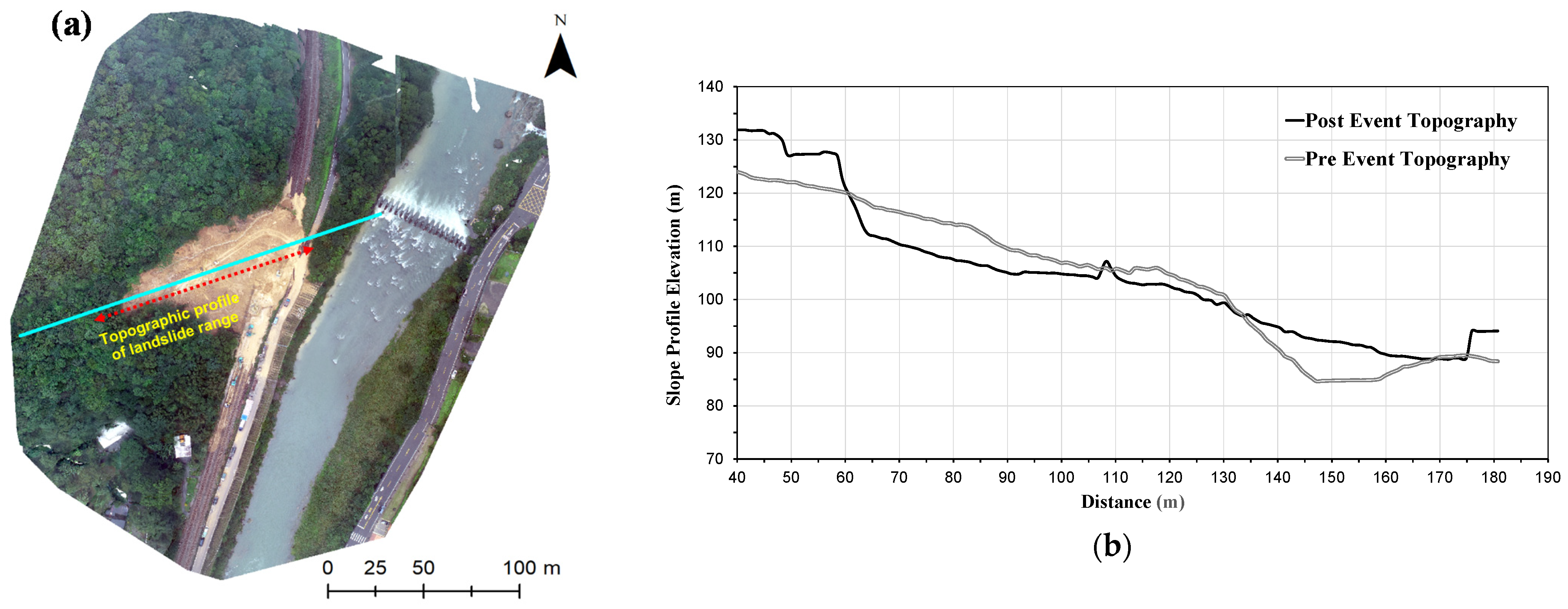
3.1. Description of the Case Landslide
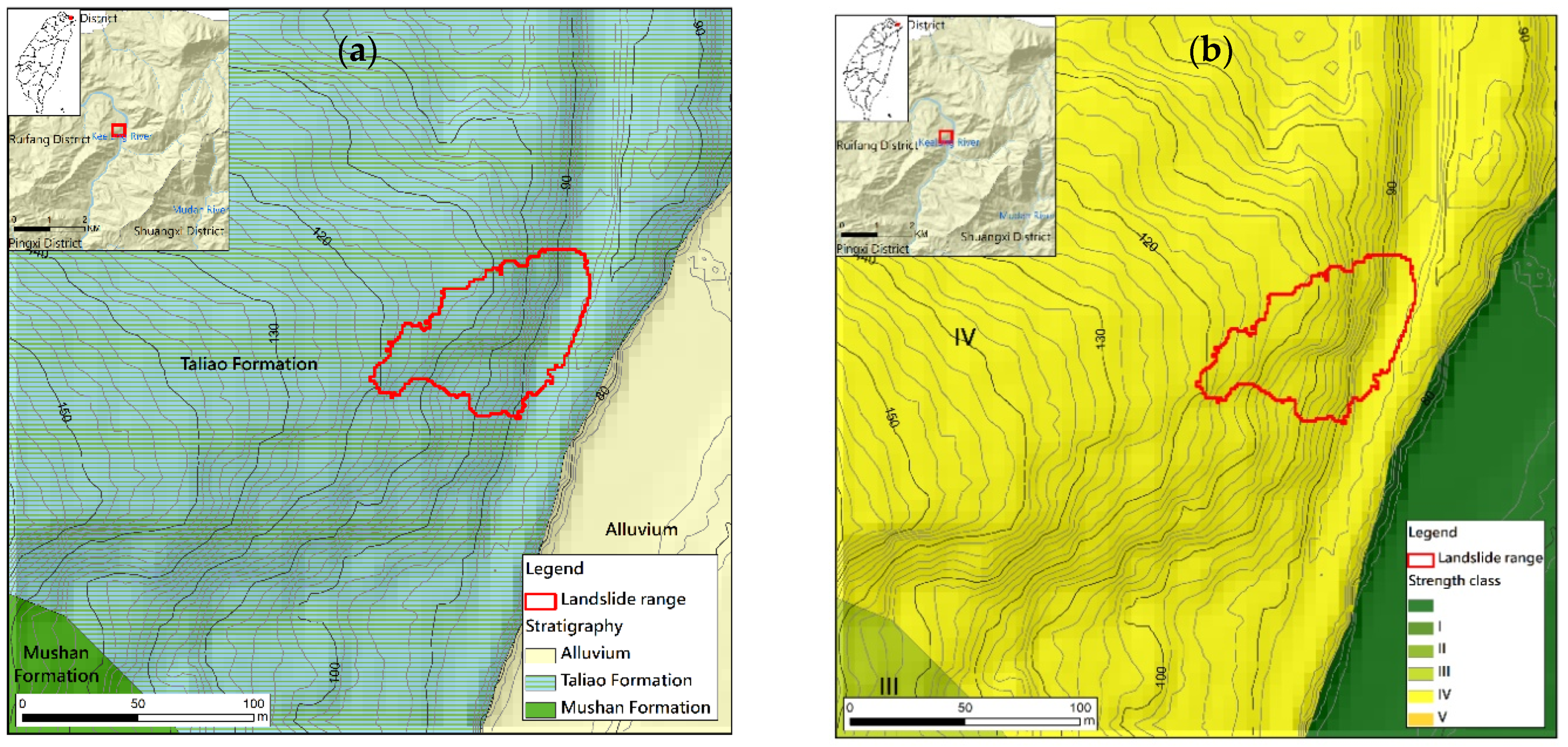
3.2. Topography and Geology of the Landslide Area
3.3. Development of a Finite Element Limit Analysis (FELA) Model and Its Parameters for the Slope
4. Examination of Key Factors Pertaining to the Stability of Closely Jointed and Weathered Rock Mass Slopes
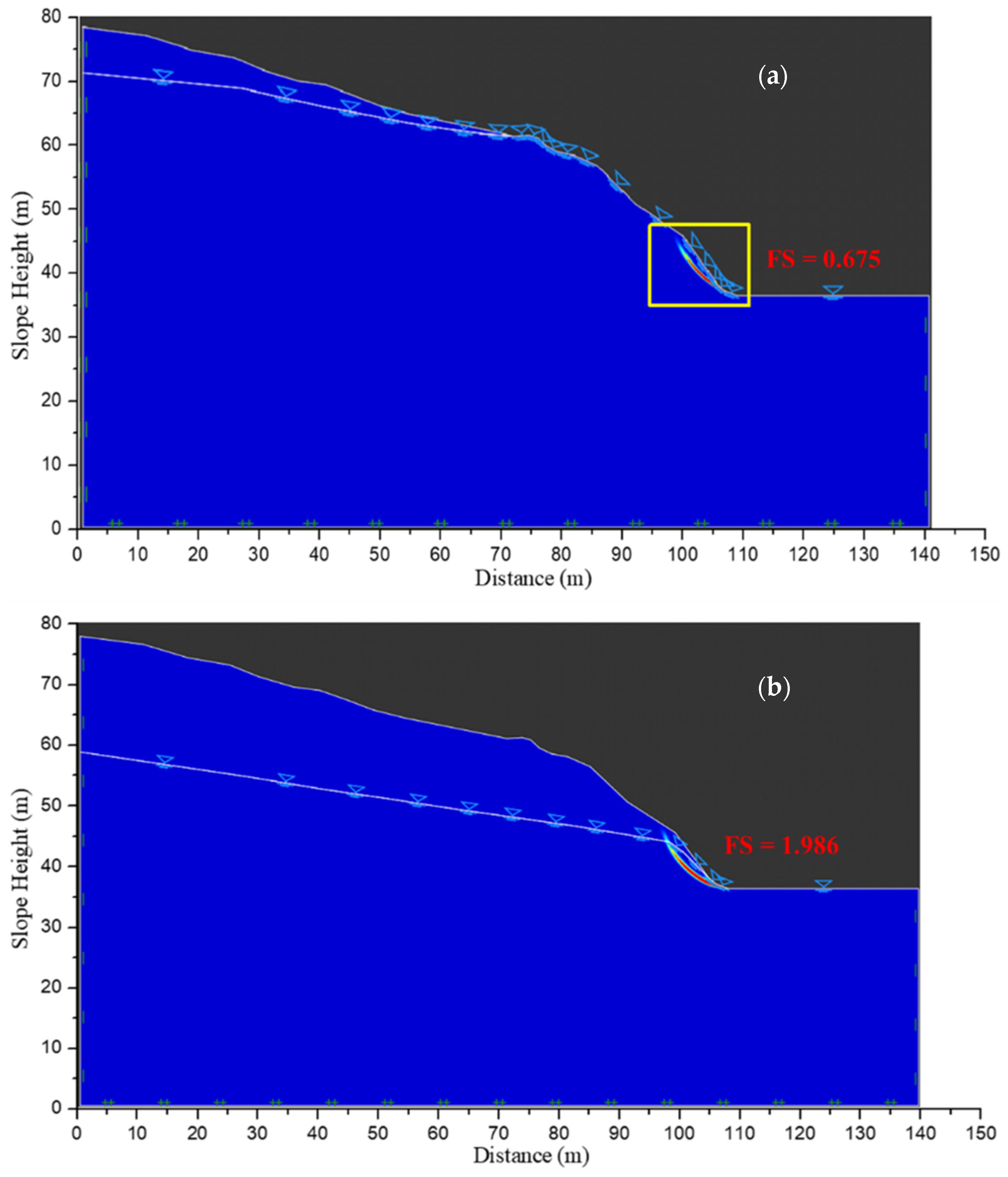
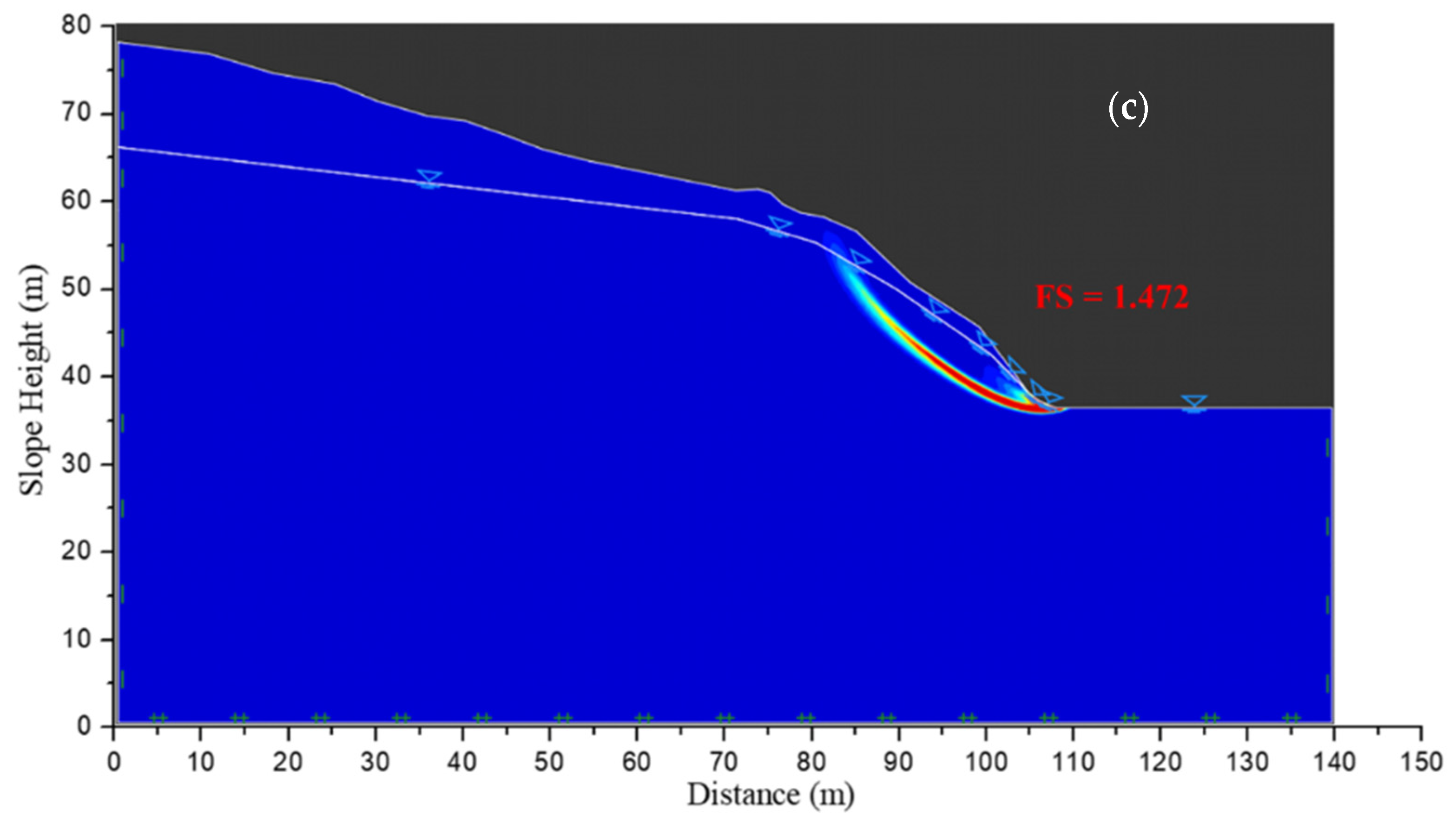
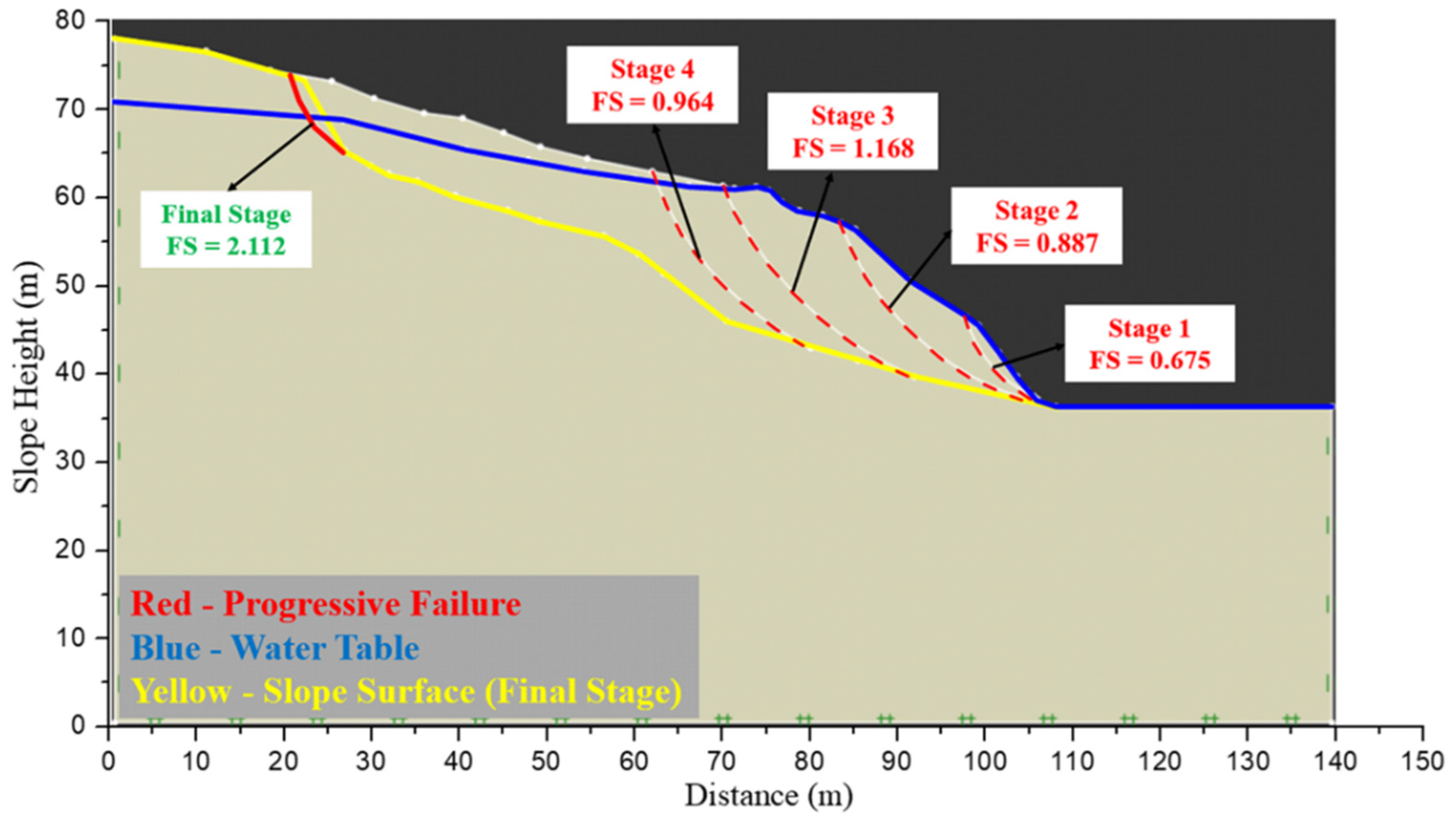
4.1. Comparison of the Numerical Simulation Results with Actual Rock Slope Failures
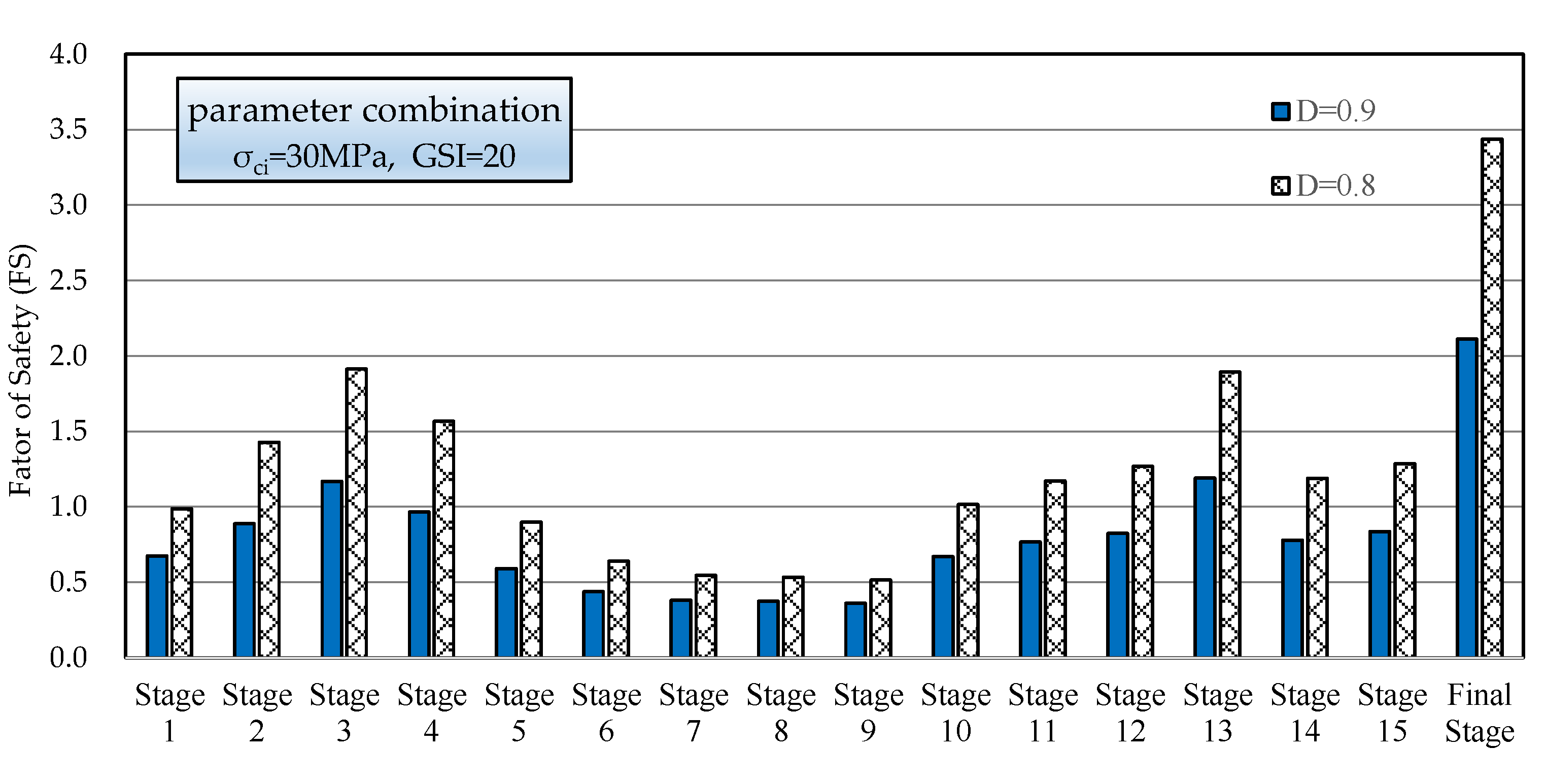
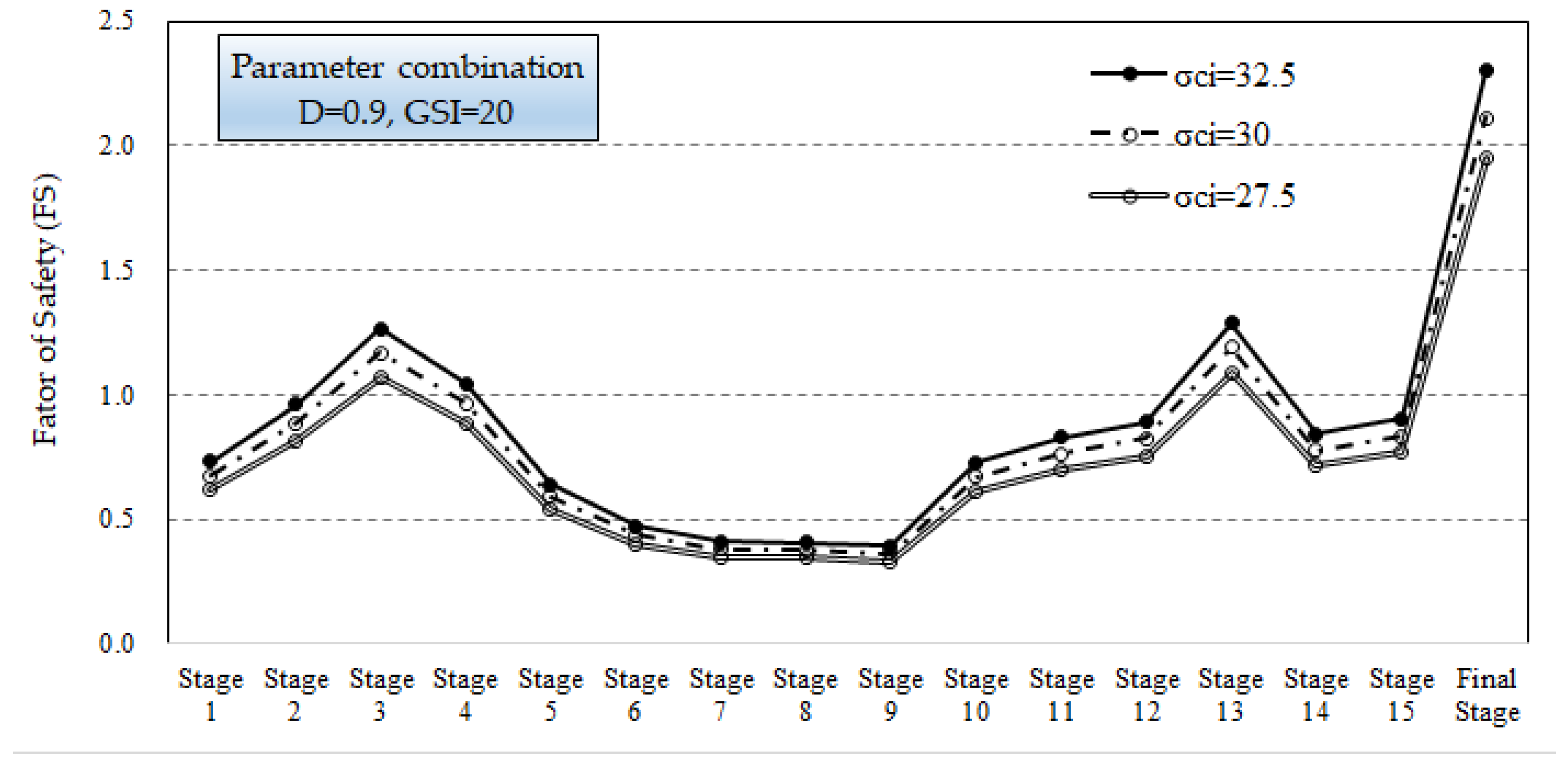
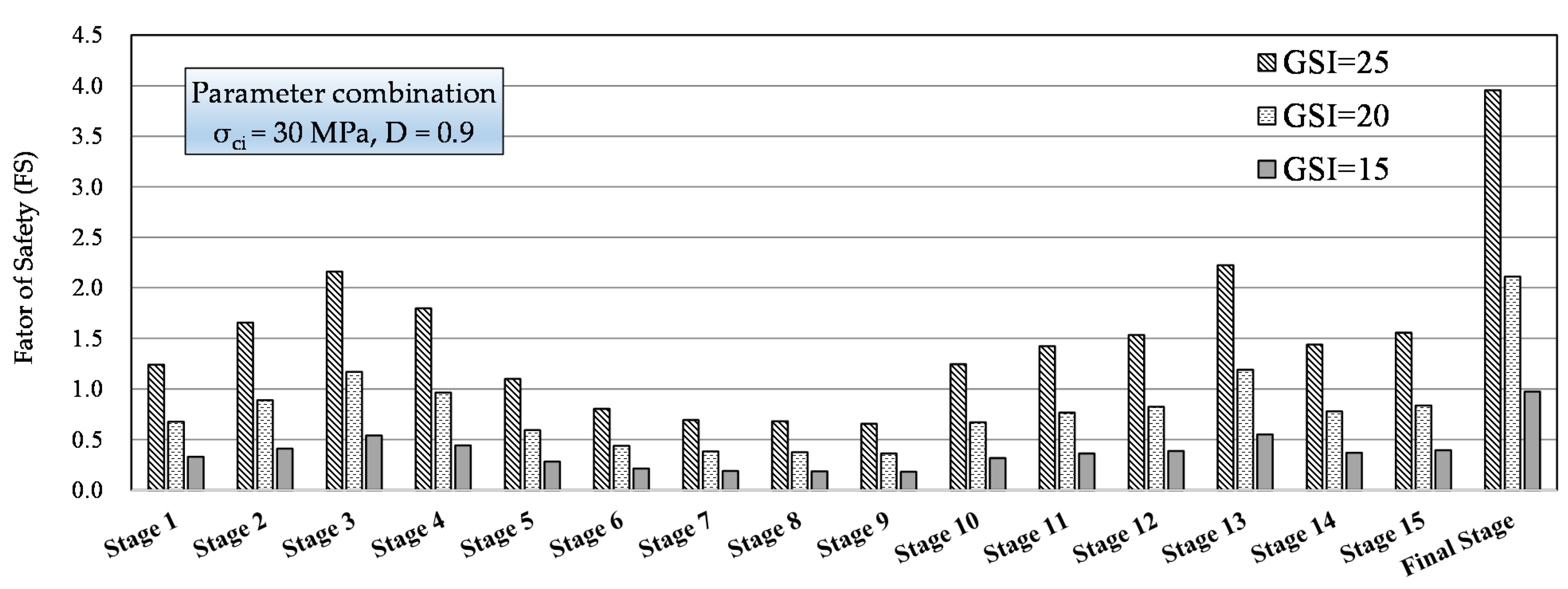
4.2. Examination of the Key Parameters of the Hoek–Brown Failure Criterion in Rock Slope Stability Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chu, H.T.; Lee, J.C.; Bergerat, F.; Hu, J.C.; Liang, S.H.; Lu, C.Y.; Lee, T.Q. Fracture patterns and their relations to mountain building in a fold-thrust belt: A case study in NW Taiwan. Bull. Soc. Géol. Fr. 2013, 184, 485–500. [Google Scholar] [CrossRef] [Green Version]
- Lacombe, O. Paleostress magnitudes associated with development of mountain belts: Insights from tectonic analyses of calcite twins in the Taiwan Foothills. Tectonics 2001, 20, 834–849. [Google Scholar] [CrossRef] [Green Version]
- Varnes, D.J. Landslide Hazard Zonation: A Review of Principles and Practice. Nat. Hazards 1984, 3, 63. [Google Scholar] [CrossRef]
- Sidle, R.C.; Pearce, A.J.; O’Loughlin, C.L. Hillslope stability and land use. Water Resour. Monogr. 1985, 11, 140. [Google Scholar]
- Carrara, A.; Cardinali, M.; Detti, R.; Guzzetti, F.; Pasqui, V.; Reichenbach, P. GIS techniques and statistical models in evaluating landslide hazard. Earth Surf. Processes Landf. 1991, 16, 427–445. [Google Scholar] [CrossRef]
- Koukis, G.; Ziourkas, C. Slope instability phenomena in Greece: A statistical analysis. Bull. Int. Assoc. Eng. Geol. 1991, 3, 47–60. [Google Scholar] [CrossRef]
- Guzzetti, F.; Carrara, A.; Cardinali, M.; Reichenbach, P. Landslide hazard evaluation: A review of current techniques and their application in a multi-Scale study, central Italy. Geomorphology 1999, 31, 181–216. [Google Scholar] [CrossRef]
- Lee, S.; Min, K. Statistical analysis of landslide susceptibility at Yongin, Korea. Environ. Geol. 2001, 40, 1095–1113. [Google Scholar] [CrossRef]
- Brenning, A. Spatial prediction models for landslide hazards: Review, comparison and evaluation. Nat. Hazards Earth Syst. Sci. 2005, 5, 853–862. [Google Scholar] [CrossRef]
- Ahmad, H.; Chen, N.S.; Rahman, M.; Islam, M.M.; Pourghasemi, H.R.; Hussain, S.F.; Habumugisha, J.M.; Liu, E.; Zheng, H.; Ni, H.; et al. Geohazards Susceptibility Assessment along the Upper Indus Basin Using Four Machine Learning and Statistical Models. Int. J. Geo-Inf. 2021, 10, 315. [Google Scholar] [CrossRef]
- Nanehkaran, Y.A.; Mao, Y.M.; Azarafza, M.; Koçkar, M.K.; Zhu, H.H. Fuzzy based multiple decision method for landslide susceptibility and hazard assessment: A case study of Tabriz, Iran. Geomech. Eng. 2021, 24, 407–418. [Google Scholar]
- Li, A.J.; Jagne, A.; Lin, H.D.; Huang, F.K. Investigation of slurry supported trench stability under seismic condition in purely cohesive soils. J. GeoEng. 2020, 15, 195–203. [Google Scholar]
- Lyamin, A.V.; Sloan, S.W. Upper bound limit analysis using linear finite elements and non-linear programming. Int. J. Numer. Anal. Methods Geomech. 2002, 26, 181–216. [Google Scholar] [CrossRef]
- Lyamin, A.V.; Sloan, S.W. Lower bound limit analysis using non-linear programming. Int. J. Numer. Methods Eng. 2002, 55, 573–611. [Google Scholar] [CrossRef]
- Krabbenhoft, K.; Lyamin, A.V.; Hjiaj, M.; Sloan, S.W. A new discontinuous upper bound limit analysis formulation. Int. J. Numer. Methods Eng. 2005, 63, 1069–1088. [Google Scholar] [CrossRef]
- Hoek, E.; Carranza-Torres, C.; Corkum, B. Hoek–Brown failure criterion-2002 edition. In Proceedings of the 5th North American Rock Mechanics Society Meeting, Toronto, ON, Canada, 7–10 July 2002. [Google Scholar]
- Hoek, E.; Brown, E.T. The Hoek-Brown failure criterion and GSI–2018 edition. J. Rock Mech. Geotech. Eng. 2019, 11, 445–463. [Google Scholar] [CrossRef]
- Pan, Y.; Wu, G.; Zhao, Z.Z.; He, L. Analysis of rock slope stability under rainfall conditions considering the water-induced weakening of rock. Comput. Geotech. 2020, 128, 10386. [Google Scholar] [CrossRef]
- Huang, C.C.; Yeh, S.H. Predicting periodic rainfall-induced slope displacement using force-equilibrium-based finite displacement method. J. GeoEng. 2015, 10, 83–89. [Google Scholar]
- Sonmez, H.; Ulusay, R.; Gokceoglu, C. A practical procedure for the back analysis of slope failures in closely jointed rock masses. Int. J. Rock Mech. Min. Sci. 1998, 35, 219–233. [Google Scholar] [CrossRef]
- Li, A.J.; Merifield, R.S.; Lyamin, A.V. Stability charts for rock slopes based on the Hoek–Brown failure criterion. Int. J. Rock Mech. Min. Sci. 2008, 45, 689–700. [Google Scholar] [CrossRef]
- Krabbenhoft, K.; Lyamin, A.; Krabbenhoft, J. Optum Computational Engineering (OptumG2) 2015. Available online: https://www.optumce.com (accessed on 20 August 2021).
- Huang, C.S.; Liu, H.C. Explanatory Text of the Geologic Map of Taiwan, Scale 1:50,000, Sheet 5, ShuangHsi; Central Geological Survey: New Taipei, Taiwan, 1988. [Google Scholar]
- Franklin, J.A. Size-Strength System for Rock Characterization; Geotechnical Ltd.: Orangeville, ON, Canada; Department of Earth Sciences University of Waterloo: Waterloo, ON, Canada, 1975. [Google Scholar]
- Liao, Y.S. Variations of Geotechnical Material Properties for In-Situ Specimen Test Results. Master’s Thesis, National Taiwan University of Science and Technology, Taoyuan, Taiwan, 2019. (In Chinese with English abstract). [Google Scholar]
- Marinos, P.; Hoek, E. GSI: A geologically friendly tool for rock-mass strength estimation. In Proceedings of the GeoEng2000 at the International conference on Geotechnical and Geological Engineering, Melbourne; Technomic Publishers: Lancaster, PA, USA, 2000; pp. 1422–1446. [Google Scholar]
- Marinos, P.; Hoek, E. Estimating the geotechnical properties of heterogeneous rock masses such as flysch. Bull. Eng. Geol. Env. 2001, 60, 82–92. [Google Scholar] [CrossRef]
- Marinos, V.; Carter, T.G. Maintaining geological reality in application of GSI for design of engineering structures in rock. Eng. Geol. 2018, 239, 282–297. [Google Scholar] [CrossRef]
- Shao, K.S. A Study of Monitoring and Deformation Behavior during Excavation Stage of Pinglin Tunnel. Master’s Thesis, National Central University, Taoyuan, Taiwan, 1997. (In Chinese with English abstract). [Google Scholar]
- Hoek, E.; Brown, E.T. Practical Estimates of Rock Mass Strength. Int. J. Rock Mech. Min. Sci. 1997, 34, 1165–1186. [Google Scholar] [CrossRef]
- Li, A.J.; Merifield, R.S.; Lyamin, A.V. Effect of rock mass disturbance on the stability of rock slopes using the Hoek-Brown failure criterion. Comput. Geotech. 2011, 38, 546–558. [Google Scholar] [CrossRef]
- Hoek, E. Reliability of Hoek–Brown estimates of rock mass properties and their impact on design. Int. J. Rock Mech. Min. Sci. 1998, 35, 63–68. [Google Scholar] [CrossRef]
- Azarafza, M.; Akgün, H.; Ghazifard, A.; AsghariKaljahi, E.; Rahnamarad, J.; Derakhshani, R. Discontinuous rock slope stability analysis by limit equilibrium approaches—A review. Int. J. Dig. Earth. 2021, 1–24. [Google Scholar] [CrossRef]
- Li, A.J.; Fatty, A.; Yang, I.T. Use of evolutionary computation to improve rock slope back analysis. Appl. Sci. 2020, 10, 2012. [Google Scholar] [CrossRef] [Green Version]






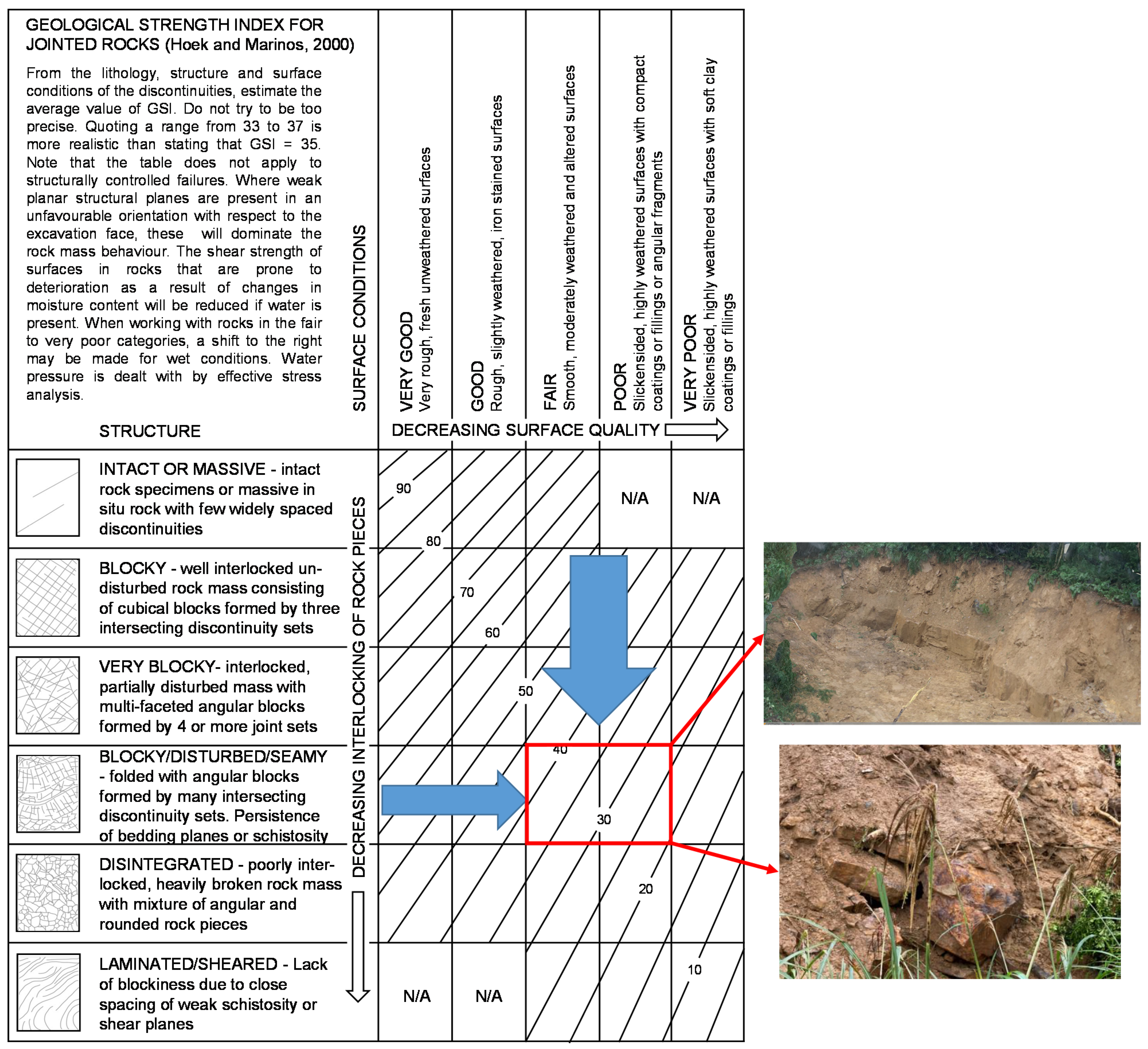

| Parameter | GSI | σci (MPa) | mi | D | γ (kN/m3) |
|---|---|---|---|---|---|
| Value Range | 15–40 | 25–35 | 15 | 0.7–0.9 | 25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, K.-S.; Li, A.-J.; Chen, C.-N.; Chung, C.-H.; Lee, C.-F.; Kuo, C.-P. Investigations of a Weathered and Closely Jointed Rock Slope Failure Using Back Analyses. Sustainability 2021, 13, 13452. https://doi.org/10.3390/su132313452
Shao K-S, Li A-J, Chen C-N, Chung C-H, Lee C-F, Kuo C-P. Investigations of a Weathered and Closely Jointed Rock Slope Failure Using Back Analyses. Sustainability. 2021; 13(23):13452. https://doi.org/10.3390/su132313452
Chicago/Turabian StyleShao, Kuo-Shih, An-Jui Li, Chee-Nan Chen, Chen-Hsien Chung, Ching-Fang Lee, and Chih-Ping Kuo. 2021. "Investigations of a Weathered and Closely Jointed Rock Slope Failure Using Back Analyses" Sustainability 13, no. 23: 13452. https://doi.org/10.3390/su132313452
APA StyleShao, K.-S., Li, A.-J., Chen, C.-N., Chung, C.-H., Lee, C.-F., & Kuo, C.-P. (2021). Investigations of a Weathered and Closely Jointed Rock Slope Failure Using Back Analyses. Sustainability, 13(23), 13452. https://doi.org/10.3390/su132313452







