Evaluating Distribution Costs and CO₂-Emissions of a Two-Stage Distribution System with Cargo Bikes: A Case Study in the City of Innsbruck

Abstract

During the last years, e-commerce has grown rapidly. As a result, the number of parcel deliveries in urban areas is increasing, which affects the inner-city traffic and leads to congestion and air pollution, thereby decreasing the quality of life in cities. City administrators and logistic service providers have been working on the optimization of parcel distribution in order to alleviate congestion and reduce the negative impact on the environment. One of the solutions for environmentally friendly parcel distribution are two-stage distribution systems with city hubs. City hubs are facilities located close to the delivery area which are used as an enabling infrastructure to store and consolidate the parcels. For the last mile delivery from the city hub to final customers, zero emission vehicles, such as cargo bikes, can be used. Many studies have been conducted on this topic in recent years. This paper contributes to this research area by evaluating the implementation of such a two-stage distribution system with a city hub and cargo bikes in Innsbruck, Austria. The goal is to determine the best location for a city hub and the composition of the delivery fleet by minimizing the total distribution and CO${}_2$-emission cost. E-vans are used for the first and cargo bikes for the second stage of the parcel delivery. The problem is modeled as a vehicle routing problem with multiple trips and is solved in ArcGIS Pro, using the built-in routing solver. The analysis shows that all hub candidates provide comparably good results, with one potential station, the main station, showing the highest improvement compared to the basic system, with delivery by conventional vans. Savings in distribution costs of up to 30% can be achieved. Furthermore, by taking into account both indirect and direct emissions with a well-to-wheel approach, CO${}_2$-emissions can be reduced by 96%.

1. Introduction

With e-commerce growing in popularity, the number of parcel deliveries increases, which leads to dense traffic situation in cities and urban areas. Furthermore, urban freight transportation is a contributor to global warming, as the transport and logistics sector accounts for 5.5% of total emissions resulting from human activity [1]. Negative externalities arise, such as traffic congestion, air pollution, noise, reduced safety, occupation of parking space and double parking on cycling infrastructure. These externalities in combination with climate goals that have to be met, motivate local authorities to implement innovative and sustainable city logistics systems.

1.1. Motivation and Goals

To overcome the challenge of reconciling the increasing demand of e-commerce as well as the environmental targets, many logistics service providers have started to act by collaborating and adopting environmentally friendly light vehicles such as cargo bikes. A smaller number and size of vehicles makes it possible to cope with the existing infrastructure in cities [2]. Cargo bikes are more adjusted to city traffic and are able to use bicycle lanes and avoid traffic congestion, thus allowing for a quicker movement through the city [3]. Additionally, deliveries with cargo bikes do not only help reduce CO${}_2$-emissions, but also result in less noise pollution, and the feeling of safety is improved as there is less traffic [4]. However, due to their comparatively low driving range and capacity, city hubs close to receivers are needed as enabling infrastructure for the transshipment from conventional vehicles to cargo bikes [5]. In a so-called two-stage distribution system, the parcels are delivered to a city hub from a regional distribution center and are afterwards distributed to the customers within the city.

In this paper, we analyze the option to implement such a logistic system with a city hub and cargo bikes for Innsbruck, Austria. Innsbruck is a small- to medium-sized city located in the alps next to the Inn river with an area of 104.9 square kilometers [6]. The population of Innsbruck is approximately 130,000 [7], of which 20- to 30-year-olds make up the largest share. According to [8], 80% of the online shoppers in Austria are 16 to 34 years old. Hence, Innsbruck is a city with a relatively high delivery volume for B2C parcel deliveries. However, Innsbruck’s geographic area poses a particular challenge for urban freight, as its topographical location leads to increased traffic congestion due to the overlapping of the various freight traffic flows without alternative routes. Furthermore, in Innsbruck’s pedestrian zones, which encompass an area of 1.34 km${}^2$ and over 6000 residents, vans are generally only allowed to drive and stop from 06:00 am to 10:30 am for the purpose of carrying out loading activities. New concepts are therefore needed to handle local freight traffic in a more resource-efficient way by using light vehicles and cooperation models.

The goal of this paper is to design a sustainable two-stage distribution system for the city of Innsbruck and evaluate it in terms of costs and resulting CO${}_2$-emissions. Three research questions are addressed: (1) Where should a city hub be located to reduce the costs of the two-stage distribution system in Innsbruck? (2) What is the best composition of vehicles for the first and the second stage? (3) How much cost and emissions can be saved by designing an effective city logistics system in comparison to the conventional delivery? Furthermore, the model has to comprise limited vehicle capacity, time windows and service time at the customers’ locations, as well as service time needed to load the parcels onto the vehicle at the depot. Moreover, working hours of drivers have to be respected and a mandatory lunch break has to be ensured.

1.2. Related Literature

This paper belongs to the area of transport optimization in city logistics. City logistics describes the efficient and effective distribution and transportation of goods in an urban area, considering different factors such as congestion, traffic, sustainability, emissions and customer convenience [9]. It addresses the logistics activities carried out in the last stage of the supply chain, the so-called last mile, in the urban environment [10]. The focus lies in optimizing these transportation activities through consolidation and coordination (see [11]). Approaches such as implementing a two-stage distribution system with a city hub are common examples of modern city logistics systems (see [12]).

A city hub acts as a transshipment point for goods (see [13,14]) and is used to sort and consolidate the dropped-off goods and store them until they are picked-up by carriers for the final distribution. In this way distribution inside a city or a city center is separated from the transportation outside the city [15]. Two-stage distribution systems with a city hub are more successful in small- to medium-sized cities comprising one hub zone that is small and close to the outskirts of the city (see [16]). For example, in Lucca, Italy, which has 87,000 inhabitants, a one-hub system to deliver to the city center has been tested and significant potential savings are reported [17]. Also, in Porto, Portugal, a city with 214,000 inhabitants, delivery with cargo bikes and one city hub is beneficial, according to [18]. However, the location of the city hub is of great importance for the success and profitability of the city logistics system, as it must be close to the urban center. By optimizing the location of warehouses or city hubs, and efficiently routing the vehicles through the city, costs and emissions can be reduced. A successfully running one-hub system is in use in Maastricht in the Netherlands, which has a population of 122,000 [19].

City hubs are often used in combination with cargo bikes for last mile delivery. The advantages of using cargo bikes as a sustainable transportation mode in urban freight distribution are numerous. The small size of the cargo bikes increases the flexibility of the vehicles in the city in general [20]. Their agility allows them to react to urgent route changes or local traffic congestion, thereby saving time and money. This is accompanied by the ability to stop the cargo bike almost everywhere and to park it on the sidewalk, thus exempting them from searching a parking space [21]. The reduced service time due to the parking ability closer to the customers, is a main advantage of cargo bikes, decreasing the overall delivery time and cost [22]. Hence, cargo bikes are the better choice in the right setting, i.e., in congested cities, or those with limited parking spaces. They are the most cost effective for urban areas with a high density of residential units and low delivery volumes per stop. Around half of the commercial trips in cities can be performed by cargo bikes without delaying the delivery by more than 2 to 10 min, compared to vans Ref. [23]. Furthermore, being less affected by traffic and parking constraints, cargo bikes allow a more precise travel time calculation, increasing the accuracy of delivery time prediction [24].

Considering a two-stage distribution system with a city hub and cargo bikes can lead to substantial decrease in CO${}_2$-emissions. In Ref. [25], the authors estimated the emissions of a two-stage distribution system to around 62% and 81% of those of the basic distribution system without a hub. In Lucca, Italy, an estimate of average yearly savings of about 50 tCO${}_2$ when implementing a city hub with light electric vehicles considering a well-to-wheel approach were reported Ref. [17]. In Ref. [22], the authors compared the emissions of cargo bikes against conventional vans and reported reduced emissions of up to 66%, when using a truck for the first stage. In Copenhagen, Denmark, the environmental and financial performance of a city hub was monitored, while evaluating the potential environmental benefits Ref. [26]. The authors report emissions savings of 68% up to 72% when replacing the previously used delivery trucks with fossil-fueled light truck. This is achieved by reducing the number of vehicles in total (by 61%) and at the same time the total distance driven (by 67%).

This paper is also closely related to the field of vehicle routing problems (VRP). The classical VRP aims at finding the optimal routes for a fleet of vehicles serving a set of spatially distributed customers while minimizing total travel costs (see [13,27]). Vehicles are assigned to one depot, which is the start and ending point of their tours. All customers must be served by a vehicle while respecting operational constraints. The VRP extension used in city logistics is the two-echelon vehicle routing problem (2E-VRP). This model represents the two-stage distribution system, where the goods are first delivered from the regional distribution center (RDC) to the city hub, and separately distributed from the city hub to the end customers [28]. The 2E-VRP aims at determining the size of the vehicle fleets and the routes in both echelons that minimize the costs. In Ref. [29], a problem was considered where the location of the city hub facilities is known but the location of the satellite facilities, as well as the number of vehicles on each level and their routes need to be determined. The purpose of the paper was to develop an efficient algorithm for the 2E-VRP. A detailed analysis of two-echelon systems and the impact of parameters on total cost was studied in [30]. In this paper different locations of the depot, the satellites, the impact of customer locations and the number of satellites was investigated. The authors concluded that the 2E-VRP performs better compared to classical distribution, i.e., the solution of a vehicle routing problem, when the depot is located externally with respect to the customer area. The 2E-VRP is in general useful in city logistics where the RDC is not close to the delivery area and a city hub is implemented to keep the heavy vehicles outside the inner city (see [29,31]). Another extension of the VRP is the VRP with multiple trips [32]. In Ref. [33], a multi-trip vehicle routing problem with time windows and release dates was introduced. This variation of the VRP addresses a city logistics system with a hub and last mile delivery where vehicles perform several trips per day because of the limited capacity and fleet size. Further, the availability date of the parcels at the depot is variable and defined with a release date per customer demand. In Ref. [22], a problem was considered where cargo bikes are allowed to return to the depot to renew their load.

The remainder of the paper is organized as follows: First, the two-stage distribution system is introduced, covering the methodology and problem description, as well as the mathematical model that forms the basis of the subsequent analysis. Thereafter follows the numerical analysis, divided into data description and presentation of results. In Section 4 the results are discussed and contextualized, followed by a conclusion.

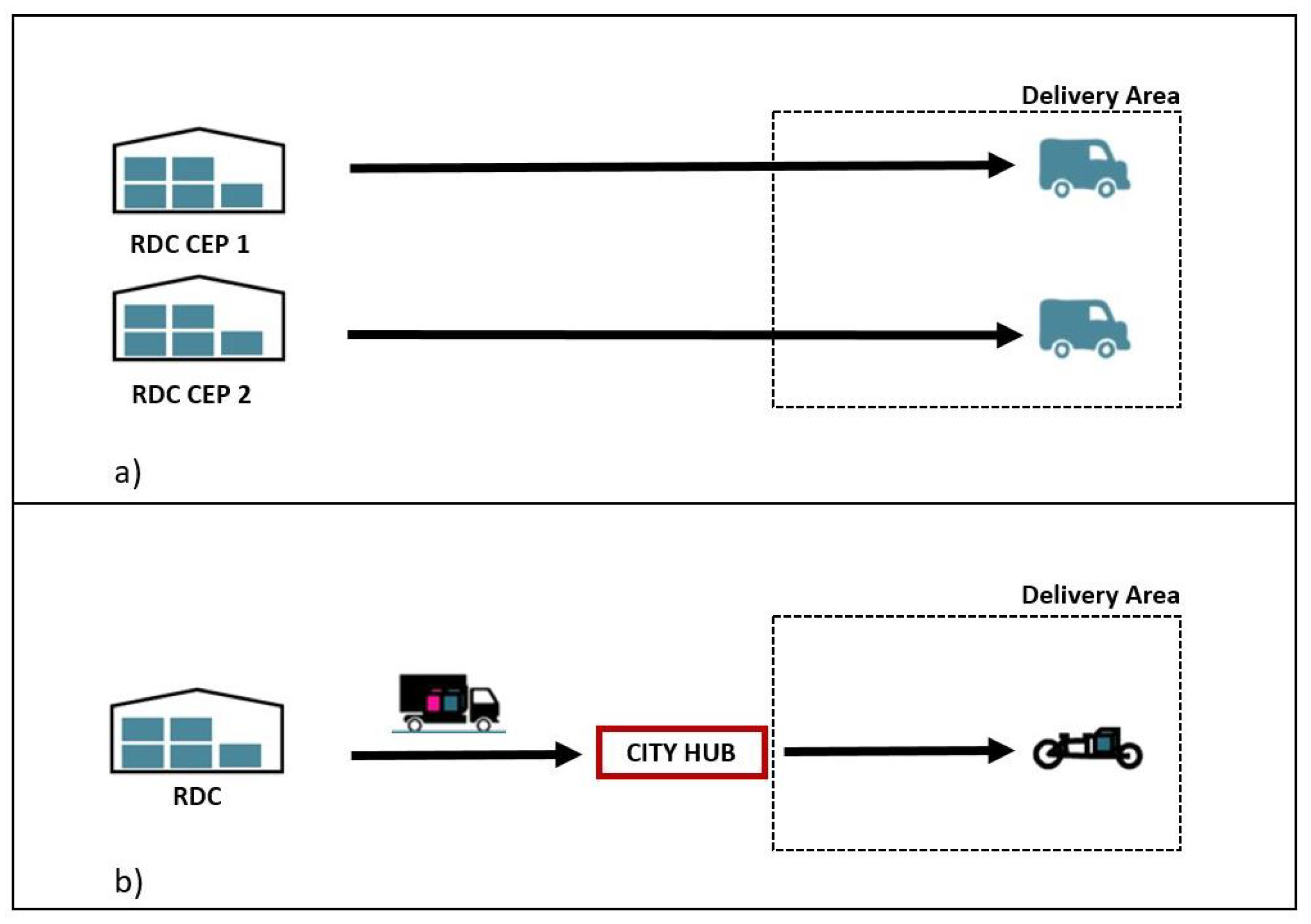
2. Two-Stage City Distribution System

In this paper we propose and evaluate a two-stage distribution system as a sustainable solution for parcel delivery in the city of Innsbruck. The new distribution system is evaluated in terms of costs and impact on the environment and the results are compared to the current distribution system used in the city.

2.1. Problem Description

The proposed two-stage distribution system and its difference from the basic concept is illustrated in Figure 1. Figure 1a shows the basic distribution system, where the parcels are distributed from a RDC directly to the end customers. Traditionally, the logistics service providers do not cooperate and/ or consolidate their shipments. Therefore, each logistics service provider manages and optimizes their own vehicle fleet individually. As a result, delivery vehicles belonging to different logistics service providers often traverse the same path from the regional distribution center to the delivery area, which not only leads to high costs and congestion, but also to high CO${}_2$-emissions, due to the non-environmentally friendly vehicles used for delivery. This problem is especially alarming in the city of Innsbruck, as several logistics service providers use the same compound for RDCs, thus a benefit from cooperation could be substantial.

Figure 1b illustrates a proposed solution for the distribution system problem, where delivery and distribution of parcels are carried out in 2 stages. In the first stage, the parcels are delivered from a joint RDC to a city hub, which is located close to the delivery area. In the basic concept, goods are delivered to delivery area by trucks or vans, however, the vehicles used for the first stage delivery could be environmentally friendly vehicles, such as electric trucks and vans. Electric vans have a limited battery range of about 130–220 km [34] currently, which would impose a challenge in their usage for direct delivery from a RDC to customers. However, as a round trip from a RDC to the city hub is substantially shorter than a daily tour, it is feasible to use the electric vans for this first stage delivery. In the city hub the parcels are reloaded onto short-distance vehicles for the final distribution in the city, such as (electric) cargo bikes. Due to their limited capacity, cargo bikes would complete several trips during the day, each time returning to the city hub, reloading the parcels and delivering them to the end customers.

2.2. Mathematical Model

The two-stage problem is formulated as a mixed integer linear program (MILP) with the objective function covering economic costs. The first stage problem includes the parcel delivery from the regional distribution center to a selected hub location, which is done by several pendulum tours. The second stage problem, i.e., last mile delivery from the selected hub location to the end customers, is formulated as a VRP with multiple trips. The model formulation for the second stage is based on formulations proposed in [33,35].

Let $N=\{1,\dots ,n\}$ be the set of customers that has to be served by a set of vehicles, $K=\{1,\dots ,m\}$. The homogeneous vehicle fleet consists of low-emission vehicles such as electric cargo bikes, which all have the same capacity Q. The vehicles are allowed to return to the depot to reload the parcels and are, hence, serving customers on multiple trips. Let set $R=\{1,\dots ,r^{max}\}$ denote the trips completed by vehicles throughout the day. Vehicles have a maximum working time of $T^{max}$.

Vehicles start and end their tour at the depot, i.e., the selected hub location. For modelling purposes, node 0 is used to denote the start and $n+1$ the end depot. Both 0 and $n+1$ are duplicates of the selected hub location. $N^I$ is used to denote the set of customers plus the starting depot, and $N^O$ the set of customers plus the end depot with $N^I=N\cup 0$ and $N^O=N\cup \{n+1\}$, respectively. Every driver has to make a 30 min rest break during the working day. The breaks are incorporated into the model by using an additional node $n+2$. Set $N^{\prime }$ is used to denote the customers plus the break node with $N^{\prime }=N\cup \{n+2\}$. The set of all vertices is defined with $V=\{0,\dots ,n+2\}$.

Service time of $s_i$ occurs at every node. Demand at each customer i is defined with $q_i$. Each customer has to be visited within a time window (TW). The start and end time of the time window at node i are given by $E_i$ and $L_i$, respectively. Time required for traveling between nodes i and j is denoted by $t{t}_{ij}$.

Distribution costs are expressed by using the following notation: Time-based costs of traveling from customer i to customer j are given by $t{c}_{ij}$. Distance-based costs include the operating costs as well as the emissions costs and are denoted by $d{c}_{ij}$. The fixed costs are given by $f_k$ and include the amortization and the maintenance of the cargo bike k. Furthermore, let $TC$ represent the transportation costs from the first stage delivery, dependent on the hub location. $TC$ comprises the total distribution costs for the pendulum tours from the regional distribution center to a selected hub location.

Binary variable $z_k$ indicates whether vehicle k is used for delivery or not. The assignment of customers to vehicles is modeled by binary decision variable $y_i^{rk}$, which is 1 if node i is visited by vehicle k on trip r and 0 otherwise. Binary flow variable, $x_{ij}^{rk}$, is equal to 1, if vehicle k travels from node i to node j on trip r, and 0 otherwise. Variable $a_i^{rk}$ represents the arrival time at node i by vehicle k on trip r.

The two-stage city distribution system problem can be formulated as follows:

$$min\sum _{i\in N^I}\sum _{j\in N^O}\sum _{r\in R}\sum _{k\in K}(t{c}_{ij}+d{c}_{ij})x_{ij}^{rk}+\sum _{k\in K}{f}_k{z}_k+TC$$

subject to

$$\begin{array}{cccc}\hfill & \sum _{r\in R}\sum _{k\in K}{y}_i^{rk}=1\hfill & \hfill & \forall i\in N\hfill \end{array}$$

(1)

$$\begin{array}{cccc}\hfill & \sum _{j\in N^{\prime }}{x}_{0j}^{rk}=\sum _{j\in N^{\prime }}{x}_{j,n+1}^{rk}\le 1\hfill & \hfill & \forall r\in R,k\in K\hfill \end{array}$$

(2)

$$\begin{array}{cccc}\hfill & \sum _{r\in R}{y}_{n+2}^{rk}=1\hfill & \hfill & \forall k\in K\hfill \end{array}$$

(3)

$$\begin{array}{cccc}\hfill & \sum _{j\in N^I}{x}_{ji}^{rk}=\sum _{j\in N^O}{x}_{ij}^{rk}\hfill & \hfill & \forall i\in N^{\prime },r\in R,k\in K\hfill \end{array}$$

(4)

$$\begin{array}{cccc}\hfill & \sum _{i\in N}{q}_i{y}_i^{rk}\le Q\hfill & \hfill & \forall r\in R,k\in K\hfill \end{array}$$

(5)

$$\begin{array}{cccc}\hfill & a_i^{rk}+s_i+t{t}_{ij}\le a_j^{rk}+(1-x_{ij}^{rk})M\hfill & \hfill & \forall i\in N^I,j\in N^O,r\in R,k\in K\hfill \end{array}$$

(6)

$$\begin{array}{cccc}\hfill & a_{n+1}^{rk}+s_{n+1}\le a_0^{r+1,k}+(1-\sum _{i\in N^{\prime }}{x}_{0j}^{r+1,k})M\hfill & \hfill & \forall r\in R|r\le r^{max}-1,k\in K\hfill \end{array}$$

(7)

$$\begin{array}{cccc}\hfill & E_i{y}_i^{rk}\le a_i^{rk}\le L_i{y}_i^{rk}\hfill & \hfill & \forall i\in N^{\prime },r\in R,k\in K\hfill \end{array}$$

(8)

$$\begin{array}{cccc}\hfill & a_{n+1}^{rk}-a_0^{r^{\prime }k}\le T^{max}\hfill & \hfill & \forall r,r^{\prime }\in R,k\in K\hfill \end{array}$$

(9)

$$\begin{array}{cccc}\hfill & \sum _{i\in N}\sum _{r\in R}{y}_i^{rk}\le z_{k}M\hfill & \hfill & \forall r\in R,k\in K\hfill \end{array}$$

(10)

$$\begin{array}{cccc}\hfill & x_{ij}^{rk}\in \{0,1\}\hfill & \hfill & \forall i,j\in V,r\in R,k\in K\hfill \end{array}$$

(11)

$$\begin{array}{cccc}\hfill & y_i^{rk}\in \{0,1\}\hfill & \hfill & \forall i\in N^{\prime },r\in R,k\in K\hfill \end{array}$$

(12)

$$\begin{array}{cccc}\hfill & z_k\in \{0,1\}\hfill & \hfill & \forall k\in K\hfill \end{array}$$

(13)

$$\begin{array}{cccc}\hfill & a_i^{rk}\ge 0\hfill & \hfill & \forall i\in V,r\in R,k\in K\hfill \end{array}$$

(14)

The objective function minimizes the transportation costs for both the first and the second stage of delivery. Constraints (1) make sure that every customer is visited, and constraints (2) ensure that a vehicle that leaves the depot for trip r also returns to the depot again. The break constraints are specified in (3). Constraints (4) are flow conservation constraints, and constraints (5) are capacity constraints for trip r of vehicle k. While constraints (6) compute the arrival time at each node, the connectivity of the tours is guaranteed by constraints (7), where M represents a big number. Constraints (8) ensure the feasibility with respect to the time windows and (9) to the maximum working time. Vehicle employment is determined with constraints (10). Finally, constraints (11)–(14) define domains of the decision variables.

2.3. Solution Method

To implement and solve the pendulum tours for the first stage and VRP with multiple trips for the second stage problem and the basic concept, ArcGIS Pro with the vehicle routing problem analysis layer is used. The layer is created from the network analysis toolset. ArcGIS Pro is a single desktop GIS application that supports data visualization, advanced analysis, data maintenance, and data sharing, among others. By applying location-based analytics such as finding patterns or optimizing routes, greater insights into the data can be gained [36]. To use the analysis layer in the network analysis tool, a street network must be connected [37]. The latter defines the underlying distances and traffic regulations needed to create the cost matrix when running the analysis (see

Table A5. VRP analysis layer settings—travel settings.

Feature	Cargo Bike VRP	Van VRP	E-Van VRP
Mode	Cargo bike cycling time (max 25 km/h)	Driving time	Driving time
Time Fields Unit	Minutes	Minutes	Minutes
Distance Fields Unit	Kilometers	Kilometers	Kilometers

). For this purpose, the online street network of ArcGIS is used by changing the network data source to ArcGIS Online. This is a ready-to-use street network with real time traffic data provided by Esri [36]. However, specific travel settings for cargo bikes and vans have to be defined and implemented manually (see

Table A1. Cargo Bike Travel mode.

ArcGIS Parameter	Selected	Option
Time Field Units		Minutes
Distance Field Units		Kilometers
Impedance		Travel Time
Type		Other
Time Cost		Travel Time
Distance Cost		Kilometers
Cost Parameter, Travel Time, Vehicle Max. Speed		25
Cost Parameter, Truck Travel Time, Vehicle Max. Speed		0
Cost Parameter, Walk Time, Vehicle Max. Speed		5
Any Hazmat Prohibited		Prohibited
Avoid Carpool Roads		Prohibited
Avoid Express Lanes	X	Prohibited
Avoid Ferries		Avoid
Avoid Gates	X	Avoid
Avoid Limited Access Roads	X	Prohibited
Avoid Private Roads	X	Prefer (low)
Avoid Roads Unsuitable for Pedestrians	X	Avoid (high)
Avoid Stairways	X	Avoid (high)
Avoid Toll Roads	X	Prohibited
Avoid Toll Roads for Trucks		Avoid (high)
Avoid Truck Restricted Roads		Avoid (high)
Avoid Unpaved Roads	X	Avoid (low)
Axle Count Restriction		Prohibited, 0
Driving a Bus (Does not include roads where buses are prohibited. Using this restriction will also ensure that the results will honor one-way streets.)		Prefer (high)
Driving a Taxi		Prefer (high)
Driving a Truck		Prohibited
Driving an Automobile		Prefer (low)
Driving an Emergency Vehicle		Prohibited
Height Restriction		Prohibited, 0
Kingpin to Rear Axle Length Restriction		Prohibited, 0
Length Restriction		Prohibited, 0
Preferred for Pedestrians	X	Prefer (medium)
Riding a Motorcycle		Prefer (high)
Roads under Construction Prohibited	X	Avoid (high)
Semi or Tractor with One or More Trailers Prohibited		Prohibited
Single Axle Vehicles Prohibited		Prohibited
Tandem Axle Vehicles Prohibited		Prohibited
Through Traffic Prohibited	X	Prefer (high)
Truck with Trailers Restriction		Prohibited, 0
Use Preferred Hazmat Routes		Prefer
Use Preferred Truck Routes		Prefer
Walking		Prohibited
Weight per Axle Restriction		Prohibited, 0
Weight Restriction		Prohibited, 0
Width Restriction		Prohibited, 0
U-Turns (agility)		All
Hierarchical road classification preferred		No
Simplify Output Geometry (max allowable offset that simplified line can deviate from original line)	X	10 m
Output Geometry		Along Network

and

Table A2. Van Travel Mode.

ArcGIS Parameter	Selected	Option
Time Field Units		Minutes
Distance Field Units		Kilometers
Type		Driving
Impedance		Travel Time
Time Cost		Travel Time
Distance Cost		Kilometers
Cost Parameter, Travel Time, Vehicle Max. Speed		0
Cost Parameter, Truck Travel Time, Vehicle Max. Speed		0
Cost Parameter, Walk Time, Vehicle Max. Speed		5
Any Hazmat Prohibited		Prohibited
Avoid Carpool Roads	X	Prohibited
Avoid Express Lanes	X	Prohibited
Avoid Ferries		Avoid
Avoid Gates	X	Avoid
Avoid Limited Access Roads		Avoid
Avoid Private Roads	X	Avoid
Avoid Roads Unsuitable for Pedestrians		Avoid (high)
Avoid Stairways		Avoid (high)
Avoid Toll Roads		Avoid
Avoid Toll Roads for Trucks		Avoid
Avoid Truck Restricted Roads		Avoid (high)
Avoid Unpaved Roads	X	Avoid (high)
Axle Count Restriction		Prohibited, 0
Driving a Bus (Does not include roads where buses are prohibited. Using this restriction will also ensure that the results will honor one-way streets.)		Prohibited
Driving a Taxi		Prohibited
Driving a Truck		Prohibited
Driving an Automobile		Prohibited
Driving an Emergency Vehicle		Prohibited
Height Restriction		Prohibited, 0
Kingpin to Rear Axle Length Restriction		Prohibited, 0
Length Restriction		Prohibited, 0
Preferred for Pedestrians		Prefer (low)
Riding a Motorcycle		Prohibited
Roads under Construction Prohibited	X	Prohibited
Semi or Tractor with One or More Trailers Prohibited		Prohibited
Single Axle Vehicles Prohibited		Prohibited
Tandem Axle Vehicles Prohibited		Prohibited
Through Traffic Prohibited	X	Avoid (high)
Truck with Trailers Restriction		Prohibited, 0
Use Preferred Hazmat Routes		Prefer
Use Preferred Truck Routes		Prefer
Walking		Prohibited
Weight per Axle Restriction		Prohibited, 0
Weight Restriction		Prohibited, 0
Width Restriction		Prohibited, 0
U-Turns (agility)		Dead-Ends and Intersections
Hierarchical road classification preferred		No
Simplify Output Geometry (max allowable offset that simplified line can deviate from original line)	X	10 m
Output Geometry		Along Network

). Further, to account for the multiple trips, an extra feature class is added to the analysis layer (see

Table A4. VRP analysis layer settings—route renewals feature class.

Feature	Cargo Bike VRP	Van VRP	E-Van VRP
RouteName	Bike n	Van n	eVan n
DepotName	Main station, west station, fair, congress	RDC	RDC
ServiceTime	10	30	30

). Here, the routes are linked to a depot where they will renew the load for the next trip. The solver in ArcGIS Pro then ensures the connectivity.

To model the first stage of the two-stage distribution problem with the e-van delivery, i.e., the pendulum tours, the tours between the RDC and each hub candidate are determined with ArcGIS Pro. The required number of e-vans is calculated for each hub location by measuring the time an e-van takes for one tour including start and end service time, and extrapolating that to the required numbers of deliveries within the capacity and time constraints.

The VRP with multiple trips in ArcGIS Pro is solved using a tabu search algorithm. As Esri, the company behind ArcGIS Pro, is the global market leader in GIS and location intelligence software [38], a performance estimation of the solver is beyond the scope of the paper. Tabu search is a local search metaheuristic and a well-structured algorithm that enables manageable implementations to solve various VRPs [39]. Solutions are examined sequentially, and the next move is made to the best neighbor based on the current solution. A neighbor is a solution that can be reached from the current solution by local modifications, such as changing one vertex within one or between 2 routes [27]. The algorithm gets its name from the tabu list, a short-term memory that stores recently visited solutions to make moves towards them tabu [40]. This measure prevents cycling, as solutions that are recently visited are forbidden. When a new best solution is found, the algorithm adds it to the tabu list and removes a solution in the list. Different strategies are used to enhance the solution quality and speed, including diversification and intensification. Intensification means that parts of the search space are explored more thoroughly, while diversification relates to forcing the search into unexplored areas of the search space. For every metaheuristic, a proper balance of these mechanisms is essential. The aspiration criterion in tabu search makes sure that tabu moves can be canceled for certain situations, for example if a new best-known solution is found.

ArcGIS Pro uses tabu search metaheuristics in combination with construction heuristics. The VRP solver first generates a cost matrix of the shortest paths along the network between all order and depot locations. Based on that, it constructs an initial solution, inserting the orders one at a time onto the most appropriate route. The initial solution is improved by changing the sequence of the orders in each route, moving orders from one route to another, and exchanging orders between routes [37].

3. Numerical Analysis

To evaluate a sustainable city hub distribution system in Innsbruck, a numerical analysis is performed. Data and assumptions for the analysis are collected using an extensive literature review and in collaboration with project partners.

3.1. Scope of the Study and Data Description

Similar to studies in other medium-sized cities (see [10,16,17,18,19]), the installation of one city hub for the distribution system is proposed. Therefore, the goal of the following analysis is to determine the best hub location from a set of hub location candidates.

The study area defines the region for the last mile delivery, i.e., where the customers are located. It cannot exceed a certain size to keep cargo bike delivery with one hub feasible. However, it must also be big enough to exploit the economies of scale. Because cargo bikes are more efficient in areas with a high density of residential buildings, we consider the population density of the city districts to determine an appropriate study area for the analysis (see [41]). The study area is defined and visualized in Figure 2. Similar to [42], a delivery radius of 3 km is maintained for the defined study area from the city hub candidates.

Cargo bikes must fulfill all demand within the study area, starting the delivery at one of the potential hub locations. The demand for parcels in the B2C sector is provided by the research project partners as annual demand per statistical sector. It was made available by a logistics service provider and modified accordingly to represent the daily demand. For the analysis in ArcGIS Pro, the averaged demand per city district must be transformed to demand points that represent individual receiver addresses. Therefore, when generating demand points, the demand per statistical sector is specified as the constraining feature class. Further, a factor of 1.3 parcels per stop for cargo bikes and 1.8 parcels per stop for vans is assumed (see [22]) to account for the case that one customer gets 2 or more parcels, or several customers are located in the same building.

This paper considers four potential city hub locations within the inner city of Innsbruck. They are well connected to high-ranked roads and railways making them easily accessible to delivery vans. Furthermore, they are located in close proximity to the geographical area they serve. Since the decision on the location of the hub is made in cooperation with the state of Tyrol, the hub candidates are all located in or near public buildings. Here, the local authorities like the city council or the state of Tyrol have storage rooms available or can create additional storage rooms as they manage the stated buildings. The potential four hub location candidates are the Innsbruck main station (Main St. or M, German: Hauptbahnhof), the Innsbruck west station (West St. or W, German: Westbahnhof), fair Innsbruck (F, German: Messe), and congress Innsbruck (C, German: Kongress).

3.2. Parameter Settings

For the implementation of the model in ArcGIS Pro, various parameters need to be defined. They are added as an input to the VRP and define the parameters and settings of the analysis. The parameters include technical information about cargo bikes such as speed or capacity, and practical experience with cargo bike delivery, e.g., the operating time per day. Furthermore, the first stage of the two-stage distribution system, i.e., the e-van delivery of the parcels from the regional distribution center to the city hub, as well as the van delivery as the base case scenario of the analysis must also be incorporated into the analysis. An overview of the assessed parameters required for the analysis is provided in

Table 1. Different parameter values for bike, van, and e-van delivery.

	Parameter	Cargo Bike	Van (Base Case)	E-Van (First Stage)
Travel	Max Speed	25 km/h	-	100 km/h
Depots	Locations	Main St., West St.	RDC	RDC
		Fair, Congress
Routes	Earliest Start Time	06:00:00	06:00:00	-
	Latest Start Time	08:00:00	08:00:00	-
	Start Depot Service Time	20 min	30 min	30 min
	End Depot Service Time	10 min	10 min	10 min
	Capacity	40 parcels	160 parcels	160 parcels
	Fixed Cost	15.00 €	30.00 €	40.00 €
	Cost Per Unit Time	0.33 €/min	0.33 €/min	0.33 €/min
	Cost Per Unit Distance	0.04 €/km	0.14 €/km	0.04 €/km
	Max. Total Distance	80 km	500 km	200 km
	Max. Total Time	480 min	480 min	480 min
Orders	Service Time	2 min	4 min	30 min
	Number Parcels per Stop	1.3 parcels	1.8 parcels	4154 parcels
	TW Start	-	(06:00:00)	-
	TW End	-	(10:30:00)	06:00:00
Route Renewals	Service Time	10 min	30 min	30 min

.

Scientific publications and reports from relevant projects are studied to collect the parameters. We compared the values found in the literature and, based on that, chose parameters for the implementation of the standard vehicle routing problem in ArcGIS Pro. Table 1 contrasts the different parameter values for cargo bikes, vans, and e-vans. Furthermore, the collected parameter values from literature are summarized in

Table A6. Parameters values.

Parameter	Literature	Chosen
Cargo bike speed	8 km/h [43]; 12 km/h [14]; 15 km/h [5], [4], [25]; 16 km/h [44], [23]; 17.6 km/h [25]; 15–25 km/h [46]; 20 km/h [18], [3]	Average 18 km/h; Max. 25 km/h
Cargo bike capacity	16 parcels [4]; 40 parcels [3], [22]; 1000 parcels for swap-containers [25]; 50 kg [46]; 50–250 kg [44]; 300–1300 L [23]	40 parcels
Cargo bike battery range	19–40 km [3]; 42 km [48]; 48 km [43]; 80 km [44]	80 km
Time per day	5 h [4]; 6 h [3]; 7h [43]; 7.5 h [22]; 8 h [5]; [44]	8 h
Deliveries per day	Average: 77 orders [44]; Min: 80 orders [46]; Average: 100–150 parcels, Max: 200–250 parcels [45]	Max. 200 orders
Delivery service time	2 min [46]; 2.5 min [14]; 3 min [22], [44]; 6–16 min [4]	2 min
Depot service time	24 min [22]; 96–132 min [44]	Start: 20 min; End: 10 min
Renewal depot service time	1 min per parcel [44]; 5 min [14]; 24 min [22]	10 min
Time-based costs	13.90 €/h [43]; 16.70 €/h [44]; 18 €/h [4]; 18 €/h [14]; 21 €/h [26]; 21.44 €/h [3]	20 €/h
Distance-based costs	0.01 €/km [43], [52], [18]; 0.024 €/km [44]; 0.04 €/km [4]	0.04 €/km
Fixed costs	10 €/day [4]; 12.88 €/day [44]; 47 €/day, including operating costs [3]	15 €/day

and explained in more detail below.

In the scientific literature, different values for cargo speed are assumed. The values for the average speed range from 8 km/h [43] to 20 km/h [18]. As we have to define the maximum bicycle speed in ArcGIS Pro, we choose the value of 25 km/h that is in line with the scientific literature and results in an average speed of about 18 km/h. In contrast, the vans’ speed limit is much higher and only follows the prescribed speed limit on the roads, which is included in the ArcGIS Online street network. However, vans have to respect the time windows for deliveries in the limited access zone of the inner city, where delivery is possible only between 6:00 am and 10:30 am.

Another important parameter is the capacity of cargo bikes. The cargo bike capacity varies depending on the type of the cargo bike and the type and size of product transported. Taking several sources into consideration, we assumed a capacity of 40 parcels (see [3,22]). About 160 parcels fit into a delivery van.

The depot service time varies based on the necessary tasks which have to be performed at the depot. For the analysis, a semi-sorted depot is assumed, resulting in an assumed depot service time of 20 min at the start, and 10 min to renew the load and at the end for the cargo bikes. Due to their higher capacity, the service time is greater for the vans (see Table A4). For the depot opening time, 06:00 am is assumed and the maximum allowable working time of the carriers is set to eight hours (see [5,44]). During this time, each carrier must take a 30-min break (see

Table A3. VRP analysis layer settings—breaks feature class.

Feature	Cargo Bike VRP	Van VRP	E-Van VRP
RouteName	Bike n	Van n	eVan n
Precedence	1	1	1
ServiceTime	30	30	30
TimeWindowStart	09:00	06:00	06:00
TimeWindowEnd	12:30	12:00	12:00
IsPaid	FALSE	FALSE	FALSE

). A maximum number of 200 stops per day is assumed for the analysis [45]. By setting that limit, it is ensured that the delivery quantity is feasible for the carriers. According to [14,46], it takes on average two minutes for a cargo bike driver to service a customer. A van driver, on the other hand, needs 4 min on average, because of the parking-difficulties in dense city environments, and the additional time needed to find a parking space and to walk from there to the receiver’s address [22].

Time-based costs include the drivers’ wage, which is assumed to be fixed. Typically, a cargo bike driver’s wage is lower than a van driver’s wage (see [4,46]). However, in order to obtain a fair comparison, we assume the same wages for cargo bike and van drivers.

The distance-based costs include the operating costs as well as the emissions costs. The chosen value of 0.04 €/km operating and emissions costs includes the electricity costs for charging the battery and for the caused emissions from the cargo bike delivery.

Equation (15) shows how the distance-based costs are calculated. Let $C_e$ represent the energy costs per kilometer. It is calculated from the fuel consumption per 100 km for a fossil-fueled van or from the kilometer range per kwh for an e-van or e-bike. The CO${}_2$ emission and the CO${}_2$ price per tCO${}_2$ are defined by $ϵ$ and $\rho$, respectively, and measured in tCO${}_2$ and €, respectively.

$$\mathrm{Distance}-\mathrm{Based}\mathrm{Cos}\mathrm{ts}=C_e+ϵ\ast \rho$$

(15)

The potential CO${}_2$-emissions savings are based on calculations, which are explained in the following. The emissions costs are measured based on a well-to-wheel approach, considering both the production and the operation of the energy. The Austrian CO${}_2$-emissions for the production of one kwh were 77 gCO${}_2$/kwh in 2020 [47] and the kilometer range per kwh is 112 km/kwh [48]. This results in 0.69 gCO${}_2$/km. Emissions costs of 25 € per ton CO${}_2$, which are already in place, for example in Germany, are assumed (see [49,50]).

The fixed costs include the amortization of the cargo bike and the battery, the costs for regular maintenance, and the costs for repairs. While a cargo bike operates commercially for trips six days a week and has a life cycle of five years, its battery must be replaced after about two years [46].

4. Analysis Results

In the first set of experiments, we compare the costs for the last mile delivery from the potential hub locations by using the data and parameters introduced in Section 3. We then change the parameters and perform a sensitivity analysis. Last, we report the total distribution costs and compare the solution to the basic delivery system with conventional vans.

4.1. Last Mile Delivery Results

The results for the last mile delivery from the four potential hub locations are shown in

Table 2. Evaluation of the costs for the last mile delivery for the 4 hub candidate locations.

Depot	Main Station	West Station	Fair	Congress
Stop Count	3193	3193	3193	3193
Parcel Count	4154	4154	4154	4154
Total Number of Bikes	23	24	24	24
Avg. Order Count per Bike	139	133	133	133
Avg. Parcel Count per Bike	180	173	173	173
Avg. Number of Renewals	4	3.8	3.8	3.8
Total Cost	3732.14 €	3797.07 €	3775.54 €	3810.38 €
Time Cost	3361.39 €	3408.15 €	3389.64 €	3423.83 €
Distance Cost	25.75 €	28.92 €	25.91 €	26.56 €
Total Time	181 h 16 m	184 h 8 m	183 h 12 m	184 h 55 m
Avg. Time per Bike	7 h 53 m	7 h 40 m	7 h 38 m	7 h 42 m
Total Travel Time	36 h 40 m	38 h 32 m	37 h 46 m	39 h 29 m
Avg. Travel Time Per Bike	1 h 36 m	1 h 36 m	1 h 34 m	1 h 39 m
Total Distance	643.7 km	723.0 km	647.6 km	663.9 km
Avg. Distance per Bike	28.0 km	30.1 km	27.0 km	27.7 km

. The total demand of 4154 parcels resulting in an order count of 3193 stops is fulfilled in all four scenarios. For west station, fair, and congress scenario 24 cargo bikes are needed for the delivery, whereas the main station scenario results in 23 required cargo bikes to fulfill the orders within the operational constraints. On average, bikes renew their load approximately four times during the day.

The total costs are the sum of the fixed, the time-dependent, and the distance-dependent costs (see Table 2: Total Cost). Total costs are the lowest in the case of the main station scenario with 3732.14 €, followed by the fair and the west station scenario, with 3775.54 € and 3797.07 €, respectively. The highest costs are reported in the case of congress with 3810.38 €. However, it can be seen that the difference in costs between the cheapest hub location and the most expensive location are only marginal. The main advantage of choosing the main station for the hub location is the number of cargo bikes needed for the last mile delivery: In this scenario only 23 cargo bikes are needed, whereas 24 vehicles are needed in other scenarios. In the main station scenario also the lowest total time and the associated time costs can be observed, as well as the total distance and the distance costs. The lower travel time for the main station hub makes it possible to serve all orders with one bike less than in other scenarios. Hence, the average time and distance per bike is higher than in the other three scenarios and the available time of 8 h is better utilized (see Table 2: Average Time per Bike).

4.2. Sensitivity Analysis

We use sensitivity analysis to examine how the results change when selected parameter values are varied. By changing the parameter values, conclusions about the design of the city logistics system, including the location of the hub and the characteristics of the vehicle fleet, can be validated. The modified parameters are the service time, the cargo bike capacity, the renewal time, the maximum total time per route, and the fixed and distance-based costs. Percentage changes of the system’s costs and other indicators are computed by comparing the new results to the results with default parameters (reported in Table 2). The percentage differences are calculated for all four potential hub locations and are then averaged to get the mean percentage change. The results are reported in

Table 3. Sensitivity analysis results—response to different parameter changes (in percent).

Parameter	Random Demand	Service Time: 3 min	Service Time: 3.5 min	Capacity: 30 parcels	Capacity: 50 parcels	Renewal Time: 20 min	Renewal Time: 5 min	Max. Time: 510 min	Fixed Cost: 20.00 €	Distance Cost: 0.01 €
No. Bikes	0.00	31.60	48.50	6.30	−7.00	13.00	−6.30	−7.30	0.00	0.00
Avg. no. Parcels	0.00	−24.00	−32.00	−5.90	7.60	−11.00	6.80	8.00	0.00	0.00
Avg. No. Renewals	−1.50	−25.00	−37.00	27.10	−18.00	−11.00	9.10	10.90	0.30	0.70
Total Cost	0.10	33.30	49.00	7.80	−5.70	10.50	−5.00	−0.90	3.30	−0.60
Time Cost	0.10	33.80	49.40	7.80	−5.50	10.30	−4.90	−0.20	0.20	0.00
Distance Cost	−0.90	2.30	0.50	20.60	−15.00	0.90	−1.50	−0.30	0.10	−74.00
Total Time	0.10	33.60	49.30	7.70	−5.60	10.50	−5.00	−0.70	0.20	0.00
Avg. Time per Bike	0.10	1.60	0.60	1.30	1.50	−2.30	1.50	7.20	0.20	0.00
Total Travel Time	0.90	3.10	0.70	19.30	−13.00	2.20	−0.50	0.30	0.70	−0.50
Avg. Travel Time per Bike	0.90	−21.00	−32.00	12.20	−6.70	−9.60	6.30	8.30	0.70	−0.50
Total Distance	−0.90	2.30	0.50	20.60	−15.00	0.90	−1.50	−0.30	0.10	3.30
Avg. Distance per Bike	−0.90	−22.00	−32.00	13.50	−8.80	−10.00	5.20	7.60	0.10	3.30

. Each column represents one changed parameter and the rows represent the performance indicators.

As demand points are randomly generated from average demand per statistical sector, their applicability must be evaluated. To do so, a second demand set with different locations is created. The total demand per statistical sector is still the same, only the locations of the random demand points are changed. The column Random Demand shows the results. As can be seen, no significant changes occurred when running the same model with slightly different demand data.

The service time per order, which is originally set to 2 min, is changed to 3 and 3.5 min (see Table 3: Service Time: 3 min and Service Time: 3.5 min). As the table shows, the change in the service time has great effects on the indicators. Increasing the delivery service time by 50% leads to an increase in the number of cargo bikes of 31.6%. If the service time is increased to 3.5 min, 50% more cargo bikes are required. To put that into absolute terms, the required number of cargo bikes for the main station increases from 23 to 31 with a service time of 3 min. For 3.5 min delivery service time, 35 bikes are needed to deliver entire demand in the study area. Also, the order count per bike decreases significantly. The travel time per bike is reduced because the carrier spends more time on service. Due to the increase in number of bikes, which leads to an increase in fixed costs, the total costs also grow by 33.3% and 49.0%, respectively, for a service time of 3 and 3.5 min.

The standard parameter for cargo bikes capacity is 40 parcels. For the sensitivity analysis, this parameter is changed to 30 parcels and 50 parcels. New solutions are presented in the fifth and sixth column of Table 3. If the capacity is decreased, the total cost increase, as more bikes are needed as they have to return to the depot more often. Hence, the average parcel count per bike decreases. Of the 8 working hours, more time is spent travelling back and forth to the hub to renew the load. A significant increase of about 20% can be observed for the renewal count, the total distance, and the travel time and costs. The opposite holds for increasing the capacity to 50 parcels. Again, the renewal count, the total distance, and the travel time and costs have the most significant changes. However, the improvements when increasing the capacity by 10 parcels are not as significant as the deterioration when the capacity is decreased by 10.

The third parameter changed is the renewal service time. In the standard model, the renewal time is 10 min. For the sensitivity analysis, this parameter is changed to 20 and 5 min (see Table 3: Renewal Time: 20 min and Renewal Time: 5 min). As expected, the number of bikes increases and the average order count per bike decreases, if more time is needed for renewal. The opposite is true for a shorter renewal time. Also, the number of renewals decreases or increases if the renewal time is doubled or halved, respectively. Reducing the renewal time by 5 min can reduce the total cost by 5%. Increasing it by 10 min increases the total costs by 10%, because more bikes are needed. The average travel time per bike decreases, since more time is used for renewal. Since the maximum allowable total time is usually the binding constraint, one analysis is conducted where the total time is increased by 30 min to 510 min, to consider the fact that in some cases the lunch break is not included in the 8 h contract. As a result, 7.3% fewer bikes are required, and 8% more parcels are delivered per bike (Table 3: Max. Time: 510 min). The number of renewals increases by over 10%, since a driver completes more tours during the extended working day. Also, the distance and the time per bike increase. Even through increasing the maximum total time by 30 min has big effects on some indicators, the total costs only change slightly. Since the positive and negative effects cancel each other out, the change in maximum total time does not have a significant effect on the total costs.

Changing the fixed cost, i.e. the daily cost for a cargo bike, including amortization and maintenance, does not greatly affect the analysis output. The standard parameter for fixed costs per bike is 15 €. For the sensitivity analysis, this value is changed to 20 €, leading to minor effects on most indicators (Table 3: Fixed Cost: 20.00 €). Even though the costs per bike increase, the number of bikes does not decrease. Due to the time constraint a feasible solution is not possible with fewer bikes, therefore, only the total costs increase.

Last, the distance-based costs are reduced to 0.01 €. As can be seen in Table 3: Distance Cost: 0.01 €, this change has a significant effect on the overall distance cost. With a decrease of the value by 75%, the overall distance costs are reduced by 74.2%. Additionally, the total distance increases by 3.3%, which has a small effect on the total travel time and thus the total cost. The other parameters are not much affected by the distance cost change.

4.3. Evaluation of the Two-Stage Distribution System

In

Table 4. Comparison of the two-stage distribution system and the basic system.

	Hub Solution with Cargo Bikes and E-Vans				Basic System
Depot	Main St.	West St.	Fair	Congress
Nr. Bikes and Vans	23 bikes,	24 bikes,	24 bikes,	24 bikes,	28 vans
	5 e-vans	5 e-vans	6 e-vans	6 e-vans
Total Cost	4639.16 €	4705.67 €	4763.83 €	4781.36 €	4860.81 €
Regular Time Cost	4050.57 €	4098.79 €	4121.19 €	4138.51 €	3907.95 €
Distance Cost	43.59 €	46.88 €	42.64 €	42.86 €	112.86 €
Emissions	8.4 kgCO${}_2$	8.5 kgCO${}_2$	9.9 kgCO${}_2$	9.0 kgCO${}_2$	242 kgCO${}_2$

we report the daily distribution costs for the first and second stage of the two-stage system as well as the caused emissions per day and compare the results with the basic system without city hubs. The latter is also modelled as a vehicle routing problem with the RDC as depot and vans for the routes. The costs for the first stage of the two-stage system are calculated as the total fixed, the time-dependent, and the distance-dependent costs for delivery of parcels from the RDC to potential depot locations. It is based on the distance between the RDC and the hub locations and the required time for an e-van to travel this route. It is noteworthy that the total costs are lower in the case of the two-stage distribution system for all four possible hub locations. For the first scenario, the difference between the costs for the most efficient hub location, i.e., the main station, and the basic system is 22,165 €. The least efficient hub location—the congress—results in a reduction of total cost of 79.45 €. Placing the hub at the west station or the fair could lead to potential financial savings of 155.14 € and 96.98 €, respectively. Also, the daily emissions of the distribution system can be reduced significantly to 8.4 kgCO${}_2$ in the best case and to 9.9 kgCO${}_2$ in the worst case, compared to 242 kgCO${}_2$ in the basic system. The emissions per day are determined based on the calculation explained in Section 3.2. While the current system needs 28 vans to fulfill the demand, the two-stage distribution system requires 23 cargo bikes and five e-vans in the best scenario with the main station hub.

Table 4 does not include the city hub costs. Most related studies in the literature do not consider depot costs when evaluating a two-stage distribution system (see [25,44]). The costs, however, play an important role when determining the efficiency of the whole system. According to [44], we need to consider additional costs for pre-sorting and handling of parcels at the city hub into individual loads for the bike carriers. Hiring an additional person for this task which would be employed daily for 8 h results in 160 € of fixed costs per day if the same wage as for the carriers is assumed. Renting a depot space that can fit about 4000 parcels can add up to about 60 € per day, which leads to potential hub costs of about 220 € per day. Adding the hub costs to the total costs of the system, the efficiency of the two-stage distribution system decreases. However, choosing the main station as a hub location is still as cost efficient as the basic system.

In order to investigate the financial and environmental savings that can be achieved, we designed three different scenarios for the main station case.

Table 5. Distribution costs for the main station scenario in the worst, realistic, and best case.

	Worst Case	Realistic Case	Best Case
Average Parcel Count per Bike	119	160	189
Difference in Costs compared to the Basic System	−1372.09 €	110.40 €	695.29 €
CO${}_2$-emissions Savings	96.50%	96.50%	96.60%

gives an overview of the distribution costs in the worst case, the realistic case, and the best case scenario. For the realistic case, we assume that the vehicles can deliver the same number of packages in the two-stage model as in the basic model. Therefore, we used the adapted parameter Renewal Time of 20 min (see Table 3: Renewal Time: 20 min), because the number of packages per vehicle is about the same as in the basic system. The worst and best cases are also extracted from the sensitivity analysis, taking the cases with the greatest negative and positive change in total costs, i.e., the Service Time of 3.5 min where total costs are 49% higher than in the regular scenario and the parameter Capacity of 50 parcels, where the total costs are 5.7% lower. Since the same number of parcels delivered, namely 160 per day, is also reported by DHL (see [51]), the realistic case is more likely than the worst case scenario. The best case scenario can occur especially on days with high demand, such as the Christmas season. The respective financial and environmental differences compared to the basic system are reported.

The financial benefit of a two-stage system is only noticeable in the realistic and the best case scenario, however, without considering the costs for a city hub. When taking the assumed hub costs of 220 € into consideration, only the best case scenario results in a financial benefit. On the other hand, the emissions can be reduced by about 96% per year compared to the basic system. This holds for all four hub candidates, making them a worthwhile alternative to the basic system, even with higher costs.

The financial savings from the hub solution could be even higher in real life, as the driver’s wages are typically lower for bike carriers than for van drivers. The former are usually less qualified, needing less experience and no driver’s license. For a fair comparison in this paper,however, we assumed the same wage for the cargo and van drivers. Furthermore, e-vans and cargo bikes could be subsidized or a public support for the city hub could be obtained. Since the implementation of a two-stage distribution system is in the interest of the city of Innsbruck and the local authorities, subsidies could be negotiated, that could lead to a higher positive difference in cost compared to the basic system. Moreover, the attempt to de-congest the city and improve the cityscape through the adopting of cargo bikes could outweigh the slightly increased costs.

5. Discussion and Conclusions

In this paper a two-stage city logistics system in Innsbruck with one city hub, e-van delivery to the city hub and cargo bike delivery from the city hub to the final customers was evaluated. The study showed that by using cargo bikes for the inner-city delivery, annual emission reduction of about 96% or about 70 tCO${}_2$ can be achieved. Furthermore, the city’s streets are less congested, and the cityscape improves. This addresses the main concern of the city’s authorities and the project partners and can outweigh potentially higher economic costs. The study also showed that financial savings can be achieved, depending on the parameter values. In the best case scenario, the two-stage system outperforms the traditional system also in terms of daily total distribution costs by 695.29 €.

A comparison between four different potential city hub locations showed that the main station is the best city hub location for the defined study area, which minimizes total distribution costs. The differences to the other three hub candidates, however, were only marginal. To serve the delivery area in Innsbruck, counting ca. 4000 parcels, about 23 cargo bikes for the last mile delivery and five e-vans for the first stage were required, leading to the total distribution costs of 4639.16 €. The results depend on the chosen parameter values used in the analysis. Various parameter settings were tested in a sensitivity analysis, to ensure the robustness of the solution. Different logistics parameters, such as service time, cargo bike capacity, renewal time, and the maximum allowable time were modified in the course of the analysis. Furthermore, the fixed, time-based, and distance-based costs were increased or decreased to analyze the consequences for the solution output. It showed that small changes in the fixed or variable costs did not lead to significantly different total cost. The greatest reduction in last mile distribution cost can be achieved by reducing the renewal time, or by increasing the capacity, with savings of 5% and 5.7%, respectively.

To evaluate the two-stage distribution system, total distribution costs of both stages were compared to the distribution costs of traditional parcel delivery in Innsbruck carried out by conventional vans. Three scenarios were developed for the analysis: a realistic scenario, the best case scenario and the worst case scenario. In the realistic and the best case scenario total distribution costs could be reduced by 110.40 € and 695.29 € respectively. In the best case scenario, the surplus in the budget would be enough to finance the city hub. Comparing the base case and the two-stage distribution system in terms of emissions, relative annual emissions savings of about 96% or about 70 tCO${}_2$ could be recorded. Here, the well-to-wheel approach was considered, where both the direct and the indirect emissions caused by the delivery are incorporated. Because the initial delivery happened with conventional, fossil-fueled delivery vans, while the two-stage distribution system used e-vans and electrically assisted cargo bicycles which cause no direct emissions, the CO${}_2$-emission savings were significant. Furthermore, shorter ways within the inner city and increased utilization resulting from the consolidation of orders of different logistic service providers led to a higher savings potential. Additional positive impact of the two-stage delivery system would be de-congestion of the city and improvement the cityscape. Moreover, by exchanging vans with cargo bikes for parcel delivery it will allow potential employees without a drivers’ license to apply for the job, thereby helping to creating new employment opportunities.

One limitation of the study was the data used. Demand data was not available as point pattern data, but aggregated per statistical sector. Random demand points were generated to overcome this. Furthermore, data on parameter values and settings for the analysis were collected through a literature review, and not in the course of an empirical study.

Future work could focus on extending the model to incorporate additional constraints such as time windows for the orders. Then one of the main advantages of cargo bikes, the better planning accuracy, could be incorporated and evaluated in the comparison with traditional van-based delivery. Another avenue of future research is the design of a more efficient algorithm to solve the problem. In terms of evaluation, further environmental and social indicators could be included, since currently only CO${}_2$-emissions are used.