BEPU Analysis in LBLOCA Safety Review Calculation
Abstract
:1. Introduction
2. BEPU Methods
3. APPWR BEPU Evaluation Model and EM Verification
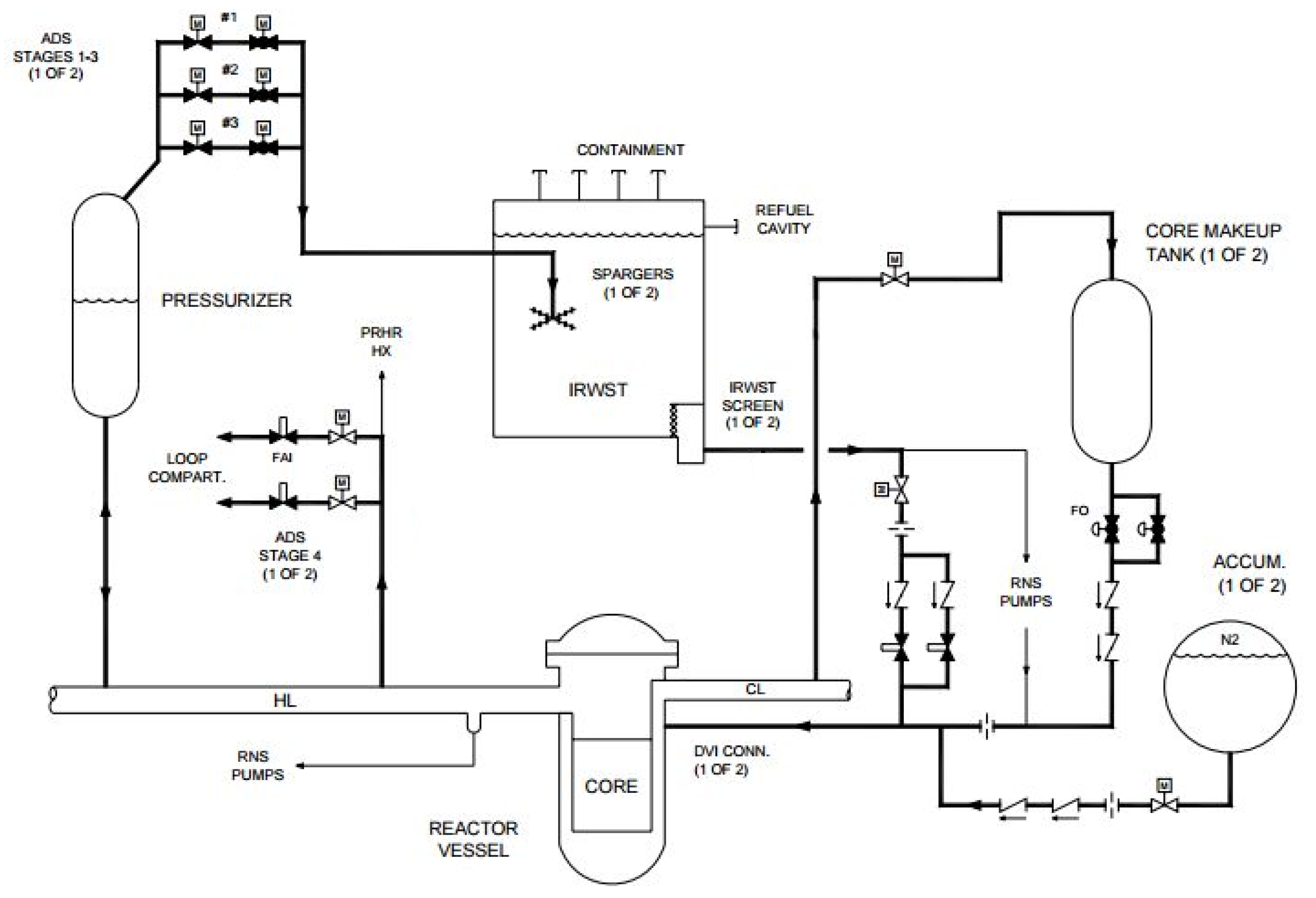
3.1. APPWR Introduction
3.2. Evaluation Models
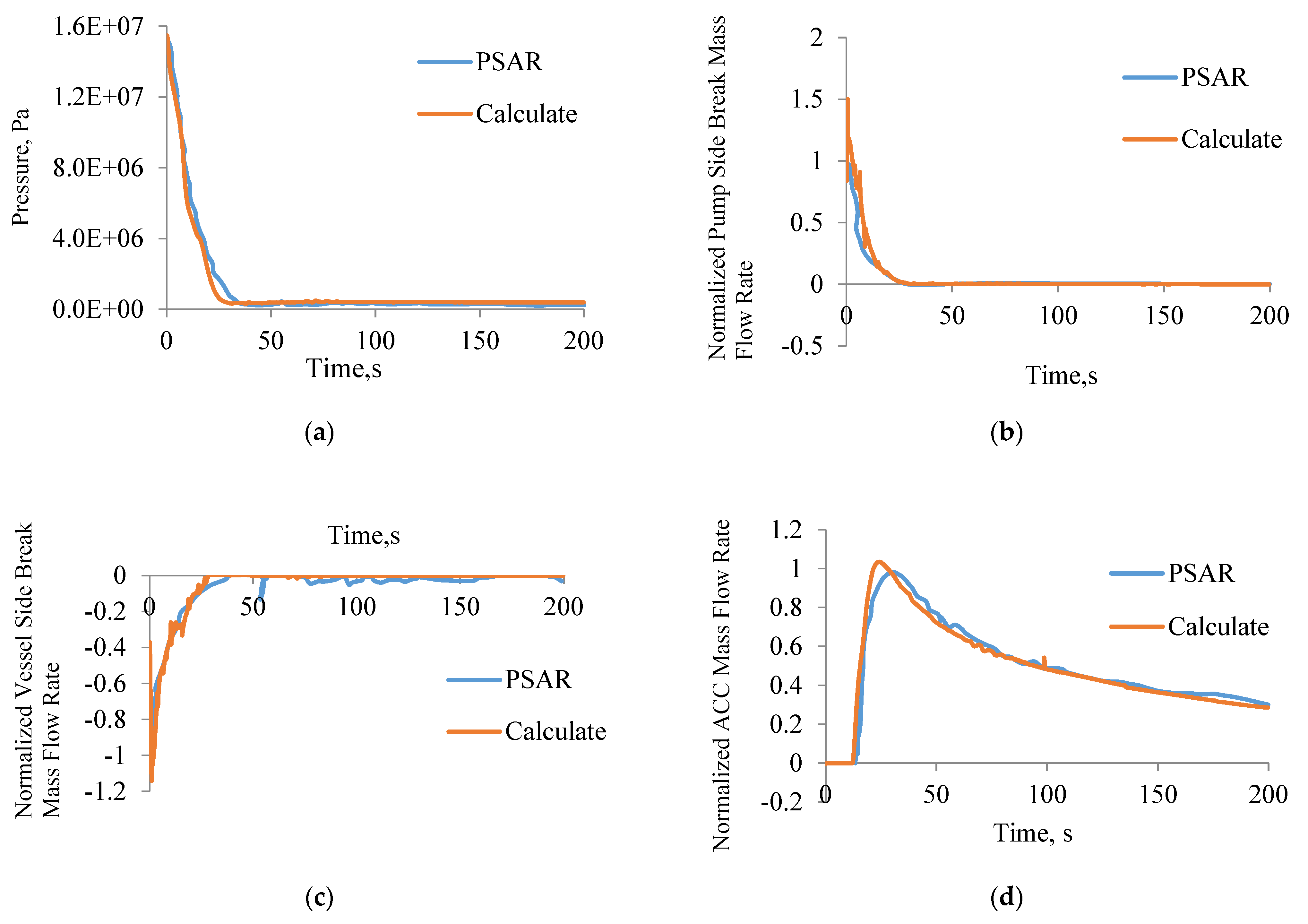
3.3. Model Verification of BEPU
4. APPWR BEPU Analysis
4.1. Uncertainty Parameters for BEPU Analysis
4.2. Uncertainty Analysis
4.3. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Roh, S.; Choi, J.Y. Exploring Signals for a Nuclear Future Using Social Big Data. Sustainability 2020, 12, 5563. [Google Scholar] [CrossRef]
- Cui, M.; Yi-Bao, L.; Liguo, Z. Application of Anticoincidence Technology to Burn-Up Measurement Systems in High-Temperature Gas-Cooled Reactors. Sustainability 2018, 10, 2883. [Google Scholar]
- Chajduk, E.; Kalbarczyk, P.; Dudek, J.; Pyszynska, M.; Bojanowska-Czajka, A.; Samczyński, Z. Development of Analytical Procedures for Chemical Characterization of Substrates for the Production of TRISO Coated Particles as Nuclear Fuel in High Temperature Gas-Cooled Reactors. Sustainability 2020, 12, 7221. [Google Scholar] [CrossRef]
- Di Ronco, A.; Giacobbo, F.; Lomonaco, G.; Lorenzi, S.; Wang, X.; Cammi, A. Preliminary Analysis and Design of the Energy Conversion System for the Molten Salt Fast Reactor. Sustainability 2020, 12, 10497. [Google Scholar] [CrossRef]
- International Atomic Energy Agency. Deterministic Safety Analysis for Nuclear Power Plants; IAEA Safety Standards Series No. SSG-2 (Rev.1); International Atomic Energy Agency: Vienna, Austria, 2019. [Google Scholar]
- Queral, C.; Montero-Mayorga, J.; Gonzalez-Cadelo, J.; Jimenez, G. AP1000 Large-Break LOCA BEPU analysis with TRACE code. Ann. Nucl. Energy 2015, 85, 576–589. [Google Scholar] [CrossRef]
- Frepoli, C. An Overview of Westinghouse Realistic Large Break LOCA Evaluation Model. Sci. Technol. Nucl. Install. 2008, 2008, 1–15. [Google Scholar] [CrossRef]
- D’Auria, F.; Camargo, C.; Mazzantini, O. The Best Estimate Plus Uncertainty (BEPU) approach in licensing of current nuclear reactors. Nucl. Eng. Des. 2012, 248, 317–328. [Google Scholar] [CrossRef]
- U.S. Nuclear Regulatory Commission. Quantifying Reactor Safety Margins: Application of Code Scaling, Applicability, and Uncertainty Evaluation Methodology to a Large-Break, Loss-of-Coolant Accidentl; NUREG/CR-5249; U.S. Nuclear Regulatory Commission: Washington, DC, USA, 1989. [Google Scholar]
- Sanchez-Saez, F.; Carlos, S.; Villanueva, J.F.; Sanchez, A.I.; Martorell, S. Uncertainty analysis of PKL SBLOCA G7.1 test simulation using TRACE with Wilks and GAM surrogate methods. Nucl. Eng. Des. 2017, 319, 61–72. [Google Scholar] [CrossRef] [Green Version]
- International Atomic Energy Agency. Best Estimate Safety Analysis for Nuclear Power Plants: Uncertainty Evaluation; Safety Reports Series No. 52; International Atomic Energy Agency: Vienna, Austria, 2008. [Google Scholar]
- Wilks, S.S. Order statistics. Bull. Am. Math. Soc. 1948, 54, 6–50. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.-L.; Wang, Z.; Wang, G.-D. Comparative Study on Statistical Methods for Application to Best-estimate plus Uncertainty Accident Analysis. At. Energy Sci. Technol. 2016, 1, 98–104. [Google Scholar]
- Somerville, P.N. Tables for Obtaining Non-parametric Tolerance Limits. Ann. Math. Statist. 1958, 29, 599–601. [Google Scholar] [CrossRef]
- Zheng, M.; Yan, J.; Jun, S.; Tian, L.; Wang, X.; Qiu, Z. The General Design and Technology Innovations of CAP1400. Engineering 2016, 2, 97–102. [Google Scholar] [CrossRef] [Green Version]
- Lin, S.-X.; Zhang, M.; Fang, Y.; Ding, Z.-H.; Yang, P.; Wang, S.; Zhang, W.; Liang, Y.-J. Overview of the CAP1400 Reactor Hydraulic Simulation Tests. In Proceedings of the 2017 25th International Conference on Nuclear Engineering. Volume 2: Plant Systems, Structures, Components and Materials, V002T03A085, Shanghai, China, 2–6 July 2017. [Google Scholar]
- Li, Y.-Q.; Chang, H.-J.; Ye, Z.-S.; Fang, F.-F.; Shi, Y.; Yang, K.; Cui, M.-T. Analyses of ACME Integral Test Results on CAP1400 Small-Break Loss-Of-Coolant-Accident Transient. Prog. Nucl. Energy 2016, 88, 375–397. [Google Scholar] [CrossRef]
- Shi, G.; Xu, C.; Yan, J.; Fan, P.; Yang, Z.; Cai, X.; Zhu, S. CAP1400 passive core cooling integral testing and application in code validation. Ann. Nucl. Energy 2021, 154, 107997. [Google Scholar] [CrossRef]
- Wang, W.-W.; Lu, L. Effect of Fuel Thermal Conductivity Degradation (TCD) on Large Break Loss of Coolant Accident for CAP 1000. At. Energy Sci. Technol. 2017, 1, 79–83. [Google Scholar]
- Hu, B.-X.; Wang, Z.; Wang, W.-W.; Wang, G.-D.; Wang, Z.-L.; Tang, G.-F.; Zhang, J.-Z.; Yang, P.; Liu, X. Application of Sampling Based Sensitivity Analysis in Evaluation of LBLOCA Mass and Energy Release PIRT. At. Energy Sci. Technol. 2016, 2, 290–294. [Google Scholar]
- Kang, D.-G. Analysis of LBLOCA using best estimate plus uncertainties for three-loop nuclear power plant power uprate. Ann. Nucl. Energy 2016, 90, 318–330. [Google Scholar] [CrossRef]
- Fernandez-Cosials, K.; Queral, C.; Robledo, F.; Sánchez-Perea, M. Analysis of a LBLOCA with FLEX actuations in a PWR-W. Nucl. Eng. Des. 2020, 370, 110908. [Google Scholar] [CrossRef]
- Yang, J.-H.; Lin, H.-T.; Wang, J.-R.; Shih, C. Evaluations of the CCFL and critical flow models in TRACE for PWR LBLOCA analysis. Kerntechnik 2012, 77, 442–448. [Google Scholar] [CrossRef]
- Deng, C.; Chen, L.; Yang, J.; Wu, Q. Best-estimate calculation plus uncertainty analysis of SBLOCA transient for the scale-down passive test facility. Prog. Nucl. Energy 2019, 112, 191–201. [Google Scholar] [CrossRef]
- Martínez-Quiroga, V.; Freixa, J.; Pérez-Ferragut, M.; Reventós, F. Significance of the Input Parameters Selection and the Nodalization Qualification in the Final Results of an IBLOCA BEPU Calculation. In Proceedings of the 11th International Topical Meeting on Nuclear Reactor Thermal Hydraulics, Operation and Safety, Gyeongju, Korea, 9–13 October 2016. [Google Scholar]
- Baccou, J.; Zhang, J.-Z.; Fillion, P.; Damblin, G.; Petruzzi, A.; Mendizábal, R.; Reventós, F.; Skorek, T.; Couplet, M.; Iooss, B.; et al. Development of good practice guidance for quantification of thermal-hydraulic code model input uncertainty. Nucl. Eng. Des. 2019, 354, 110173. [Google Scholar] [CrossRef]
- Nuclear Energy Agency/Organisation for economic co-operation and development. Uncertainty and Sensitivity Analysis of a LBLOCA in Zion Nuclear Power Plant; NEA/CSNI/R(2009)13; OECD/NEA: Paris, France, 2009. [Google Scholar]
- Young, M.-Y.; Bajorek, S.M.; Nissley, M.E.; Hochreiter, L.E. Application of code scaling applicability and uncertainty methodology to the large break loss of coolant. Nucl. Eng. Des. 1998, 186, 39–52. [Google Scholar] [CrossRef]
- Zhang, Z.-Z.; Wang, H.-L.; Meng, H.-Y.; Liu, M.-L. Uncertainty Evaluation and Correlation Analysis of ingle-particle energies in phenomenological nuclear mean field: An investigation into propagating uncertainties for independent model parameters. Nucl. Sci. Tech. 2021, 32, 45–57. [Google Scholar] [CrossRef]
- D’auria, F.; Galassi, G.M. Code validation and uncertainties in system thermalhydraulics. Prog. Nucl. Energy 1998, 33, 175–216. [Google Scholar] [CrossRef]





| Real Quantile Figure-of-Merit | Max. after 59 Trials | 2nd Max. after 93 Trials | 3rd Max. after 124 Trials | 4th Max. after 153 Trials |
|---|---|---|---|---|
| 95% | 95% | 95% | 95% | 95% |
| 97% | 83% | 77% | 72% | 68% |
| 99% | 45% | 24% | 13% | 7% |
| Design Parameters | Values |
|---|---|
| Plant life (years) | 60 |
| Thermal power output (MWt) | 4040 |
| Electric power output (MWt) | 1400 |
| First loop pressure (MPa) | 15.5 |
| Fuel assemblies | 193 |
| Hot legs | 2 |
| Cold legs | 4 |
| SG | 2 |
| Parameter | Error/Target |
|---|---|
| Thermal power | 0 |
| PZR water volume | 0 |
| Pressure of PZR | 0 |
| Pump-head | −0.09 |
| Pump-rotational-speed | −0.06 |
| Mass flow rate of cold leg | 0 |
| Mass flow rate of core | 0.003 |
| Mass flow rate of core bypass | 0.005 |
| Mass flow rate of upper head bypass and inlet and outlet | 0.06 |
| Average temperature of coolant | 0.0005 |
| Temperature of inlet | −0.0006 |
| Pressure of SG-out-dome | 0.035 |
| Event | Design Data (s) | BEPU (s) |
|---|---|---|
| Break | 0 | 0 |
| Safeguards signal | 2.2 | 2 |
| CMT valve open | 4.2 | 4 |
| RCPs trip | 9.5 | 9.3 |
| ACC injection/Begin of late blowdown | 13.5 | 13 |
| End of late blowdown/Begin of refill | 27 | 28.5 |
| Core bottom water level resumes in the core | 42.8 | 56.4 |
| PCT occurs | 62 | 69 |
| No | Parameter | Reference Value | Distribution | Range/ Standard Deviation |
|---|---|---|---|---|
| 1 | Gap conductance | 1 | Uniform | 0.8–1.2 |
| 2 | Fdh | 1.65 | Normal | σ = 1.9% |
| 3 | Decay heat | 1 | Normal | σ = 3.89% |
| 4 | Average linear power density, kW/ft | LP | Uniform | (LP − 0.057) to (LP + 0.056) |
| 5 | RCS pressure, MPa | PR | Uniform | (PR − 0.34) to (PR + 0.35) |
| 6 | ACC pressure, MPa | PA | Uniform | (PA − 0.44) to (PA + 0.47) |
| 7 | ACC temperature, K | TA | Uniform | (TA − 19.5) to (TA + 19.5) |
| 8 | ACC friction factor | 1 | Uniform | 0.8–1.2 |
| 9 | RCS temperature, K | TR | Uniform | (TR − 4.2) to (TR + 4.2) |
| 10 | Discharge coefficient | 1 | Uniform | 0.75–1.35 |
| 11 | ACC volume, m3 | VA | Uniform | (VA − 1.3) to (VA + 1.3) |
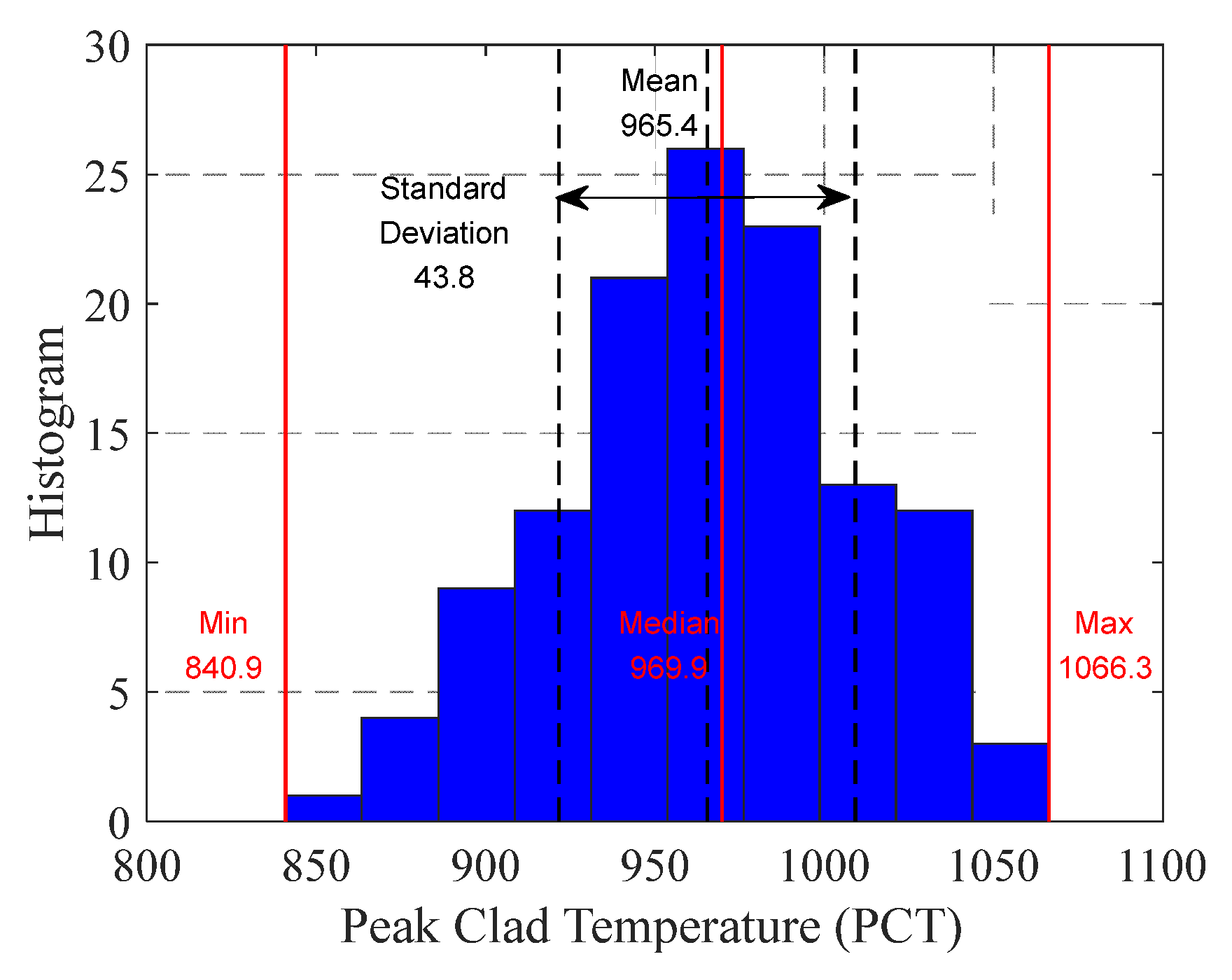
| Highest PCT | PCT, K |
|---|---|
| 1st | 1066.26 |
| 2nd | 1061.67 |
| 3rd | 1050.53 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Xu, C.; Wang, Y.-Z.; Qiu, S.-Z.; Liu, Y.-S.; Fu, H. BEPU Analysis in LBLOCA Safety Review Calculation. Sustainability 2021, 13, 14042. https://doi.org/10.3390/su132414042
Sun W, Xu C, Wang Y-Z, Qiu S-Z, Liu Y-S, Fu H. BEPU Analysis in LBLOCA Safety Review Calculation. Sustainability. 2021; 13(24):14042. https://doi.org/10.3390/su132414042
Chicago/Turabian StyleSun, Wei, Chao Xu, Yi-Zhen Wang, Sui-Zheng Qiu, Yu-Sheng Liu, and Hao Fu. 2021. "BEPU Analysis in LBLOCA Safety Review Calculation" Sustainability 13, no. 24: 14042. https://doi.org/10.3390/su132414042
APA StyleSun, W., Xu, C., Wang, Y.-Z., Qiu, S.-Z., Liu, Y.-S., & Fu, H. (2021). BEPU Analysis in LBLOCA Safety Review Calculation. Sustainability, 13(24), 14042. https://doi.org/10.3390/su132414042






