A New Sustainable Warehouse Management Approach for Workforce and Activities Scheduling

Abstract

Sustainable engineering is very important for logistics systems. Nowadays, sustainable warehouse management is a key factor in market success. Workforce fluctuation and inverting the number of customers’ demands make a lot of problems in distribution warehouses. This study addresses a sustainable approach for the workforce scheduling problem recognized in a real distribution warehouse. The problem arises from the high variability of demand for workers over one workday, which causes workforce surplus in some periods of the workday and shortages in others. Engineering managers of the distribution warehouse already use different full-time and part-time shifts, and schedule workers on different activities, but they still have significant workforce surpluses or shortages in some periods. This study proposes the scheduling of activities’ execution together with workers to face that variability and decrease the cost of the workforce. This idea comes from the fact that some activities in a distribution warehouse can be done in a specific time period after the need for them occurs. In this way, the variability of demand for workers can be decreased, and a lower workforce cost may be ensured. Based on this idea, the entire problem is modeled as integer linear programming. The real example of the problem is solved, and the proposed model is tested on randomly generated instances of the problem in Python by means of the PuLP linear programming package. The results indicate different positive effects in the manner of sustainable warehouse management: lower workforce costs, time savings, better utilization of all types of resources and equipment, increased employee satisfaction, and so on. For even 61% of instances of the introduced problem, the obtained cost of the workforce is lower by more than 20% if activities’ executions are scheduled together with employees.

1. Introduction

The warehouse is one of the most important parts of companies with distribution functions, on whose sustainability the entire company’s sustainability largely depends. It has a particularly important impact on economic and social sustainability as a part of the company that most absorbs the consequences of changes in demand. This has been best demonstrated nowadays where there are large differences in demand. Recently, more and more attention has also been paid to the ecological sustainability of warehouses. Warehouses are the most responsible for the increase in greenhouse gas emissions in the supply chain [1], primarily due to the increase in energy consumption for lighting, heating, cooling, air conditioning, and the handling of goods [2]. In this regard, companies are being invested in to provide renewable energy sources, green technologies, recycling systems, and so on. In addition, the number of works on the topic of green warehousing has increased significantly in recent years [1].

Nevertheless, economic, social, and environmental sustainability are equally important for achieving overall warehouse sustainability [2]. Tan et al. [3] describe in detail their importance, and point out that any change in goals in one type affects the achievement of the goals of the other two types of sustainability. Therefore, it is very important to maintain a balance between the factors of all three types of sustainability [4]. In this regard, engineering has the task to go a step further than seeking sustainable resources and offer systems in which sustainable resources are used in a sustainable way [5]. Operations research should get more attention in this process [6].

The sustainability of the warehouse largely depends on the utilization of the warehouse’s resource (i.e., on their schedule in space and time). If the warehouse is observed only between four walls, then its main resources are space, equipment, and workforce. The schedule in the use of space and stationary equipment is more a tactical or strategic decision and generally does not require daily optimization. On the other hand, workers and the mobile part of the equipment are scheduled every day. Without the efficient use of these resources, there is no sustainable order picking. Since order picking is an extremely intensive process that consumes a lot of energy, capital, and human resources, its impact on overall warehouse sustainability is extremely high. Andriansyah et al. [7] point out that an efficient use of resources is a prerequisite for sustainable order picking and thus for sustainable warehousing.

Numerous papers deal with scheduling, routing, and other methods that optimize the use of mobile resources in the warehouse. The aim is to minimize their costs, energy consumption, and greenhouse emission while performing activities. Burinskiene et al. [8] scheduled forklift driving and picking vehicle routes to reduce travel time and cost in replenishment and order picking. Boenzi et al. [9] optimized forklift operation in terms of both energy consumption and environmental impacts. Pashkevich et al. [10] examined which factors cause an increase in forklift energy consumption. Lorenc and Lehrer [11] scheduled products in warehouses of modern companies to achieve more efficient use of resources in the order-picking process. On the other hand, studies such as [12,13,14] and others have scheduled workers. In general, workers have been scheduled on tasks, jobs, activities, days, and so on, following a work execution plan. Papers dedicated to the workforce in the warehouse and workforce scheduling on activities are represented in the literature review in more detail.

However, to achieve optimal utilization of mobile resources, it is not enough just to optimally schedule them according to a work execution plan; the work execution must also be optimally scheduled when scheduling mobile resources. With this approach, this paper goes a step ahead compared to the existing literature, which deals only with the effects of scheduling of mobile resources on work. In addition, this paper gives preference to the workforce over the mobile equipment in the scheduling process in the warehouse and defines all types of works in the warehouse as activities. In a similar sense as in this paper, Carli et al. [15] scheduled activities and forklifts in a warehouse to optimize the charging batteries. Their aim was to charge forklift batteries less often during peak hours. In contrast, this paper takes into account the economic and social aspects when scheduling activities. It exploits the possibility of postponing the execution of some activities and the use of workers in different types of activities to lower workforce costs. It provides a more even use of workers over the workday and a break on time, and eliminates overcrowding in the warehouse to improve working conditions. All of that increases economic and social sustainability and creates a potential for investment in environmental sustainability solutions.

The workforce scheduling and planning is hence very important but also a complicated task for companies with distribution warehouses (DW). Like in many other service systems, the complexity comes from the variability of workload during a planning horizon. As a result, a different number of workers is needed in different periods of the planning horizon. However, on a daily basis, this problem might be resolved in a DW better than in other service systems. During the analysis of activities in the real DW, it was noticed that many activities could be postponed completely or partially. It means that the execution of these activities can be scheduled in a specific time period after the need for their execution occurs. In that way, the variability of demand for workers may be decreased, and a lower workforce cost may be ensured. The main aim of this study was to incorporate this specificity in the scheduling of workers on activities in DW and provide a solution with a lower cost of the workforce. At the same time, the solution should contribute to a more balanced workload for workers during the day, respecting the period for a break. In this way, the solution should help increase the efficiency and sustainability of the warehouse.

The idea for this study came from cooperating with engineering managers of the real DW to decrease the cost of the workforce. After analyzing activities in their warehouse, and how they schedule workers, the workforce scheduling problem in DW (DW-WSP) was defined. Based on the defined DW-WSP, the idea of applying an activities execution scheduling (AES) for decreasing the cost of the workforce in DW was developed. This idea and the DW-WSP are presented in the rest of this section, together with the main contributions of the paper and implications for engineering managers. The position of the study among the existing literature and related studies are discussed in the next section. The approach to solving the introduced problem, which allows the scheduling of workers and execution of activities at the same time, is presented next. This approach explains the concept for solving the problem and a mathematical model of the problem, named a workforce and activities execution scheduling model (the WAES model). The WAES model is tested for the input values obtained from the considered DW, and for the 100 randomly generated instances of the problem. Each instance of the problem is solved with the WAES model and the model that excludes the AES (the WS model). The results of the testing, final discussion, and future research conclude the paper.

1.1. The DW-WSP

The DW-WSP is introduced as follows. The workforce has to be determined by shifts and by worker profiles, along with scheduling workers’ activities over the workday. Jobs of the same type perform an activity that lasts the entire workday and requires a different number of workers in different intervals of a workday. The required number of workers for executing an activity in an interval is equal to the sum of workers needed for performing all jobs belonging to that activity that occurred in that interval. For each activity, there is a deadline for finishing. The needed number of workers by intervals and by activities is calculated based on the history of jobs’ occurrence. The exceptions are activities whose workload depends on the workload of one or more other activities. For such an activity, the needed number of workers in an interval is calculated based on the number of workers that are scheduled on the activities it depends on. In DW, there are full-time and part-time shifts. Each full-time worker needs to take their break within a prescribed time window, which depends on the shift. Different worker profiles are employed, which can execute different activities following their qualifications. Based on the overall definition, this problem can be characterized as a relatively extended version of the shift-scheduling problem, in which a worker can perform more than one activity in the same shift. Ultimately, the conclusion can be drawn that the defined problem belongs to the group of multi-activity shift scheduling problems (MASSPs).

1.2. The AES

The scheduling of activities’ execution, together with workforce scheduling, is the main idea for decreasing the cost of the workforce in DW. The AES in this paper refers to the scheduling of some activities’ execution in a time period after the need for their execution occurs. This scheduling is possible due to the opportunities that some activities provide in terms of their completion. The execution of these activities can be completely or partially postponed. The following example explains the AES from the workforce scheduling perspective. Let it be prescribed that each truck checked in for the unloading has to be unloaded in three hours. The truck can be unloaded completely in the first, the second, or the third hour after arrival. The unloading can also be scheduled partly in two or three of these hours. Accordingly, the requirements for workers of unloading activity can be fulfilled in different ways after they occur.

Further, assume it is measured that four workers can unload the truck in one hour. If the workday is divided into one-hour intervals, then a truck checked in for unloading creates the job that requires four workers to work for one hour. As the unloading has to be finished in three hours, all four workers can be scheduled to unload the truck in the first, in the second, or the third hour after the truck is checked in. However, the truck can also be unloaded by one worker over all three hours and by another worker during one of these three hours, and so on. Therefore, there are many combinations to schedule the execution of activities (i.e., to fulfill requirements for workers of activities that have a deadline for finishing). The idea of using the AES for decreasing the cost of the workforce in DW is represented by the example in Figure 1.

1.3. Main Contributions

It is believed that this study might contribute to knowledge and practice by offering novelties that were not identified in other research. Careful investigation of the literature showed that many studies are dealing with MASSPs, but trying to develop a better technique to solve a familar MASSP. In this work, the MASSP model is adjusted for application in DW and increasing the sustainability thereof. Despite the overall MASSP complexity, the entire problem is extended with the AES to decrease the cost of the workforce in DW. Therefore, it is believed that the study has two potential contributions:

• The first is practical, and refers to developing a model for workforce scheduling in DW, which the literature lacks, and which can decrease the cost of the workforce in DW and increase its sustainability.
• The second is methodological, and refers to the introduction of the AES to an MASSP as a novelty that might provide a better solution of MASSPs in general.

2. Literature Review

This study can be positioned among the studies that consider workforce scheduling problems, activity scheduling problems, and warehouse sustainability.

Regarding workforce scheduling problems, this study can be positioned among studies that consider shift scheduling problems. According to Ernst et al. [16], “shift scheduling deals with the problem of selecting from a potentially large pool of candidates; what shifts are to be worked together with an assignment of the number of employees to each shift to meet demand.” The position of the break within selected shifts is also considered unless it is fixed. Usually, the problem is considered in a single-day planning horizon divided into a certain number of equal intervals. If the number of available workers is specified, then the objective is usually to find a schedule that minimizes understaffing and overstaffing. If the number of available workers is not provided, the aim is to find a schedule that provides the minimal cost of the workforce. Some of the other objectives in use are minimizing a gap between assignments and employees’ preferences, balancing a workload between employees, minimizing workforce size, and maximizing employees’ satisfaction.

This study can be classed among the studies that consider MASSPs. MASSPs are a relatively extended type of shift scheduling problem. The multi-activity context in shift scheduling problems extends these problems to determining when and which activity each worker performs. Demand for workers is represented by activities and by intervals of a workday. Hence, MASSPs generally imply solving two problems. One problem is to select working shifts and, subsequently, assign workers to them. The second one is to assign workers to activities by intervals of shifts. If activities require different qualified workers, then for each selected shift, the number of every worker profile needs to be determined.

Finally, this study can be classed among the studies that consider warehouse sustainability. These studies are related to the ideas of green warehousing, sustainable warehouse management, development of operational research tools for solving sustainable engineering problems in the warehouse, and so on.

2.1. Literature Review of Workforce Scheduling in Warehouses

Despite the significant number of studies addressing the workforce scheduling problem, a small number of studies have investigated that problem in a warehouse. Out of more than 700 papers about workforce scheduling published between 1954 and 2003, included and described in the review paper by Ernst et al. [17], not one mentions the warehouse. In the second review paper by Van der Bergh et al. [18], which includes papers from 2003 to 2012, the warehouse is mentioned in four papers. After 2012, to the best of the authors’ knowledge, only two papers mention the warehouse. All of these papers are briefly described below.

De Causmaecker et al. [19] classified real-world personnel planning problems by investigating a small yet representative sample of Belgian companies. In a warehouse company, a call center, a fast-food restaurant, and an employment agency, they encountered personnel planning based on fluctuating demands. As the required number of personnel fluctuated, they described the problem in these companies as a fluctuation-centered personnel planning problem. Authors have pointed out that these companies maintain a historical record for demand forecasting, whereas the warehouse company has at least three workers qualified for each task and hires temporary employees.

Günther and Nissen [20,21] scheduled workers on workstations (jobs) in one German logistics provider, where most of the jobs are related to the warehouse. Both papers have solved the same problem, but used different techniques to do so, with both aimed at improving the existing schedule of workers during the day. Accordingly, the objectives of the studies were obtained by allowing workers to perform more than one job during the day. The objective function was the minimizing of over-satisfying and under-satisfying of demands for workers, as well as changing jobs. Bard and Wan [22] presented a model for determining the optimal size of the permanent workforce, where workstation groups specify the demand for workers for up to 24 h a day, seven days a week. The model was tested using the data provided by the U.S. Postal Service (USPS) mail processing and distribution center (P&DC) in Dallas.

Ladier et al. [23] defined three phases of making weekly and daily schedules for workers. In the first phase, the number of temporary workers of every profile and the number of hours by task for each worker (temporary or permanent employee) are determined for each day of the one-week horizon. In the second phase, for each employee, the shift and the percentage of time spent on the assigned task are calculated for each day and each hour. In the third phase, an assignment of tasks to employees is made for each interval. The solution in each phase is obtained by minimizing the deviation of the solution from the given demands, conditions, rules, and so on. Ladier and Alpan [24] solved the cross-dock truck scheduling problem and the employee rostering problem in an integrated manner. Two iterative procedures were proposed for solving the problem, encompassing employees-first and trucks-first.

2.2. Literature Review of Multi-Activity Shift Scheduling

An in-depth review of literature in the workforce planning and scheduling sphere revealed that the multi-activity context had been rarely noted. Moreover, the term “activity” is quite newly introduced. Referring to the study conducted by Ernst et al. [17], it is uncovered that none of the papers that have been reviewed described jobs as activities. Besides, Van den Bergh et al. [18] conducted a review study in which the scheduling of workers on activities was only identified in cited studies such as [25,26,27]. However, before these, it is also worth mentioning the papers in which jobs are activities following this paper’s definition, but they were not described in that way.

Ritzman et al. [28] and Loucks and Jacobs [29] are among the first papers that introduce the multi-activity context. Ritzman et al. [28] assigned every worker to a particular work, every hour, within a post office. Similarly, Loucks and Jacobs [29] allocated different types of work (called tasks) to restaurant workers, where each task required workers to have adequate skills. Bard and Wan [22] scheduled workers on workstations in a way that the demand for workers of every workstation was defined in half-hour intervals, every day, five days a week. The scheduling of workers on workstations, which corresponded to the activities, was conducted in a study by Günther and Nissen [21]. The results of the study indicate that on each workstation, in each interval of the day, a certain number of workers are needed. In a study conducted by Ladier et al. [24], tasks in a warehouse were considered in two ways, which is to say, they defined their workload precisely (hour-by-hour) and for a whole time slot. Tasks defined for the whole time slot could be realized at any time. Given the definition of activity from this paper, the first group of tasks corresponds to activities, and the second one to tasks.

It can be asserted that Demassey et al. [12,25] and Cote et al. [30] first introduced the term “activities” in reference to workforce problems. However, the problems in their papers are described as the employee timetabling problem. Besides, these studies also introduced the constraints that are subsequently used in almost every paper concerning MASSP and are presented below (ended with Lequy et al. [31]). Accordingly, the constraints can be regulated as allowed and forbidden assignments of activities to shift intervals; a minimum and a maximum number of consecutive periods assigned to an activity or break for an employee; allowed and forbidden activity changes; and a required number of break periods after changing activities or consecutive working periods; and so on. Followings studies could have solved a quite similar MASSP, but using different solving techniques.

Demassey et al. [12,25] determined valid schedules to which an employee can be assigned (valid shifts) by using constraint programming considering two sequences. Firstly, they have fulfilled intervals of valid shifts with activities and a break/lunch according to various constraints. Secondly, they have deployed the column generation approach to cover demand. They identified the required number of workers to work in specific shifts. Additionally, Demassey et al. [12] solved this problem when the set of valid shifts is determined for each worker separately. In studies conducted by Cote et al. [30,32], they determined, for each worker, which activity to perform in which interval, without using a set of feasible shifts. For each employee, a shift was formed by using various constraints (i.e., an implicit way was used to form shifts).

Cote et al. [32] and the subsequent papers described a solved problem as MASSP, or by a slightly modified name. Cote et al. [26] continued to use the implicit way for defining shifts. However, this time, the decision variable denoted the number of workers assigned to an activity in an interval. Cote et al. [13] selected a working shift for each worker from his/her set of feasibility shifts by using a column generation approach. Each valid shift for an employee was fulfilled with a break, a lunch, or an activity, according to defined constraints. The pricing sub-problem was modeled by using a context-free grammar that allowed extracting the set of feasible shifts for each employee.

Lequy et al. [14] assumed that shifts (with breaks) are already assigned to workers. Accordingly, they have assigned activities to shifts (i.e., to the periods of shifts). An activity was assigned to a period of a shift, considering only if there was an adequate number of qualified workers to perform the activity in that shift. Ultimately, they have proposed three integer programming formulations of the problem, and subsequently, they have developed three heuristics based on branch and bound or column generation methods. This problem was extended in Lequy et al. [31] by assigning tasks to shifts besides activities. Tasks were assigned to shifts in the same way as activities; however, they obeyed different rules. Similarly, Boyer et al. [33] extended the model of Cote et al. [13] by including tasks besides activities in the problem.

Dahmen and Rekik [34] solved an MASSP over a multi-day planning horizon, where workdays were known for each worker. The study aimed at constructing admissible shifts followed by assigning them to workers in a way that minimizes under-staffing and over-staffing costs over their workdays. They have proposed a tabu-search-based constructive algorithm and a mixed integer linear programming (MILP) model of the shift scheduling problem. Restrepo et al. [27] solved another real case of MASSP. The problem was concerned with finding the schedule for security staff and cashiers over 100 parking lots in the city of Bogotá. They modeled parking lots as work activities and the staff movements between parking lots as changes between work activities. The solution was articulated as the number of workers in selected shifts and the assignment of activities to time slots of those shifts.

2.3. Literature Review of Sustainable Warehouse Studies

Tan et al. [3] define a sustainable warehouse as a warehouse where all economic, environmental, and social inputs are integrated, balanced, and managed. In their work, they developed a model for testing warehouse sustainability. The model also provides decision support that leads to sustainable warehousing. Bank and Murphy [35] emphasize the importance of warehouse sustainability for the sustainability of the entire supply chain. They introduced warehouse sustainability metrics, measurements, and guidelines. Similarly, Torabizadeh et al. [36] provided a list of 33 performance indicators that can be used to assess the sustainability of a sustainable warehouse management system. Bartolini et al. [1] pointed out that warehouses make a major contribution to increasing greenhouse gas in supply chains. For that reason, they provided an overview of the literature dealing with green warehousing and warehouse sustainability. They identified 38 papers related to this topic. Carli et al. [15] scheduled mobile electrical equipment in the warehouse, taking into account the cost of electricity and the cost of penalties related to the makespan. In this way, they ensured a reduction in the impact of mobile electrical equipment on the economic and environmental sustainability of the warehouse. Freis et al. [37] proposed a methodology to determine the energy demand of logistics centers and evaluate the impacts of design options to create energy-efficient and CO₂-neutral systems. They concluded that the energy demand and CO₂ emissions of logistics centers can be reduced if the energy interrelations between the sub-systems intra-logistics, building technology, and building skin are taken into account when improving the base elements of these sub-systems. They also provided energy-saving measures, depending on the degree of automation of the logistics center. Kamarulzaman et al. [38] made a list of green initiatives that can be applied when performing activities in the warehouse and evaluated Malaysian food-based manufacturers according to the application of these initiatives. Amjed et al. [39] defined a sustainable warehouse model that shows elements and constructs that impact sustainability. Elements were grouped into nine constructs, and the dimensions of sustainability that impacted each element were defined. They named the constructs as warehouse facility design, warehouse layout, inventory management, mechanical handling equipment, warehouse staff, warehouse operations, onsite facilities, and warehouse management system. Malinowska et al. [40] defined criteria for warehouse assessment in regards to sustainable functioning, and created a roadmap to gain a better level of sustainable warehouse. The road map for each criterion contains activities to achieve better results of the evaluation criteria and advantages of their application. Durmić [41] determined the importance of various factors and dimensions of sustainability in the selection of a sustainable supplier in BIH. Based on expert assessments, it was obtained that economic factors and sustainability are the most important when selecting a supplier. Đalić et al. [42] presented a model for evaluation and supplier selection based on seven environmental criteria: environmental image, recycling, pollution control, environmental management system, environmentally friendly products, resource consumption, and green competencies.

3. The Sustainable Warehouse Management Approach for Workforce and Activities Scheduling

3.1. Problem Statement

The problem has its roots in selecting working shifts, as well as in determining the number of workers for each profile in each selected shift. Accordingly, the aim is to figure out a solution so that the cost of the workforce is minimized, and every constraint and demand for workers is satisfied over a workday. Depending on activity, demand for workers has to be fulfilled within the prescribed time window or by the end of the prescribed interval of a workday. Since the solution to this problem is robustly tied to the scheduling of workers on activities, then obtaining such a schedule is also part of the problem. Besides, the prospective schedule has to specify a break for each worker within a prescribed time window. Therefore, the overall solution is expected to address the following issues:

• How many workers of each profile are needed to work in each selected shift?
• Which activity is performed by each of the workers in each interval of their shift, and when do they take a rest?

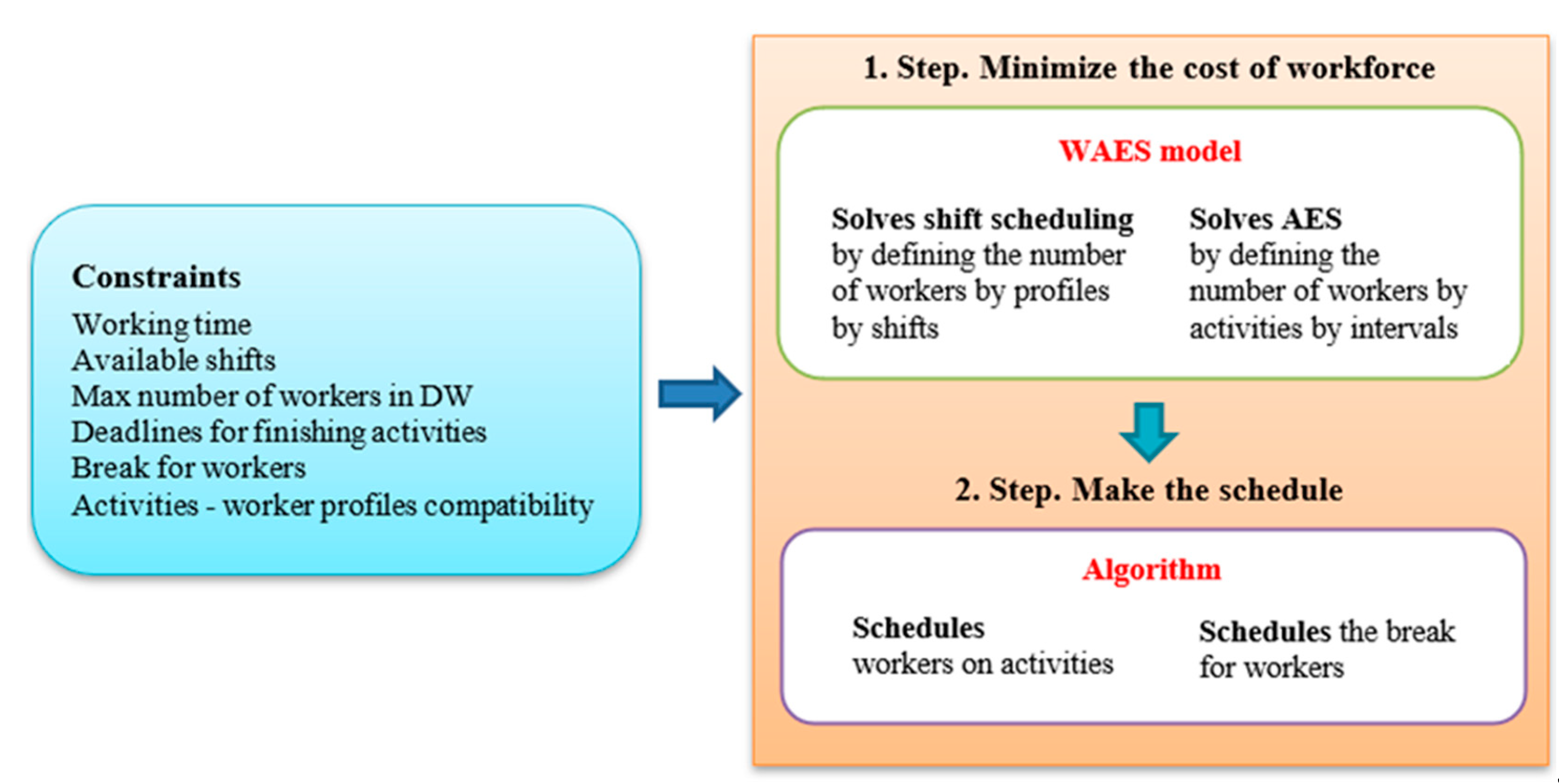
3.2. Conceptual Framework for Solving the Problem

Based on the introduced issues, an entire conceptual framework for solving the problem is developed. It implies solving the WAES model first and then making the schedule for each worker. The solution of WAES provides the number of workers employed in each shift by profile, and the number of workers assigned to each activity in each interval by profile. However, the solution does not specify personally for each worker which activity he performs in which interval and when he has a break. For that need, an algorithm is developed in Python. Based on the obtained solution, the algorithm for each worker assigns an activity or a break in each interval of his shift. The entire conceptual framework for solving the problem is presented in Figure 2.

3.3. Assumptions, Limitations, and Notation

The problem is considered over one workday, which is divided into $n$ intervals of equal length. Each interval is represented by an ordinal number, where $n$ is also the ordinal number of the last interval in the workday. Intervals of a workday are contained in set $N$ (i.e., $N=\left\{1,2,\dots ,n\right\}$). The workday can have full-time and part-time shifts. All possible full-time shifts are contained in set $M_1$, and all possible part-time shifts are contained in set $M_2$. Together, they form the set of all possible shifts $M$. The working environment of the warehouse can include independent and dependent activities. Independent activities are included in set $B$, whereas dependent activities are incorporated into set $C$. All considered activities are included in set $A$.

For activity $a\in B$ and interval $k\in N$, a required number of workers by intervals of the workday is assumed to be known. This is represented as demand for workers $\left(d_{ai}\right)$. On the other hand, for activity $a\in C$ and interval $k\in N$, the demand for workers $\left(d_{ai}\right)$ is equal to the sum of the percentages of the number of workers assigned to each activity from set $G_a$ in interval $k$. Set $G_a$ contains activities on which activity $a\in C$ depends. Therefore, for activity $a\in C$ and activity $a^{,}\in G_a$, there is a percent of dependence ($s_{a^{,}}$). Since demand for workers of dependent activities can be a non-integer number, it has to be fulfilled by an integer number that is equal to or greater than demand.

Each activity has to be executed within a defined time window. The time window for fulfilling a demand for workers on an activity is set according to the time window available for that activity’s execution. There are two types of time windows. For activity $a\in A_1$, demand for workers needs to be fulfilled within the exact number of intervals $\left(v_a\right)$, starting from the one in which it occurs. For example, if the policy of a distribution company is to unload each truck within two intervals after checking in, then each demand for workers of the unloading activity needs to be fulfilled within two intervals.

For activity $a\in A_1$, demand for workers generated before interval $r_a$ needs to be fulfilled by the end of that interval. Requests for performing these activities are received until the interval $r_a$ or an interval before it starts. For example, if a distribution company operates until 22:00, and all orders received by 16:00 are distributed in the morning of the subsequent workday, then all orders received by 16:00 have to be prepared by 22:00. Accordingly, each demand for workers of an order-picking activity needs to be fulfilled by 22:00.

Different worker profiles are employed in the warehouse. All considered worker profiles are represented by set $T$. For each activity, it is defined which of the workers’ profiles are allowed to perform it. Set $T_a$ denotes the set of worker profiles who are allowed to perform an activity $a$. Similarly, set $H_t$ denotes activities which a worker of the profile $t\in T$ is allowed to perform. A worker of profile $t$ costs $c_t$. The maximal number of workers who can work at the same tim (i.e., the maximal number of active warehouse workers) is $q$. In each full-time shift, there is a break of $p$ intervals long, which needs to be taken by each worker employed in a full-time shift within the time window made of $f$ intervals. For activity $j\in M_1$, intervals available for the break are given in set $O_j$.

Demand for workers on independent activities over a workday is considered predictable based on a previous archived record about the workload. However, workload prediction and its conversion into demand for workers are not considered in this paper. The model is also limited to application in distribution warehouses.

Mathematical notations used in the model are presented in

Table 1. Table of notation.

Inputs
Time
$\mathit{N}$	Set of intervals of a workday
$\mathit{M}$	Set of shifts
${\mathit{M}}_1$	Set of full-time shifts
${\mathit{M}}_2$	Set of part-time shifts
$\mathit{n}$	Ordinal number of the last interval in a workday
${\mathit{b}}_{\mathit{k}\mathit{j}}$	A parameter that has a value of 1 if an interval $k\in N$ is part of a shift $j\in M$; otherwise, it is 0.
Activities
$\mathit{A}$	Set of all activities
$\mathit{B}$	Set of independent activities
$\mathit{C}$	Set of dependent activities
${\mathit{G}}_{\mathit{a}}$	Set of activities that activity $a\in C$ depends on
${\mathit{d}}_{\mathit{a}\mathit{i}}$	Demand for workers of activity $a$ in interval $i$
${\mathit{s}}_{{\mathit{a}}^{\prime }}$	Percent of the dependence of activity $a\in C$ on activity $a^{\prime }\in G_a/$100
Deadlines
${\mathit{A}}_1$	Set of activities with a deadline represented by the time window
${\mathit{v}}_{\mathit{a}}$	Duration of the time window for finishing activity $a\in A_1$ (in intervals)
${\mathit{A}}_2$	Set of activities with a deadline represented by number of interval
${\mathit{r}}_{\mathit{a}}$	The interval by which demand for workers of activity $\mathrm{a}\in {\mathrm{A}}_2$ needs to be fulfilled
Workers
$\mathit{T}$	Set of all worker profiles
${\mathit{T}}_{\mathit{a}}$	Set of worker profiles who are allowed to perform activity $a$
${\mathit{H}}_{\mathit{t}}$	Set of activities which a worker of profile $t\in T$ is allowed to perform
${\mathit{c}}_{\mathit{t}}$	Cost of worker of profile $t$
q	Maximal number of workers who can work at the same time
$\mathit{p}$	Duration of the break (in intervals)
$\mathit{f}$	Duration of time window available for breaks (in intervals)
${\mathit{O}}_{\mathit{j}}$	Intervals available for the break in shift $j\in M_1$
w	Percent of workers employed in part-time shifts/100
Outputs
${\mathit{y}}_{\mathit{t}\mathit{j}}$	Number of workers of a profile $t\in T$ assigned to shift $j\in M$
${\mathit{y}}_{\mathit{t}\mathit{i}\mathit{j}\mathit{a}}$	Number of workers of profile $t\in T$ assigned to interval $i\in N$ of shift $j\in M$ on activity $a\in A$
${\mathit{x}}_{\mathit{a}\mathit{i}\mathit{j}\mathit{k}}$	Number of workers provided in interval $i\in N$ of shift $j\in M$ to fulfill the demand for workers of activity $a\in A$ from interval $k\in N$

, separately for model inputs and outputs. The model inputs are presented in the context of time, activities, deadlines for finishing activities, and workers.

3.4. Optimization Model

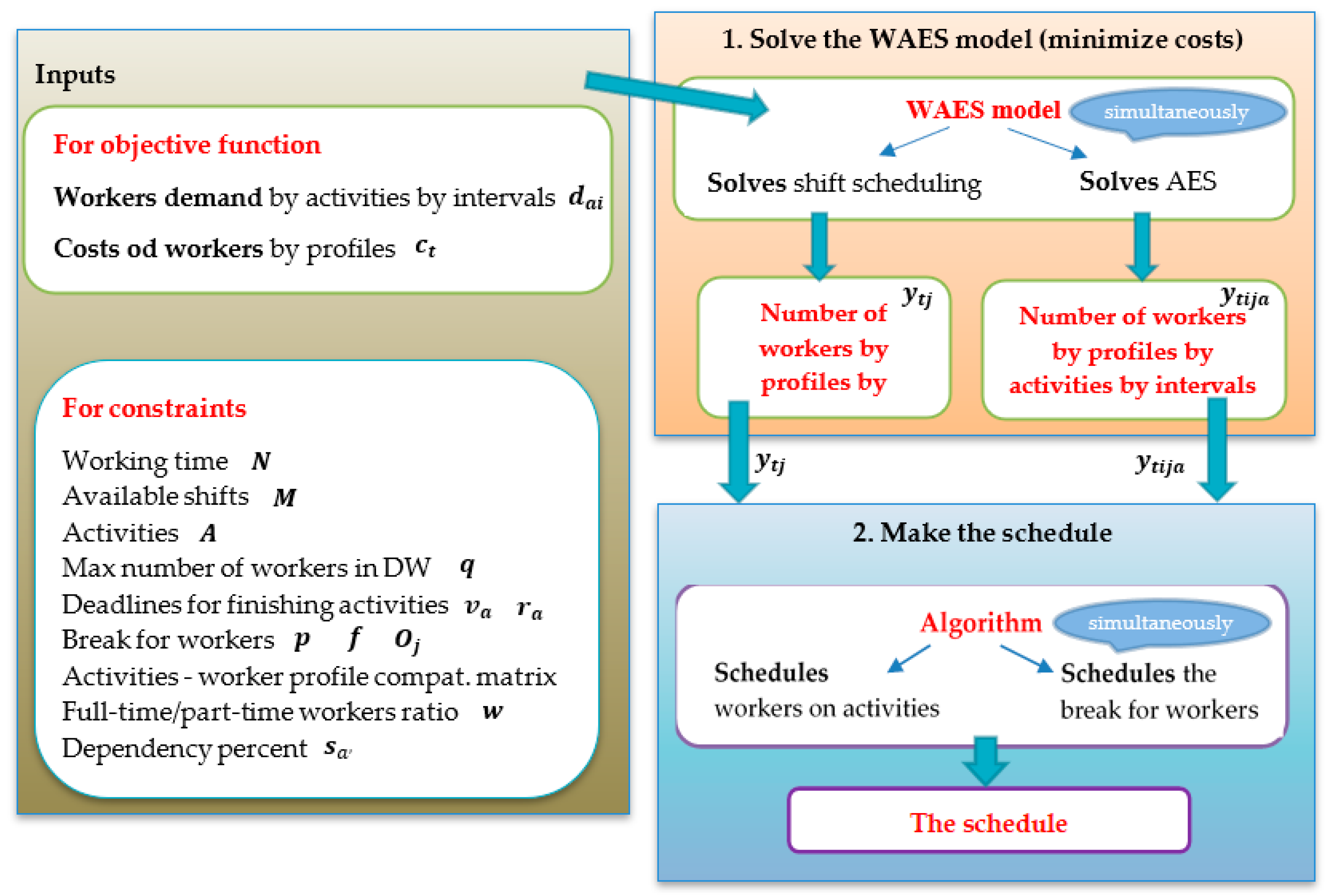
Before introducing the optimization model, the working mechanism of the proposed approach for solving DW-WSP is presented to indicate the position of the model in the process of reaching a solution (Figure 3).

Following the conceptual framework, the working mechanism for solving the DW-WSP, and the introduced notation, the WAES model of the problem is developed in the form of a linear program. The WAES model has the following form:

$$min: {\displaystyle \sum }_{j\in M}{\displaystyle \sum }_{t\in T}{c}_t\ast y_{tj}$$

(1)

Subject to:

$${\displaystyle \sum }_{j\in M}{\displaystyle \sum }_{k=i}^{until}{x}_{aijk}\ast b_{kj}=d_{ai},\hspace{1em}\hspace{1em}\forall i\in N, \forall a\in B{{\displaystyle \cap }}^{\text{}}{A}_1; until=\min \left(i+v_a, n\right)$$

(2)

$${\displaystyle \sum }_{j\in M}{\displaystyle \sum }_{k=i}^{until}{x}_{aijk}\ast b_{kj}=d_{ai},\hspace{1em}\hspace{1em}\forall i\in N, \forall a\in B{{\displaystyle \cap }}^{}{A}_2;until=r_a$$

(3)

$${\displaystyle \sum }_{j\in M}{\displaystyle \sum }_{k^{,}=k}^{until}{x}_{akj{k}^{,}}\ast b_{kj}\ge {\displaystyle \sum }_{a^{,}\in G_a}{s}_{a^{,}}\ast {\displaystyle \sum }_{j\in M}{\displaystyle \sum }_{i\in N}{x}_{aijk}, \forall k\in N, \forall a\in C{{\displaystyle \cap }}^{\text{}}{A}_1; until=\min \left(k+v_a, n\right)$$

(4)

$${\displaystyle \sum }_{j\in M}{\displaystyle \sum }_{k^{,}=k}^{until}{x}_{akj{k}^{,}}\ast b_{kj}\ge {\displaystyle \sum }_{a^{,}\in G_a}{s}_{a^{,}}\ast {\displaystyle \sum }_{j\in M}{\displaystyle \sum }_{i\in N}{x}_{aijk}, \forall k\in N, \forall a\in C{{\displaystyle \cap }}^{\text{}}{A}_2; until=r_a$$

(5)

$${\displaystyle \sum }_{i=1}^k{x}_{aijk}\le {\displaystyle \sum }_{t\in T_a}{y}_{tija},\hspace{1em}\hspace{1em}\forall k\in N; \forall j\in M, \forall a\in A$$

(6)

$${\displaystyle \sum }_{a\in H_t}{y}_{tija}\le y_{tj},\hspace{1em}\hspace{1em}\forall i\in N, \forall j\in M, \forall t\in T$$

(7)

$${\displaystyle \sum }_{t\in T}{\displaystyle \sum }_{j\in M}{\displaystyle \sum }_{a\in A}{y}_{tija}\le q,\hspace{1em}\hspace{1em}\forall i\in N$$

(8)

$${\displaystyle \sum }_{\forall i\in O_j}{\displaystyle \sum }_{a\in H_t}{y}_{tija}\le \left(f-p\right)\ast y_{tj},\hspace{1em}\hspace{1em}\forall t\in T,\forall j\in M_1$$

(9)

$${\displaystyle \sum }_{j\in M}{\displaystyle \sum }_{t\in T}{y}_{tj}\le w\ast {\displaystyle \sum }_{j\in M_2}{\displaystyle \sum }_{t\in T}{y}_{tj}$$

(10)

$$integer: x_{aijk},y_{tija},y_{tj},\hspace{1em}\hspace{1em}\forall i\in N, \forall j\in M, \forall a\in A, \forall t\in T, \forall k\in N$$

(11)

The objective function (1) aims at minimizing the total cost of the workforce. Constraints (2)–(5) ensure that demand for workers on all activities is fulfilled within a prescribed time. Constraint (6) regulates the overall fulfillment of the demand for workers on an activity in an interval not to be larger than the number of workers of all profiles assigned to that activity in that interval. Constraint (7) regulates, for each worker profile, the number of workers by intervals of a shift not to be larger than the number of workers assigned to that shift. Constraint (8) ensures that the number of workers in the warehouse does not exceed the maximum allowed number in any interval of the workday. Constraint (9) ensures that every worker has a break of the defined duration in the defined period. Constraint (10) prevents a situation in which workers are coming and leaving all the time. Constraint (11) defines the nature of the variables.

4. Numerical Experiments

The potential of the WAES model to provide workforce scheduling solutions with a lower workforce cost is firstly tested for the input values provided by engineering managers of the real DW and then on randomly generated instances.

4.1. The Real DW-WSP

The DW operates from 8:00 to 22:00 and employs full-time workers and part-time workers. Full-time shifts consist of 8 h of work and 1 h of break. Part-time shifts are 4-h shifts without a break. Let the minimal time interval of the day be 1 h. Accordingly, there are 14 intervals in one workday and six potential full-time shifts (i.e., $n=14$, $p=1$, and $M_1=\left\{1,\dots ,6\right\}$). The number of potential part-time shifts is nine, and they are denoted by numbers following the number of the last full-time shift (i.e., $M_2=\left\{7,\dots ,15\right\}$). The number of workers employed in part-time shifts is limited to 30% of the total number of employed workers (i.e., $w=0.3)$.

There are ten different activities in the DW and nine profiles of workers that can be employed. The compatibility matrix (

Table 2. Compatibility matrix.

Worker Profile	Activities										Cost
	1	2	3	4	5	6	7	8	9	10
1	*	*	*	*							1.28
2	*	*	*	*							1.4
3	*	*	*	*							1
4	*	*	*	*							1.28
5	*	*	*	*	*				*	*	1.6
6	*					*					1.6
7	*						*	*		*	1.4
8	*	*	*	*					*		1.36
9	*	*	*	*			*	*	*	*	1.4
Legend Worker profiles 1- Order picker 2- Controller 3- Auxiliary worker 4- Packer			5- Supervisor 6- Controller at reception 7- Forklift driver 8- WMS receiver 9- WMS forklift driver			Activities 1- Order picking 2- Control 3- Auxiliary jobs 4- Preparing goods for loading 5- Supervision			6- Control at reception 7- Loading vehicles 8- Unloading vehicles 9- WMS goods receiving 10-Putting away and extracting of goods

* Worker is qualified for a certain activity

) specifies for each worker profile the activities which they can perform. The costs of worker profiles were not available, but the ratio between the cost of each worker profile and the lowest cost among them were available. These ratios are used as costs of worker profiles in the model. The last column of the compatibility matrix presents these costs. The costs are valid for the engagement in full-time shifts in one workday. For part-time shifts, the costs of workers’ engagement are half of the presented costs. For example, the cost of full-time engagement of one worker of profile 1 is 1.28 for one workday.

For the sake of discussion and ease of presentation, the problem is restricted to activities $1, 6, 7$, and $8$, and worker profiles $1, 6,$ and $7$. Activities $6,7$, and $8$ belong to set $A_1$, whereas activity $1$ belongs to set $A_2$. Activity $6$ depends on activity $8$ with a dependence of 50% (i.e., $G_6\in \left\{8\right\}$ and $s_8=0.5$). The other three activities are independent. Demand for workers of independent activities was obtained from the engineering managers of the DW and is presented in

Table 3. The solution of the real DW-WSP.

Interval		Shifts																		Workers Demand
		1					2								8		11
No.	h.	e7	e7	e7	e7	e7	e1	e1	e1	e1	e1	e1	e1	e1	e7	e7	e6	e6	e6	a7	a1	a8
1	8	a7	a7	a7	a7	a7	/	/	/	/	/	/	/	/	/	/	/	/	/	7	11	0
2	9	a7	a7	a7	a7	a7	a1	a1	a1	a1	a1	a1	a1	a1	a7	a7	/	/	/	8	10	0
3	10	a7	a7	a7	a7	a7	a1	a1	a1	a1	a1	a1	a1	a1	a7	a7	/	/	/	5	7	0
4	11	a7	B	B	a7	a7	a1	a1	a1	a1	a1	a1	a1	a1	a7	a7	/	/	/	4	8	0
5	12	a8	a8	a8	a8	B	B	B	B	B	B	B	B	B	a8	a8	a6	a6	a6	0	7	6
6	13	B	a8	a8	B	a8	a1	a1	a1	a1	a1	a1	X	X	a8	a8	a6	a6	a6	0	6	5
7	14	a1	a1	a8	a8	a8	a1	a1	a1	a1	a1	a1	a1	X	/	/	a1	a6	a6	0	9	3
8	15	a1	a1	a1	a8	a8	a1	a1	a1	a1	a1	a1	a1	a1	/	/	a1	a1	a6	0	10	2
9	16	a1	a1	a1	a1	a1	a1	a1	a1	a1	a1	a1	a1	a1	/	/	a1	a1	a1	0	9	0
10	17	/	/	/	/	/	a1	a1	a1	a1	a1	a1	a1	a1	/	/	/	/	/	0	0	0
11	18	/	/	/	/	/	/	/	/	/	/	/	/	/	/	/	/	/	/	0	0	0
12	19	/	/	/	/	/	/	/	/	/	/	/	/	/	/	/	/	/	/	0	0	0
13	20	/	/	/	/	/	/	/	/	/	/	/	/	/	/	/	/	/	/	0	0	0
14	21	/	/	/	/	/	/	/	/	/	/	/	/	/	/	/	/	/	/	0	0	0
Legend
			Worker profiles e1—Order picker e6—Controller at receptione7—Forklift driver							Activities a1—Order picking a6—Control at reception a7—Loading vehicles a8—Unloading vehicles								Other B—Break X—Without work /—Interval is not part of the shift

. From the compatibility matrix, it follows that $T_1\in \left\{1,6,7\right\}$, $T_6=\left\{6\right\}$, $T_7=\left\{1\right\}$, and $T_8=\left\{1\right\}$, while $c_1=1.28$, $c_6=1.6$, and $c_7=1.4$. In addition, it follows that $H_1\in \left\{1\right\}$, $H_6\in \left\{1,6\right\}$, and $H_7\in \left\{1,7,8\right\}$. Each full-time worker needs to have the fourth, fifth, or sixth interval of his shift free (for example, $O_2=\left\{5, 6, 7\right\}$). Accordingly, it follows that $p=1$ and $f=3$. The maximum number of active workers in the warehouse is set to be 30 (i.e., $q=30$).

The policy of the distribution company defines that trucks for loading can wait up to two intervals to be loaded. Trucks for unloading need to be unloaded within one interval, starting from the interval in which they checked in for unloading. During the unloading, shipments are controlled at the reception without delay. The distribution company dispatches all orders received before 16:00 in the morning of the following workday. As trucks do not arrive strictly at the beginning of an interval, a truck checked in for unloading or loading during an interval is considered as checked in at the beginning of the subsequent interval. Therefore, the execution of these four activities needs to be finished according to the following parameters: $v_6=0,v_7=1,v_8=0$, and $r_1=14$. The exceptions are trucks checked in for unloading in the next to last interval of the workday. They need to be processed until the end of the last interval. Trucks that arrive during the last interval are not processed.

Currently, engineering managers of the DW do not consider the AES and strive to execute each activity when the need for it occurs. To examine the cost of the DW-WSP solution in such circumstances, the problem is solved with the WS model of the problem that excludes the possibility of the AES. This model is obtained by setting all deadline parameters to zero ($v_6=0, v_7=0, v_8=0$ and $r_1=0)$ in the WAES model. In that case, the obtained solution of DW-WSP has a cost of 22.95. If the WAES model is used—that is, if deadline parameters have real values $(v_6=0, v_7=1, v_8=0$, and $r_1=14)$ and the AES is possible—a solution with the cost of 21.04 is obtained. In both cases, the problem is solved in Python by means of the PuLP linear programming package. The integrality gap is set to be up to 3%. The workforce schedule that follows from the last obtained solution is demonstrated in Table 3. For making the schedule from the solution of the model, an algorithm in Python was developed.

The solution implies a schedule with three full-time shifts and two part-time shifts. Full-time shifts are 1 and 2. Shift 1 starts at 8 o’clock and shift 2 at 9 o’clock. Part-time shifts are 8 and 11. Shift 8 starts at 9:00 and shift 11 at 12:00. In shift 1, there are five workers of profile 7, in shift 2 there are eight workers of profile 1, and so on. If one of the workers is observed individually, it can be seen what activity he is engaged in at each interval of his shift and when he has a break. For example, the first worker in shift 1 works on activity 7 in the first four intervals; in the fifth interval, he works on activity 8; in the seventh interval, he has a rest; and then until the end of the workday, he works on activity 1. If the execution of an activity is observed, it can be seen which workers execute the activity in each interval. For example, activity 7 in the first interval requires seven workers of profile 7. According to the schedule, five workers perform this activity in the first interval. The need for two workers is transferred to the next interval because this activity allows a delay in execution of one hour. The solution also contains three intervals in which some workers do not work due to lack of work. This is the sixth interval for the seventh and the eighth worker in shift 2, and the seventh interval for the eighth worker in the same shift. With the application of the WAES model, the number of such intervals is reduced and the costs of the solutions are decreased. The main reason for this is the application of the AES within the WAES model.

4.2. Randomly Generated Instances of the DW-WSP

The idea of using the AES to decrease the cost of the workforce has been shown to be very helpful in the solved example. To generalize this observation, 100 instances of the same problem were solved as in the real example. Instances of the problem differ in the number of required workers by intervals for activities. The required numbers of workers are randomly generated for each interval of the workday and each independent activity. Randomly generated values are set to be between 0 (included) and 10 (included). All other features and input values are the same for each instance of the problem and correspond to those in the solved example. Results of the testing show that for each instance of the problem, a lower cost is obtained if the WAES model is used for solving the problem. For 61% of instances of the problem, the obtained cost of the workforce is lower by more than 20% compared to the cost obtained by using the WS model (Figure 4).

If we consider efficiency as the ratio of realized costs to costs that are theoretically sufficient to perform a given workload, then changes in the efficiency of the workforce can also be calculated to examine the effects of solving the problem as the WAES model (i.e., performing workforce scheduling together with the AES). For an activity, the theoretical lowest costs can be calculated by multiplying the hours required to perform the activity with the cost per hour of the cheapest profile of a worker who can perform the activity. By using theoretical costs of activities, the overall theoretical costs are obtained. For the real example of DW-WSP, the overall theoretical costs are 18.24. The efficiency of the workforce in the case of using the WS model for solving the problem is 79%, whereas in the case of using the WAES model, it is 87%. Therefore the efficiency is increased by 9%. The increases in efficiency for the randomly generated instances of the same problem are presented in the next figure (Figure 5).

5. Discussion

The solutions of the example and the randomly generated instances indicate the importance of taking into account the possibility of AES in workforce scheduling in DW. It has proved to be good assistance for minimizing the variability of demand for workers and for better utilization of workers. The number of intervals without work for workers is decreased, and the use of workers in activities that are primarily intended for them is increased. The consequence is decreasing the cost of the workforce in DW if the WAES model is used for the DW-WSP.

Taking into account that the execution of some activities in DW can be completely or partly postponed, the model allows engineering managers to schedule workers in a better way and optimize the cost of the workforce. In workforce planning and scheduling models, jobs are usually considered as tasks that last only a certain period and require the same number of workers during that time. Interrupting a task that is being performed or replacing an assigned worker by another is not considered, or it is penalized. In other words, demand for workers has to be fulfilled at the time when it occurs. In this model, the fulfillment of some activities’ demand for workers is scheduled following the available time for fulfillment. In addition, a worker scheduled on an activity can be replaced by another during the same shift. These features of some activities in DW enable more flexible workforce scheduling and provide an additional opportunity for optimizing the cost of the workforce.

At the same time, the model allows engineering managers to shape the final solution by setting certain parameters of the model. With these parameters, they can set the period allowed for a break during a shift, the break duration, the maximum allowed number of active workers, deadlines for finishing activities, the percent of part-time workers, the duration of shifts, and so on. The model can also be used for determining the number of part-time workers by days. If a workweek includes seven workdays, then the model can be used for obtaining inputs for a day-off scheduling problem as well. A model for solving such a problem, that also includes different worker profiles, can be found in Billionnet et al. [43].

Previously, not many studies have been devoted to raising warehouse sustainability through scheduling the execution of activities over time, especially not with limitations that take into account working conditions. Many studies dealing with sustainable warehousing are dedicated to building models for assessing warehouse sustainability. Other studies deal with energy savings in the process of handling goods. This paper offers a model that enables the raising of economic sustainability in a specific way, taking into account the social aspects of sustainability as well. A special feature of the paper is that it takes into account the needs of workers in optimizing work processes. It not only improves social sustainability, but indirectly enables the achievement of economic benefits as well. Workers are more productive, fewer costs are spent on training new workers, expenses due to workers going to competing companies are lowered, expenses caused by absences from work are decreased, and so on. According to Andriansyah et al. [7], sustainable development implies an efficient use of both natural and human resources. Human capital is a company’s greatest asset [44].

6. Conclusions

This study provides engineering managers with a sustainable engineering model that integrates workforce scheduling of workers on activities and of the execution of activities. By integrating the scheduling of the workforce and activities, greater opportunities are achieved for optimizing workforce utilization and raising the sustainability of warehouses to a higher degree. Frequent changes in demand have forced companies with distribution functions to attach more importance to the sustainability of their warehouses today. The success of these companies largely depends on the sustainability of their warehouses. Given that insufficient use of resources leads to losses and the unsustainability of the warehouse, it is very important to plan and schedule activities in the warehouse and of its resources.

This article provides a solution that allows for the reduction of costs in the warehouse and an increase in its efficiency and sustainability. Optimal scheduling of activities in the warehouse over time reduces the necessary resources and costs and opens space for processing even larger quantities of goods with the same or fewer resources. By optimal scheduling, the stress on the warehouse system in certain periods is reduced, and thus the possibility of errors in operation, damage of goods and equipment, delays in delivery, and so on. All of this provides opportunities for raising economic sustainability. Optimal scheduling of activities and resources in the warehouse also reduces the stress on external systems such as the power grid or roads in certain periods, thus increasing environmental sustainability. In addition, the workload of workers is scheduled more evenly over time, as well as between workers. Each worker has a break in the planned period, and no more workers operate at the same time than allowed for the given space. In this way, it is possible to increase the productivity of workers, reduce their mistakes, turnover, and injuries, and increase the overall social sustainability of the warehouse.

This paper contributes primarily to raising the economic and social sustainability of the warehouse. From that point of view, it could be said that this is a limitation of this paper. However, if we take into account approaches for raising environmental sustainability, then it can be said that this paper complements these approaches. The environmental sustainability within the warehouse can be raised by reducing energy consumption, primarily for cooling, heating, air conditioning, and handling of goods. Some studies [37,45,46] have dealt with how to accomplish this. Moreover, environmental sustainability in the warehouse can be raised by reducing waste production and water consumption, and through the recycling and reuse of packaging, pallets, paper, and so on. Other studies [39,47,48] have dealt with these issues. By providing a solution for increasing social and economic sustainability, this paper provides a sustainable basis for investing in solutions that improve the environmental sustainability of the warehouse.

Having all of the above in mind, the new sustainable warehouse management approach for workforce and activities scheduling should be a useful tool for increasing the sustainability of the warehouse. In addition, the achievements of this study represent a good base for further research, which should make this model even more useful in practice. The cost of the workforce can be decreased even more if some of the parameters in the model also become the subject of optimization. In future models, it would be useful to pay more attention to other aspects of sustainability in DW using similar approaches, but also using hybrid approaches that combine several different methods. Future research may also be aimed at predicting the warehouse’s workload and the needed number of workers. One of the most important tasks should be to define the factors influencing the prediction of workload and the needed number of workers in addition to historical data on the workload. The current situation, government measures, and announcements regarding the COVID-19 crisis should be recognized in this prediction.