Implementation of a Stable Solar-Powered Microgrid Testbed for Remote Applications
Abstract
:1. Introduction
- (1)
- Develop a physical parameter-based model for self-stabilizing operation of interactive inverters borrowing from synchronous generator dynamics;
- (2)
- Introduce a systematic design method for an intrinsically stable microgrid, operated by I-DERs using a “governor + SG” mechanism;
- (3)
- Interpret inverter inertia via dc-link capacitance and;
- (4)
- Implement a stable microgrid without using battery storage systems. That is, dc-link voltage stability and frequency stability is achieved with no battery storage utilization, although they can still be used for other purposes such as peak shaving and load shifting.
2. System Topology and Proposed Control Scheme
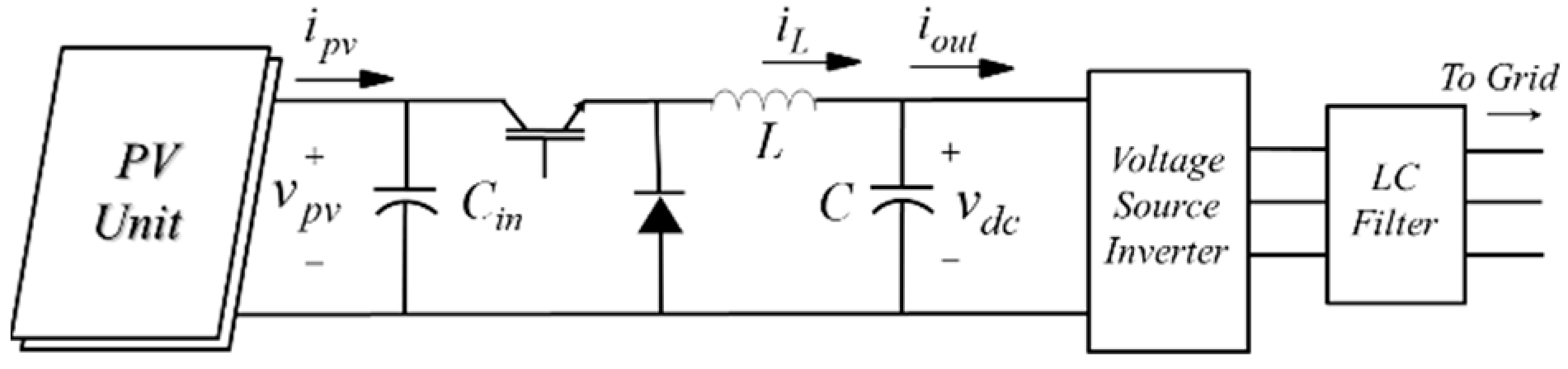
2.1. System Topology
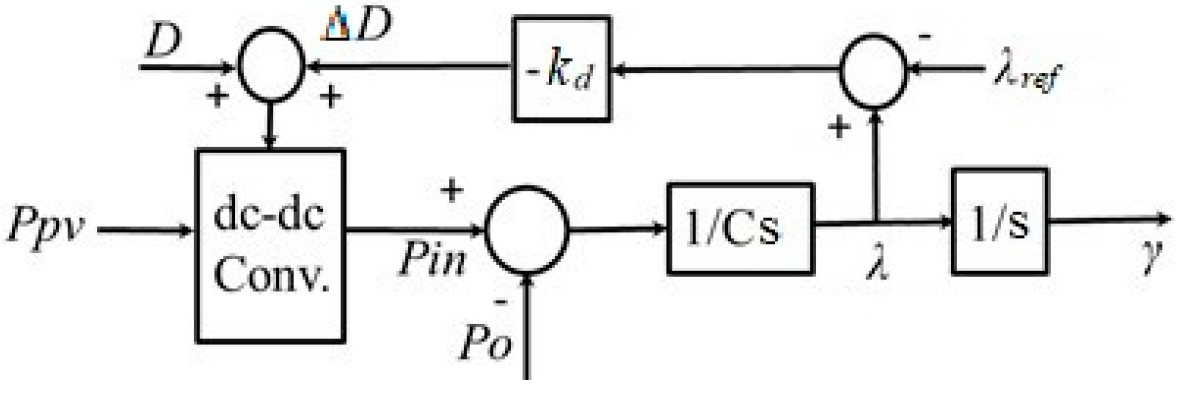
2.2. System Model and Control Scheme
2.3. Parameter Design
3. Results
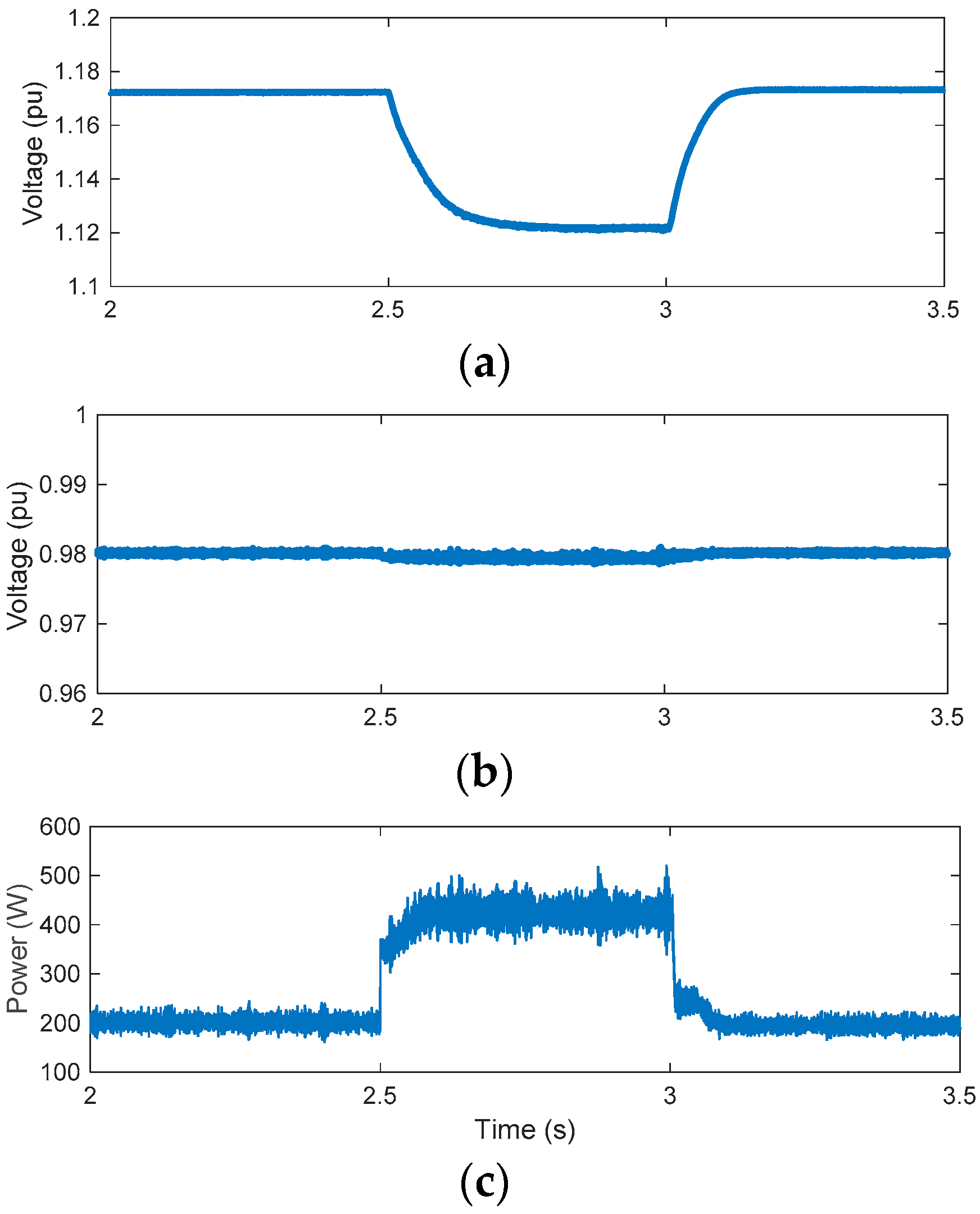
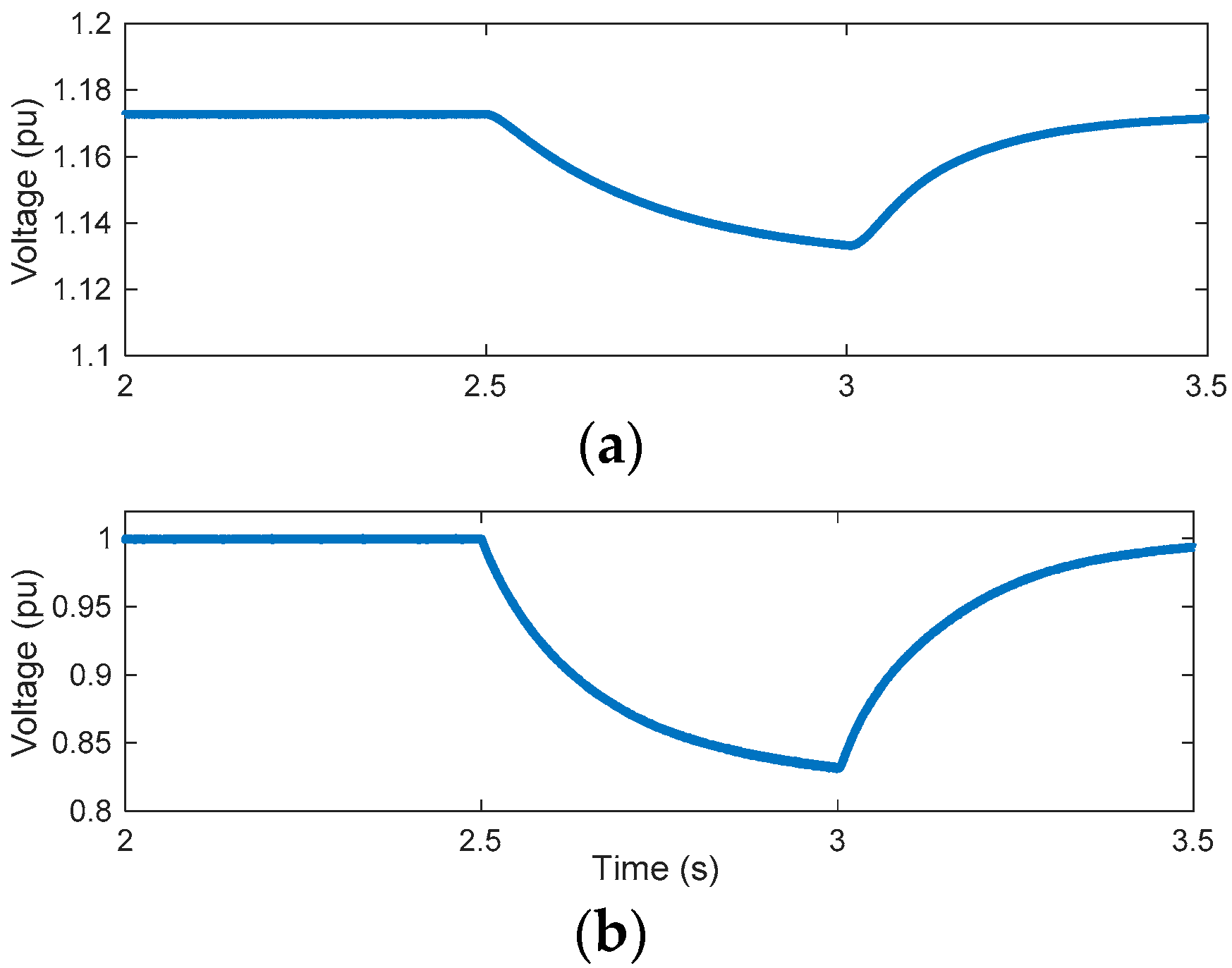
3.1. Simulation Results
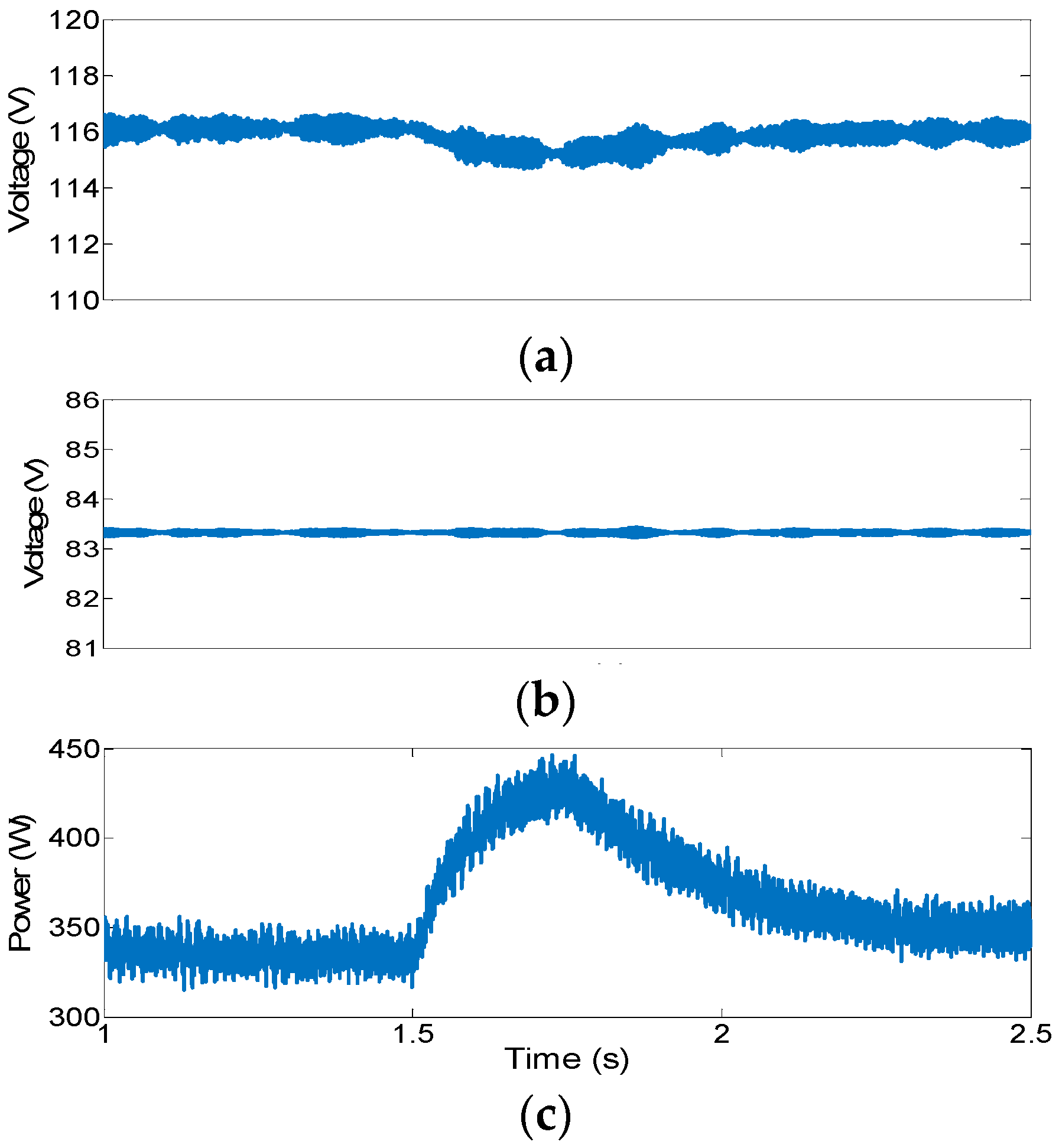
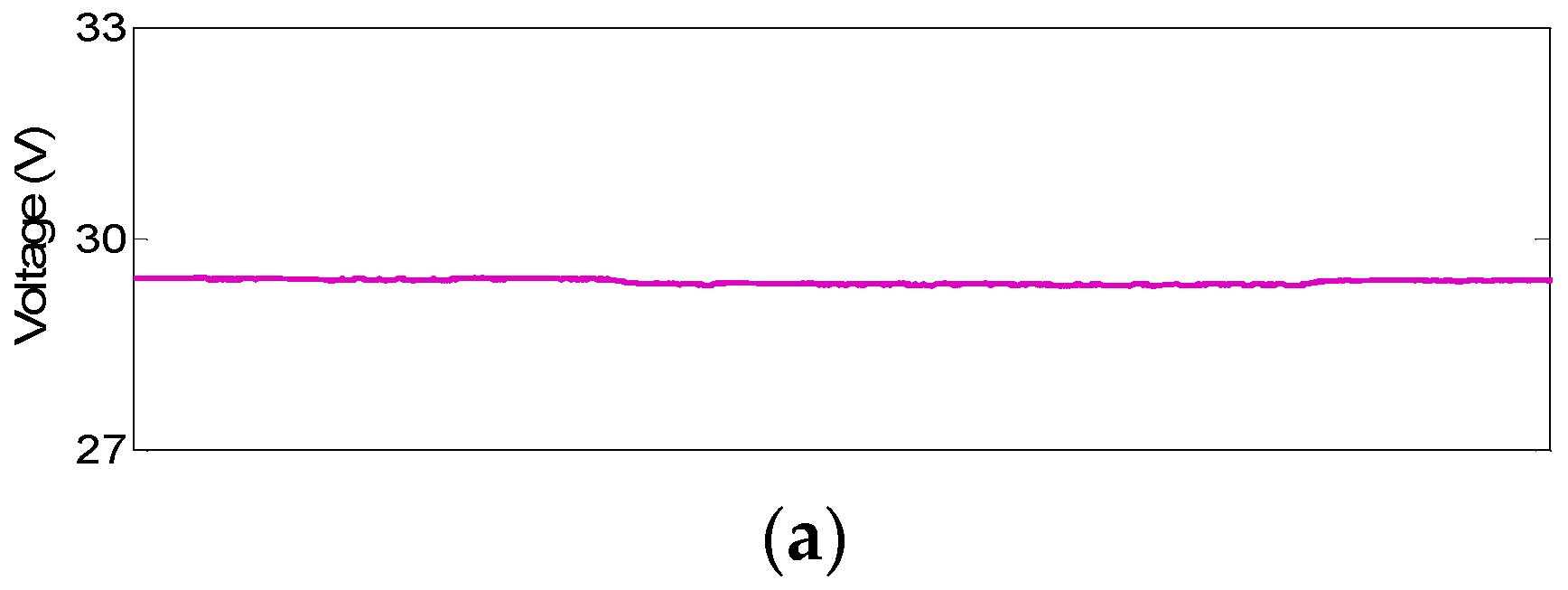
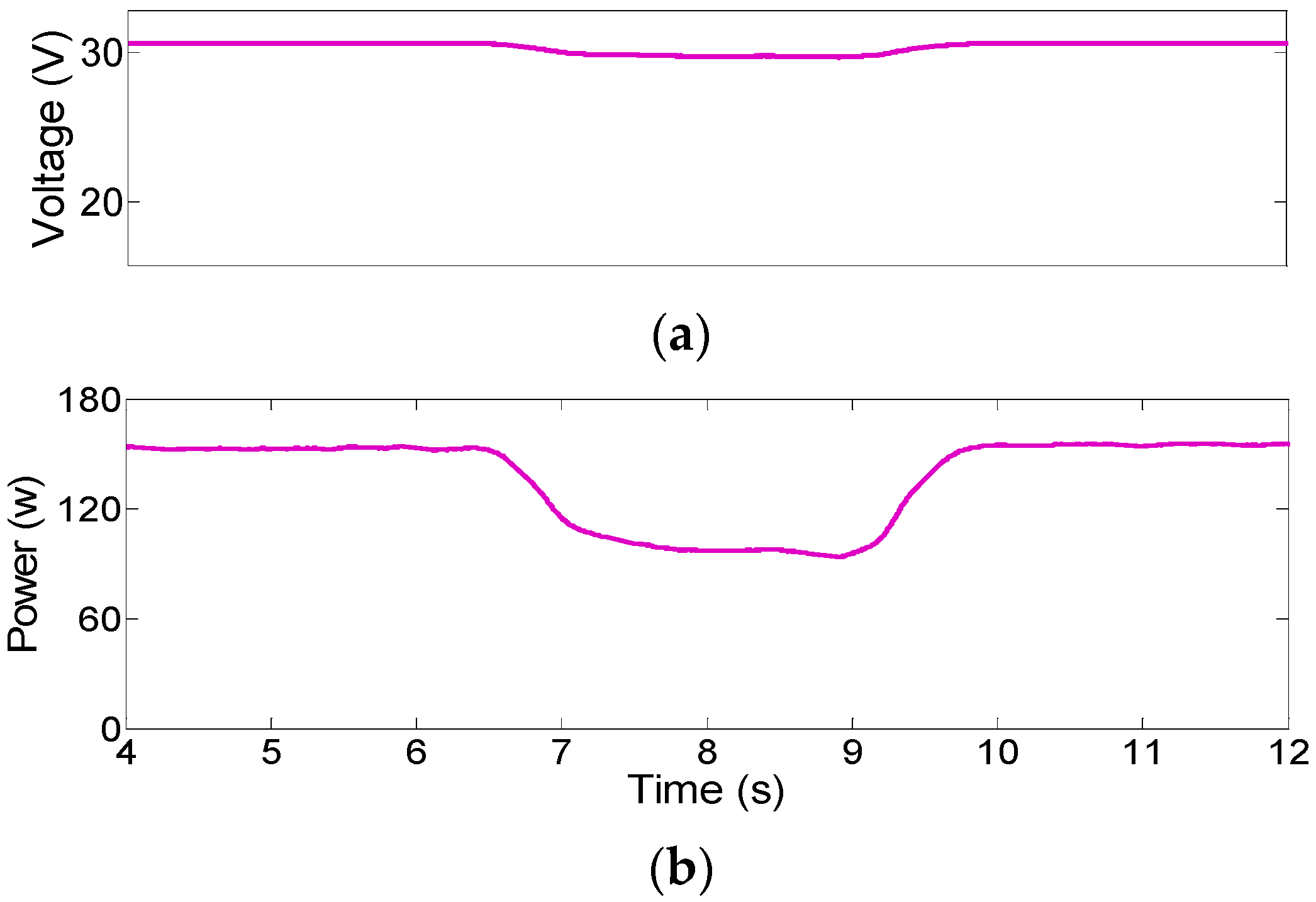
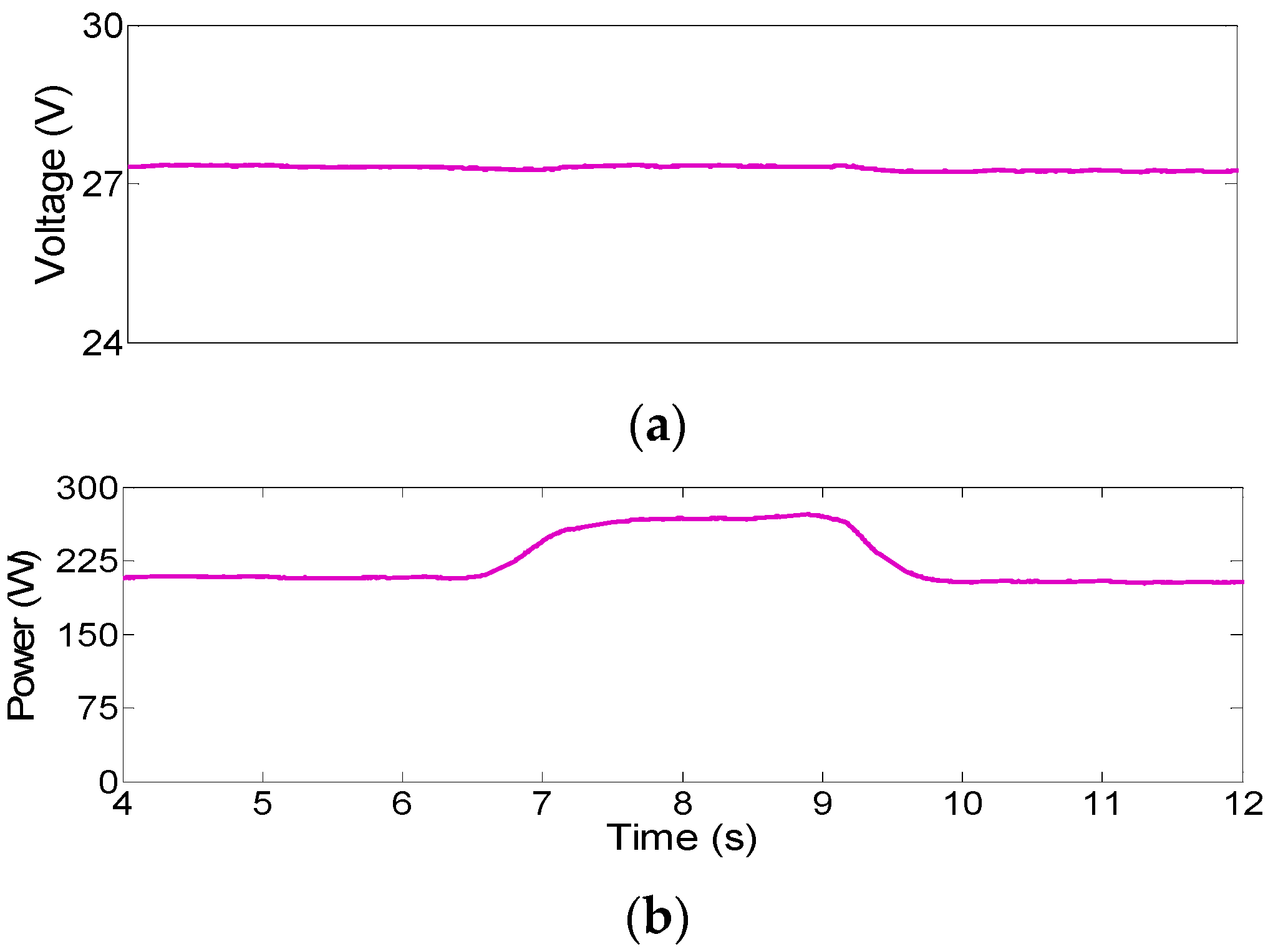
3.2. Experimental Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Photovoltaic power | |
| power injected to the dc-link capacitor from the dc-dc converter | |
| delivered power to the inverter | |
| delivered power to the grid by inverter | |
| input mechanical power | |
| output electrical power | |
| dc-link capacitor voltage | |
| dc base voltage | |
| voltage magnitude of the fundamental harmonic at the inverter’s output terminal | |
| grid bus voltage magnitude | |
| Photovoltaic voltage | |
| phase angle of the fundamental harmonic at the inverter’s output terminal | |
| grid bus voltage phase angle | |
| magnitude of element ik in the admittance matrix of the network | |
| base power | |
| direct-axis synchronous reactance | |
| quadrature-axis synchronous reactance | |
| direct-axis transient reactance | |
| Quadrature-axis transient reactance | |
| direct-axis transient open-circuit time constant | |
| direct-axis field flux linkages | |
| field voltage in a synchronous generator | |
| inverter modulation factor | |
| the admittance that connects the inverter to the grid | |
| ω | rotor speed in the synchronous generator |
| angular momentum | |
| inertia constant | |
| angle of element ik in the admittance matrix of the network |
References
- IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces. In IEEE Std 1547-2018 (Revision of IEEE Std 1547-2003); IEEE: Piscataway, NJ, USA, 2018.
- Zhang, L.; Harnefors, L.; Nee, H.-P. Power-synchronization control of grid-connected voltage-source converters. IEEE Trans. Power Syst. 2010, 25, 809–820. [Google Scholar] [CrossRef]
- Hu, J.; Hu, Q.; Wang, B.; Tang, H.; Chi, Y. Small signal instability of PLL-synchronized type-4 wind turbines connected to high-impedance AC grid during LVRT. IEEE Trans. Energy Convers. 2016, 31, 1676–1687. [Google Scholar] [CrossRef]
- Huang, L.; Xin, H.; Wang, Z.; Wu, K.; Wang, H.; Hu, J.; Lu, C. A virtual synchronous control for voltage-source converters utilizing dynamics of DC-link capacitor to realize self-synchronization. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1565–1577. [Google Scholar] [CrossRef]
- Wen, T.; Zhu, D.; Zou, X.; Jiang, B.; Peng, L.; Kang, Y. Power coupling mechanism analysis and improved decoupling control for virtual synchronous generator. IEEE Trans. Power Electron. 2021, 36, 3028–3041. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Z.; Wong, K.P. Advanced control strategies of PMSG-based wind turbines for system inertia support. IEEE Trans. Power Syst. 2017, 32, 3027–3037. [Google Scholar] [CrossRef]
- Zhong, Q.-C.; Weiss, G. Synchronverters: Inverters that mimic synchronous generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- Hu, W.; Wu, Z.; Dinavahi, V. Dynamic analysis and model order reduction of virtual synchronous machine based microgrid. IEEE Access 2020, 8, 106585–106600. [Google Scholar] [CrossRef]
- Roldán-Pérez, J.; Rodríguez-Cabero, A.; Prodanovic, M. Design and Analysis of Virtual Synchronous Machines in Inductive and Resistive Weak Grids. IEEE Trans. Energy Convers. 2019, 34, 1818–1828. [Google Scholar] [CrossRef]
- Sun, D.; Liu, H.; Gao, S.; Wu, L.; Song, P.; Wang, X. Comparison of different virtual inertia control methods for inverter-based generators. J. Mod. Power Syst. Clean Energy 2020, 8, 768–777. [Google Scholar] [CrossRef]
- Chen, M.; Zhou, D.; Blaabjerg, F. Modelling, implementation, and assessment of virtual synchronous generator in power systems. J. Mod. Power Syst. Clean Energy 2020, 8, 399–411. [Google Scholar] [CrossRef]
- VanDoorn, T.L.; Meersman, B.; De Kooning, J.D.M.; Vandevelde, L. Analogy between conventional grid control and islanded microgrid control based on a global DC-link voltage droop. IEEE Trans. Power Deliv. 2012, 27, 1405–1414. [Google Scholar] [CrossRef] [Green Version]
- Peng, Q.; Yang, Y.; Liu, T.; Blaabjerg, F. Coordination of virtual inertia control and frequency damping in PV systems for optimal frequency support. CPSS Trans. Power Electron. Appl. 2020, 5, 305–316. [Google Scholar] [CrossRef]
- Zhong, Q.-C.; Nguyen, P.-L.; Ma, Z.; Sheng, W. Self-synchronized synchronverters: Inverters without a dedicated synchronization unit. IEEE Trans. Power Electron. 2014, 29, 617–630. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S.H.; Park, J.-W. Inertia-free stand-alone microgrid—Part II: Inertia control for stabilizing DC-link capacitor voltage of PMSG wind turbine system. IEEE Trans. Ind. Appl. 2018, 54, 4060–4068. [Google Scholar] [CrossRef]
- Lamichhane, S.; Nazaripouya, H.; Mehraeen, S. Micro Grid Stability Improvements by Employing Storage. In Proceedings of the 2013 IEEE Green Technologies Conference (GreenTech), Denver, CO, USA, 4–5 April 2013. [Google Scholar]
- Fang, J.; Tang, Y.; Li, H.; Li, X. A battery/ultracapacitor hybrid energy storage system for implementing the power management of virtual synchronous generators. IEEE Trans. Power Electron. 2018, 33, 2820–2824. [Google Scholar] [CrossRef]
- Kazemlou, S.; Mehraeen, S. Novel decentralized control of power systems with penetration of renewable energy sources in small-scale power systems. IEEE Trans. Energy Convers. 2014, 29, 851–861. [Google Scholar] [CrossRef]
- Saberi, H.; Mehraeen, S. A simultaneous voltage and frequency control scheme for photovoltaic distributed generation units in small-scale power systems. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017. [Google Scholar]
- Pilawa-Podgurski, R.C.N.; Perreault, D.J. Submodule integrated distributed maximum power point tracking for solar photovoltaic applications. IEEE Trans. Power Electron. 2013, 28, 2957–2967. [Google Scholar] [CrossRef] [Green Version]
- Walker, G.; Sernia, P. Cascaded DC–DC converter connection of photovoltaic modules. IEEE Trans. Power Electron. 2004, 19, 1130–1139. [Google Scholar] [CrossRef]
- Mohan, N.; Undeland, T.M.; Robbins, W.P. Power Electronics: Converters, Applications, and Design; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
- Sauer, P.W.; Pai, M.A. Power System Dynamics and Stability; Prentice Hall: Upper Saddle River, NJ, USA, 1998; Volume 101. [Google Scholar]
- IEEE Recommended Practice for Excitation System Models for Power System Stability Studies. In IEEE Std 421.5-2016 (Revision of IEEE Std 421.5-2005); IEEE: Piscataway, NJ, USA, 2016; pp. 1–207.
- IEEE Guide for Identification, Testing, and Evaluation of the Dynamic Performance of Excitation Control Systems. In IEEE Std 421.2-2014 (Revision of IEEE Std 421.2-1990); IEEE: Piscataway, NJ, USA, 2014; pp. 1–63.
- Nazaripouya, H.; Mehraeen, S. Modeling and nonlinear optimal control of weak/islanded grids using FACTS device in a game theoretic approach. IEEE Trans. Control. Syst. Technol. 2015, 24, 158–171. [Google Scholar] [CrossRef]

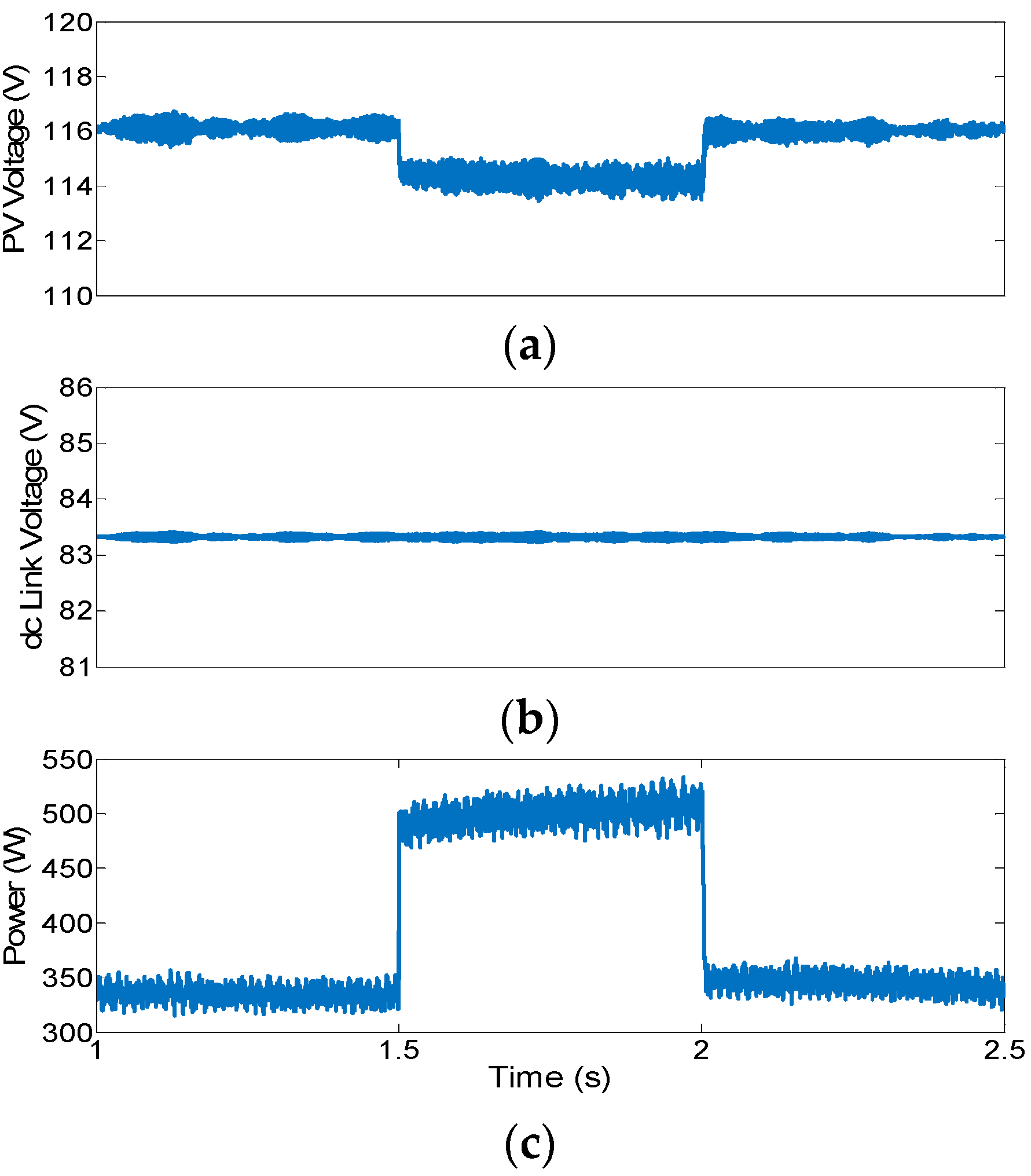
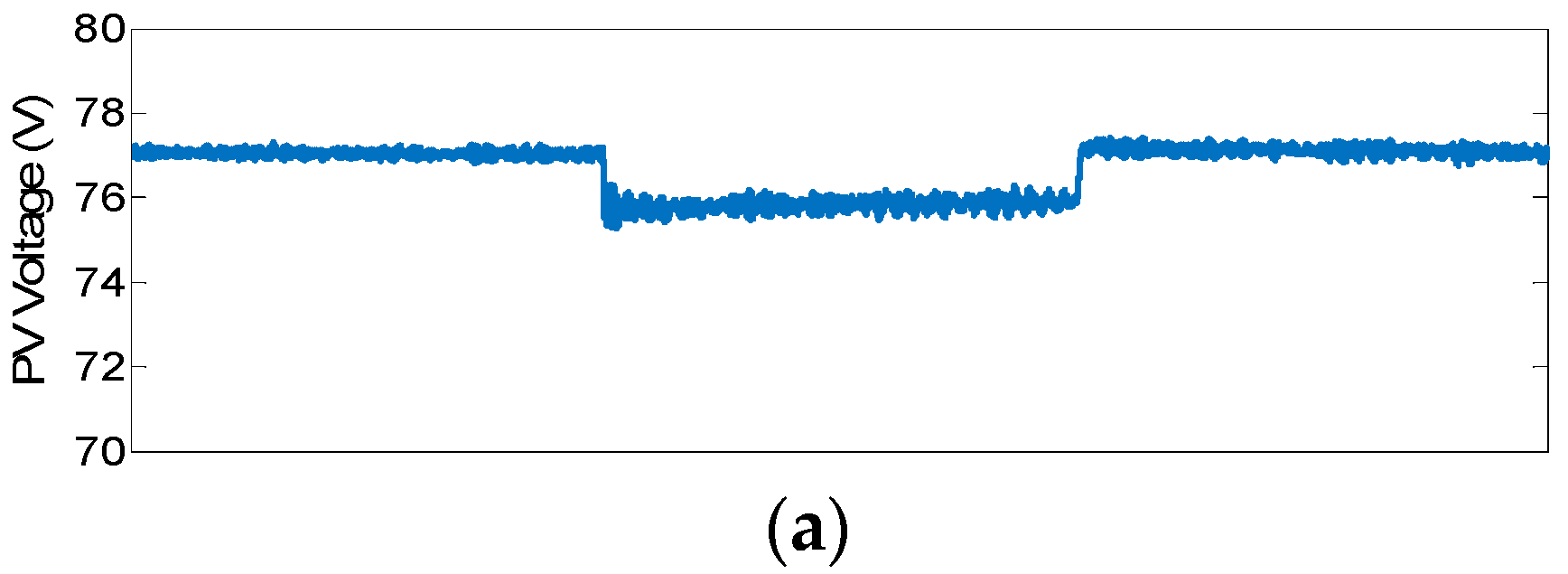
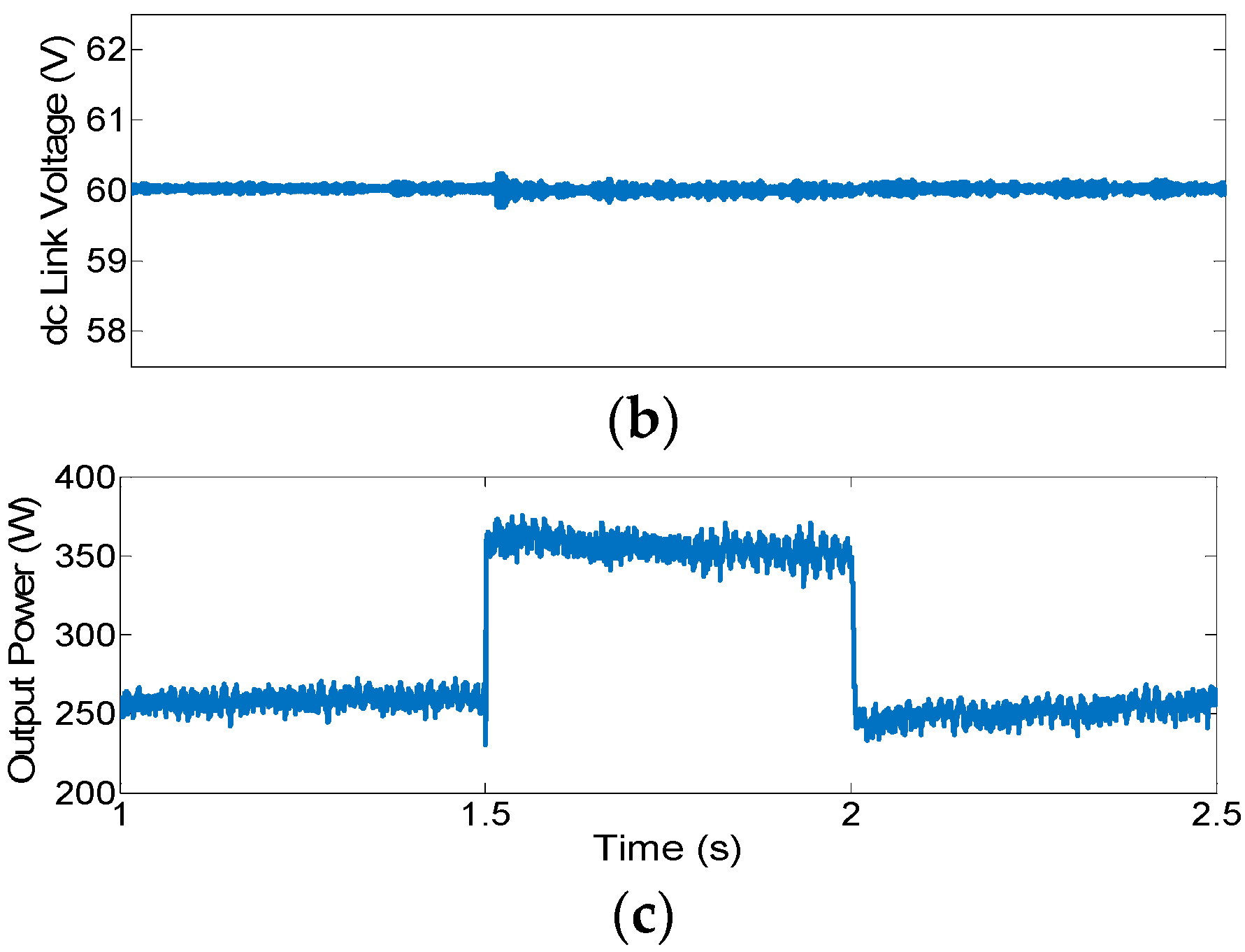

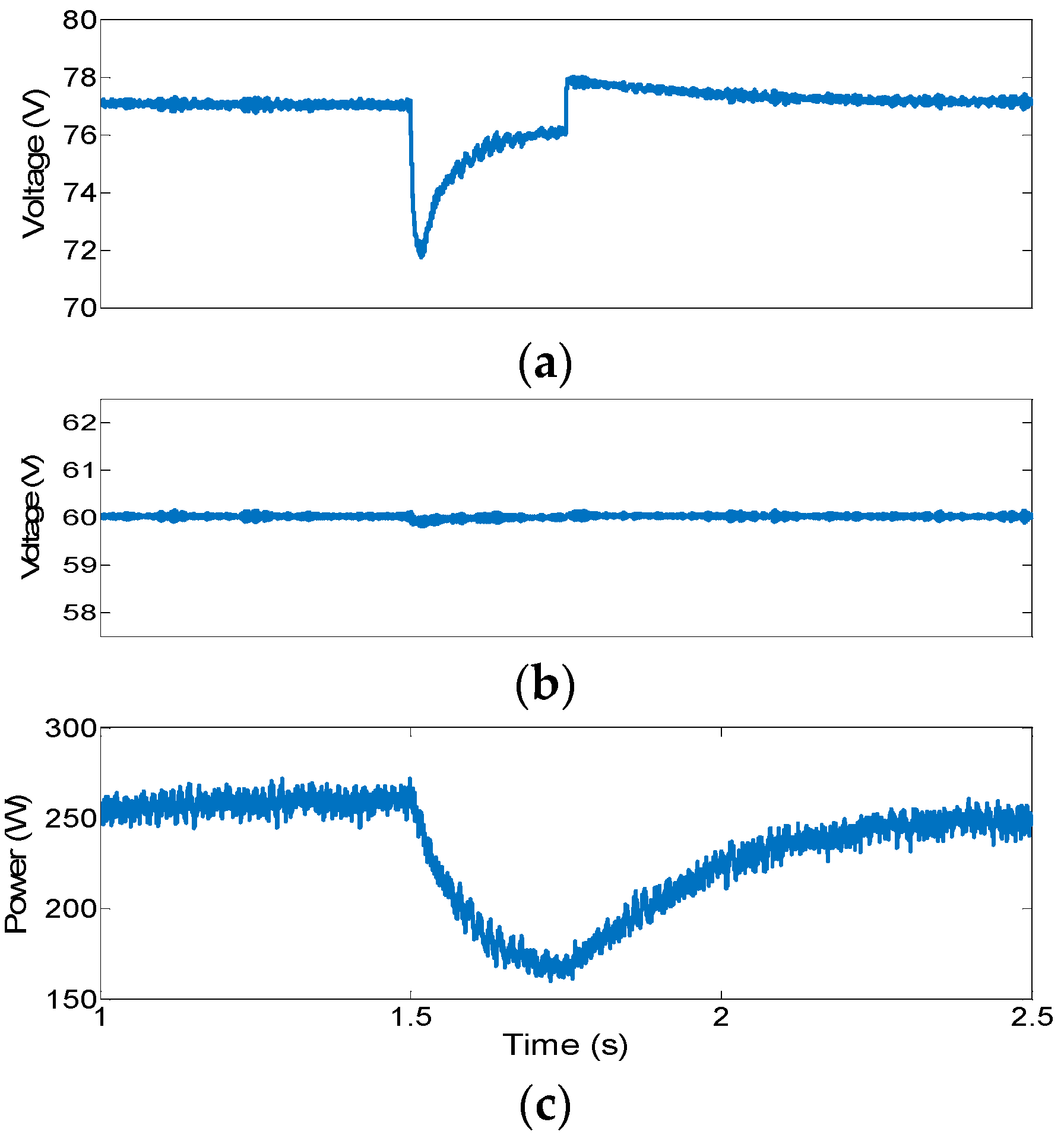




| Parameters | SG 1 | SG 2 |
|---|---|---|
| d-axis synchronous reactance () | 0.295 pu | 0.2495 pu |
| d-axis transient reactance () | 0.0697 pu | 0.0531 pu |
| d-axis open-circuit time constant () | 6.56 s | 5.7 s |
| q-axis synchronous reactance () | 0.282 pu | 0.237 pu |
| inertia constant H (s) | 0.0302 s | 0.0358 s |
| Eigenvalues | |
|---|---|
| −7.9299 + 0.0000i | −1.0419 − 135.5989i |
| −4.9906 + 61.2965i | −0.3522 + 0.0000i |
| −4.9906 − 61.2965i | −0.1629 + 0.0000i |
| −1.0419 + 135.5989i | −5.5 × 10−7 + 0.0000i |
| Hardware | Values | Model | Values |
|---|---|---|---|
| Pannel Voc | 39.5 V | 0.295 pu | |
| Pannel Vmpp | 34 V | 0.069 pu | |
| Pannel Pmpp | 280 W | 0.282 pu | |
| Cin and C | 1 mF | Td0 | 6.56 s |
| L | 2.5 mH | B | 5 pu |
| fs | 10 kHz | Dp | 0.2026 |
| Line Inductance (LL) | 20 mH | Line Resistance (RL) | 0.5 Ω |
| Vdc-base | 80 Vdc | Pbase | 2 kVA |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saberi, H.; Nazaripouya, H.; Mehraeen, S. Implementation of a Stable Solar-Powered Microgrid Testbed for Remote Applications. Sustainability 2021, 13, 2707. https://doi.org/10.3390/su13052707
Saberi H, Nazaripouya H, Mehraeen S. Implementation of a Stable Solar-Powered Microgrid Testbed for Remote Applications. Sustainability. 2021; 13(5):2707. https://doi.org/10.3390/su13052707
Chicago/Turabian StyleSaberi, Hossein, Hamidreza Nazaripouya, and Shahab Mehraeen. 2021. "Implementation of a Stable Solar-Powered Microgrid Testbed for Remote Applications" Sustainability 13, no. 5: 2707. https://doi.org/10.3390/su13052707
APA StyleSaberi, H., Nazaripouya, H., & Mehraeen, S. (2021). Implementation of a Stable Solar-Powered Microgrid Testbed for Remote Applications. Sustainability, 13(5), 2707. https://doi.org/10.3390/su13052707







