Gaussian Kernel Methods for Seismic Fragility and Risk Assessment of Mid-Rise Buildings
Abstract
1. Introduction
2. Case Study Description
2.1. Structural Models
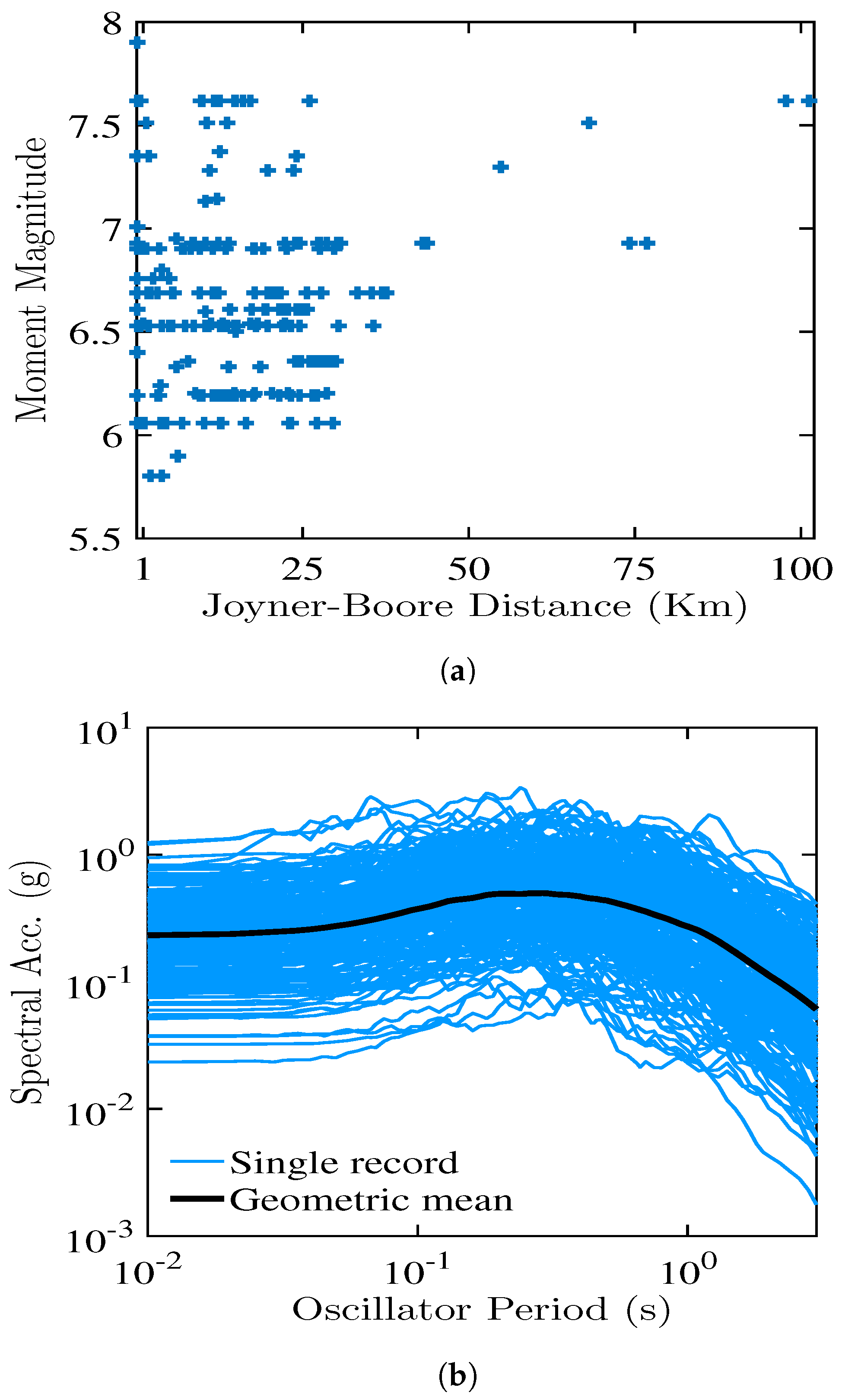
2.2. Ground Motion Records
2.3. Seismic Response Analyses
3. Data-Driven Seismic Response Modeling Using Gaussian Kernels
3.1. Overview of the Kernel Function in Kernel Regression
3.2. Predictive Models for Median Structural Response
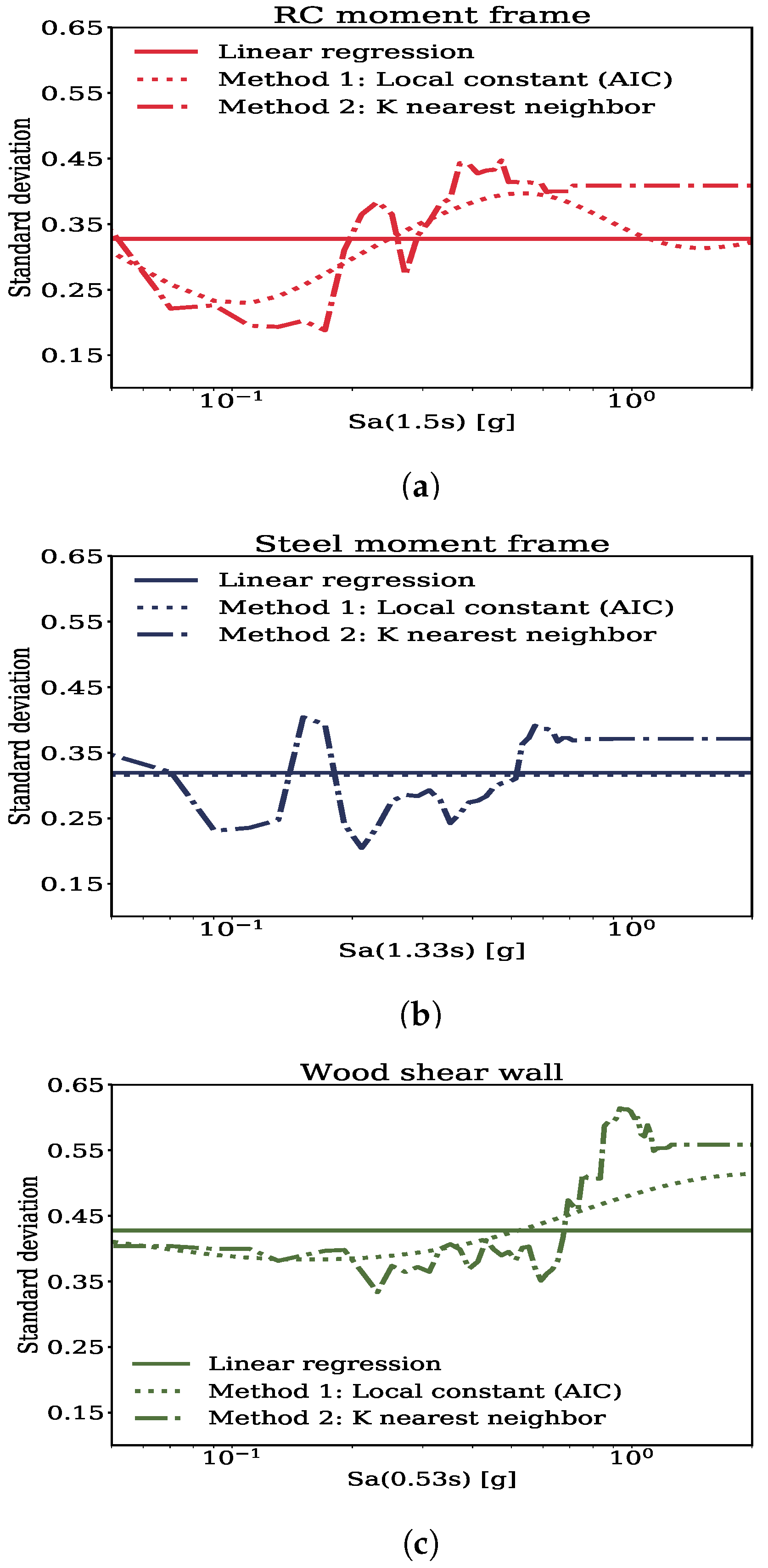
3.3. Predictive Models for Standard Deviation around the Median Response
3.4. Characterizing the Distribution of Peak Interstory Drift Prediction Residuals
- At each IM level, K residuals nearest to the IM level are selected using a nearest neighbor algorithm with uniform weights.
- The K samples are randomly divided into training and test subsets in 77–33 proportion thirty times.
- The standard deviation variation across the different IM levels is independently computed for the training and the test subsets across all the thirty partitions.
- Then, the sum of squared differences (SSD) between the standard deviation from training and test subsets is averaged across the thirty partitions:where, M is the number of IM levels and is the standard deviation.
- For a low K, the SSD value would be high due to overfitting. As the K increases, the SSD starts decreasing as enough samples are available in the training and test subsets to predict similar standard deviation variations across the IM levels. The K at which the reduction in SSD starts being small is the one required for subsequent analysis.
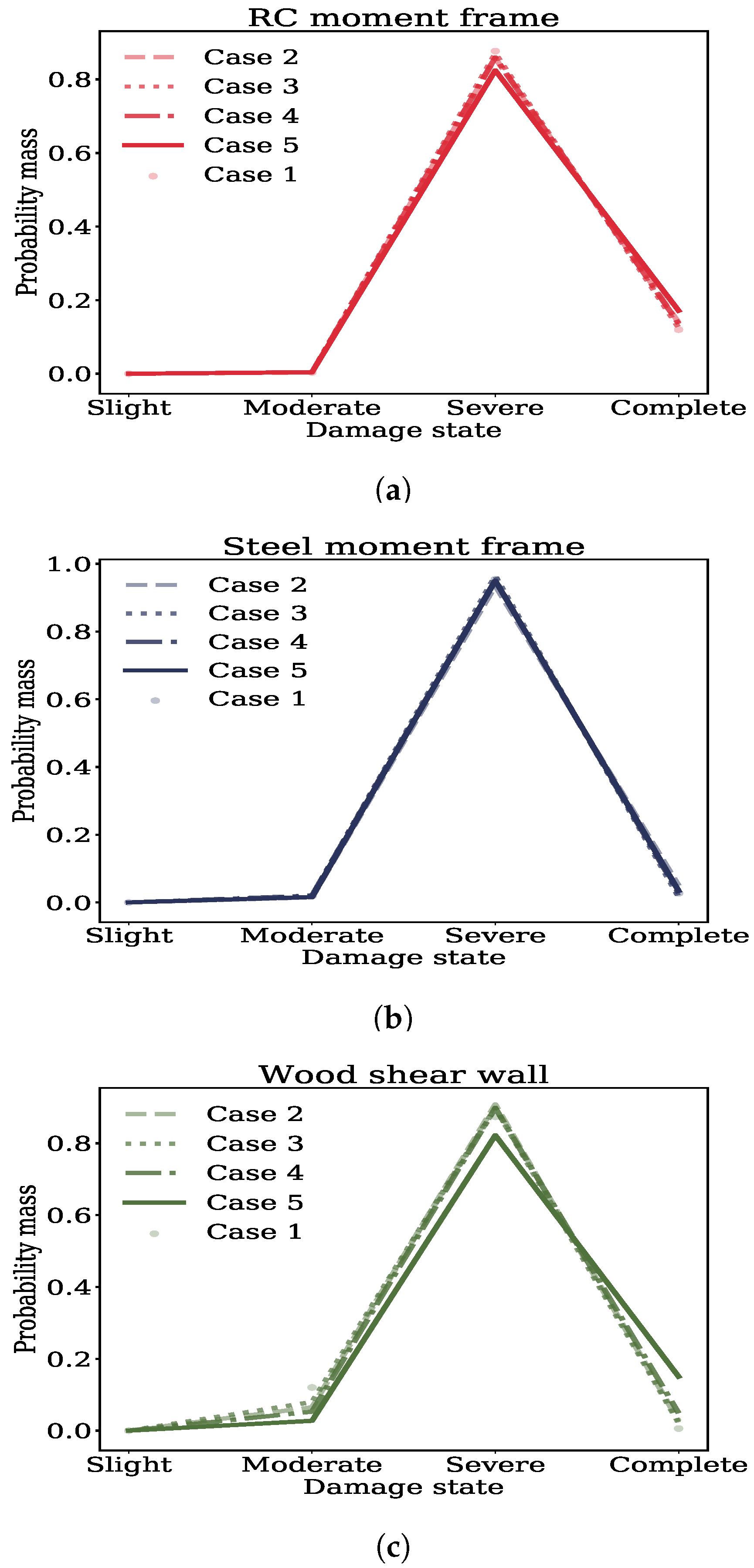
4. Impacts on Fragility Functions
4.1. Cases and Drift Limits for Fragility Evaluation
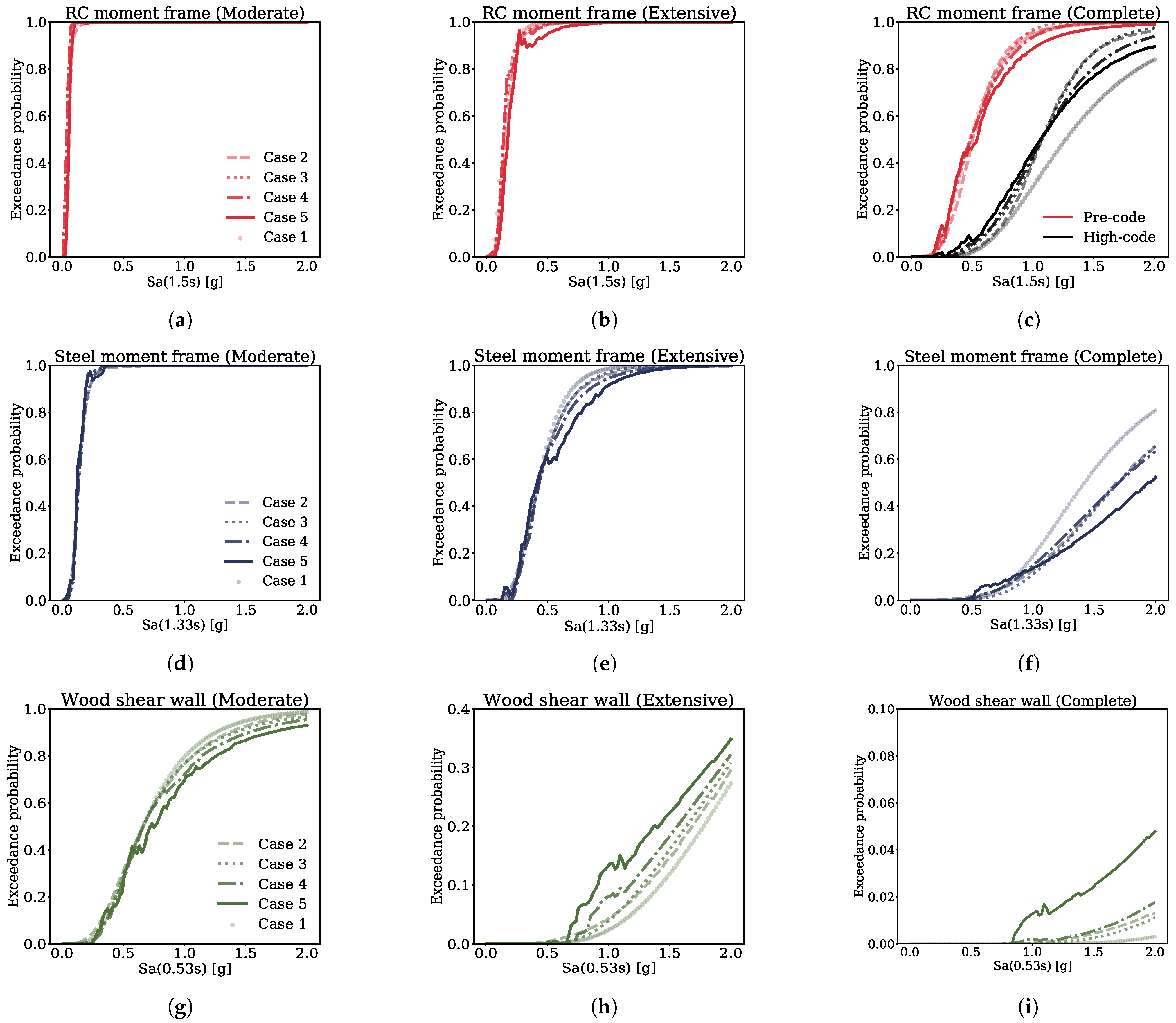
4.2. Computing the Fragility Functions Using the Different Cases
4.3. Results
5. Impacts on Seismic Risk Quantified through the Demand and Loss Hazards
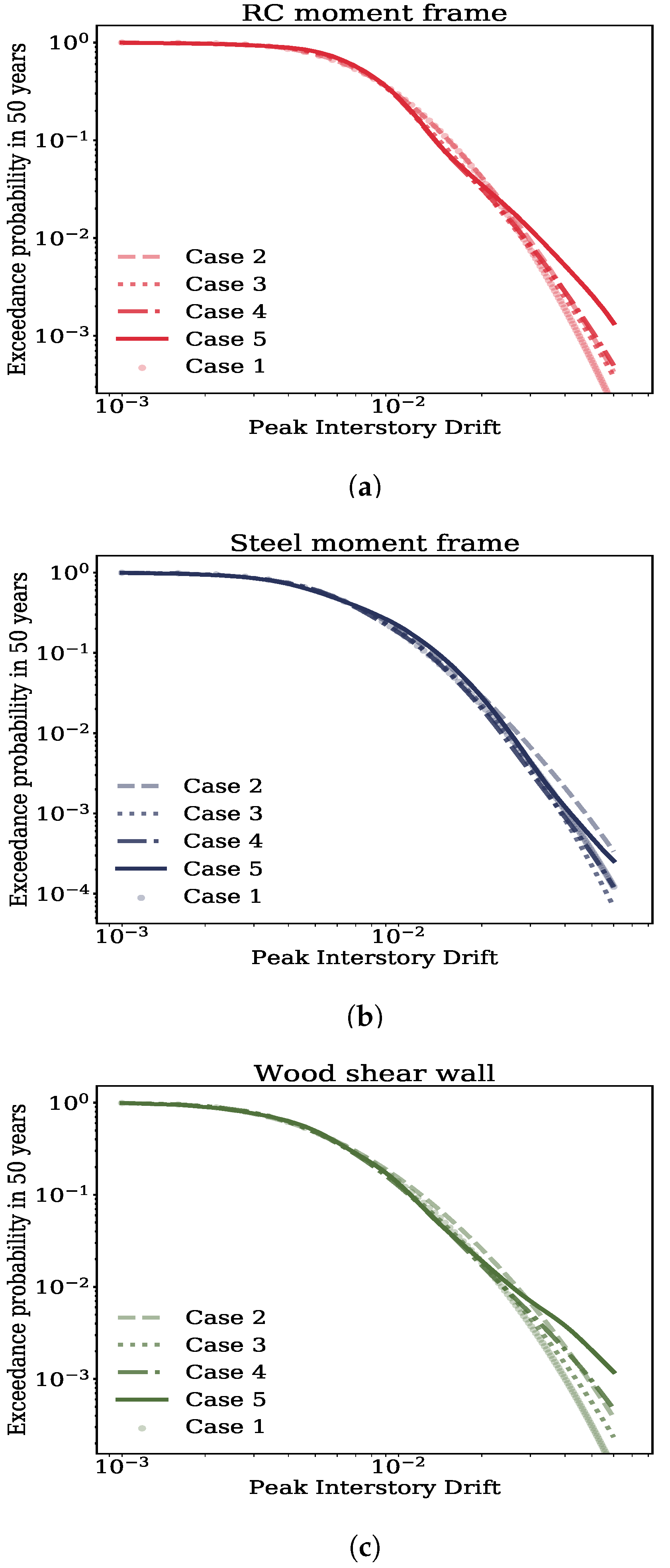
5.1. Results: Demand Hazard
5.2. Results: Loss Hazard
6. Summary and Conclusions
- For characterizing the relation between response and intensity, local linear regression with LS-CV bandwidth criterion was considered since it made more physical predictions of response within the intensity bounds of interest.
- Variation of standard deviation with the intensity was captured using local constant regression with AIC bandwidth criterion since it predicted constant estimates of standard deviation beyond the data bounds and this is more conservative.
- Distribution of residuals were characterized using a Gaussian kernel density given the residuals closest to the input intensity level. These closest residuals were selected using the K Nearest Neighbor algorithm with a conservative value for K to avoid over-fitting.
- The compounded effects of alleviating the assumptions made by linear regression on fragilities is more significant than any of those individually.
- Alleviating the linear regression assumptions impact the Complete damage state to a significant extent and the Severe damage state to a marginal extent but not any of the lower damage states.
- For all practical purposes, linear regression assumptions seem to have lesser impacts on the loss hazard, even for large downtime levels. Deaggregation of the loss hazard at a large downtime level revealed that these subtle impacts are due to the concentration of probability mass mostly in the Severe damage state. For this damage state, it was noted that the assumptions made by linear regression had marginal impacts on the fragility functions.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bruneau, M.; Chang, S.; Eguchi, R.; Lee, G.; O’Rourke, T.; Reinhorn, A.; Shinozuka, M.; Tierney, K.; Wallace, W.; Von Winterfeldt, D. A framework to quantitatively assess and enhance the seismic resilience of communities. Earthq. Spectra 2003, 4, 733–752. [Google Scholar] [CrossRef]
- Cimellaro, G.; Reinhorn, A.; Bruneau, M. Framework for analytical quantification of disaster resilience. Eng. Struct. 2010, 32, 3639–3649. [Google Scholar] [CrossRef]
- Burton, H.; Deierlein, G.; Lallemant, D.; Lin, T. Framework for Incorporating Probabilistic Building Performance in the Assessment of Community Seismic Resilience. J. Struct. Eng. 2016, 142, C4015007. [Google Scholar] [CrossRef]
- Dhulipala, S.; Flint, M. Series of semi-Markov processes to model infrastructure resilience under multihazards. Reliab. Eng. Syst. Saf. 2020, 193, 106659. [Google Scholar] [CrossRef]
- Kia, M.; Banazadeh, M.; Bayat, M. Rapid seismic vulnerability assessment by new regression-based demand and collapse models for steel moment frames. Earthq. Struct. 2018, 14, 203–214. [Google Scholar]
- Kia, M.; Banazadeh, M.; Bayat, M. Rapid seismic loss assessment using new probabilistic demand and consequence models. Bull. Earthq. Eng. 2019, 17, 3545–3572. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Cornell, A.C. Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- Jalayer, F.; Cornell, C. Alternative non-linear demand estimation methods for probability-based seismic assessments. Earthq. Eng. Struct. Dyn. 2009, 38, 951–972. [Google Scholar] [CrossRef]
- Baker, J.W. Efficient Analytical Fragility Function Fitting Using Dynamic Structural Analysis. Earthq. Spectra 2015, 31, 579–599. [Google Scholar] [CrossRef]
- Luco, N.; Cornell, C.A. Structure-specific scalar intensity measures for near-source and ordinary earthquake ground motions. Earthq. Spectra 2007, 23, 357–392. [Google Scholar] [CrossRef]
- Jalayer, F. Direct Probabilistic Seismic Analysis: Implementing Non-Linear Dynamic Assessments. Ph.D. Thesis, Stanford University, Menlo Park, CA, USA, 2003. [Google Scholar]
- Luco, N.; Bazzurro, P. Does amplitude scaling of ground motion records result in biased nonlinear structural drift responses? Earthq. Eng. Struct. Dyn. 2007, 36, 1813–1835. [Google Scholar] [CrossRef]
- Dávalos, H.; Miranda, E. Evaluation of bias on the probability of collapse from amplitude scaling using spectral-shape-matched records. Earthq. Eng. Struct. Dyn. 2019, 48, 970–986. [Google Scholar] [CrossRef]
- Tubaldi, E.; Freddi, F.; Barbato, M. Probabilistic seismic demand model for pounding risk assessment. Earthq. Eng. Struct. Dyn. 2016, 45, 1743–1758. [Google Scholar] [CrossRef]
- Modica, A.; Stafford, P. Vector fragility surfaces for reinforced concrete frames in Europe. Bull. Earthq. Eng. 2014, 12, 1725–1753. [Google Scholar] [CrossRef]
- Chu, M.; Katerina, K.; Sudret, B. Seismic fragility curves for structures using non-parametric representations. Front. Struct. Civ. Eng. 2017, 11, 169–186. [Google Scholar]
- Moehle, J.; Deierlein, G.G. A framework methodology for performance-based earthquake engineering. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Trifunac, M.; Ivanović, S.; Todorovska, M. Instrumented 7-Story Reinforced Concrete Building in Van Nuys, California: Description of the Damage from the 1994 Northridge Earthquake and Strong Motion Data; Technical Report; University of Southern California: Los Angeles, CA, USA, 1999. [Google Scholar]
- Krawinkler, H. Van Nuys Hotel Building Testbed Report: Exercising Seismic Performance Assessment; Technical Report; Pacific Earthquake Engineering Research (PEER) Center: Berkeley, CA, USA, 2005. [Google Scholar]
- Mazzoni, S.; McKenna, F.; Scott, M.H.; Fenves, G.L. Open System for Earthquake Engineering Simulation (OpenSEES); Technical Report; Pacific Earthquake Engineering Research (PEER) Center: Berkeley, CA, USA, 2006. [Google Scholar]
- Kalkan, E. Available online: www.quakelogic.net/research (accessed on 15 August 2019).
- Paspuleti, C. Seismic Analysis of an Older Reinforced Concrete Frame. Master’s Thesis, University of Washington, Washington, DC, USA, 2002. [Google Scholar]
- Lignos, D. Sidesway Collapse of Deteriorating Structural Systems under Seismic Excitations. Ph.D. Thesis, Stanford University, Menlo Park, CA, USA, 2008. [Google Scholar]
- Eads, L. Seismic Collapse Risk Assessment of Buildings: Effects of Intensity Measure Selection and Computational Approach. Ph.D. Thesis, Stanford University, Menlo Park, CA, USA, 2013. [Google Scholar]
- Ibarra, L.F.; Medina, R.A.; Krawinkler, H. Hysteretic models that incorporate strength and stiffness deterioration. Earthq. Eng. Struct. Dyn. 2005, 34, 1489–1511. [Google Scholar] [CrossRef]
- Jayamon, J.R. Seismic Performance Assessment of Wood-Frame Shear Wall Structures. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 2017. [Google Scholar]
- Folz, B.; Filiatrault, A. SAWS—Version 1.0, A Computer Program for the Seismic Analysis of Woodframe Structures; Technical Report; Consortium of Universities for Research in Earthquake Engineering: Richmond, CA, USA, 2001. [Google Scholar]
- Ancheta, T.; Darragh, R.; Stewart, J.; Seyhan, E.; Silva, W.; Chiou, B.; Wooddell, K.; Graves, R.; Kottke, A.; Boore, D.; et al. NGA-West2 database. Earthq. Spectra 2014, 30, 989–1005. [Google Scholar] [CrossRef]
- Sehhati, R.; Rodriguez-Marek, A.; ElGawady, M.; Cofer, W. Effects of near-fault ground motions and equivalent pulses on multi-story structures. Eng. Struct. 2011, 33, 767–779. [Google Scholar] [CrossRef]
- Archila, M.; Ventura, C.E.; Liam Finn, W.D. New insights on effects of directionality and duration of near-field ground motions on seismic response of tall buildings. Struct. Des. Tall Spec. Build. 2017, 26, e1363. [Google Scholar] [CrossRef]
- Dhulipala, S.; Rodriguez-Marek, A.; Ranganathan, S.; Flint, M. A site-consistent method to quantify sufficiency of alternative IMs in relation to PSDA. Earthq. Eng. Struct. Dyn. 2018, 47, 377–396. [Google Scholar] [CrossRef]
- Dhulipala, S. Bayesian Methods for Intensity Measure and Ground Motion Selection in Performance-Based Earthquake Engineering. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 2019. [Google Scholar]
- Racine, J. Nonparametric econometrics: A primer. Found. Trends Econom. 2008, 3, 1–88. [Google Scholar] [CrossRef]
- Noh, H.; Lallemant, D.; Kiremidjian, A. Development of empirical and analytical fragility functions using kernel smoothing methods. Earthq. Eng. Struct. Dyn. 2015, 44, 1163–1180. [Google Scholar] [CrossRef]
- Loader, C. Bandwidth selection: Classical or plug-in? Ann. Stat. 1999, 27, 415–438. [Google Scholar] [CrossRef]
- Al Mamun, A.; Saatcioglu, M. Seismic fragility analysis of pre-1975 conventional concrete frame buildings in Canada. Can. J. Civ. Eng. 2018, 45, 728–738. [Google Scholar] [CrossRef]
- Muller, H.; Stadtmuller, U. Variable bandwidth kernel estimators of regression curves. Annal. Stat. 1987, 15, 182–201. [Google Scholar] [CrossRef]
- Hassanat, A.; Abbadi, M.; Altarawneh, G.; Alhasanat, A. Solving the Problem of the K Parameter in the KNN Classifier Using an Ensemble Learning Approach. arXiv 2014, arXiv:1409.0919. [Google Scholar]
- FEMA. Multi-Hazard Loss Estimation Methodology Earthquake Model (HAZUS-MH MR5): Technical Manual; Technical Report; Federal Emergency Management Agency: Washington, DC, USA, 2010. [Google Scholar]
- Field, E.; Jordan, T.; Cornell, C. OpenSHA: A developing community-modeling environment for seismic hazard analysis. Seismol. Res. Lett. 2003, 74, 406–419. [Google Scholar] [CrossRef]
- Boore, D.M.; Atkinson, G.M. Ground-motion prediction equations for the average horizontal component of PGA, PGV, and 5%-damped PSA at spectral periods between 0.01 s and 10.0 s. Earthq. Spectra 2008, 24, 99–138. [Google Scholar] [CrossRef]








| Predictive Model for Mean Response | Predictive Model for Standard Deviation | Distribution of Residuals | Plot Type | |
|---|---|---|---|---|
| Case 1 | Log-linear | Constant | Gaussian distribution | Circles |
| Case 2 | Kernel regression: local linear (LS-CV) | Constant | Gaussian kernel density | Dashdot |
| Case 3 | Kernel regression: local linear (LS-CV) | Kernel regression: local constant (AIC) | Gaussian distribution | Dotted |
| Case 4 | Kernel regression: local linear (LS-CV) | K nearest neighbor | Gaussian distribution | Dashed |
| Case 5 | Kernel regression: local linear (LS-CV) | K nearest neighbor | Gaussian kernel density | Solid |
| Structure Type | DS 1: Slight | DS 2: Moderate | DS 3: Extensive | DS 4: Complete |
|---|---|---|---|---|
| RC moment frame | 0.0027 | 0.0043 | 0.0107 | 0.0267 0.0533 (High) |
| Steel moment frame | 0.004 | 0.008 | 0.02 | 0.0533 |
| Wood shear wall | 0.004 | 0.012 | 0.04 | 0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dhulipala, S.L.N. Gaussian Kernel Methods for Seismic Fragility and Risk Assessment of Mid-Rise Buildings. Sustainability 2021, 13, 2973. https://doi.org/10.3390/su13052973
Dhulipala SLN. Gaussian Kernel Methods for Seismic Fragility and Risk Assessment of Mid-Rise Buildings. Sustainability. 2021; 13(5):2973. https://doi.org/10.3390/su13052973
Chicago/Turabian StyleDhulipala, Somayajulu L. N. 2021. "Gaussian Kernel Methods for Seismic Fragility and Risk Assessment of Mid-Rise Buildings" Sustainability 13, no. 5: 2973. https://doi.org/10.3390/su13052973
APA StyleDhulipala, S. L. N. (2021). Gaussian Kernel Methods for Seismic Fragility and Risk Assessment of Mid-Rise Buildings. Sustainability, 13(5), 2973. https://doi.org/10.3390/su13052973






