Spatial-Temporal Flows-Adaptive Street Layout Control Using Reinforcement Learning
Abstract
:1. Introduction
2. Literature Review
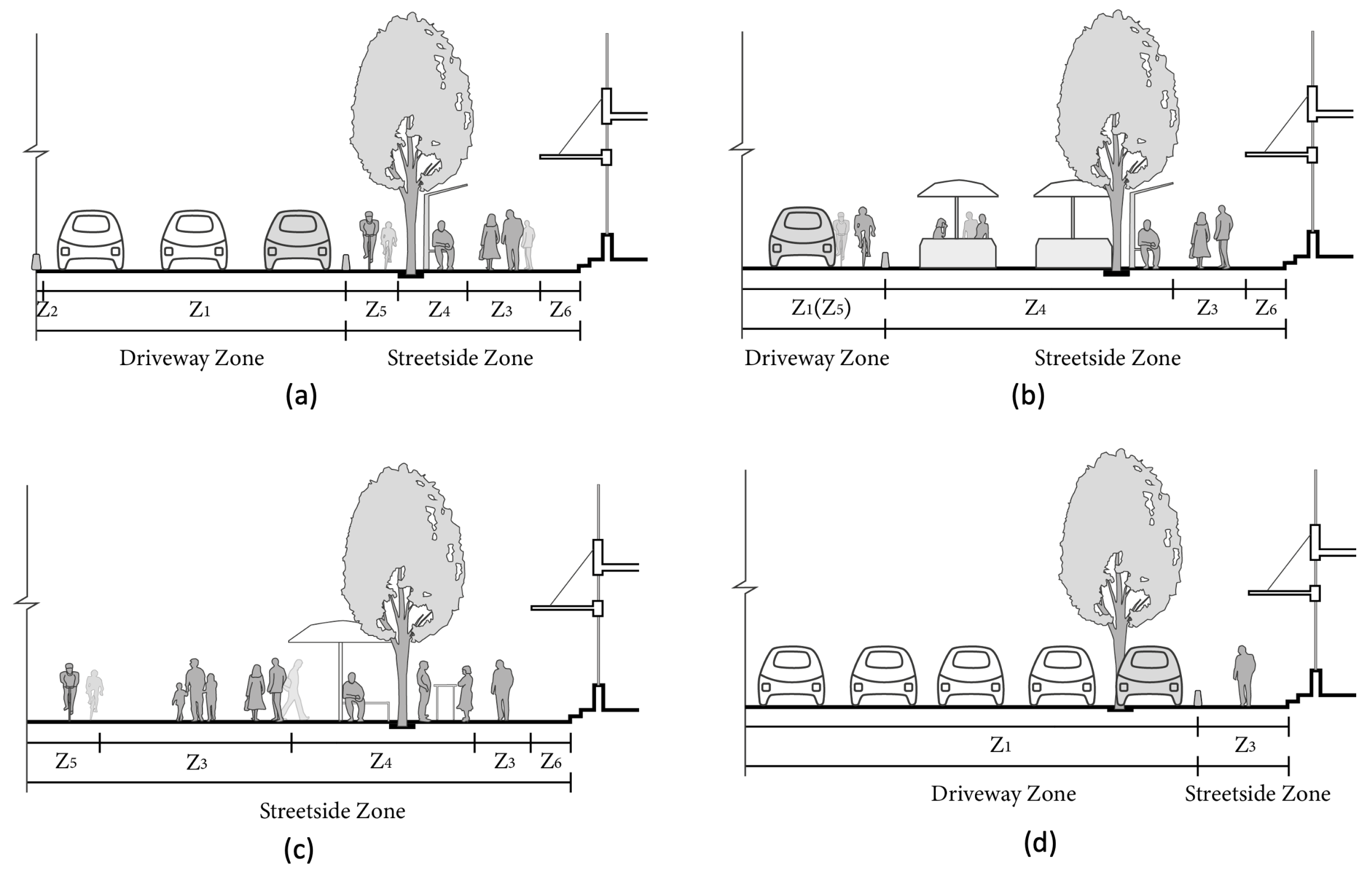
2.1. Public Right-of-Way of Complete Streets Scheme
2.2. Challenges Facing Complete Streets Scheme
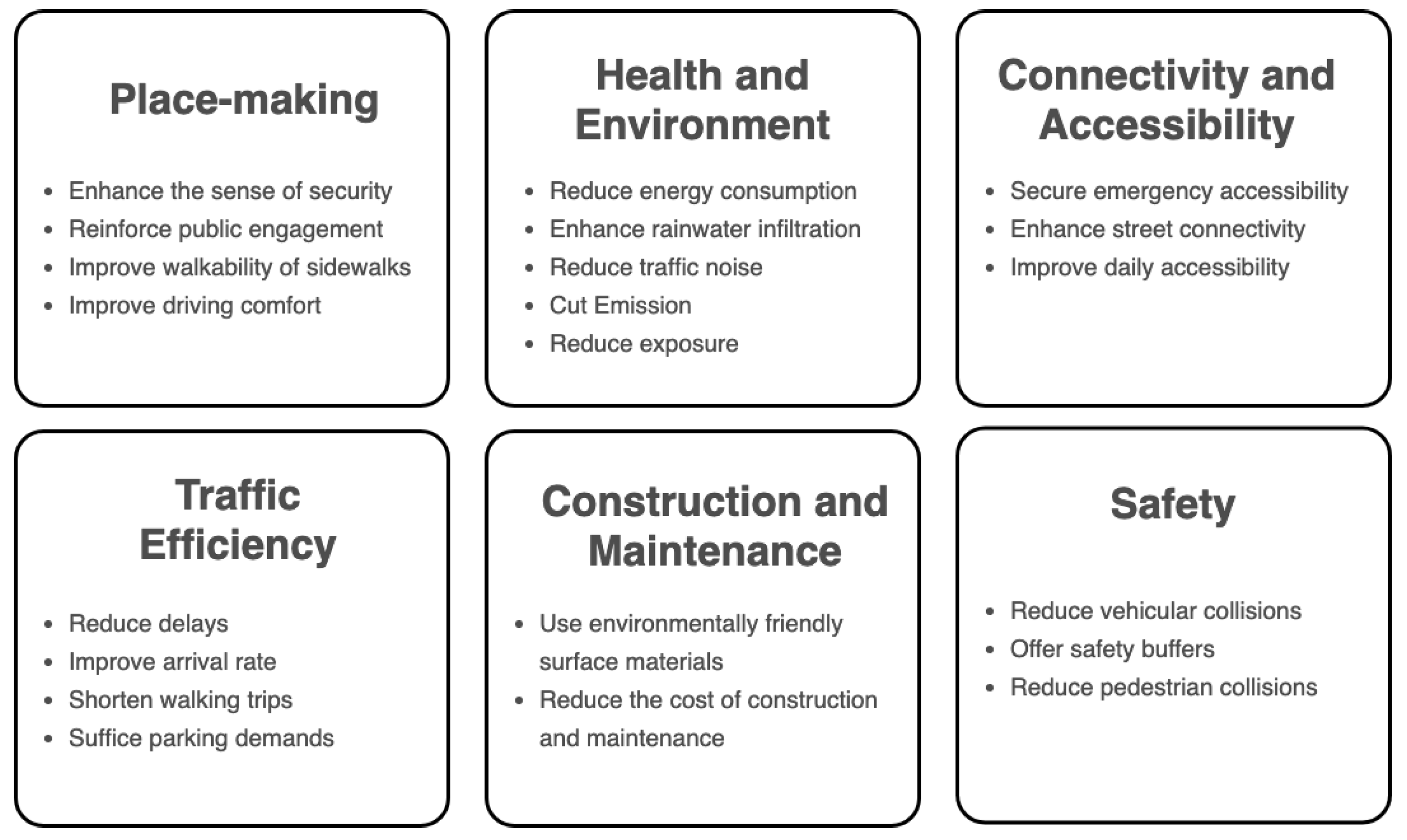
2.3. Performance Metrics Regarding Street Design and Management
2.4. Summary of Literature Review
3. Preliminaries of Reinforcement Learning
3.1. Reinforcement Learning and Markov Decision Process
3.2. Deep Deterministic Policy Gradient (DDPG) Algorithm
4. Methodology
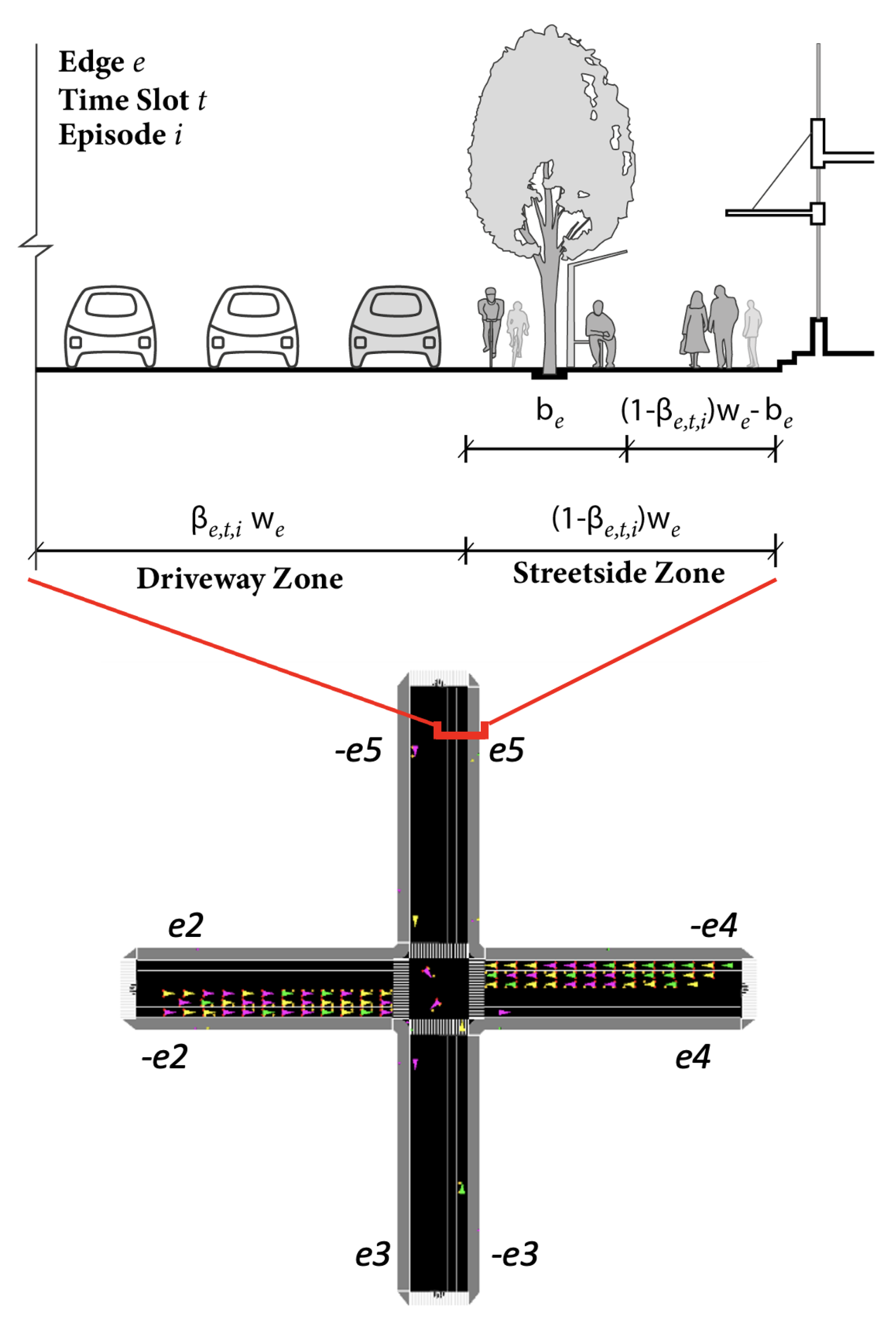
4.1. Modelling Formulation
4.2. SUMO Traffic Simulation Incorporated DDPG Modelling Framework
4.3. DDPG Algorithm Structure
4.3.1. State
4.3.2. Action
4.3.3. Reward
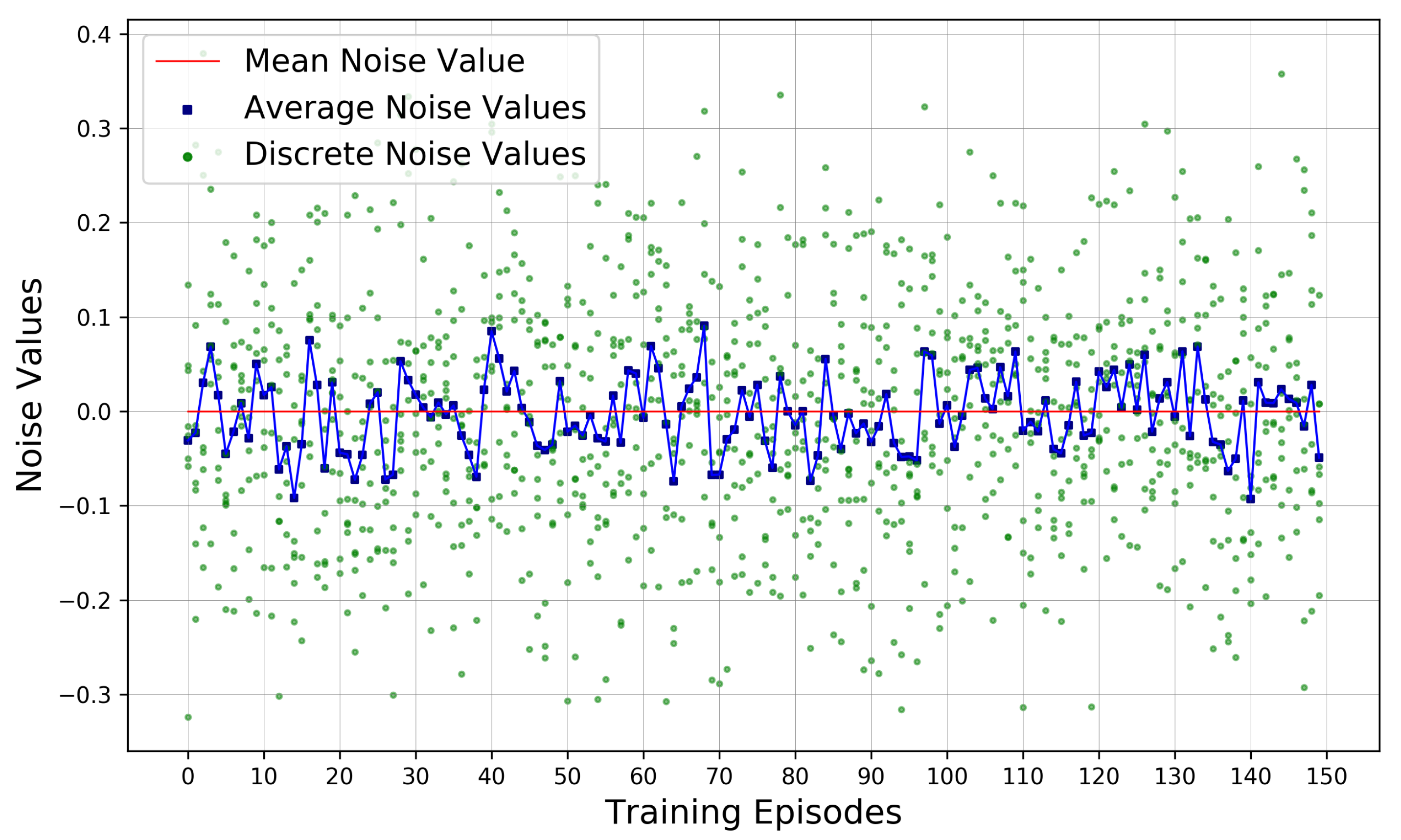
4.3.4. Experience Replay Buffer
4.3.5. Actor Networks
4.3.6. Critic Networks
4.3.7. Keras Neural Networks
5. Model Training and Results
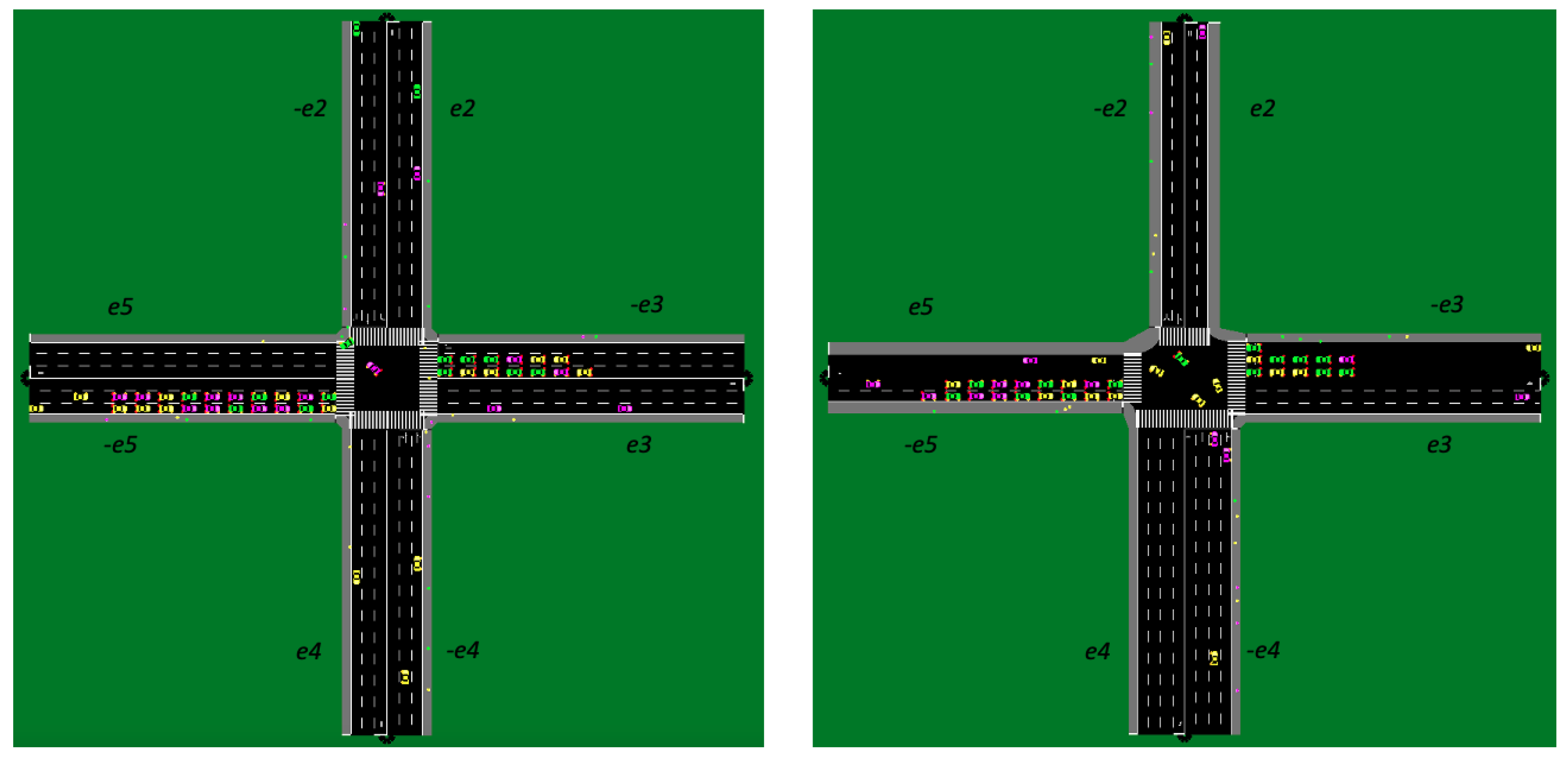
5.1. Specification of Travel Plans and Testing Case
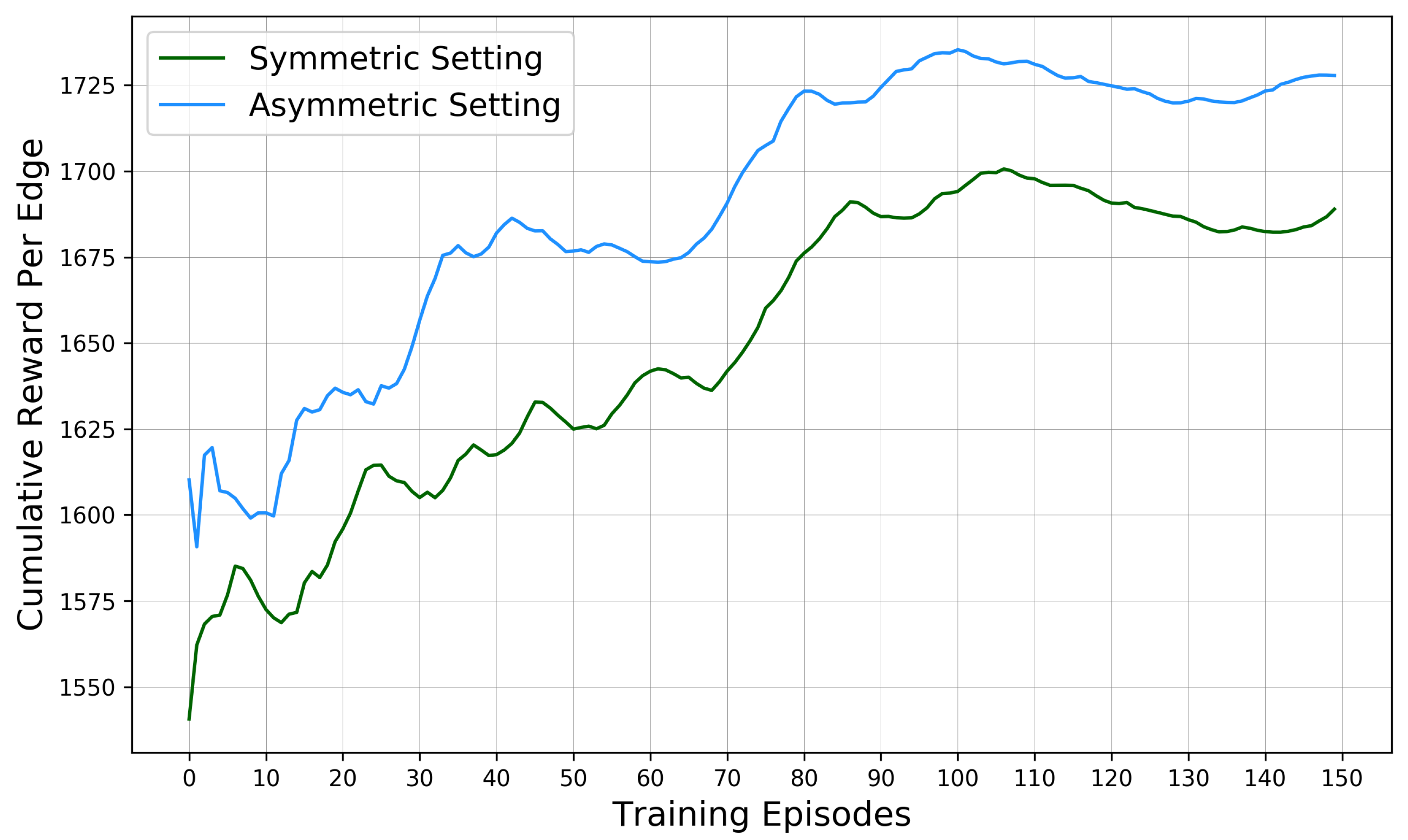
5.2. Training Performance of SUMO-DDPG
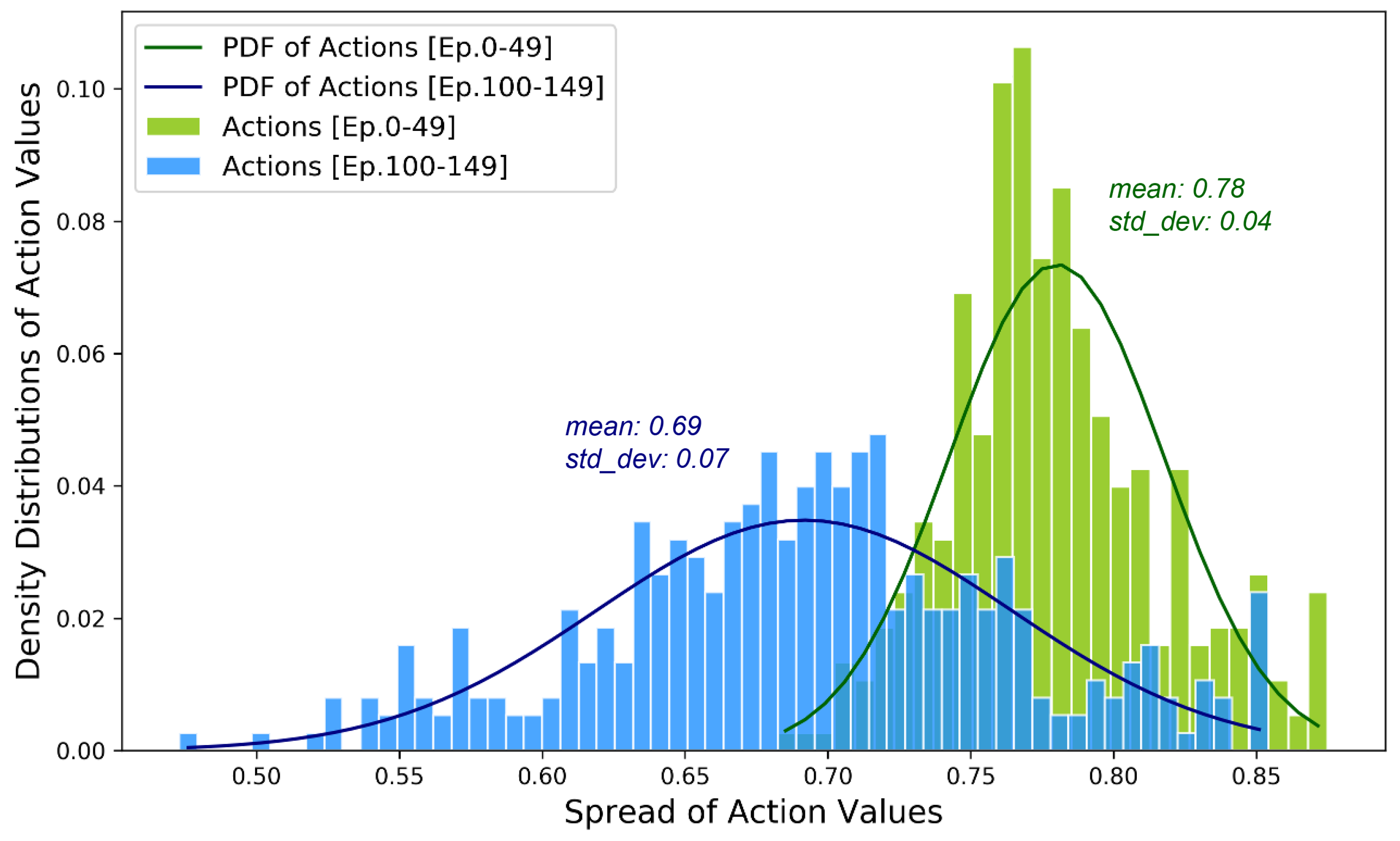
5.3. Improved ROW Assignment Strategies
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ROW | Right-of-Way |
| AV | Autonomous Vehicles |
| RL | Reinforcement Learning |
| MDP | Markov Decision Process |
| DPG | Deterministic Policy Gradient method |
| DDPG | Deep Deterministic Policy Gradient algorithm |
| SUMO | Simulation of Urban Mobility software |
| OU | Ornstein–Uhlenbeck |
References
- Prytherch, D.L. Legal geographies—Codifying the right-of-way: Statutory geographies of urban mobility and the street. Urban Geogr. 2012, 33, 295–314. [Google Scholar] [CrossRef]
- Shinar, D. Safety and mobility of vulnerable road users: Pedestrians, bicyclists, and motorcyclists. Accid. Anal. Prev. 2011, 44, 1–2. [Google Scholar] [CrossRef] [PubMed]
- Slinn, M.; Matthews, P.; Guest, P. Traffic Engineering Design. Principles and Practice; Taylor & Francis: Milton Park, UK, 1998. [Google Scholar]
- Donais, F.M.; Abi-Zeid, I.; Waygood, E.O.D.; Lavoie, R. Assessing and ranking the potential of a street to be redesigned as a Complete Street: A multi-criteria decision aiding approach. Transp. Res. Part A Policy Pract. 2019, 124, 1–19. [Google Scholar] [CrossRef]
- Hui, N.; Saxe, S.; Roorda, M.; Hess, P.; Miller, E.J. Measuring the completeness of complete streets. Transp. Rev. 2018, 38, 73–95. [Google Scholar] [CrossRef]
- McCann, B. Completing Our Streets: The Transition to Safe and Inclusive Transportation Networks; Island Press: Washington, DC, USA, 2013. [Google Scholar]
- O’Flaherty, C.A. Transport Planning and Traffic Engineering; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Mofolasayo, A. Complete Street concept, and ensuring safety of vulnerable road users. Transp. Res. Procedia 2020, 48, 1142–1165. [Google Scholar] [CrossRef]
- Dumbaugh, E.; King, M. Engineering Livable Streets: A Thematic Review of Advancements in Urban Street Design. J. Plan. Lit. 2018, 33, 451–465. [Google Scholar] [CrossRef]
- Desai, M. Reforming Complete Streets: Considering the Street as Place. Ph.D. Thesis, University of Cincinnati, Cincinnati, OH, USA, 2015. [Google Scholar]
- Loukaitou-Sideris, A.; Brozen, M.; Abad Ocubillo, R.; Ocubillo, K. Reclaiming the Right-of-Way Evaluation Report: An Assessment of the Spring Street Parklets; Technical Report; UCLA: Los Angeles, CA, USA, 2013. [Google Scholar]
- Ewing, R.; Brown, S.J. US Traffic Calming Manual; Routledge: London, UK, 2017. [Google Scholar]
- Wolf, S.A.; Grimshaw, V.E.; Sacks, R.; Maguire, T.; Matera, C.; Lee, K.K. The impact of a temporary recurrent street closure on physical activity in New York City. J. Urban Health 2015, 92, 230–241. [Google Scholar] [CrossRef] [Green Version]
- Fischer, J.; Winters, M. COVID-19 street reallocation in mid-sized Canadian cities: Socio-spatial equity patterns. Can. J. Public Health 2021, 112, 376–390. [Google Scholar] [CrossRef]
- González-González, E.; Nogués, S.; Stead, D. Automated vehicles and the city of tomorrow: A backcasting approach. Cities 2019, 94, 153–160. [Google Scholar] [CrossRef] [Green Version]
- Sadik-Khan, J.; Reynolds, S.; Hutcheson, R.; Carroll, M.; Spillar, R.; Barr, J. Blueprint for Autonomous Urbanism: Second Edition; Technical Report; National Association of City Transportation Officials: New York, NY, USA, 2017. [Google Scholar]
- Hungness, D.; Bridgelall, R. Model Contrast of Autonomous Vehicle Impacts on Traffic. J. Adv. Transp. 2020, 2020, 8935692. [Google Scholar] [CrossRef]
- Moavenzadeh, J.; Lang, N.S. Reshaping Urban Mobility with Autonomous Vehicles: Lessons from the City of Boston; World Economic Forum: New York, NY, USA, 2018. [Google Scholar]
- Zhang, W.; Wang, K. Parking futures: Shared automated vehicles and parking demand reduction trajectories in Atlanta. Land Use Policy 2020, 91, 103963. [Google Scholar] [CrossRef]
- Anastasiadis, E.; Angeloudis, P.; Ainalis, D.; Ye, Q.; Hsu, P.Y.; Karamanis, R.; Escribano Macias, J.; Stettler, M. On the Selection of Charging Facility Locations for EV-Based Ride-Hailing Services: A Computational Case Study. Sustainability 2021, 13, 168. [Google Scholar] [CrossRef]
- Yu, B.; Xu, C.Z. Admission control for roadside unit access in intelligent transportation systems. In Proceedings of the 2009 17th International Workshop on Quality of Service, Charleston, SC, USA, 13–15 July 2009; pp. 1–9. [Google Scholar]
- Liu, Y.; Ye, Q.; Feng, Y.; Escribano-Macias, J.; Angeloudis, P. Location-routing Optimisation for Urban Logistics Using Mobile Parcel Locker Based on Hybrid Q-Learning Algorithm. arXiv 2021, arXiv:2110.15485. [Google Scholar]
- Chu, T.; Wang, J.; Codecà, L.; Li, Z. Multi-agent deep reinforcement learning for large-scale traffic signal control. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1086–1095. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Ke, L.; Qiao, Z.; Chai, X. Large-scale traffic signal control using a novel multiagent reinforcement learning. IEEE Trans. Cybern. 2020, 51, 174–187. [Google Scholar] [CrossRef]
- Wei, H.; Liu, X.; Mashayekhy, L.; Decker, K. Mixed-Autonomy Traffic Control with Proximal Policy Optimization. In Proceedings of the 2019 IEEE Vehicular Networking Conference (VNC), Honolulu, HI, USA, 22–25 September 2019; pp. 1–8. [Google Scholar]
- Keyue, G. Analysis Right-of-Way Concept of Urban Road Width. Urban Transp. China 2012, 10, 62–67. [Google Scholar]
- National Association of City Transportation Officials. Global Street Design Guide; Island Press: Washington, DC, USA, 2016. [Google Scholar]
- Urban Planning Society of China. Street Design Guideline. Available online: http://www.planning.org.cn/news/uploads/2021/03/6062c223067b9_1617084963.pdf (accessed on 7 April 2021).
- National Association of City Transportation Office. Urban Street Design Guide. Available online: https://nacto.org/publication/urban-street-design-guide/ (accessed on 7 April 2021).
- Department for Transport, United Kingdom. Manual for Streets. Available online: https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/341513/pdfmanforstreets.pdf (accessed on 7 April 2021).
- Hamilton-Baillie, B. Shared space: Reconciling people, places and traffic. Built Environ. 2008, 34, 161–181. [Google Scholar] [CrossRef] [Green Version]
- Beske, J. Placemaking. In Suburban Remix; Springer; Island Press: Washington, DC, USA, 2018; pp. 266–289. [Google Scholar]
- Schlossberg, M.; Millard-Ball, A.; Shay, E.; Riggs, W.B. Rethinking the Street in an Era of Driverless Cars; Technical Report; University of Oregon: Eugene, OR, USA, 2018. [Google Scholar]
- Meeder, M.; Bosina, E.; Weidmann, U. Autonomous vehicles: Pedestrian heaven or pedestrian hell. In Proceedings of the 17th Swiss Transport Research Conference, Ascona, Switzerland, 17–19 May 2017; pp. 17–19. [Google Scholar]
- Javanshour, F.; Dia, H.; Duncan, G. Exploring system characteristics of autonomous mobility on-demand systems under varying travel demand patterns. In Intelligent Transport Systems for Everyone’s Mobility; Springer: Singapore, 2019; pp. 299–315. [Google Scholar]
- Javanshour, F.; Dia, H.; Duncan, G.; Abduljabbar, R.; Liyanage, S. Performance Evaluation of Station-Based Autonomous On-Demand Car-Sharing Systems. IEEE Trans. Intell. Transp. Syst. 2021. [Google Scholar] [CrossRef]
- Kondor, D.; Santi, P.; Basak, K.; Zhang, X.; Ratti, C. Large-scale estimation of parking requirements for autonomous mobility on demand systems. arXiv 2018, arXiv:1808.05935. [Google Scholar]
- Sabar, N.R.; Chung, E.; Tsubota, T.; de Almeida, P.E.M. A memetic algorithm for real world multi-intersection traffic signal optimisation problems. Eng. Appl. Artif. Intell. 2017, 63, 45–53. [Google Scholar] [CrossRef]
- Sánchez-Medina, J.J.; Galán-Moreno, M.J.; Rubio-Royo, E. Traffic signal optimization in “La Almozara” district in Saragossa under congestion conditions, using genetic algorithms, traffic microsimulation, and cluster computing. IEEE Trans. Intell. Transp. Syst. 2009, 11, 132–141. [Google Scholar] [CrossRef]
- Aragon-Gómez, R.; Clempner, J.B. Traffic-signal control reinforcement learning approach for continuous-time markov games. Eng. Appl. Artif. Intell. 2020, 89, 103415. [Google Scholar] [CrossRef]
- Brauers, W.K.M.; Zavadskas, E.K.; Peldschus, F.; Turskis, Z. Multi-objective decision-making for road design. Transport 2008, 23, 183–193. [Google Scholar] [CrossRef]
- Vaudrin, F.; Erdmann, J.; Capus, L. Impact of autonomous vehicles in an urban environment controlled by static traffic lights system. Proc. Sumo. Simul. Auton. Mobil. 2017, 81, 81–90. [Google Scholar]
- Puiutta, E.; Veith, E.M. Explainable reinforcement learning: A survey. In International Cross-Domain Conference for Machine Learning and Knowledge Extraction; Springer: Cham, Switzerland, 2020; pp. 77–95. [Google Scholar]
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement learning: A survey. J. Artif. Intell. Res. 1996, 4, 237–285. [Google Scholar] [CrossRef] [Green Version]
- Qiang, W.; Zhongli, Z. Reinforcement learning model, algorithms and its application. In Proceedings of the 2011 International Conference on Mechatronic Science, Electric Engineering and Computer (MEC), Budapest, Hungary, 3–7 July 2011; pp. 1143–1146. [Google Scholar]
- Saravanan, M.; Ganeshkumar, P. Routing using reinforcement learning in vehicular ad hoc networks. Comput. Intell. 2020, 36, 682–697. [Google Scholar] [CrossRef]
- Passalis, N.; Tefas, A. Continuous drone control using deep reinforcement learning for frontal view person shooting. Neural Comput. Appl. 2020, 32, 4227–4238. [Google Scholar] [CrossRef]
- Wu, C.; Kreidieh, A.; Parvate, K.; Vinitsky, E.; Bayen, A.M. Flow: Architecture and benchmarking for reinforcement learning in traffic control. arXiv 2017, arXiv:1710.05465. [Google Scholar]
- Sutton, R.S.; McAllester, D.A.; Singh, S.P.; Mansour, Y. Policy gradient methods for reinforcement learning with function approximation. NIPs. Citeseer 1999, 99, 1057–1063. [Google Scholar]
- Schulman, J.; Moritz, P.; Levine, S.; Jordan, M.; Abbeel, P. High-dimensional continuous control using generalized advantage estimation. arXiv 2015, arXiv:1506.02438. [Google Scholar]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic policy gradient algorithms. In Proceedings of the International Conference on Machine Learning, PMLR, Beijing, China, 21 June 2014; pp. 387–395. [Google Scholar]
- Plappert, M.; Houthooft, R.; Dhariwal, P.; Sidor, S.; Chen, R.Y.; Chen, X.; Asfour, T.; Abbeel, P.; Andrychowicz, M. Parameter space noise for exploration. arXiv 2017, arXiv:1706.01905. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Treiber, M.; Kesting, A. Car-following models based on driving strategies. In Traffic Flow Dynamics; Springer: Berlin/Heidelberg, Germany, 2013; pp. 181–204. [Google Scholar]
- Fernandes, P.; Nunes, U. Platooning of autonomous vehicles with intervehicle communications in SUMO traffic simulator. In Proceedings of the 13th International IEEE Conference on Intelligent Transportation Systems, Funchal, Portugal, 19–22 September 2010; pp. 1313–1318. [Google Scholar]
- Safarov, K.; Kent, T.; Wilson, E.; Richards, A. Emergent Crossing Regimes of Identical Autonomous Vehicles at an Uncontrolled Intersection. arXiv 2021, arXiv:2104.04150. [Google Scholar]
- Crabtree, M.; Lodge, C.; Emmerson, P. A Review of Pedestrian Walking Speeds and Time Needed to Cross the Road. 2015. Available online: https://trid.trb.org/View/1378632 (accessed on 22 November 2021).
- Susilawati, S.; Taylor, M.A.; Somenahalli, S.V. Distributions of travel time variability on urban roads. J. Adv. Transp. 2013, 47, 720–736. [Google Scholar] [CrossRef]
- Bibbona, E.; Panfilo, G.; Tavella, P. The Ornstein–Uhlenbeck process as a model of a low pass filtered white noise. Metrologia 2008, 45, S117. [Google Scholar] [CrossRef]
- Baird, L.; Moore, A.W. Gradient descent for general reinforcement learning. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1999; pp. 968–974. [Google Scholar]



| Notation | Specification | Value | |
|---|---|---|---|
| E | Set of edges | ||
| V | Set of vehicles | ||
| P | Set of pedestrians | ||
| OD | Set of origin-destination pairs | ||
| Sets | V | Set of vehicles on edge e | V V |
| P | Set of pedestrians on edge e | P P | |
| V | Set of vehicles with assignment | V V | |
| P | Set of pedestrians with assignment | P P | |
| CF | following cars of vehicle v | ||
| e | an edge | E | |
| v | a vehicle | V | |
| Indices | p | a pedestrian | P |
| t | a time slot | ||
| an origin-destination pair | OD | ||
| number of lanes on edge e | |||
| , | unit travel demand of a vehicle/a pedestrian | V, P | |
| , | position of a vehicle/ a pedestrian | V, P | |
| direction of edge e | - | ||
| longitudinal distance between | V | ||
| Variables | , | velocity of a vehicle/ a pedestrian | V, P |
| , | acceleration of a vehicle/ a pedestrian | V, P | |
| arrival rate at t | |||
| departure rate at t | |||
| (Decision Variable) driving lane ratio of e at t | |||
| edge width of edge e | |||
| width of a facility belt of edge e | |||
| k | length of a time slot | 30 | |
| T | Simulation time period | 3600 s | |
| number of edges | 8 | ||
| vehicular travel demand at t | |||
| pedestrian travel demand at t | |||
| minimal space gap between pedestrians | 0.25 m | ||
| Parameters | distance between origin o and destination d | ||
| reward amplifier | 1000 | ||
| vehicle length | 4.5 m | ||
| maximum speed of AV | 13 m/s | ||
| maximum speed of pedestrian | 1.2 m/s | ||
| speed deviation | 0.05 | ||
| h | time headway | 0.6 s | |
| maximum acceleration of vehicles | 2.6 m/s2 | ||
| maximum acceleration of a pedestrian | 0.3 m/s2 |
| Notation | Specification | Value |
|---|---|---|
| Ornstein–Uhlenbeck noise | - | |
| mean rate of noise regression | 0.15 | |
| standard deviation of noise distribution | 0.2 | |
| mean of noise distribution | 0 | |
| soft update parameter | 0.005 | |
| discount factor | 0.99 | |
| B | replay buffer capacity | 100,000 |
| m | mini-batch size | 64 |
| Episodes | 150 | |
| I | Intervals per Step | 36 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Q.; Feng, Y.; Candela, E.; Escribano Macias, J.; Stettler, M.; Angeloudis, P. Spatial-Temporal Flows-Adaptive Street Layout Control Using Reinforcement Learning. Sustainability 2022, 14, 107. https://doi.org/10.3390/su14010107
Ye Q, Feng Y, Candela E, Escribano Macias J, Stettler M, Angeloudis P. Spatial-Temporal Flows-Adaptive Street Layout Control Using Reinforcement Learning. Sustainability. 2022; 14(1):107. https://doi.org/10.3390/su14010107
Chicago/Turabian StyleYe, Qiming, Yuxiang Feng, Eduardo Candela, Jose Escribano Macias, Marc Stettler, and Panagiotis Angeloudis. 2022. "Spatial-Temporal Flows-Adaptive Street Layout Control Using Reinforcement Learning" Sustainability 14, no. 1: 107. https://doi.org/10.3390/su14010107
APA StyleYe, Q., Feng, Y., Candela, E., Escribano Macias, J., Stettler, M., & Angeloudis, P. (2022). Spatial-Temporal Flows-Adaptive Street Layout Control Using Reinforcement Learning. Sustainability, 14(1), 107. https://doi.org/10.3390/su14010107






