A New Collaborative Multi-Agent Monte Carlo Simulation Model for Spatial Correlation of Air Pollution Global Risk Assessment
Abstract
:1. Introduction
2. Materials and Methods
2.1. Air Pollution Datasets
2.1.1. Malaysia Air Pollution Dataset
2.1.2. China Air Pollution Dataset
2.2. Prediction Methods
2.2.1. Descriptive Statistics
2.2.2. ARIMA Algorithm
2.2.3. Monte Carlo Simulation
- Build an appropriate probability model according to the simulated object’s characteristics;
- Find a suitable distribution function to the desired solution.
- Generate a random variable (or random vector) with a known probability distribution;
- Generate a random variable of a sample;
- Establish the sampling method of the random distribution.
- Simulate a random variable as the solution to the object problem;
- Find the unbiased estimator.
2.3. Modeling Dynamic and Distributed Behavior
2.4. Evaluation Metrics
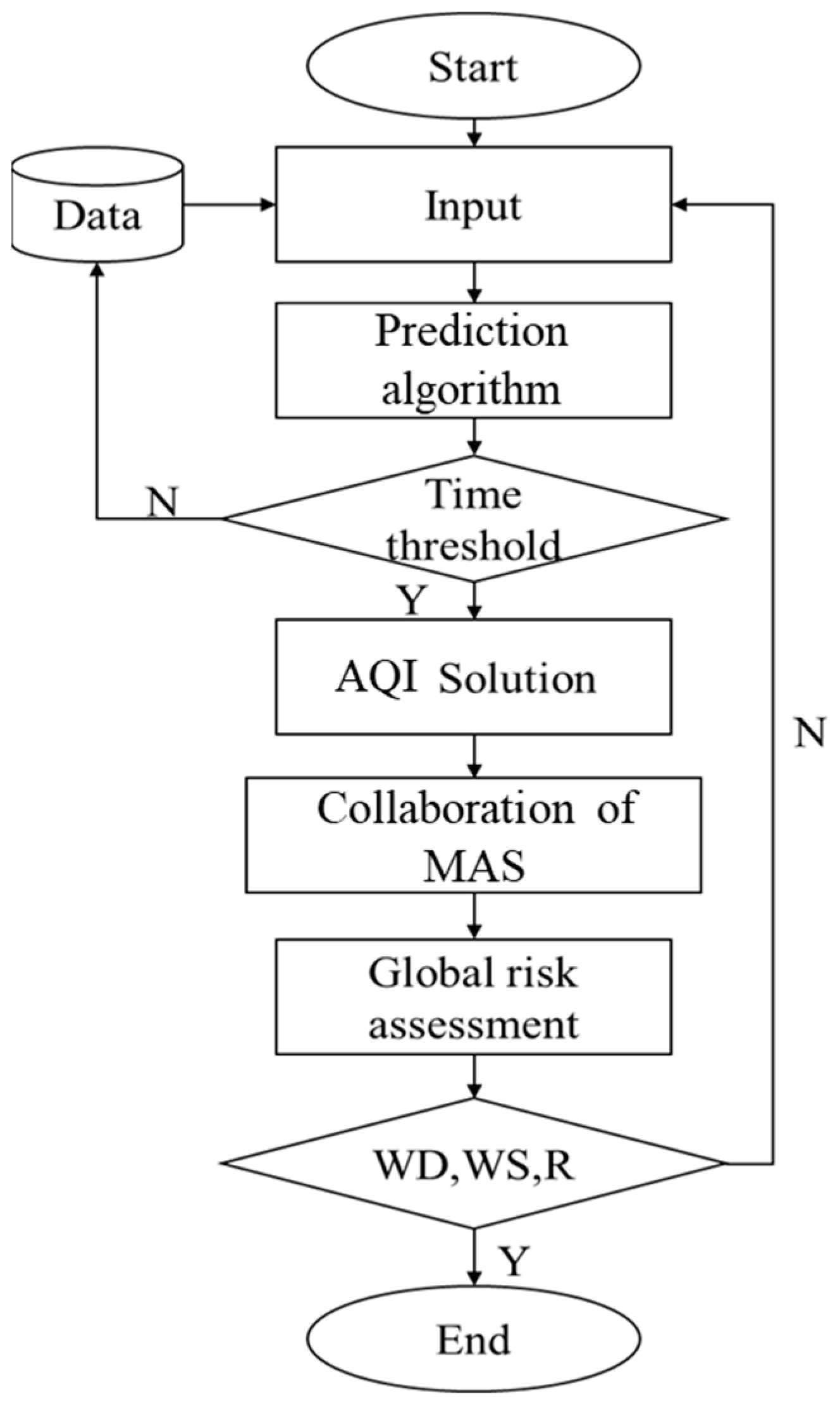
3. Air Pollution Global Risk Assessment (APGRA) Model
3.1. Air Pollution Local Risk Assessment
| Algorithm 1 Air Pollution Local Risk Assessment Algorithm |
| Input initial input < ARIMA (p, I, q, i, j); T_past; T future; N_runs; y_history >; initial output < y_forecasted, σ_forecasted >; Output Y = []; y_forecasted; σ_forecasted; Start prediction model = fitARIMA (p, I, q, i, j, T_past, N_runs, y_history); for t = 1 until No_runs do: y_forecasted = forecast (model, T_past, T_future); Y = add(y_forecasted); end σ_forecasted = sqrt(variance(Y)); y_forecasted = avg(Y); End |
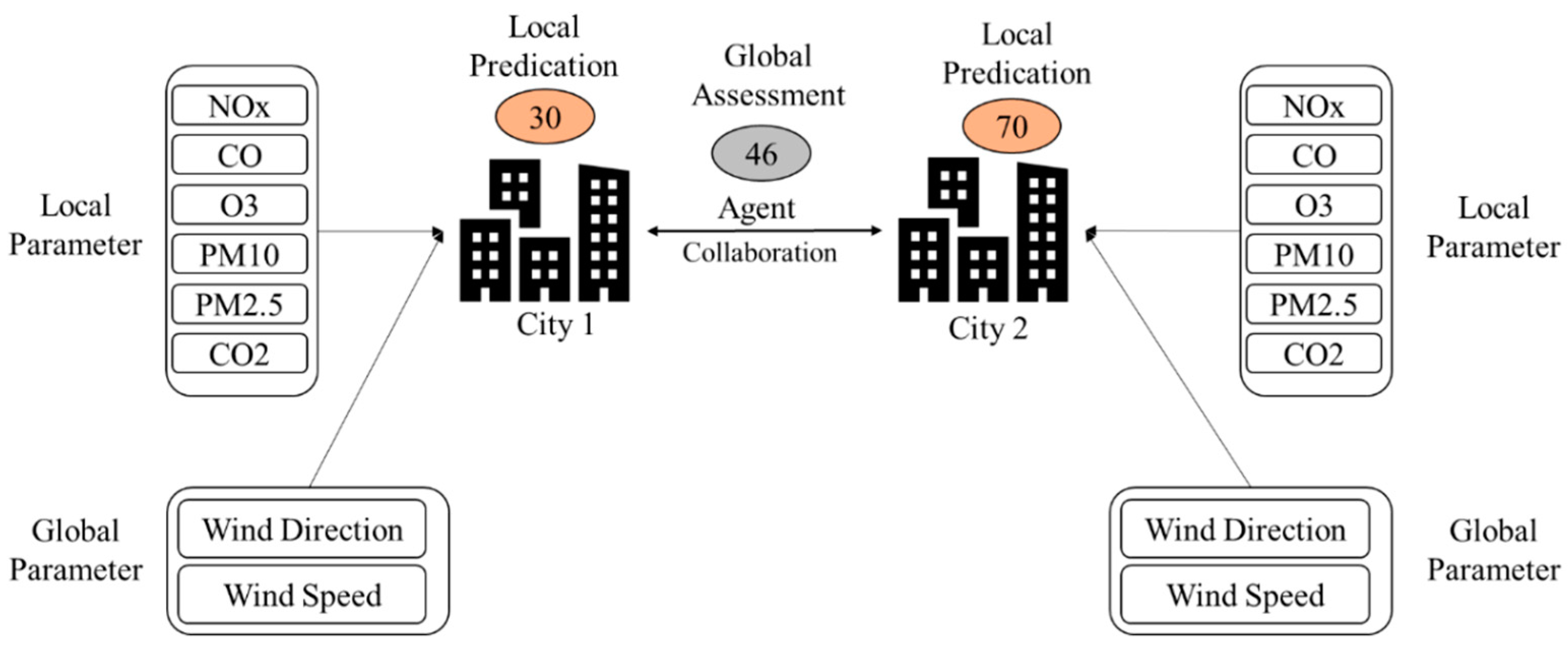
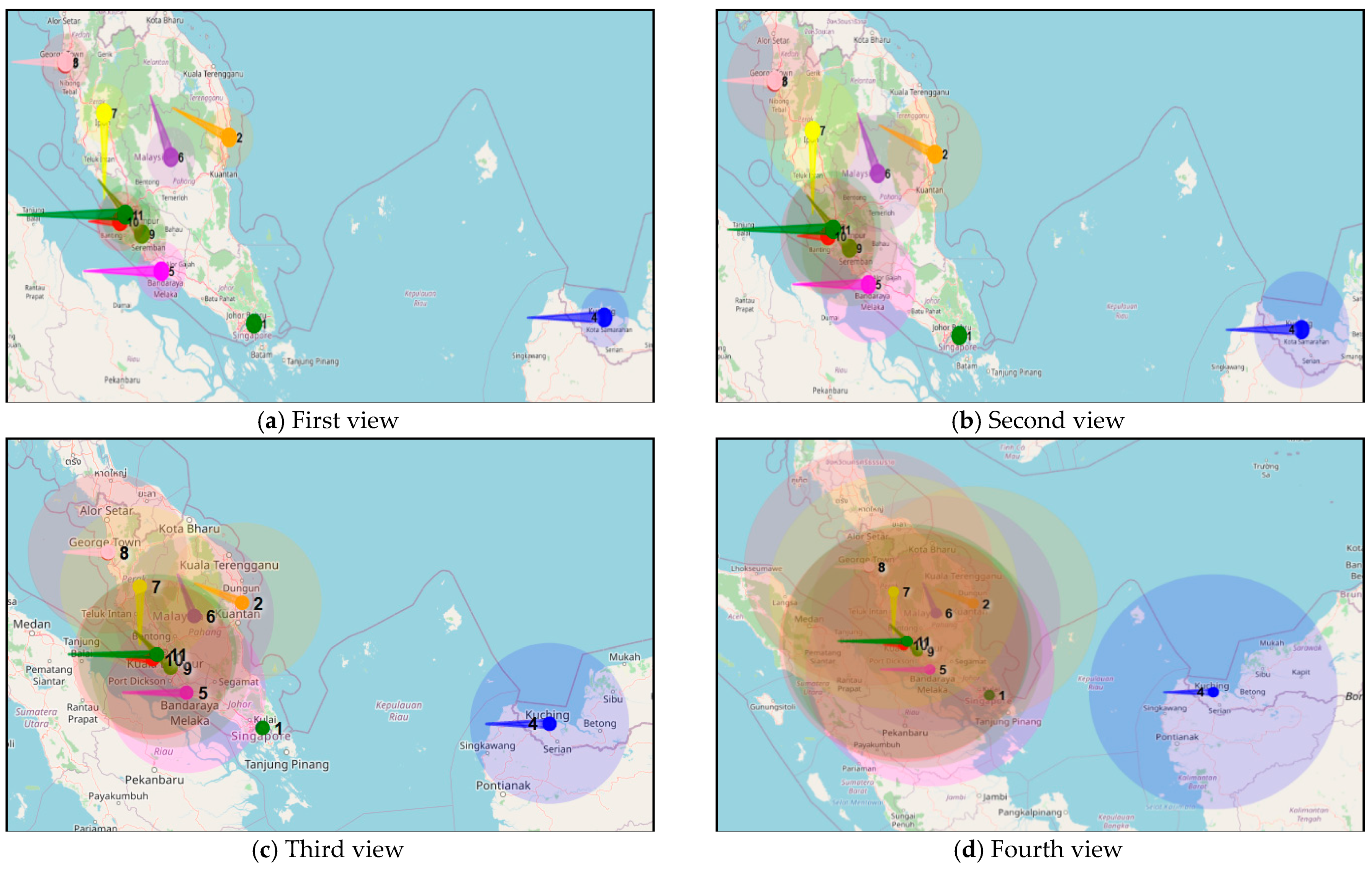
3.2. Air Pollution Global Risk Assessment
| Algorithm 2 Air Pollution Global Risk Assessment Algorithm |
| Input A(i, j) // I = 1, 2, ..., n umber of cities; j = 1, 2, ..., m number of time series // this represents the original agent’s models WS(i) // wind speed at city i WD(i) // wind direction at city i R // Radius of interaction SpeedT // lower speed effec Output AI (i, j) // this represents the model after modifying with global interaction Start for i = 1: n // to go through all cities cities = find Cities (i, R) // for each city we find influencing city for k = 1: length(cities) if(WS(k) > SpeedT and WD(i) is toward location of city k) for j = 1:m AI (i, j) = alpha*WS(k)*A (k, j) // to change all-time series to be affect by the source city end AI (i, j) = A (i, j) + AI (i, j) end end end End |
3.3. Risk Forecasting
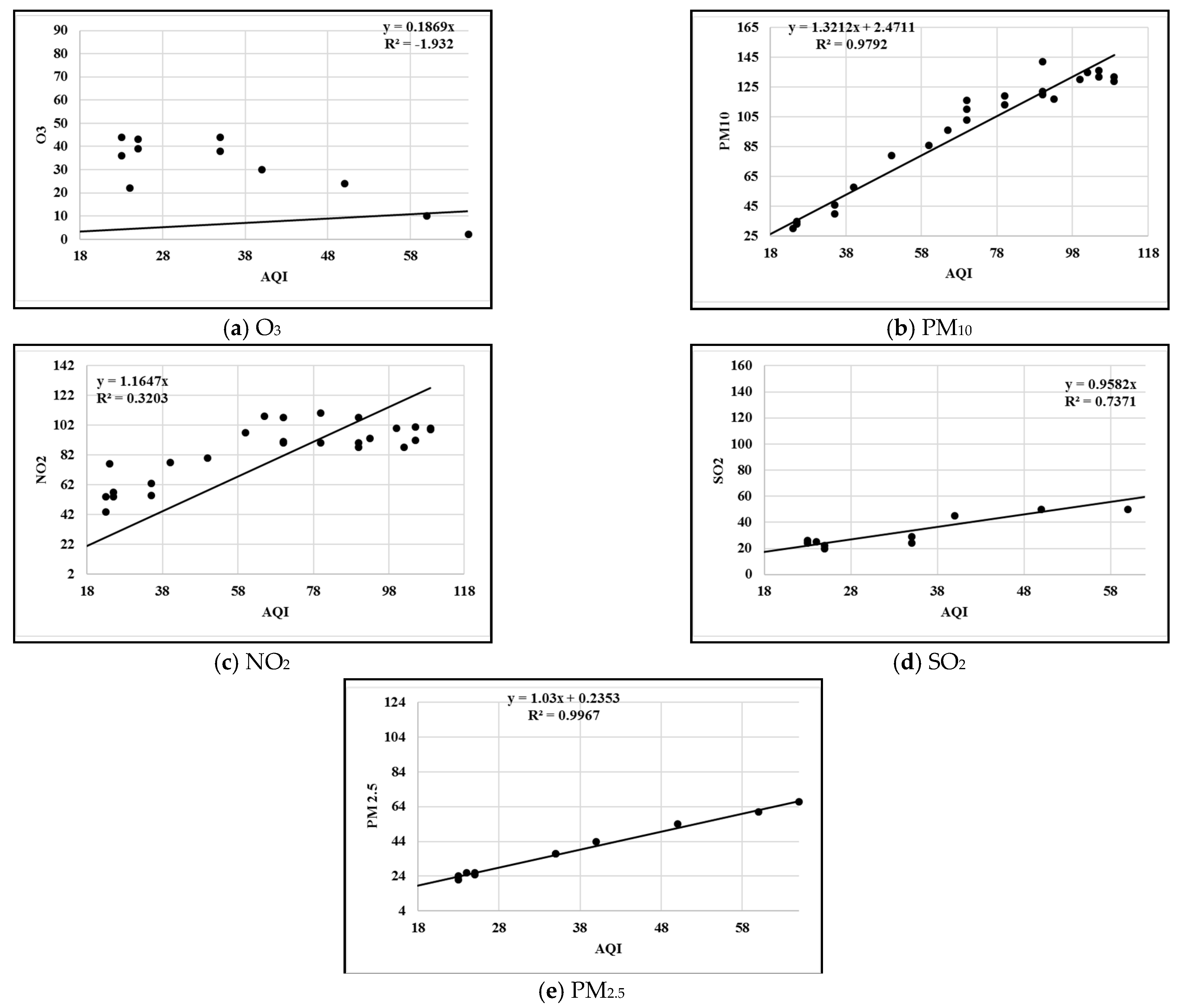
3.4. Correlation Analysis
4. Results and Discussion
4.1. Comparison between AQI Prediction Models
4.2. Results of Global Air Pollution Risk Assessment Model
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, S.; Guo, B.; Dong, A.; He, J.; Xu, Z.; Chen, S.X. Cautionary tales on air-quality improvement in Beijing. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20170457. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.S.; Cao, Y.; Hou, J.J.; Zhang, J.T.; Yang, Y.O.; Liu, L.C. Identifying common paths of CO2 and air pollutants emissions in China. J. Clean. Prod. 2020, 256, 120599. [Google Scholar] [CrossRef]
- Li, J.; Tartarini, F. Changes in air quality during the COVID-19 lockdown in Singapore and associations with human mobility trends. Aerosol Air Qual. Res. 2020, 20, 1748–1758. [Google Scholar] [CrossRef]
- Nyoni, T.; Mutongi, C. Modeling and forecasting carbon dioxide emissions in China using Autoregressive Integrated Moving Average (ARIMA) models. EPRA Int. J. Multidiscip. Res. 2019, 5, 215–224. [Google Scholar]
- Bakhtavar, E.; Hosseini, S.; Hewage, K.; Sadiq, R. Air pollution risk assessment using a hybrid fuzzy intelligent probability-based approach: Mine blasting dust impacts. Nat. Resour. Res. 2021, 30, 2607–2627. [Google Scholar] [CrossRef]
- Siwek, K.; Osowski, S. Data mining methods for prediction of air pollution. Int. J. Appl. Math. Comput. Sci. 2016, 26, 467–478. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Wang, J. A new air quality monitoring and early warning system: Air quality assessment and air pollutant concentration prediction. Environ. Res. 2017, 158, 105–117. [Google Scholar] [CrossRef]
- Tong, R.; Cheng, M.; Zhang, L.; Liu, M.; Yang, X.; Li, X.; Yin, W. The construction dust-induced occupational health risk using Monte-Carlo simulation. J. Clean. Prod. 2018, 184, 598–608. [Google Scholar] [CrossRef]
- Song, C.; Fu, X. Research on different weight combination in air quality forecasting models. J. Clean. Prod. 2020, 261, 121169. [Google Scholar] [CrossRef]
- Yang, H.; O’Connell, J.F. Short-term carbon emissions forecast for aviation industry in Shanghai. J. Clean. Prod. 2020, 275, 122734. [Google Scholar] [CrossRef]
- Feng, X.; Li, Q.; Zhu, Y.; Hou, J.; Jin, L.; Wang, J. Artificial neural networks forecasting of PM2.5 pollution using air mass trajectory based geographic model and wavelet transformation. Atmos. Environ. 2015, 107, 118–128. [Google Scholar] [CrossRef]
- Prasad, K.; Gorai, A.K.; Goyal, P. Development of ANFIS models for air quality forecasting and input optimization for reducing the computational cost and time. Atmos. Environ. 2016, 128, 246–262. [Google Scholar] [CrossRef]
- Zio, E. Challenges in the vulnerability and risk analysis of critical infrastructures. Reliab. Eng. Syst. Saf. 2016, 152, 137–150. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, H.; Qin, Z.; Zhang, G. A novel hybrid-Garch model based on ARIMA and SVM for PM2. 5 concentrations forecasting. Atmos. Pollut. Res. 2017, 8, 850–860. [Google Scholar] [CrossRef]
- Hernandez-Matamoros, A.; Fujita, H.; Hayashi, T.; Perez-Meana, H. Forecasting of COVID19 per regions using ARIMA models and polynomial functions. Appl. Soft Comput. 2020, 96, 106610. [Google Scholar] [CrossRef] [PubMed]
- Benvenuto, D.; Giovanetti, M.; Vassallo, L.; Angeletti, S.; Ciccozzi, M. Application of the ARIMA model on the COVID-2019 epidemic dataset. Data Brief 2020, 29, 105340. [Google Scholar] [CrossRef] [PubMed]
- Westerlund, J.; Urbain, J.P.; Bonilla, J. Application of air quality combination forecasting to Bogota. Atmos. Environ. 2014, 89, 22–28. [Google Scholar] [CrossRef]
- Mannshardt, E.; Benedict, K.; Jenkins, S.; Keating, M.; Mintz, D.; Stone, S.; Wayland, R. Analysis of short-term ozone and PM2. 5 measurements: Characteristics and relationships for air sensor messaging. J. Air Waste Manag. Assoc. 2017, 67, 462–474. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qazi, A.; Shamayleh, A.; El-Sayegh, S.; Formaneck, S. Prioritizing risks in sustainable construction projects using a risk matrix-based Monte Carlo Simulation approach. Sustain. Cities Soc. 2021, 65, 102576. [Google Scholar] [CrossRef]
- Zhao, L.; Ji, Y.; Yao, J.; Long, S.; Li, D.; Yang, Y. Quantifying the fate and risk assessment of different antibiotics during wastewater treatment using a Monte Carlo simulation. J. Clean. Prod. 2017, 168, 626–631. [Google Scholar] [CrossRef]
- Gordy, M.B.; Juneja, S. Nested simulation in portfolio risk measurement. Manag. Sci. 2010, 56, 1833–1848. [Google Scholar] [CrossRef] [Green Version]
- Mostafa, S.A.; Ahmad, M.S.; Annamalai, M.; Ahmad, A.; Gunasekaran, S.S. A dynamically adjustable autonomic agent framework. In Advances in Information Systems and Technologies; Springer: Berlin/Heidelberg, Germany, 2013; pp. 631–642. [Google Scholar]
- Hassan, M.H.; Mostafa, S.A.; Mustapha, A.; Abd Wahab, M.H.; Nor, D.M. A survey of multi-agent system approach in risk assessment. In Proceedings of the 2018 International Symposium on Agent, Multi-Agent Systems and Robotics (ISAMSR), Putrajaya, Malaysia, 27–28 August 2018; Institute of Electrical and Electronics Engineers (IEEE): Putrajaya, Malaysia, 2018; pp. 1–6. [Google Scholar]
- Mostafa, S.A.; Ahmad, M.S.; Ahmad, A.; Annamalai, M. Formulating situation awareness for multi-agent systems. In Proceedings of the 2013 International Conference on Advanced Computer Science Applications and Technologies, Kuching, Malaysia, 23–24 December 2013; Institute of Electrical and Electronics Engineers (IEEE): Kuching, Malaysia, 2013; pp. 48–53. [Google Scholar]
- Kashinath, S.A.; Mostafa, S.A.; Mustapha, A.; Mahdin, H.; Lim, D.; Mahmoud, M.A.; Yang, T.J. Review of data fusion methods for real-time and multi-sensor traffic flow analysis. IEEE Access 2021, 9, 51258–51276. [Google Scholar] [CrossRef]
- Mostafa, S.A.; Hazeem, A.A.; Khaleefahand, S.H.; Mustapha, A.; Darman, R. A collaborative multi-agent system for oil palm pests and diseases global situation awareness. In Proceedings of the Future Technologies Conference, Vancouver, BC, Canada, 13–14 November 2018; Springer: Cham, Switzerland, 2018; pp. 763–775. [Google Scholar]
- Mostafa, S.A.; Mustapha, A.; Gunasekaran, S.S.; Ahmad, M.S.; Mohammed, M.A.; Parwekar, P.; Kadry, S. An agent architecture for autonomous UAV flight control in object classification and recognition missions. Soft Comput. 2021, 1–14. [Google Scholar] [CrossRef]
- Khalaf, B.A.; Mostafa, S.A.; Mustapha, A.; Mohammed, M.A.; Mahmoud, M.A.; Al-Rimy, B.A.S.; Marks, A. An Adaptive Protection of Flooding Attacks Model for Complex Network Environments. Secur. Commun. Netw. 2021, 2021. [Google Scholar] [CrossRef]
- Mostafa, S.A.; Gunasekaran, S.S.; Ahmad, M.S.; Ahmad, A.; Annamalai, M.; Mustapha, A. Defining tasks and actions complexity-levels via their deliberation intensity measures in the layered adjustable autonomy model. In Proceedings of the 2014 International Conference on Intelligent Environments (IE ’14), Shanghai, China, 30 June–4 July 2014; Institute of Electrical and Electronics Engineers (IEEE): Shanghai, China, 2014; pp. 52–55. [Google Scholar]
- Mostafa, S.A.; Mustapha, A.; Mohammed, M.A.; Ahmad, M.S.; Mahmoud, M.A. A fuzzy logic control in adjustable autonomy of a multi-agent system for an automated elderly movement monitoring application. Int. J. Med. Inform. 2018, 112, 173–184. [Google Scholar] [CrossRef] [PubMed]
- Bellifemine, F.L.; Caire, G.; Greenwood, D. Developing Multi-Agent Systems with JADE; John Wiley & Sons: Chichester, UK, 2007. [Google Scholar]
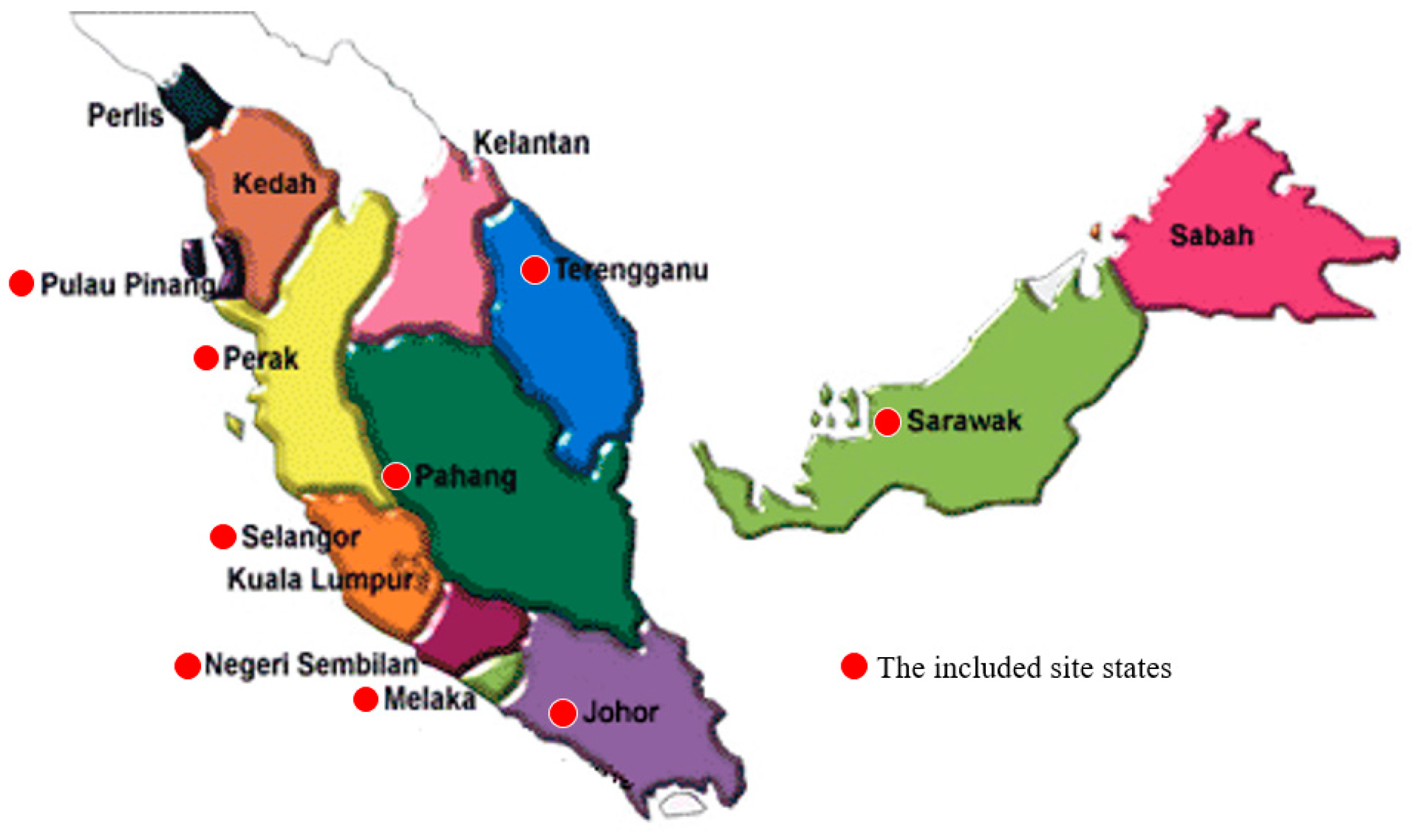






| NO | Site State | Site ID | Location | Latitude | Longitude | Type |
|---|---|---|---|---|---|---|
| 1 | Johor | CAS 001 | SM Pasir Gudang 2, Pasir Gudang, Johor | N01° 28.225 | E103° 53.637 | Residential |
| 2 | Terengganu | CAE 002 | SRK Bukit Kuang, Teluk Kalung, Kemaman. | N04° 16.260 | E103° 25.826 | Residential |
| 3 | Pulau Pinang | CAN 003 | Sek. Keb. Cenderawasih, Tmn. Inderawasih, Perai | N05° 23.470 | E100° 23.213 | Residential |
| 4 | Sarawak | CAK 004 | Medical Store, Kuching, Sarawak | N01° 33.734 | E110° 23.329 | Residential |
| 5 | Melaka | CAS 006 | Sek. Men. Keb. Bukit Rambai, Melaka | N02° 15.510 | E102° 10.364 | Residential |
| 6 | Pahang | CAE 007 | Pej. Kajicuaca, Batu Embun, Jerantut, Pahang | N03° 58.238 | E102° 20.863 | Residential |
| 7 | Perak | CAN 008 | SM Jalan Tasek, Ipoh, Perak | N04° 37.781 | E101° 06.964 | Residential |
| 8 | Pulau Pinang | CAN 009 | SK Seberang Jaya II, Perai, Pulau Pinang | N05° 23.890 | E100° 24.194 | Residential |
| 9 | Negeri Sembilan | CAC 010 | Taman Semarak (Phase II), Nilai, N.Sembilan | N02° 49.246 | E101° 48.877 | Residential |
| 10 | Selangor | CAC 011 | SM(P) Raja Zarina, Klang, Selangor | N03° 00.620 | E101° 24.484 | Residential |
| Dataset Characteristics | Multivariate, Time-Series |
|---|---|
| Number of Instances: | 420,768 |
| Area: | Physical |
| Number of Attributes: | 18 |
| Attribute Characteristics: | Integer, Real |
| Missing Values? | Yes |
| Associated Tasks: | Regression |
| AQI 1-Day Advance Prediction | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Metric | City 1 | City 2 | City 3 | City 4 | City 5 | City 6 | City 7 | City 8 | City 9 | City 10 | |
| ARIMA | R2 | 0.83 | 0.24 | 0.33 | 0.47 | 0.87 | 0.34 | 0.48 | 0.92 | 0.89 | 0.34 |
| RMSE | 3.84 | 2.83 | 4.99 | 2.66 | 3.78 | 2.77 | 2.18 | 3.11 | 4.71 | 1.33 | |
| MAE | 3.45 | 2.69 | 4.40 | 2.32 | 3.40 | 2.26 | 2.04 | 2.78 | 4.30 | 1.10 | |
| Time | 7.20 | 6.30 | 5.20 | 6.30 | 6.50 | 4.70 | 3.80 | 6.60 | 6.90 | 6.20 | |
| MCS | R2 | 0.91 | 0.75 | 0.50 | 0.64 | 0.89 | 0.88 | 0.73 | 0.94 | 0.92 | 0.56 |
| RMSE | 2.15 | 1.08 | 2.05 | 1.24 | 3.08 | 1.92 | 1.02 | 2.47 | 3.10 | 0.80 | |
| MAE | 1.90 | 1.03 | 1.89 | 1.06 | 2.60 | 1.60 | 0.88 | 2.11 | 2.70 | 0.65 | |
| Time | 8.40 | 8.30 | 6.20 | 8.30 | 7.50 | 6.70 | 6.80 | 7.50 | 7.90 | 8.10 | |
| ANFIS | R2 | 0.8 | 0.6 | 0.4 | 0.3 | 0.8 | 0.1 | 0.1 | 0.9 | 0.7 | 0.1 |
| RMSE | 4.3 | 3.3 | 5 | 3.2 | 4.5 | 4 | 2.3 | 3.4 | 5 | 2 | |
| MAE | 4 | 3.1 | 4.4 | 2.7 | 4.1 | 3.5 | 2 | 3 | 4.8 | 1.7 | |
| Time | 10.40 | 12.30 | 9 | 11 | 9 | 9 | 9 | 11 | 12 | 11 | |
| AQI 2-Day Advance Prediction | |||||||||||
| Metric | City 1 | City 2 | City 3 | City 4 | City 5 | City 6 | City 7 | City 8 | City 9 | City10 | |
| ARIMA | R2 | 0.12 | 0.20 | 0.30 | 0.39 | 0.01 | 0.02 | 0.25 | 0.82 | 0.80 | 0.10 |
| RMSE | 19.40 | 9.20 | 5.90 | 22.30 | 14.80 | 8.10 | 3.60 | 6.76 | 12.60 | 16.20 | |
| MAE | 15.30 | 7.20 | 5.31 | 16.80 | 12.00 | 6.90 | 3.36 | 3.80 | 10.50 | 11.38 | |
| Time | 9.20 | 7.40 | 7.20 | 7.30 | 7.50 | 6.70 | 6.80 | 8.80 | 8.30 | 7.30 | |
| MCS | R2 | 0.20 | 0.50 | 0.40 | 0.40 | 0.89 | 0.08 | 0.75 | 0.90 | 0.88 | 0.49 |
| RMSE | 10.90 | 5.36 | 4.52 | 11.30 | 4.47 | 2.50 | 1.72 | 4.14 | 9.00 | 4.60 | |
| MAE | 7.96 | 3.75 | 3.77 | 8.51 | 3.54 | 1.95 | 1.42 | 2.66 | 7.00 | 2.80 | |
| Time | 9.80 | 9.40 | 9.80 | 9.50 | 9.20 | 8.70 | 8.30 | 9.80 | 9.30 | 9.30 | |
| ANFIS | R2 | 0.1 | 0.4 | 0.6 | 0.4 | 0.1 | 0.1 | 0.3 | 0.9 | 0.8 | 0.2 |
| RMSE | 19 | 9.3 | 3.9 | 22 | 14 | 8 | 2.7 | 3.2 | 12 | 16.4 | |
| MAE | 15.6 | 7.4 | 3.3 | 17 | 12 | 7 | 2.3 | 2.9 | 10 | 11.7 | |
| Time | 13 | 15 | 14 | 15 | 14 | 13 | 14 | 15 | 15 | 14 | |
| AQI 1-Day Advance Prediction | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Metric | City 1 | City 2 | City 3 | City 4 | City 5 | City 6 | City 7 | City 8 | City 9 | City 10 | |
| ARIMA | R2 | 0.97 | 0.94 | 0.55 | 0.89 | 0.58 | 0.45 | 0.66 | 0.40 | 0.81 | 0.93 |
| RMSE | 4.45 | 9.78 | 6.14 | 10.0 | 5.46 | 20.2 | 21.4 | 30.4 | 19.1 | 14.24 | |
| MAE | 3.32 | 8.39 | 5.38 | 8.54 | 4.88 | 15.1 | 16.7 | 26.3 | 17.4 | 12.46 | |
| Time | 2.70 | 3.00 | 2.50 | 2.80 | 2.30 | 2.70 | 2.70 | 2.80 | 2.90 | 2.10 | |
| MCS | R2 | 0.98 | 0.95 | 0.83 | 0.91 | 0.73 | 0.81 | 0.93 | 0.50 | 0.91 | 0.97 |
| RMSE | 2.70 | 4.64 | 2.95 | 5.70 | 2.30 | 16.7 | 9.80 | 11.0 | 12.9 | 6.40 | |
| MAE | 1.80 | 3.75 | 2.40 | 4.54 | 2.00 | 11.7 | 7.10 | 9.80 | 10.7 | 5.30 | |
| Time | 3.10 | 3.90 | 3.10 | 3.90 | 3.10 | 3.10 | 3.90 | 3.10 | 3.10 | 3.10 | |
| ANFIS | R2 | 0.8 | 0.8 | 0.40 | 0.79 | 0.63 | 0.25 | 0.69 | 0.14 | 0.73 | 0.92 |
| RMSE | 4.43 | 10.3 | 6.09 | 8.99 | 6.12 | 13.3 | 19.7 | 30.0 | 20.5 | 14.7 | |
| MAE | 3.22 | 8.6 | 5.1 | 7.9 | 5.41 | 10.8 | 15.9 | 26 | 18.3 | 12.9 | |
| Time | 7 | 8 | 7 | 8 | 8 | 7 | 8 | 9 | 8 | 7 | |
| AQI 2-Day Advance Prediction | |||||||||||
| Metric | City 1 | City 2 | City 3 | City 4 | City 5 | City 6 | City 7 | City 8 | City 9 | City 10 | |
| ARIMA | R2 | 0.90 | 0.86 | 0.69 | 0.64 | 0.89 | 0.74 | 0.52 | 0.30 | 0.58 | 0.817 |
| RMSE | 15.8 | 22.1 | 11.1 | 15.0 | 13.2 | 30.3 | 25.2 | 38.7 | 21.6 | 18.98 | |
| MAE | 9.91 | 17.2 | 8.42 | 11.1 | 9.38 | 25.6 | 21.5 | 30.3 | 20.1 | 16.25 | |
| Time | 3.20 | 4.10 | 4.10 | 4.10 | 4.30 | 3.20 | 3.20 | 3.20 | 4.30 | 4.30 | |
| MCS | R2 | 0.94 | 0.87 | 0.76 | 0.75 | 0.96 | 0.85 | 0.82 | 0.40 | 0.81 | 0.90 |
| RMSE | 11.6 | 15.7 | 7.20 | 11.2 | 9.70 | 21.9 | 15.0 | 27.0 | 13.7 | 11.50 | |
| MAE | 6.80 | 10.6 | 4.70 | 7.40 | 6.00 | 17.9 | 11.8 | 17.0 | 12.1 | 9.00 | |
| Time | 4.10 | 4.90 | 4.80 | 4.90 | 4.80 | 4.80 | 4.80 | 4.10 | 4.80 | 4.10 | |
| ANFIS | R2 | 0.9 | 0.8 | 0.5 | 0.6 | 0.8 | 0.7 | 0.5 | 0.5 | 0.5 | 0.8 |
| RMSE | 16 | 22 | 11 | 15 | 13.5 | 30 | 24 | 39 | 23 | 19 | |
| MAE | 10 | 17 | 8 | 11 | 9.5 | 26 | 21 | 30 | 20 | 16 | |
| Time | 9 | 9 | 8 | 8 | 9.20 | 9.30 | 9.20 | 9.40 | 8.90 | 8.60 | |
| AQI 1-Day Advance Assessment of Risk Level in Malaysia Dataset | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Results | City 1 | City 2 | City 3 | City 4 | City 5 | City 6 | City 7 | City 8 | City 9 | City 10 |
| Risk level | good | good | moderate | good | good | good | good | moderate | moderate | good |
| Affected by | none | none | 7,9 | none | 3,8 | none | none | 7,9 | none | 9 |
| Effect on | none | none | 5 | none | none | none | 3 | 5 | 7,3,10 | none |
| Effect zone | 1 | 2 | 0.5 | 1 | 1 | 0.5 | 2 | 2 | 2 | 1 |
| R2 | 0.9 | 0.6 | 0.5 | 0.8 | 0.7 | 0.6 | 0.6 | 0.7 | 0.8 | 0.6 |
| RMSE | 1.06 | 2.6 | 2.98 | 1.7 | 1.8 | 2 | 2.2 | 3.1 | 1.3 | 1.9 |
| MAE | 0.7 | 1.2 | 1.7 | 1.2 | 1.37 | 1.5 | 1.55 | 1.78 | 0.9 | 1.3 |
| Time | 3.20 | 5.30 | 4.20 | 3.30 | 3.20 | 4.90 | 4.80 | 3.20 | 3.90 | 5.10 |
| AQI 1-Day Advance Assessment of Risk Level in China Dataset | ||||||||||
| Results | City 1 | City 2 | City 3 | City 4 | City 5 | City 6 | City 7 | City 8 | City 9 | City 10 |
| Risk level | moderate | good | moderate | good | good | moderate | good | moderate | good | good |
| Affected by | none | 9 | 4 | none | none | none | none | 4 | none | 4 |
| Effect on | none | none | none | 8,3,10 | none | none | none | none | 2 | none |
| Effect zone | 0.5 | 0.5 | 1 | 1 | 0.5 | 0.5 | 0.5 | 2 | 0.5 | 0.5 |
| R2 | 0.6 | 0.6 | 0.8 | 0.8 | 0.9 | 0.5 | 0.7 | 0.7 | 0.8 | 0.9 |
| RMSE | 2.8 | 3.2 | 4.5 | 5 | 5.2 | 5.1 | 4.8 | 5.8 | 6.8 | 4 |
| MAE | 2.1 | 2.4 | 3.2 | 3.75 | 4.1 | 3.6 | 3.4 | 4 | 4.5 | 2.8 |
| Time | 3.70 | 3.20 | 3.10 | 3.20 | 3.20 | 3.20 | 3.20 | 3.70 | 3.90 | 3.20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassan, M.H.; Mostafa, S.A.; Mustapha, A.; Saringat, M.Z.; Al-rimy, B.A.S.; Saeed, F.; Eljialy, A.E.M.; Jubair, M.A. A New Collaborative Multi-Agent Monte Carlo Simulation Model for Spatial Correlation of Air Pollution Global Risk Assessment. Sustainability 2022, 14, 510. https://doi.org/10.3390/su14010510
Hassan MH, Mostafa SA, Mustapha A, Saringat MZ, Al-rimy BAS, Saeed F, Eljialy AEM, Jubair MA. A New Collaborative Multi-Agent Monte Carlo Simulation Model for Spatial Correlation of Air Pollution Global Risk Assessment. Sustainability. 2022; 14(1):510. https://doi.org/10.3390/su14010510
Chicago/Turabian StyleHassan, Mustafa Hamid, Salama A. Mostafa, Aida Mustapha, Mohd Zainuri Saringat, Bander Ali Saleh Al-rimy, Faisal Saeed, A.E.M. Eljialy, and Mohammed Ahmed Jubair. 2022. "A New Collaborative Multi-Agent Monte Carlo Simulation Model for Spatial Correlation of Air Pollution Global Risk Assessment" Sustainability 14, no. 1: 510. https://doi.org/10.3390/su14010510
APA StyleHassan, M. H., Mostafa, S. A., Mustapha, A., Saringat, M. Z., Al-rimy, B. A. S., Saeed, F., Eljialy, A. E. M., & Jubair, M. A. (2022). A New Collaborative Multi-Agent Monte Carlo Simulation Model for Spatial Correlation of Air Pollution Global Risk Assessment. Sustainability, 14(1), 510. https://doi.org/10.3390/su14010510









