A Novel Hybrid Sine Cosine Algorithm and Pattern Search for Optimal Coordination of Power System Damping Controllers
Abstract
:1. Introduction
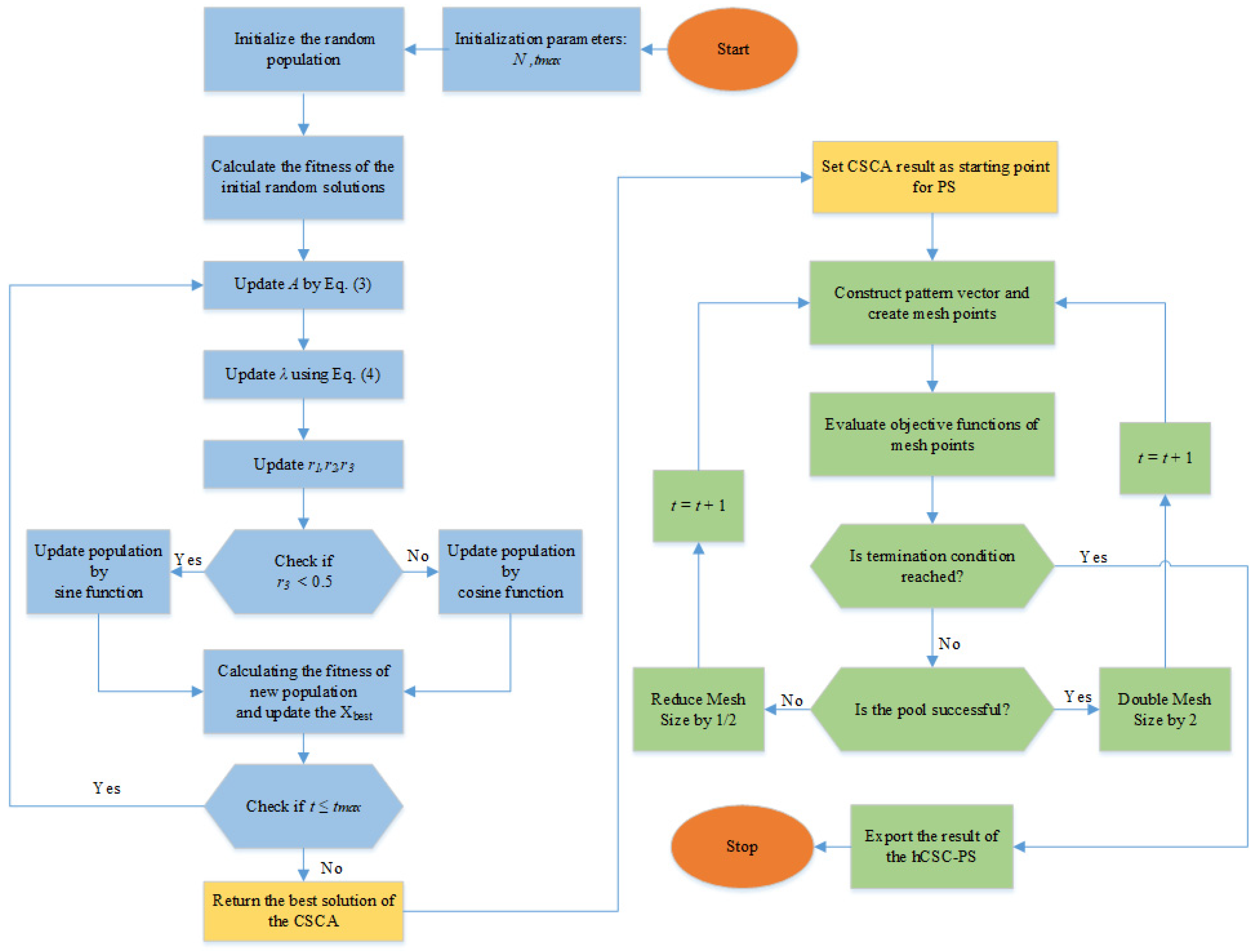
2. Proposed Hybrid Algorithm
2.1. CSCA
| Algorithm 1. CSCA. |
| Initialization algorithm parameters: population size (N), maximum iteration number (). |
| Initialize random population X |
| For i = 1 to N |
| Calculate the fitness of each random solution |
| Record the optimal individual as Xbest |
| End |
| While (t ≤ ) |
| Update A using Equation (3) |
| Update λ using Equation (4) |
| For i = 1 to N |
| For j = 1 to dim |
| Update r3 |
| If r3 < 0.5 |
| Update X by the sine part of Equation (5) |
| Else |
| Update X by the cosine part of Equation (5) |
| End if |
| End for |
| Calculate the fitness of the updated X |
| Update Xbest |
| End for |
| t = t + 1 |
| End |
| Return the best solution |
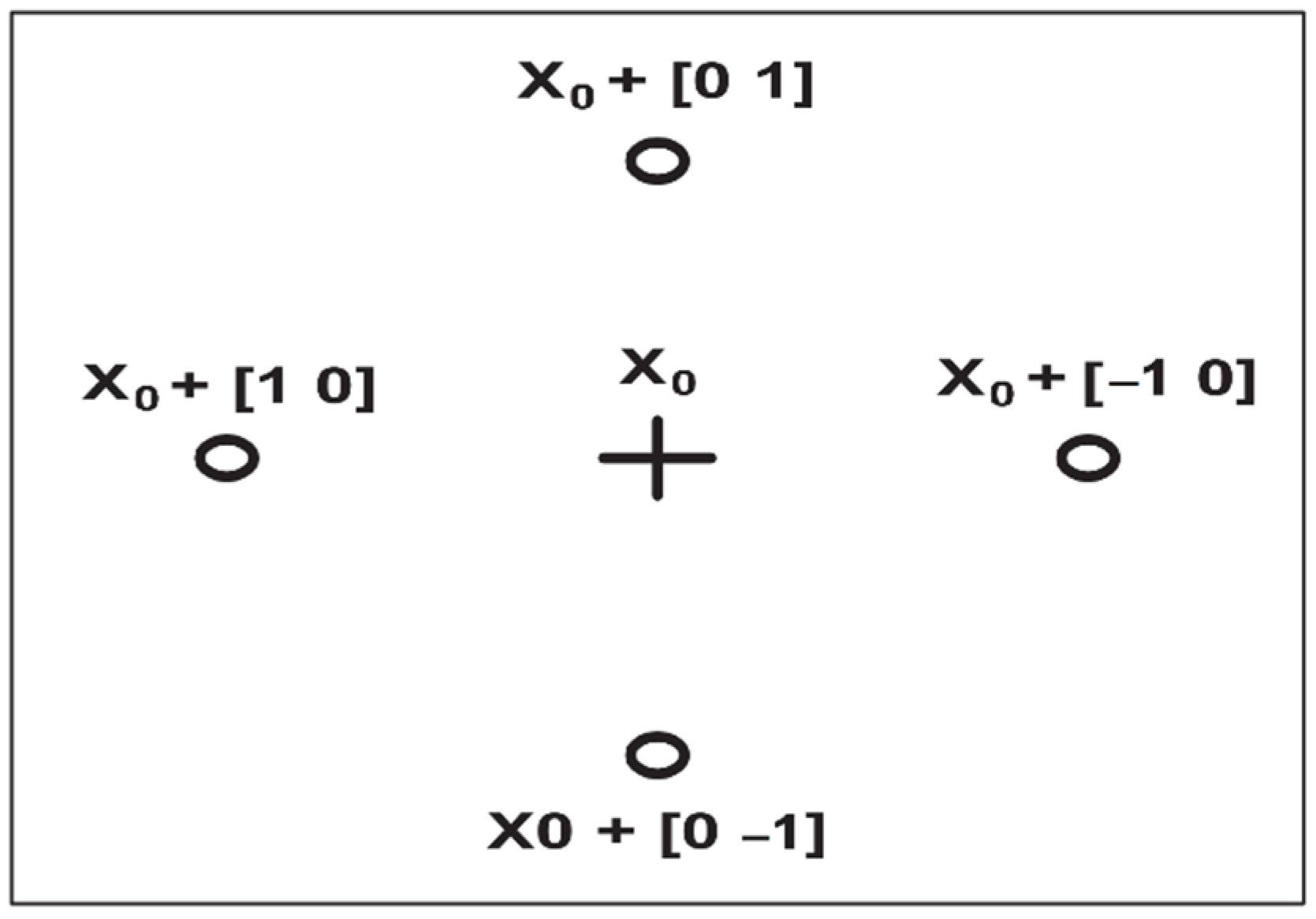
2.2. Pattern Search (PS)
| Algorithm 2. Pattern search method. |
| Initialization: |
| Initialize the starting point X0 and step size factor SF |
| Set t = 0 |
| Iteration: |
| 1. Search step: evaluate f at a finite number of points with the goal of decreasing the objective function value at Xk. If Xk+1 is found satisfying f (Xk+1) < f (Xk), go to step 4. |
| Otherwise, go to step 2. |
| 2. Poll step: If f (Xk ) ≤ f (X) for every X in the mesh neighborhood, go to step 3. |
| Otherwise, choose a point Xk+1 such that f (Xk+1) < f (Xk), go to step 4. |
| 3. Mesh reduction: let SFk+1 = 1/2 × SFk. Set k ← k + 1 and return to step 1 for a new iteration. |
| 4. Mesh expansion: let SFk+1 = 2 × SFk. Set k ← k + 1 and return to step 1 for a new iteration |
2.3. Proposed Method (hCSC-PS)
3. Optimization Problem Formulation
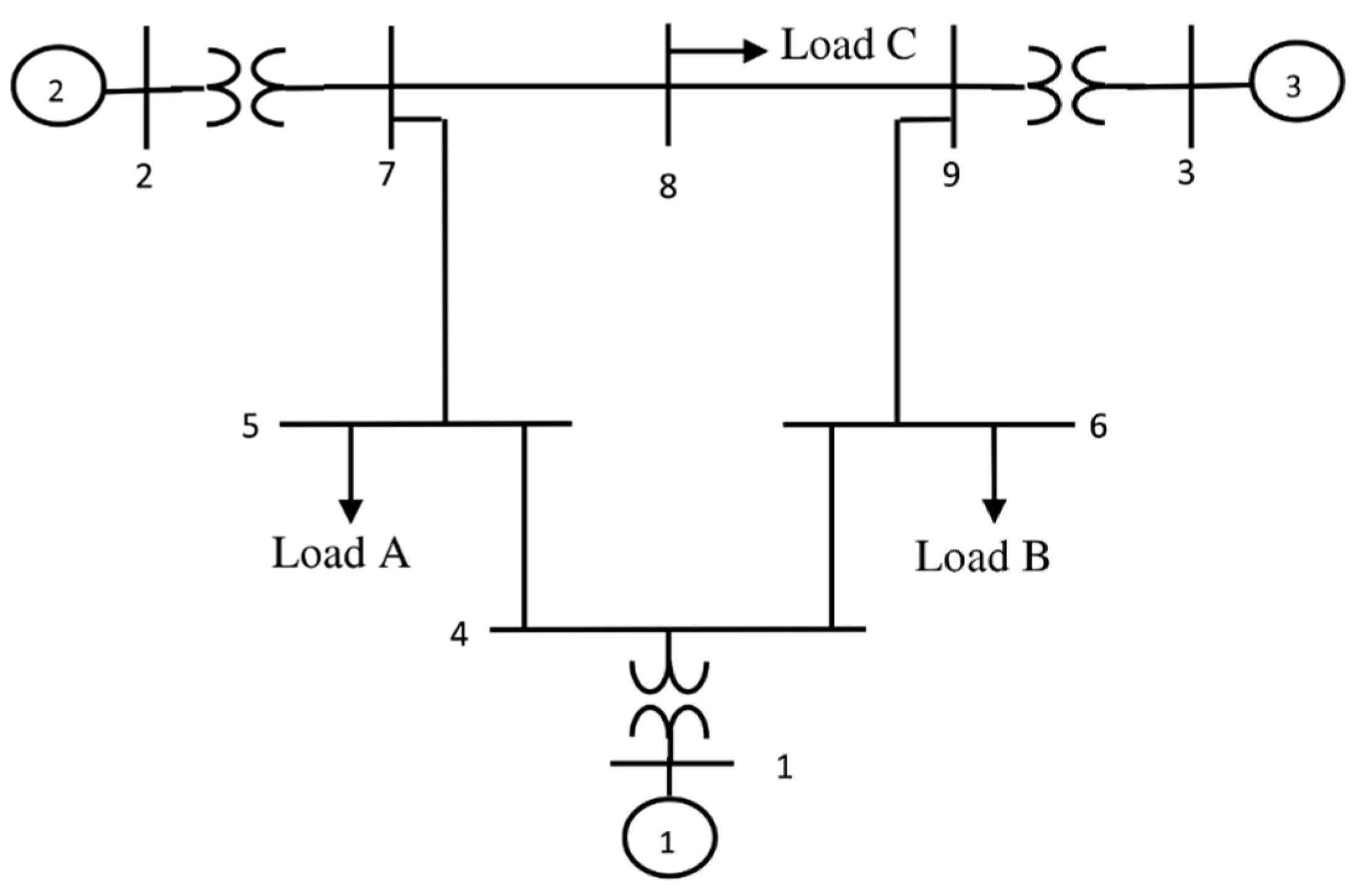
3.1. Power System Model
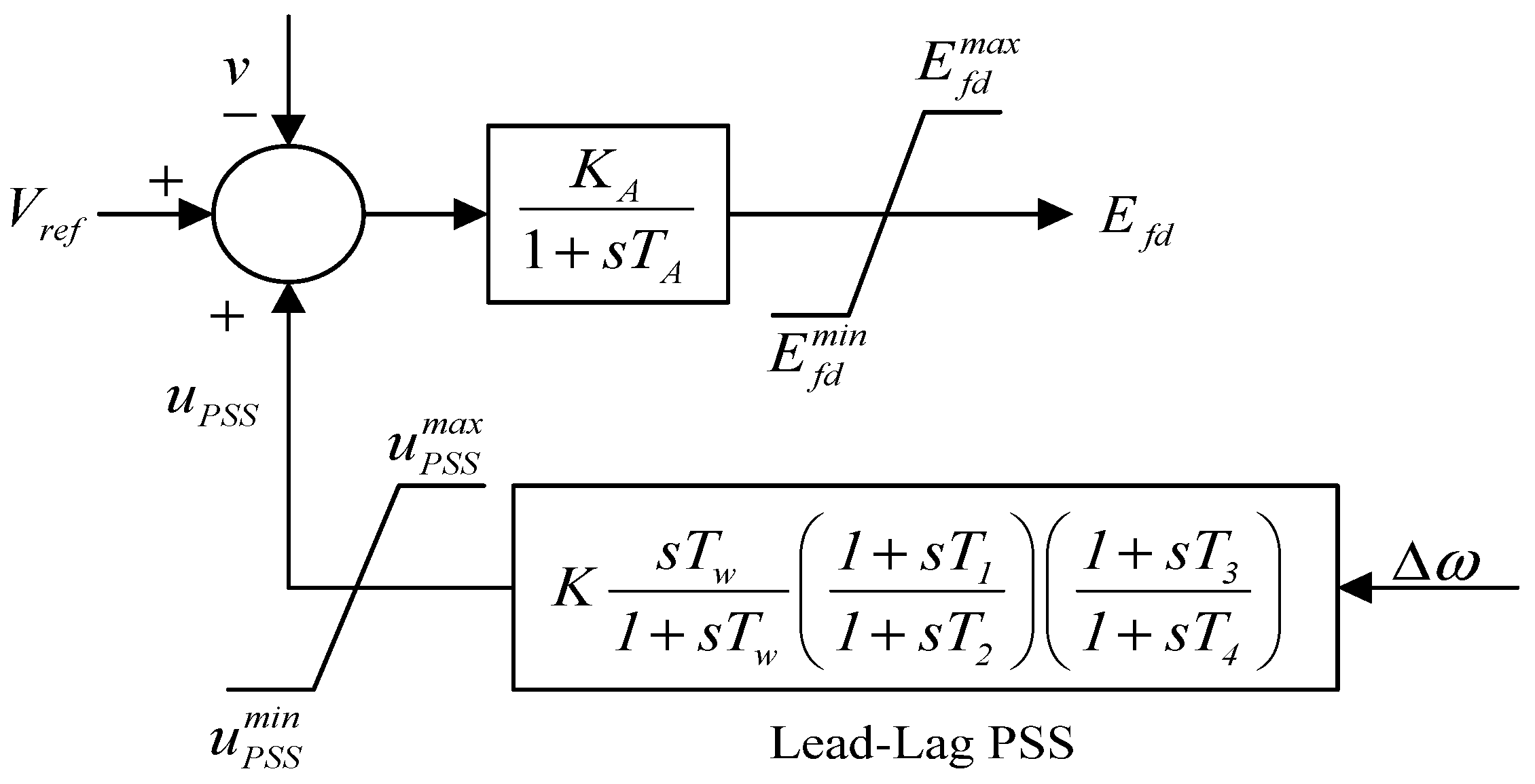
3.1.1. PSS Structure
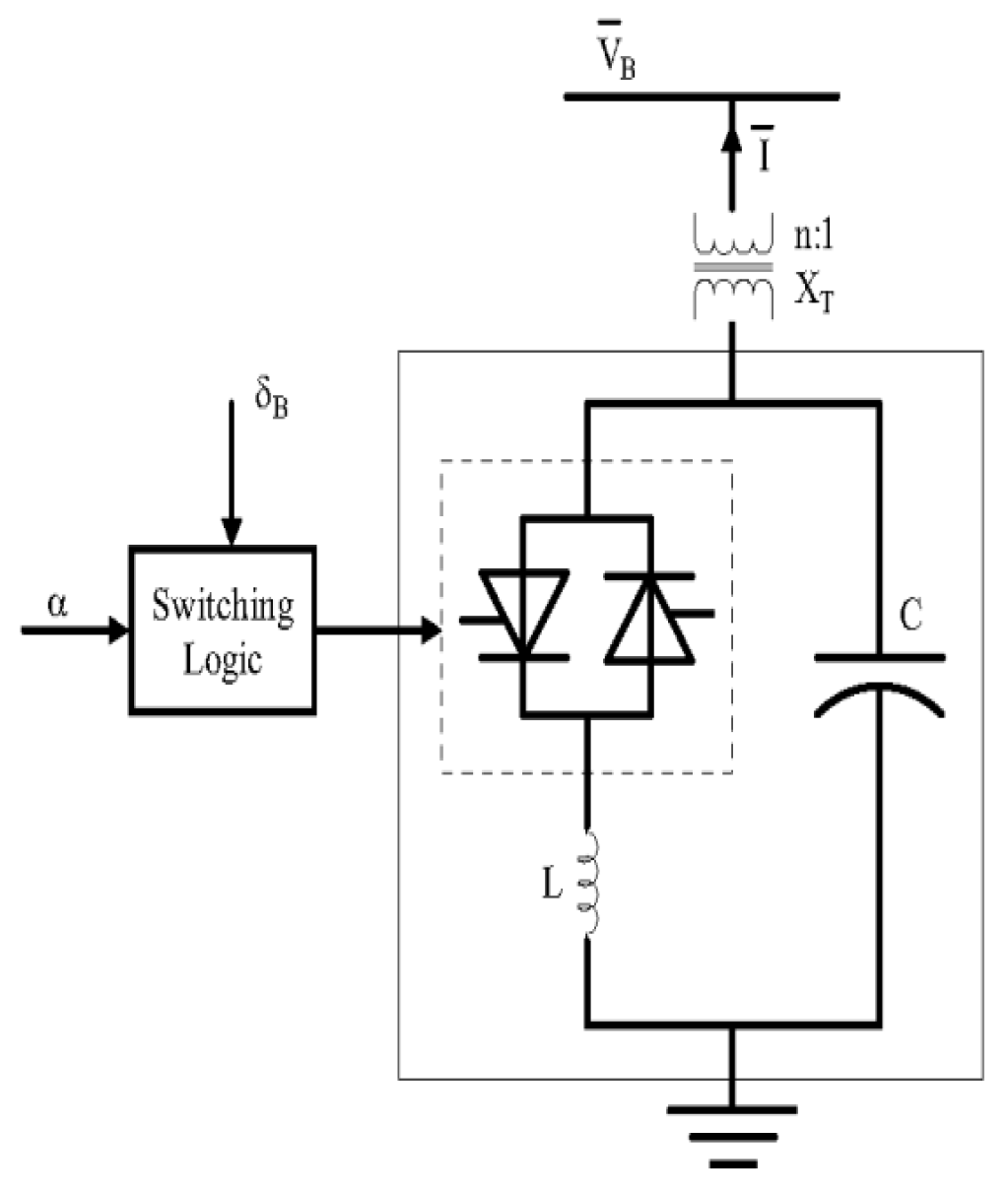
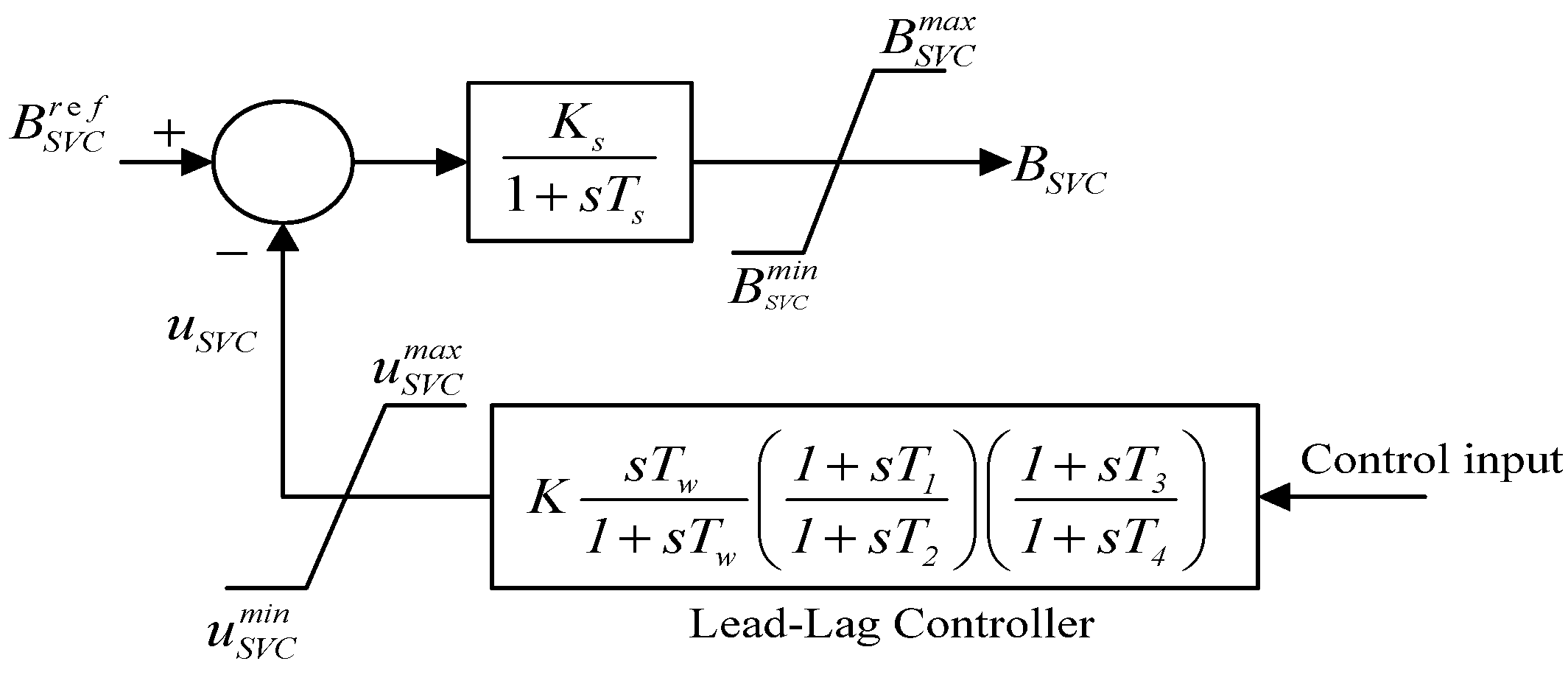
3.1.2. SVC Based Damping Controller Model
3.2. Problem Formulation
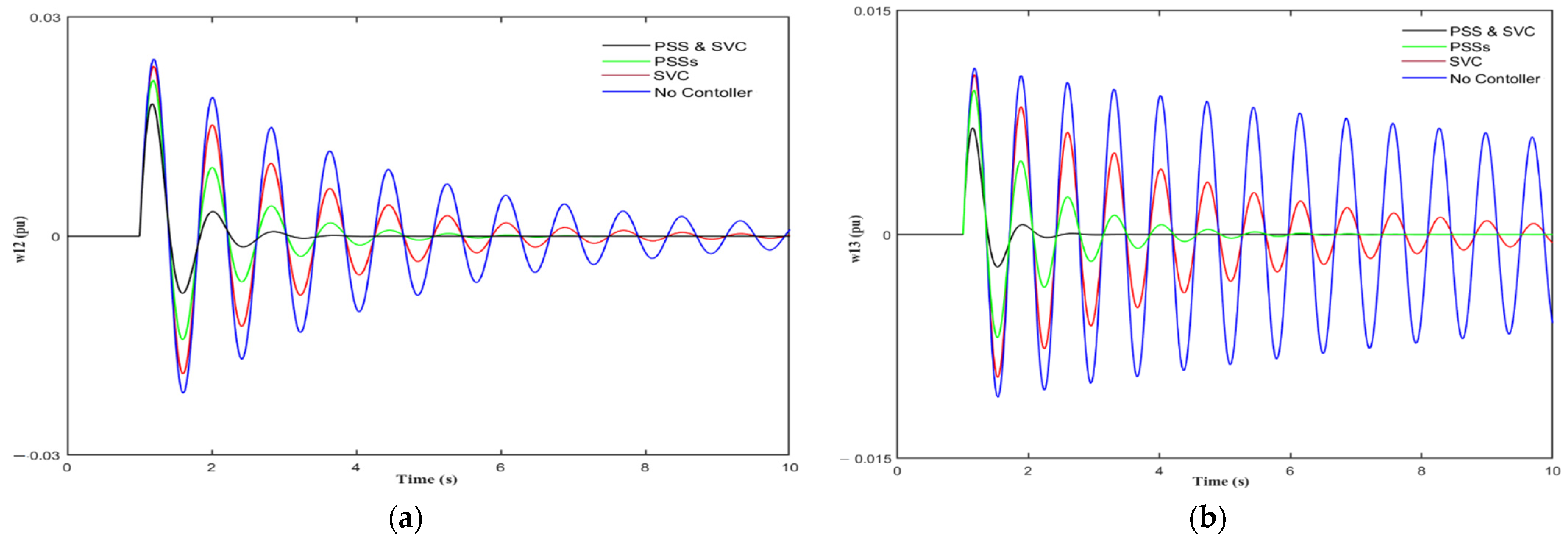
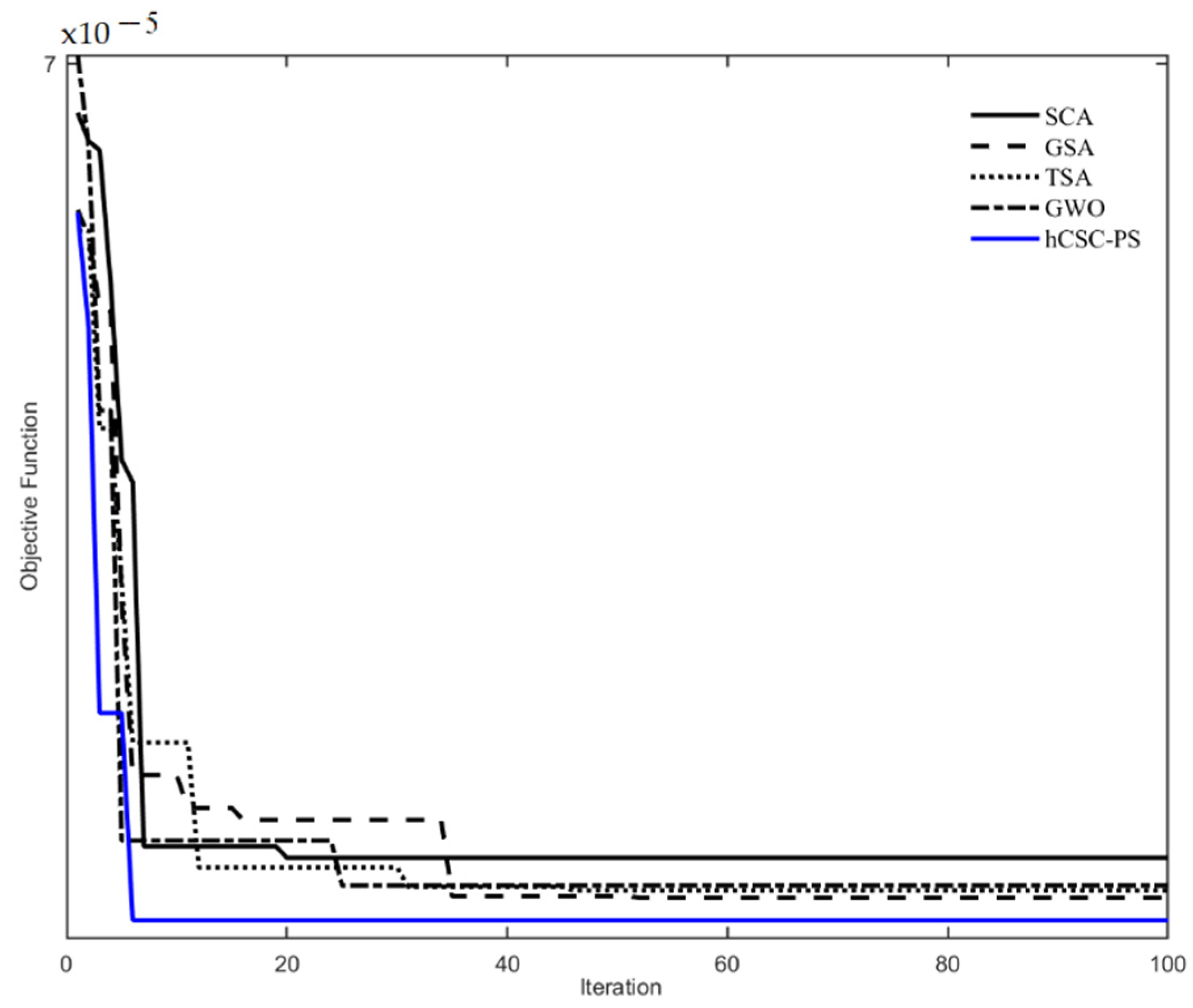
4. Performance Verification of hCSC-PS
5. Practical Applications
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Generator
Appendix A.2. Exciter and PSS
Appendix A.3. SVC- Based Controller
Appendix A.4. Linearized Model
Appendix B
| Variables & Abbreviation | Description | Variables & Abbreviation | Description |
|---|---|---|---|
| f(X) | Fitness function | dim | Dimension |
| g(X) | Inequality constraints | SF | Size factor |
| h(X) | Equality constraints | Mechanical input power | |
| X | Dimensional vector of design variables | Active power | |
| XL & XU | Boundary constraints | M | Machine inertia |
| δ | Rotor angle | D | Damping the coefficient |
| ω | Speed deviation | Reference voltage | |
| Eq | Internal voltages | Open circuit field time constant | |
| Efa | Field voltages | Stator currents in d- and q -axis circuits | |
| u | Input control parameters | x | Vector of state variables |
| tsim | time of simulation | y | Vector of algebraic variables |
| N | Number of machines | BSVC | Susceptance of SVC |
| M | Number of operating points | ξ | Damping ratio |
| K | Gain | Fmin | Minimum value of the objective function |
| T1–T4 | Time constants | dim | dimension |
| TWi | Time constant of washout | A | 4n × 4n matrix |
| Placement of ith solution in the search space | B | 4n × m matrix | |
| Upper bounds | a | Control parameter | |
| Lower bounds | m | PSS and SVC | |
| r3 | Random number among 0 and 1 | X | 4n × 1 state vector |
| Position of ith solution at iteration t | SF | Size factor | |
| Best solution in the population | PSS | Power system stabilizer | |
| r1 | Random numbers in the range of [0, 2π] | SVC | Static VAR compensator |
| r2 | Random weight of the best solution | CSCA | Chaotic sine cosine algorithm |
| Maximum number of iterations | PS | Pattern search | |
| λ (t) | Chaotic map | FACTS | Flexible AC transmission systems |
| t | Iteration number | hCSC-PS | Hybrid CSCA and PS |
| a | Constant equal to 4 | LFO | Low frequency oscillations |
| W12 | Speed difference response of G1–G2 | SQP | Sequential quadratic programming |
| W13 | Speed difference response of G1–G3 | SCA | Sine cosine algorithm |
| K1–K6 | Linearization constants | Kp, Kq, KB | Linearization constants |
References
- Kundur, P.; Balu, N.J.; Lauby, M.G. Power System Stability and Control; McGraw Hill: New York, NY, USA, 1994; p. 7. [Google Scholar]
- Hingorani, N.G. FACTS-flexible AC transmission system. In International Conference on AC and DC Power Transmission; IET: London, UK, 1991; pp. 1–7. [Google Scholar]
- Eslami, M.; Shareef, H.; Mohamed, A.; Khajehzadeh, M. A Survey on Flexible AC Transmission Systems (FACTS). Przeglad Elektrotechniczny 2012, 88, 1–11. [Google Scholar]
- Chen, J.-H.; Lee, W.-J.; Chen, M.-S. Using a static var compensator to balance a distribution system. In Proceedings of the IAS’96 Conference Record of the 1996 IEEE Industry Applications Conference Thirty-First IAS Annual Meeting, San Diego, CA, USA, 6–10 October 1996; IEEE: Piscataway, NJ, USA, 1996; pp. 2321–2326. [Google Scholar]
- Anderson, P.M.; Fouad, A.A. Power System Control and Stability; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Noroozian, M.; Adersson, G. Damping of power system oscillations by use of controllable components. IEEE Trans. Power Deliv. 1994, 9, 2046–2054. [Google Scholar] [CrossRef]
- Eslami, M.; Shareef, H.; Khajehzadeh, M. Optimal design of damping controllers using a new hybrid artificial bee colony algorithm. Int. J. Electr. Power Energy Syst. 2013, 52, 42–54. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.R.; El-Shafie, A.; Eslami, M. Search for critical failure surface in slope stability analysis by gravitational search algorithm. Int. J. Phys. Sci. 2011, 6, 5012–5021. [Google Scholar]
- Talaat, M.; Hatata, A.; Alsayyari, A.S.; Alblawi, A. A smart load management system based on the grasshopper optimization algorithm using the under-frequency load shedding approach. Energy 2020, 190, 116423. [Google Scholar] [CrossRef]
- Talaat, M.; Farahat, M.; Mansour, N.; Hatata, A. Load forecasting based on grasshopper optimization and a multilayer feed-forward neural network using regressive approach. Energy 2020, 196, 117087. [Google Scholar] [CrossRef]
- Talaat, M.; Said, T.; Essa, M.A.; Hatata, A. Integrated MFFNN-MVO approach for PV solar power forecasting considering thermal effects and environmental conditions. Int. J. Electr. Power Energy Syst. 2022, 135, 107570. [Google Scholar] [CrossRef]
- Rana, M.J.; Shahriar, M.S.; Shafiullah, M. Levenberg–Marquardt neural network to estimate UPFC-coordinated PSS parameters to enhance power system stability. Neural Comput. Appl. 2019, 31, 1237–1248. [Google Scholar] [CrossRef]
- Shafiullah, M.; Abido, M.; Coelho, L. Design of robust PSS in multimachine power systems using backtracking search algorithm. In Proceedings of the 2015 18th International Conference on Intelligent System Application to Power Systems (ISAP), Porto, Portugal, 11–16 September 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–6. [Google Scholar]
- Firouz, M.H.; Ghadimi, N. Concordant controllers based on FACTS and FPSS for solving wide-area in multi-machine power system. J. Intell. Fuzzy Syst. 2016, 30, 845–859. [Google Scholar] [CrossRef]
- Farah, A.; Guesmi, T.; Abdallah, H.H.; Ouali, A. A novel chaotic teaching–learning-based optimization algorithm for multi-machine power system stabilizers design problem. Int. J. Electr. Power Energy Syst. 2016, 77, 197–209. [Google Scholar] [CrossRef]
- Abd-Elazim, S.; Ali, E. Coordinated design of PSSs and SVC via bacteria foraging optimization algorithm in a multimachine power system. Int. J. Electr. Power Energy Syst. 2012, 41, 44–53. [Google Scholar] [CrossRef]
- Choudhury, S.; Dash, T. Modified brain storming optimization technique for transient stability improvement of SVC controller for a two machine system. World J. Eng. 2021, 18, 841–850. [Google Scholar] [CrossRef]
- Guesmi, T.; Alshammari, B.M.; Almalaq, Y.; Alateeq, A.; Alqunun, K. New Coordinated Tuning of SVC and PSSs in Multimachine Power System Using Coyote Optimization Algorithm. Sustainability 2021, 13, 3131. [Google Scholar] [CrossRef]
- Kamarposhti, M.A.; Colak, I.; Iwendi, C.; Band, S.S.; Ibeke, E. Optimal Coordination of PSS and SSSC Controllers in Power System Using Ant Colony Optimization Algorithm. J. Circuits Syst. Comput. 2021, 2250060. [Google Scholar] [CrossRef]
- Baadji, B.; Bentarzi, H.; Bakdi, A. Comprehensive learning bat algorithm for optimal coordinated tuning of power system stabilizers and static VAR compensator in power systems. Eng. Optim. 2020, 52, 1761–1779. [Google Scholar] [CrossRef]
- Abido, M.; Abdel-Magid, Y. Coordinated design of a PSS and an SVC-based controller to enhance power system stability. Int. J. Electr. Power Energy Syst. 2003, 25, 695–704. [Google Scholar] [CrossRef]
- Kamari, N.A.M.; Musirin, I.; Ibrahim, A.A. Swarm intelligence approach for angle stability improvement of PSS and SVC-based SMIB. J. Electr. Eng. Technol. 2020, 15, 1001–1014. [Google Scholar] [CrossRef]
- Abdelaziz, A.Y.; Ali, E.S. Static VAR compensator damping controller design based on flower pollination algorithm for a multi-machine power system. Electr. Power Compon. Syst. 2015, 43, 1268–1277. [Google Scholar] [CrossRef]
- Eslami, M.; Shareef, H.; Mohamed, A.; Khajehzadeh, M. PSS and TCSC damping controller coordinated design using GSA. Energy Procedia 2012, 14, 763–769. [Google Scholar] [CrossRef] [Green Version]
- Eslami, M.; Shareef, H.; Mohamed, A.; Khajehzadeh, M. Gravitational search algorithm for coordinated design of PSS and TCSC as damping controller. J. Cent. South Univ. 2012, 19, 923–932. [Google Scholar] [CrossRef]
- Kar, M.K.; Kumar, S.; Singh, A.K.; Panigrahi, S. A modified sine cosine algorithm with ensemble search agent updating schemes for small signal stability analysis. Int. Trans. Electr. Energy Syst. 2021, 31, e13058. [Google Scholar] [CrossRef]
- Bhukya, J.; Naidu, T.A.; Vuddanti, S.; Konstantinou, C. Coordinated control and parameters optimization for PSS, POD and SVC to enhance the transient stability with the integration of DFIG based wind power systems. Int. J. Emerg. Electr. Power Syst. 2021. [Google Scholar] [CrossRef]
- Pandey, R.K.; Gupta, D.K. Performance evaluation of power oscillation damping controller—Firefly algorithm based parameter tuning. Electr. Power Compon. Syst. 2017, 45, 2164–2174. [Google Scholar] [CrossRef]
- Panda, S. Robust coordinated design of multiple and multi-type damping controller using differential evolution algorithm. Int. J. Electr. Power Energy Syst. 2011, 33, 1018–1030. [Google Scholar] [CrossRef]
- Karthikeyan, K.; Lakshmi, P. Optimal design of PID controller for improving rotor angle stability using BBO. Procedia Eng. 2012, 38, 889–902. [Google Scholar] [CrossRef] [Green Version]
- Abd Elazim, S.; Ali, E. Optimal power system stabilizers design via cuckoo search algorithm. Int. J. Electr. Power Energy Syst. 2016, 75, 99–107. [Google Scholar] [CrossRef]
- Naresh, G.; Raju, M.R.; Narasimham, S. Coordinated design of power system stabilizers and TCSC employing improved harmony search algorithm. Swarm Evol. Comput. 2016, 27, 169–179. [Google Scholar] [CrossRef]
- Afzalan, E.; Joorabian, M. Analysis of the simultaneous coordinated design of STATCOM-based damping stabilizers and PSS in a multi-machine power system using the seeker optimization algorithm. Int. J. Electr. Power Energy Syst. 2013, 53, 1003–1017. [Google Scholar] [CrossRef]
- Bijami, E.; Marnani, J.A. Imperialist Competitive Algorithm for Optimal Simultaneous Coordinated Tuning of Damping Controller. Int. J. Tech. Phys. Probl. Eng. (IJTPE) 2012, 11, 34–41. [Google Scholar]
- Devarapalli, R.; Bhattacharyya, B. Application of modified harris hawks optimization in power system oscillations damping controller design. In Proceedings of the 2019 8th International Conference on Power Systems (ICPS), Jaipur, India, 20–22 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Eslami, M.; Babaei, B.; Shareef, H.; Khajehzadeh, M.; Arandian, B. Optimum Design of Damping Controllers using modified Sperm Swarm Optimization. IEEE Access 2021, 9, 145592–145604. [Google Scholar]
- Abido, M.; Abdel-Magid, Y. A tabu search based approach to power system stability enhancement via excitation and static phase shifter control. Electr. Power Syst. Res. 1999, 52, 133–143. [Google Scholar] [CrossRef]
- Abido, M. Simulated annealing based approach to PSS and FACTS based stabilizer tuning. Int. J. Electr. Power Energy Syst. 2000, 22, 247–258. [Google Scholar] [CrossRef]
- Dhal, P. Multi-verse Optimizer for Dynamic Stability Analysis Using STATCOM and Power System Stabilizer. Advanced Computing and Intelligent Engineering: Proceedings of ICACIE 2018; Springer Nature Singapore Pte Ltd.: Singapore, 2020; Volume 2, p. 117. [Google Scholar]
- Devarapalli, R.; Bhattacharyya, B.; Kumar, V.; Kumar, S. Improved Moth Flame Optimization in Systematization of STATCOM and PSS. In Smart Grid Automation and Industry 4.0. Lecture Notes in Electrical Engineering; Springer: Singapore, 2021; Volume 693, pp. 481–491. [Google Scholar] [CrossRef]
- Aribowo, W.; Muslim, S.; Suprianto, B.; Haryudo, S.I. Tunicate Swarm Algorithm-Neural Network for Adaptive Power System Stabilizer Parameter. Sci. Technol. Asia 2021, 26, 50–63. [Google Scholar]
- Dey, P.; Bhattacharya, A.; Das, P. Tuning of power system stabilizer for small signal stability improvement of interconnected power system. Appl. Comput. Inform. 2017, 16, 3–28. [Google Scholar] [CrossRef]
- Asghari, K.; Masdari, M.; Gharehchopogh, F.S.; Saneifard, R. Multi-swarm and chaotic whale-particle swarm optimization algorithm with a selection method based on roulette wheel. Expert Syst. 2021, 38, e12779. [Google Scholar] [CrossRef]
- Farah, A.; Belazi, A.; Alqunun, K.; Almalaq, A.; Alshammari, B.M.; Ben Hamida, M.B.; Abbassi, R. A New Design Method for Optimal Parameters Setting of PSSs and SVC Damping Controllers to Alleviate Power System Stability Problem. Energies 2021, 14, 7312. [Google Scholar] [CrossRef]
- Sahu, P.R.; Hota, P.K.; Panda, S. Modified whale optimization algorithm for coordinated design of fuzzy lead-lag structure-based SSSC controller and power system stabilizer. Int. Trans. Electr. Energy Syst. 2019, 29, e2797. [Google Scholar] [CrossRef]
- Eslami, M.; Shareef, H.; Mohamed, A.; Khajehzadeh, M. Optimal location of PSS using improved PSO with chaotic sequence. In Proceedings of the International Conference on Electrical, Control and Computer Engineering 2011 (InECCE), Kuantan, Malaysia, 21–22 June 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 253–258. [Google Scholar]
- Khajehzadeh, M.; Taha, M.R.; Eslami, M. A new hybrid firefly algorithm for foundation optimization. Natl. Acad. Sci. Lett. 2013, 36, 279–288. [Google Scholar] [CrossRef]
- Eslami, M.; Shareef, H.; Mohamed, A. Optimization and coordination of damping controls for optimal oscillations damping in multi-machine power system. Int. Rev. Electr. Eng. 2011, 6, 1984–1993. [Google Scholar]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A. Advances in sine cosine algorithm: A comprehensive survey. Artif. Intell. Rev. 2021, 54, 2567–2608. [Google Scholar] [CrossRef]
- Ji, Y.; Tu, J.; Zhou, H.; Gui, W.; Liang, G.; Chen, H.; Wang, M. An adaptive chaotic sine cosine algorithm for constrained and unconstrained optimization. Complexity 2020, 2020, 6084917. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Torczon, V. On the convergence of pattern search algorithms. SIAM J. Optim. 1997, 7, 1–25. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Kaur, S.; Awasthi, L.K.; Sangal, A.; Dhiman, G. Tunicate swarm algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020, 90, 103541. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Pai, M.; Gupta, D.S.; Padiyar, K. Small Signal Analysis of Power Systems; Alpha Science Int’l Ltd.: Oxford, UK, 2004. [Google Scholar]
- Sadikovic, R.; Andersson, G.; Korba, P. Damping controller design for power system oscillations. Intell. Autom. Soft Comput. 2006, 12, 51–62. [Google Scholar] [CrossRef]



| Function | Range | n (Dim) | 3D View | |
|---|---|---|---|---|
| 0 | 30 |  | ||
| 0 | 30 |  | ||
| 0 | 30 |  | ||
| 0 | 30 |  | ||
| 0 | 30 |  | ||
| 0 | 30 |  | ||
| 0 | 30 |  |
| Function | Range | n (Dim) | 3D View | |
|---|---|---|---|---|
| 428.9829 × n | 30 |  | ||
| 0 | 30 |  | ||
| 0 | 30 |  | ||
| 0 | 30 |  | ||
| 0 | 30 |  | ||
| 0 | 30 |  |
| Function | Range | n (Dim) | 3D View | |
|---|---|---|---|---|
| 1 | 2 |  | ||
| 0.00030 | 4 |  | ||
| −1.0316 | 2 |  | ||
| 0.398 | 2 |  | ||
| 3 | 2 |  | ||
| −3.86 | 3 |  | ||
| −3.32 | 6 |  | ||
| −10.1532 | 4 |  | ||
| −10.4028 | 4 |  | ||
| −10.5363 | 4 |  |
| Year | Algorithm | Parameter | Specifications |
|---|---|---|---|
| 2021 | hCSC-PS | Search agents Number of elites Number of function evaluations | 50 2 50,000 |
| 2016 | SCA | Search agents Number of elites Number of function evaluations | 50 2 50,000 |
| 2009 | GSA | Search agents Gravitational constant Alpha coefficient Number of function evaluations | 50 100 20 50,000 |
| 2014 | GWO | Search agents Control parameter (→a) Number of function evaluations | 50 [2,0] 50,000 |
| 2020 | TSA | Search agents Parameter Pmin Parameter Pmax Number of function evaluations | 50 1 4 50,000 |
| Function | Statistics | hCSC-PS | SCA | GSA | TSA | GWO |
|---|---|---|---|---|---|---|
| F1 | Best Worst Mean Median Std. | 0.000 0.000 0.000 0.000 0.000 | 1.551 × 10−6 2. 030 × 10−3 2.340 × 10−5 1.874 × 10−4 7.929 × 10−5 | 1.101 × 10−17 3.186 × 10−17 2.117 × 10−17 2.007 × 10−17 5.815 × 10−17 | 5.145 × 10−60 1.058 × 10−55 8.215 × 10−55 7.401 × 10−55 2.390 × 10−55 | 2.391× 10−61 3.564× 10−58 4.116× 10−59 1.153× 10−59 1.123× 10−58 |
| F2 | Best Worst Mean Median Std. | 0.000 0.000 0.000 0.000 0.000 | 1.500 × 10−6 9.830 × 10−6 1.687 × 10−6 5.402 × 10−7 2.304 × 10−6 | 1.528 × 10−8 3.331 × 10−8 2.393 × 10−8 2.347 × 10−8 4.002 × 10−8 | 1.119 × 10−35 3.281 × 10−32 2.151 × 10−33 3.104 × 10−34 6.023 × 10−33 | 8.362 × 10−36 5.340 × 10−34 8.361 × 10−35 5.929 × 10−35 9.850 × 10−35 |
| F3 | Best Worst Mean Median Std. | 0.000 0.000 0.000 0.000 0.000 | 7.172 × 10 2.660 × 103 7.991 × 102 6.294 × 102 7.562 × 102 | 1.029 × 102 4.686 × 102 2.454 × 102 2.211 × 102 1.001 × 102 | 2.568 × 10−32 2.449 × 10−17 8.174 × 10−19 1.869 × 10−24 4.471 × 10−18 | 1.253 × 10−19 3.557 × 10−13 1.509 × 10−14 2.074 × 10−17 6.554 × 10−14 |
| F4 | Best Worst Mean Median Std. | 0.000 0.000 0.000 0.000 0.000 | 1.161 3.467 × 10 9.208 6.080 8.672 | 2.230 × 10−9 5.085 × 10−9 3.303 × 10−9 3.200 × 10−9 7.444 × 10−9 | 3.235 × 10−8 6.342 × 10−5 1.011 × 10−5 2.027 × 10−6 1.692 × 10−5 | 9.821 × 10−16 2.441 × 10−13 1.948 × 10−14 6.381 × 10−15 4.491 × 10−14 |
| F5 | Best Worst Mean Median Std. | 5.061 × 10−1 8.123× 10−1 7.183× 10−1 7.270× 10−1 1.063× 10−1 | 2.712 × 10 4.951 × 10 2.911 × 10 2.900 × 10 4.152 | 2.574 × 10 2.209 × 102 4.228 × 10 2.617 × 10 4.544 × 10 | 2.562 × 10 2.954 × 10 2.844 × 10 2.891 × 10 7.619 × 10−1 | 2.521 × 10 2.872 × 10 2.690 × 10 2.713 × 10 8.408 × 10−1 |
| F6 | Best Worst Mean Median Std. | 0.000 0.000 0.000 0.000 0.000 | 3.457 4.843 4.436 4.457 2.850 × 10−1 | 9.712 × 10−18 8.642 × 10−17 3.097 × 10−17 2.933 × 10−17 6.169 × 10−17 | 2.054 4.772 3.670 3.561 0.693 | 2.456 × 10−1 1.291 6.476 × 10−1 7.252 × 10−1 3.053 × 10−1 |
| F7 | Best Worst Mean Median Std. | 3.305 × 10−10 1.221× 0−14 7.280× 0−16 3.300× 0−10 2.488× 10−5 | 4.150 × 10−2 3.100 × 10−3 4.116 × 10−1 8.780 × 10−2 5.010 × 10−2 | 8.100 × 10−3 9.620 × 10−2 3.370 × 10−2 1.220 × 10−2 8.800 × 10−3 | 6.710 × 10−4 3.100 × 10−2 4.800 × 10−2 5.800 × 10−2 7.7266 × 10−4 | 1.523 × 10−4 4.200 × 10−2 7.995 × 10−4 7.069 × 10−4 4.678 × 10−4 |
| Function | Statistics | hCSC-PS | SCA | GSA | TSA | GWO |
|---|---|---|---|---|---|---|
| F8 | Best Worst Mean Median Std. | −1.100 × 104 −1.001× 104 −1.100× 104 −1.102× 104 1.734× 102 | −5.399 × 103 −3.432 × 103 −4.576 × 103 −3.672 × 103 3.768 × 102 | −3.627 × 103 −2.103 × 103 −2.882 × 103 −2.846 × 103 3.754 × 102 | −7.999 × 103 −5.376 × 103 −6.412 × 103 −6.513 × 103 5.692 × 1023 | −8.917 × 103 −4.878 × 103 −6.357 × 103 −6.426 × 103 8.524 × 1023 |
| F9 | Best Worst Mean Median Std. | 0.000 0.000 0.000 0.000 0.000 | 1.066 × 10−6 4.143 × 10 5.969 8.339 × 10−4 1.124 × 10 | 8.854 2.788 × 10 1.672 × 10 1.531 × 10 3.204 | 7.877 × 10 2.949 × 102 1.014 × 102 1.096 × 102 3.387 × 10 | 0.000 1.105 × 10 8.553 × 10−1 0.000 2.4938 |
| F10 | Best Worst Mean Median Std. | 8.881 × 10−16 8.881 × 10−16 8.881 × 10−16 8.881 × 10−16 0.000 | 1.556 × 10−5 2.121 × 10 1.336 × 10 2.112 × 10 7.977 | 2.428 × 10−9 4.582 × 10−9 4.691 × 10−9 3.486 × 10−9 5.133 × 10−10 | 1.569 × 10−14 4.012 2.409 2.765 1.097 | 1.560 × 10−14 2.020 × 10−14 1.547 × 10−15 1.459 × 10−14 2.376 × 10−15 |
| F11 | Best Worst Mean Median Std. | 0.000 0.000 0.000 0.000 0.000 | 4.348 × 10−7 7.654 × 10−1 2.148 × 10−1 1.320 × 10−2 2.218 × 10−1 | 1.654 1.028 × 10 4.452 3.565 2.023 | 0.00 1.090 × 10−2 6.700 × 10−2 7.200 × 10−2 5.700 × 10−2 | 0.000 8.400 × 10−2 9.400 × 10−3 0.000 4.100 × 10−3 |
| F12 | Best Worst Mean Median Std. | 4.611 × 10−32 4.611× 10−32 4.611× 10−32 4.611× 10−32 1.044× 10−47 | 2.456 × 10−1 5.632 9.654 × 10−1 4.209 × 10−1 1.144 | 8.214 × 10−20 1.343 × 10−1 4.580 × 10−2 1.303 × 10−19 4.230 × 10−2 | 2.876 × 10−1 1.398 × 10 6.094 6.765 3.409 | 2.540 × 10−2 4.200 × 10−2 6.640 × 10−2 8.290 × 10−2 5.010 × 10−2 |
| F13 | Best Worst Mean Median Std. | 1.245 × 10−32 1.000× 10−2 5.000 × 10−3 1.000× 10−2 4.000× 10−3 | 1.945 2.298 × 10 3.541 2.366 3.980 | 1.354 × 10−18 1.000 × 10−2 6.334 × 10−4 2.109 × 10−18 1.800 × 10−2 | 1.9876 3.2305 1.9976 1.8574 6.436 × 10−1 | 1.001 × 10−1 1.041 5.283 × 10−1 5.235 × 10−1 3.351 × 10−1 |
| Function | Statistics | hCSC-PS | SCA | GSA | TSA | GWO |
|---|---|---|---|---|---|---|
| F14 | Best Worst Mean Median Std. | 9.980 × 10−1 9.980 × 10−1 9.980 × 10−1 9.980 × 10−1 1.472 × 10−11 | 9.980 × 10−1 2.982 1.196 9.980 × 10−1 6.054 × 10−1 | 9.980 × 10−1 8.085 3.621 3.045 2.194 | 9.980 × 10−1 1.267 × 10 7.665 1.076 × 10 4.884 | 9.980 × 10−1 1.267× 10 4.131 2.982 4.144 |
| F15 | Best Worst Mean Median Std. | 3.138 × 10−4 3.968× 10−4 3.364 × 10−4 3.232 × 10−4 2.458 × 10−5 | 3.406 × 10−4 1.400 × 10−2 8.597 × 10−4 7.309 × 10−4 3.808 × 10−4 | 1.200 × 10−2 1.180 × 10−1 2.500 × 10−2 2.100 × 10−2 1.900 × 10−2 | 3.751 × 10−4 5.660 × 10−2 4.300 × 10−2 4.539 × 10−4 1.160 × 10−1 | 3.174 × 10−4 2.040 × 10−2 4.400 × 10−2 3.075 × 10−4 8.100 × 10−2 |
| F16 | Best Worst Mean Median Std. | −1.031 −1.031 −1.031 −1.031 1.859 × 10−6 | −1.031 −1.031 −1.031 −1.031 1.039 × 10−5 | −1.031 −1.031 −1.031 −1.031 5.608 × 10−5 | −1.031 −1.000 −1.030 −1.031 5.800 × 10−2 | −1.031 −1.031 −1.031 −1.031 4.738 × 10−9 |
| F17 | Best Worst Mean Median Std. | 3.979 × 10−1 3.979 × 10−1 3.979 × 10−1 3.979 × 10−1 0.000 | 3.979 × 10−1 3.992 × 10−1 3.982 × 10−1 3.982 × 10−1 3.488 × 10−4 | 3.979 × 10−1 3.979 × 10−1 3.979 × 10−1 3.979 × 10−1 0.000 | 3.979 × 10−1 3.980 × 10−1 3.979 × 10−1 3.979 × 10−1 1.371 × 10−5 | 3.979 × 10−1 3.979 × 10−1 3.979 × 10−1 3.979 × 10−1 1.105 × 10−6 |
| F18 | Best Worst Mean Median Std. | 3.000 3.000 3.000 3.000 1.098 × 10−14 | 3.000 3.000 3.000 3.000 5.349 × 10−6 | 3.000 3.000 3.000 3.000 1.592 × 10−15 | 3.000 8.400 × 10 5.700 3.000 14.7885 | 3.000 3.000 3.000 3.000 9.505 × 10−6 |
| F19 | Best Worst Mean Median Std. | −3.862 −3.862 −3.862 −3.862 4.186 × 10−16 | −3.862 −3.854 −3.875 −3.806 2.800 × 10−2 | −3.862 −3.862 −3.862 −3.862 2.479 × 10−5 | −3.862 −3.954 −3.062 −3.962 1.500 × 10−2 | −3.862 −3.954 −3.962 −3.962 2.100 × 10−2 |
| F20 | Best Worst Mean Median Std. | −3.322 −3.322 −3.322 −3.322 1.355× 10−15 | −3.191 −2.048 −3.015 −3.013 1.974 × 10−1 | −3.322 −1.855 −2.953 −2.987 2.446 × 10−1 | −3.321 −3.088 −3.253 −3.202 6.710 × 10−2 | −3.322 −3.029 −3.249 −3.262 8.210 × 10−2 |
| F21 | Best Worst Mean Median Std. | −1.015 × 10 −1015 × 10 −1.015× 10 −1.015 × 10 2.499 × 10−17 | −8.137 −8.800 × 10−1 −4.318 −4.905 2.078 | −1.015 × 10 −2.682 −6.396 −3.954 3.590 | −1.013 × 10 −2.666 −7.287 −7.419 2.859 | −1.015 × 10 −5.099 −9.479 −1.015 × 10 1.746 |
| F22 | Best Worst Mean Median Std. | −1.040 × 10 −1.040 × 10 −1.040 × 10 −1.040 × 10 5.420 × 10−15 | −9.054 −9.064 × 10−1 −5.415 −5.037 1.738 | −1.040 × 10 −1.040 × 10 −1.040 × 10 −1.040 × 10 4.661 × 10−6 | −1.039 × 10 −2.748 −7.838 −1.025 × 10 3.184 | −1.040 × 10 −5.085 −1.022 × 10 −1.040 × 10 9.723 × 10−1 |
| F23 | Best Worst Mean Median Std. | −1.053 × 10 −1.053 × 10 −1.053 × 10 −1.053 × 10 2.485 × 10−18 | −9.3851 −3.2531 −5.2925 −5.0398 1.0982 | −1.053 × 1.0 −1053 × 10 −1.053 × 10 −1.053 × 10 1.836 × 10−15 | −1.051 × 10 −1.675 −7.673 −1.041 × 10 3.7585 | −1.053 × 10 −1.053 × 10 −1.053 × 10 −1.053 × 10 2.585 × 10−4 |
| Generator | Normal Case | Case 1 | Case 2 | Case 3 | ||||
|---|---|---|---|---|---|---|---|---|
| P(p.u) | Q(p.u) | P(p.u) | Q(p.u) | P(p.u) | Q(p.u) | P(p.u) | Q(p.u) | |
| G1 | 1.79 | 0.28 | 2.11 | 1.19 | 0.33 | 1.12 | 1.47 | 1.05 |
| G2 | 1.65 | 0.08 | 1.22 | 0.57 | 2.00 | 0.57 | 2.01 | 0.6 |
| G3 | 0.85 | −0.11 | 1.29 | 0.38 | 1.50 | 0.38 | 1.5 | 0.7 |
| Load | ||||||||
| A | 1.25 | 0.54 | 2.10 | 0.70 | 1.50 | 0.90 | 1.5 | 0.9 |
| B | 0.90 | 0.31 | 1.81 | 0.450 | 1.20 | 0.80 | 1.2 | 0.8 |
| C | 1.10 | 0.25 | 1.70 | 0.80 | 1.00 | 0.5 | 1 | 0.5 |
| Algorithm | K | T1 | T2 | T3 | T4 | |
|---|---|---|---|---|---|---|
| Uncoordinated design | PSS1 | 20.45 | 0.070 | 0.073 | 0.030 | 0.045 |
| PSS2 | 19.36 | 0.128 | 0.050 | 0.068 | 0.055 | |
| SVC | 65.56 | 0.028 | 0.121 | 0.523 | 0.048 | |
| Coordinated design | PSS1 | 24.06 | 0.095 | 0.043 | 0.283 | 0.050 |
| PSS2 | 15.03 | 0.056 | 0.050 | 0.054 | 0.029 | |
| SVC | 25.02 | 0.028 | 0.230 | 0.058 | 0.493 |
| Algorithm | K | T1 | T2 | T3 | T4 | |
|---|---|---|---|---|---|---|
| Coordinated by SCA | PSS1 | 20.30 | 0.254 | 0.854 | 0.221 | 1.214 |
| PSS2 | 17.24 | 0.052 | 0.563 | 0.034 | 0.376 | |
| SVC | 36.92 | 0.058 | 0.034 | 0.031 | 0.098 | |
| Coordinated by TSA | PSS1 | 18.24 | 0.021 | 0.267 | 0.181 | 0.276 |
| PSS2 | 26.08 | 0.854 | 0.189 | 0.023 | 1.149 | |
| SVC | 18.65 | 0.523 | 0.123 | 0.081 | 0.100 | |
| Coordinated by GSA | PSS1 | 25.45 | 0.283 | 0.854 | 0.63 | 1.312 |
| PSS2 | 18.05 | 0.054 | 0.561 | 0.101 | 0.734 | |
| SVC | 51.23 | 0.058 | 0.034 | 0.045 | 0.087 |
| Uncoordinated Design | Coordinated Design | Coordinated by SCA | Coordinated by TSA | Coordinated by GSA | |
|---|---|---|---|---|---|
| Case 1 | 0.0696 | 0.7779 | 0.5654 | 0.5412 | 0.2524 |
| Case 2 | 0.2868 | 0.8379 | 0.5003 | 0.5177 | 0.5215 |
| Case 3 | 0.2139 | 0.7686 | 0.4538 | 0.4417 | 0.5459 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eslami, M.; Neshat, M.; Khalid, S.A. A Novel Hybrid Sine Cosine Algorithm and Pattern Search for Optimal Coordination of Power System Damping Controllers. Sustainability 2022, 14, 541. https://doi.org/10.3390/su14010541
Eslami M, Neshat M, Khalid SA. A Novel Hybrid Sine Cosine Algorithm and Pattern Search for Optimal Coordination of Power System Damping Controllers. Sustainability. 2022; 14(1):541. https://doi.org/10.3390/su14010541
Chicago/Turabian StyleEslami, Mahdiyeh, Mehdi Neshat, and Saifulnizam Abd. Khalid. 2022. "A Novel Hybrid Sine Cosine Algorithm and Pattern Search for Optimal Coordination of Power System Damping Controllers" Sustainability 14, no. 1: 541. https://doi.org/10.3390/su14010541
APA StyleEslami, M., Neshat, M., & Khalid, S. A. (2022). A Novel Hybrid Sine Cosine Algorithm and Pattern Search for Optimal Coordination of Power System Damping Controllers. Sustainability, 14(1), 541. https://doi.org/10.3390/su14010541







