Determination and Comparative Analysis of Critical Velocity for Five Objects of Railway Vehicle Class
Abstract
:1. Introduction
2. The Basics of the Motion Stability Analysis
3. Methods of Determining the Value of Critical Velocity
4. Critical Velocity Determined for the Objects Tested
4.1. The Method Used
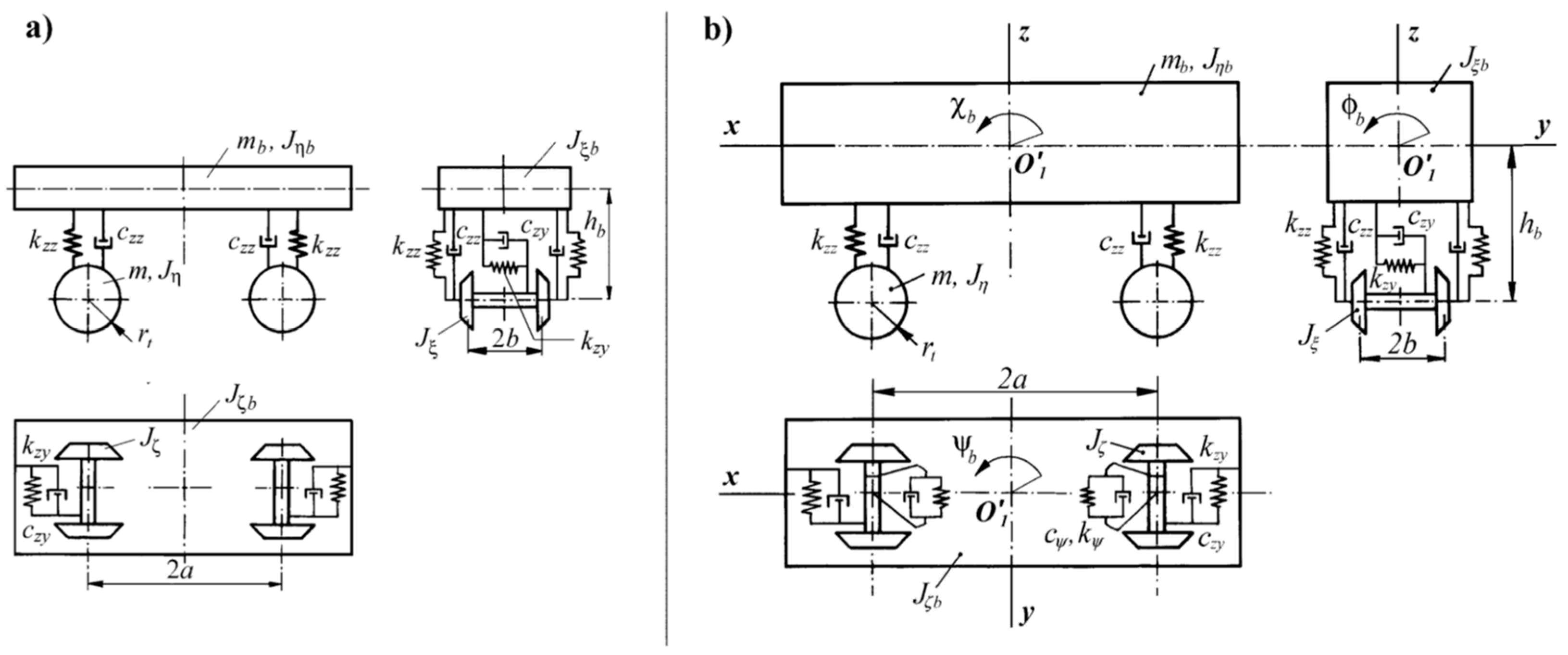
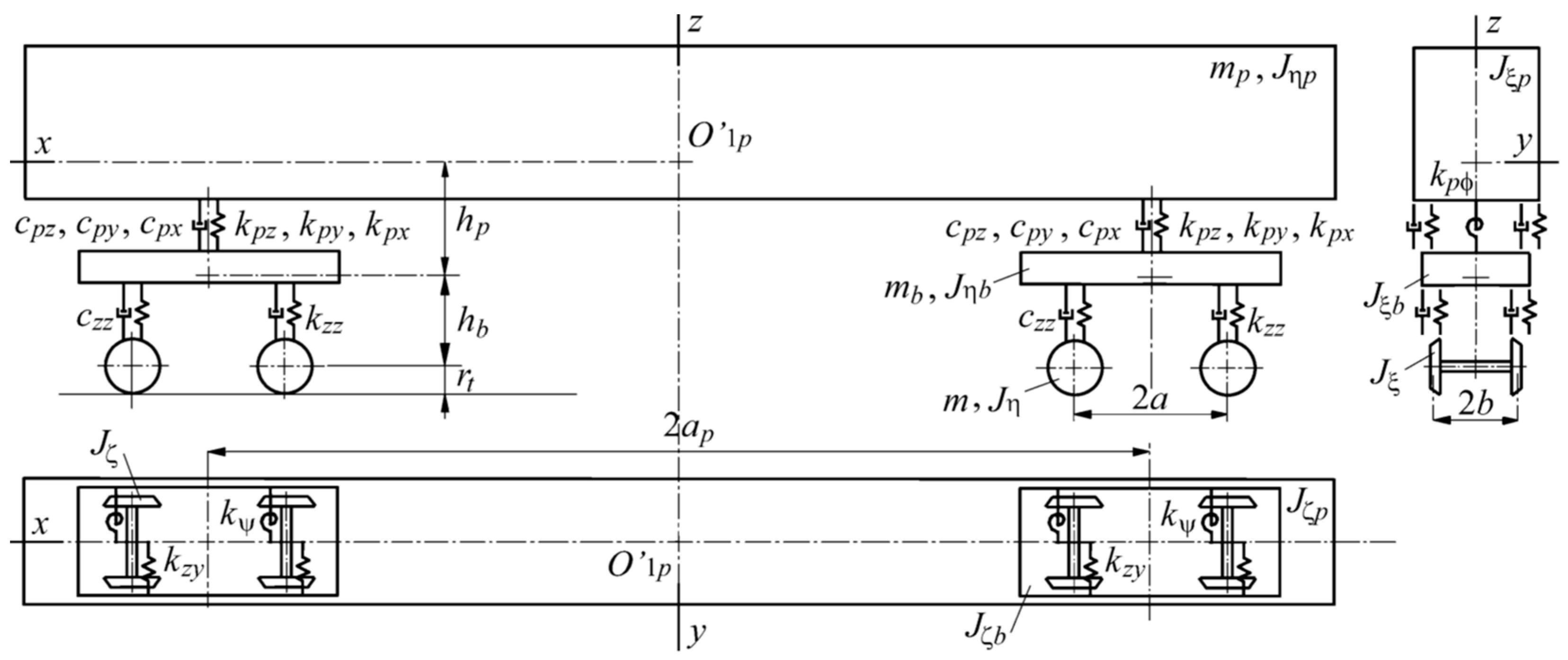
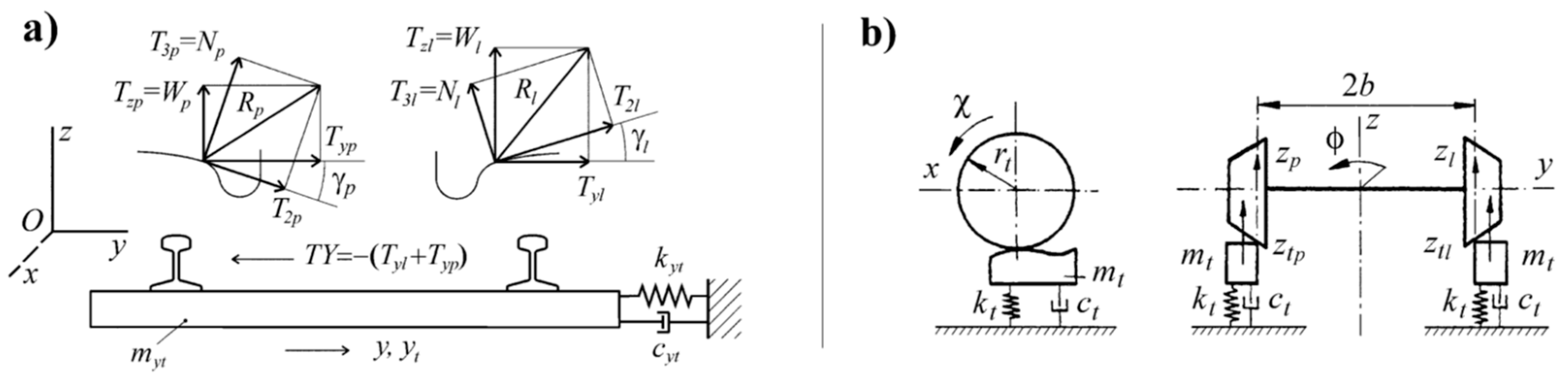
4.2. Models of the Considered Objects
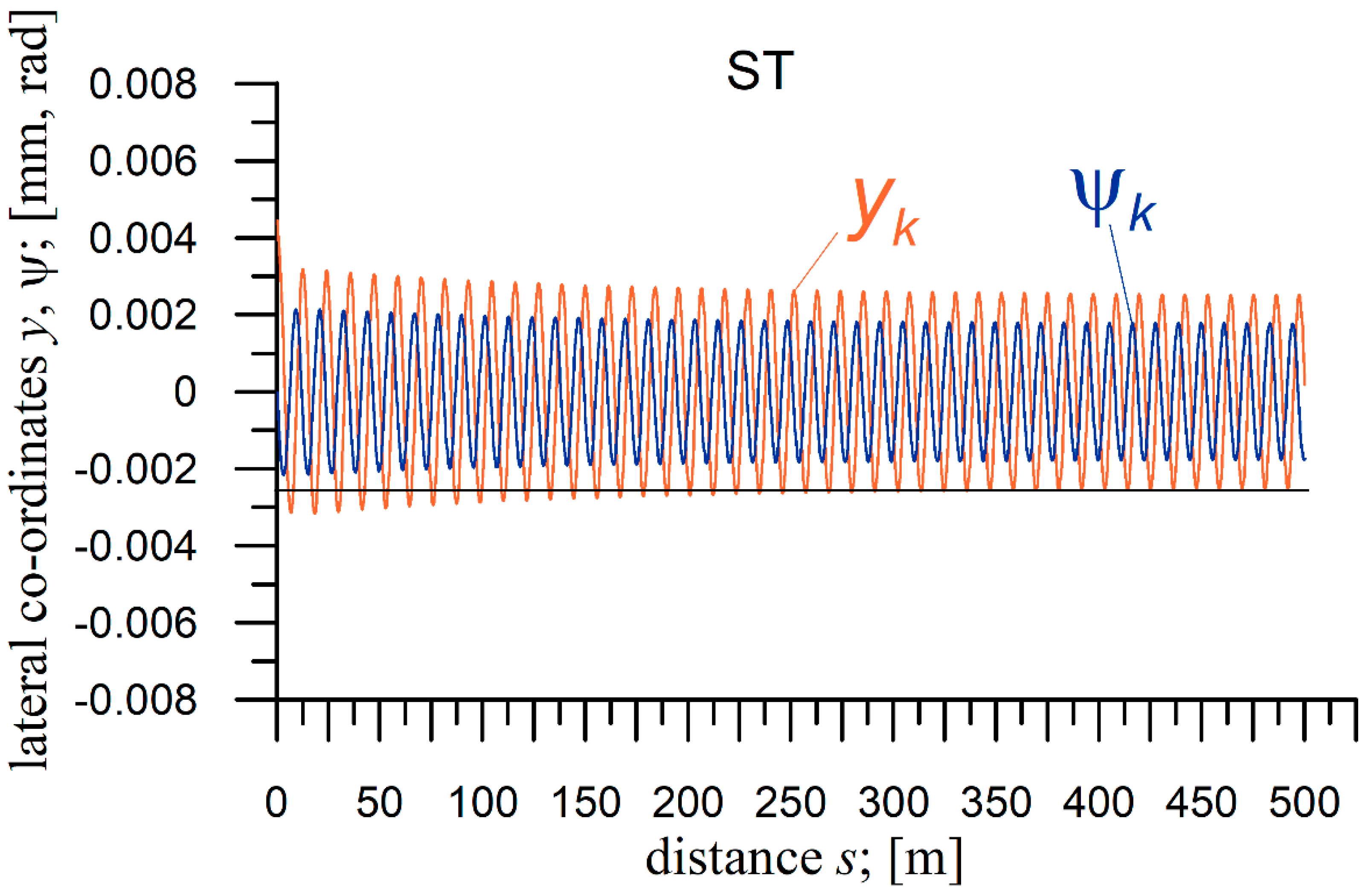
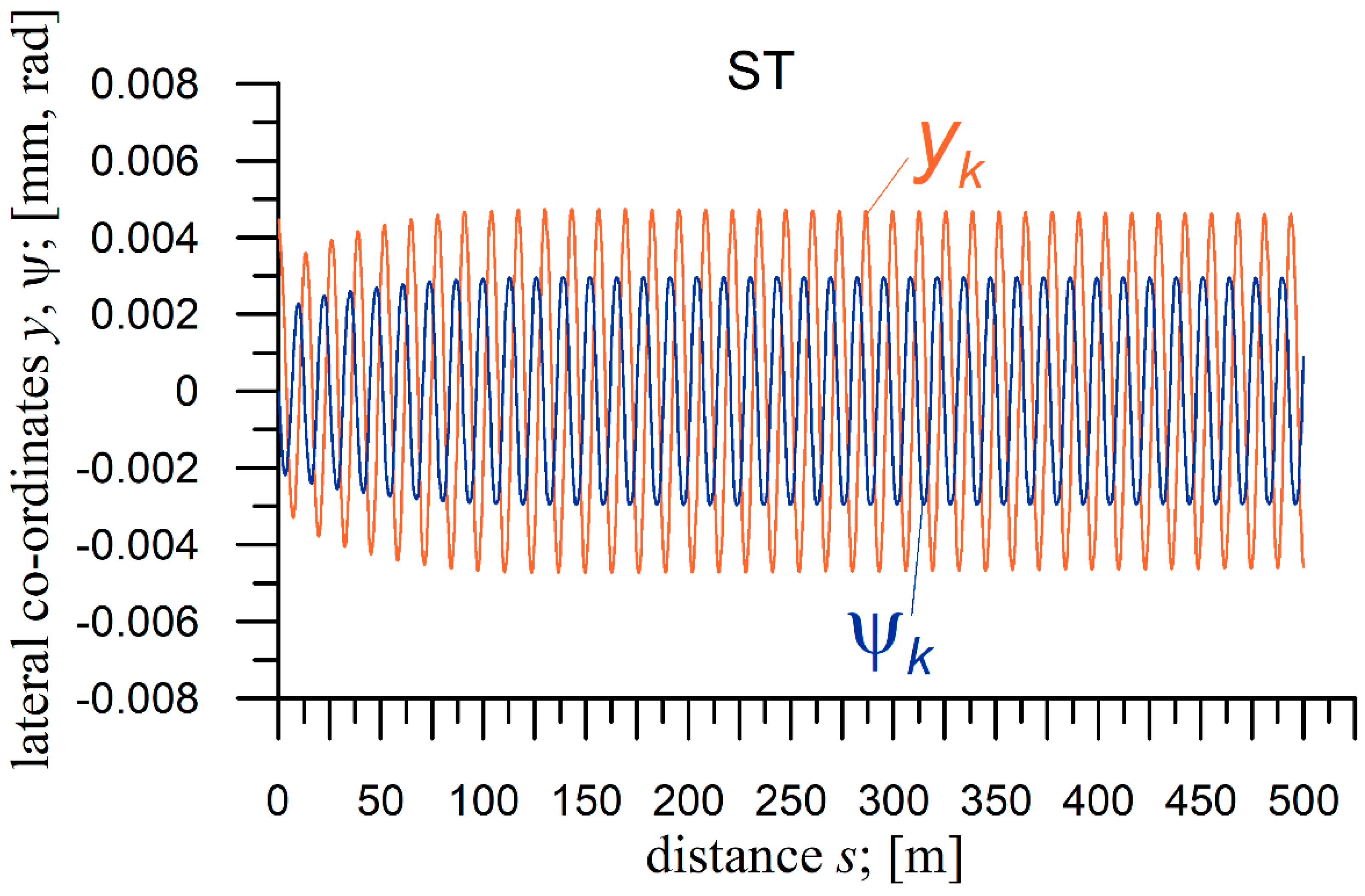
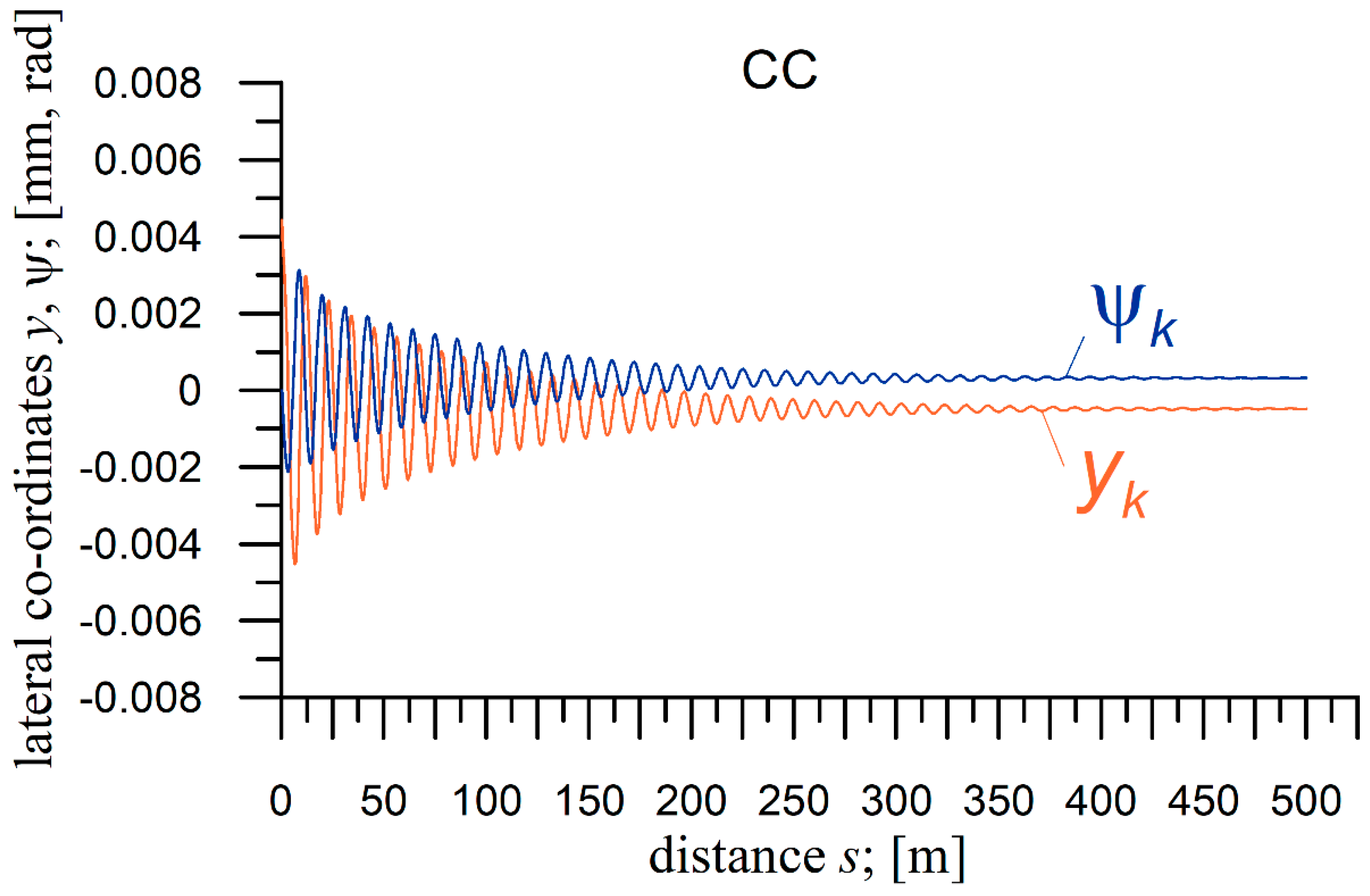
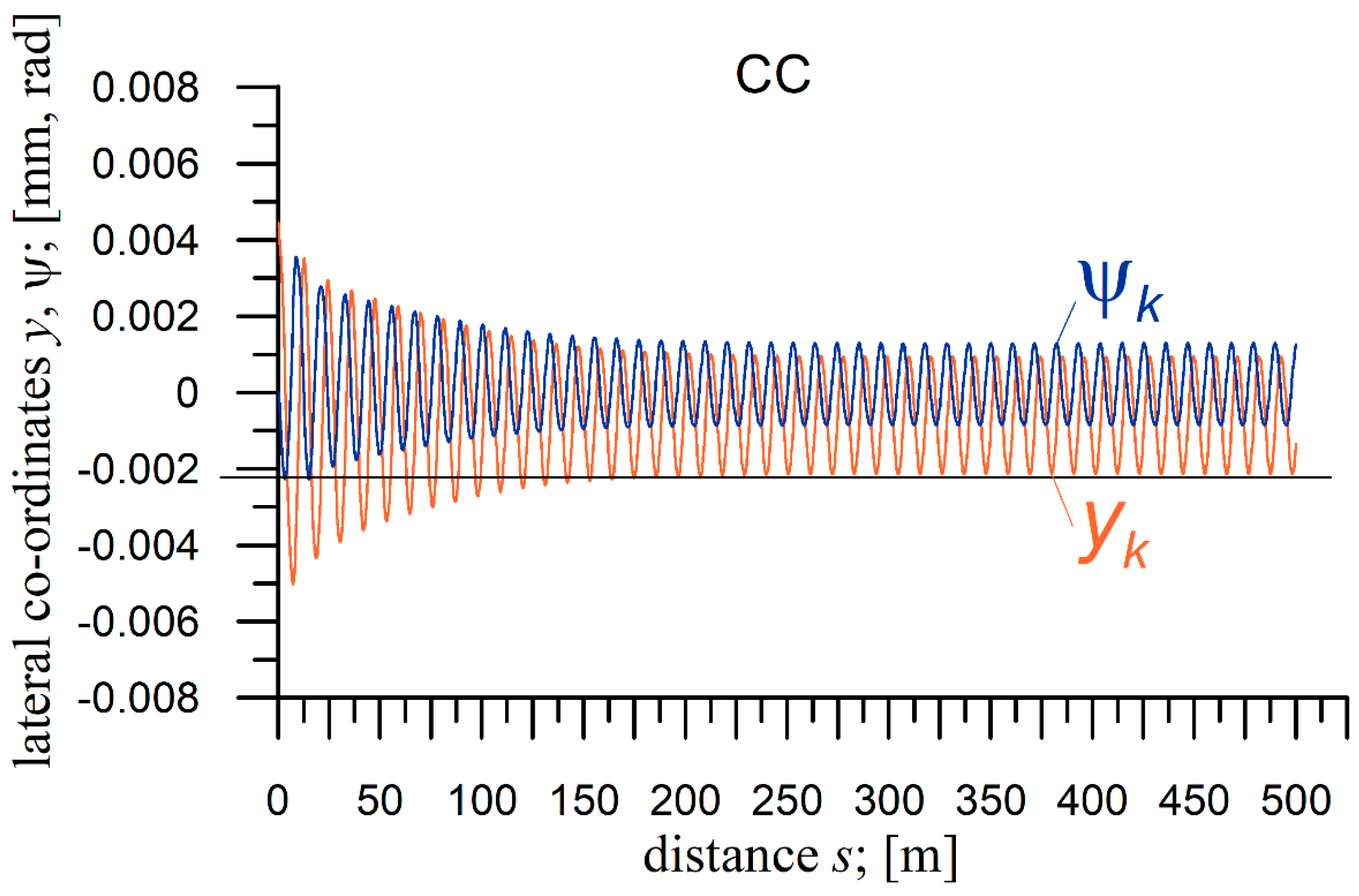
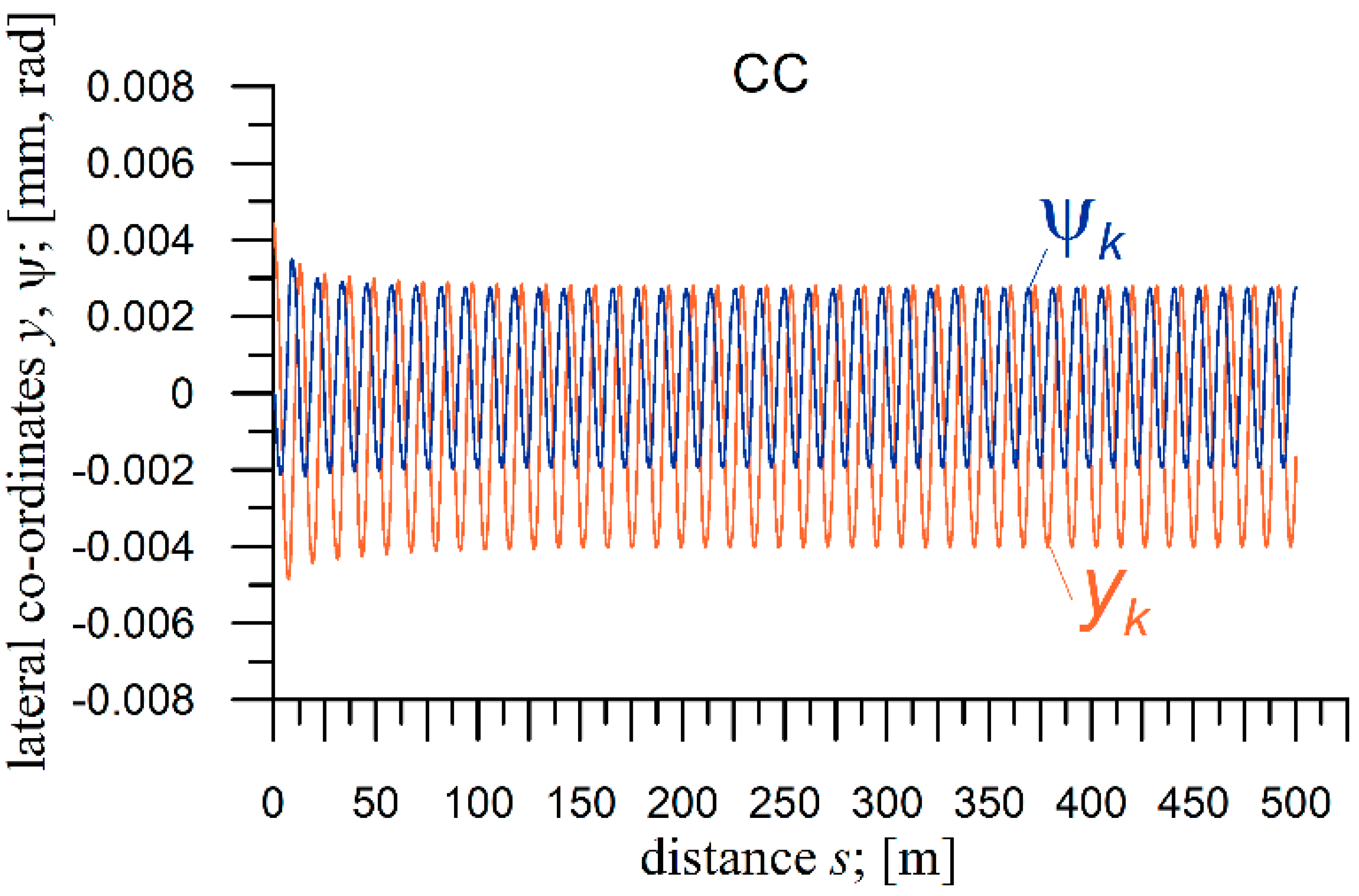
4.3. Conditions of the Critical Velocity Determination and Example Simulation Results
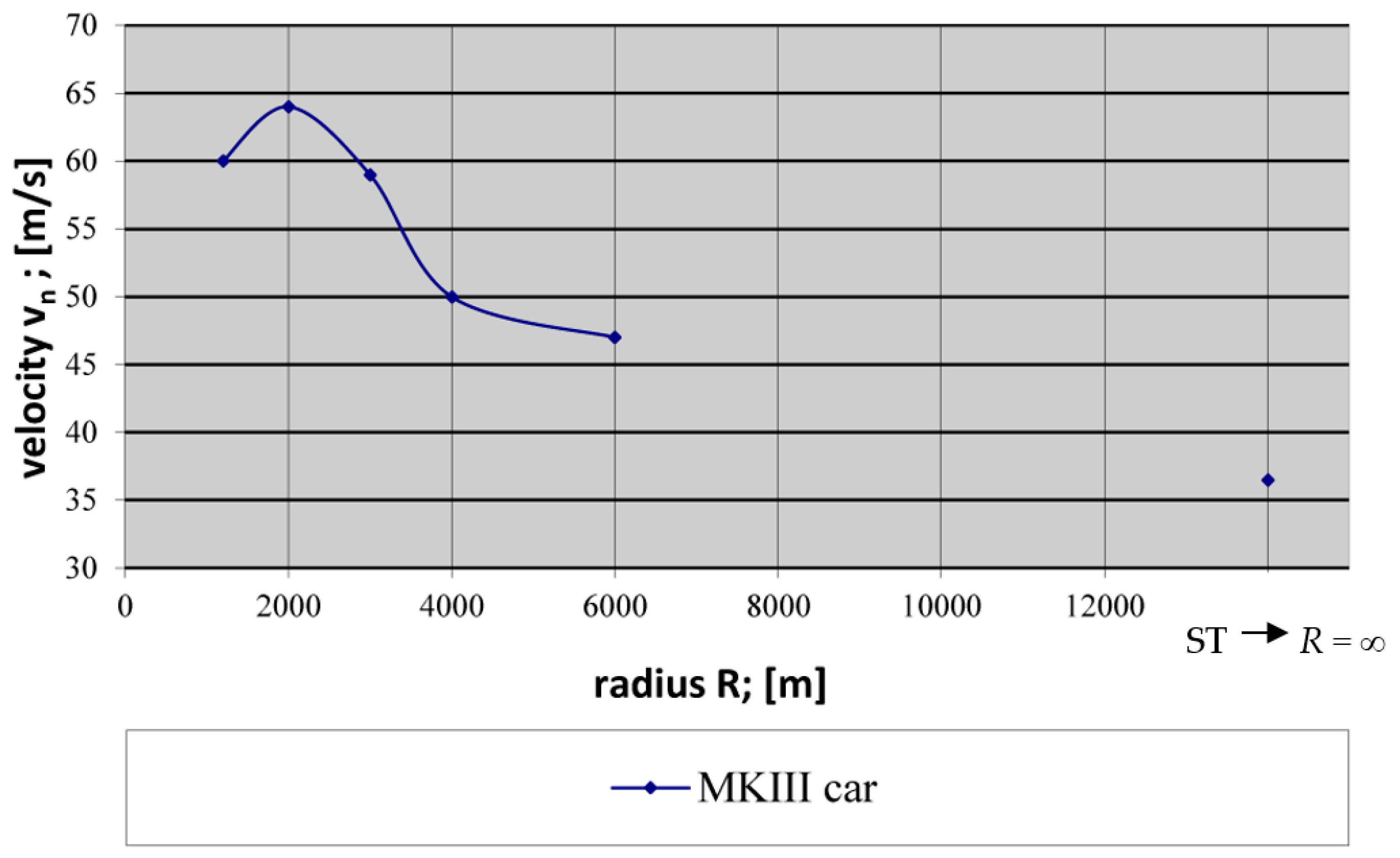
4.4. Results of the Critical Velocity Determination
5. Discussion of the Results and Conclusions
5.1. Detailed Discussion of the Results
5.2. General Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zboinski, K.; Dusza, M. Bifurcation analysis of 4-axle rail vehicle models in a curved track. Nonlinear Dyn. 2017, 89, 863–885. [Google Scholar] [CrossRef]
- Zboinski, K.; Golofit-Stawinska, M. Investigation into nonlinear phenomena for various railway vehicles in transition curves at velocities close to critical one. Nonlinear Dyn. 2019, 98, 1555–1601. [Google Scholar] [CrossRef] [Green Version]
- Zboiński, K. Dynamical investigation of railway vehicles on a curved track. Eur. J. Mech. Part A Solids 1998, 17, 1001–1020. [Google Scholar] [CrossRef]
- Knothe, K.; Bohm, F. History of Stability of Railway and Road Vehicles. Veh. Syst. Dyn. 1999, 31, 283–323. [Google Scholar] [CrossRef]
- Zboinski, K. Nieliniowa Dynamika Pojazdow Szynowych w Luku; Wydawnictwo Naukowe Instytutu Technologii Eksploatacji-Państwowego Instytutu Badawczego (ITE PIB): Warszawa-Radom, Poland, 2012; p. 371. ISBN 98-83-7789-129-2. [Google Scholar]
- Knothe, K.; Stichel, S. Rail Vehicle Dynamics; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Ding, W. Self-Excited Vibration: Theory, Paradigms, and Research Methods; Springer: Berlin/Heidelberg, Germany, 2012; p. 399. ISBN 978-3540697404. [Google Scholar]
- Zboinski, K.; Dusza, M. Self-exciting vibrations and Hopf’s bifurcation in non-linear stability analysis of rail vehicles in curved track. Eur. J. Mech. Part A Solids 2010, 29, 190–203. [Google Scholar] [CrossRef] [Green Version]
- Zboinski, K.; Dusza, M. Extended study of rail vehicle lateral stability in a curved track. Veh. Syst. Dyn. 2011, 49, 789–810. [Google Scholar] [CrossRef]
- Gasch, R.; Moelle, D. Nonlinear Bogie Hunting. In Proceedings of the 7th IAVSD Symposium on Dynamics of Vehicles on Roads and Tracks, Cambridge, UK, 7–11 September 1981; Swets & Zeitlinger: Lisse, The Netherlands, 1982; pp. 455–467. [Google Scholar]
- Goodall, R.M.; Iwnicki, S. Non-linear Dynamic Techniques v. Equivalent Conicity Methods for Rail Vehicle Stability Assessment. In Proceedings of the 18th IAVSD Symposium on Dynamics of Vehicles on Roads and Tracks, Vehicle System Dynamics, Kanagawa, Japan, 24–30 August 2003; Taylor & Francis: London, UK, 2004; Volume 41, pp. 791–799. [Google Scholar]
- Hoffmann, M. Dynamics of European Two-Axle Freight Wagons; Technical University of Denmark, Informatics and Mathematical Modelling: Lyngby, Denmark, 2006. [Google Scholar]
- Xu, G.; Steindl, A.; Troger, H. Nonlinear stability analysis of a bogie of a low-platform wagon. Veh. Syst. Dyn. 1992, 20 (Suppl. S1), 653–665. [Google Scholar] [CrossRef]
- Zboinski, K.; Dusza, M. Analysis and method of the analysis of non-linear lateral stability of railway vehicles in curved track. Veh. Syst. Dyn. 2004, 41, 222–231. [Google Scholar]
- Dusza, M. The study of track gauge influence on lateral stability of 4-axle rail vehicle model. Arch. Transp. 2014, 30, 7–20. [Google Scholar] [CrossRef]
- Zboinski, K.; Dusza, M. Development of the method an analysis for non-linear lateral stability of railway vehicles in curved track. Veh. Syst. Dyn. 2006, 44 (Suppl. S1), 147–157. [Google Scholar] [CrossRef]
- True, H.; Jensen, J.C. Chaos and asymmetry in railway vehicle dynamics. Period. Polytech. Ser. Transp. Eng. 1994, 22, 55–68. [Google Scholar]
- Schupp, G. Computational Bifurcation Analysis of Mechanical Systems with Applications to Railway Vehicles. In Proceedings of the 18th IAVSD Symposium on Dynamics of Vehicles on Roads and Tracks, Vehicle System Dynamics, Kanagawa, Japan, 24–30 August 2003; Taylor & Francis: London, UK, 2004; Volume 41, pp. 458–467. [Google Scholar]
- Iwnicki, S. Handbook of Railway Vehicle Dynamics; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Oxfordshire, UK, 2006. [Google Scholar]
- Hoffmann, M.; True, H. The dynamics of European two-axle railway freight wagons with UIC standard suspension. Veh. Syst. Dyn. 2008, 46 (Suppl. S1), 225–236. [Google Scholar] [CrossRef]
- Dusza, M.; Zboinski, K. Comparison of Two Different Methods for Identification of Railway Vehicle Critical Velocity. In Proceedings of the 12th Mini Conference on Vehicle System Dynamics, Identification and Anomalies, Budapest, Hungary, 8–10 November 2010; pp. 161–170. [Google Scholar]
- True, H. Multiple attractors and critical parameters and how to find them numerically: The right, the wrong and the gambling way. Veh. Syst. Dyn. 2013, 51, 443–459. [Google Scholar] [CrossRef]
- Iwnicki, S.; Stichel, S.; Orlova, A.; Hecht, M. Dynamics of railway freight vehicles. Veh. Syst. Dyn. 2015, 53, 995–1033. [Google Scholar] [CrossRef] [Green Version]
- Toumi, M.; Chollet, H.; Yin, H. Effect of Elasto-Plasticity on the Creep Force Characteristic and the Railway Vehicle Stability. In The Dynamics of Vehicles on Roads Track; CRC Press: Boca Raton, FL, USA, 2016; pp. 1015–1025. [Google Scholar]
- Schiehlen, W. Dynamical Analysis of Vehicle Systems: Theoretical Foundations and Advanced Applications; Springer Wien: New York, NY, USA; Udine, Italy, 2007. [Google Scholar]
- True, H. Does a Critical Speed for Railroad Vehicles Exist? In Proceedings of the ASME/IEEE Joint Railroad Conference, Chicago, IL, USA, 22–24 March 1994; pp. 125–131. [Google Scholar]
- True, H. On the theory of nonlinear dynamics and its applications in vehicle systems dynamics. Veh. Syst. Dyn. 1999, 31, 393–421. [Google Scholar] [CrossRef]
- True, H. Recent advances in the fundamental understanding of railway vehicle dynamics. Int. J. Veh. Des. 2006, 40, 251–264. [Google Scholar] [CrossRef]
- Zboinski, K.; Woznica, P. Optimization of railway transition curves’ shape with use of vehicle-track dynamical model. Arch. Transp. 2010, 22, 387–407. [Google Scholar] [CrossRef]
- Kalker, J.J. A fast algorithm for the simplified theory of rolling contact. Veh. Syst. Dyn. 1982, 11, 1–13. [Google Scholar] [CrossRef]
- Kik, W. Comparison of the behaviour of different wheelset-track models. Vehicle Syst. Dyn. 1992, 20 (Suppl. S1), 325–339. [Google Scholar] [CrossRef]
- Zboinski, K. Modelling dynamics of certain class of discrete multi-body systems based on direct method of the dynamics of relative motion. Meccanica 2012, 47, 1527–1551. [Google Scholar] [CrossRef] [Green Version]

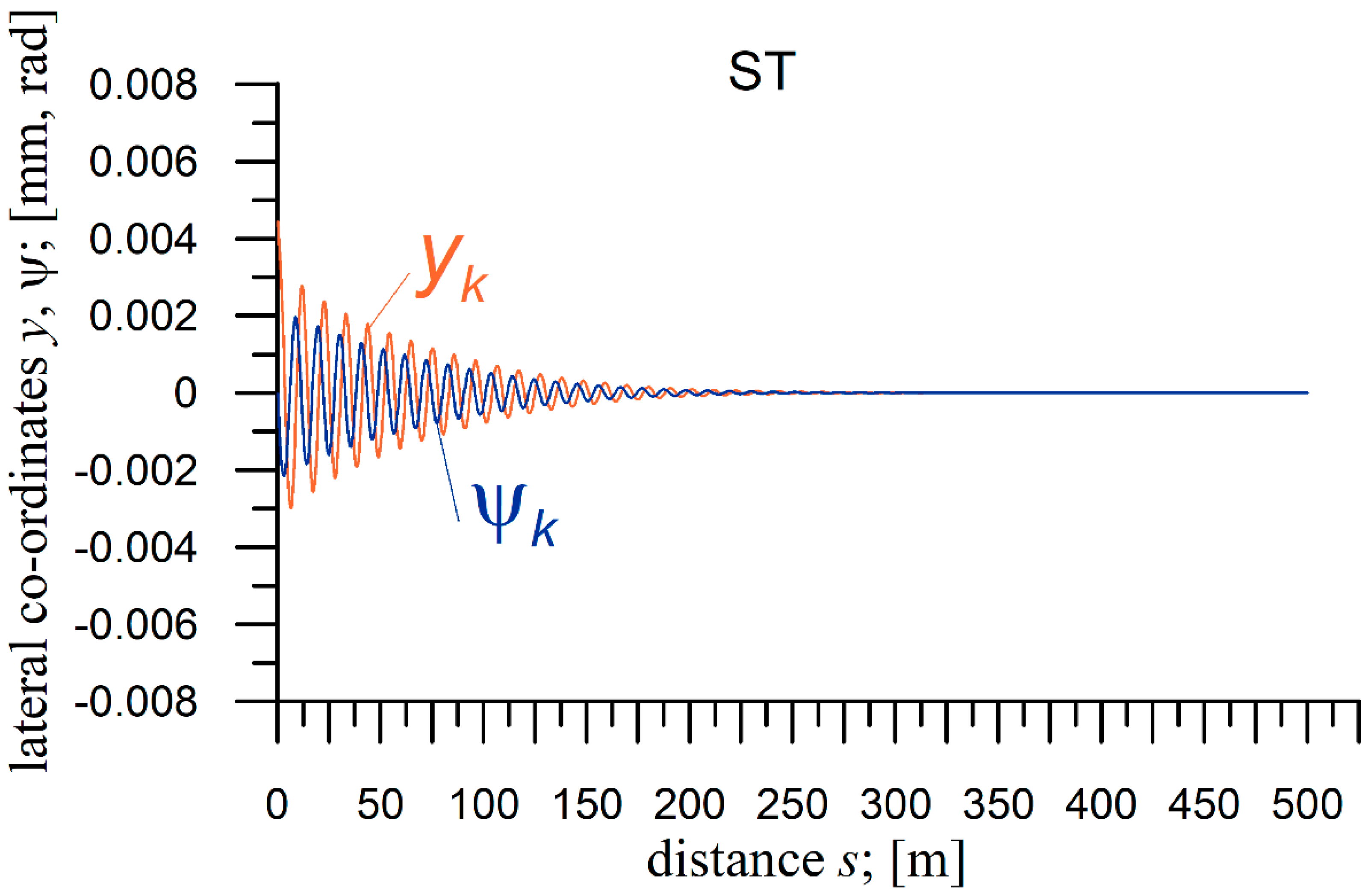
| Object | Initial Conditions yi(0) (m) | ST Length; l (m) | CC Length; l (m) | CC Radius; R (m) | Superelevation h (m) |
|---|---|---|---|---|---|
| Bogie of MKIII car, Bogie with averaged parameters | 0.0045 | 500 | - | - | 0 |
| 0.0045 | - | 500 | 600 | 0.1500 | |
| 0.0045 | - | 500 | 1200 | 0.0750 | |
| 0.0045 | - | 500 | 2000 | 0.0450 | |
| 0.0045 | - | 500 | 4000 | 0.0225 | |
| 0.0045 | - | 500 | 6000 | 0.0150 | |
| 0.0045 | - | 500 | 10,000 | 0.0090 | |
| 25TN bogie | 0.0045 | 500 | - | - | 0 |
| 0.0045 | - | 500 | 300 | 0.1500 | |
| 0.0045 | - | 500 | 600 | 0.1500 | |
| 0.0045 | - | 500 | 900 | 0.1420 | |
| 0.0045 | - | 500 | 1200 | 0.0750 | |
| 0.0045 | - | 500 | 2000 | 0.0450 | |
| 0.0045 | - | 500 | 4000 | 0.0225 | |
| 0.0045 | - | 500 | 6000 | 0.0150 | |
| 0.0045 | - | 500 | 10,000 | 0.0090 |
| Object | Initial Conditions yi(0) (m) | ST Length l (m) | CC Length l (m) | CC Radius R (m) | Superelevation h (m) |
|---|---|---|---|---|---|
| hsfv1 car, Vehicle with averaged parameters | 0.0045 | 500 | - | - | 0 |
| 0.0045 | - | 500 | 300 | 0.1500 | |
| 0.0045 | - | 500 | 600 | 0.1500 | |
| 0.0045 | - | 500 | 900 | 0.1420 | |
| 0.0045 | - | 500 | 1200 | 0.0750 | |
| 0.0045 | - | 500 | 2000 | 0.0450 | |
| 0.0045 | - | 500 | 4000 | 0.0225 | |
| 0.0045 | - | 500 | 6000 | 0.0150 | |
| 0.0045 | - | 500 | 10,000 | 0.0090 |
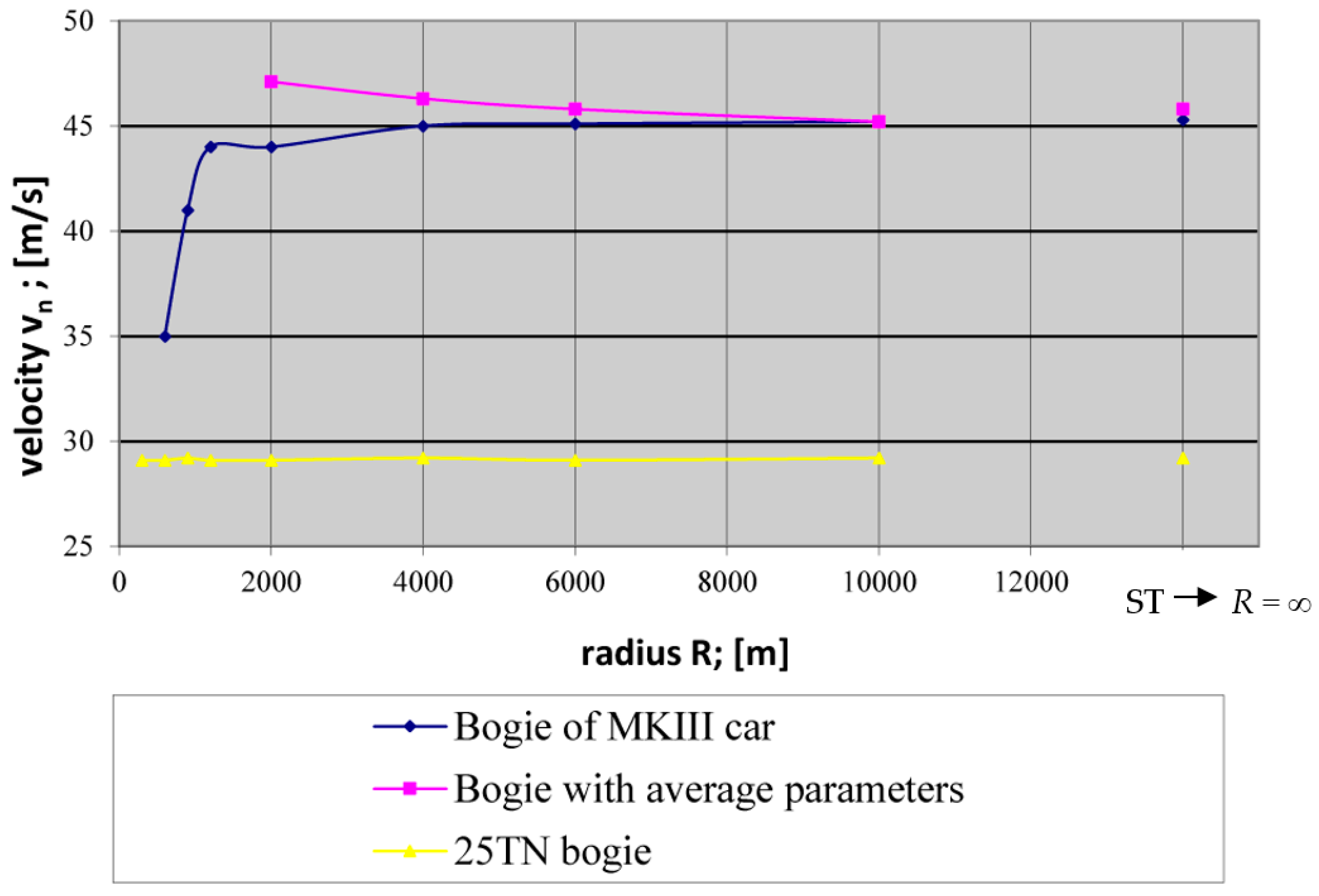
| Object | ST; vn (m/s) | CC; R (m) | CC; vn (m/s) |
|---|---|---|---|
| Bogie of MKIII car | 45.3 | - | - |
| 600 | 35.0 | ||
| 900 | 41.0 | ||
| 1200 | 44.0 | ||
| 2000 | 44.0 | ||
| 4000 | 45.0 | ||
| 6000 | 45.1 | ||
| 10,000 | 45.2 | ||
| Bogie with averaged parameters | 45.8 | - | - |
| 600 | n. derailment—at 42 * | ||
| 1200 | n. derailment—at 59 * | ||
| 2000 | 47.1 | ||
| 4000 | 46.3 | ||
| 6000 | 45.8 | ||
| 10,000 | 45.2 | ||
| 25TN bogie | 29.2 | - | - |
| 300 | 29.1 | ||
| 600 | 29.1 | ||
| 900 | 29.2 | ||
| 1200 | 29.1 | ||
| 2000 | 29.1 | ||
| 4000 | 29.2 | ||
| 6000 | 29.1 | ||
| 10,000 | 29.2 |
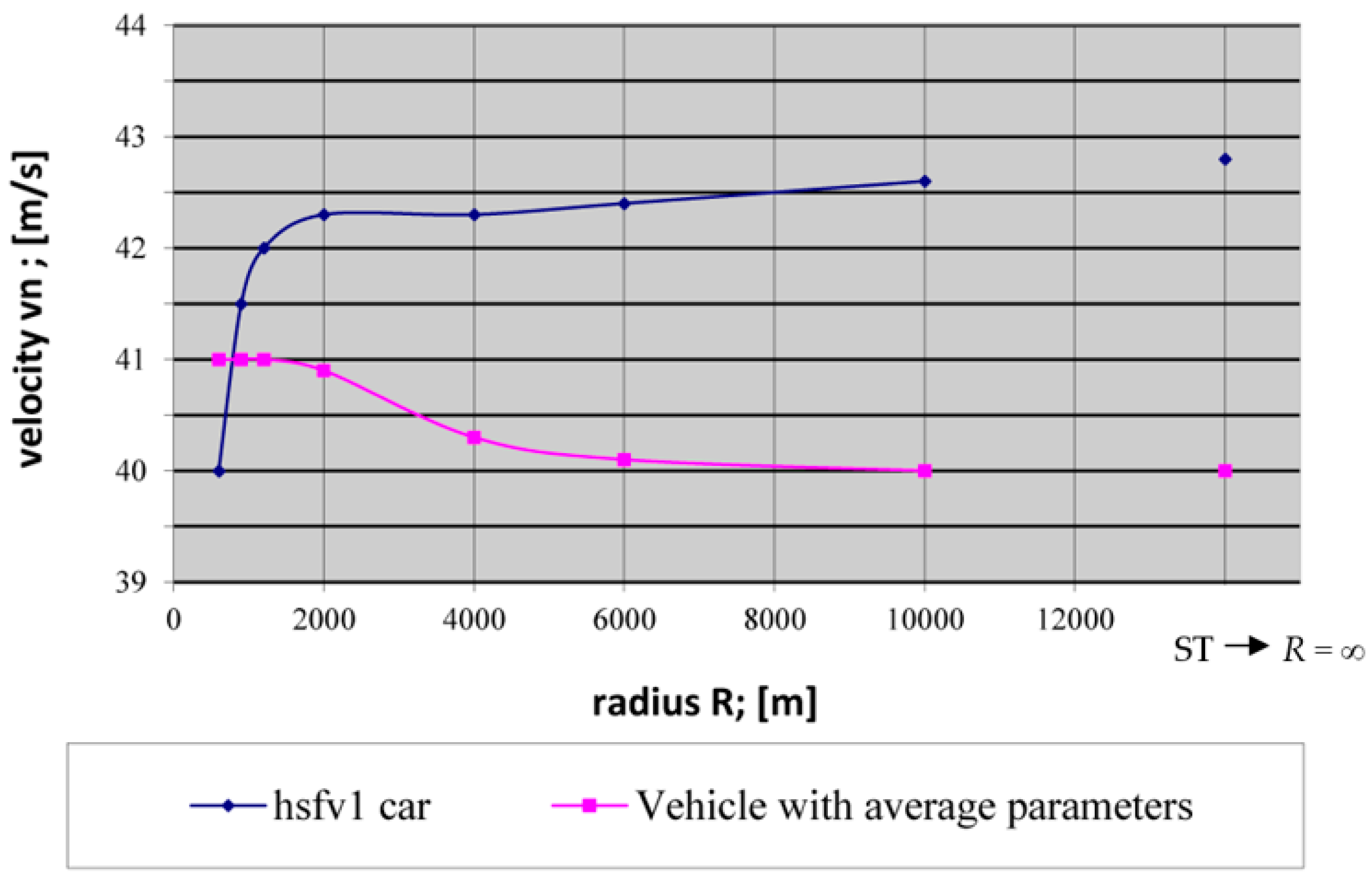
| Object | ST vn (m/s) | CC R (m) | CC vn (m/s) |
|---|---|---|---|
| hsfv1 car ** | 42.8 | - | - |
| 300 | n. derailment—at 39.0 * | ||
| 600 | 40.0 | ||
| 900 | 41.5 | ||
| 1200 | 42.0 | ||
| 2000 | 42.3 | ||
| 4000 | 42.3 | ||
| 6000 | 42.4 | ||
| 10,000 | 42.6 | ||
| Vehicle with averaged parameters | 40.0 | - | - |
| 300 | n. derailment—at 10.2 * | ||
| 600 | 41.0 | ||
| 900 | 41.0 | ||
| 1200 | 41.0 | ||
| 2000 | 40.9 | ||
| 4000 | 40.3 | ||
| 6000 | 40.1 | ||
| 10,000 | 40.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zboinski, K.; Golofit-Stawinska, M. Determination and Comparative Analysis of Critical Velocity for Five Objects of Railway Vehicle Class. Sustainability 2022, 14, 6649. https://doi.org/10.3390/su14116649
Zboinski K, Golofit-Stawinska M. Determination and Comparative Analysis of Critical Velocity for Five Objects of Railway Vehicle Class. Sustainability. 2022; 14(11):6649. https://doi.org/10.3390/su14116649
Chicago/Turabian StyleZboinski, Krzysztof, and Milena Golofit-Stawinska. 2022. "Determination and Comparative Analysis of Critical Velocity for Five Objects of Railway Vehicle Class" Sustainability 14, no. 11: 6649. https://doi.org/10.3390/su14116649