Time History Method of Three-Dimensional Dynamic Stability Analysis for High Earth-Rockfill Dam and Its Application
Abstract
:1. Introduction
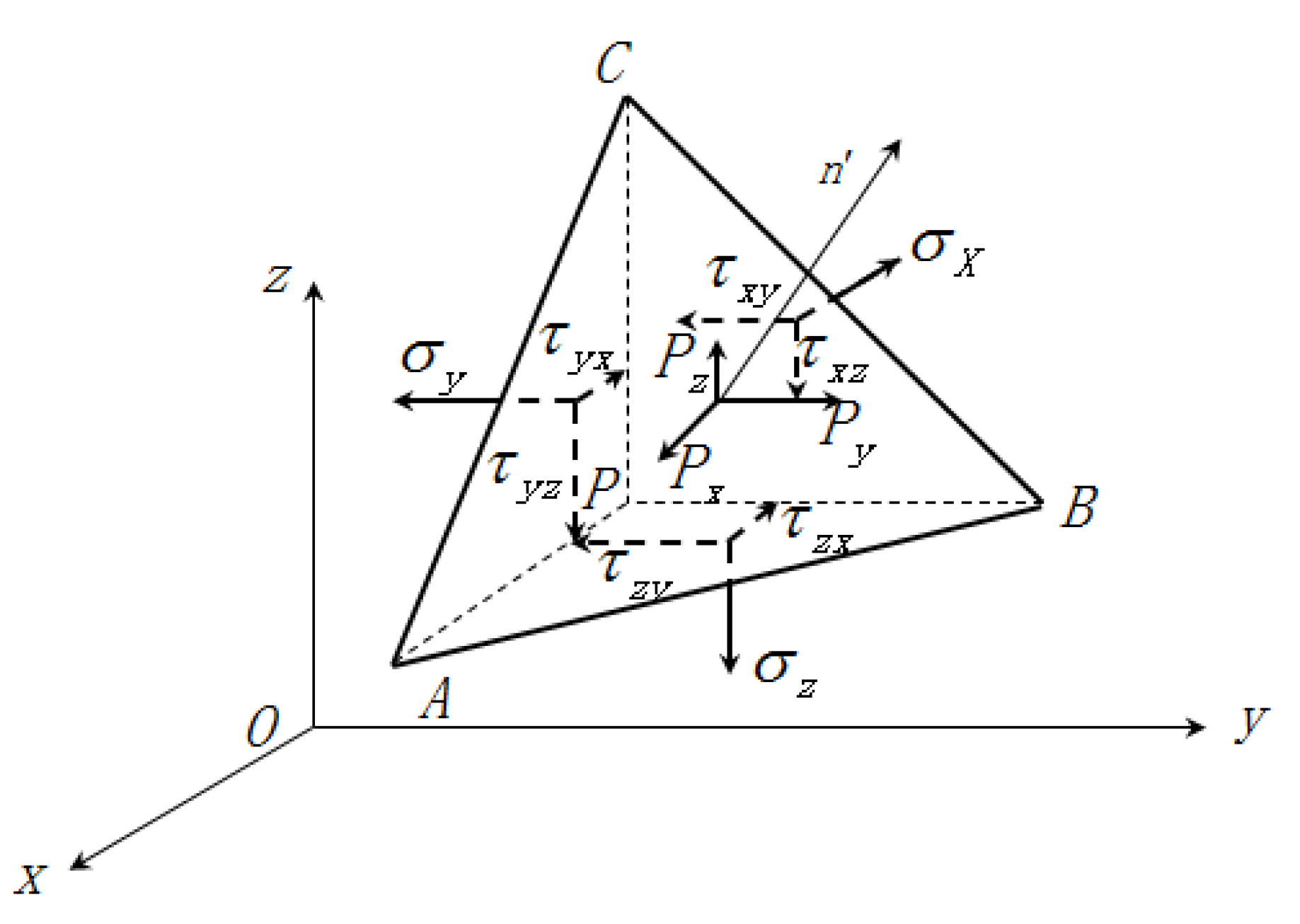
2. Finite Element Sliding Surface Stress Method
3. Time History Method of Three-Dimensional Dynamic Stability Analysis
3.1. Analysis Method
3.2. Features of Software
3.2.1. Software Framework
3.2.2. The Software Features
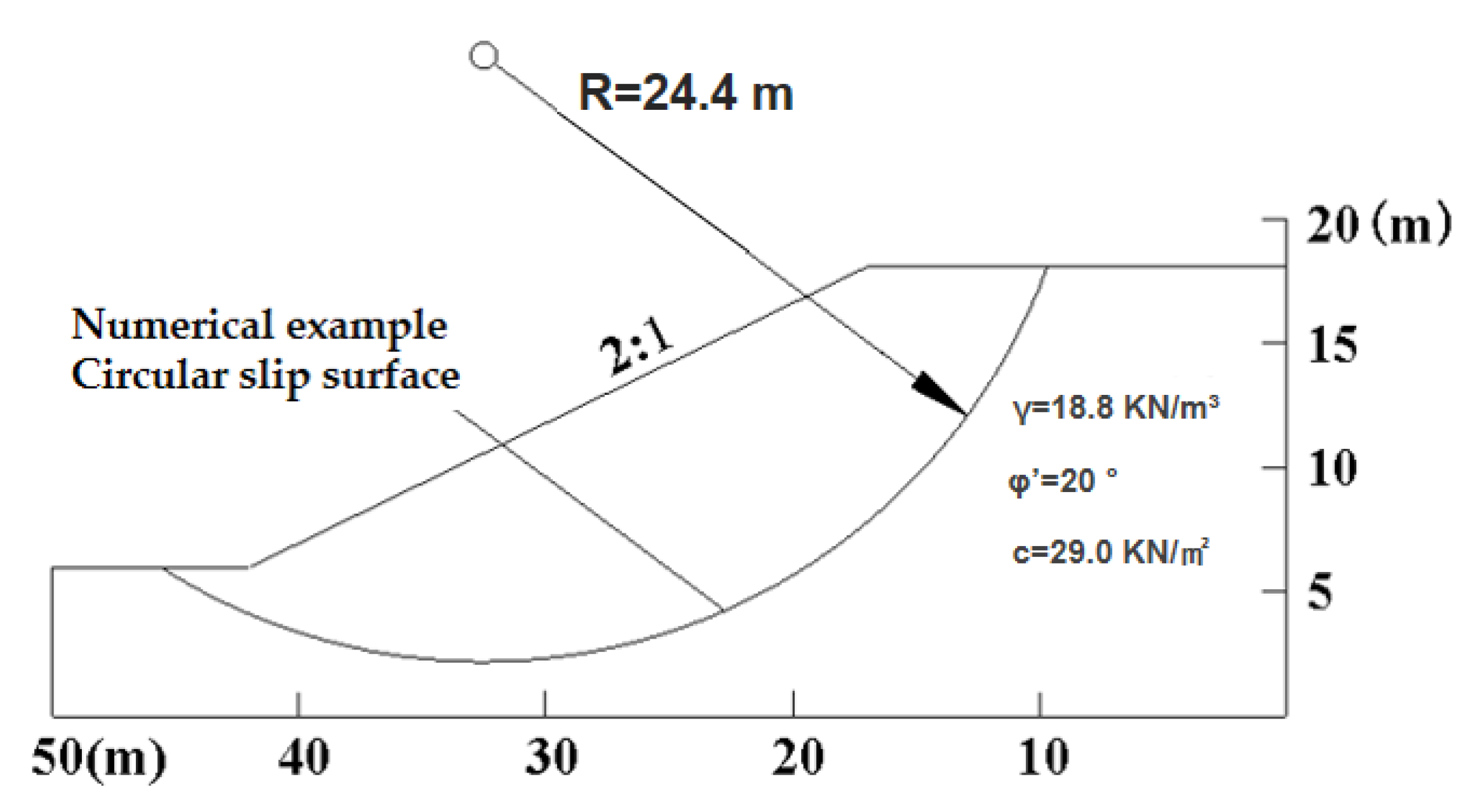
3.2.3. Verification and Analysis
4. Three-Dimensional Dynamic Stability Analysis of Faced Rockfill Dam
4.1. Numerical Model
4.2. Material Parameters
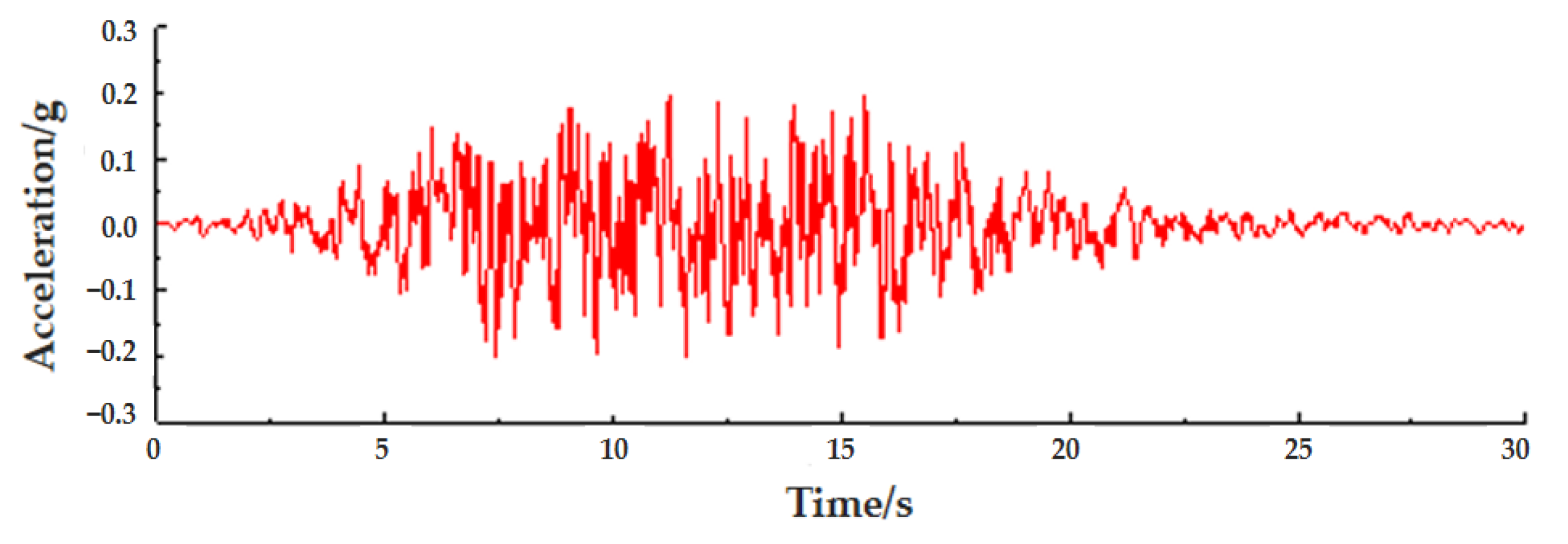
4.3. Ground Motion Input
4.4. Analysis of Calculation Results
5. Conclusions
- Based on the finite element sliding surface stress method and dynamic response analysis, a time history method of three-dimensional stability analysis is presented and realized using in-house software. The developed software is verified to be feasible and efficient by examples. It provides a basis for seismic design and the local reinforcement of high earth-rock dams, helps in the understanding of the time history variation of safety factors and the sliding process and optimizes the efficiency of dynamic stability analysis of high earth-rock dams.
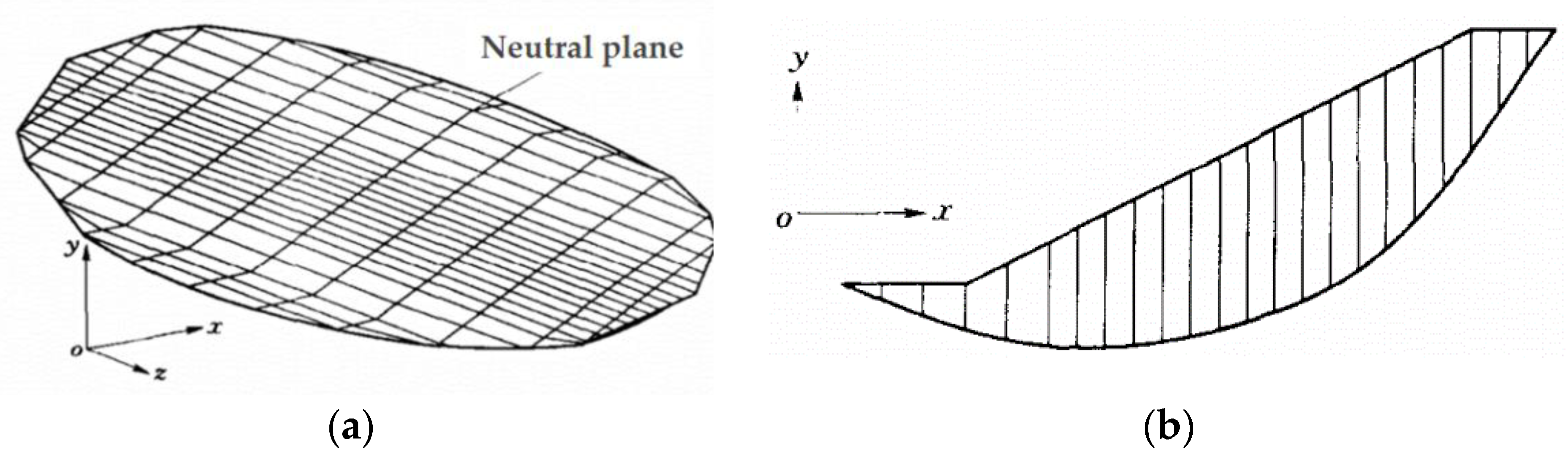
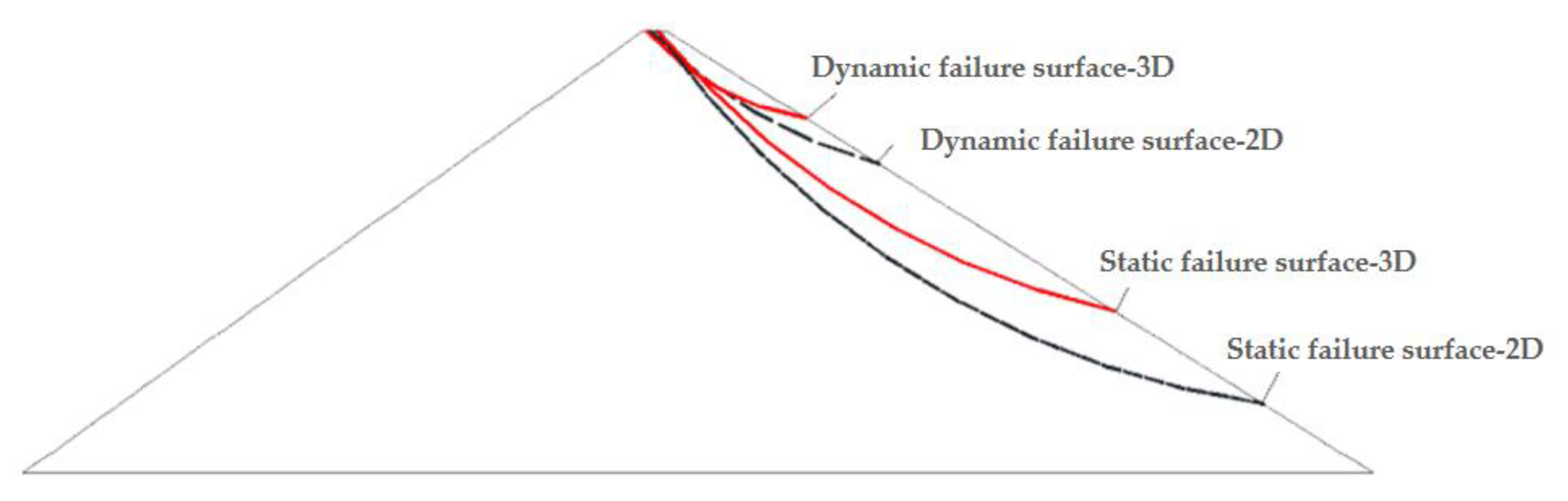
- The stability analysis method based on finite element analysis is more reasonable and has obvious advantages. It is suitable for analyzing earth-rockfill dam slopes with long seismic duration and complicated action forms. In addition, there is a great difference between traditional two-dimensional stability analysis and three-dimensional stability analysis. The two-dimensional analysis assumes that the sliding body extends indefinitely along the dam axis which is not in line with reality. The most dangerous sliding body captured by three-dimensional stability analysis is shallower. The soil body in the sliding surface at the dam crest tends to be pulled apart. The local sliding direction of the sliding surface is symmetrical and the lower and middle sides are inclined outwards.
- The three-dimensional dynamic stability time history analysis not only adopts the 3D finite element dynamic response, which is closer to the real response of the dam, but also reflects the local instability characteristics of the dam slope. It can also reflect and consider the development process of the stress-strain state of the potential sliding surface, as well as the local security of the potential sliding face, time history of safety factor, overall form and space position of the dangerous sliding body, even the sliding process of the failure body and the analysis results are closer to the reality.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, X.; Wang, Y.; Tulamaiti, Y.; Zhou, C.; Zhou, Y.; Wang, G. Refined numerical simulation of a concrete cut-off wall in the thick overburden of dam foundation. Structures 2021, 33, 4407–4420. [Google Scholar] [CrossRef]
- Wang, F.; Liu, C.; Zhou, J.; Yang, Z. Review of seismic safety study on high earth-rockfill dam in China. Hydropower Pumped Storage 2017, 3, 33–37. [Google Scholar]
- Liu, X.; Zhao, J.; Yang, Y.; Wang, Z. Advances in seismic design of earth-rockfill dams and foundations in China and revision of code based on lessons from Wenchuan Earthquake. Chin. J. Geotech. Eng. 2015, 37, 2111–2118. [Google Scholar]
- Qu, Y.; Zou, D.; Chen, K.; Liu, J. Three-dimensional refined analysis of seismic cracking and anti-seismic measures performance of concrete face slab in CFRDs. Comput. Geotech. 2021, 139, 104376. [Google Scholar] [CrossRef]
- Zhang, J.; Li, X.; Wang, X.; Chi, M.; Wang, Y. Method for judging seismic stability state of soil slopes. Chin. J. Geotech. Eng. 2018, 40, 2096–2102. [Google Scholar]
- Cui, P. Research on System Reliability of Deep Anti-Sliding Stability of Gravity Dam Bedrock Considering Stochastic Sracture Network. Master’s Thesis, Dalian University of Technology, Dalian, China, 2021. [Google Scholar]
- Kong, L.; Chen, H. Advancement in the techniques for special soils and slopes. China Civ. Eng. J. 2012, 45, 141–161. [Google Scholar]
- Chen, K.; Zou, D.; Kong, X.; Zhou, Y. Global concurrent cross-scale nonlinear analysis approach of complex CFRD systems considering dynamic impervious panel-rockfill material-foundation interactions. Soil Dyn. Earthq. Eng. 2018, 114, 51–68. [Google Scholar] [CrossRef]
- Schnaid, F.; de Mello, L.G.F.S.; Dzialoszynski, B.S. Guidelines and recommendations on minimum factors of safety for slope stability of tailings dams. Soils Rocks 2020, 43, 369–395. [Google Scholar] [CrossRef]
- Matsui, T.; San, K.C. Finite element slope stability analysis by shear strength reduction technique. Soils Found 1992, 32, 59–70. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.; Huang, R.; Shi, Y.; Xu, Q. Stability analysis of slope based on dynamic and whole strength reduction methods. Chin. J. Rock Mech. Eng. 2014, 33, 243–256. [Google Scholar]
- Guo, Y.; Chen, T.; Qian, H. The determination method of dynamic safety factor for slope based on strength reduction. China Civ. Eng. J. 2012, 45, 117–120. [Google Scholar]
- Nian, T.K.; Huang, R.Q.; Wan, S.S.; Chen, G.Q. Three-dimensional strength-reduction finite element analysis of slopes: Geometric effects. Can. Geotech. J. 2012, 49, 574–588. [Google Scholar] [CrossRef]
- Gong, J.; Zou, D.; Kong, X.; Liu, J.; Qu, Y. An approach for simulating the interaction between soil and discontinuous structure with mixed interpolation interface. Eng. Struct. 2021, 237, 112035. [Google Scholar] [CrossRef]
- Reddy, J.N. An Introduction to the Finite Element Method; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2013. [Google Scholar]
- Giams, K.; Donaldi, B. Determination of critical slip surfaces for slopes via stress strain calculations. Opt. Quantum Electron. 1988, 5, 1–9. [Google Scholar]
- Wu, W.; Chen, Z.; Huang, L. A New Method for Searching Critical Folded Sliding Surface. China Water Transp. 2014, 14, 94–95. [Google Scholar]
- Li, J.; Chen, S.; Yu, F. A method for searching potential failure surface of slope based on maximum shear strain increment. Rock Soil Mech. 2013, 34, 371–378. [Google Scholar] [CrossRef]
- Lin, Y.; Chen, S. Search of three-dimensional slip surface for slope based on finite element calculation. Rock Soil Mech. 2013, 34, 1191–1196. [Google Scholar] [CrossRef]
- Gao, W.; Zhang, F. Study of applications of meeting ant colony algorithm to search non-circular critical slip surface of slope. Rock Soil Mech. 2014, 35, 391–398. [Google Scholar] [CrossRef]
- Gao, W.; Zhang, L.; Zhang, F. Critical slip surface searching for slope based on premium-penalty ant colony optimization. J. Hydraul. Eng. 2012, 43, 209–215. [Google Scholar] [CrossRef]
- Xing, Y.; Wang, X.; Liu, F.; Gao, J. Study on the Search and Evaluation of the Most Dangerous Sliding Surface of Two-dimensional Slope. Subgrade Eng. 2021, 1, 14–18. [Google Scholar] [CrossRef]
- Guo, M.; Li, C.; Wang, S. Three-dimensional slope stability analysis based on finite element stress. Chin. J. Rock Mech. Eng. 2012, 31, 2494–2500. [Google Scholar]
- Guo, M.; Ge, X.; Wang, S.; Wang, H. Dynamic stability analysis of slope based on vector sum analysis method. Chin. J. Rock Mech. Eng. 2011, 30, 572–579. [Google Scholar]
- Guo, M.; Li, C.; Ge, X.; Wang, S.; Lv, Y. Searching potential slip surface of slopes based on the vector sum analysis method. Rock Soil Mech. 2009, 30, 1775–1781. [Google Scholar]
- Pang, R.; Xu, B.; Zhou, Y. Seismic time-history response and system reliability analysis of slopes considering uncertainty of multi-parameters and earthquake excitations. Comput. Geotech. 2021, 136, 104245. [Google Scholar] [CrossRef]
- Yu, X.; Wang, Y.; Wang, G.; Xue, B.; Zhao, X.; Du, X. Study on working behaviors and improvement strategies of concrete cutoff wall with slurry cake in thick soil foundation. Int. J. Geomech. 2022, 22, 04022075. [Google Scholar] [CrossRef]
- Liu, X.; Zou, D.; Liu, J.; Zheng, B.; Bai, J. A gradation-dependent particle shape factor for characterizing small-strain shear modulus of sand-gravel mixtures. Transp. Geotech. 2021, 28, 100548. [Google Scholar] [CrossRef]
- Xu, B.; Zhou, Y.; Zou, D. Numerical Simulation on Slabs Dislocation of Zipingpu Concrete Faced Rockfill Dam during the Wenchuan Earthquake Based on a Generalized Plasticity Model. Sci. World J. 2014, 2014, 572407. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Chu, X. Failure Mechanism and Factor of Safety for Spatially Variable Undrained Soil Slope. Adv. Civ. Eng. 2019, 2019, 8575439. [Google Scholar] [CrossRef]
- Kulhawy, F. Finite Element Analysis of the Behavior of Embankments. Ph.D. Thesis, University of California, Los Angeles, CA, USA, 1969. [Google Scholar]
- Czienkiewicz, O.; Humpheson, C.; Wlewis, R. Associated and non-associated visco-plasticity and plasticity in soil mechanics. Géotechnique 1975, 25, 671–689. [Google Scholar] [CrossRef]
- Donaldi, B.; Tanc, P. Stability of geomechanical structures assessed by finite element method. In Proceedings of the Second International Conference on Computing in Civil Engineering, Hangzhou, China, 5–9 June 1985; Science Press: Beijing, China, 1985. [Google Scholar]
- Shao, L.; Liu, S. Extension of limit equilibrium conditions and stability analysis of geotechnical structures. Rock Soil Mech. 2015, 36, 71–75. [Google Scholar]
- Shen, J.; Karakus, M. Three-dimensional numerical analysis for rock slope stability using shear strength reduction method. Can. Geotech. J. 2014, 51, 164–172. [Google Scholar] [CrossRef]
- Liu, J.; Zou, D.; Kong, X. A two-mechanism soil-structure interface model for three-dimensional cyclic loading. Int. J. Numer. Anal. Met. 2020, 44, 2042–2069. [Google Scholar] [CrossRef]
- Kong, X.; Lou, S.; Zou, D.; Jia, G.; Han, G. The equivalent dynamic shear modulus and equivalent damping ratio of rockfill material for dam. J. Hydraul. Eng. 2001, 8, 20–25. [Google Scholar]
- Wang, Y.; Li, J.; Wu, Z.; Chen, J.; Bian, K. Dynamic Risk Evaluation and Early Warning of Crest Cracking for High Earth-Rockfill Dams through Bayesian Parameter Updating. Appl. Sci. 2020, 10, 7627. [Google Scholar] [CrossRef]
- Huang, C.; Tsai, C. New method for 3D and asymmetrical slope stability analysis. J. Geotech. Geoenviron. 2000, 126, 917–927. [Google Scholar] [CrossRef]
- Pang, R.; Xu, B.; Zhou, Y.; Zhang, X.; Wang, X. Fragility analysis of high CFRDs subjected to mainshock-aftershock sequences based on plastic failure. Eng. Struct. 2020, 206, 110152. [Google Scholar] [CrossRef]



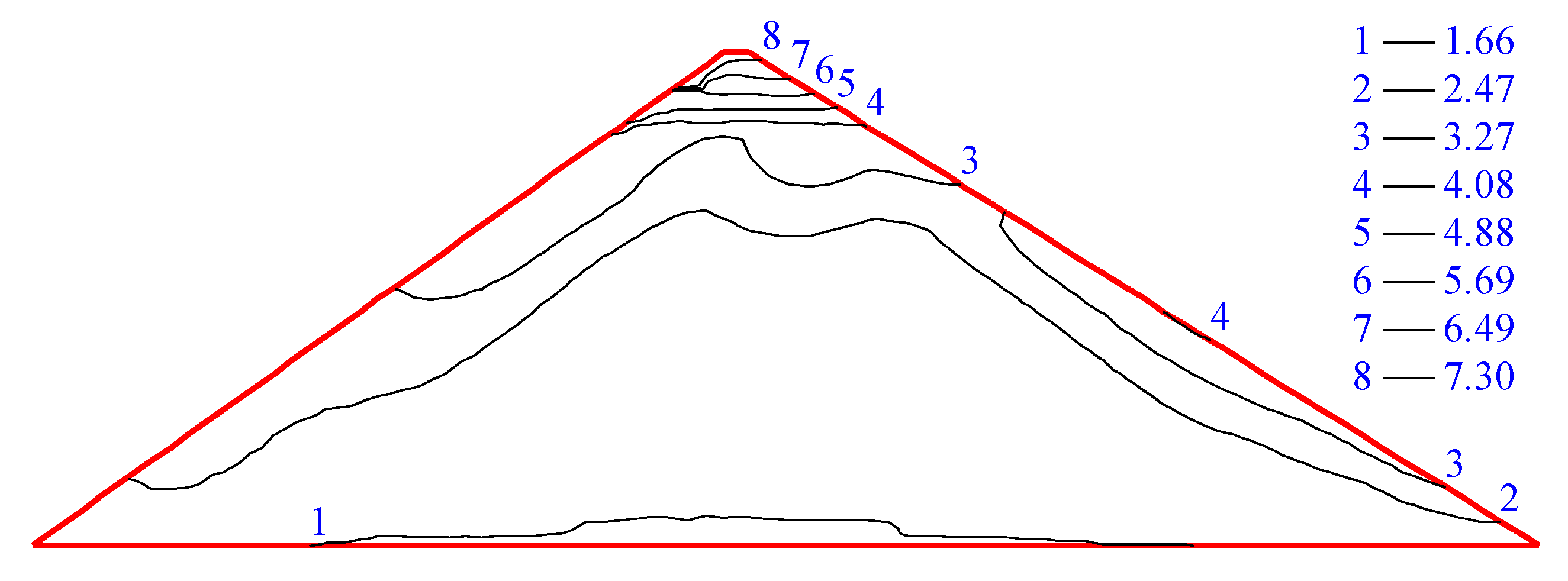
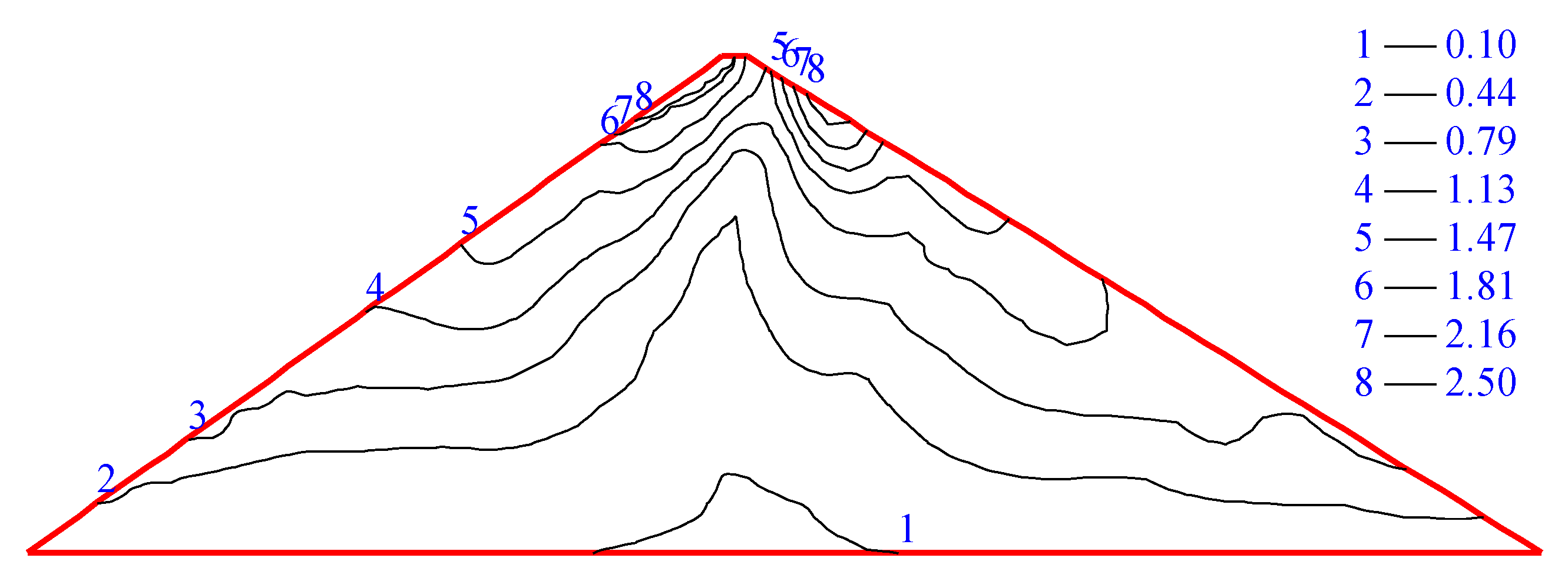
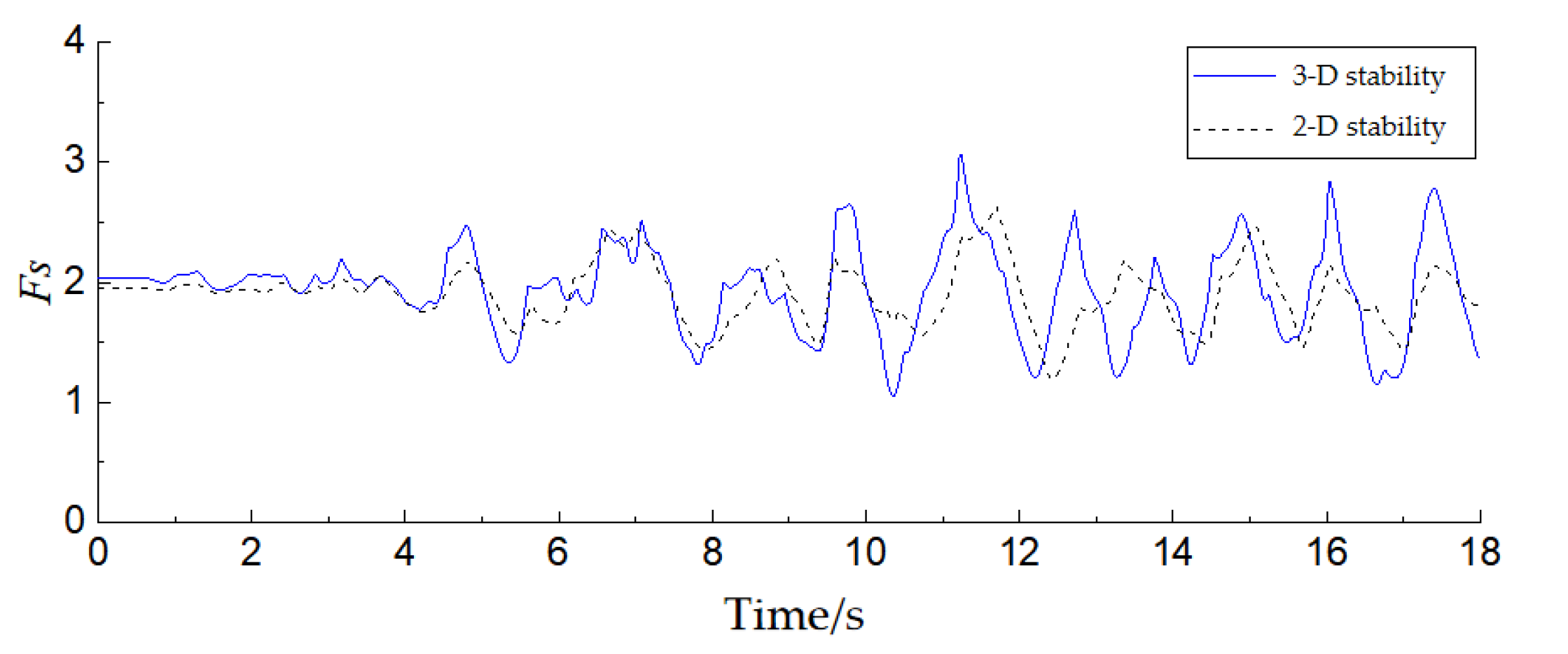
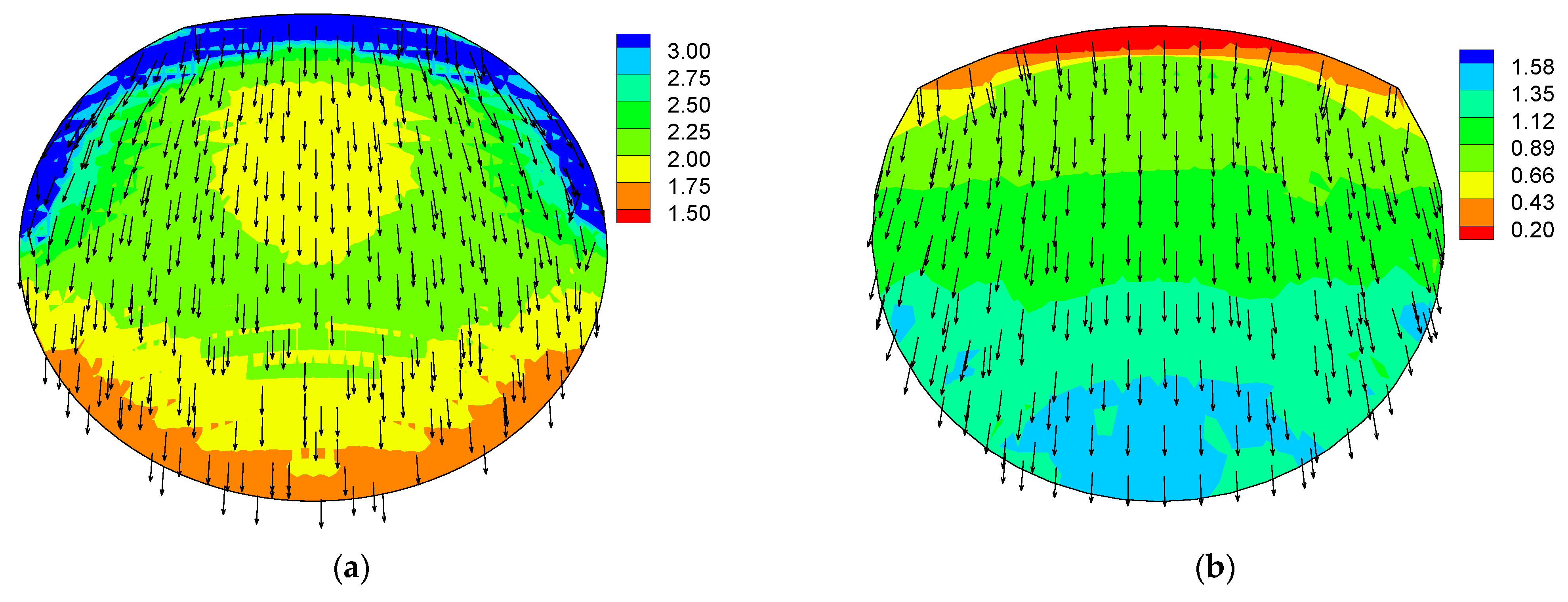

| Number of Elements/Piece | Number of Sliding Surfaces/Piece | Number of Seismic Wave Calculation Time/Piece | Serial Calculation Time/h | Parallel Computing Time/h |
|---|---|---|---|---|
| 149,984 | 41,039 | 900 | 3.7 | 0.5 |
| K | n | Rf | Kb | m | |||
|---|---|---|---|---|---|---|---|
| 2150 | 52 | 8.5 | 1100 | 0.35 | 0.82 | 600 | 0.1 |
| Calculation Example (Year) | Computing Method | Safety Factor |
|---|---|---|
| Zhang Xing (1988) | Three-dimensional limit equilibrium analysis method | 2.122 |
| Chen Zuyu (2003) | Three-dimensional limit equilibrium analysis method | 2.187 |
| Fang Jianrui (2007) | Direct Search Method for 3-D Finite Element | 2.386 |
| Zhang Changliang (2008) | Three dimensional Sarma method | 2.241 |
| Zheng Yingren (2010) | Strength reduction method—(M-C) | 2.150 |
| Strength Reduction Method—Inner Corner Point Outer Circle | 2.217 | |
| Strength Reduction Method—Outer corner point circumference | 2.489 | |
| Wang Ke (2013) | Improved three-dimensional limit equilibrium analysis method | 2.213 |
| This Paper | Finite element sliding surface stress method | 2.214 |
| K | n | |
|---|---|---|
| 2339 | 0.5 | 0.33 |
| Material Type | Modulus of Elasticity (GPa) | Poisson’s Ratio | ρ (kg /m3) |
|---|---|---|---|
| Bedrock | 20.0 | 0.250 | 2600 |
| Concrete face material | 25.5 | 0.167 | 2400 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, H.; Yu, X.; Zou, D.; Wang, Y.; Li, M.; Liu, J. Time History Method of Three-Dimensional Dynamic Stability Analysis for High Earth-Rockfill Dam and Its Application. Sustainability 2022, 14, 6671. https://doi.org/10.3390/su14116671
Yuan H, Yu X, Zou D, Wang Y, Li M, Liu J. Time History Method of Three-Dimensional Dynamic Stability Analysis for High Earth-Rockfill Dam and Its Application. Sustainability. 2022; 14(11):6671. https://doi.org/10.3390/su14116671
Chicago/Turabian StyleYuan, Han, Xiang Yu, Degao Zou, Yuke Wang, Minghao Li, and Junchi Liu. 2022. "Time History Method of Three-Dimensional Dynamic Stability Analysis for High Earth-Rockfill Dam and Its Application" Sustainability 14, no. 11: 6671. https://doi.org/10.3390/su14116671
APA StyleYuan, H., Yu, X., Zou, D., Wang, Y., Li, M., & Liu, J. (2022). Time History Method of Three-Dimensional Dynamic Stability Analysis for High Earth-Rockfill Dam and Its Application. Sustainability, 14(11), 6671. https://doi.org/10.3390/su14116671







