Reactive Power Management Based Hybrid GAEO
Abstract
:1. Introduction
- Solving the RPD problem using a new algorithm, GAEO, for the first time as far as the authors know based on literature review.
- The validity of the GAEO algorithm for minimizing power loss is investigated and compared with results of other techniques.
- GAEO is applied to optimize the RPD problem for the first time on three test systems: IEEE14-bus, IEEE-30bus, and IEEE57-bus.
2. Hybrid Genetic Algorithm Equilibrium Optimizer (GAEO)
3. Modelling of Power System
3.1. Objective Function
3.2. System Constraints
3.2.1. Equality Constraints
3.2.2. Inequality Constraints
4. Modeling and Implementation of GAEO Algorithm
4.1. Initialization
4.2. Main Loop
4.2.1. Using GA (Crossover and Mutations)
4.2.2. Using EO on the Best Half Population Members
4.2.3. Balancing of Both Exploration and Exploitation
4.3. Adjusting Operating Parameters
- The exploration ability of control variables (a1).
- The exploitation ability of control variables (a2).
- Mutrate.
- Selection and participation probability of concentration updating by the generation rate control variable (GP).
5. Simulation and Results
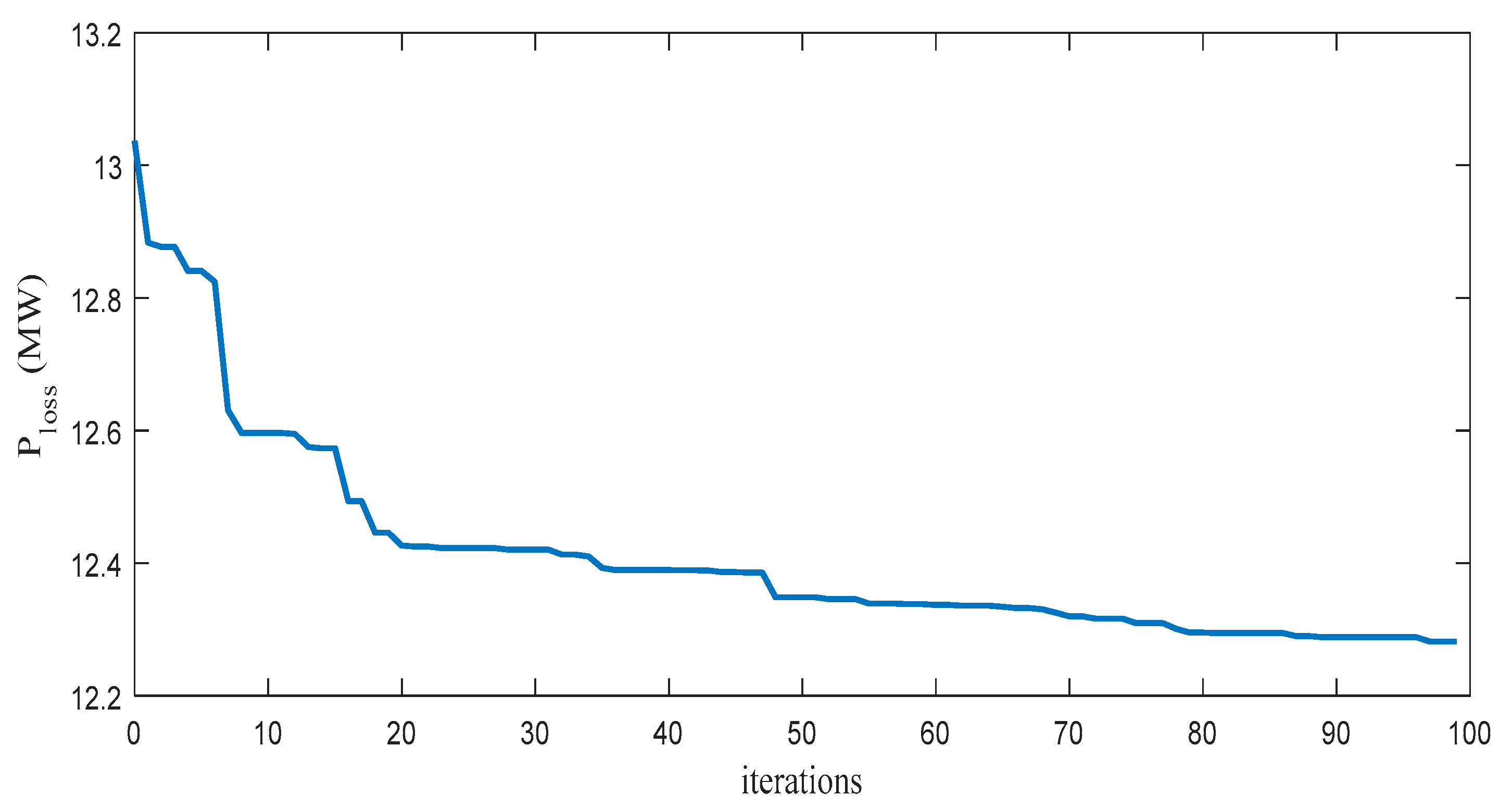
5.1. Case I IEEE 14-Bus System
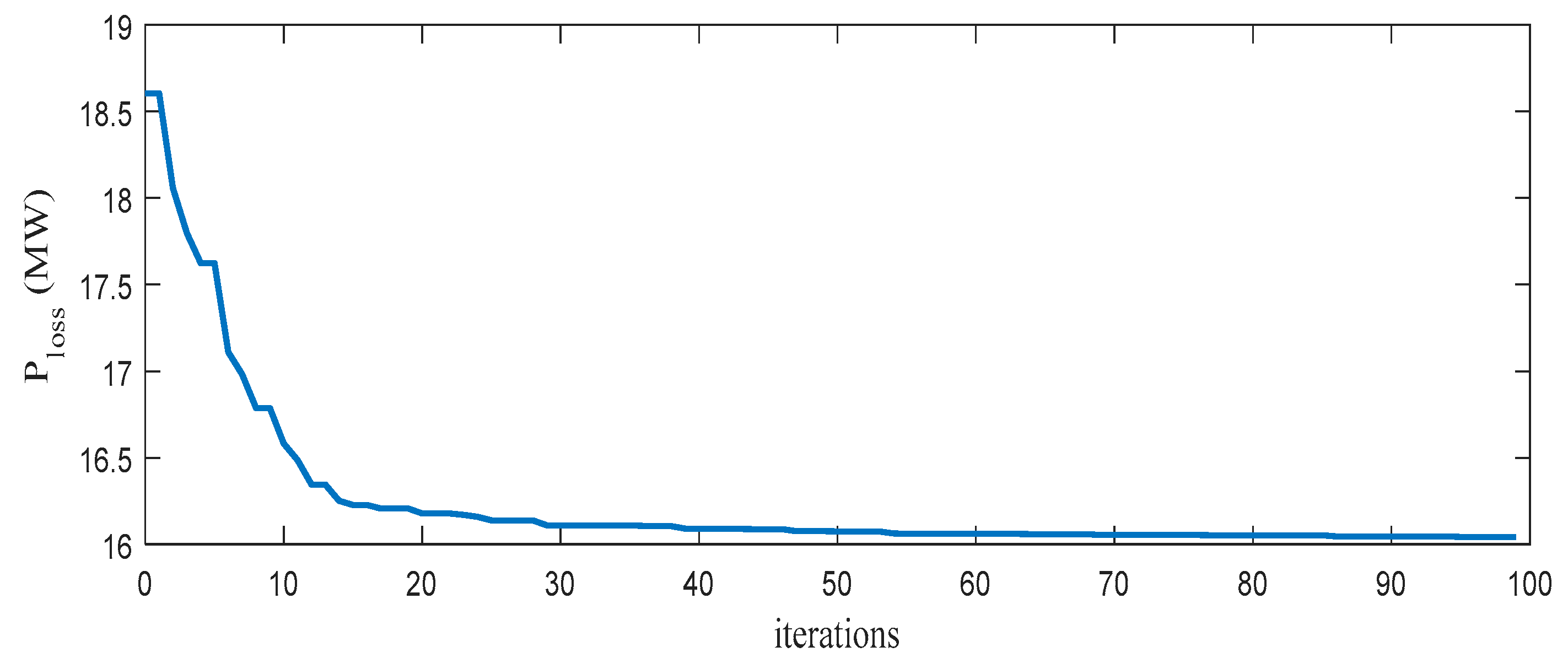
5.2. Modified IEEE 30-Bus System
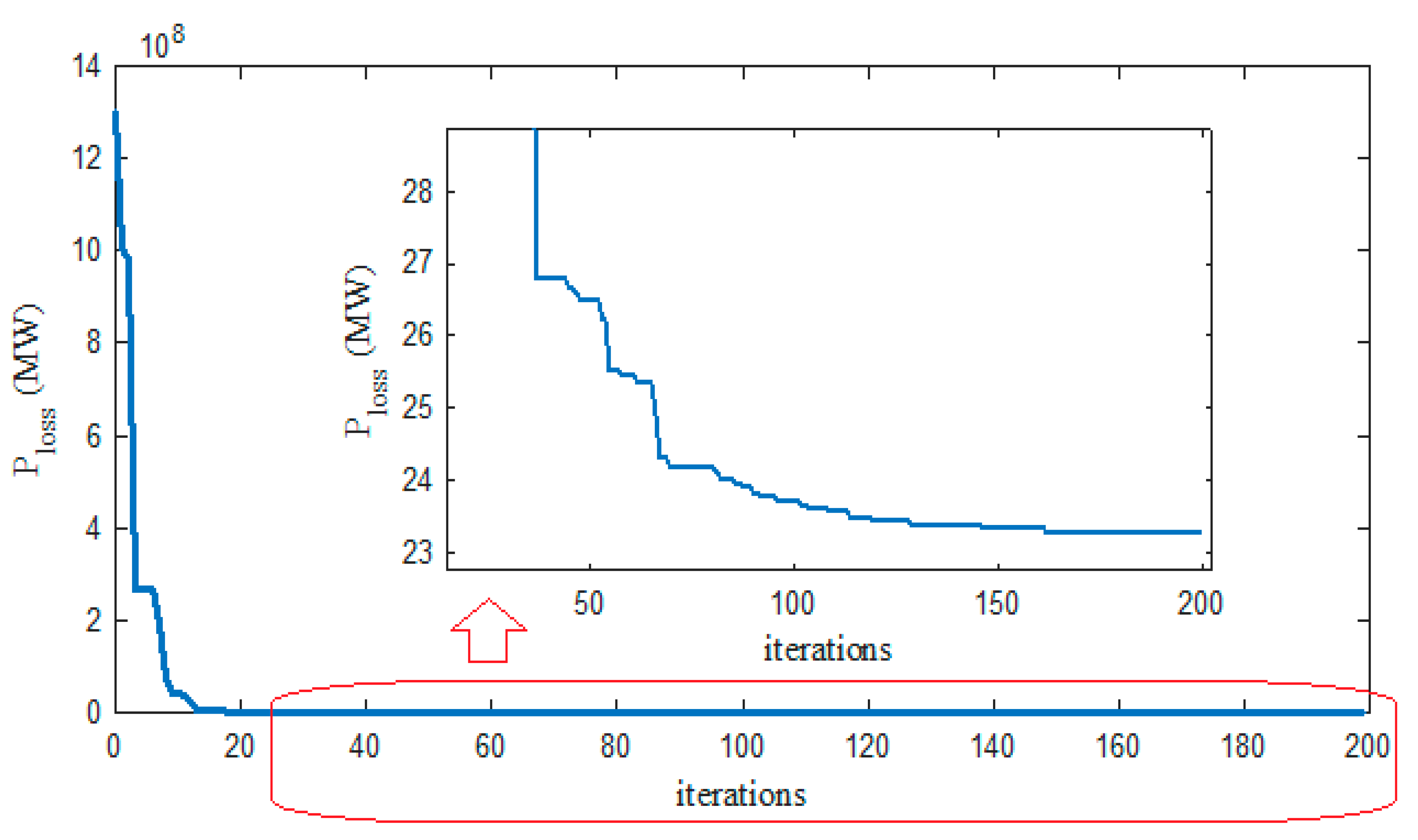
5.3. Case III IEEE 57-bus System
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mobarak, Y.; Hemeida, A.; El-Bahnasawy, A.; Hamada, M. Reactive power compensation on Egypt Electricity Network for optimal energy saving. Eng. Technol. Appl. Sci. Res. 2019, 9, 3699–3704. [Google Scholar] [CrossRef]
- Hemeida, A.M.; Hamada, M.M.; Mobarak, Y.A.; El-Bahnasawy, A.; Ashmawy, M.G.; Senjyu, T. TCSC with auxiliary controls based voltage and reactive power controls on grid power system. Ain Shams Eng. J. 2020, 11, 587–609. [Google Scholar] [CrossRef]
- Ben oualid Medani, K.; Sayah, S.; Bekrar, A. Whale optimization algorithm based optimal reactive power dispatch: A case study of the Algerian power system. Electr. Power Syst. Res. 2018, 163, 696–705. [Google Scholar] [CrossRef]
- Gilvaei, M.N.; Jafari, H.; Ghadi, M.J.; Li, L. A novel hybrid optimization approach for reactive power dispatch problem considering voltage stability index. Eng. Appl. Artif. Intell. 2020, 96, 103963. [Google Scholar] [CrossRef]
- Mugemanyi, S.; Qu, Z.; Rugema, F.X.; Dong, Y.; Bananeza, C.; Wang, L. Optimal reactive power dispatch using chaotic bat algorithm. IEEE Access 2020, 8, 65830–65867. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, J.; Yang, X.; Ling, Y. Optimal reactive power dispatch using water wave optimization algorithm. Oper. Res. 2020, 20, 2537–2553. [Google Scholar] [CrossRef]
- Hemeida, A.M.; Hassan, S.A.; Mohamed, A.-A.A.; Alkhalaf, S.; Mahmoud, M.M.; Senjyu, T.; El-Din, A.B. Nature-inspired algorithms for feed-forward neural network classifiers: A survey of one decade of research. Ain Shams Eng. J. 2020, 11, 659–675. [Google Scholar] [CrossRef]
- Mohamed, A.-A.A.; Mohamed, Y.S.; El-Gaafary, A.A.; Hemeida, A.M. Optimal power flow using moth swarm algorithm. Electr. Power Syst. Res. 2017, 142, 190–206. [Google Scholar] [CrossRef]
- Mohamed, A.-A.A.; El-Gaafary, A.A.; Mohamed, Y.S.; Hemeida, A.M. Multi-objective modified grey wolf optimizer for optimal power flow. In Proceedings of the 2016 Eighteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 27–29 December 2016; pp. 982–990. [Google Scholar] [CrossRef]
- El-Gaafary, A.A.; Mohamed, Y.S.; Hemeida, A.M.; Mohamed, A.-A.A. Grey wolf optimization for multi input multi output system. Univers. J. Commun. Netw. 2015, 3, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Saleh, A.A.; Mohamed, A.-A.A.; Hemeida, A.M.; Ibrahim, A.A. Comparison of different optimization techniques for optimal allocation of multiple distribution generation. In Proceedings of the 2018 International Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 19–21 February 2018; pp. 317–323. [Google Scholar] [CrossRef]
- Hemeida, A.M.; Bakry, O.M.; Mohamed, A.A.A.; Mahmoud, E.A. Genetic Algorithms and Satin Bowerbird Optimization for optimal allocation of distributed generators in radial system. Appl. Soft Comput. 2021, 111, 107727. [Google Scholar] [CrossRef]
- Saleh, A.A.; Mohamed, A.-A.A.; Hemeida, A.M.; Ibrahim, A.A. Multi-objective whale optimization algorithm for optimal allocation of distributed generation and capacitor bank. In Proceedings of the 2019 International Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 2–4 February 2019; pp. 459–465. [Google Scholar] [CrossRef]
- Saleh, A.A.; Senjyu, T.; Alkhalaf, S.; Alotaibi, M.A.; Hemeida, A.M. Water cycle algorithm for probabilistic planning of renewable energy resource, considering different load models. Energies 2020, 13, 5800. [Google Scholar] [CrossRef]
- Saleh, A.A.; Mohamed, A.-A.A.; Hemeida, A.M. Optimal allocation of distributed generations and capacitor using multi-objective different optimization techniques. In Proceedings of the 2019 International Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 2–4 February 2019; pp. 377–383. [Google Scholar] [CrossRef]
- Alkhalaf, S.; Senjyu, T.; Saleh, A.A.; Hemeida, A.M.; Mohamed, A.-A.A. A MODA and MODE comparison for optimal allocation of distributed generations with different load levels. Sustainability 2019, 11, 5323. [Google Scholar] [CrossRef] [Green Version]
- Mei, R.N.S.; Sulaiman, M.H.; Mustaffa, Z.; Daniyal, H. Optimal reactive power dispatch solution by loss minimization using moth-flame optimization technique. Appl. Soft Comput. 2017, 59, 210–222. [Google Scholar] [CrossRef] [Green Version]
- Abaza, A.; Fawzy, A.; El-Sehiemy, R.A.; Alghamdi, A.S.; Kamel, S. Sensitive reactive power dispatch solution accomplished with renewable energy allocation using an enhanced coyote optimization algorithm. Ain Shams Eng. J. 2021, 12, 1723–1739. [Google Scholar] [CrossRef]
- Saddique, M.S.; Bhatti, A.R.; Haroon, S.S.; Sattar, M.K.; Amin, S.; Sajjad, I.A.; ul Haq, S.S.; Awan, A.B.; Rasheed, N. Solution to optimal reactive power dispatch in transmission system using meta-heuristic techniques―Status and technological review. Electr. Power Syst. Res. 2020, 178, 106031. [Google Scholar] [CrossRef]
- Ettappan, M.; Vimala, V.; Ramesh, S.; Kesavan, V.T. Optimal reactive power dispatch for real power loss minimization and voltage stability enhancement using artificial bee colony algorithm. Microprocess. Microsyst. 2020, 76, 103085. [Google Scholar] [CrossRef]
- Mouassa, S.; Bouktir, T.; Salhi, A. Ant lion optimizer for solving optimal reactive power dispatch problem in power systems. Eng. Sci. Technol. Int. J. 2017, 20, 885–895. [Google Scholar] [CrossRef]
- Heidari, A.A.; Abbaspour, R.A.; Jordehi, A.R. Gaussian bare-bones water cycle algorithm for optimal reactive power dispatch in electrical power systems. Appl. Soft Comput. 2017, 57, 657–671. [Google Scholar] [CrossRef]
- Jamal, R.; Men, B.; Khan, N.H. A novel nature inspired meta-heuristic optimization approach of GWO optimizer for optimal reactive power dispatch problems. IEEE Access 2020, 8, 202596–202610. [Google Scholar] [CrossRef]
- Barakat, A.F.; El-Sehiemy, R.; Elsaid, M.; Osman, E. Solving reactive power dispatch problem by using JAYA optimization algorithm. In International Journal of Engineering Research in Africa; Trans Tech Publications Ltd.: Bäch SZ, Switzerland, 2018; Volume 36, pp. 12–24. [Google Scholar] [CrossRef]
- Khan, N.H.; Wang, Y.; Tian, D.; Raja, M.A.Z.; Jamal, R.; Muhammad, Y. Design of fractional particle swarm optimization gravitational search algorithm for optimal reactive power dispatch problems. IEEE Access 2020, 8, 146785–146806. [Google Scholar] [CrossRef]
- Abdel-Fatah, S.; Ebeed, M.; Kamel, S. Optimal reactive power dispatch using modified sine cosine algorithm. In Proceedings of the 2019 International Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 2–4 February 2019; pp. 510–514. [Google Scholar] [CrossRef]
- Muhammad, Y.; Khan, R.; Ullah, F.; Aslam, M.S.; Raja, M.A.Z. Design of fractional swarming strategy for solution of optimal reactive power dispatch. Neural Comput. Appl. 2020, 32, 10501–10518. [Google Scholar] [CrossRef]
- Sahli, Z.; Hamouda, A.; Bekrar, A.; Trentesaux, D. Reactive power dispatch optimization with voltage profile improvement using an efficient hybrid algorithm. Energies 2018, 11, 2134. [Google Scholar] [CrossRef] [Green Version]
- Aljohani, T.M.; Ebrahim, A.F.; Mohammed, O. Single and multiobjective optimal reactive power dispatch based on hybrid artificial physics–particle swarm optimization. Energies 2019, 12, 2333. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, T.T.; Vo, D.N. Improved social spider optimization algorithm for optimal reactive power dispatch problem with different objectives. Neural Comput. Appl. 2020, 32, 5919–5950. [Google Scholar] [CrossRef]
- Shaheen, M.A.; Hasanien, H.M.; Alkuhayli, A. A novel hybrid GWO-PSO optimization technique for optimal reactive power dispatch problem solution. Ain Shams Eng. J. 2021, 12, 621–630. [Google Scholar] [CrossRef]
- Bakry, O.; Dardeer, M.; Senjyu, T.; Alkhalaf, S. Multi-Objective Hybrid Genetic Algorithms and Equilibrium Optimizer GAEO to Integrate Renewable Energy Sources with Distribution Networks. Aswan Univ. J. Sci. Technol. 2021, 1, 34–69. [Google Scholar]
- Albadr, M.A.; Tiun, S.; Ayob, M.; Al-Dhief, F. Genetic algorithm based on natural selection theory for optimization problems. Symmetry 2020, 12, 1758. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl.-Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Saddique, M.S.; Habib, S.; Haroon, S.S.; Bhatti, A.R.; Amin, S.; Ahmed, E.M. Optimal Solution of Reactive Power Dispatch in Transmission System to Minimize Power Losses using Sine-Cosine Algorithm. IEEE Access 2022, 10, 20223–20239. [Google Scholar] [CrossRef]
- Zhang, M.; Li, Y. Multi-Objective Optimal Reactive Power Dispatch of Power Systems by Combining Classification-Based Multi-Objective Evolutionary Algorithm and Integrated Decision Making. IEEE Access 2020, 8, 38198–38209. [Google Scholar] [CrossRef]
- Tudose, A.M.; Picioroaga, I.I.; Sidea, D.O.; Bulac, C. Solving single-and multi-objective optimal reactive power dispatch problems using an improved salp swarm algorithm. Energies 2021, 14, 1222. [Google Scholar] [CrossRef]
- Vishnu, M.; TK, S.K. An improved solution for reactive power dispatch problem using diversity-enhanced particle swarm optimization. Energies 2020, 13, 2862. [Google Scholar] [CrossRef]




| IEEE 14-Bus | IEEE 30-Bus | IEEE 57-Bus | |
|---|---|---|---|
| Number of buses | 14 | 30 | 57 |
| Number of line flow | 20 | 41 | 80 |
| Generating units | 5 | 6 | 7 |
| Transformer tap changer | 3 | 4 | 15 |
| Reactive compensator | 2 | 3 | 3 |
| Control variables | 10 | 13 | 25 |
| P load (MW) | 259.0 | 283.40 | 1250.8 |
| Q load (MVAR) | 73.5 | 126.20 | 336.40 |
| P gen (MW) | 272.0 | 289.211 | 1279.26 |
| Q gen (MVAR) | 82.44 | 108.922 | 345.45 |
| P loss (MW) base case | 13.49 | 17.557 | 28.462 |
| Range | Vg | Vl | tap | Qc |
|---|---|---|---|---|
| Minimum | 0.95 | 0.95 | 0.9 | 0 |
| maximum | 1.1 | 1.5 | 1.1 | 0.3 |
| Parameters | Values |
|---|---|
| No. of iterations | 100 |
| Number of populations | 40 |
| The exploration ability control variables (a1) | 2 |
| The exploitation ability control variables (a2) | 1 |
| Participation probability of concentration updating by the generation rate control variable (GP) | 0.3 |
| Mutrate | 0.09 |
| Selection | 0.5 |
| Variable Name | Base Value | CBA-IV [5] | SCA [35] | ISSA [37] | GAEO |
|---|---|---|---|---|---|
| V1 | 1.06 | 1.092 | 1.09 | 1.1 | 1.0600 |
| V2 | 1.045 | 1.0884 | 1.08 | 1.085802 | 1.0450 |
| V3 | 1.01 | 1.0558 | 1.05 | 1.056346 | 1.0100 |
| V6 | 1.07 | 1.0325 | 1.09 | 1.096919 | 1.0700 |
| V8 | 1.09 | 1.0951 | 1.09 | 1.1 | 1.0900 |
| T1 | 0.9467 | 0.9746 | 0.95 | 1.03 | 0.9780 |
| T2 | 0.9524 | 1.0676 | 0.94 | 0.9 | 0.9690 |
| T3 | 0.9091 | 1.0599 | 1.03 | 0.98 | 0.9320 |
| Q9 | 0.18 | 0.2208 | 0.16 | 0.18 | 0.1900 |
| Qc14 | 0.18 | 0.0786 | 0.05 | 0 | 0.1900 |
| Real power loss (MW) | 13.49 | 12.2923 | 12.27 | 12.2834 | 12.2694 |
| Parameters | Values |
|---|---|
| No. of iterations | 100 |
| Number of populations | 40 |
| The exploration ability control variables (a1) | 2 |
| The exploitation ability control variables (a2) | 1 |
| Participation probability of concentration updating by the generation rate control variable (GP) | 0.4 |
| Mutrate | 0.09 |
| Selection | 0.5 |
| Variable Name | Base Value | DEPSO [38] | CPSMOEA [36] | GAEO |
|---|---|---|---|---|
| V1 | 1.06 | 0.9925 | 1.01 | 1.0600 |
| V2 | 1.043 | 0.9989 | 1.0778 | 1.0450 |
| V5 | 1.01 | 1.0646 | 1.0417 | 1.0100 |
| V8 | 1.01 | 1.0017 | 1.0478 | 1.0100 |
| V11 | 1.082 | 1.0448 | 1.0393 | 1.0820 |
| V13 | 1.071 | 1.0252 | 1.0293 | 1.0710 |
| T1 | 0.98 | 1.017 | 1.05 | 0.9780 |
| T2 | 0.97 | 1.0461 | 1.05 | 0.9690 |
| T3 | 0.93 | 1.0363 | 1.05 | 0.9320 |
| T4 | 0.97 | 1.0299 | 1 | 0.9680 |
| Q3 | 5 | 14.7 | 12 | 19.0000 |
| Q10 | 19 | 13.99 | 20 | 4.3000 |
| Q24 | 4 | 12.03 | 12 | 0.9000 |
| Real power loss | 17.55 | 17.52 | 16.17 | 16.0428 |
| Parameters | Values |
|---|---|
| No. of iterations | 200 |
| Number of populations | 40 |
| The exploration ability control variables (a1) | 2 |
| The exploitation ability control variables (a2) | 1 |
| Participation probability of concentration updating by the generation rate control variable (GP) | 0.2 |
| Mutrate | 0.09 |
| Selection | 0.5 |
| Variable Name | SCA [35] | CBA-IV [5] | GAEO |
|---|---|---|---|
| V1 | 1.096 | 1.0964 | 1.0400 |
| V2 | 1.089 | 1.0949 | 1.0100 |
| V3 | 1.083 | 1.0906 | 0.9850 |
| V6 | 1.082 | 1.0838 | 0.9800 |
| V8 | 1.091 | 1.100 | 1.0050 |
| V9 | 1.075 | 1.0869 | 0.9800 |
| V12 | 1.070 | 1.0822 | 1.0150 |
| T4-18 | 1.004 | 0.9002 | 0.9700 |
| T4-18 | 1.029 | 0.9005 | 0.9780 |
| T21-20 | 1.039 | 0.9958 | 1.0430 |
| T24-25 | 1.022 | 1.0086 | 1.0430 |
| T7-29 | 0.99 | 0.9061 | 0.9670 |
| T34-32 | 1.029 | 0.9990 | 0.9750 |
| T11-41 | 0.998 | 0.9087 | 0.9550 |
| T15-45 | 1.023 | 0.9003 | 0.9550 |
| T14-46 | 1.016 | 0.9002 | 0.9000 |
| T10-51 | 0.999 | 0.9123 | 0.9300 |
| T13-49 | 1.022 | 0.9002 | 0.8950 |
| T11-43 | 0.998 | 0.9000 | 0.9580 |
| T40-56 | 1.022 | 1.0267 | 0.9580 |
| T39-57 | 0.992 | 0.9729 | 0.9800 |
| T9-55 | 0.984 | 0.9220 | 0.9400 |
| Qc18 | 0.066 | 0.1827 | 10.0000 |
| Qc25 | 0.046 | 0.1335 | 5.9000 |
| Qc53 | 0.030 | 0.0858 | 6.3000 |
| Active power loss | 24.05 | 21.9627 | 23.2514 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hemeida, M.; Senjyu, T.; Alkhalaf, S.; Fawzy, A.; Ahmed, M.; Osheba, D. Reactive Power Management Based Hybrid GAEO. Sustainability 2022, 14, 6933. https://doi.org/10.3390/su14116933
Hemeida M, Senjyu T, Alkhalaf S, Fawzy A, Ahmed M, Osheba D. Reactive Power Management Based Hybrid GAEO. Sustainability. 2022; 14(11):6933. https://doi.org/10.3390/su14116933
Chicago/Turabian StyleHemeida, Mahmoud, Tomonobu Senjyu, Salem Alkhalaf, Asmaa Fawzy, Mahrous Ahmed, and Dina Osheba. 2022. "Reactive Power Management Based Hybrid GAEO" Sustainability 14, no. 11: 6933. https://doi.org/10.3390/su14116933
APA StyleHemeida, M., Senjyu, T., Alkhalaf, S., Fawzy, A., Ahmed, M., & Osheba, D. (2022). Reactive Power Management Based Hybrid GAEO. Sustainability, 14(11), 6933. https://doi.org/10.3390/su14116933










