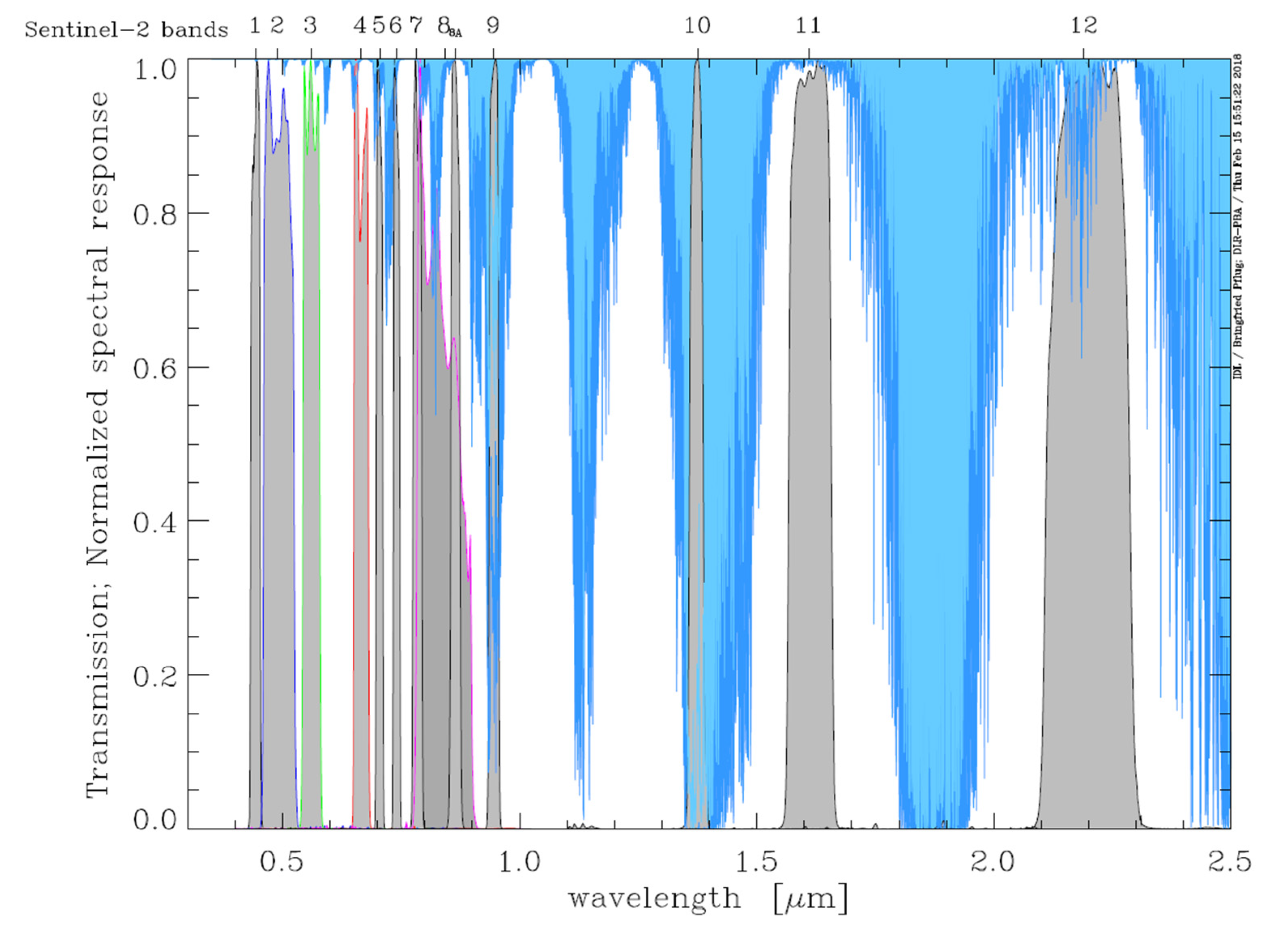
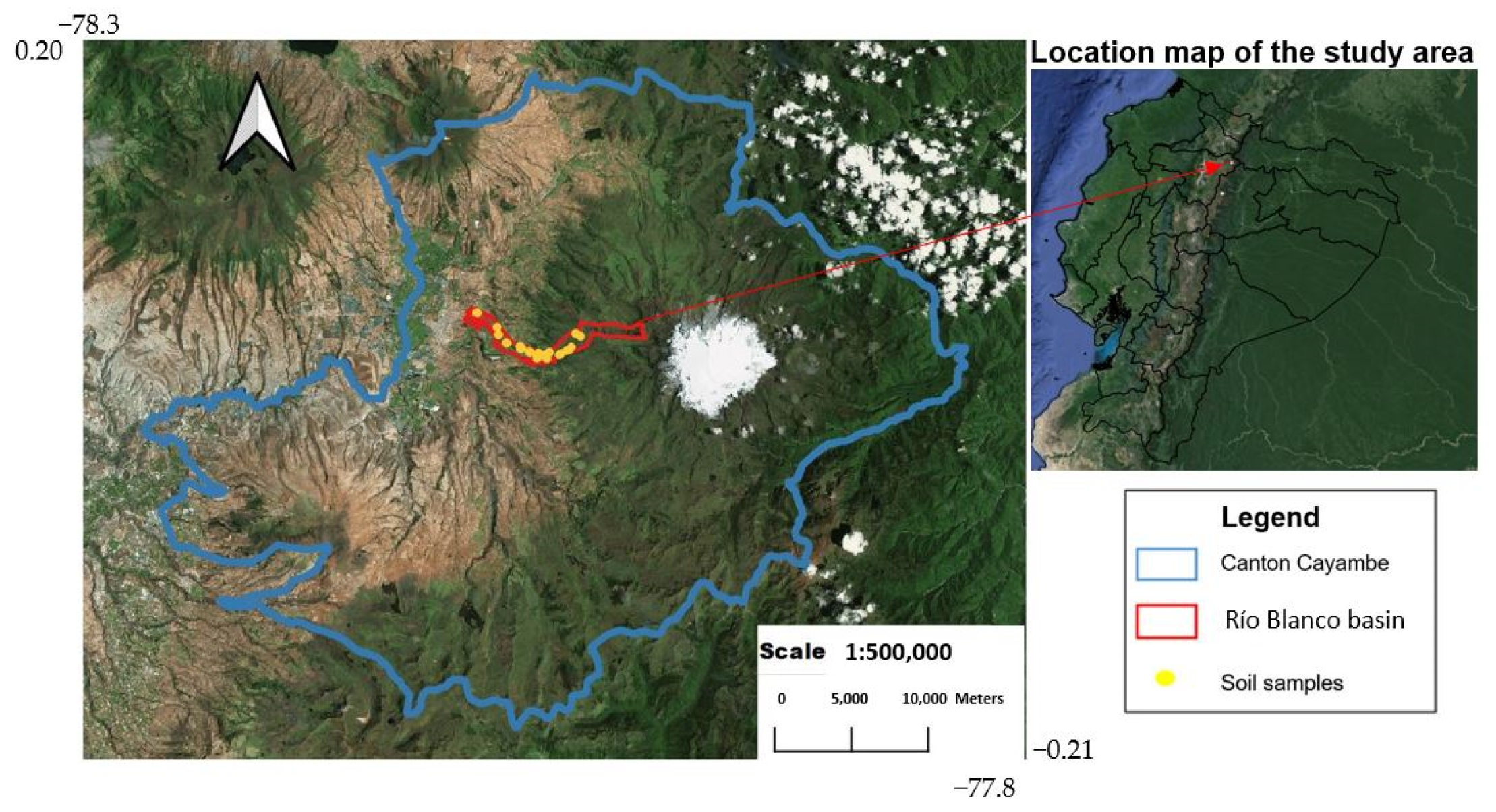
1. Introduction
Soil is the main natural resource for food and energy production [
1]. It controls the movement of water in the landscape and functions as a biological filter for the possible leaching of pollutants into environmental spheres [
2]. However, soil can be degraded by chemical and physical processes, which reduces its ability to function as a base for the development of a healthy layer for vegetation. Therefore, acknowledging soil conditions by the effects on vegetation can represent site conditions [
3,
4].
Gholizadeh and Kopačková (2019) [
1] considered that conventional methods of soil health evaluation in large areas involve several expensive and time-consuming variables such as collection of field data, chemical analysis in a laboratory, and geostatistical interpolation. Alternately, several studies have shown the possibility of characterizing soils and identifying their quality by correlating both physicochemical and spectral parameters [
5]. Therefore, the use of remote sensing spectrometry products in environmental evaluation studies offers a complementary alternative to in situ monitoring procedures to aid in research, control, and monitoring of the soil component. The application field for these tools in the soil component is extensive [
6] through the study of soil characteristics such as reflectance, degradation, and possible polluting agents with the processing of satellite images permitting the inspection and monitoring of large areas in a fixed time and place [
7].
In Ecuador, the properties and pedogenetic processes of soil have been studied in terms of rock type, geomorphology, taxonomic classification, and soil order. An increasing breach between the available information on the main soils and their quality [
8] leads to understanding the condition of the soil to allow for the planification of healthy and sustainable territories, as determined by goals 12 and 15 of the Sustainable Development Goals (SDG) [
9]. These goals correspond to responsible consumption and production, and life on land. Therefore, it is necessary to determine the quality of soil to develop fast, feasible, and affordable estimation methods for monitoring and assessing areas.
In the study area, the predominate soils are Andisol and Mollisol, which originate from weathering of volcanic material (ash) [
10]. These relatively young soils can convey high agricultural potential [
11]. Andisols, also known as
páramos, are clay loam soils capable of retaining enormous amounts of water; on the contrary, Mollisols are fertile soils with a high organic matter content that cover approximately 70% of the Cayambe canton, a political–administrative unit of Ecuador, where the research’s basin is located. However, the lack of land use and occupation policies has caused the expansion of agricultural activity boundaries [
12], causing the loss of the
páramo. The main goal is to understand whether there is any relationship between the spectra measured in the samples collected in field with the corresponding bands measured by satellite, combining physicochemical analysis to quantify and model the quality of Andean soils caused by agricultural activity. This will be achieved by (i) compiling and analyzing the physicochemical parameters of soil based on quality standards for agricultural activities, obtaining indices that classify the soils based on their order (Andisol and Mollisol) and use, and (ii) determining whether the soil is associated with some of the physicochemical qualities considered, validating land use and order models based on field reflectance data, satellite reflectance, and physicochemical qualities.
There are several studies based on national models capable of predicting spectra limited in an infrared laboratory with statistical algorithm analysis [
13,
14]. In this research, with the use of these spectroscopic methods for the evaluation of soil quality, models were developed for estimating indicators based on the combination of soil order, land use, and physicochemical characteristics, using logistic regression analysis, linear discriminant analysis, and regression trees. The approach offers a method that derives the estimates using the ratio of laboratory/satellite spectra when the soil is well represented by the calibration samples used to build the predictive models [
13]. Therefore, the performance of these local models can be used in other geographic spaces by incorporating the spectra into a dataset for that area [
15].
Consequently, the combination of laboratory spectroscopy and multispectral images with environmental covariates is an adequate methodological alternative to obtain models that are adjusted for the prediction of the quality of Andean soils, independently of other methodological approaches that have been used [
16,
17,
18,
19].
3. Results
3.1. Physicochemical Analysis
The different soil samples were analyzed using standardized physicochemical methods. The soil moisture results were in a range from 12.23% to 74.99%. The areas that predominated with the highest percentage of soil moisture were moors, and those with the lowest soil moisture were forest and shrub areas. The lowest water content was observed in Mollisol.
Regarding pH, the most acidic soils corresponded to undisturbed moors, whereas the least acidic soils corresponded to cultivated pastures. The range was 4.55 to 5.76, which, according to Mexican regulations, ranges from moderately acidic to strongly acidic, and according to Ecuadorian regulations, it would be out of range.
The electrical conductivity of the soils was within the limits established by both the Ecuadorian and Mexican regulations, <200 µS/cm and <1 dS/m, respectively. The areas with the lowest electrical conductivity were moors, whereas the highest electrical conductivity was observed in grasses.
For OM, the values ranged from 2.78% to 16.06%. According to Mexican standards, the zones range from very low to very high levels for soils of volcanic origin. The zone with the lowest OM percentage was forest, followed by passage areas, and the zone with the highest OM content was páramo areas.
3.2. Analysis of Spectral Signatures
In this section the behavior of each band was determined with respect to the intensity of reflectance of the soil samples. For each cylinder, two spectral measurements were made in opposite sections of the same tube, and for each soil sample 10 spectral measurements per section were averaged for a single representative spectrum per homogeneous area, which resulted in graphs (
Figure 9a,b) as a function of reflectance and wavelength per sample in each homogeneous area.
The reflectance of the spectra was graphically analyzed in the laboratory to determine the behavior of the soils related to their spectral signatures of the Andisol and Mollisol orders. The spectral signatures obtained in the laboratory presented a pattern related to the typical spectral signature of soils, ranging from the visible range (VNIR) to near-infrared (NIR) to short-wave infrared (SWIR).
The graph in
Figure 9a shows the pasture curves, where sample ID11 of the Andisol soil order presented the same intensity of reflectance as sample ID14 of the Mollisol order, which were the highest compared to the other samples. Sample ID10 of the Mollisol order had a medium intensity of reflectance, unlike sample ID15 of the Mollisol order and sample ID13 of the Mollisol order with lower values of reflectance intensity. This variation in the curves is related to the properties and state of these soils [
51], considering the variation of each of the land uses. Thus, in the graph in
Figure 9b, sample ID16 of the Mollisol order, with agricultural land use, may indicate changes in the characteristics and status of agricultural use in the months of June, July, and August.
It can be said that the graphs made a difference in the behavior of the soil order based on the associated land use.
This could be related to the reflectance records of the Sentinel-2 satellite images (
Figure 10a,b) to improve spectral differences by calculating soil order indices based on land use and physicochemical parameters, as explained in the next section.
3.3. Development and Validation of Models Based on Soil Reflectance Levels in Laboratory and Satellite Image
3.3.1. Model 1, by the Orders of Andisol and Mollisol Soils
From the logistic regression calculation, Model 1 was obtained, whose structure is shown in
Table 6.
The coefficients of Model 1 were both positive and negative. This model was composed of explanatory variables, consisting of a combination of the spectral behavior of the soil in the laboratory and satellite image, with the particularity that there are reflectance levels related to the characteristics of red, red border, and near-infrared. Classical vegetation indices were composed, but in this case, the objective was to classify the order of the soil in Andisol and Mollisol. Furthermore, one of the independent variables was not significant (B08c), which did not influence the global significance of this logistic regression model (p < 0.0001).
Based on the training dataset, we obtained a confusion matrix (
Table 7).
The confusion matrix indicated a training error of 3.5%, which means that the model was good for classifying soils in relation to their order in Andisol or Mollisol based on the spectral behavior of the soil in laboratory and satellite image, and satellite related to the red reflectance of any modality. The false-positive and false-negative coefficients were relatively low (
Table 7), at 1.9% (2615/139,762) and 5.89% (6006/102,024), respectively. In other words, 2615 soil samples of the Andisol order were classified as Mollisol, and 6006 Mollisol soil samples were classified as Andisol. We then evaluated the model using a test dataset to describe the validation process.
Model 1 Validation
The diagnostic evaluation of Model 1, from the diagnostic statistics using the test dataset, was generally good because the accuracy, sensitivity, and specificity were above 95%. On the other hand, the
p-value of the Kappa statistic (
Table 8) was more significant than 0.05 (
p > 0.05), indicating that the null hypothesis that the measurements obtained through Model 1 were equivalent to the real data is not rejected.
3.3.2. Model 2 for Variable Land Use of the Andisol Order
As explained in
Section 2.8.1, to classify land use according to the Andisol soil order, linear discriminant analysis was applied (
Figure 8). The following results were obtained (
Table 9).
The spectral values of the soil in the laboratory had greater weight in the classification of the different land uses than in the satellite image as a function of spectrometry in the laboratory and satellite image. Regardless of the sign, the coefficients of the soil spectral values in the laboratory were greater than the coefficients of the values in the satellite image. Consequently, the first component of this linear discriminant function explains that 96.5% of the total variability of the three different land uses had lower coefficients; even though the reflectance values in the satellite image were lower, these variables were important for the classification of land use as a function of the Andisol soil order. The first and second discriminant components were the linear combinations of the variables that best discriminate between the three land uses of the Andisol order, which in this case corresponded to the entire spectrum of soil in the laboratory and satellite image, respectively.
Figure 11 shows the results of the soil classification based on the linear discriminant function model (Model 2).
The numbers 1, 2, and 3 represent the mean of each dataset. The means were quite separate, which implies a good classification of the land use of the Andisol order. In addition, based on the first linear discriminator, better discrimination was observed between the soils of Pasture and Páramo or between soils of Shrub and Páramo use than between the soils of Shrub and Pasture use. This situation could be because these land uses, in some cases, have relatively small neighboring units. Based on the training dataset, a confusion matrix was obtained (
Table 10). In
Figure 11 and
Table 10, a good classification of the land uses of the Andisol order was observed, with a classification error of 0.51%.
Model 2 Validation
From the first group data for Shrub, Páramo, and Pasture land uses of the Andisol order, corresponding to the 30% that were not part of the model calculation, a confusion matrix was obtained (
Table 11) from which a good classification of the land uses of the Andisol order was obtained, whose classification error was only 0.50% and accuracy 99.5%. Similar results were obtained for the second set of randomly selected data.
3.3.3. Model for Variable Land Use of the Mollisol Order
- (a)
Model 3 for the variable of land use of the Mollisol order 1 from all wavelengths of the soil spectrum in laboratory and satellite image
The results were obtained from the application of LDA (
Table 12).
For the Mollisol 1 order, observing the coefficients of the linear discriminant function (
Table 12), it resulted that the spectral behavior of soils measured in the laboratory exhibited a higher contribution to discriminate land uses Forest, Páramo, and Pasture for the Mollisol 1 order, compared to the coefficients derived from the satellite image. Consequently, the first component of this linear discriminant function (LD1) explained 70.9% of the total variability of the three different land uses, implying that although the reflectance values in the satellite image had lower coefficients, these variables were important for the classification of land use from the Mollisol 1 soil order. The first and second discriminant components were the linear combinations of the variables that best discriminated between the three Mollisol 1 land use types.
Figure 12 shows a representation of the linear discriminant function for this particular case of Mollisol 1 land use, with a minimum overlap between Páramo and Pasture, with a classification error of only 0.47% and an accuracy of 99.52%.
- (b)
Model 4 for the variable of land use of the Mollisol 2 order from all wavelengths of the soil spectra in laboratory and satellite image
The following results were obtained from the application of LDA (
Table 13):
In relation to the coefficients of the linear discriminant function (
Table 13), it was found that the soil spectral values measured in the laboratory had a higher contribution for the classification of the considered land uses compared to those of the satellite image. Regardless of the sign, the coefficients of the soil spectrum in the laboratory were higher than the coefficients of the spectrum in the satellite image. Consequently, the only component of this linear discriminant function explained 100% of the total variability of the two different land uses, which implies that even though the spectral values of the satellite image had lower coefficients, these variables were important for the classification of these land uses as a function of the Mollisol 2 soil order.
Figure 13 represents a good classification of the uses of soils order Mollisol 2.
Model 4 Validation
For the validation of Model 4, we tested 30% of the remaining data, called the test dataset, to classify the soils based on Model 4, and obtained the following confusion matrix, shown in
Table 14.
In
Table 14, for the remaining 30%, a good classification of the land use was observed in Agriculture and Shrub for the Mollisol 2 order, considering the same behavior indicated in the training data.
3.4. Index Development
3.4.1. Index for Andisol and Mollisol Soil Orders from Model 1
According to the methodological process indicated in
Section 2.8.1, the index.ma.1 (Mollisol Andisol Index) was obtained (Equation (4)):
The index.ma.1 separates the soils according to their order into Andisol and Mollisol. If the index values are positive, they correspond to soils of the Andisol order; if index.ma.1 takes negative values, they correspond to soils of the Mollisol order. The descriptive statistics of index.ma.1 are shown in
Table 15.
For the soils of the Andisol order, the mean level of the index was 0.2377 with a relatively low level of variability, equal to 0.1792. For soils of the Mollisol order, the mean level of the index was lower, −1.4961, presenting a higher level of variability equal to 0.5688, which can also be classified as a high level of variability. In this way, index.ma.1 classifies soils according to their order.
3.4.2. Indices Depending on the Variable of Land Use of the Andisol and Mollisol Orders
- (a)
Index for the Land Use of the Andisol Order from Model 2
The index obtained from the discriminant function of Model 2 was expressed as follows (Equation (5)):
The descriptive statistics of Index 2 are displayed in
Table 16.
For land use of the Andisol order, the mean level of Index 2 was higher in Páramo (0.54), with a level of variability equal to 0.06 (the table in
Section 3.5.2). For the land use of the Pasture type of the Andisol order, the average level of Index 2 was −1.12, with a level of variability equal to 0.22 (the table in
Section 3.5.2). In the use of bushland of the Andisol order, the mean level of Index 2 was −1.04, with a level of variability of 0.33. The level of variability of the groups defined according to the land use of the Andisol order was very different, representing the natural behavior of these variables.
- (b)
Index for the Land Use of the Mollisol 1 Order from Model 3.
The index obtained from the discriminant function of Model 3 is expressed as follows (Equation (6)).
For land uses of the Mollisol 1 order, the mean level of Index 3 was higher in forest land use, at 0.79, with the highest level of variability, equal to 0.22 (the table in
Section 3.5.3). For the use of páramo land of the Mollisol 1 order, the mean level of Index 5 was −0.06, with the lowest level of variability, equal to 0.12 (
Table 17). The level of variability of the groups defined as a function of the land use of the Mollisol order was different, representing the natural behavior of these variables.
- (c)
Index for the land Use of the Mollisol 2 Order from Model 4
The fourth index obtained from the discriminant function (Model 4) was obtained by standardizing the coefficients of this model. Each coefficient of Model 4 was divided by the sum of its coefficients in such a way that the sum of the coefficients of Index 4 was equal to 1, obtaining (Equation (7)):
For land uses of the Mollisol 2 order, the mean Index 4 was higher in agricultural land use, at 0.12, with the highest level of variability, equal to 0.02 (
Table 18). For the use of shrub soil of the Mollisol 2 order, the mean level of Index 6 was −0.07, with the lowest level of variability, equal to 0.01 (
Table 18). The level of variability of the groups defined as a function of the land use of the Mollisol order was different, representing the natural behavior of these variables.
3.5. Regression Tree Models to Define Association between Indices and Physicochemical Parameters
3.5.1. Regression Tree Models of Physicochemical Parameters as a Function of Soil Order through Model 1 (index.ma.1)
The first model predicted the values of index.ma.1. as a function of the covariates, soil order, and physicochemical parameters. An example with soil moisture is presented, where for soils of the Andisol order, the mean of the index.ma.1 (
Figure 14) is equal to −0.134. If the soil moisture (HU) is greater than or equal to 36.7 for soils of the Andisol order, the predicted value of the index.ma.1 is on average equal to 0.109 (i = 0.109) for
n = 74,000 soil samples. However, if the soil moisture is less than 36.7, the predicted value of index.ma.1 is on average equal to 0.382 (i = 0.382), for
n = 65,700 soil samples. The same interpretation for soils of Mollisol order.
Likewise, if the value of the index is positive, it corresponds to an Andisol soil order and negative to a Mollisol soil order. The predicted moisture value is at least 36.7.
3.5.2. Regression Tree Models of Physicochemical Parameters as a Function of Land Use of the Andisol Order through Model 2 (index.2)
As shown in
Table 19, it was possible to obtain the effect of land use of the Andisol order on the physicochemical parameters.
An example of the non-parametric regression tree model is presented below (
Figure 15), with the dependent variable as index.2 and the independent variables as soil use and organic matter (OM) for soils of the Andisol order (
Table 20) (ARUSAMO).
3.5.3. Regression Tree Models of Physicochemical Parameters as a Function of Land Use of the Mollisol Order through Model 3 (index.3)
In
Figure 16, the regression tree model of index.3 can be observed as an example in the function of land use of soil order Mollisol 1 and organic matter, which are related based on
Table 21 (ARUSM3MO).
OM was greater in Páramo (≥8.6%) than Forest and Pasture, with a misclassification of 22% for Forest and 17% for Pasture (
Table 21).
3.5.4. Regression Tree Models of Physicochemical Parameters as a Function of Land Use of the Mollisol Order through Model 4 (index.4)
The land use regression tree model for soil order Mollisol 2 and OM, which are related based on
Table 22 (ARUSM4MO), are shown in
Figure 17.
OM was greater in Shrub (≥6.1%) than Agriculture (<6.1%), with a misclassification of 1% for Shrub (
Table 22).
4. Discussion
The results of this study allow for a description of the correlation between the physicochemical parameters with index.2 (Andisol), index.3 (Mollisol 1), index.4 (Mollisol 2), according to the soil order–land use homogeneous zones defined in
Section 2.7 and based on the criteria of Zebrowski 1997 [
52]. In the case of the Mollisol order soil, the prediction values for Páramo were ≥8.6% (
Table 21), which maintained the characteristic behavior of the Ecuadorian Andean zone, as cited by Podwojewski (1999) [
53]. On the contrary, for Forest and Pasture, the prediction models presented a behavior with a lower value in organic matter (<8.6%) (
Table 21), a less acidic pH and lower soil moisture percentage, and a higher electrical conductivity [
10]. This behavior shows the effects of the impact of human activity, with a lesser value of OM in the Agriculture land use (<6.1%) (
Table 22).
The results presented in this study differ from other studies that compared different classification techniques using Sentinel-2 images [
18,
54], or considered the capacity of satellite observations to monitor and determine the state of the vegetation due to environmental stress factors by evaluating vegetation and chlorophyll indices [
1].
Unlike other methodological approaches [
17,
55,
56,
57], this study demonstrates that the combination of laboratory spectroscopy and multispectral images with environmental covariates is an adequate alternative to establish spatial analysis models to predict the quality of Andean soils in terms of physicochemical variables such as CE, OM, pH, and HU. For this purpose, performing soil order–land use associations was revealed to be an important possible tool for assessing the accomplished predictive models.
- (1)
Performance of the Models
Equation (4) shows the distributions of the logistic regression coefficients in the R-NIR spectral range for soil order, with low false-positive (1.9%) and false-negative (5.89%) coefficients. For the Andisol soil order, the mean level of the index (index.ma.1) was 0.2377, with a level of variability equal to 0.1792 (
Table 15). For the Mollisol soil order, the mean level of the index (index.ma.1) was −1.4961, with a level of variability equal to 0.5688 (
Table 15). The index values ranged from approximately −6 to 2, with some outliers below −4 and a very low frequency of occurrence. This corroborates the potential of promoting soil studies based on laboratory spectral data and remote sensors, such as Ali Aldabaa et al. (2014) [
19], who evaluated the feasibility of the methods for the prediction of soil surface salinity by visible near-infrared diffuse reflectance spectroscopy (VisNIR) and remote sensing (RS). Equations (5)–(7) show the distributions of the coefficients of the linear discriminant function in the VIS-NIR-SWIR spectral range for the order–land use both in laboratory and S2 configurations. For land uses of the Andisol order, the level of variability of the defined groups was very different, which represents the natural behavior of these variables (Shrub, Páramo, Pasture), which, unlike previous research on the VIS-NIR, presented greater sturdiness considering SWIR.
- (2)
Predictions of Physicochemical Parameters
The prediction performance of the R-NIR model, based on the Student t-test with p < 0.0001 for OM, CE, pH, and soil moisture, shows that the mean of each parameter in the Andisol and Mollisol soil order were different, concluding that the mean of each one was lower for the Mollisol soil order, unlike CE, where its mean was higher in Mollisol.
Regarding the results obtained from the VIS-NIR-SWIR or full spectrum model, using non-parametric regression tree models, excellent results were obtained for OM, pH, CE, and soil moisture as explanatory variables of order–land use [
57]. For Mollisol 1, the 95% confidence intervals for the difference in means for the set of physicochemical parameters (CE, OM, pH, HU) were negative for Pasture and Páramo, and for Forest. This means that on average the given set of parameters had higher values in Forest. For the Mollisol 2 soil type, the 95% confidence intervals for the difference in means for the considered set of physicochemical parameters were negative for Shrub and positive for Agriculture. For Andisol-type soils, the 95% confidence intervals for the difference in means for OM in Páramo are higher than the average OM in Shrub. Similarly, but in an opposite direction, when comparing the mean OM in Pasture and Páramo land uses (
p = 0.0000 < 0.05), the 95% confidence interval for the mean difference was negative, which implies that the average OM in soils used for pasture was less than the average OM in soils used for Páramo. Very similar results were obtained in relation to the pH physicochemical parameter, and in relation to CE and HU in all pairs of established comparisons there were statistically significant differences.
In the methodological process, the nonparametric regression tree method was successfully applied to predict the values of the model covariates by soil order or land use order (
Figure 8). This statistical analysis methodology differed from those applied to date, like Adeline (2017) [
41], Bao (2017) [
40], Soriano-Disla (2014) [
17], and Ali Aldabaa (2014) [
19], where it was established that soil properties were derived from reflectance spectra that can be applied from various sources of spectral measurements, such as measurements in the laboratory, in the field, or from remote sensing systems.
These regression tree models were more flexible than those presented by Hill (2011) [
55], because they did not consider non-compliance with statistical assumptions such as normality or collinearity problems between predictor variables. The regression tree models allowed for approximate estimates supported by 95% confidence intervals as a measure of the variation range of each physicochemical parameter, allowing for a reading of this from the top to the final nodes and vice versa, which was not possible in other applied models (
Figure 14,
Figure 15,
Figure 16 and
Figure 17;
Table 21 and
Table 22) [
19,
55,
56].
Soil quality and soil degradation are crucial to develop sustainable agricultural activities [
58]. The usual methods for environmental soil monitoring are very labor intensive and costly to cover large areas of land [
1,
13]. Satellite data in this field open up new research opportunities with great applications, as large areas of land can be analyzed and soil quality can be assessed in areas that are difficult to access [
6,
51].
Finally, this study is very valuable for the Ecuadorian Andean region for soil sustainability. Additionally, the results obtained in this study could be adapted in future research to other geographical regions after reviewing the soil order and land use that allow the relationships observed in the proposed model indices to be confirmed.
5. Conclusions
Soil quality is an important factor in sustainable land management. Its evaluation allows for the development and implementation of sustainable agriculture management techniques. Thus, in this study, an alternative method for the prediction of the parameters OM, CE, pH, and soil moisture based on the R-NIR and VIS-NIR-SWIR models is presented to demonstrate its applicability in the Ecuadorian Andean region. For this purpose, logistic regression analysis and linear discriminant function analysis were used. This required the establishment of homogeneous zones defined by soil order and land use combinations to design and implement soil-sampling strategies and field–satellite spectral measurements. The findings of this study suggest that soil + RS spectroscopy is a useful technique to predict soil properties, presenting good potential as an impetus towards future soil studies.
According to the results of this study:
- (1)
The logistic regression function made it possible to predict the values as a soil order function and each of the physicochemical parameters described above.
- (2)
The linear discriminant function made it possible to treat the data based on the linear combination of the Andisol soil order variables by land use (Shrub, Páramo, Pasture), Mollisol soil order by land use (group 1: Forest, Páramo and Pasture; group 2: Agriculture and Shrub).
- (3)
Non-parametric models had the advantage of predicting the values of the independent variables OM, CE, pH, and soil moisture (soil properties).
Therefore, because of the achieved results, the proposed methodology might be applied to other regions and adapted to predict soil properties as a function of the site-specific soil order and land use properties. Future research should explore the variability of soil quality parameters geographically with the aim of building regional models.