Research and Analysis on the Influencing Factors of China’s Carbon Emissions Based on a Panel Quantile Model
Abstract
:1. Introduction
2. Literature Review
3. Data and Models
3.1. Data Description
3.2. Analysis of Carbon Emission Status
3.3. Model Description
4. Empirical Results and Analysis
4.1. Stationary Test
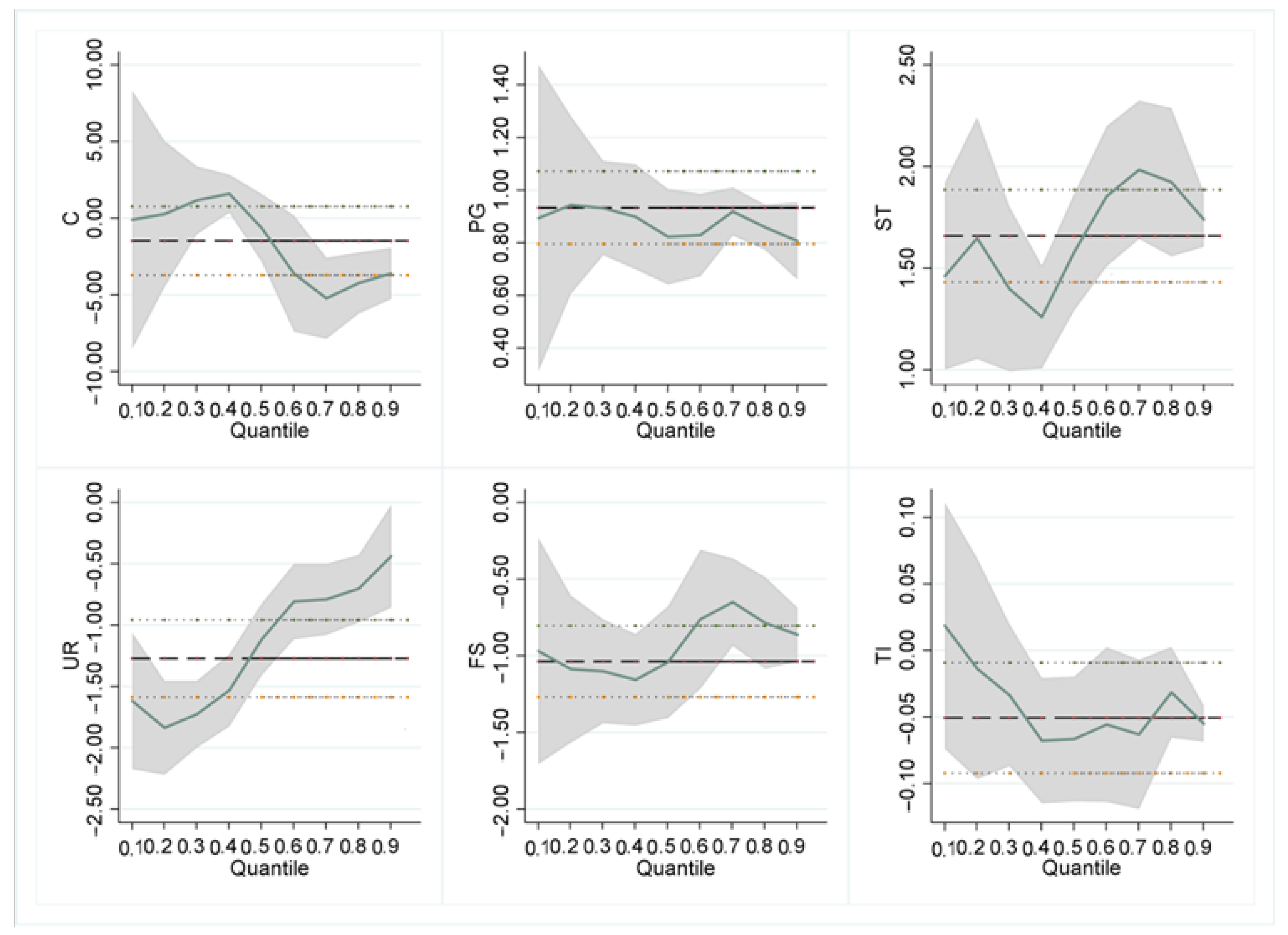
4.2. Results and Discussion of Quantile Regression
5. Conclusions and Suggestions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, C.; Lin, Y. Panel estimation for urbanization, energy consumption and CO2 emissions: A regional analysis in China. Energy Policy 2012, 49, 488–498. [Google Scholar] [CrossRef]
- Meng, L.; Guo, J.E.; Chai, J.; Zhang, Z. China’s regional CO2 emissions: Characteristics, inter-regional transfer and emission reduction policies. Energy Policy 2011, 39, 6136–6144. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Liu, H.; Wang, Y. The Robust Causal Relationships among Domestic Tourism Demand, Carbon Emissions, and Economic Growth in China. SAGE Open 2021, 11, 21582440211054478. [Google Scholar] [CrossRef]
- Sirag, A.; Matemilola, B.T.; Law, S.H.; Bany-Ariffin, A.N. Does environmental Kuznets curve hypothesis exist? Evidence from dynamic panel threshold. J. Environ. Econ. Policy 2018, 7, 145–165. [Google Scholar] [CrossRef]
- Nasir, M.; Rehman, F.U. Environmental Kuznets Curve for carbon emissions in Pakistan: An empirical investigation. Energy Policy 2011, 39, 1857–1864. [Google Scholar] [CrossRef]
- Ozturk, I.; Acaravci, A. The long-run and causal analysis of energy, growth, openness and financial development on carbon emissions in Turkey. Energy Econ. 2013, 36, 262–267. [Google Scholar] [CrossRef]
- Jorgenson, A.K.; Clark, B. Assessing the temporal stability of the population/environment relationship in comparative perspective: A cross-national panel study of carbon dioxide emissions, 1960–2005. Popul. Environ. 2010, 32, 27–41. [Google Scholar] [CrossRef]
- Song, M.; Wu, J.; Song, M.; Zhang, L.; Zhu, Y. Spatiotemporal regularity and spillover effects of carbon emission intensity in China′s Bohai Economic Rim. Sci. Total Environ. 2020, 740, 140184. [Google Scholar] [CrossRef]
- Qi, X.; Han, Y.; Kou, P. Population urbanization, trade openness and carbon emissions: An empirical analysis based on China. Air Qual. Atmos. Health 2020, 13, 1–10. [Google Scholar] [CrossRef]
- Zhu, H.M.; You, W.H.; Zeng, Z.F. Urbanization and CO2 emissions: A semi-parametric panel data analysis. Econ. Lett. 2012, 117, 848–850. [Google Scholar] [CrossRef]
- Al-Mulali, U.; Sab, C.N.B.C.; Fereidouni, H.G. Exploring the bi-directional long run relationship between urbanization, energy consumption, and carbon dioxide emission. Energy 2012, 46, 156–167. [Google Scholar] [CrossRef]
- Poumanyvong, P.; Kaneko, S. Does urbanization lead to less energy use and lower CO2 emissions? A cross-country analysis. Ecol. Econ. 2010, 70, 434–444. [Google Scholar] [CrossRef]
- Chuai, X.; Feng, J. High resolution carbon emissions simulation and spatial heterogeneity analysis based on big data in Nanjing City, China. Sci. Total Environ. 2019, 686, 828–837. [Google Scholar] [CrossRef] [PubMed]
- Robert, J.R.; Shanshan, W.U. Industrial activity and the environment in China: An industry-level analysis. China Econ. Rev. 2008, 19, 393–408. [Google Scholar]
- York, R.; Rosa, E.A.; Dietz, T. STIRPAT, IPAT and ImPACT: Analytic tools for unpacking the driving forces of environmental impacts. Ecol. Econ. 2003, 46, 351–365. [Google Scholar] [CrossRef]
- Ota, T.; Kakinaka, M.; Kotani, K. Demographic effects on residential electricity and city gas consumption in the aging society of Japan. Energy Policy 2018, 115, 503–513. [Google Scholar] [CrossRef] [Green Version]
- Martínez-Zarzoso, I.; Maruotti, A. The Impact of Urbanization on CO2 Emissions: Evidence from Developing Countries. Ecol. Econ. 2011, 70, 1344–1353. [Google Scholar] [CrossRef] [Green Version]
- Shahbaz, M.; Loganathan, N.; Sbia, R.; Afza, T. The effect of urbanization, affluence and trade openness on energy consumption: A time series analysis in Malaysia. Renew. Sustain. Energy Rev. 2015, 47, 683–693. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Mao, Y.; Morrison, A.M. Impacts of Environmental Regulations on Tourism Carbon Emissions. International. J. Environ. Res. Public Health 2021, 18, 12850. [Google Scholar] [CrossRef]
- Chen, X.; Chen, Z. Can Green Finance Development Reduce Carbon Emissions? Empirical Evidence from 30 Chinese Provinces. Sustainability 2021, 13, 12137. [Google Scholar] [CrossRef]
- Tiba, S.; Belaid, F. The pollution concern in the era of globalization: Do the contribution of foreign direct investment and trade openness matter? Energy Econ. 2020, 92, 104966. [Google Scholar] [CrossRef]
- Bassett, K.G. Regression Quantiles. Econometrica 1978, 46, 33–50. [Google Scholar]
- Kato, K.; Galvao, A.F.; Montes-Rojas, G.V. Asymptotics for panel quantile regression models with individual effects. J. Econom. 2012, 170, 76–91. [Google Scholar] [CrossRef] [Green Version]
- Koenker, R. Quantile regression for longitudinal data. J. Multivar. Anal. 2004, 91, 74–89. [Google Scholar] [CrossRef] [Green Version]
- Lamarche, C. Measuring the incentives to learn in Colombia using new quantile regression approaches. J. Dev. Econ. 2011, 96, 278–288. [Google Scholar] [CrossRef]
- Damette, O.; Delacote, P. On the economic factors of deforestation: What can we learn from quantile analysis? Econ. Model. 2012, 29, 2427–2434. [Google Scholar] [CrossRef] [Green Version]
- Maddala, G.S.; Wu, S. A Comparative Study of Unit Root Tests with Panel Data and a New Simple Test. Oxf. Bull. Econ. Stat. 1999, 61, 631–652. [Google Scholar] [CrossRef]
- Pedroni, P. Critical Values for Cointegration Tests in Heterogeneous Panels with Multiple Regressors. Oxf. Bull. Econ. Stat. 1999, 61, 653–670. [Google Scholar] [CrossRef]
- Kao, C. Spurious regression and residual-based tests for cointegration in panel data. J. Econom. 2004, 90, 1–44. [Google Scholar] [CrossRef]
- Huo, T.; Cao, R.; Du, H.; Zhang, J.; Cai, W.; Liu, B. Nonlinear influence of urbanization on China′s urban residential building carbon emissions: New evidence from panel threshold model. Sci. Total Environ. 2021, 772, 145058. [Google Scholar] [CrossRef]
- Dhakal, S.; Kaneko, S.; Imura, H. An analysis on driving factors for CO2 emissions from energy use in Tokyo and Seoul by factor decomposition method. Environ. Syst. Res. 2002, 30, 295–303. [Google Scholar] [CrossRef] [Green Version]
- Underwood, A.; Fremstad, A. Does sharing backfire? A decomposition of household and urban economies in CO2 emissions. Energy Policy 2018, 123, 404–413. [Google Scholar] [CrossRef]


| Variable Symbol | Meaning | Computing Method |
|---|---|---|
| CE | Carbon emissions | As shown in Formula (1) |
| PG | Per capita Disposable income | Provincial Statistical Yearbook |
| ST | Industrial structure | Percentage of added value of secondary industry in total GDP |
| UR | Urbanization level | Urban population as a percentage of the total population |
| FS | Average family size | Total population divided by total households |
| TI | Scientific and technological innovation level | Number of patent applications per 10,000 people |
| CE | PG | ST | UR | FS | TI | |
|---|---|---|---|---|---|---|
| Mean | 5.204 | 9.652 | 3.612 | 3.876 | 3.216 | 1.023 |
| Median | 5.248 | 9.666 | 3.677 | 3.874 | 3.197 | 0.291 |
| Maximum | 7.384 | 11.128 | 3.971 | 4.532 | 4.394 | 11.951 |
| Minimum | −0.211 | 8.460 | 2.471 | 2.976 | 2.356 | 0.003 |
| Std. Dev. | 0.991 | 0.621 | 0.261 | 0.297 | 0.357 | 1.788 |
| Skewness | −1.352 | −0.051 | −1.668 | −0.116 | 0.237 | 3.032 |
| Kurtosis | 8.205 | 1.995 | 6.457 | 2.959 | 2.841 | 13.036 |
| Jarque–Bera | 817.171 | 24.235 | 548.201 | 1.311 | 5.944 | 3265.320 |
| Probability | 0.000 | 0.000 | 0.000 | 0.519 | 0.051 | 0.000 |
| Sum | 2966.111 | 5501.564 | 2058.671 | 2209.569 | 1833.325 | 582.975 |
| Sum Sq. Dev. | 559.283 | 219.400 | 38.791 | 50.193 | 72.615 | 1819.072 |
| Variables | Levels | First Difference | ||
|---|---|---|---|---|
| Fisher-ADF Test | Fisher-PP Test | Fisher-ADF Test | Fisher-PP Test | |
| CE | 22.961 (1.000) | 29.723 (0.999) | 171.092 (0.000) | 335.635 (0.000) |
| PG | 25.588 (1.000) | 10.566 (1.000) | 108.885 (0.000) | 158.832 (0.000) |
| ST | 26.349 (1.000) | 13.823 (1.000) | 100.521 (0.000) | 124.090 (0.000) |
| UR | 81.973 (0.031) | 119.675 (0.000) | 131.938 (0.000) | 237.285 (0.000) |
| FS | 67.253 (0.242) | 92.8540 (0.004) | 164.446 (0.000) | 449.673 (0.000) |
| TI | 47.3507 (0.882) | 101.904 (0.000) | 213.177 (0.000) | 577.459 (0.000) |
| Inspection Method | Inspection Form | Statistical Value | p Value |
|---|---|---|---|
| Pedroni test | Modified Phillips–Perron t | 6.229 | 0.000 |
| Phillips–Perron t | −4.4193 | 0.000 | |
| Augmented Dickey–Fuller t | −4.3482 | 0.000 | |
| Kao test | Modified Dickey–Fuller t | −1.8535 | 0.031 |
| Dickey–Fuller t | −5.5930 | 0.000 | |
| Augmented Dickey–Fuller t | −10.3112 | 0.000 |
| Variables | OLS | Quantile Statistics | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 10th | 20th | 30th | 40th | 50th | 60th | 70th | 80th | 90th | ||
| PG | 0.933 (0.000) | 0.893 (0.003) | 0.943 (0.000) | 0.932 (0.000) | 0.898 (0.000) | 0.823 (0.000) | 0.829 (0.000) | 0.919 (0.000) | 0.859 (0.000) | 0.806 (0.000) |
| ST | 1.658 (0.000) | 1.460 (0.000) | 1.648 (0.000) | 1.397 (0.000) | 1.260 (0.000) | 1.580 (0.000) | 1.854 (0.000) | 1.984 (0.000) | 1.923 (0.000) | 1.739 (0.000) |
| UR | −1.272 (0.000) | −1.618 (0.000) | −1.838 (0.000) | −1.727 (0.000) | −1.532 (0.000) | −1.116 (0.000) | −0.808 (0.000) | −0.790 (0.000) | −0.702 (0.000) | −0.438 (0.016) |
| FS | −1.036 (0.000) | −0.970 (0.017) | −1.087 (0.000) | −1.101 (0.000) | −1.157 (0.000) | −1.042 (0.000) | −0.762 (0.000) | −0.651 (0.000) | −0.786 (0.000) | −0.863 (0.000) |
| TI | −0.050 (0.011) | 0.019 (0.615) | −0.014 (0.687) | −0.034 (0.236) | −0.068 (0.004) | −0.067 (0.005) | −0.056 (0.055) | −0.063 (0.045) | −0.032 (0.176) | −0.055 (0.000) |
| C | −1.478 (0.192) | −0.103 (0.982) | 0.267 (0.913) | 1.163 (0.494) | 1.596 (0.235) | −0.639 (0.686) | −3.621 (0.063) | −5.228 (0.000) | −4.230 (0.000) | −3.609 (0.000) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Chang, X.; Huang, C. Research and Analysis on the Influencing Factors of China’s Carbon Emissions Based on a Panel Quantile Model. Sustainability 2022, 14, 7791. https://doi.org/10.3390/su14137791
Liu Y, Chang X, Huang C. Research and Analysis on the Influencing Factors of China’s Carbon Emissions Based on a Panel Quantile Model. Sustainability. 2022; 14(13):7791. https://doi.org/10.3390/su14137791
Chicago/Turabian StyleLiu, Yunlong, Xianlin Chang, and Chengfeng Huang. 2022. "Research and Analysis on the Influencing Factors of China’s Carbon Emissions Based on a Panel Quantile Model" Sustainability 14, no. 13: 7791. https://doi.org/10.3390/su14137791
APA StyleLiu, Y., Chang, X., & Huang, C. (2022). Research and Analysis on the Influencing Factors of China’s Carbon Emissions Based on a Panel Quantile Model. Sustainability, 14(13), 7791. https://doi.org/10.3390/su14137791





